PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
- 2 Механика
- 2.1 Кинематика
- 2.2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
- 3 Термодинамика и МКТ
- 3.1 МКТ
- 3.2 Термодинамика
- 4 Электродинамика
- 4.
 1 Электростатика
1 Электростатика - 4.2 Электрический ток
- 4.3 Магнетизм
- 4.4 Электромагнитные колебания и волны
- 4.
- 5 Оптика. СТО
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5.
 6 СТО
6 СТО
- 6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
- 7 Общие темы
- 8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике
Новые страницы
Запрос не дал результатов.
Значение, Определение, Предложения . Что такое векторная величина
- Онлайн-переводчик
- Грамматика
- Видео уроки
- Учебники
- Лексика
- Специалистам
- Английский для туристов
- Рефераты
- Тесты
- Диалоги
- Английские словари
- Статьи
- Биографии
- Обратная связь
- О проекте
Примеры
Значение слова «ВЕКТОРНЫЙ»
Смотреть все значения слова ВЕКТОРНЫЙ
Значение слова «ВЕЛИЧИНА»
Размер, объём, протяжённость предмета.
Смотреть все значения слова ВЕЛИЧИНА
Предложения с «векторная величина»
Градиент определяется как векторная величина с компонентами, равными частным производным поверхности в направлениях x и Y. | |
| Другие результаты | |
GP определяется средней функцией и ковариационной функцией, которые определяют средние векторы и ковариационные матрицы для каждого конечного набора случайных величин. | |
Вектор Лапласа-Рунге-Ленца также может быть обобщен для идентификации сохраненных величин, применимых к другим ситуациям. | |
Вектор LRL отличается от других сохраненных величин следующим свойством. | |
И наоборот, система из n величин vi, преобразующихся подобно координатам xi в V, определяет контравариантный вектор. | |
Система из n величин, которые преобразуются противоположно координатам, является тогда ковариантным вектором. | |
Геометрически это произведение евклидовых величин двух векторов и косинуса угла между ними. | |
S-AWC использует технологию векторизации крутящего момента для передачи различных величин крутящего момента на задние колеса. | |
Вторая космическая скорость — величина не векторная, а скалярная. | |
Поскольку up-единичный вектор, его величина фиксирована, и он может изменяться только в направлении, то есть его изменение dup имеет компонент только перпендикулярный up. | |
Величина и направление вектора градиента не зависят от конкретного координатного представления. | |
Кинетическая энергия является скалярной величиной, поскольку она зависит от квадрата скорости, однако связанная с ней величина, Импульс, является вектором и определяется им. | |
Величина радиальной скорости является точечным произведением вектора скорости и единичного вектора в направлении перемещения. | |
Величина дисбаланса и угол дисбаланса дают вектор дисбаланса. | |
Красная линия и связанные с ней векторы поля показывают, как изменяется величина и направление электрического поля вдоль направления движения. | |
Он отличается от евклидова вектора тем, как определяется его величина. | |
Плотность линейного импульса электромагнитного поля равна S/c2, где S-величина вектора Пойнтинга, а c-скорость света в свободном пространстве. | |
Величина вектора эксцентриситета представляет собой эксцентриситет орбиты. | |
Этот масштабированный вектор e имеет то же направление, что и A, и его величина равна эксцентриситету орбиты, и, таким образом, исчезает для круговых орбит. | |
Скорость вращения-это вектор, величина которого равна скорости вращения. | |
Величина силы задается величиной заряда, умноженной на величину вектора электрического поля. | |
Единичная величина этих векторов является следствием эквалайзера. 1. | |
Скорость частиц — это еще одна величина, связанная с акустическими волнами, однако, в отличие от звукового давления, скорость частиц-это вектор. | |
В России математик Леонид Канторович разработал экономические модели в частично упорядоченных векторных пространствах, которые подчеркивали двойственность между величинами и ценами. | |
Это происходит потому, что дипольные моменты являются евклидовыми векторными величинами с величиной и направлением, и два равных вектора, которые противостоят друг другу, будут аннулированы. | |
В двух или более измерениях xi являются векторными величинами. | |
Как и линейный импульс, угловой момент является векторной величиной, и его сохранение подразумевает, что направление оси вращения имеет тенденцию оставаться неизменным. | |
Крутизна склона в этой точке определяется величиной вектора градиента. | |
Поскольку полная производная векторного поля является линейным отображением от векторов к векторам, она является тензорной величиной. | |
Единичный толчок в любом направлении зависит от полного вектора относительной скорости v с величиной |v / = v, которая не может равняться или превышать c, так что 0 ≤ v | |
На данной странице приводится толкование (значение) фразы / выражения «векторная величина», а также синонимы, антонимы и предложения, при наличии их в нашей базе данных. Мы стремимся сделать толковый словарь English-Grammar.Biz, в том числе и толкование фразы / выражения «векторная величина», максимально корректным и информативным. Если у вас есть предложения или замечания по поводу корректности определения «векторная величина», просим написать нам в разделе «Обратная связь».
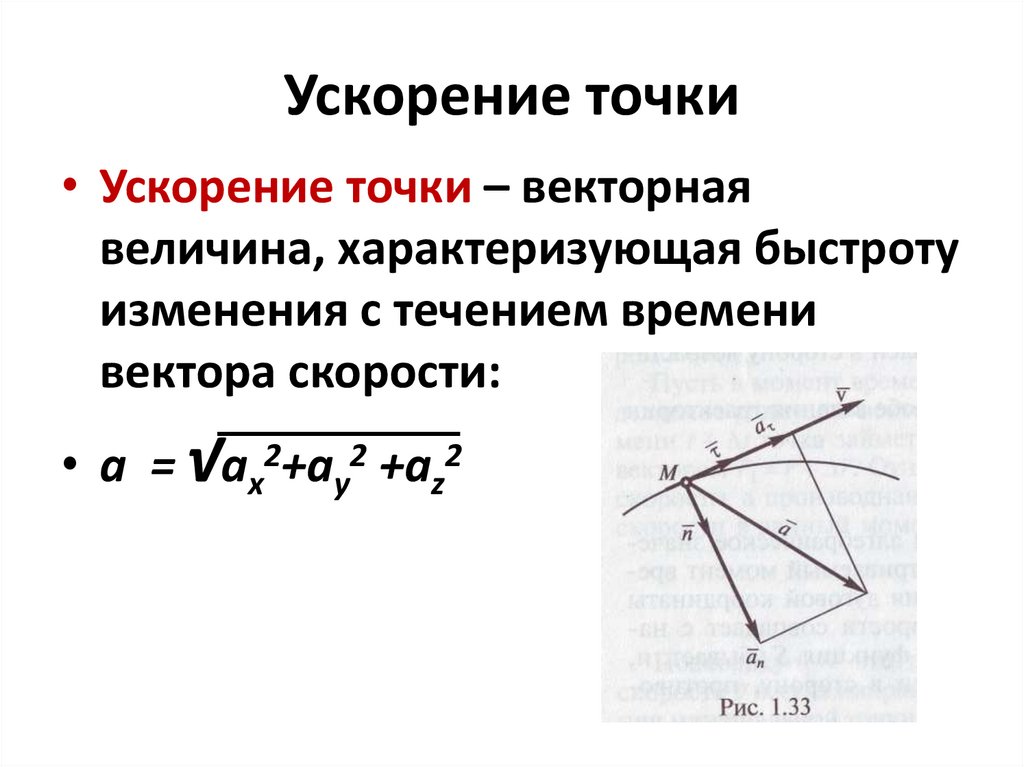
Является ли энергия векторной величиной: почему, как, подробные факты?
В физике физические величины подразделяются на две основные категории: скалярные и векторные.
Величина, которая относится к величине и направлению, известна как вектор, то есть скорость. А величина, которая имеет дело только с величиной, известна как скалярная величина, то есть масса, заряд и т. Д.
Энергия — это физическая величина, которая дает представление о способности объекта или системы выполнять работу.
Чтобы ответить на вопрос: является ли энергия векторной величиной? , прочтите этот пост.
Является ли энергия векторной величинойВ физике энергия также определяется как работа, совершаемая над системой или телом.
«Энергия» by Шон МакИнти под лицензией CC BY 2.0
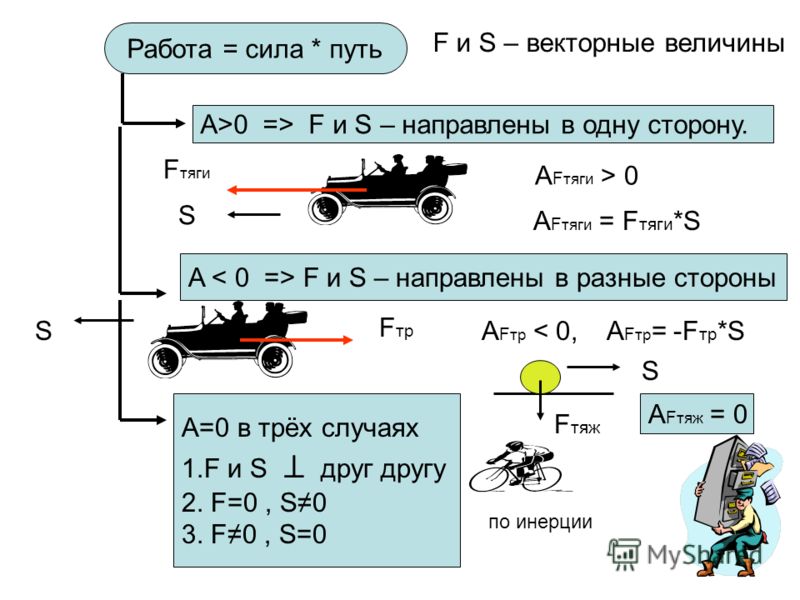
энергия = проделанная работа
Работа = сила. смещение
Если мы приложим силу к системе или телу, и оно смещается в направлении силы; потом говорят, что работа была сделана на теле.
Теперь, как мы знаем, сила и смещение являются векторными величинами, так как также требуется направление, чтобы получить полную информацию о них. Скалярное произведение двух физических величин, таких как сила и смещение, дает скалярное (обычное) значение — скалярную величину.
Следовательно, мы можем заключить, что физическая величина — энергия НЕ является векторной величиной.
Почему энергия — это скалярная величина.Поскольку мы изучили, что энергия, физическая величина попадает в категорию скалярных величин.
- Как мы знаем, скалярные величины связаны только с величиной, а не с направлением, и здесь энергия не имеет направления.
- В дополнение или вычитание энергий векторная алгебра не применима.
- Формула энергии показывает скалярное произведение двух физических величин (сила, смещение, которые являются векторными).
Следовательно, приведенные выше пункты показывают, почему энергия является скалярной величиной.
Хотя в некоторых случаях энергия имеет определенное направление. Например, тепловая энергия, при которой тепловая энергия всегда течет от более горячего тела к более холодному.
Но,
Сложение или вычитание количества выполняется с помощью обычного закона алгебры, а не векторной алгебры.
Энергия всегда имеет только положительное, отрицательное или нулевое действительное значение.
Давайте посмотрим на несколько примеров, связанных с этим.
Проблема 1: на частицу действует сила F = i + 2j + 3k, и частица перемещается на расстояние S = 4i + 6j. Найдите работу, проделанную над частицей, если сила и смещение направлены в одном направлении.Решение: данные количества:
Сила, F= я + 2j + 3к
Расстояние,s= 4i + 6j
Теперь работа, проделанная с телом, дается
Работа = сила. смещение
W = (i + 2j + 3k).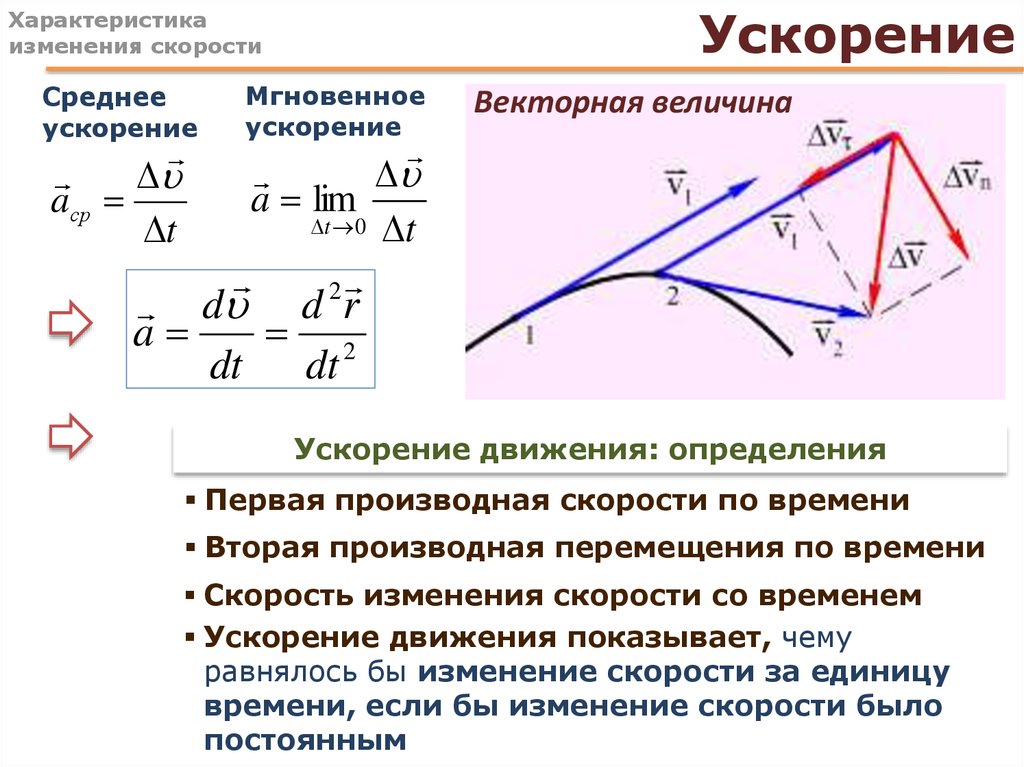 (4i + 6j)
(4i + 6j)
W = 4+ 12 + 0
W = 16 Дж
Задача 2: частица перемещается из положения a = 3i + 2j-6k в положение b = 14i + 13j-9k под действием силы (4i + j + 3k) ньютона. Посчитайте проделанную работу.Решение: С учетом количества
Сила, F= 4i + j + 3k ньютон
a= 3i + 2j-6k
b= 14i + 13j-9k
r= b–a
r= (14i+13j-9k)-(3i+2j-6k) = 11i+11j-3k
W = Пт
W = (4i+j+3k).(11i+11j-3k)
W = 44 + 11-9 = 46 Дж
Задача 3: Найдите работу, проделанную при перемещении частицы по вектору s = 4i-j + 7k метров, если приложенная сила равна F = i + 2j-k ньютон.Решение: при заданных количествах
Сила, F= i + 2j-k ньютон
s= 4i-j + 7k метров
Теперь проделанная работа выражается как W = Сила * смещение.
W = (i + 2j-k) * (4i-j + 7k)
W = 4-2-7 = -5 Дж
Работа, выполняемая при перемещении частицы, эквивалентна энергии, полученной частицей.
Решение: данные количества:
Форс-мажор F= -2i + 15j + 6k ньютон
Водоизмещение s= 10 Дж метр
Проделанная работа выражается как работа = сила * смещение.
работа = (-2i + 15j + 6k) .10j
работа = 150 Дж
Отсюда проделанная работа по кузову составляет 150 Дж.
Часто задаваемые вопросы: FAQВопрос. Что такое скалярный продукт?Есть два способа выполнить умножение двух векторных величин, и один из них — скалярное произведение.
Скалярное произведение, иногда также известное как скалярное произведение, поскольку мы получаем скалярную величину путем умножения двух векторов. В векторной алгебре мы не можем перемножить два вектора, как в математике.
Точечное произведение можно определить двумя способами. Один из них является алгебраическим — суммирование произведений соответствующих элементов, а другой — геометрическим — произведением величины двух векторных величин и косинусоидального угла между ними.
Интересной особенностью скалярного произведения является то, что результирующий вектор лежит в одной плоскости.
Скалярное произведение двух векторов может иметь положительное, отрицательное или нулевое значение.
Предположим, что a и b — два вектора, тогда его скалярное произведение можно записать как
Точечное произведение также полезно для определения проекции (тени) одного вектора на другой. Когда мы говорим о проекции одного вектора на другой, это означает, что тень первого вектора на втором. Результирующий вектор имеет скалярное значение.
Пусть AB = b и AC =a , — два вектора, а тета — угол между ними. Нарисуйте нормальный BD на линии переменного тока.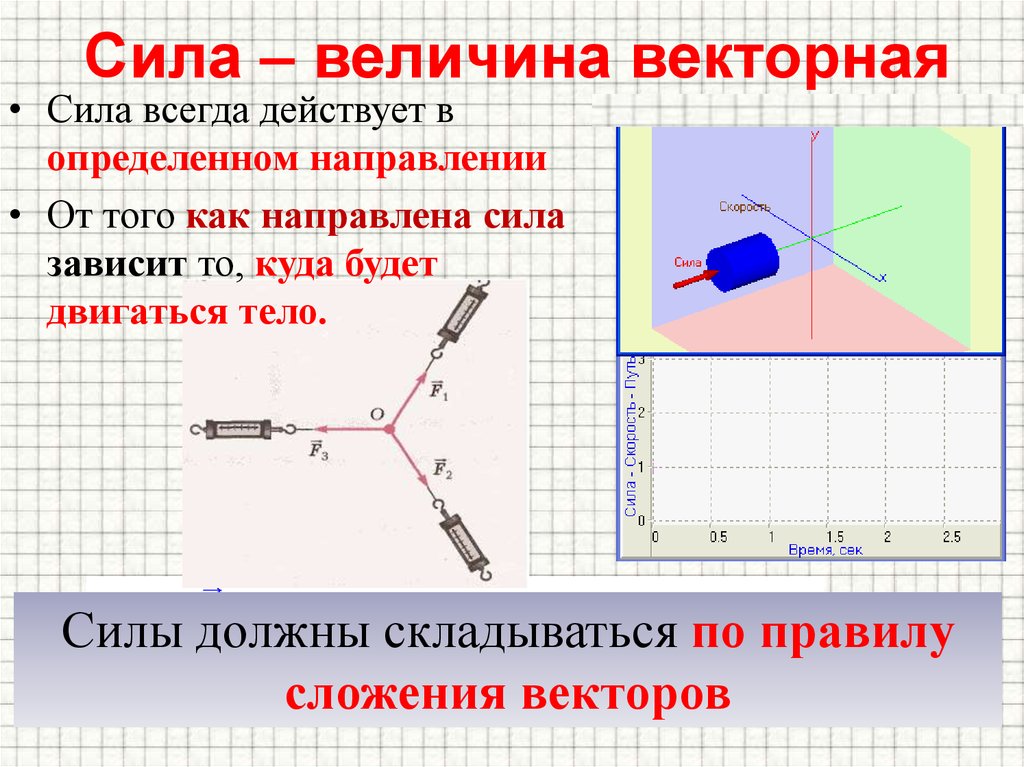
AD — векторная проекция
ab = a (проекция b на a)
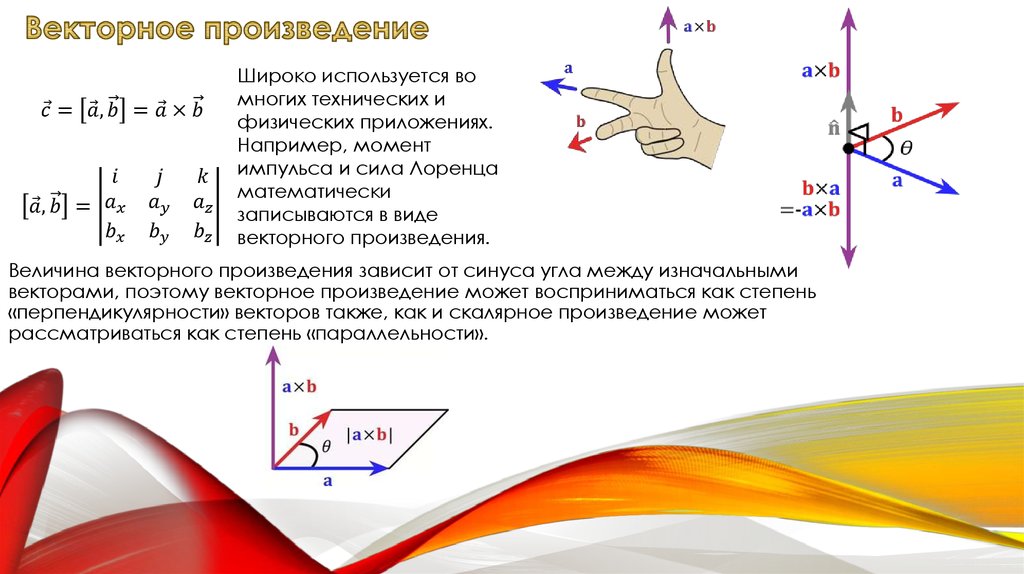
Вопрос. Что такое перекрестный продукт?Другой способ выполнения умножения двух векторных величин — это векторное произведение, также называемое векторным произведением.
В результате получается векторная величина. Он находится в плоскости, перпендикулярной обоим векторам, и чтобы знать его направление, нужно использовать глубокое или основное правило — правило большого пальца правой руки.
Следовательно, перекрестное произведение оказывается в трех измерениях, в то время как скалярное произведение ограничено только двумя измерениями.
Перекрестный продуктгде n — единичный вектор, задающий направление результирующего вектора.
где a и b — величины векторов a и b соответственно.
Вопрос. Запишите разницу между скалярной и векторной величинами. .
.Вот несколько моментов, по которым различают скалярные и векторные величины.
Скалярная величина:- Чтобы описать количество, нужна только величина.
- Чтобы складывать или вычитать или делить и умножать, нам не нужно развивать какую-либо другую алгебру. Достаточно обычного закона алгебры.
- Он только одномерный.
- Он представлен только одной буквой алфавита.
- Может иметь положительные и отрицательные значения.
- Это относится как к величине, так и к направлению.
- Чтобы сложить, вычесть или умножить, нам нужно использовать векторную алгебру.
- У него может быть более одного измерения.
- Он обозначается одной буквой, выделенной жирным шрифтом, или однобуквенной стрелкой на голове.
- Величина количества определяется его модулем.

Ниже приведен список некоторых физических величин, которые являются скалярными.
- Температура
- Заряд
- Масса
- Расстояние
- Давление
- Плотность
- Громкости
- Энтропия
- Сопротивление
- Показатель преломления
- Питания
- Поверхностная энергия
- Напряжение
Вот несколько примеров векторных величин.
- Водоизмещение
- Форс-мажор
- Крутящий момент
- Скорость
- Импульс
- Район
- Ускорение
- Магнитное поле интенсивность
- Электрическое поле
Тест с ответами: «Векторные величины»
1. Какое правило используется для сложения двух неколлинеарных векторов?
Какое правило используется для сложения двух неколлинеарных векторов?
а) Правило Пифагора
б) Правило параллельных прямых
в) Правило параллелограмма +
2. Если два ненулевых вектора лежат на параллельных прямых или на одной прямой, то они называются:
а) сонаправленные
б) коллинеарные +
в) нулевые
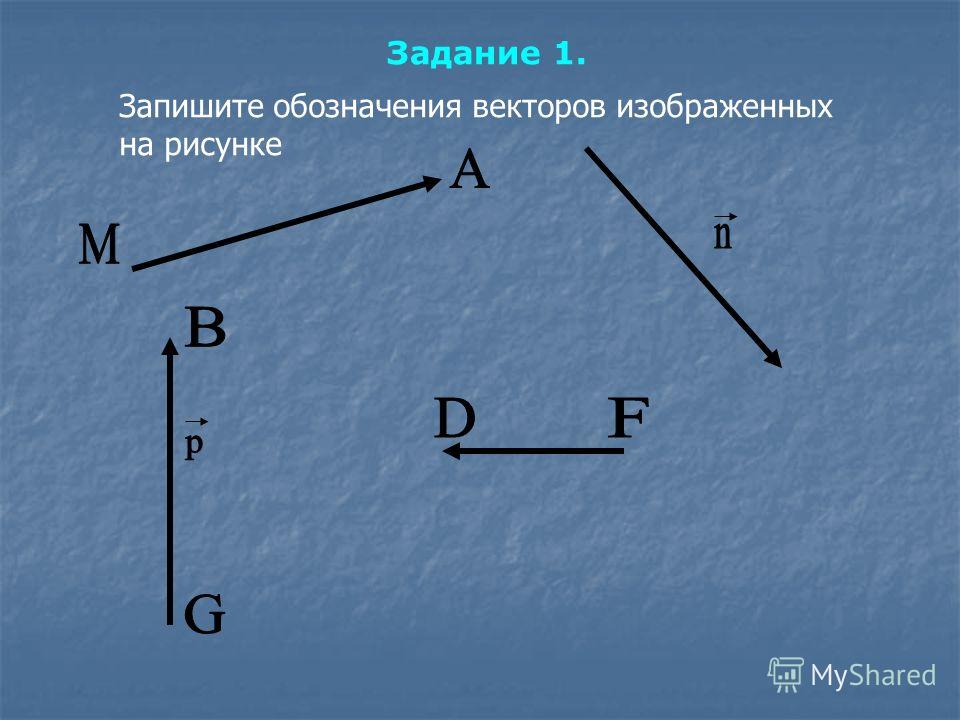
3. Отрезок, для которого указано, какая из его граничных точек — начало, а какая – конец это:
а) Прямая
б) Луч
в) Вектор +
4. Выберите векторную физическую величину:
а) время
б) скорость тела +
в) масса тела
5. Нескольких векторов сложили по правилу многоугольника. Начало первого вектора совпало с концом последнего. Чему равна сумма векторов?
а) нулевому вектору +
б) вектору равному разнице первого вектора и последнего
в) единичному вектору
6. Как называются векторы, если они сонаправленные и имеют равные модули?
а) нулевые
б) Коллинеарные
г) Равные +
7. Чем характеризуются векторные величины?
а) численным значением и направлением +
б) только численным значением
в) только направлением
8. Два вектора коллинеарны и направлены в противоположные стороны. Их модули равны 3 и 4 соответственно. Чему равен модуль суммы этих векторов?
Два вектора коллинеарны и направлены в противоположные стороны. Их модули равны 3 и 4 соответственно. Чему равен модуль суммы этих векторов?
а) 1 +
б) 5
в) 7
9. Если из произвольной точки отложить первый вектор, из конца полученного вектора отложить второй вектор, и построить вектор, соединяющий начало первого с концом второго – это будет:
а) разность первого и второго векторов
б) сумма первого и второго векторов +
в) нулевой вектор
10. Чем характеризуются скалярные величины?
а) численным значением и направлением
б) только численным значением +
в) только направлением
11. В чего изображается на графике нулевой вектор?
б) В виде точки +
а) В виде прямой
в) В виде направленного отрезком
12. Какое правило используется для сложения двух любых векторов?
а) Правило Пифагора
б) Правило треугольника
в) Правило параллелограмма +
13. Как называется вектор, начало которого совпадает с его концом
а) Нулевой +
б) Начальный
в) Точечный
14. Какой вектор направлен вниз к поверхности Земли?
Какой вектор направлен вниз к поверхности Земли?
а) вектор скорости свободно падающего тела +
б) вектор скорости автомобиля, движущего по горизонтальной дороге
в) вектор скорости взлетающей вверх ракеты
15. Как называется закон: сумма двух векторов не изменится от порядка слагаемых?
a) Переместительный законом +
б) сочетательный законом
в) правило параллелограмма
16. Автомобиль двигался по прямой дороге со скоростью 60 км/час. После знака ограничения скорости, автомобилист снизил скорость до 40 км час. Как изменился вектор скорости автомобиля.
а) Модуль вектора скорости увеличился в 1,5 раза, направление не изменилось
б) Модуль вектора скорости уменьшился в 1,5 раза, направление не изменилось
в) Модуль вектора скорости уменьшился в 1,5 раза, направление изменилось
17. Выберите скалярную физическую величину:
а) перемещение тела
б) скорость тела
в) масса тела +
18. При умножении векторной величины на скалярную получается:
а) скалярная величина
б) векторная величина +
в) в одних случаях скалярная, а в других векторная величина
19. Что такое модуль вектора?
Что такое модуль вектора?
а) направление вектора
б) числовое значение вектора +
в) координата вектора
20. Ракета вылетает под углом 30 градусов к горизонту со скоростью 300 м/с. Чему равен модуль вертикальной составляющей вектора скорости ракеты?
а) 150 м/с +
б) 260 м/с
в) 300 м/с
21. Как обозначают векторы?
а) буквами со стрелкой над ними +
б) буквами без стрелки над ними
в) цифрами
22. Угол между вектором силы и осью х составляет z. Модуль вектора силы равен F. Чему равен модуль составляющей вектора силы вдоль оси x?
а) F*sin(z)
б) F*cos(z) +
в) F*tg(z)
23. Как обозначают модуль вектора?
а) буквами со стрелкой над ними
б) буквами без стрелки над ними +
в) цифрами
24. Как называются два вектора с равными модулями, лежащие на параллельных прямых, если их направления противоположны?
а) противоположными +
б) коллинеарными
в) сонаправленными
25. Равными считаются векторы, у которых одинаковы:
а) модули
б) и модули, и направления +
в) направления
26. Какой вектор получится в результате умножения любого вектора на ноль?
Какой вектор получится в результате умножения любого вектора на ноль?
а) единичный вектор
б) начальный вектор
в) нулевой вектор
27. Два вектора направлены перпендикулярно друг к другу. Их модули равны 3 и 4 соответственно. Чему равен модуль суммы этих векторов?
а) 5 +
б) 6
в) 7
28. Если при равномерном прямолинейном движении тела вектор перемещения разделить на время перемещения, что получится?
а) модуль скорости
б) вектор скорости +
в) модуль перемещения
29. Два вектора сонаправлены. Их модули равны 3 и 4 соответственно. Чему равен модуль суммы этих векторов?
а) 5
б) 6
в) 7 +
30. Если два вектора коллинеарны и их направления совпадают, то они называются:
а) сонаправленные +
б) коллинеарные
в) нулевые
31. Если из произвольной точки отложить первый вектор, а также второй вектор, и построить вектор, соединяющий конец второго вектора с концом первого – это будет:
а) разность первого и второго векторов +
б) сумма первого и второго векторов
в) нулевой вектор
Что такое векторное измерение?
Что такое векторное измерение? Вектор, в физике величина, имеющая как величину, так и направление. Обычно он изображается стрелкой, направление которой совпадает с направлением величины, а длина пропорциональна величине величины. Хотя вектор имеет величину и направление, он не имеет положения.
Обычно он изображается стрелкой, направление которой совпадает с направлением величины, а длина пропорциональна величине величины. Хотя вектор имеет величину и направление, он не имеет положения.
Что является примером векторного измерения? Примеры векторных величин включают смещение, скорость, положение, силу и крутящий момент. На языке математики физические векторные величины представлены математическими объектами, называемыми векторами ((Рисунок)).
Что такое вектор и скаляр? Величина, имеющая величину, но не имеющую определенного направления, называется скалярной. Величина, имеющая величину и действующая в определенном направлении, называется вектором.
В чем разница между скалярным измерением и векторным измерением? Скаляры — это величины, которые полностью описываются только величиной (или числовым значением). Векторы — это величины, которые полностью описываются как величиной, так и направлением.
Что такое векторный краткий ответ?
Векторные величины. Векторные величины относятся к физическим величинам, характеризующимся наличием как величины, так и направления. Например, смещение, сила, крутящий момент, импульс, ускорение, скорость и т. д.
Векторные величины относятся к физическим величинам, характеризующимся наличием как величины, так и направления. Например, смещение, сила, крутящий момент, импульс, ускорение, скорость и т. д.
Что такое векторная величина и ее примеры?
Вектор, в физике величина, имеющая как величину, так и направление. Например, перемещение, скорость и ускорение являются векторными величинами, а скорость (величина скорости), время и масса являются скалярными величинами.
Что такое векторная диаграмма?
Векторные диаграммы — это диаграммы, которые изображают направление и относительную величину векторной величины с помощью векторной стрелки. Если размер стрелки в каждом последующем кадре векторной диаграммы одинаков, то величина этого вектора постоянна. На приведенных ниже диаграммах изображена скорость автомобиля во время его движения.
Является ли работа скалярной или векторной?
Работа – это не векторная величина, а скалярная величина.
Позиция — это вектор или скаляр?
Расстояние — скалярная величина, это число, выраженное в некоторых единицах. Позиция является векторной величиной. Он имеет величину, а также направление. Величина векторной величины — это число (с единицами измерения), говорящее вам, какая часть величины существует, а направление говорит вам, в какую сторону оно указывает.
Позиция является векторной величиной. Он имеет величину, а также направление. Величина векторной величины — это число (с единицами измерения), говорящее вам, какая часть величины существует, а направление говорит вам, в какую сторону оно указывает.
Является ли вектор током?
Примечание: ток — это вектор, потому что он имеет величину и направление. Но дело в том, что вектор всегда подчиняется закону сложения векторов. Поскольку ток ему не подчиняется и следует алгебраическому сложению, токи являются скалярными.
Почему сила является векторной величиной?
Сила имеет как величину, так и направление, поэтому: Сила есть векторная величина; его единицы — ньютоны, Н. Силы могут вызывать движение; в качестве альтернативы силы могут действовать, чтобы удерживать объект (объекты) в покое.
Является ли расстояние векторной величиной?
Перемещение является примером векторной величины. Расстояние является примером скалярной величины. Вектор – это любая величина, имеющая как величину, так и направление. Некоторые физические величины, такие как расстояние, либо не имеют направления, либо не указываются.
Некоторые физические величины, такие как расстояние, либо не имеют направления, либо не указываются.
Как называется векторная величина?
Математики и ученые называют векторной величиной величину, зависящую от направления. Величина, не зависящая от направления, называется скалярной величиной. Векторные величины имеют две характеристики: величину и направление. Скалярные величины имеют только величину.
Для чего используется вектор?
Вектор — это любой носитель, часто вирус или плазмида, который используется для доставки желаемой последовательности ДНК в клетку-хозяин в рамках процедуры молекулярного клонирования. В зависимости от цели процедуры клонирования вектор может способствовать размножению, выделению или экспрессии вставки чужеродной ДНК.
Что такое векторная величина в одном предложении?
Определение количества векторов
Физические величины, для которых четко определены и величина, и направление, известны как векторные величины. Например, мальчик едет на велосипеде со скоростью 30 км/ч в северо-восточном направлении.
Что такое векторная величина в математике?
Вектор, в математике величина, которая имеет как величину, так и направление, но не положение. Примерами таких величин являются скорость и ускорение. С тех пор векторы стали необходимы в физике, механике, электротехнике и других науках для математического описания сил.
Какая из следующих величин не является векторной?
Ответ: Скорость не является векторной величиной. У него есть только величина, но нет направления, и, следовательно, это скалярная величина.
Является ли электричество векторным зарядом?
Ничто не является вектором, пока не определено направление.
Электрический заряд является скалярной величиной, потому что заряд никогда не переходил на уровень векторов или тензоров, которым нужны и величина, и направление.
Какие существуют два метода построения векторной диаграммы?
Существует множество методов определения величины и направления результата сложения двух или более векторов. Два метода, которые будут обсуждаться в этом уроке и использоваться на протяжении всего раздела: теорема Пифагора и тригонометрические методы. метод «голова к хвосту» с использованием масштабированной векторной диаграммы.
Два метода, которые будут обсуждаться в этом уроке и использоваться на протяжении всего раздела: теорема Пифагора и тригонометрические методы. метод «голова к хвосту» с использованием масштабированной векторной диаграммы.
Что такое векторное уравнение?
В общем, векторное уравнение — это любая функция, которая принимает любую одну или несколько переменных и возвращает вектор. Векторное уравнение линии — это уравнение, определяющее вектор положения каждой точки на линии. Это работает как для прямых линий, так и для кривых.
Что такое электрическая векторная диаграмма?
Векторная диаграмма — это диаграмма, на которой может быть представлен один или несколько векторов. На векторной диаграмме переменные величины изображаются стрелкой. Когда электрическая величина действует от источника в направлении нагрузки, вектор, представляющий величину, считается положительным вектором.
Что такое пример нулевого вектора?
Нулевой вектор — это вектор, величина которого равна нулю и который не имеет направления. Это равнодействующая двух или более равных векторов, действующих противоположно друг другу. Наиболее распространенным примером нулевого вектора является натяжение веревки с обоих концов с одинаковыми силами в противоположном направлении.
Это равнодействующая двух или более равных векторов, действующих противоположно друг другу. Наиболее распространенным примером нулевого вектора является натяжение веревки с обоих концов с одинаковыми силами в противоположном направлении.
Какие существуют виды векторов?
Четыре основных типа векторов — это плазмиды, вирусные векторы, космиды и искусственные хромосомы. Из них наиболее часто используемыми векторами являются плазмиды.
Может ли работа быть отрицательной?
Отрицательная проделанная работа. Проделанная работа называется отрицательной, если сила и перемещение направлены в противоположные стороны. Следовательно, работа отрицательна. Примечание: Работа, совершаемая трением, всегда равна нулю, поскольку сила трения и перемещение действуют в противоположных направлениях.
Какова формула положения?
Функция положения также указывает направление
Обычное применение производных — это соотношение между скоростью, скоростью и ускорением. В этих задачах вам обычно дается уравнение положения в форме «x=» или «s(t) = s(t)= s(t)=», которое говорит вам о расстоянии объекта от некоторой контрольной точки.
1.1: Векторы — Физика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 16286
- Калифорнийский университет, Дэвис
Определение вектора
Для описания природы недостаточно просто присвоить числа физическим величинам. Очень часто физические величины имеют направления. Например, описание движения чего-либо будет неполным, если вы просто укажете, с какой скоростью оно движется. [ Итак, астероид движется со скоростью 35 000 миль в час, но направляется ли он к Земле?! ] Таким образом, мы имеем следующее определение физических величин, обладающих обоими этими свойствами:
Определение: Вектор
Вектор – это величина, имеющая как величину, так и направление.
Мы будем часто представлять векторную величину стрелкой, где направление вектора — это направление, на которое указывает стрелка, а величина вектора представлена длиной стрелки. Это не означает, что векторы — это стрелок — стрелки просто создают удобное геометрическое представление. Таким образом, хотя стрелка, представляющая вектор, может быть 6 см в длину, это не означает, что вектор имеет величину 6 см . Например, вектор может представлять скорость и направление движущегося объекта, и тогда величина вектора даже не выражается в единицах см . Однако если мы нарисуем две стрелки, представляющие одну и ту же величину, и одна из них в два раза длиннее другой, подразумевается, что более длинная стрелка представляет вектор с удвоенной величиной вектора, представленного более короткой стрелкой.
Предупреждение
Невозможно сравнить величины различных физических величин. Если вектор расстояния нарисован в виде стрелки на той же странице, что и стрелка вектора скорости, относительные размеры двух стрелок не имеют смысла.
Есть несколько других вещей, которые мы должны сказать о векторах и стрелках, которые их представляют:
- Расположение стрелки, представляющей вектор, не является отличительной чертой вектора. То есть стрелку, представляющую вектор, можно перемещать по желанию, и пока она не растягивается, не сжимается и не поворачивается, она будет представлять тот же вектор. Простое изменение положения стрелки не меняет ее величины или направления, если ее перемещать осторожно.
- Направления векторов (и, следовательно, направления соответствующих стрелок) могут быть математически изменены на противоположные путем умножения на –1.
- Длина вектора может быть увеличена или уменьшена (масштабирована) посредством умножения на обычное число (называемое скаляром). Если число больше 1, вектор увеличивается в длину, а если меньше 1, то сжимается.
И еще одно… Когда мы пишем символ для векторной величины, мы делаем это с маленькой стрелкой над буквой, например: \(\overrightarrow A\). Предполагается, что переменные с той же буквой, что и заданный вектор, но не содержащие стрелку, представляют величина этого вектора. Так, например, при использовании в том же контексте переменная A представляет величину \(\overrightarrow A\).
Предполагается, что переменные с той же буквой, что и заданный вектор, но не содержащие стрелку, представляют величина этого вектора. Так, например, при использовании в том же контексте переменная A представляет величину \(\overrightarrow A\).
Сложение/вычитание векторов
Чтобы математические величины, которые мы называем векторами, имели для нас какое-либо значение, они должны позволять выполнять простые математические операции, такие как сложение. Направленный характер векторов делает сложение намного сложнее, чем простое суммирование двух величин. Оказывается, правильное сложение векторов требует простой геометрии. Это происходит так: перенесите один из векторов (параллельно, чтобы не менять его направление) так, чтобы его хвост соприкасался с головой другого вектора. Затем создайте новый вектор таким образом, чтобы его хвост находился на открытом хвосте, а голова — на открытой голове.
Рисунок 1.1.1 — Дополнение графического вектора
Рисунок 1. 1.2 — Дополнение вектора является коммутативным
1.2 — Дополнение вектора является коммутативным
. Что около подтереалов. Что ж, мы можем сделать это, следуя тому же методу, что и для обычных чисел: какой бы вектор мы ни хотели вычесть, мы умножаем на –1, а затем прибавляем результат к другому вектору, что мы делаем, как описано выше. Мы уже знаем, что умножение вектора на –1 меняет его направление на противоположное (и оставляет его величину неизменной), поэтому для нас это четко определенная операция. 92 -2AB \cos \theta\]
Имея все длины катетов треугольника и один из углов (тот, что между \(A\) и \(B\)), мы можем получить другие углы, используя Закон синусов.
Пример \(\PageIndex{1}\)
Значения двух векторов, показанных на диаграмме ниже: \(A=132\) и \(B=145\). Найдите величину и направление (угол, образованный с осью \(х\)) вектора, являющегося разностью этих двух векторов.
- Решение
Используя тот факт, что отрицательный вектор — это тот же вектор, указывающий в противоположном направлении, а также сложение векторов «хвост к голове», мы получаем следующую диаграмму для трех векторов:
Угол между \(\overrightarrow A\) и \(\overrightarrow B\), очевидно, равен 65º – 30º = 35º, поэтому для этого треугольника у нас есть длины двух сторон и угол между ними.
 Следовательно, мы можем найти длину третьей стороны (\(\overrightarrow C\)) по закону косинусов: 9о\номер\]
Следовательно, мы можем найти длину третьей стороны (\(\overrightarrow C\)) по закону косинусов: 9о\номер\] Если мы повернем \(\overrightarrow C\) против часовой стрелки на этот угол, он будет параллелен \(\overrightarrow A\), если мы затем повернем его назад по часовой стрелке на 30º (угол \(\overrightarrow A\) составляет с осью \(х\), то он будет параллелен оси \(х\). Следовательно, угол \(\overrightarrow C\) с осью \(x\) равен: -81° + 30° = -51° (ниже оси \(x\)). Этот ответ, безусловно, соответствует приведенной выше диаграмме, на которой \(\overrightarrow C\) имеет меньшую величину, чем \(\overrightarrow A\) и \(\overrightarrow B\), и указывает вниз вправо.
Хотя мы можем использовать эти инструменты для математического нахождения суммы двух векторов, оказывается, что есть и другой способ сделать это, не требующий стольких геометрических рассуждений. Этот метод использует три простых факта:
- Мы можем заменить любой отдельный вектор суммой двух (или более) векторов.

- Легко сложить два параллельных вектора.
- Если мы используем прямоугольные треугольники, с тригонометрией работать легче, чем с обычными треугольниками и законом косинусов/синусов.
Хитрость заключается в том, чтобы выбрать две (или три, если необходимо) перпендикулярные оси (они не обязательно должны быть горизонтальными и вертикальными, они должны быть только перпендикулярны друг другу) и разбить каждый вовлеченный вектор в сумму двух перпендикулярные векторы, параллельные этим осям. Длины этих перпендикулярных векторов называются компонентами вектора вдоль этих осей. Возвращаясь к приведенному выше списку преимуществ, помните, что мы можем добавлять подобные компоненты, такие как числа, и мы можем легко определить эти компоненты с помощью тригонометрии.
Рисунок 1.1.3 — Векторные компоненты
Рисунок 1.1.4 — Суммирование векторов с использованием компонентов
333333. Суммины, такие Summs of Commons, Такие Summs of Commons of Summs of Summs of Summs of The Summs of Summs of The Summs of The Summs of The Summs of The Summs of The Summs of The Summs of The Summs. те же оси могут быть добавлены. В результате получаются дополнительные компоненты, которые затем необходимо преобразовать в вектор.
Суммины, такие Summs of Commons, Такие Summs of Commons of Summs of Summs of Summs of The Summs of Summs of The Summs of The Summs of The Summs of The Summs of The Summs of The Summs of The Summs. те же оси могут быть добавлены. В результате получаются дополнительные компоненты, которые затем необходимо преобразовать в вектор.
Единичные векторы
Таким образом, мы можем использовать перпендикулярные системы координат для описания векторов с точки зрения их компонентов. По сути это означает, что для описания вектора в терминах набора трех осей нам нужно знать три числа. Но может быть полезно выразить эти векторы как единую математическую единицу, и именно здесь понятие 9Приходит единичный вектор 0034 . Векторы имеют величину и направление, и с помощью единичных векторов мы можем математически разбить вектор на эти две части. Величина — это просто число (с физическими единицами) без направления, а единичный вектор — это вектор (без единиц), длина которого равна 1, поэтому его можно масштабировать до любой длины, ничего не добавляя к величине. Следовательно, мы можем записать вектор как простое произведение:
Следовательно, мы можем записать вектор как простое произведение:
\[\overrightarrow A = A\widehat A\]
, где \(\widehat A\) — единичный вектор (обычно произносится как «\(A\)-hat »). Это безразмерный вектор длины 1, указывающий в направлении вектора \(\overrightarrow A\). Значение \(A\) — это число в физических единицах, равное величине. Диаграмма ниже дает графическое описание того, как эта конструкция работает для нескольких распространенных физических векторов. Единичные векторы обеспечивают очень простой шаблон, определяя направление, а величина заполняет шаблон, добавляя обхват и «аромат» (физические единицы) вектора.
Рисунок 1.1.4 – Единичные векторы и величины
Если мы объединим это понятие с компонентами, мы можем записать любой вектор как сумму компонентов, умноженных на единичные векторы в направлениях трех пространственных измерений. По соглашению мы даем этим единичным векторам имена \(\widehat i\), \(\widehat j\) и \(\widehat k\) для осей \(x\), \(y\) и \(г\) соответственно. В частности, у нас есть:
В частности, у нас есть:
\[\overrightarrow A = A_x\widehat i + A_y\widehat j + A_z\widehat k \]
Теперь мы можем просто использовать это как математическое представление векторов, и нам вообще не нужно обращаться к геометрии. Например,
\[ \begin{align} \overrightarrow C &= \overrightarrow A + \overrightarrow B \nonumber\\[5pt] &= (A_x\widehat i + A_y\widehat j + A_z\widehat k) + (B_x\widehat i + B_y\widehat j + B_z\widehat k) \nonumber\\[5pt] &= C_x\widehat i + C_y\widehat j + C_z\widehat k\nonumber\\[5pt] &= (A_x+ B_x) \widehat i + (A_y + B_y) \widehat j + (A_z + B_z) \widehat k \end{align}\]
Дает нам тот же результат, что и ранее для компонентов суммы двух векторов.
Пример \(\PageIndex{2}\)
Повторите расчет примера 1.1.1, но на этот раз с использованием компонентов.
- Раствор
Разделение двух векторов на их компоненты \(x\) и \(y\) дает:
\[\begin{array}{c} \overrightarrow A = {A_x}\widehat i + {A_y}\widehat j = A\cos \theta \;\widehat i + A\sin \theta \;\widehat j = 132\cos {30^o}\widehat i + 132\sin {30^o}\widehat j = 114,3\;\widehat i + 66,0\;\widehat j\\ \overrightarrow B = {A_x}\widehat я + {A_y}\widehat j = B\cos\theta\;\widehat i + B\sin\theta\;\widehat j = 145\cos {65^o}\widehat i + 145\sin {65^o }\widehat j = 61,3\;\widehat i + 131,4\;\widehat j \end{массив}\nonumber\] 9о} \end{массив}\номер\]
Это соответствует ответу из примера 1.
 1.1.
1.1.
Эта страница под названием 1.1: Vectors публикуется в соответствии с лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Томом Вайдеманом непосредственно на платформе LibreTexts.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Том Вайдеман
- Лицензия
- CC BY-SA
- Версия лицензии
- 4,0
- Показать оглавление
- нет
- Теги
- источник@родной
Примеры векторных и скалярных величин в физике
При изучении физики существует множество различных аспектов измерения и множество типов инструментов измерения. Скалярные и векторные величины являются двумя из этих типов инструментов измерения. Продолжайте читать примеры скалярной величины и примеры векторной величины в физике.
Скалярные и векторные величины являются двумя из этих типов инструментов измерения. Продолжайте читать примеры скалярной величины и примеры векторной величины в физике.
инфографические скалярные и векторные примеры
Advertisement
Определение скалярных и векторных величин
Понимание разницы между скалярными и векторными величинами является важным первым шагом в физике. Основное различие в их определениях:
- Скаляр является измерением единицы строго в величине .
- Вектор представляет собой измерение, которое относится как к величине единицы, так и к направлению движения, которое совершила единица.
Другими словами, скалярная величина имеет величину, такую как размер или длина, но не имеет определенного направления. Когда у него есть конкретное направление, это векторная величина.
Примеры скалярных величин
Скалярные величины, как указано выше, являются измерениями, строго относящимися к величине среды. В скалярной величине совершенно нет направленных составляющих — только величина среды. Исследуйте 10 примеров скалярных величин.
Площадь
Если вы измеряете площадь поверхности участка земли или двумерного объекта, у него нет направления, только величина. Вы можете связать с ним направление, когда рассматриваемый объект является трехмерным, поскольку вы измеряете его в разных направлениях. Но площадь является скалярной, когда измерение простое и двумерное.
Плотность
Плотность объекта можно найти, разделив его массу на объем. Поскольку в этом расчете требуется только две точки, это скалярная величина. Направление не влияет на плотность объекта.
Расстояние
Сколько вы прошли? Измеряя расстояние, вы определяете величину пройденного вами пространства. Он не включает водоизмещение или скорость; скалярная величина расстояния обсуждает только то, сколько земли было пройдено.
Энергия
Как и другие скалярные величины, энергия является произведением двух факторов (в данном случае силы и перемещения). Он описывает величину использования энергии без измерения направления.
Реклама
Масса
Многие люди используют слова «вес» и «масса» как синонимы, но это не одно и то же. Масса – это количество материи, присутствующей в объекте. Это не зависит от направления; масса объекта одинакова независимо от того, в каком направлении движется объект.
Скорость
Может быть трудно понять разницу между скоростью и скоростью. Однако знание того, что скорость является скалярной величиной, может оказаться полезным, поскольку при измерении скорости направление не имеет значения.
Реклама
Температура
Когда вы измеряете температуру термометром, вы измеряете свою среднюю тепловую энергию. Поскольку вы уже знаете, что энергия является скалярной величиной, вы, вероятно, можете понять, что температура также скалярна.
Время
Скалярные величины часто относятся ко времени, которое включает в себя измерение лет, месяцев, недель, дней, часов, минут, секунд и даже миллисекунд. При измерении времени не учитывается или не измеряется направление, хотя кажется, что время всегда движется вперед.
Объем
Скалярное количество может относиться к объему среды, например, к ее объему. Все, от тонн и унций до граммов, миллилитров и микрограммов, — все это скалярные величины, если они применяются к измеряемой среде, а не к движению среды.
Работа
Работа — это энергия, переданная объекту силой. Это скалярная величина, поскольку она является произведением силы и перемещения. Работа — это не то же самое, что сила, которая является векторной величиной, потому что работа — это результат действия силы.
Примеры векторных величин
Векторные величины относятся как к направлению движения среды, так и к измерению скалярной величины. Вы можете заметить, что скалярные произведения часто являются произведениями двух векторных величин. Ознакомьтесь с этими 10 примерами векторных величин, встречающихся в вашей повседневной жизни.
Ознакомьтесь с этими 10 примерами векторных величин, встречающихся в вашей повседневной жизни.
Ускорение
Хотя скорость является скалярной величиной, ускорение отличается. Ускорение измеряет скорость изменения скорости объекта. Он учитывает период времени, а также направление, что делает его векторной величиной.
Реклама
Перемещение
Скалярная величина расстояния измеряет землю, пройденную движением, а перемещение измеряет, насколько далеко она переместилась от своего первоначального местоположения. Вы можете видеть, что направление и величина очень важны при измерении смещения!
Сила
Сила имеет как величину, так и направление. В отличие от скалярного количества работы, сила заставляет объект изменять свою скорость. Думайте о таких силах, как гравитация, когда решаете, является ли это векторной величиной.
Повышение/снижение температуры
Измерение температуры среды является скалярной величиной. Однако измерение повышения или понижения температуры среды является векторной величиной. У него есть направление и величина.
У него есть направление и величина.
Магнитная поляризация
Поляризация указывает на то, что два устройства отошли друг от друга. Направление (вдали друг от друга), а также величина (насколько далеко или насколько) являются важными факторами при измерении поляризации.
Импульс
Импульс указывает на то, что объект находится в движении. Это произведение массы и скорости, и его можно рассчитать только в том случае, если вы знаете, как быстро движется объект (величина) и в каком направлении.
Положение
Может показаться, что фиксированное положение не имеет ни величины, ни направления. И это правильно — если вы определяете «позицию» таким образом. Вектор положения берется относительно начала системы координат; то есть он существует в конце прямой линии, которая соединяется с серединой оси. С этой точки зрения легко увидеть направление и величину.
Реклама
Тяга
Тяга — это тип силы реакции, которая также имеет величину и направление. Подумайте о том, что вас толкают или толкают по воздуху — вы определенно движетесь в направлении, имеющем огромную величину! Чаще всего он используется в механике и аэронавтике.
Подумайте о том, что вас толкают или толкают по воздуху — вы определенно движетесь в направлении, имеющем огромную величину! Чаще всего он используется в механике и аэронавтике.
Скорость
Измерение скорости, с которой объект меняет положение, является векторной величиной. Чтобы измерить векторную величину среды, необходимо применить направленное измерение к скалярной величине. Другим элементом направления, который может быть применен к векторной величине, является разница между вертикальным и горизонтальным перемещениями.
Вес
Вес объекта является произведением его массы и действующего на него гравитационного ускорения. Поскольку это связано с силой тяжести, вес имеет направление (вниз), а также величину.
Реклама
Источник дополнительной технической информации в Интернете
Высокотехнические примеры и пояснения, касающиеся скалярных и векторных величин, можно найти на веб-сайте National Aeronautics and Space. Он содержит полное описание скаляров и векторов, а также примеры и способы их использования.
Физика вокруг нас
Итак, теперь у вас есть несколько примеров скалярных и векторных величин, и вы понимаете некоторые различия между ними. Для получения дополнительной информации о физике ознакомьтесь с этими примерами контактной силы, которые вы, вероятно, увидите в физическом мире. Вы также можете больше углубиться в законы физики с повседневными примерами инерции.
Штатный писатель
Скаляр и вектор: определение, количество, примеры
В повседневной жизни мы взаимозаменяемо используем расстояние, перемещение, скорость, скорость, ускорение и т. д. Для физиков все величины, будь то статические или движущиеся, могут быть дифференцированы путем их классификации как скаляры или векторы.
Величина с величиной (размером) только называется скалярной величиной . Масса, энергия, мощность, расстояние и время — вот некоторые примеры скалярных величин, потому что с ними не связано направление.
Величина, имеющая величину и связанное с ней направление , является векторной величиной . Ускорение, сила, сила тяжести и вес являются некоторыми векторными величинами. Все векторные величины связаны с определенным направлением.
Скаляры и векторы: значение и примеры
Как мы уже говорили, величина, имеющая величину и направление, называется векторной величиной.
Вес является примером векторной величины, поскольку он является произведением массы и ускорения свободного падения. Ускорение свободного падения направлено вертикально вниз , что делает вес векторной величиной.
Давайте рассмотрим несколько примеров скаляров и векторов.
Предположим, у вас есть ящик, и вы перемещаете его на расстояние 5 метров.
Рис. 1. Движение объекта из точки A в точку B в заданном направлении представляет собой вектор. Oğulcan Tezcan – StudySmarter Originals
Если вы скажете кому-нибудь, что расстояние между точками A и B равно 5 метрам, вы говорите о скалярной величине , потому что вы не указываете направление . Пять метров — это всего лишь величина (расстояние), а направление может быть любым. Таким образом, расстояние является скалярной величиной.
Пять метров — это всего лишь величина (расстояние), а направление может быть любым. Таким образом, расстояние является скалярной величиной.
Однако, если вы расскажете кому-нибудь вы переместили ящик на 5 метров вправо (на восток) , как показано на рисунке 1, теперь вы говорите о векторной величине . Почему? Поскольку у вас есть , теперь указано направление, связанное с движением . А в физике это называется смещения . Следовательно, перемещение является векторной величиной.
Теперь предположим, что вам потребовалось 2 секунды, чтобы переместить коробку вправо.
Рис. 2. Диаграмма, показывающая вектор смещения относительно времени. Огулкан Тезкан – StudySmarter Originals
Если бы вам нужно было вычислить, как быстро вы переместили коробку, вы вычислили скорость движения . В приведенном выше примере скорость равна:
Скорость является скалярной величиной , поскольку она не имеет направления.
Однако, если вы скажете, что ящик двигался со скоростью 2,5 м/с вправо , это становится векторной величиной . Скорость с направлением есть скорость, и изменение скорости, в свою очередь, известно как ускорение (м/с 2 ), что также является векторной величиной.
| Скаляр | Вектор |
| Расстояние | |
| SPEED | VELOCITE и ACCELORET |
| Скаля | Vectors | Vectors | 330Vectors | 330 . величину и направление. величину и направление. |
| Они меняются с изменением величины. | Они меняются с изменением величины или направления, или того и другого. |
| Их можно складывать, вычитать, умножать или делить по обычным правилам алгебры. | Их можно складывать, вычитать или умножать, используя законы векторов. |
| Обозначается обычными буквами. | Обозначается жирным шрифтом или стрелкой над буквой. Например: A или |
Вектор положения и вектор смещения
Рисунок 1: Вектор положенияВектор, представляющий положение объекта (точки) A относительно начала координат O, называется вектором положения
объекта. Он может быть представлен стрелкой с концом в точке О и острием в точке А. Вектор положения указывает расстояние и направление объекта относительно выбранного источника.
Рис. 2: Вектор смещения
Пусть A — положение движущегося объекта в момент времени t, и аналогично A’ — положение движущегося объекта в более позднее время t’ (рис. 2).
и
— векторы положения в моменты времени t и t’ соответственно. Таким образом, вектор
называется вектором смещения, соответствующим движению за время от t до t’. Фактический путь, пройденный объектом, может не совпадать с прямой линией, соединяющей А с А’.
Представление вектора
Вектор может быть представлен либо одной жирной буквой, либо одной буквой со стрелкой на ней. Например, сила представлена как
или F . Его величина представлена , называемым модулем вектора силы. Модуль или величина вектора является скалярной величиной.
Вектор может быть представлен графически или геометрически прямой линией со стрелкой. Длина линии дает величину вектора, а стрелка указывает его направление.
Рисунок 3 представляет вектор
= . Здесь OA — величина данного вектора, а направление показано стрелкой (головкой). Начальная или начальная точка O линии стрелки называется началом или концом вектора. Точка A, которая находится в конце линии стрелки, называется вершиной, или головой, или конечной точкой вектора.
Модуль вектора
Модуль вектора — это положительное число, которое измеряет величину вектора.
Например, модуль вектора
представлен как или, просто как A.
Характеристики вектора
Характеристики вектора приведены ниже:
- Вектор имеет как величину, так и направление.
- Вектор не подчиняется обычным правилам алгебры.
- Вектор может измениться с изменением величины или направления, или того и другого.
Надеюсь, вы поняли концепцию и разницу между скалярами и векторами, представление и характеристики вектора и т. д. Также поделитесь своими отзывами об этой статье в комментариях.
д. Также поделитесь своими отзывами об этой статье в комментариях.
Оставайтесь с HelpYouBetter, чтобы узнать больше интересных тем и связанных с ними концепций.
Почему, как, доказательства и подробные факты – Lambda Geeks
Сила является векторной величиной, и ее единицей S.I. является Ньютон.
Чтобы быть векторной величиной, нужно иметь не только величину, но и направление. Поскольку сила имеет как направление, так и величину, она является векторной величиной.
Является ли сила векторной величиной? Безусловно, это векторная величина. Очевидно, что каждая величина имеет величину. Но в этом случае было бы очень запутанно, если бы не знать направления, было бы невозможно решить головоломку. Следовательно, сила имеет как величину, так и направление. Таким образом, это векторная величина.
Что такое Сила?Сила — внешний фактор, отвечающий за изменение состояния тела.
Он либо подтолкнет тело, чтобы привести его в движение, либо остановит его; это может работать в обе стороны. Знаменитый греческий философ Аристотель сказал, что сила вызывает «неестественное движение».
Знаменитый греческий философ Аристотель сказал, что сила вызывает «неестественное движение».
Поскольку сила является векторной величиной, она обозначается стрелкой над ней как:
Формула для получения силы дается как: F = m.a
| Где, | F = сила | м = Масса объекта |
| a = Ускорение |
Сила S. I. Единицей измерения является Ньютон (Н) или кг. м/с 2 .
Размеры силы даны как: LMT -2
Далее, с силой связаны три понятия. Во-первых, это Thrust, при котором скорость объекта увеличивается. Перетаскивание, при котором скорость объекта уменьшается. И Torque, в котором изменяется скорость вращения объекта. Давление можно отнести к еще одному виду силы, и это распределение малых сил, приложенных к телу.
Существует контактная сила, для которой необходим физический контакт между двумя объектами. К контактным силам относятся некоторые неосновные силы, примеры которых приведены ниже. Тогда есть бесконтактные силы, которые не нуждаются в физическом контакте между объектами. Неконтактные силы включают основные силы, приведенные ниже.
К контактным силам относятся некоторые неосновные силы, примеры которых приведены ниже. Тогда есть бесконтактные силы, которые не нуждаются в физическом контакте между объектами. Неконтактные силы включают основные силы, приведенные ниже.
В природе существует четыре основных типа сил.
- Гравитационная сила – это универсальная сила, действующая между массами и всегда притягивающая.
- Электромагнитная сила – действует между заряженными частицами и в десять раз мощнее гравитационной силы. Оно может быть привлекательным или отталкивающим. Магнитная сила является разновидностью электромагнитной силы.
- Слабая Ядерная сила – проявляется только в определенных ядерных процессах, таких как бета-распад ядра (β-распад). Она более мощная, чем сила гравитации, но слабее, чем электромагнитная и сильная ядерная сила.
- Сильная ядерная сила — сильнее всех основных сил природы.
 Он удерживает вместе протоны и нейтроны в ядре. Электроны не испытывают этой силы.
Он удерживает вместе протоны и нейтроны в ядре. Электроны не испытывают этой силы.
При взаимодействии фундаментальных сил друг с другом, как следствие, возникают нефундаментальные силы. Некоторые из неосновных сил:
- Нормальная сила – действует перпендикулярно поверхности, с которой контактирует объект.
- Сила трения – это поверхностная сила, препятствующая движению объекта. Далее его можно разделить на статическое трение и кинетическое трение.
- Натяжение – действует, когда объект тянут веревками, веревками или тросами и т. д.
- Сила упругости – действует, когда тело возвращается к своей первоначальной форме и размеру после растяжения. Говорят, что сила не действует на тело.
- Напряжение – это сила, действующая на единицу площади тела.
- Центростремительная сила – ее еще называют фиктивной или псевдосилой.
 Объект обязан следовать по кривой траектории. Он имеет тенденцию тянуть объект в центре.
Объект обязан следовать по кривой траектории. Он имеет тенденцию тянуть объект в центре. - Центробежная сила – это тоже фиктивная или псевдосила. Это противоположно центростремительной силе и имеет тенденцию оттягивать объект от центра.
Подробнее на Виды сил.
Почему сила является векторной величиной?Объект должен иметь как величину, так и направление, чтобы быть векторной величиной.
Как мы узнали выше, чтобы быть векторной величиной, объект должен иметь как величину, так и направление, но этого недостаточно. Чтобы быть векторной величиной и чтобы доказать это математически, объект должен подчиняться законам сложения или вычитания векторов.
В качестве примера рассмотрим коробку, лежащую на столе, на которую действуют различные силы. Сила гравитации будет тянуть его вниз, а равная и противоположная нормальная сила будет тянуть его вверх. Теперь эти силы уравновешивают друг друга, и в результате результирующая сила будет равна нулю, и мы говорим, что ящик не движется.
Теперь, если мы хотим переместить коробку, нам нужно применить к ней некоторую силу. Но с какой стороны? Если мы скажем, что приложили к ящику силу в 3 ньютона, как мы узнаем, куда движется ящик? Таким образом, необходимо упомянуть направление. Будет логично, если мы скажем, что нам нужно приложить силу в 3 ньютона с правой стороны, чтобы было легче понять, что ящик движется в правильном направлении.
Таким образом, если мы хотим сдвинуть коробку на левую сторону, мы толкаем (прикладываем силу) с левой стороны, а если мы хотим сдвинуть коробку с правой стороны, мы прикладываем силу к правой стороне.
Представление вектораСуществует множество различных методов сложения или вычитания векторов, которые мы рассмотрим далее в этой статье.
Законы сложения векторов включают
- Сложение или вычитание компонентов вектора
- Треугольный закон сложения векторов
- Параллелограммный закон сложения векторов
- Полигональный закон сложения векторов
Сначала давайте кратко разберемся с законами сложения векторов.
- Треугольный закон сложения векторов применяется, когда два вектора расположены в формате «голова к хвосту».
- Закон сложения векторов в виде параллелограмма применяется, когда два вектора располагаются голова к голове или хвост к хвосту.
- Сложение и вычитание выполняются в простой математике.
- Векторы нельзя складывать или вычитать из скаляров и наоборот.
- Векторы точного характера можно добавлять или вычитать. Например, сила должна добавляться или вычитаться только с силой, а не со скоростью или любым другим вектором.
Подробнее о Типы внешних сил .
Как доказать, что сила является векторной величиной?Как упоминалось выше, необходимо математически доказать, что сила является вектором.
- Сложение или вычитание компонентов вектора
Для сложения или вычитания вектора необходимо складывать или вычитать компоненты вектора.
Например, пусть ниже два вектора.
Тогда сумма двух векторов будет:
Разница между двумя векторами будет:
- Треугольный закон сложения векторов
другой вектор, и в результате образуется диагональ, которая и является результирующим вектором. Он следует формату «голова к хвосту».
Треугольный закон сложения векторовНапример,
Следовательно,
Если нужно найти угол между векторами
, его можно найти по формуле:
- Закон сложения векторов
В этом методе хвост или голова одного вектора соединяется с хвостом или головой другого вектора соответственно, в результате чего образуется диагональ. Он следует формату «голова к голове» или «хвост к хвосту».
Параллелограммный закон сложения векторовСледовательно, формула нахождения равнодействующей останется такой же, как и треугольный закон сложения векторов. т. е.
- Закон сложения векторов полигонов
В этом методе каждая сторона многоугольника будет представлять вектор. Этот многоугольник будет разбит на треугольники, и с помощью треугольного закона сложения векторов будет легко вычислить все векторы.
Этот многоугольник будет разбит на треугольники, и с помощью треугольного закона сложения векторов будет легко вычислить все векторы.
Этот закон справедлив для любого количества векторов и всегда представлен в циклическом порядке.
Полигональный закон сложения векторов Почему электрическая линия силы является векторной величиной?Воображаемые линии, иллюстрирующие направление электрического поля, известны как электрические силовые линии.
Электрическая силовая линия является силой, следовательно, это векторная величина. На самом деле сила — это вектор, поэтому электрическая линия силы явно становится векторной величиной. Следовательно, она имеет как величину, так и направление.
Электрическая силовая линия широко известна как электрическое поле и выражается как сила на единицу заряда. Единица S.I. для электрического поля — ньютон на кулон (Н/Кл), или иногда также указывается как вольт на метр (В/м).
The formula for electric field is given as:
E=F/q
| Where, | E = Electric Field |
| F = Force | |
| q = Charge |
Как видно из рисунка выше, линии электрического поля представлены векторными стрелками. Как показано выше, если заряд положительный, линии выходят из заряда, а если заряд отрицательный, линии входят в заряд.
Если в пространстве присутствует только положительный заряд, то говорят, что электрические силовые линии исходят из положительного заряда и уходят в бесконечность. Точно так же, если в пространстве присутствует только отрицательный заряд, то говорят, что электрические силовые линии идут из бесконечности к отрицательному заряду.
Линии становятся короче вблизи заряда и длиннее вдали от него. Электрические силовые линии никогда не пересекаются друг с другом, но при этом чрезвычайно плотны. Когда электрические силовые линии встречаются с поверхностью любого объекта, электрические силовые линии становятся перпендикулярными поверхности. Эти линии не видны, но экспериментально доказаны.
Когда электрические силовые линии встречаются с поверхностью любого объекта, электрические силовые линии становятся перпендикулярными поверхности. Эти линии не видны, но экспериментально доказаны.
Следовательно, с помощью направления мы можем показать, что положительные заряды притягивают отрицательные заряды, но отталкивают другие положительные заряды. Точно так же отрицательные заряды притягиваются к положительным зарядам, но отталкивают другие отрицательные заряды.
Таким образом, если кто-то хочет описать электрические силовые линии, это невозможно сделать без помощи направления. Установить, положительный заряд или отрицательный, можно только с помощью направления. После установления неизвестного заряда заряда можно найти электрическое поле, его напряженность, электрический поток и т. д. Таким образом, мы можем сказать, что электрические силовые линии являются векторной величиной.
В чем разница между векторами и скалярами?
Скаляр — это величина, которая полностью определяется своей величиной и не имеет направления. Скаляр может быть описан либо безразмерно, либо в терминах некоторой физической величины. Примеры скаляров: масса, объем, расстояние, энергия и время.
Скаляр может быть описан либо безразмерно, либо в терминах некоторой физической величины. Примеры скаляров: масса, объем, расстояние, энергия и время.
Скалярными величинами можно управлять с помощью законов арифметики, применимых к натуральным числам. Например, если я добавляю 20 граммов сахара в рецепт, а затем добавляю еще 20 граммов, в результате получается 40 граммов сахара в рецепте. Если я куплю литровую (1000 мл) бутылку воды и выпью 250 мл, останется 750 мл.
Вектор является величиной, которая определяет как величину, так и направление. Такая величина может быть представлена геометрически стрелкой длины, пропорциональной ее величине, указывающей в заданном направлении. Примеры векторов: перемещение, скорость, ускорение, сила и электрическое поле. Векторы можно складывать простыми способами, как и скаляры. Например: Самолет летит на юг со скоростью 500 миль/час. Ветер дует с востока со скоростью 100 миль в час. Результирующая скорость не 600 миль в час и не 400 миль в час. 92)
92)
R = 509,9 миль/ч.
Направление плоскости можно вычислить с помощью функции косинуса.
тангенс = 100/500 = 11,31 градуса
(Примечание: рисунок выполнен не в масштабе)
1. ___ _ пример скалярной величины
а) скорость
б) сила
в) том
г) ускорение
2. ___ является примером векторной величины
а) масса
б) сила
в) том
г) плотность
3. Скалярная величина:
а) всегда имеет массу
б) есть величина, полностью определяемая своей величиной
в) показывает направление
г) не имеет единиц
4. Векторная величина
а) может быть безразмерной величиной
б) указывает только величину
в) указывает только направление
г) указывает как величину, так и направление 90 036
5. Мальчик давит на стену с силой 50 фунтов. Стена не двигается. Результирующая сила:
Мальчик давит на стену с силой 50 фунтов. Стена не двигается. Результирующая сила:
а) -50 фунтов
б) 100 фунтов
в) 0 фунтов
г) -75 фунтов
6. Человек прошел 3 мили на север, затем повернул направо и прошел 4 мили на восток. Результирующее смещение:
а) 1 миля ЮЗ
б) 7 миль NE
в) 5 миль NE
d) 5 миль E
7. Самолет, летящий со скоростью 500 миль/час строго на север, имеет попутный ветер 45 миль/час, результирующая скорость:
а) 545 миль/час на юг.
б) 455 миль/час на север.
c) 545 миль/ч строго на север.
г) 455 миль/час на юг
8. Разница между скоростью и скоростью:
а) скорость не имеет единиц
б) скорость показывает только величину, а скорость представляет и величину (силу), и направление
в) они используют разные единицы для представления своей величины 90 362
г) скорость имеет большую величину
9. Результирующая величина двух векторов
Результирующая величина двух векторов
а) Всегда положительный
б) никогда не может быть нулевым
в) Никогда не может быть отрицательным
г) Обычно равен нулю
10. Что из следующего неверно.
а) скорость может быть отрицательной
б) скорость есть вектор
б) скорость является скаляром
г) скорость может быть отрицательной
Сила, работа и энергия
Скорость, скорость и ускорение: В чем разница между скоростью и скоростью? Что такое ускорение? График скорости и ускорения. Проверка вашего понимания.
Сила: Что такое сила? Измерение сил. Описание Сил. Что делает сила? Что такое трение? Оценочные вопросы.
Векторы и скаляры: Что такое векторная величина? Примеры векторов. Что такое скалярная величина? Примеры скаляров.


 1 Электростатика
1 Электростатика 6 СТО
6 СТО


 Следовательно, мы можем найти длину третьей стороны (\(\overrightarrow C\)) по закону косинусов: 9о\номер\]
Следовательно, мы можем найти длину третьей стороны (\(\overrightarrow C\)) по закону косинусов: 9о\номер\] 
 1.1.
1.1. 

 Взгляните на рисунки ниже.
Взгляните на рисунки ниже.
 Вес коробки, mg, действует вниз с массой m и гравитационным притяжением g.
Вес коробки, mg, действует вниз с массой m и гравитационным притяжением g. Силовые линии должны проходить через одну и ту же точку, чтобы тело находилось в равновесии.
Силовые линии должны проходить через одну и ту же точку, чтобы тело находилось в равновесии.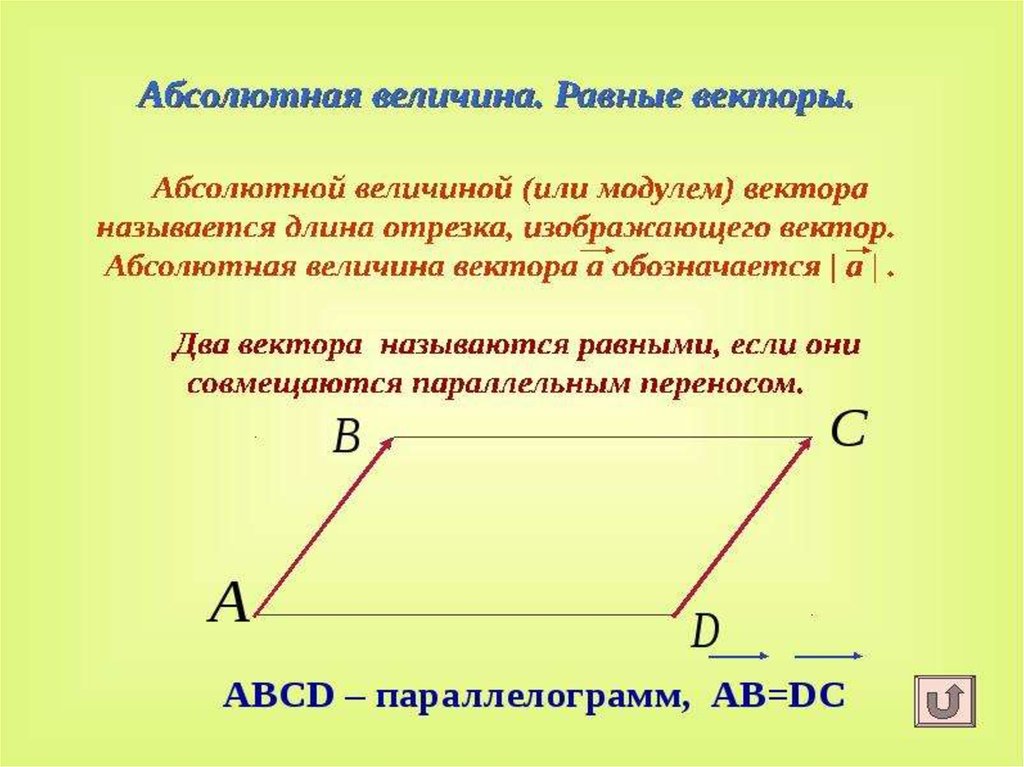 Usama Adeel – StudySmarter Originals
Usama Adeel – StudySmarter Originals
 Если тело движется к возрастающей координате положения, его скорость принимается положительной. С другой стороны, если тело движется в направлении убывания координаты, его скорость считается отрицательной.
Если тело движется к возрастающей координате положения, его скорость принимается положительной. С другой стороны, если тело движется в направлении убывания координаты, его скорость считается отрицательной.
 Он удерживает вместе протоны и нейтроны в ядре. Электроны не испытывают этой силы.
Он удерживает вместе протоны и нейтроны в ядре. Электроны не испытывают этой силы.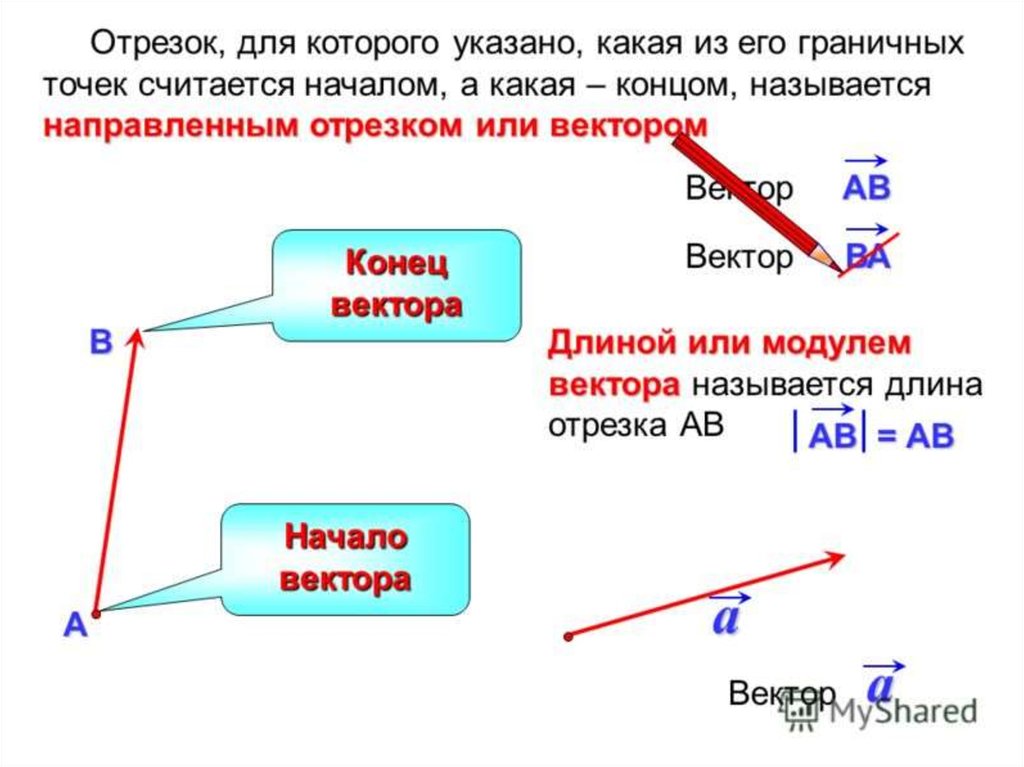 Объект обязан следовать по кривой траектории. Он имеет тенденцию тянуть объект в центре.
Объект обязан следовать по кривой траектории. Он имеет тенденцию тянуть объект в центре.