Векторные величина: Что такое векторная величина? — ответ на Uchi.ru — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Скалярные и векторные величины

Даны определения и приведены примеры скалярных и векторных величин. Описаны математические операции над векторными величинами.

Физические величины бывают скалярными и векторными

Скалярные величины

Скалярная величина (от лат. scalaris – ступенчатый) в механике – величина, каждое значение которой может быть выражено одним числом.

Примеры скалярных величин: масса тела, время, температура, длина, путь, площадь.

Более подробно функционирование опорно-двигательного аппарата человека и биомеханика мышц описаны в книге:

Биомеханика опорно-двигательного аппарата человека

Векторные величины

Если величина, кроме числового значения характеризуется еще и направлением, то она называется векторной величиной или просто вектором. То есть вектор определяется численным значением и направлением.

Примеры векторных величин: перемещение, скорость, ускорение, сила, момент силы, импульс тела.

Обозначение векторных величин

На рисунках и схемах вектор отображается отрезком прямой со стрелкой на одном конце. Длина отрезка в выбранном масштабе выражает числовое значение векторной величины (его модуль), а стрелка указывает ее направление.

На рисунках, схемах и в тексте векторные величины обозначают несколькими способами:

1 способ. Векторная величина обозначается строчной или заглавной буквой со стрелкой или чертой над ней (рис. 1).

Рис.1. Вектор и его обозначение

2 способ. Векторная величина обозначается заглавными буквами, обозначающими начало и конец вектора с чертой или стрелками над ними (рис. 1).

3 способ. Иногда векторные величины в формулах обозначаются жирным шрифтом, а скалярные — обычным. Например: F=ma

Операции над векторными величинами (векторами)

Над векторными величинами возможны следующие математические операции:

Сложение и вычитание векторов.
Умножение вектора на скаляр.
Произведение векторов (скалярное и векторное).

Литература

Петров В.А., Гагин Ю.А. Механика спортивных движений. – М: Физкультура и спорт, 1974. – 232 с.

С уважением, А.В. Самсонова

Что такое вектор и векторные величины? Какие их свойства, признаки? / Справочник :: Бингоскул

Что такое вектор и векторные величины? Какие их свойства, признаки?

добавить в закладки удалить из закладок

Содержание:

Одни величины в физике называют скалярными, другие – векторными, и последним посвящён целый раздел алгебры. Кратко разберёмся, какие величины называют векторными, определим их свойства. Узнаем основные параметры этих отрезков, сферы применения, возможные манипуляции с ними.

Что такое векторная величина

К определению понятия «вектор» подходят с разных сторон. В одних источниках его называют направленным отрезком с известными началом и концом. Другие – подробнее описывают, что такое вектор, это отрезок с заданными:

Длиной, величиной либо модулем. Часто определяется выбранным масштабом.

Точкой приложения или начальной точкой.

Линией действия – прямой, на которой расположен.

Стороной действия – порядком перехода от точки приложения к концу.

Часто линия и сторона действия объединяются в направление вектора.

Очевидно, термин происходит из латинского языка: vector – несущий.

Обозначение

Векторы в физике, математике, геометрии обозначают:

Одной буквой (обычно маленькой с жирным начертанием) латинского алфавита.

Двумя большими буквами латиницы с чертой либо стрелкой над ними в обоих случаях.

В последней ситуации первая буква указывает на начальную точку или начало направленного отрезка, вторая – на его конец. Их порядок указывает на направленность вектора. Отсюда следует, что порядок указания букв важен. AB ≠ BA как в случае с обычными отрезками. На чертежах направление изображают стрелкой на конце, начало представляют точкой.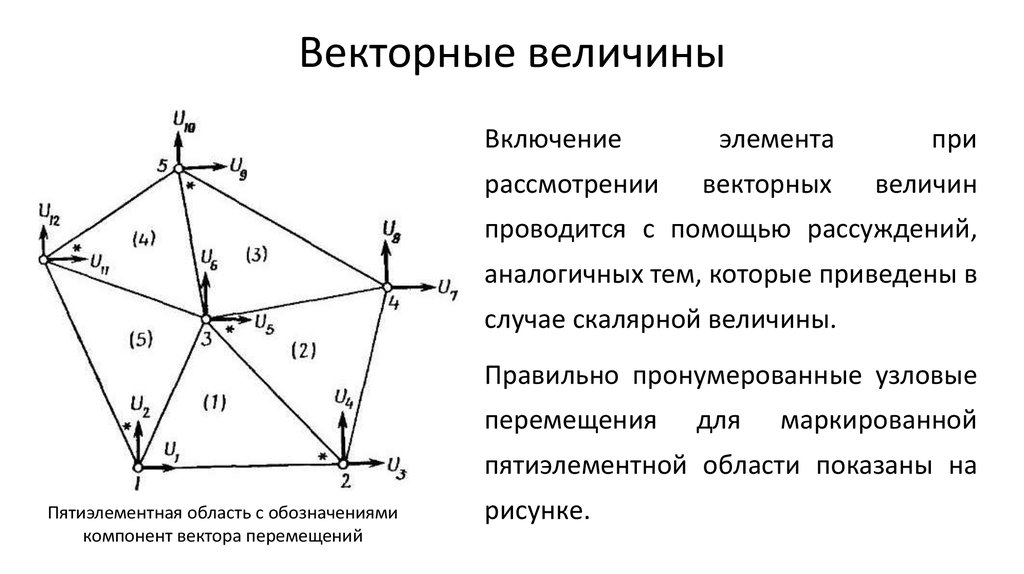 Длиной называется разница между конечной и начальной точками. Обозначается преимущественно буквой V со стрелкой/риской вверху \overrightarrow{V} .

Свойства и классификация векторов

Направленные отрезки обладают рядом особенностей. Различают следующие виды векторов:

Коллинеарные – принадлежат одной прямой либо параллельным. Правило применимо к плоскости и пространству.

Сонаправленные – коллинеарные и одновременно одинаково направлены.

Противоположно направленные – коллинеарные отрезки с противоположным направлением.

Компланарные – направленные к общему началу векторы, расположенные в одной плоскости.

Нулевые – длина равна нулю – начало совпадает с концом.

Свободные – могут передвигаться относительно начального положения.

Скользящие – подлежат перемещению вдоль линии действия.

Несвободные – не допускают изменения точки приложения.

Величины можно складывать – суммировать, отнимать – вычислять их разницу, умножать – находить произведение и определять длину (модуль). Причем операции производятся как с векторами, так и по отношению к направленному отрезку и числу.

Применение

Векторными называют величины, которые характеризуются направлением и переносом. В физике это скорость, ускорение – в большинстве случаев, направлены в сторону движения тела; тепловой поток, электрический ток, магнитная индукция, перемещение. С силой ситуация интереснее, на объект их может действовать несколько в разных направлениях, суммирующая при этом может быть нулевой.

Применение направленных отрезков упрощает определение меры углов между отрезками, лучами, прямыми, вычисление площадей геометрических фигур. В компьютерной графике векторы-нормали применяют для освещения сцен и создания масштабируемых изображений, качество которых не страдает при уменьшении или увеличении картинки. Рассматриваемые отрезки положены в основу системы полярных координат. Существует отдельный раздел компьютерной графики – векторный.

Скользящие «несущие» широко применяются в физике (механике), например, это сила. При перемещении вектора силы вдоль прямой, которой тот принадлежит, момент силы остаётся константой. При перемещении на иную прямую он зачастую меняется. Сила не рассматривается как свободный направленный отрезок.

Поделитесь в социальных сетях:

20 ноября 2021, 14:45

Геометрия

Could not load xLike class!

Векторные и скалярные величины — определение и примеры

В математике и физике есть физические величины, которые можно разделить на две категории, а именно

Скалярное количество
Количество векторов

В этой статье давайте обсудим, что такое векторные и скалярные величины на примерах.

Определение скалярной величины

Физические величины, имеющие только величину , известны как скалярные величины. Он полностью описывается величиной или числовым значением. Скалярная величина не имеет направлений. Другими словами, скаляр — это мера количества. Например, если я скажу, что высота башни – 15 метров, тогда высота башни является скалярной величиной, поскольку для определения ей нужна только величина высоты. Давайте возьмем другой пример, предположим, что время, необходимое для выполнения части работы, составляет 3 часа, тогда и в этом случае для описания времени просто нужна величина, т. е. 3 часа.

Примеры скалярных величин

Другими примерами скалярных величин являются масса, скорость, расстояние, время, энергия, плотность, объем, температура, расстояние, работа и так далее.

Определение количества векторов

Физические величины, для которых четко определены и величина, и направление , называются векторными величинами. Например, мальчик едет на велосипеде со скоростью 30 км/ч в северо-восточном направлении. Тогда, как мы видим, для определения скорости нам нужны две вещи, а именно величина скорости и ее направление. Следовательно, он представляет собой векторную величину.

Примеры количества векторов

Другими примерами векторных величин являются смещение, ускорение, сила, импульс, вес, скорость света, гравитационное поле, ток и т. д.

Разница между скалярной и векторной величиной

Давайте обсудим некоторые различия здесь:

Разница между скалярной и векторной величиной
Скалярное количество	Количество векторов
Имеет величину всего	Имеет как величину, так и направление
Не имеет направления	Имеет направление
Указывается номером и единицей измерения	Также указывается числом вместе с направлением и единицей измерения
Обозначается символом количества	Обозначается символом количества, выделенным жирным шрифтом, или стрелкой над цифрой 9. 0044
Пример: температура, скорость и т. д.	Пример: ускорение, скорость и т. д.

Векторное представление

Давайте посмотрим на отрезок, нарисованный ниже. Векторная величина всегда имеет начальную и конечную точки. Две конечные точки данного отрезка различимы как и . Представляет собой направленный отрезок

Направленный отрезок прямой с начальной точкой A и конечной точкой B условно обозначен жирным шрифтом AB .

\(\begin{array}{l}\text{Также это может быть представлено как} \ \overrightarrow{AB}\end{array} \)

Длина вектора a представляет его величину, которая обозначается |AB|. Вместо использования двухбуквенного обозначения мы можем использовать однобуквенное обозначение для представления вектора как a, b, c и обозначать их величины. Поскольку трудно писать буквы жирным шрифтом, мы используем черту над буквами для представления векторов как ā.

Следовательно,

\(\begin{array}{l}\text{If} \\overrightarrow{AB} = a,\ \text{then} |\overrightarrow{AB}| = a, \\ \text{где} \ | \overrightarrow{AB}|\ \text{указывает величину вектора.

}\end{массив} \)

Также величина называется модулем.

Характеристики векторов

Характеристики векторов следующие:

Векторы обладают как величиной, так и направлением
Не подчиняется обычному закону алгебры
Изменяется либо величина, либо направление, либо оба изменяются

Пример скалярной и векторной величины

Вопрос:

Узнать скалярную и векторную величину из заданного списка.

Сила, скорость, электрическое поле, угловой момент, магнитный момент, температура, линейный момент, средняя скорость.

Решение:

Из данного списка,

Скалярные величины – скорость, температура.
Векторные величины — сила, электрическое поле, угловой момент, магнитный момент, линейный импульс, средняя скорость.

Теперь мы знаем, что такое векторы и скаляры. Теперь, если кто-нибудь спросит, является ли ускорение вектором или скаляром, мы легко ответим, что это вектор, потому что у него есть не только величина, но и направление. Точно так же, когда спрашивают, является ли расстояние вектором или скаляром, совершенно очевидно, что, поскольку расстояние имеет только величину, оно является скалярной величиной.

Продолжайте учиться с BYJU’S — обучающим приложением, чтобы учиться лучше.

Скаляр и вектор: определение, количество, примеры

В повседневной жизни мы взаимозаменяемо используем расстояние, перемещение, скорость, скорость, ускорение и т. д. Для физиков все величины, будь то статические или движущиеся, можно дифференцировать, классифицируя их как либо скаляры, либо векторы.

Величина с величиной (размером) только называется скалярной величиной . Масса, энергия, мощность, расстояние и время — вот некоторые примеры скалярных величин, потому что с ними не связано направление.

Величина, имеющая величину и связанное с ней направление , является векторной величиной . Ускорение, сила, сила тяжести и вес являются некоторыми векторными величинами. Все векторные величины связаны с определенным направлением.

Скаляры и векторы: значение и примеры

Как мы уже говорили, величина, у которой есть величина и направление, называется векторной величиной.

Вес является примером векторной величины, поскольку он является произведением массы и ускорения свободного падения. ускорение силы тяжести направлено вертикально вниз , что делает вес векторной величиной.

Давайте рассмотрим несколько примеров скаляров и векторов.

Предположим, у вас есть ящик, и вы перемещаете его на расстояние 5 метров.

Рис. 1. Движение объекта из точки А в точку В в заданном направлении представляет собой вектор. Oğulcan Tezcan – StudySmarter Originals

Если вы скажете кому-нибудь, что расстояние между точками A и B составляет 5 метров, вы говорите о скалярная величина потому что вы не указываете направление . Пять метров — это всего лишь величина (расстояние), а направление может быть любым. Таким образом, расстояние является скалярной величиной.

Однако, если вы скажете кому-нибудь , что переместили ящик на 5 метров вправо (на восток) , как показано на рисунке 1, вы теперь говорите о векторной величине . Почему? Поскольку у вас есть , теперь указано направление, связанное с движением . А в физике это называется смещение . Следовательно, перемещение является векторной величиной.

Предположим, вам потребовалось 2 секунды, чтобы передвинуть ящик вправо.

Рис. 2. Диаграмма, показывающая вектор смещения относительно времени. Oğulcan Tezcan – StudySmarter Originals

Если бы вам нужно было вычислить, как быстро вы переместили коробку, вы вычислили бы скорость движения . В приведенном выше примере скорость равна:

Скорость=5м2с=2,5 м/с

Скорость является скалярной величиной , так как у него нет никакого направления.

Однако, если вы скажете, что ящик двигался со скоростью 2,5 м/с вправо , это становится векторной величиной . Скорость с направлением — это скорость, , а изменение скорости, в свою очередь, известно как ускорение (м/с ² ), которое также является векторной величиной.

Скаляр	Вектор
Расстояние	Смещение
скорость	скорость и ускорение

Масса и вес: какая из величин скалярная, а какая векторная?

Масса и вес тела могут казаться одинаковыми, но это не так.

Масса: Количественная мера инерции тела , которая представляет собой тенденцию тела сопротивляться силе, которая может вызвать изменение его скорости или положения. Масса имеет единицу СИ килограмм.

Вес: Гравитационное притяжение , действующее на массу. Единицей измерения СИ являются ньютоны.

Скаляр

Масса не имеет никакого направления, и она будет одинаковой, где бы вы ни находились во Вселенной! Таким образом, мы можем классифицировать массу как скалярную величину .

Вектор

Вес, с другой стороны, это сила, действующая на объект, и поскольку сила имеет направление, вес является векторной величиной .

Другой способ посмотреть на это, если вы поместите один объект на Землю, а другой объект с той же массой на Луну. Оба объекта будут иметь одинаковую массу, но разный вес из-за гравитационного притяжения Луны (1,62 м/с ² ), что меньше по сравнению с Землей.

Как мы можем представить векторы?

Мы можем представить векторы стрелкой, как показано ниже.

Рисунок 3. Представление вектора. Wikimedia Commons

Длина отображает величину, хвост — начальную точку вектора, смысл вектора определяется порядком двух точек на линии, параллельной вектору, а ориентация говорит вам, под каким углом вектор указывает. Комбинация ориентации и смысла определяет направление вектора.

Примеры векторов: как мы можем выполнить сложение векторов?

Давайте рассмотрим несколько примеров выполнения сложения векторов.

Допустим, у вас есть два вектора 10 северной широты и 15 северной широты, и оба они указывают на восток. Сумма этих векторов становится 25N на восток.

Рисунок 4. Добавление векторов в одном направлении. Усама Адил — StudySmarter Originals.

Теперь, если мы изменим направление 15 северной широты на запад (-15 северной широты), результирующий вектор становится -5 N (указывая на запад). Векторная величина может иметь положительные и отрицательные знаки . Знак вектора показывает, что направление вектора противоположно опорному направлению (которое произвольно).

Рис. 5. Вычитаются векторы в противоположном направлении. Usama Adeel – StudySmarter Originals

Теперь, конечно, все сложения векторов не так просты, как показано выше. Что бы вы сделали, если бы два вектора были перпендикулярны друг другу? Здесь нам нужно немного импровизировать.

Правило «голова к хвосту»

С помощью этого правила мы можем вычислить результирующий вектор, соединив хвост первого вектора с началом второго вектора . Взгляните на рисунки ниже.

Рис. 6. Перпендикулярные векторы соединяются по правилу «голова к хвосту». Usama Adeel – StudySmarter Originals

Векторная сила 30 Н действует в восточном направлении, а векторная сила 40 Н действует в северном направлении. Мы можем вычислить результирующий вектор, соединив хвост вектора 30N с головой вектора 40N. Вектора перпендикулярны, поэтому мы можем используйте теорему Пифагора для решения результирующего вектора, как показано на рисунке 7.

Рисунок 7. Перпендикулярное сложение вектора. Usama Adeel – StudySmarter Originals

Немного тригонометрии и применения теоремы Пифагора результирующий вектор становится равным 50N. Теперь, как мы обсуждали, векторная величина имеет не только направление, но и величину, поэтому мы можем вычислить угол вектора 50N, используя арктангенс 40/30 (перпендикуляр/основание). Тогда угол составляет 53,1 ° от горизонтали для приведенного выше примера.

Разложение вектора на его компоненты

Используя тот же пример выше, что, если бы у нас была только векторная сила 50 Н с углом от горизонтали, и нас попросили найти ее горизонтальную и вертикальную составляющие?

Разделение одного вектора на два или более векторов, производящих эффект, аналогичный исходному вектору, называется разрешением векторов .

Давайте рассмотрим пример, объясняющий эту концепцию.

Предположим, что вектор силы F в 150 Н приложен под углом 30 градусов к поверхности.

Рис. 8. Вектор под углом. Usama Adeel – StudySmarter Originals

Мы можем разделить вектор F на горизонтальную составляющую (Fx) и вертикальную (Fy) составляющую, как показано ниже:

Рисунок 9. Разрешение векторов. Usama Adeel – StudySmarter Originals

Вычисление Fx и Fy с помощью тригонометрии дает нам:

Fx=Cos(30)·F=129,9N

Fy=Sin(30)·F=75N

Разложение компонентов силы на наклонная плоскость

Как вы, наверное, уже поняли, расчеты в физике никогда не бывают такими простыми! Не каждая поверхность горизонтальна — иногда поверхности могут быть наклонными, и вам придется рассчитывать и разрешать компоненты вдоль наклонной плоскости.

Рисунок 10. Направление веса на наклонной плоскости. Usama Adeel – StudySmarter Originals

На рис. 10 показана коробка на поверхности под углом θ к горизонтали. Вес коробки, mg, действует вниз с массой m и гравитационным притяжением g.

Если мы разделим вектор mg на горизонтальную и вертикальную составляющие,

вертикальная составляющая будет перпендикулярна наклонной поверхности, а
горизонтальная составляющая mg будет параллельна к наклонной поверхности.

Рис. 11. Разрешение вектора мг на наклонной поверхности. Usama Adeel – StudySmarter Originals

Угол θ между mg и mgcosθ будет таким же, как угол наклонной поверхности от горизонтали. Сила, которая разгонит ящик вниз по склону, составит mgsin θ (Fg) , а сила реакции Fn (из третьего закона Ньютона) будет равна mgcos θ . Отсюда

Fg=mgsinθ

Fn=mgcosθ

Рис. 12. Разрешение векторов и направление движения на наклонной плоскости. Usama Adeel – StudySmarter Originals

Равновесие копланарных силовых систем

Если силы действуют на тело, и тело неподвижно или движется с постоянной скоростью (без ускорения), такой случай называется равновесием . Силовые линии должны проходить через одну и ту же точку, чтобы тело находилось в равновесии.

На приведенной ниже диаграмме однородная лестница прислонена к гладкой стене (трение отсутствует). Вес лестницы действует вниз, а нормальная сила реакции действует под углом 90° к стене.

Рис. 13. Лестница, прислоненная к стене, является примером тела, находящегося в равновесии. Usama Adeel — StudySmarter Originals

Если вы расширите эти силы, вы увидите, что они пересекаются в определенной точке. Поскольку объект находится в равновесии, сила от земли также должна проходить через ту же точку, что и другие силы.

Рис. 14. Силовые линии пересекаются в одной точке, если тело находится в равновесии. Usama Adeel – StudySmarter Originals

При разделении силы от земли на ее вертикальную и горизонтальную составляющие, нормальная сила реакции от земли действует вверх, а сила трения от земли действует вдоль поверхности.

Рис. 15. Результирующая векторов трения и грунта.