производная / Дифференцирование векторного произведения / Математика

Есть какие-то четкие правила дифференцирования векторного произведения? Почему $% [\vec{a}\vec{b}]’=\left[\frac{d\vec{a}}{dt},\vec{b}\right]+\left[\vec{a},\frac{d\vec{b}}{dt}\right] $%? Может это как-то выводится? дифференцирование производная векторы задан 20 Авг ’16 10:46 CMTV 35●2●17 77% принятых изменен 20 Авг ’16 10:46

старыеновыеценные

Это можно вывести явно выписав формулы и воспользовавшись формулой производная произведения. .. Или воспользоваться формулой дифференцирования определителей (которая тоже есть следствие производной произведения)… $$ \begin{vmatrix} a_1&a_2\\b_1&b_2 \end{vmatrix}’= (a_1b_2-a_2b_1)’=(a_1’b_2-a_2’b_1)+(a_1b_2′-a_2b_1′)= \begin{vmatrix} a_1’&a_2’\\b_1&b_2 \end{vmatrix}+ \begin{vmatrix} a_1&a_2\\b_1’&b_2′ \end{vmatrix} $$ ссылка отвечен 20 Авг ’16 11:21 all_exist 54.8k●3●13

Ваш ответ

Если вы не нашли ответ, задайте вопрос.

Здравствуйте

Математика — это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.

Присоединяйтесь!

регистрация »

отмечен:

производная ×379

векторы ×243
дифференцирование ×110

задан
20 Авг ’16 10:46

показан
6820 раз

обновлен
20 Авг ’16 11:38

Связанные вопросы

Отслеживать вопрос

по почте:

Зарегистрировавшись, вы сможете подписаться на любые обновления

по RSS:

Ответы

Ответы и Комментарии

Как рассчитать перекрестный продукт в Excel

В этом руководстве объясняется, как рассчитать перекрестный продукт в Excel.

Перекрестное произведение — это математическая операция между двумя векторами, a и b, которая создает новый вектор, перпендикулярный обоим векторам a и b.

Оглавление

1. Реальный пример вычисления векторного произведения в Excel
2. Как вычислить векторное произведение в Excel
3. Часто задаваемые вопросы (FAQ)

Перекрестное произведение обозначается перекрестным знаком «x» между двумя векторами. Результат a×b определяется как вектор c, ортогональный как a, так и b. Ортогональный — это математический термин, связанный с прямыми углами.

Новый вектор будет иметь величину, равную площади параллелограмма, которую охватывают векторы.

Мы также можем интерпретировать векторное перекрестное произведение как три отдельных значения. Все эти компоненты трехмерного вектора (i, j и k) перпендикулярны друг другу.

Перекрестное произведение может быть выражено в матричной записи следующим образом:

Мы можем использовать правило Сарруса, чтобы расширить результат до следующего уравнения: , мы можем создать таблицу, в которой перечислены все коэффициенты.

Мы создадим три разные формулы для вычисления каждого компонента результирующего вектора.

Перекрестное произведение двух векторов эквивалентно значениям, возвращаемым этими тремя формулами.

Теперь, когда мы знаем, когда вычислять векторное произведение в Excel, давайте узнаем, как его использовать и работать с фактическим образцом электронной таблицы.

 

 

Реальный пример вычисления векторного произведения в Excel

В следующем разделе приведены несколько примеров использования этой функции. Мы также подробно расскажем о формулах и инструментах, используемых в этих примерах.

Во-первых, давайте подробнее рассмотрим два наших вектора. Наши два вектора ниже записаны как массивы. Прежде чем мы сможем найти векторное произведение этих двух векторов, нам придется разделить каждый компонент на несколько ячеек.

 

Когда у нас есть таблица каждого компонента вектора, мы можем следовать формуле перекрестного произведения, чтобы определить компоненты конечного вектора.

 

Хотите поближе познакомиться с нашими примерами? Вы можете сделать свою собственную копию таблицы выше, используя ссылку, прикрепленную ниже.

Сделайте копию нашего образца электронной таблицы

Используйте наш образец электронной таблицы, чтобы более подробно изучить формулу каждого компонента. Вы можете увидеть, как изменяется перекрестный продукт, изменив любую из компонент вектора.

Если вы готовы вычислять перекрестные произведения в Excel, перейдите к следующему разделу, чтобы прочитать пошаговую инструкцию, как это сделать!

 

 

Как вычислить векторное произведение в Excel

В этом разделе описаны все шаги, необходимые для начала вычисления векторного произведения в Excel.

Выполните следующие действия, чтобы научиться находить векторное произведение двух векторов в Excel:

1. Сначала создайте таблицу, разделяющую компоненты каждого вектора. В этом примере компоненты векторов a и b помечены буквами «i», «j» и «k».
   
2. Далее мы добавим в нашу электронную таблицу формулу перекрестного произведения каждого компонента. Алгебраическая нотация будет служить руководством для создания реальных формул Excel.
   
3. Мы можем интерпретировать нижний индекс как номер столбца. Например, a2 можно заменить ячейкой D7 , поскольку она относится ко 2-му столбцу в строке «a». Это означает, что мы можем преобразовать «a ₂ b ₃ » в 9.0102 D7 * E8 в нашей формуле.
   
   
4. Используйте тот же метод, что и на предыдущем шаге, чтобы создать вычитаемое.
   
5. Нажмите клавишу Enter , чтобы оценить формулу.
   
6. Преобразование алгебраической формулы второго компонента в формулу Excel, которая ссылается на созданную таблицу.
   
   
7. Затем преобразуйте алгебраическую формулу перекрестного произведения третьего компонента.
   
8. Окончательный вектор векторного произведения эквивалентен трем значениям, возвращаемым нашими формулами.
   
   

Это все шаги, необходимые для вычисления перекрестного произведения в Excel.

 

 

Часто задаваемые вопросы (FAQ)

1. Где можно применить векторное произведение?
   Векторное перекрестное произведение — это математическая концепция, имеющая множество применений. Области, которые полагаются на векторные силы или трехмерные взаимодействия, такие как инженерия, физика и компьютерное программирование, могут использовать перекрестное произведение, чтобы определить, что происходит, когда взаимодействуют две разные силы.
   Операция векторного произведения также используется в вычислительной геометрии для определения расстояния между двумя наклонными линиями. Операция также может определить, компланарны ли два вектора.
2. В чем разница между скалярным произведением и перекрестным произведением?
   Скалярное произведение является скалярной величиной. Это означает, что результат имеет определенную величину, но не имеет определенного направления. Перекрестное произведение дает векторную величину, которая имеет как величину, так и направление.

 

 

Это пошаговое руководство должно предоставить вам всю информацию, необходимую для начала расчета векторного произведения в Excel.

Определение векторного произведения — это лишь один из примеров многих функций Excel, которые вы можете использовать в своих электронных таблицах. Наш веб-сайт предлагает сотни других функций и методов, которые помогут вам получить больше от Microsoft Excel.

Среди множества других доступных функций Excel вы можете найти одну из них, подходящую для вашего случая использования.

Не пропустите новые советы, приемы и рекомендации нашей команды по работе с электронными таблицами. Подпишитесь на нашу рассылку, чтобы быть в курсе последних руководств от нас!

Получайте от нас электронные письма об Excel.

Наша цель в этом году — создать множество содержательных, коротких руководств для таких пользователей Excel, как вы.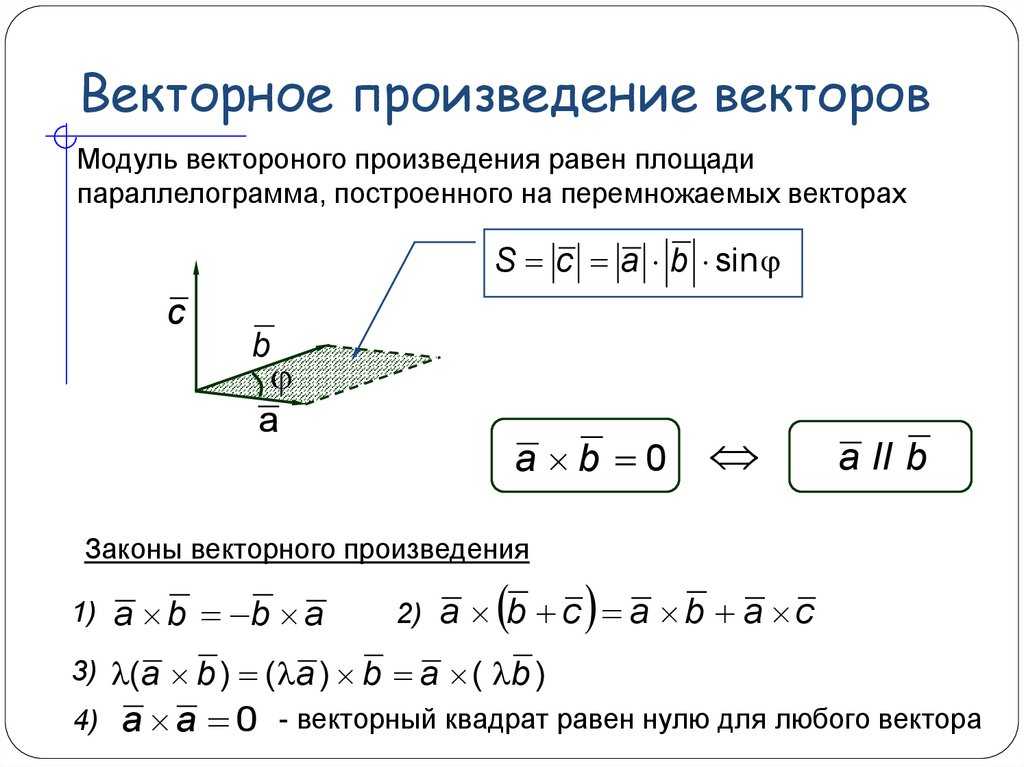

Если вам понравился этот, вам понравится то, над чем мы работаем! Читатели получают ✨ ранний доступ ✨ к новому контенту.

 

Дейон Менор

Привет! Я разработчик программного обеспечения со страстью к анализу данных. Google Таблицы помогли мне расширить возможности моих команд для принятия решений на основе данных. Всегда есть что-то новое, что можно узнать, так что давайте посмотрим, как вы можете сделать жизнь намного проще с помощью электронных таблиц!

Формула перекрестного произведения | Свойства

В этой статье вы узнаете, что такое векторное произведение двух векторов и как оно рассчитывается.

Что такое перекрестный продукт?

В векторном анализе перекрестное произведение — это мультипликативное произведение двух векторов в трехмерном пространстве, результатом которого является вектор, перпендикулярный обоим векторам. Обозначается a×b. Это бинарная операция над двумя векторами.

Перекрестное произведение также является важным ключевым моментом в физике, поскольку оно используется для графического представления двух величин и их направлений.

Формула перекрестного произведения

Перекрестное произведение также известно как векторное произведение, поскольку оно является произведением двух векторов. Если A и B являются двумя независимыми векторами, их формула векторного произведения может быть записана как:

Результирующий вектор будет перпендикулярен обоим векторам A и B.

Так как перекрестное произведение двух векторов дает другой вектор, мы можем записать это:

$$ \vec A ×\vec B \;=\;\vec C $$

Где C обозначает результирующую векторов A и B, а острие стрелки обозначает знак представления вектора.

Как найти кросс-произведение?

Если A и B два вектора, например:

$$ \vec A \;=\; ai + bj + ck \;\;и\;\; \vec В \;=\; ди + едж + фк $$

Перекрестное произведение двух векторов A и B можно рассчитать по следующей формуле.

$$ \vec A ×\vec B \;=\;\vec C $$

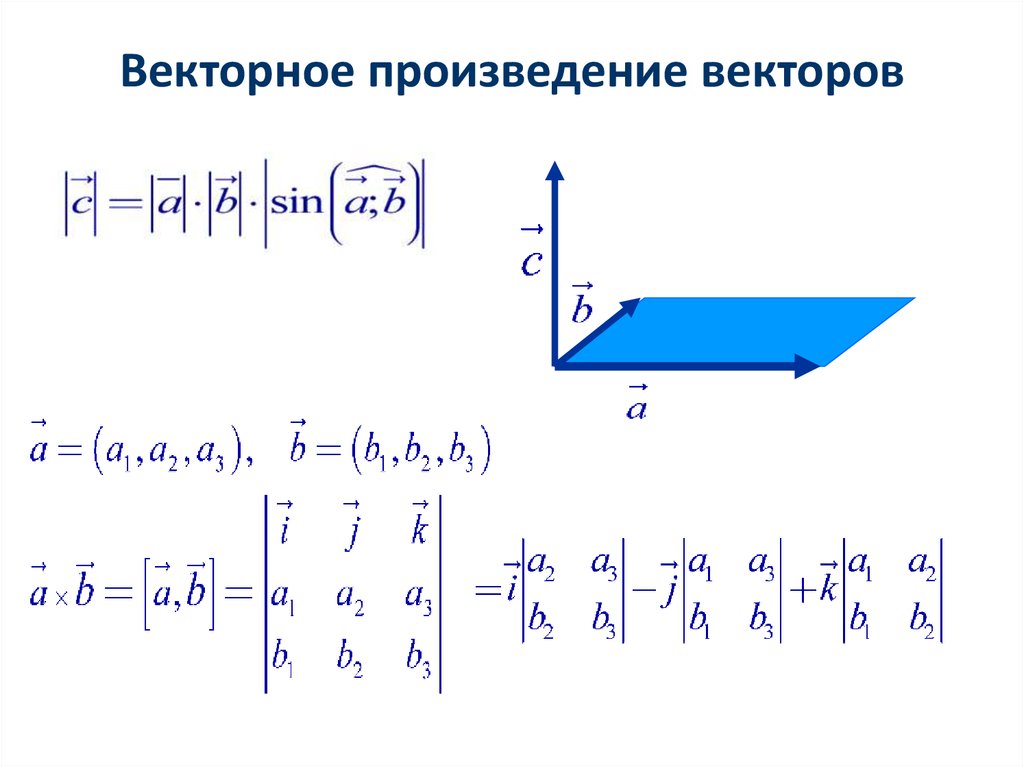
Где результирующий вектор вычисляется с использованием матричной записи.

$$ \vec C \;=\; \begin{vmatrix} i & j & k \\ a & b & c \\ d & e & f \\ \end{vmatrix} $$ $$ \vec C \;=\; i \begin{vmatrix} b & c \\ e & f \\ \end{vmatrix} \;-\; j \begin{vmatrix} a & c \\ d & f \\ \end{vmatrix} \;+\; k \begin{vmatrix} a & b \\ d & e \\ \end{vmatrix} $$

См. приведенный ниже пример, чтобы понять, как вычислить векторное произведение двух векторов.

Свойства векторного произведения

Есть некоторые свойства векторного произведения, на которых оно основано. Это:

1. Антикоммутативность:

   A × B = — B × A

2. Распределительное имущество:

A × B × C = ( A × B ) + ( A × C )

3. Перекрестное произведение нулевого вектора:

А × 0 = 0

4. Перемножение вектора с самим собой:

А × А = 0

Часто задаваемые вопросы

Как найти перекрестный продукт?

Перекрестное произведение двух векторов можно вычислить с помощью правила правой руки, которое выглядит следующим образом:

Возьмите пальцы правой руки таким образом, чтобы два пальца представляли направление двух векторов, а большой палец представлял направление результирующий вектор, который перпендикулярен исходным векторам.