Векторное умножение Википедия
 Векторное произведение в трёхмерном евклидовом пространстве
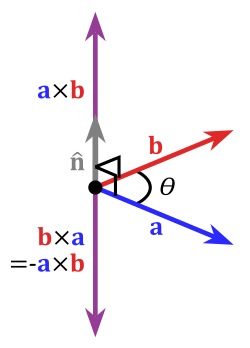
Векторное произведение в трёхмерном евклидовом пространствеВекторное произведение двух векторов в трёхмерном евклидовом пространстве — вектор, перпендикулярный обоим исходным векторам, длина которого равна площади параллелограмма, образованного исходными векторами, а выбор из двух направлений определяется так, чтобы тройка из по порядку стоящих в произведении векторов и получившегося вектора была правой[⇨]. Векторное произведение коллинеарных векторов (в частности, если хотя бы один из множителей — нулевой вектор) считается равным нулевому вектору.
Таким образом, для определения векторного произведения двух векторов необходимо задать ориентацию пространства, то есть сказать, какая тройка векторов является правой, а какая — левой. При этом не является обязательным задание в рассматриваемом пространстве какой-либо системы координат. В частности, при заданной ориентации пространства результат векторного произведения не зависит от того, является ли рассматриваемая система координат правой или левой. При этом формулы выражения координат векторного произведения через координаты исходных векторов в правой и левой ортонормированной прямоугольной системе координат отличаются знаком.
Векторное произведение не обладает свойствами коммутативности и ассоциативности. Оно является антикоммутативным и, в отличие от скалярного произведения векторов, результат является опять вектором.
Полезно для «измерения» перпендикулярности векторов — модуль векторного произведения двух векторов равен произведению их модулей, если они перпендикулярны, и уменьшается до нуля, если векторы коллинеарны.
Широко используется во многих технических и физических приложениях. Например, момент импульса и сила Лоренца математически записываются в виде векторного произведения.
Векторное умножение — это… Что такое Векторное умножение?
Правые и левые тройки векторов
Три вектора называются упорядоченной тройкой, если указано, какой из этих векторов является первым, какой — вторым, а какой — третьим.
Тройка некомпланарных векторов 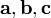 называется правой (левой), если, будучи приведёнными к общему началу, эти векторы располагаются так, как могут быть расположены соответственно большой, несогнутый указательный и средний пальцы правой (левой) руки.
называется правой (левой), если, будучи приведёнными к общему началу, эти векторы располагаются так, как могут быть расположены соответственно большой, несогнутый указательный и средний пальцы правой (левой) руки.
Определение
Векторным произведением вектора 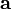 на вектор
на вектор 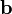 называется вектор
называется вектор 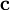 , удовлетворяющий следующим требованиям:
, удовлетворяющий следующим требованиям:
- длина вектора

 и
и  на синус угла
на синус угла  ; между ними
; между ними
Обозначение:
В различных учебных заведениях определение векторного произведения даётся по-разному. Например, в качестве определения даётся описанное далее выражение векторного произведения в координатах. А далее выводится данное выше определение.
Свойства
Геометрические свойства векторного произведения
Алгебраические свойства векторного произведения
Выражение для векторного произведения в декартовых координатах
Если два вектора 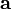 и
и 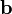 определены своими прямоугольными декартовыми координатами, а говоря точнее — представлены в ортонормированном базисе
определены своими прямоугольными декартовыми координатами, а говоря точнее — представлены в ортонормированном базисе
то их векторное произведение имеет вид
Для запоминания этой формулы удобно использовать определитель:
или
где 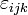 — символ Леви-Чивиты.
— символ Леви-Чивиты.
Обобщения
Кватернионы
Векторное произведение можно также записать в кватернионной форме, поэтому буквы 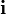 ,
, 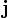 ,
, 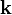 — стандартные обозначения для ортов в
— стандартные обозначения для ортов в 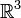 : они рассматриваются как воображаемые кватернионы.
: они рассматриваются как воображаемые кватернионы.
Заметим, что соотношения через векторное произведение между 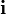 ,
, 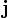 и
и 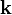 соответствуют правилам умножения для кватернионов i, j и k. Если представить вектор
соответствуют правилам умножения для кватернионов i, j и k. Если представить вектор 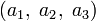 как кватернион a1i + a2j + a3k, то векторное произведение двух векторов получается взятием векторной части от произведения соответствующих им кватернионов. Скалярное произведение этих векторов противоположно скалярной части произведения этих кватернионов.
как кватернион a1i + a2j + a3k, то векторное произведение двух векторов получается взятием векторной части от произведения соответствующих им кватернионов. Скалярное произведение этих векторов противоположно скалярной части произведения этих кватернионов.
Преобразование к матричной форме
Векторное произведение двух векторов можно записать как произведение кососимметрической матрицы и вектора:
где
Пусть 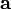 равен векторному произведению:
равен векторному произведению:
тогда
Такая форма записи позволяет обобщить векторное произведение на высшие размерности, представляя псевдовекторы (угловая скорость, индукция и т. п.) как такие кососимметричные матрицы. Ясно, что такие физические величины будут иметь n(n − 1) / 2 независимых компонент в n-мерном пространстве. В трёхмерном пространстве получаются три независимые компоненты, поэтому такие величины можно представлять как векторы этого пространства.
С такой формой записи также зачастую проще работать (например, в en:epipolar geometry).
Из общих свойств векторного произведения следует, что
![[\mathbf{a}]_{\times} \, \mathbf{a} = \mathbf{0}](//rc74.ru/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif) и
и ![\mathbf{a}^{T} \, [\mathbf{a}]_{\times} = \mathbf{0}](//rc74.ru/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif)
а так как ![[\mathbf{a}]_{\times}](/800/600/https/dic.academic.ru/pictures/wiki/files/100/d00b55ad4c7fdd0a1f2a424e0ca572ef.png) кососимметрична, то
кососимметрична, то
В такой форме записи легко доказывается тождество Лагранжа (правило «бац минус цаб»).
Распространение на матрицы
В 3-хмерном случае можно определить векторное произведение матриц и произведение матрицы на вектор. Это делает очевидным указанный выше изоморфизм и позволяет упростить многие выкладки. Представим матрицу A как столбец векторов, тогда
Умножение матрицы на вектор слева определяется аналогично, если представить A как строку векторов. Транспонирование матрицы, соответственно, переводит строку векторов в столбец векторов, и наоборот. Легко обобщить многие соотношения для векторов на соотношения для векторов и матриц, например (A — матрица, 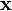 ,
, 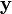 — векторы):
— векторы):
После этого можно изменить форму записи для векторного произведения:
E — единичная матрица. Отсюда очевидны существование и вид матрицы, соответствующей векторному умножению на вектор слева. Аналогично можно получить выражение для матрицы умножения на вектор справа. Распространяя операции над векторами на матрицы покомпонентно, представляя их как «векторы из векторов», стандартные соотношения для векторов легко обобщаются на матрицы. Например, теорема Стокса в 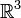 примет вид:
примет вид:
где ротор матрицы A вычисляется как векторное произведение матрицы A на оператор Гамильтона слева. В этих обозначениях очень легко доказать, например, следующие формы теоремы Стокса:
Размерности, не равные трём
Пусть D — размерность пространства.
Векторное произведение, обладающее всеми свойствами обычного трёхмерного векторного произведения, то есть бинарное билинейное антисимметричное невырожденное отображение 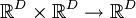 , можно ввести только для размерности 3.
, можно ввести только для размерности 3.
Однако есть простое обобщение на остальные натуральные размерности, начиная с 3, а если нужно — и на размерность 2 (последнее, правда, сравнительно специфическим образом). Тогда это обобщение, в отличие от невозможного, описанного чуть выше, вводится не для пары векторов, а лишь для набора (D − 1) векторов-сомножителей. Вполне аналогично смешанному произведению, естественно обобщаемому в D-мерном пространстве на операцию с D сомножителями. Используя символ Леви-Чивиты 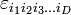 с D индексами, можно явно записать такое (D − 1)-валентное векторное произведение как
с D индексами, можно явно записать такое (D − 1)-валентное векторное произведение как
Такое обобщение дает гиперплощадь размерности (D − 1).
Если нужно ввести операцию именно для двух сомножителей, имеющую геометрический смысл, предельно близкий к смыслу векторного произведения (то есть представляющую ориентированную площадь), то результат уже не будет вектором, так как при D < > 3 не найдется единственной, однозначно определённой нормали к двумерной плоскости, натянутой на множители. Можно ввести бивектор, компоненты которого равны проекциям ориентированной площади параллелограмма, натянутого на пару векторов, на координатные плоскости:
 .
.
Эта конструкция называется внешним произведением.
Для двумерного случая эта операция называется псевдоскалярным произведением, так как получающееся пространство одномерно и результат можно отождествить с псевдоскаляром.
Алгебра Ли векторов
Векторное произведение вводит на 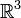 структуру алгебры Ли (поскольку оно удовлетворяет обеим аксиомам — антисимметричности и тождеству Якоби). Эта структура соответствует отождествлению
структуру алгебры Ли (поскольку оно удовлетворяет обеим аксиомам — антисимметричности и тождеству Якоби). Эта структура соответствует отождествлению 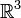 с касательной алгеброй Ли so(3) к группе Ли SO(3) ортогональных линейных преобразований трёхмерного пространства.
с касательной алгеброй Ли so(3) к группе Ли SO(3) ортогональных линейных преобразований трёхмерного пространства.
См. также
Произведения векторов
Другое
Ссылки
Литература
- Кочин Н. Е. Введение в векторный и тензорный анализ.
Wikimedia Foundation. 2010.
векторное умножение — со всех языков на русский
См. также в других словарях:
Векторное умножение — Содержание 1 Правые и левые тройки векторов 2 Определение 3 Свойства … Википедия
Векторное произведение — в трёхмерном пространстве. Векторное произведение это псевдовектор, перпендикулярный плоскости, построенной по двум … Википедия
Векторное произведение векторов — Содержание 1 Правые и левые тройки векторов 2 Определение 3 Свойства … Википедия
Векторное пространство — У этого термина существуют и другие значения, см. Пространство. Векторное (линейное) пространство основной объект изучения линейной алгебры. Содержание 1 Определение 2 Простейшие свойства … Википедия
ВЕКТОРНОЕ ИСЧИСЛЕНИЕ — устаревшее название раздела математики, в к ром изучаются свойства операций над векторами. В. и. подразделяют на векторную алгебру п векторный анализ. В векторной алгебре изучают линейные операции (сложение векторов и умножение векторов на число) … Математическая энциклопедия
Векторное исчисление — Векторное исчисление раздел математики, в котором изучаются свойства операций над векторами[1]. В связи с разнообразием особенностей векторов, зависящих от пространства, в котором они исследуются, векторный анализ подразделяется на… … Википедия
Умножение двухэлементного тензора — Тензорное произведение одно из основных понятий линейной алгебры. Содержание 1 Тензорное произведение модулей 2 Свойства … Википедия
ВЕКТОРНОЕ ПРОСТРАНСТВО — линейное пространство, над полем К, аддитивно записанная абелева группа Е, в которой определено умножение элементов на скаляры, т. е. отображение удовлетворяющее следующим аксиомам Из аксиом 1) 4) вытекают следующие важные свойства векторного… … Математическая энциклопедия
Нормированное векторное пространство — У этого термина существуют и другие значения, см. Пространство. В нашем пространстве понятие «длина вектора» понимается интуитивно как расстояние между его началом и концом. Наиболее важными свойствами «длины вектора» являются следующие: Длина… … Википедия
Позиционные коды векторов — Содержание 1 Специальная алгебра многомерных векторов[1] 1.1 Специальное умножение … Википедия
Ротор (математика) — У этого термина существуют и другие значения, см. Ротор. Ротор, или вихрь векторный дифференциальный оператор над векторным полем. Обозначается (в русскоязычной[1] литературе) или (в англоязычной литературе), а также как векторное умножение … Википедия
векторное умножение — с английского на русский
См. также в других словарях:
Векторное умножение — Содержание 1 Правые и левые тройки векторов 2 Определение 3 Свойства … Википедия
Векторное произведение — в трёхмерном пространстве. Векторное произведение это псевдовектор, перпендикулярный плоскости, построенной по двум … Википедия
Векторное произведение векторов — Содержание 1 Правые и левые тройки векторов 2 Определение 3 Свойства … Википедия
Векторное пространство — У этого термина существуют и другие значения, см. Пространство. Векторное (линейное) пространство основной объект изучения линейной алгебры. Содержание 1 Определение 2 Простейшие свойства … Википедия
ВЕКТОРНОЕ ИСЧИСЛЕНИЕ — устаревшее название раздела математики, в к ром изучаются свойства операций над векторами. В. и. подразделяют на векторную алгебру п векторный анализ. В векторной алгебре изучают линейные операции (сложение векторов и умножение векторов на число) … Математическая энциклопедия
Векторное исчисление — Векторное исчисление раздел математики, в котором изучаются свойства операций над векторами[1]. В связи с разнообразием особенностей векторов, зависящих от пространства, в котором они исследуются, векторный анализ подразделяется на… … Википедия
Умножение двухэлементного тензора — Тензорное произведение одно из основных понятий линейной алгебры. Содержание 1 Тензорное произведение модулей 2 Свойства … Википедия
ВЕКТОРНОЕ ПРОСТРАНСТВО — линейное пространство, над полем К, аддитивно записанная абелева группа Е, в которой определено умножение элементов на скаляры, т. е. отображение удовлетворяющее следующим аксиомам Из аксиом 1) 4) вытекают следующие важные свойства векторного… … Математическая энциклопедия
Нормированное векторное пространство — У этого термина существуют и другие значения, см. Пространство. В нашем пространстве понятие «длина вектора» понимается интуитивно как расстояние между его началом и концом. Наиболее важными свойствами «длины вектора» являются следующие: Длина… … Википедия
Позиционные коды векторов — Содержание 1 Специальная алгебра многомерных векторов[1] 1.1 Специальное умножение … Википедия
Ротор (математика) — У этого термина существуют и другие значения, см. Ротор. Ротор, или вихрь векторный дифференциальный оператор над векторным полем. Обозначается (в русскоязычной[1] литературе) или (в англоязычной литературе), а также как векторное умножение … Википедия
векторное умножение — с русского на английский
См. также в других словарях:
Векторное умножение — Содержание 1 Правые и левые тройки векторов 2 Определение 3 Свойства … Википедия
Векторное произведение — в трёхмерном пространстве. Векторное произведение это псевдовектор, перпендикулярный плоскости, построенной по двум … Википедия
Векторное произведение векторов — Содержание 1 Правые и левые тройки векторов 2 Определение 3 Свойства … Википедия
Векторное пространство — У этого термина существуют и другие значения, см. Пространство. Векторное (линейное) пространство основной объект изучения линейной алгебры. Содержание 1 Определение 2 Простейшие свойства … Википедия
ВЕКТОРНОЕ ИСЧИСЛЕНИЕ — устаревшее название раздела математики, в к ром изучаются свойства операций над векторами. В. и. подразделяют на векторную алгебру п векторный анализ. В векторной алгебре изучают линейные операции (сложение векторов и умножение векторов на число) … Математическая энциклопедия
Векторное исчисление — Векторное исчисление раздел математики, в котором изучаются свойства операций над векторами[1]. В связи с разнообразием особенностей векторов, зависящих от пространства, в котором они исследуются, векторный анализ подразделяется на… … Википедия
Умножение двухэлементного тензора — Тензорное произведение одно из основных понятий линейной алгебры. Содержание 1 Тензорное произведение модулей 2 Свойства … Википедия
ВЕКТОРНОЕ ПРОСТРАНСТВО — линейное пространство, над полем К, аддитивно записанная абелева группа Е, в которой определено умножение элементов на скаляры, т. е. отображение удовлетворяющее следующим аксиомам Из аксиом 1) 4) вытекают следующие важные свойства векторного… … Математическая энциклопедия
Нормированное векторное пространство — У этого термина существуют и другие значения, см. Пространство. В нашем пространстве понятие «длина вектора» понимается интуитивно как расстояние между его началом и концом. Наиболее важными свойствами «длины вектора» являются следующие: Длина… … Википедия
Позиционные коды векторов — Содержание 1 Специальная алгебра многомерных векторов[1] 1.1 Специальное умножение … Википедия
Ротор (математика) — У этого термина существуют и другие значения, см. Ротор. Ротор, или вихрь векторный дифференциальный оператор над векторным полем. Обозначается (в русскоязычной[1] литературе) или (в англоязычной литературе), а также как векторное умножение … Википедия
векторное умножение — с русского на все языки
См. также в других словарях:
Векторное умножение — Содержание 1 Правые и левые тройки векторов 2 Определение 3 Свойства … Википедия
Векторное произведение
Векторное произведение векторов — Содержание 1 Правые и левые тройки векторов 2 Определение 3 Свойства … Википедия
Векторное пространство — У этого термина существуют и другие значения, см. Пространство. Векторное (линейное) пространство основной объект изучения линейной алгебры. Содержание 1 Определение 2 Простейшие свойства … Википедия
ВЕКТОРНОЕ ИСЧИСЛЕНИЕ — устаревшее название раздела математики, в к ром изучаются свойства операций над векторами. В. и. подразделяют на векторную алгебру п векторный анализ. В векторной алгебре изучают линейные операции (сложение векторов и умножение векторов на число) … Математическая энциклопедия
Векторное исчисление — Векторное исчисление раздел математики, в котором изучаются свойства операций над векторами[1]. В связи с разнообразием особенностей векторов, зависящих от пространства, в котором они исследуются, векторный анализ подразделяется на… … Википедия
Умножение двухэлементного тензора — Тензорное произведение одно из основных понятий линейной алгебры. Содержание 1 Тензорное произведение модулей 2 Свойства … Википедия
ВЕКТОРНОЕ ПРОСТРАНСТВО
Нормированное векторное пространство — У этого термина существуют и другие значения, см. Пространство. В нашем пространстве понятие «длина вектора» понимается интуитивно как расстояние между его началом и концом. Наиболее важными свойствами «длины вектора» являются следующие: Длина… … Википедия
Позиционные коды векторов — Содержание 1 Специальная алгебра многомерных векторов[1] 1.1 Специальное умножение … Википедия
Ротор (математика) — У этого термина существуют и другие значения, см. Ротор. Ротор, или вихрь векторный дифференциальный оператор над векторным полем. Обозначается (в русскоязычной[1] литературе) или (в англоязычной литературе), а также как векторное умножение … Википедия
Векторное произведение
Векторное произведениеВ. Г. Автор. Векторная и тензорная алгебра для будущих физиков и техников
Суперобложка / Обложка / Содержание
..Векторное произведение векторов
Мы уже знаем несколько операций, которые можно выполнять с векторами: векторы можно складывать, умножать на число, умножать друг на друга скалярно.
Каждое новое понятие в любой науке возникает в силу необходимости отразить некоторый новый элемент наших знаний. Создание новых элементов языка – это процесс творческий. Если бы это было не так, на Земле не было бы столько национальных языков. И на всех существующих языках легко и свободно может быть выражена вся та информация, которая на сегодняшний день является достоянием всего . Однако иногда бывает, что какое-то открытие, новое явление или просто принципиально новую идею невозможно объяснить – не хватает слов. Если открытие, явление или идея действительно важны, то через какое-то время язык с этими проблемами обязательно справляется. Если нам есть, что сказать, то необходимые для этого языковые возможности обязательно появятся. Но никому не приходит в голову побеспокоиться об этом заранее. Никогда не ставилась цель изобрести язык, на котором можно было бы не только правильно и непротиворечиво отразить все то, что мы знаем, но и то, что мы когда-либо сможем узнать. Мало того, что это невозможно, но это еще и неудобно. Языком, который обременен всеми будущими проблемами, которые к тому же могут и не возникнуть, никто не захочет пользоваться. Он обречен на забвение.
Абсолютно все то же самое можно сказать и о научном языке, который является расширением языка естественного. Любая новая информация обязательно находит средства для своего выражения на языке той или иной науки. Не является исключением и язык математики. С одной стороны, он является результатом творчества многих ученых. С другой стороны, каждое новое понятие в математике, обязательно связано с необходимостью правильно отобразить наше сегодняшнее понимание природы и ее законов.
Математика – это наука о наиболее общих, а следовательно, и наиболее абстрактных, законах природы, и именно для выражения этих законов и конструируется ее язык. Другими словами, сначала – новые знания и новые идеи, и только потом – новый язык. При изучении же математики мы вынуждены почти всегда идти в обратном направлении: сначала – определения новых понятий, затем – теоремы и их следствия, и только после этого – приложения (и то, только если на это остается время). В результате, иногда складывается неверное представление о том, что математика развивается совершенно независимо от всего остального естествознания. Можно даже услышать мнение, будто бы
«математика является блестящим примером чистого разума, удачно расширяющегося самопроизвольно, без применения опыта».
Мы не собираемся вступать здесь в полемику по этому вопросу. Проблема эта бесконечная. Мы хотим только выразить нашу точку зрения, которая заключается в том, что все, что мы можем сказать на любом языке, так или иначе связано с природой, и если кто-то сможет сказать что-то сверх того, то вряд ли он сам поймет, что он такое сказал. И раз мы до сих пор понимаем, о чем мы говорим, следовательно, мы говорим о природе или, по крайней мере, о языке, на котором можно что-либо полезное о ней сказать.
До сих пор у нас не было повода для разговора об отношении математики к опыту. В дальнейшем же мы не намерены больше к этому возвращаться, поскольку это непростой самостоятельный вопрос. То, что мы решили сказать хотя бы несколько слов об этом сейчас, связано с векторным умножением. Векторное умножение – это первое понятие векторной алгебры, необходимость введения которого трудно осознать, не выходя за рамки математической теории. Это понятие своими корнями уходит в естествознание и, прежде всего, в механику. У нас же нет возможности об этом говорить. Мы вынуждены ввести это понятие каким-то другим способом, который ничего общего не имеет с действительными причинами его возникновения. Конечно, мы постараемся, чтобы это понятие не возникло, как кролик из шляпы фокусника. Но, как это ни парадоксально, для лучшего понимания математики необходимо изучать ее историю и, конечно, естествознание, хотя это отдельная тема и, соответственно, другие книги.
Итак, векторное умножение. Еще одно. Мы уже знаем два вида умножения, которые можно выполнять с векторами.
Можно вектор умножить на число, и при этом мы снова получим вектор. При скалярном умножении перемножаются два вектора, а в результате мы получаем число. Векторное умножение – это чисто векторная операция: перемножаются два вектора, и в результате снова получается вектор.
Операция векторного умножения в скрытой или, как говорят, в латентной форме уже содержится в понятии ориентированного объема. Покажем, как ее можно извлечь оттуда на свет божий.
Начнем с формулы для ориентированного объема, которую мы получили в предыдущем разделе.
Формально используя правило скалярного умножения векторов в декартовой системе координат, мы можем продолжить:
Следовательно:
.
Мы получили, что с формальной точки зрения ориентированный объем равен скалярному произведению вектора на некоторый вектор, который в свою очередь определяется векторами и . Этот формальный вектор и называется векторным произведением векторов и и обозначается .
Следовательно, векторным произведением векторов и называется вектор
.
Вот он уже и появился, хотя и не в той форме, в которой он традиционно записывается – поэтому продолжим преобразования.
Раскладывая каждый из определителей по первому столбцу, мы можем упростить выражение:
.
В таком виде оно выглядит менее громоздко, зато труднее запоминается. Можно еще упростить выражение, если заметить, что формально оно представляет собой результат разложения определителя третьего порядка по первому столбцу.
, следовательно, совсем коротко можно записать:
.
Алгебраическое определение векторного умножения в декартовой системе координат
Определение (26)
|
Выражение и его краткая форма могут быть приняты за определение для векторного умножения в декартовой системе координат. |
В дальнейшем мы получим выражение для векторного умножения в произвольных косоугольных координатах. Но даже если придерживаться только ортонормированных систем, можно заметить особенность данного вектора. Если мы поменяем местами два любых вектора базиса, скажем i и j , векторное произведение изменит направление на противоположное.
В самом деле,
, где
– векторное произведение в базисе {ijk}, а
– векторное произведение в базисе {jik}.
То есть .
Но если придерживаться только правых декартовых систем координат, то векторное произведение определяется однозначно.
С использованием векторного умножения формула для ориентированного объема приобретает следующий вид:
.
Выражение в векторной алгебре называется смешанным умножением векторов, и оно, следовательно, равно:
.
Смешанное произведение равно ориентированному объему. Отсюда вытекают и все его свойства.
Свойства смешанного умножения векторов
1. Знаки скалярного и векторного умножения можно менять местами
.
2. При перестановке любых двух сомножителей смешанное произведение изменяет знак на противоположный.
3. Смешанное произведение векторов равно нулю тогда и только тогда, когда эти векторы компланарны.
4. Если смешанное произведение векторов больше нуля, то векторы образуют правую тройку векторов.
Для смешанного произведения часто вводится специальное обозначение, например, [10, с. 110] или [12, с. 65]. Однако, нам кажется, что более удачным обозначением, если оно вообще необходимо, является следующее: . По крайней мере, оно вполне логично вытекает из связи смешанного произведения, ориентированного объема и его выражения через определитель.
Поскольку со смешанным произведением все более или менее ясно, вернемся к векторному умножению.
До сих пор мы придерживались геометрической теории векторов. Геометрический вектор для нас был первичным понятием. Вводя в векторном пространстве тот или иной базис, мы могли выразить вектор через его координаты. Этот шаг часто является удобным, но до сих пор никогда не был обязательным. Принятое нами определение непосредственно исходит из координатного представления векторов. Здесь возникает важный вопрос: является ли наше определение инвариантным по отношению к произвольному выбору координатной системы? А что если мы в качестве базисных выберем другие векторы; получим ли мы в результате векторного умножения тот же самый вектор? На эти вопросы мы сразу даем отрицательный ответ. Наше определение справедливо только для декартовых систем координат. Для любых других систем оно не годится. Для того чтобы прийти к более универсальному определению, выясним геометрический смысл, содержащийся в том, которое у нас есть.
Рис. 37Во-первых, из того, что
и, аналогично: – откуда следует, что векторное произведение ортогонально к вектору и к вектору . Следовательно, оно ортогонально плоскости параллелограмма, построенного на этих векторах (рис. 37).
Во-вторых, ,
где h – высота параллелепипеда.
С другой стороны:
,
где , как обычно, – площадь параллелограмма, построенного на векторах и . Следовательно, модуль векторного произведения равен площади параллелограмма, построенного на этих векторах. А сам вектор направлен вдоль прямой n–n, перпендикулярной плоскости параллелограмма. Но мы пока еще не знаем, в какую сторону вдоль этой прямой он направлен.
Если векторы , и образуют правую тройку, то
.
А если векторы , и образуют левую тройку, то
.
Но это возможно только, если векторы , и образуют правую тройку.
Теперь мы готовы дать геометрическое определение векторного умножения.
Геометрическое определение векторного произведения (27)
Расшифровывая данное определение, мы можем выразить площадь параллелограмма через его стороны и угол (рис. 37). В этом случае пункт два определения будет звучать так:
2(а). Модуль векторного произведения равен произведению модулей векторов на синус угла между ними .
Данное определение является чисто геометрическим и не зависит от произвола в выборе систем координат. Но и у него есть слабое место. В самом деле, что означает понятие «правая тройка векторов» на языке математики? Правую тройку от левой мы можем отличить только благодаря тому, что по неизвестной на сегодняшний день причине правшей на Земле больше, чем левшей. Не существует математических средств для того, чтобы одну из систем координат идентифицировать, как правую. Не существует таких средств и в классической физике. Такие средства появляются только в технике, поскольку правши наточили больше правых винтов, чем левши левых.
Поэтому для векторного произведения имеется альтернативное определение.
Альтернативное определение векторного умножения (28)
До тех пор пока мы в качестве базиса выбираем только правые тройки векторов, оба определения приводят к одному и тому же результату. Но стоит только перейти к левому базису, и вектор, построенный в соответствии с альтернативным определением, поменяет направление на противоположное. Такие векторы называются относительными, псевдовекторами или аксиальными векторами, в отличие от обычных (полярных) векторов. Единственное преимущество такого определения – полная эквивалентность его алгебраическому определению, что удобно при выполнении алгебраических преобразований в координатной форме. Можно не заботиться о том левая или правая тройка векторов выбрана в качестве базиса – алгебраическое выражение для векторного произведения от этого не зависит. Единственное беспокойство вызывает вопрос: существует ли такая геометрическая и физическая реальность, для описания которой могут быть использованы псевдовекторы? Очень даже существует. Например, для задания свойств вращательного движения можно использовать вектор. Для этого его достаточно совместить с осью вращения и величину скорости связать в его модулем. А вот каким образом связать два возможных направления его вдоль оси с двумя возможными направлениями вращения вокруг этой оси – это все равно. А раз все равно, то вполне можно использовать для этих целей аксиальные векторы. По крайней мере, они правильно отражают то свойство подобных процессов, что направление вектора вдоль выбранной оси не имеет физического или геометрического смысла и выбирается по соглашению.
В математике примерно одинаково часто используются оба определения. Мы будем в дальнейшем придерживаться второго.
Свойства векторного умножения
Все свойства проще всего выводятся из первого его алгебраического определения.
1. Векторное произведение векторов и равно нулю тогда и только тогда, когда векторы и коллинеарны.
В самом деле, если
, то и все определители равны нулю, и, следовательно, столбцы пропорциональны:
; ; .
Отсюда следует, что
, что и означает коллинеарность векторов.
Обратное утверждение автоматически следует из пропорциональности координат коллинеарных векторов.
2. При изменении порядка сомножителей векторное произведение изменяет знак на противоположный. В отношении этого свойства говорят, что векторное произведение антикоммутативно.
.
3. Векторное умножение ассоциативно относительно числового множителя.
, где λ произвольное действительное число.
4. Векторное умножение дистрибутивно относительно сложения векторов.
.
Докажем последнее свойство.
Из свойств определителей сразу вытекает, что
.
..Векторное умножение векторов базиса декартовой системы координат
При выполнении алгебраических операций полезно иметь таблицу умножения для базисных векторов декартовой системы координат, аналогичную той, которую мы в свое время получили для скалярного умножения.
Из свойств векторного умножения сразу следует, что
, далее ,
и, аналогично,
, .
Разберемся с направлениями векторов.
Вектор ортогонален к каждому из векторов i и j, следовательно, он направлен по оси z. Поскольку он должен составлять с этими векторами правую тройку, он должен быть направлен в положительном направлении оси z. Отсюда следует, что
, и, аналогично,
;
.
Составим таблицу умножения, учитывая при этом, что при изменении порядка сомножителей, знак произведения изменяется на противоположный.
|
× |
i |
j |
k |
|
i |
0 |
k |
-j |
|
j |
-k |
0 |
i |
|
k |
j |
-i |
0 |
Для запоминания таблицы умножения удобно пользоваться правилом циклической подстановки или «правилом треугольника» (рис. 38).
Рис. 38Обход треугольника, в вершинах которого изображены векторы базиса, можно производить, начиная с любой вершины. При этом, если обход совершается против часовой стрелки, то произведение вектора, с которого начинается обход, на вектор следующий за ним, равно третьему вектору. Если же обход совершается по часовой стрелке, то результирующий вектор следует умножить на 1.
Умножим два вектора друг на друга, используя правила перемножения базисных векторов. Для этого разложим векторы по векторам базиса и используем свойства векторного умножения.
.
Результат вполне ожидаемый и, тем более приятный.
|
Д |
остоинство алгебры в том, что она работает подобно хорошо отлаженному механизму, который достаточно только слегка подтолкнуть, а дальше он все сделает сам. |


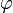 ; между ними
; между ними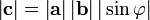
![\mathbf c = \left[ \mathbf a \mathbf b \right] = \left[ \mathbf a,\; \mathbf b \right] = \mathbf a \times \mathbf b](/800/600/https/dic.academic.ru/pictures/wiki/files/101/ed09d9154faf68b1a7783004b4cbc46c.png)
![[ \mathbf a,\; \mathbf b ] = S\, \mathbf e](/800/600/https/dic.academic.ru/pictures/wiki/files/50/28395f1def81662c027a8cbd7f6f8aa9.png)
![\left[ \mathbf a,\; \mathbf c \right] = \mathrm{Pr}_{ \mathbf e }\, \mathbf a \left](/800/600/https/dic.academic.ru/pictures/wiki/files/48/04002beabcb294e180266aa94180d9b9.png)
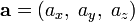
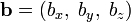
![[ \mathbf a,\; \mathbf b ] = (a_y b_z - a_z b_y,\; a_z b_x - a_x b_z,\; a_x b_y - a_y b_x).](/800/600/https/dic.academic.ru/pictures/wiki/files/52/4c3df91a2cfe53408b07f333a175565a.png)
![[ \mathbf a,\; \mathbf b ] = \begin{vmatrix} \mathbf i &amp; \mathbf j &amp; \mathbf k \\ a_x &amp; a_y &amp; a_z \\ b_x &amp; b_y &amp; b_z \end{vmatrix}](/800/600/https/dic.academic.ru/pictures/wiki/files/49/16ea255c911b3e4c07cc2adae3d7626e.png)
![[ \mathbf a,\; \mathbf b ]_i = \sum_{j,k=1}^3 \varepsilon_{i j k} a_j b_k,](/800/600/https/dic.academic.ru/pictures/wiki/files/55/7c8e6ab7e9c7e3607e920bb75caae299.png)
![\mathbf{a} \times \mathbf{b} = [\mathbf{a}]_{\times} \mathbf{b} = \begin{bmatrix}\,0&amp;\!-a_3&amp;\,\,a_2\\ \,\,a_3&amp;0&amp;\!-a_1\\-a_2&amp;\,\,a_1&amp;\,0\end{bmatrix}\begin{bmatrix}b_1\\b_2\\b_3\end{bmatrix}](/800/600/https/dic.academic.ru/pictures/wiki/files/98/bb0828317b64e54d924e3d9dabb54234.png)
![\mathbf{b} \times \mathbf{a} = \mathbf{b}^T [\mathbf{a}]_{\times} = \begin{bmatrix}b_1&amp;b_2&amp;b_3\end{bmatrix}\begin{bmatrix}\,0&amp;\!-a_3&amp;\,\,\,a_2\\\,\,\,a_3&amp;\,0&amp;\!-a_1\\-a_2&amp;\,\,a_1&amp;\,0\end{bmatrix}](/800/600/https/dic.academic.ru/pictures/wiki/files/97/a1999aed4c7add8bb1d9f291beb9a7e9.png)
![[\mathbf{a}]_{\times} \stackrel{\rm def}{=} \begin{bmatrix}\,\,0&amp;\!-a_3&amp;\,\,\,a_2\\\,\,\,a_3&amp;0&amp;\!-a_1\\\!-a_2&amp;\,\,a_1&amp;\,\,0\end{bmatrix}](/800/600/https/dic.academic.ru/pictures/wiki/files/52/42367ea2bfc38aaf3870e9a3aba428bb.png)
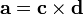
![[\mathbf{a}]_{\times} = (\mathbf{c}\mathbf{d}^T)^T - \mathbf{c}\mathbf{d}^T.](/800/600/https/dic.academic.ru/pictures/wiki/files/53/55d46afc14c256de89aa56b17ef38491.png)
![[\mathbf{a}]_{\times} \, \mathbf{a} = \mathbf{0}](/800/600/https/dic.academic.ru/pictures/wiki/files/98/b00e919750be3b08a60e4757f3cf9cf9.png) и
и ![\mathbf{a}^{T} \, [\mathbf{a}]_{\times} = \mathbf{0}](/800/600/https/dic.academic.ru/pictures/wiki/files/55/762d1d364c16664eff7d042f99842e70.png)
![\mathbf{b}^{T} \, [\mathbf{a}]_{\times} \, \mathbf{b} = 0.](/800/600/https/dic.academic.ru/pictures/wiki/files/98/b0e7a57333b3ebbdf3c81c827152e5fa.png)
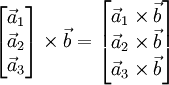
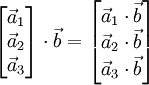
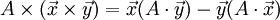
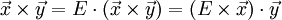
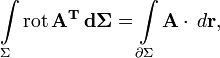
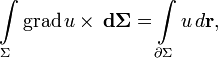
![\int\limits_{\Sigma} \left[ \mathbf{d\Sigma}; \left[ \nabla; \vec a \right] \right] = \int\limits_{\partial\Sigma} \vec a \times d \mathbf{r}.](/800/600/https/dic.academic.ru/pictures/wiki/files/53/552f7432c2a90d787f641f23287017c2.png)
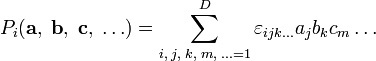
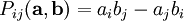 .
.