Что такое векторное умножение, матричное произведение (умножение), внутреннее произведение, скалярное произведение, реализация кода Python, разность и связь
Table of Contents
предисловие
вектор
определение
Связь с матрицей
Умножение вектора
матрица
определение
Матрица продукта работы
Код Python
Отличия и связи
Примеры
подводить итоги
Ключевые отличия
Связь между точечным произведением и умножением матриц
Смотреть»Цветочная книга«Обнаружил такое предложение в процессе
Точечное произведение двух векторов x и y одного измерения можно рассматривать как матричное произведение x⊤y.
Разумеется, говоря о умножении матриц, как же снова прийти к точечному произведению? И векторы …
Я научился невежеству раньше. Для глубокого изучения я тщательно нашел информацию для написания этого блога и передал ее своим друзьям в той же ситуации, что и я.
PS:“Цветочная книга«За книгу А.И. Библия»Глубокое обучение
определение
Вектор представляет собой столбец чисел.
Пример: вектор
Связь с матрицей
Вектор можно рассматривать как матрицу с одним столбцом
Транспонирование векторов можно рассматривать как матрицу с одной строкой
Транспонировать вектора х:
Умножение вектора
У векторов много операций, в этой статье рассказывается только о умножении векторов.
Количественный продукт (также называемый внутренним продуктом, точечный продукт; скалярный продукт)
Предположим, что в двумерном пространстве есть два вектора с участием Определите их количественный продукт (также называемый внутренним продуктом и точечным продуктом) как следующие действительные числа:
В более общем смысле, внутреннее произведение n-мерного вектора определяется следующим образом:
ссылкаBaidu энциклопедия
определение
Матрица представляет собой двумерный массив
Матрица продукта работы
Матрица имеет много операций, в этой статье рассказывается только о работе матричного продукта.
ПредполагатьAДляМатрица,BДляМатрица, то называетсяматрицаCматрицаAпротивBПродукт ,
Где матрица СЛинияЭлементы столбца могут быть выражены как:
Предпосылки для умножения матриц:
Форма матрицы А, Форма матрицы B, Форма С
Есть две матрицы A, B следующим образом:
Размер матрицы A равен 3×2, а размер матрицы B равен 2×3, тогда матрица C умножения A и B должна быть 3×3, где m = 3, p = 2, n = 3.
В соответствии с формулой
Элементы матрицы C следующие
То есть матрица С представляет собой матрицу 3х3
Код PythonНапишите простой метод матричного произведения с помощью np.dot (A, B, C)Результат тот же. для справки.
Недостаток следующего метода состоит в том, что невозможно вычислить матрицу больших чисел, например, размер A равен 1000 * 10000, а размер B равен 10000 * 10000.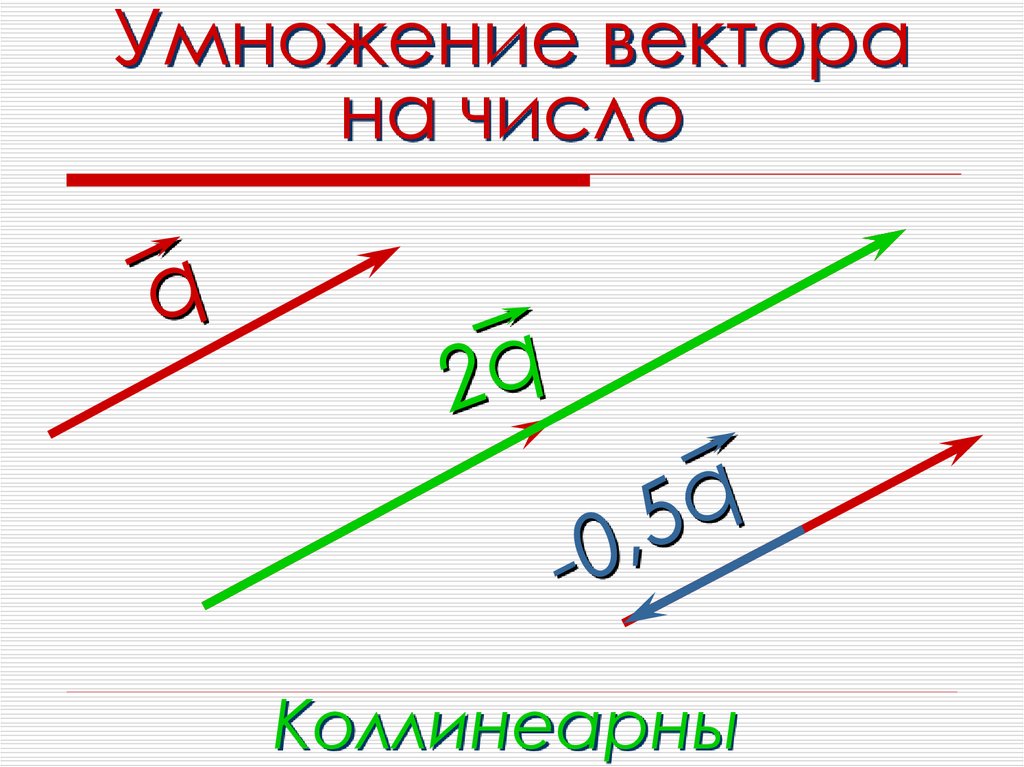
np.dot (A, B, C) не может выполнять матричные вычисления таких больших чисел.
Если у вас есть лучший способ, пожалуйста, оставьте сообщение.
#! /usr/bin/env python
# -*- coding: utf-8 -*-
import numpy as np
def dot(A, B):
row = A.shape[0]
column = B.shape[1]
p = A.shape[1]
if A.shape[1] != B.shape[0]:
return
# Создайте матрицу C с размерной строкой * столбца и все ее значения равны нулю
C = np.zeros((row, column), dtype=A.dtype)
print("A.shape, B.shape, C.shape:", A.shape, B.shape, C.shape)
# Рассчитать результат умножения матриц
for i in range(row):
for j in range(column):
for k in range(p):
C[i, j] += A[i, k] * B[k, j]
return C
if __name__ == '__main__':
A = np.arange(3, 9).reshape(2, 3)
B = np.arange(1, 7).reshape(3, 2)
C = np.zeros((2, 2), dtype=int)
print("matrix A:\n", A)
print("matrix B:\n",B)
np.dot(A, B, C)
print("np.
dot C:\n", C)
c = dot(A, B)
print("my dot C:\n", c)
assert C.any() == c.any()
assert C.all() == c.all()Точечное произведение двух векторов x и y одного измерения можно рассматривать как матричное произведение x⊤y.
Примеры
Если взять в качестве примера двумерный вектор, это относительно просто и легко понять. Если вы понимаете это в двух измерениях, вы можете расширить, чтобы понять больше измерений.
Предположим, что двумерные векторы x и y соответственно
Точечное произведение х и у выглядит следующим образом
Запишите их в матричной форме следующим образом
Матрица х транспонируется в, Размерность равна 1×2, размерность матрицы y равна 2×1, две матрицы умножаются, и матрица 1×1 получается в соответствии с формулой следующим образом
Постучал по доске!
Ключевые отличия
Точечное произведение двух векторов равноНастоящий номер(То есть скаляр)
Результатом умножения двух матриц является одинматрица
Ключевой момент: «Может быть видно» в оригинальных словах в книге не означает, что
Связь между точечным произведением и умножением матриц
Вы можете умножить матрицуC = ABвДумайте об этом как о точечном произведении между i-й строкой матрицы A и j-м столбцом матрицы B.
cross | NumPy
numpy.cross(a, b, axisa=-1, axisb=-1, axisc=-1, axis=None)
Функция cross() вычисляет векторное произведение двух векторов a и b в трехмерном пространстве. Так как речь идет о трехмерном пространстве, то векторы a и b, должны содержать три компоненты: x, y, z. Если один из векторов содержит две компоненты, то третья компонента предполагается равной 0 и вычисление производится как обычно. Если оба вектора состоят всего из двух компонент, то будет возвращено одно число — z компонента векторного произведения.
Массивы a и 
- Параметры:
- a — массив NumPy или подобный массиву объект
- Компоненты первого вектора (векторов).
- b — массив NumPy или подобный массиву объект
- Компоненты второго вектора (векторов).
- Определяет ось, в направлении которой формируются компоненты вектора
a(по умолчанию последняя ось). - axisb — массив NumPy или подобный массиву объект
- Определяет ось, в направлении которой формируются компоненты вектора
b(по умолчанию последняя ось). - axisc — массив NumPy или подобный массиву объект
- Определяет ось, в направлении которой формируются компоненты векторного произведения
a(по умолчанию последняя ось).
- axis — массив NumPy или подобный массиву объект
- Определяет одинаковую ось всех трех массивов.
- Возвращает:
- результат — число или массив NumPy
- Число, вектор или массив с результатом векторного произведения.
Замечание
С версии 1.9.0 поддерживает транслирование входных массивов.
Примеры
Векторное произведение двух векторов из трех компонет:
>>> import numpy as np >>> >>> a = [2, 3, 5] >>> b = [7, 11, 13] >>> >>> np.cross(a, b) array([-16, 9, 1])
Если один из векторов состоит всего из двух компонент, то предполагается, что у него все-таки есть третья компонента, которая просто равна нулю:
>>> a = [1, 7] >>> x = [1, 7, 0] >>> b = [1, 3, 7] >>> >>> np.cross(a, b) array([49, -7, -4]) >>> np.cross(x, b) array([49, -7, -4])
Если оба вектора состоят всего из двух компонент, то возвращается длина (третья компонента) результирующего вектора:
>>> a = [2, 5] >>> b = [1, 4] >>> np.cross(a, b) array(3)
Если a и b — это массивы векторов, то будет выполнено их поэлементное векторное умножение:
>>> a = np.arange(1, 10).reshape(3, 3)
>>> b = np.arange(9, 0, -1).reshape(3, 3)
>>>
>>> a
array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
>>> b
array([[9, 8, 7],
[6, 5, 4],
[3, 2, 1]])
>>>
>>>
>>> # Обратите внимание на выполнение правила правой руки
.
.. # при вычислении векторного произведения:
... np.cross(a, b)
array([[-10, 20, -10],
[-10, 20, -10],
[-10, 20, -10]])
>>>
>>> np.cross(b, a)
array([[ 10, -20, 10],
[ 10, -20, 10],
[ 10, -20, 10]])
>>>
>>>
>>> # Данная функция поддерживает механизм
... # транслирования массивов:
>>> a = np.arange(1, 10).reshape(3, 3)
>>> a
array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
>>> b = [9, 8, 7]
>>>
>>> np.cross(a, b)
array([[-10, 20, -10],
[-13, 26, -13],
[-16, 32, -16]]) Изменить ориентацию выхоного массива можно с помощью параметра axisc:
>>> a = np.arange(1, 13).reshape(4, 3)
>>> b = np.arange(12, 0, -1).reshape(4, 3)
>>>
>>> a
array([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12]])
>>> b
array([[12, 11, 10],
[ 9, 8, 7],
[ 6, 5, 4],
[ 3, 2, 1]])
>>>
>>>
>>> np. cross(a, b) # по умолчанию, axisc = 1
array([[-13, 26, -13],
[-13, 26, -13],
[-13, 26, -13],
[-13, 26, -13]])
>>>
>>> np.cross(a, b, axisc = 0)
array([[-13, -13, -13, -13],
[ 26, 26, 26, 26],
[-13, -13, -13, -13]])
>>>
cross(a, b) # по умолчанию, axisc = 1
array([[-13, 26, -13],
[-13, 26, -13],
[-13, 26, -13],
[-13, 26, -13]])
>>>
>>> np.cross(a, b, axisc = 0)
array([[-13, -13, -13, -13],
[ 26, 26, 26, 26],
[-13, -13, -13, -13]])
>>> Так же мы можем изменить направление векторов a и b, указав их в соответствующих параметрах axisa и axisb:
>>> a = np.arange(1, 10).reshape(3, 3)
>>> b = np.arange(9, 0, -1).reshape(3, 3)
>>>
>>> a
array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
>>> b
array([[9, 8, 7],
[6, 5, 4],
[3, 2, 1]])
>>>
>>>
>>> np.cross(a, b)
array([[-10, 20, -10],
[-10, 20, -10],
[-10, 20, -10]])
>>>
>>> np.cross(a, b, axisa = 0)
array([[-28, 56, -28],
[-20, 40, -20],
[-12, 24, -12]])
>>>
>>> # Эквивалентно:
>>> np. cross(a.T, b)
array([[-28, 56, -28],
[-20, 40, -20],
[-12, 24, -12]])
cross(a.T, b)
array([[-28, 56, -28],
[-20, 40, -20],
[-12, 24, -12]]) Задать одинаковую ось всех трех массивов можно с помощью параметра axis:
>>> np.cross(a, b, axis = 0)
array([[-30, -30, -30],
[ 60, 60, 60],
[-30, -30, -30]])
>>>
>>> np.cross(a, b, axisa = 0, axisb = 0, axisc = 0)
array([[-30, -30, -30],
[ 60, 60, 60],
[-30, -30, -30]])| о векторном произведении | [авг. 28, 2014|08:45 pm] Anatoly Vorobey |
| Я прочитал замечательную книгу, называется «Геометрические векторы», которая хороший порядок в голове навела.  Помимо прочего, разобрался с тем, что мне с юности мешало и не нравилось в векторном произведении. Помимо прочего, разобрался с тем, что мне с юности мешало и не нравилось в векторном произведении.Мне казались странными две вещи. Во-первых, что векторное произведение, в отличие от скалярного, «привязано» к трехмерному пространству, а в другом количестве измерений его непонятно, как определять. Во-вторых, что для его определения нужно правило правой руки (оно же «правило буравчика»): мне казалось очень странным, что этот произвольный выбор правила правой руки (а не левой, например) может быть «зашит» в законы физики. Про первый вопрос, о сути векторного произведения не только в трехмерном пространстве, я напишу потом в записи о всей книге и ее подходе, если соберусь. А о правиле правой руки постараюсь вкратце рассказать тут. Будем смотреть на вектор «по-физически» как на отрезок в пространстве, с заданным на нем направлением. Длина отрезка определяет величину вектора. Направление, которое мы обозначаем стрелкой — просто выбор одного из двух концов отрезка. Если в векторе поменять направление на обратное, получится обратный вектор, и эту операцию логично обозначать знаком минус, потому что сложение двух этих векторов дает ноль (вектор нулевой величины).
Далее, векторное произведение двух векторов определяется обычно так: это отрезок, перпендикулярный плоскости, в которой лежат оба вектора, и его длина равна произведению их длин умноженному на синус угла между ними. Но чтобы этот отрезок стал вектором, осталось еще дать ему направление, т.е. решить, в каком конце рисуется стрелка. Или — что то же самое — в какую из двух сторон от плоскости он уходит. Для этого используют правило правой руки: если расположить руку так, чтобы четыре пальца загибались от первого вектора ко второму, то отставленный большой палец покажет направление векторного произведения. При этом векторное произведение несколько странно ведет себя по сравнению с обычными векторами, и поэтому, если нужна точность, его называют псевдовектором (или аксиальным вектором). Вот что это значит. Предположим, мы используем векторы для изображения каких-то физических величин, которые мы в принципе можем измерить: например, скорость, или сила, или магнитное поле и так далее. Но векторное произведение так не работает. Оно в зеркальном отражении меняется на обратное тому, каким, казалось бы, должно быть. И понятно, почему так происходит: из-за правила правой руки. Ведь в зеркальном отражении правая рука становится левой, а векторное произведение там, в отражении, все равно нужно по определению делать по правилу правой. Поток тока по замкнутому контуру создает магнитное поле, которое определяется с помощью векторного произведения. В зеркальном отражении нам хотелось бы, чтобы оно указывало в том же направлении, снизу вверх, но из-за правила правой руки оно теперь направлено сверху вниз. У колес машины есть угловая скорость, которая определяется через векторное произведение. У машины слева оно направлено влево (красная стрелка). Справа зеркальное отражение той же машины. Мы бы ожидали, что в зеркальном направлении стрелка будет теперь идти вправо, но из-за правила правой руки она опять направлена влево. В общем, векторное произведение ведет себя как обычный вектор, если мы всего лишь поворачиваем систему координат (т. Теперь другой взгляд на все это, из книги Вайнрайха «Геометрические векторы». У нас есть отрезок в пространстве, и мы хотим дать ему направление, чтобы он стал вектором. Мы привыкли к тому, что это значит — выбрать одну из его вершин и назвать ее началом, а другую концом (или хвостом и головой), и нарисовать стрелку. Но давайте представим себе, что на самом деле есть два разных вида «направления». Есть два разных способа выбрать что-то, одно из двух, касающееся этого отрезка. Один, когда мы выбираем одну из вершин и рисуем стрелку, называется «полярное направление». Отрезок может вращаться (или вокруг него можно описывать круги, если желаете) в одном из двух направлений. Обратите внимание, это важно! — неверно называть их «по часовой стрелке» или «против часовой стрелки», это неправильно, потому что каждое из этих аксиальных направлений будет «по часовой стрелке», если смотреть с одного конца отрезка, и «против часовой стрелки», если смотреть с другого. Это просто два противоположных направления. Отрезок, у которого задано такое аксиальное направление, называется аксиальным вектором. Важно уяснить, что у такого вектора нигде нет стрелки, у него нет выбранной вершины, у него есть только выбранное аксиальное направление (направление вращения). Такие векторы можно складывать друг с другом, или умножать на скаляры, так же легко, как и обычные полярные векторы. Например, как мы складываем обычные векторы? Мы сдвигаем их так, чтобы начало одного уткнулось в конец другого, т. Зачем нужны аксиальные векторы? Так вот векторное произведение как раз естественным образом и является аксиальным вектором. Мы умножаем два вектора a и b, получаем отрезок определенной величины, перпендикулярный их плоскости. Для того, чтобы дать ему «стрелку», нам нужно что-то вроде правила правой руки. Но чтобы дать ему аксиальное направление, ничего особенного не нужно: оно естественным образом задается как направление вращения от a к b. Теперь при зеркальном отражении аксиальный вектор ведет себя так же естественно, как и (обычный) полярный вектор. Его направление вращение может измениться на противоположное, в зависимости от его ориентации в пространстве, но это нормально, обычный вектор тоже может измениться на противоположный, если он направлен к зеркалу. Главное — это что все происходит в точности как мы ожидаем: изогнутая стрелка вокруг вектора отражается в зеркале точно так же, как и все остальное. Нет этого странного прыжка стрелки от сверху вниз к снизу вверх, как было, когда мы рисовали у векторного произведения стрелку. Нет такого, что есть обычный нормальный вектор и «плохой» псевдовектор: полярный и аксиальный векторы равноправны и симметричны по своим свойствам. В этом подходе мы работаем с двумя разными видами векторов, и соответственно разных операций получается больше, и надо с ними разобраться. Скалярное произведение двух аксиальных векторов дает обычный скаляр, как и скалярное произведение двух полярных векторов. Обычный скаляр можно считать «полярным», и у него задано «направление» — просто его знак: 10 и -10 это два полярных скаляра противоположного направления. А какое же отношение ко всему этому имеет «правило правой руки», спросите вы? Очень просто. Мы определили новый вид вектора, и с его помощью векторное произведение, без правила правой руки. Но если нам хочется, то правило правой руки просто-напросто дает способ перевести любой аксиальный вектор в полярный, и наоборот. То, как загибаются пальцы — это аксиальное направление, то, куда указывает большой палец — полярное. Поскольку аксиальное и полярное направления не зависят друг от друга, нет естественного способа перевести одно в другое. По-моему, очень красиво. | |
Умножение матрицы на вектор — Мэтью Н. Бернштейн . В этом посте я дам определение умножения матрицы на вектор, а также три угла, с которых можно рассматривать эту концепцию. Третий аспект подразумевает просмотр матриц как функций между векторными пространствами
Введение
В предыдущем посте мы обсуждали три способа просмотра матрицы: как таблицу значений, как список векторов и, наконец, как функцию. Это третий способ просмотра матриц, который действительно придает матрицам их силу. Здесь мы представим операцию между матрицами и векторами, называемую умножением матрицы на вектор , которая позволит нам использовать матрицы как функции.
Умножение матрицы на вектор — это операция между матрицей и вектором, в результате которой получается новый вектор. Примечательно, что умножение матрицы на вектор определяется только между матрицей и вектором, где длина вектора равна количеству столбцов матрицы. Он определяется следующим образом: 9n$ матрично-векторное умножение $\boldsymbol{A}$ и $\boldsymbol{x}$ определяется как
Примечательно, что умножение матрицы на вектор определяется только между матрицей и вектором, где длина вектора равна количеству столбцов матрицы. Он определяется следующим образом: 9n$ матрично-векторное умножение $\boldsymbol{A}$ и $\boldsymbol{x}$ определяется как
, где $\boldsymbol{a}_{*, i}$ — $i$-й вектор-столбец $\boldsymbol{A}$.
Как и большинство математических понятий, умножение матрицы на вектор можно рассматривать с разных точек зрения на разных уровнях абстракции. Эти взгляды пригодятся, когда мы попытаемся концептуализировать различные способы использования матричного умножения на вектор для моделирования реальных проблем. Ниже приведены три способа, которые я считаю полезными для концептуализации умножения матрицы на вектор в порядке от наименее к наиболее абстрактному:0004
- В качестве «построчного» процесса генерации вектора: Умножение матрицы на вектор определяет процесс создания нового вектора с использованием существующего вектора, где каждый элемент нового вектора «генерируется» путем взятия взвешенной суммы каждой строки матрицы с использованием элементов вектора в качестве коэффициентов
- Как взятие линейной комбинации столбцов матрицы: Умножение матрицы на вектор — это процесс взятия линейной комбинации пространства столбцов матрицы используя элементы вектора в качестве коэффициентов
- Как вычисление функции между векторными пространствами: Умножение матрицы на вектор позволяет матрице определить отображение между двумя векторными пространствами.

Я считаю полезными все три точки зрения. Первые две перспективы обеспечивают способ понимания механизма умножения матрицы на вектор, тогда как третья перспектива обеспечивает суть умножения матрицы на вектор. Именно эта третья перспектива умножения матрицы на вектор позволяет нам рассматривать матрицы как функции, как мы обсуждали в предыдущем посте.
Умножение матрицы на вектор как «построчный» процесс генерации вектора
Полезный способ просмотра механизма умножения матрицы на вектор между матрицей $\boldsymbol{A}$ и вектором $\boldsymbol{x }$ заключается в том, чтобы рассматривать его как своего рода «процесс» (или даже как компьютерную программу), который создает каждый элемент выходного вектора итеративным образом, когда мы перебираем каждую строку $A$. В частности, для каждой строки $i$ матрицы $\boldsymbol{A}$ мы берем $\boldsymbol{x}$ и вычисляем скалярное произведение между $\boldsymbol{x}$ и $i$-й строкой матрицы, тем самым производя $i$-й элемент выходного вектора (см.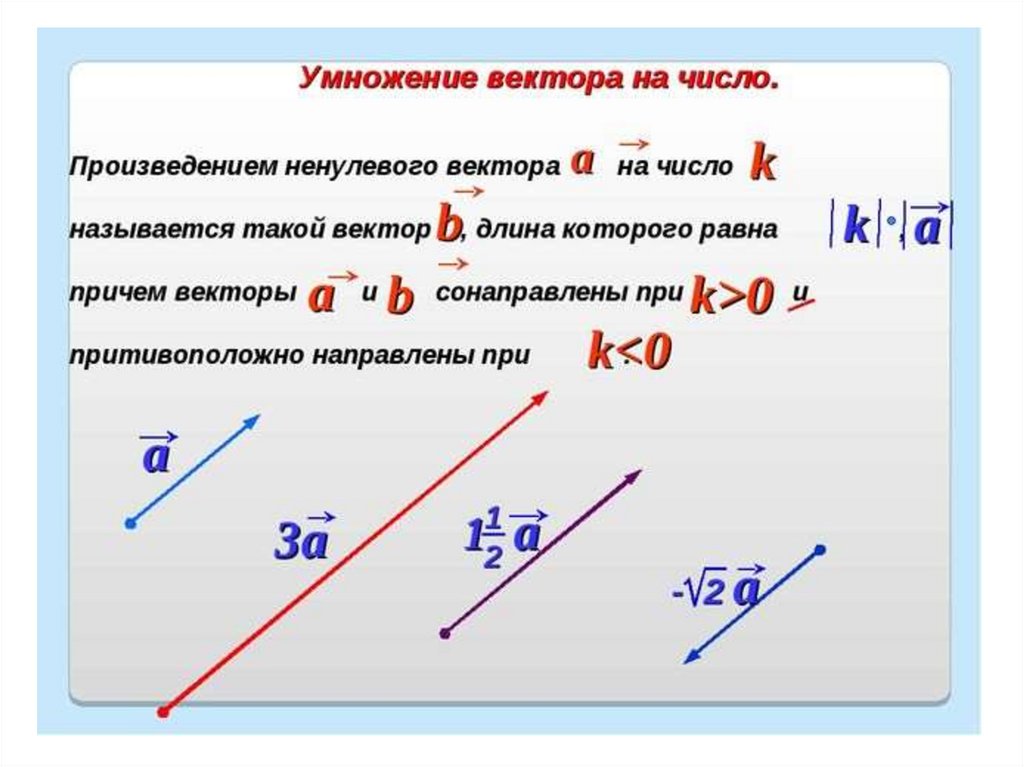 n$, считается, что
n$, считается, что
, где $\boldsymbol{a}_{i,* }$ — это $i$-й вектор-строка в $\boldsymbol{A}$.
Доказательство:
\[\begin{align*} \boldsymbol{A}\boldsymbol{x} &:= x_1\boldsymbol{a}_{*,1} + x_2\boldsymbol{a}_{* ,2} + \dots + x_n\boldsymbol{a}_{*,n} \\ &= x_1 \begin{bmatrix}a_{1,1} \\ a_{2,1} \\ \vdots \\ a_ {m, 1} \end{bmatrix} + x_2\begin{bmatrix}a_{1,2} \\ a_{2,2} \\ \vdots \\ a_{m, 2} \end{bmatrix} + \ точки + x_n\begin{bmatrix}a_{1,n} \\ a_{2,n} \\ \vdots \\ a_{m, n} \end{bmatrix} \\ &= \begin{bmatrix}x_1a_{ 1,1} \\ x_1a_{2,1} \\ \vdots \\ x_1a_{m, 1} \end{bmatrix} + \begin{bmatrix}x_2a_{1,2} \\ x_2a_{2,2} \ \ \vdots \\ x_2a_{m, 2} \end{bmatrix} + \dots + \begin{bmatrix}x_na_{1,n} \\ x_na_{2,n} \\ \vdots \\ x_na_{m, n } \end{bmatrix} \\ &= \begin{bmatrix} x_1a_{1,1} + x_2a_{1,2} + \dots + x_na_{1,n} \\ x_1a_{2,1} + x_2a_{2 ,2} + \dots + x_na_{2,n} \\ \vdots \\ x_1a_{m,1} + x_2a_{m,2} + \dots + x_na_{m,n} \\ \end{bmatrix} \ \ &= \begin{bmatrix} \sum_{i=1}^n a_{1,i}x_i \\ \sum_{i=1}^n a_{2,i}x_i \\ \vdots \\ \sum_ {i=1}^n a_{m,i}x_i \\ \end{bmatrix} \\ &= \begin{bma trix}\boldsymbol{a}_{1,*} \cdot \boldsymbol{x} \\ \boldsymbol{a}_{2,*} \cdot \boldsymbol{x} \\ \vdots \\ \boldsymbol{a }_{m,*} \cdot \boldsymbol{x} \\ \end{bmatrix}\end{align*}\]$\square$
Теги: линейная алгебра, линейное преобразование, математика, матрицы, учебник
Умножение векторов — GCSE Maths
Введение
Что такое векторное умножение?
Как умножить вектор
наРабочий лист векторного умножения
Распространенные заблуждения
Практикуйте вопросы умножения векторов
Умножение векторов GCSE вопросы
Контрольный список обучения
Следующие уроки
Вы знали?
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Еженедельные онлайн-уроки повторения математики GCSE теперь доступны
Узнать больше
Введение
Что такое векторное умножение?
Как умножить вектор
Рабочий лист векторного умножения
Распространенные заблуждения
Упражнения на умножение векторов
Умножение векторов GCSE вопросы
Контрольный список обучения
Следующие уроки
Вы знали?
Все еще застряли?
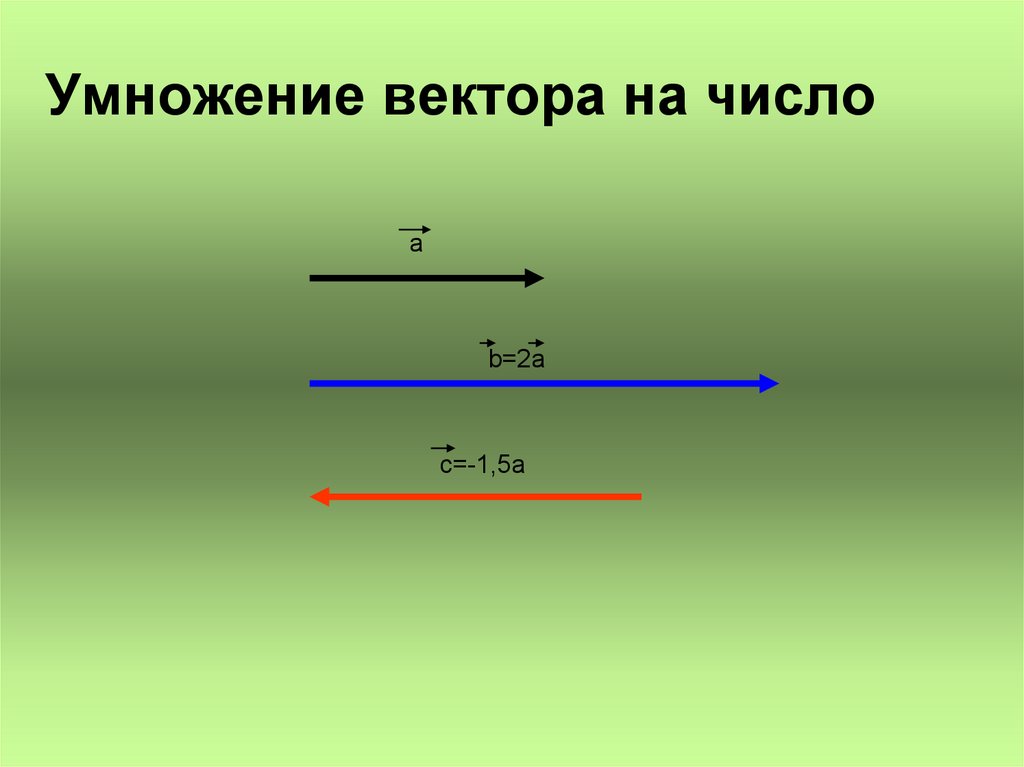
Здесь мы узнаем о векторном умножении, в том числе на скалярное умножение вектора (умножение вектора на число).
Существуют также векторные рабочие листы на основе экзаменационных вопросов Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.
Что такое векторное умножение?
Умножение векторов — это умножение вектора на число. Число является скаляром и имеет только величину, тогда как вектор имеет величину и направление.
Для этого умножаем каждую из составляющих на скалярное число.
Вот пример:
Вектор a равно
\[\textbf{a}= \left(\begin{массив}{1} 2\\ 1\\ \end{array}\right)\]
Таким образом, умножение вектора a на 3 будет
\[3\textbf{a}= 3\влево(\начать{массив}{1} 2\\ 1\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} 3\раз2\\ 3\умножить на 1\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} 6\\ 3\\ \end{array}\right)\]
Это работает, потому что умножение — это многократное сложение. Другим способом умножения вектора на на 3 будет 9. 0004
0004
\[3\textbf{а}=\textbf{а}+\textbf{а}+\textbf{а}= \left(\begin{массив}{1} 2\\ 1\\ \конец{массив}\справа) +\влево(\начать{массив}{1} 2\\ 1\\ \конец{массив}\справа) +\влево(\начать{массив}{1} 2\\ 1\\ \конец{массив}\справа) =\влево(\начать{массив}{1} 6\\ 3\\ \end{array}\right)\]
Это видно на диаграмме. Вы можете видеть 3 лота компонента x и 3 лота компонента y.
Направление вектора, умноженного на скалярное число, такое же, как у исходного вектора, но величина вектора (также называемая абсолютным значением вектора) изменилась.
Что такое векторное умножение?
Как умножить вектор
Чтобы умножить вектор на скаляр:
- Умножьте компонент x на скаляр.
- Умножьте компонент y на скаляр.
- Запишите результирующий вектор.
Как умножить вектор
Рабочий лист векторного умножения
Получите бесплатный векторный лист умножения, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
Включает рассуждения и прикладные вопросы.
СКОРО
ИксЛист векторного умножения
Получите бесплатный лист векторного умножения, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКОРО
Связанные уроки по векторам
Умножение векторов является частью нашей серии уроков для поддержки повторения на векторов . Возможно, вам будет полезно начать с урока по основным векторам, чтобы получить общее представление о том, чего ожидать, или воспользоваться пошаговыми руководствами, приведенными ниже, для получения более подробной информации по отдельным темам. Другие уроки этой серии включают:
- Векторы
- величина вектора
- Колоночный вектор
- Векторная обозначения
- Вектор Добавление
- ВЕКТОР SUBTRACTION
- Вектор.0017
Пример 1: векторное умножение
Вычисление:
\[2\left(\begin{array}{1} 4\\ 5\\ \end{массив}\right)\]
- Умножьте компонент x на скаляр.

Умножить скалярное число на верхнее число
2\раз4=8
2 Умножьте компонент y на скаляр.
Умножить скалярное число на нижнее число
2\х5=10
3 Запишите результирующий вектор.
Запишите два ответа в виде вектор-столбца
\[2\left(\begin{array}{1} 4\\ 5\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} 2\раз4\\ 2\раз5\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} 8\\ 10\\ \end{array}\right)\]
Пример 2: векторное умножение
Вычисление:
\[4\left(\begin{array}{1} 8\\ 3\\ \end{массив}\right)\]
Умножьте компонент x на скаляр.
Умножить скалярное число на верхнее число
4\х8=32
Умножьте компонент y на скаляр.
Умножить скалярное число на нижнее число
4\times3=12
Запишите результирующий вектор.

Запишите два ответа в виде вектор-столбца
\[4\left(\begin{array}{1} 8\\ 3\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} 4\раз8\\ 4\раз3\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} 32\\ 12\\ \конец{массив}\справа)\]
Пример 3: векторное умножение, десятичный скаляр
Вычисление:
\[0,5\left(\begin{array}{1} 10\\ 8\\ \end{массив}\right)\]
Умножьте компонент x на скаляр.
Умножить скалярное число на верхнее число
0,5\×10=5
Умножьте компонент y на скаляр.
Умножить скалярное число на нижнее число
0,5\х8=4
Запишите результирующий вектор.
Запишите два ответа в виде вектор-столбца
\[0,5\left(\begin{array}{1} 10\\ 8\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} 0,5\х10\\ 0,5\х8\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} 5\\ 4\\ \end{array}\right)\]
Пример 4: векторное умножение, дробный скаляр
Вычисление:
\[\frac{1}{3}\left(\begin{array}{1} -6\\ 9\\ \end{массив}\right)\]
Умножить 9Компонент 0008 x скаляром.

Умножить скалярное число на верхнее число
\frac{1}{3}\times-6=-2
Умножьте компонент y на скаляр.
Умножить скалярное число на нижнее число
\frac{1}{3}\times9=3
Запишите результирующий вектор.
Запишите два ответа в виде вектор-столбца
\[\frac{1}{3}\left(\begin{array}{1} -6\\ 9\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} \frac{1}{3}\times-6\\ \frac{1}{3}\times9\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} -2\\ 3\\ \end{array}\right)\]
Пример 5: векторное умножение
Вычисление:
\[4\left(\begin{array}{1} -5\\ -2\\ \end{массив}\right)\]
Умножьте компонент x на скаляр.
Умножить скалярное число на верхнее число
4\раз-5=-20
Умножьте компонент y на скаляр.

Умножить скалярное число на нижнее число
4\раз-2=-8
Запишите результирующий вектор.
Запишите два ответа в виде вектор-столбца
\[4\left(\begin{array}{1} -5\\ -2\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} 4\раз-5\\ 4\раз-2\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} -20\\ -8\\ \end{array}\right)\]
Пример 6: векторное умножение, отрицательный скаляр
Вычисление:
\[-3\left(\begin{array}{1} -2\\ 5\\ \конец{массив}\справа)\]
Умножить компонент x на скаляр.
Умножить скалярное число на верхнее число
-3\раз-2=6
Умножьте компонент y на скаляр.
Умножить скалярное число на нижнее число
-3\times5=-15
Запишите результирующий вектор.

Запишите два ответа в виде вектор-столбца
\[-3\left(\begin{array}{1} -2\\ 5\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} -3\раз-2\\ -3\раз5\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} 6\\ -15\\ \конец{массив}\справа)\]
Распространенные заблуждения
- Убедитесь, что вы умножили оба компонента на скалярное число
Компоненты x и y необходимо умножить на скалярное число.
- Векторы-столбцы имеют только 2 числа в скобках
Векторы-столбцы имеют верхний номер и нижний номер в скобках. Нет необходимости в каких-либо других знаках препинания, таких как запятые или точки с запятой. Нет необходимости в линии для разделения чисел.
Вопросы по умножению векторов
\begin{pmatrix} \; 5 \;\\ \; 7\; \end{pmatrix}
\begin{pmatrix} \; 6 \;\\ \; 4\; \end{pmatrix}
\begin{pmatrix} \; 12 \;\\ \; 6\; \end{pmatrix}
\begin{pmatrix} \; 6 \;\\ \; 12\; \end{pmatrix}
3\textbf{a}= 3\begin{pmatrix} \; 2 \;\\\; 4\; \end{pmatrix} = \begin{pmatrix} \; 3\умножить на 2\;\\\; 3\х4\; \end{pmatrix} = \begin{pmatrix} \; 6 \;\\\; 12\; \end{pmatrix}
\begin{pmatrix} \; 6 \;\\ \; 8\; \end{pmatrix}
\begin{pmatrix} \; 5 \;\\ \; 3 \; \end{pmatrix}
\begin{pmatrix} \; 5 \;\\ \; 15 \; \end{pmatrix}
\begin{pmatrix} \; 6 \;\\ \; 15 \; \end{pmatrix}
5\textbf{b}= 5\begin{pmatrix} \; 1 \;\\ \; 3 \; \end{pmatrix} = \begin{pmatrix} \; 5\умножить на 1\;\\\; 5\раз3\; \end{pmatrix} = \begin{pmatrix} \; 5 \;\\\; 15 \; \end{pmatrix}
\begin{pmatrix} \; 21 \;\\ \; 31\; \end{pmatrix}
\begin{pmatrix} \; 20.
 1 \;\\
\; 30,1 \;
\end{pmatrix}
1 \;\\
\; 30,1 \;
\end{pmatrix}\begin{pmatrix} \; 2 \;\\ \; 3 \; \end{pmatrix}
\begin{pmatrix} \; 20 \;\\ \; 3 \; \end{pmatrix}
0.1\textbf{c}= 0.1\begin{pmatrix} \; 20 \;\\ \; 30 \; \end{pmatrix} = \begin{pmatrix} \; 0,1\раз 20\;\\\; 0,1\х30\; \end{pmatrix} = \begin{pmatrix} \; 2 \;\\\; 3 \; \end{pmatrix}
\begin{pmatrix} \; -4 \;\\ \; 3 \; \end{pmatrix}
\begin{pmatrix} \; -4 \;\\ \; 6\; \end{pматрица}
\begin{pmatrix} \; -2 \;\\ \; 3 \; \end{pmatrix}
\begin{pmatrix} \; -10 \;\\ \; 6\; \end{pmatrix}
\frac{2}{5}\textbf{a}= \frac{2}{5}\begin{pmatrix} \; -10\;\\\; 15 \; \end{pmatrix} = \begin{pmatrix} \; \frac{2}{5}\times -10 \;\\ \; \frac{2}{5}\times15 \; \end{pmatrix} = \begin{pmatrix} \; -4\;\\\; 6\; \end{pmatrix}
\begin{pmatrix} \; 12 \;\\ \; 18\; \end{pmatrix}
\begin{pmatrix} \; 4 \;\\ \; 3 \; \end{pmatrix}
\begin{pmatrix} \; -12 \;\\ \; -18\; \end{pматрица}
\begin{pmatrix} \; -4 \;\\ \; -3\; \end{pmatrix}
6\textbf{d}= 6\begin{pmatrix} \; -2 \;\\\; -3\; \end{pmatrix} = \begin{pmatrix} \; 6\раз -2\;\\\; 6\раз -3\; \end{pmatrix} = \begin{pmatrix} \; -12\;\\\; -18\; \end{pmatrix}
\begin{pmatrix} \; -15 \;\\ \; -12 \; \end{pmatrix}
\begin{pmatrix} \; -2 \;\\ \; -1\; \end{pmatrix}
\begin{pmatrix} \; 15 \;\\ \; 12\; \end{pmatrix}
\begin{pmatrix} \; -15 \;\\ \; -4\; \end{pматрица}
-3\textbf{f}= -3\begin{pmatrix} \; -5 \;\\\; -4\; \end{pmatrix} = \begin{pmatrix} \; -3\раз -5\;\\\; -3\раз -4\; \end{pmatrix} = \begin{pmatrix} \; 15 \;\\\; 12\; \end{pmatrix}
Умножение векторов Вопросы GCSE
1.
 Вектор \textbf{v} равен
Вектор \textbf{v} равен\textbf{v}= \begin{pматрица} \; -3 \;\\ \; 5 \; \end{pматрица}
Какой из приведенных ниже векторов эквивалентен 4\textbf{v} ?
А \ четырехъядерный \ четырехъядерный Б \ четырехъядерный \ четырехъядерный С \ четырехъядерный \ четырехъядерный Д \begin{pmatrix} \; -12 \;\\ \; 5 \; \end{pmatrix} \ четырехъядерный \ четырехъядерный \begin{pmatrix} \; -1 \;\\ \; 20 \; \end{pmatrix} \ четырехъядерный \ четырехъядерный \begin{pmatrix} \; -1 \;\\ \; 5 \; \end{pmatrix} \ четырехъядерный \ четырехъядерный \begin{pmatrix} \; -12 \;\\ \; 20 \; \end{pматрица} (1 балл)
Показать ответ
2. Вектор \textbf{a} равен
\textbf{а}= \begin{pматрица} \; 3 \;\\ \; -6 \; \end{pматрица}
Вычислить 5\textbf{a}
(2 балла)
Показать ответ
\begin{pmatrix} \; 15 \;\\ \; -30 \; \end{pматрица}
Для компонента x (верхнее число)
(1)
Для компонента y (нижний номер)
(1)
3.
 Вот векторное умножение
Вот векторное умножение3 \begin{pматрица} \; -4 \;\\ \; \текст{б} \; \end{pматрица} знак равно \begin{pматрица} \; \текст{а} \;\\ \; 24\; \end{pматрица}
(a) Найдите значение a .
(b) Найдите значение b .
(2 балла)
Показать ответ
(а)
а=-12
(1)
(б)
б=8
(1)
Контрольный список обучения
Вы теперь узнали, как:
- Умножить вектор на скаляр
.
- Умножьте компонент x на скаляр.
Знаете ли вы?
Не входит в GCSE: мы можем транспонировать вектор-столбец, чтобы записать его как вектор-строку (и наоборот). Они выглядят как координаты, но без запятых.
Векторы также можно расширить до математики уровня A и высшей математики, научившись умножать два вектора вместе с помощью скалярного произведения. Это также известно как скалярное произведение двух векторов. Векторы можно умножать, и это известно как векторное произведение. Это также известно как векторное произведение двух векторов. Перекрестное произведение связано с правилом правой руки.
Это также известно как скалярное произведение двух векторов. Векторы можно умножать, и это известно как векторное произведение. Это также известно как векторное произведение двух векторов. Перекрестное произведение связано с правилом правой руки.
Мы также можем расширять векторы до трех измерений. Мы также можем посмотреть на вектор, перпендикулярный плоскости, чтобы получить уравнение плоскости.
Векторы-столбцы являются простым примером матриц. В математике GCSE у нас есть один столбец. Матрицы изучаются на уровне A Level Additional Maths. Количество столбцов и строк будет больше 1 . Умножение матриц можно изучать вместе с нахождением обратной матрицы. Мы также можем найти определитель матрицы и пойти дальше и изучить собственные значения и собственные векторы.
Если величина вектора равна 1 , этот вектор называется единичным вектором.
Все еще зависает?
Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning. Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.
Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.
Узнайте больше о нашей программе повторения GCSE по математике.
Умножение матрицы на вектор
Видео академии Хана выше называет внутренний продукт просто скалярным произведением и использует обозначение
x.yвместоНачиная с
яшироко используется в качестве индекса в этом примечании.видео на самом деле является 2D-DFT, а не точно таким же DFT, как определено выше.
Я намеренно не даю понять, что именно я имею в виду под цифрами. Но для этого раздела подойдет практически любой разумный набор чисел (например, целые числа, действительные числа, комплексные числа). Если вы спросите, множество чисел, для которых выполняется этот закон (плюс некоторые другие требования), называется полукольцом 9.
 0198 .
0198 .Если проблема кажется слишком эзотерической, просто держитесь за своих (оценочных) лошадей. Вскоре мы увидим, что эта сумма произведений соответствует очень естественной задаче.
Для этой заметки мы будем предполагать, что числа достаточно малы, так что все основные операции (сложение, умножение, вычитание и деление) занимают постоянное время.
В этой заметке мы будем работать с матрицами и векторами. Проще говоря, матрицы — это двумерные массивы, а векторы — одномерные массивы (или «обычное» понятие массивов). Мы будем использовать нотацию, совместимую с нотацией массива. Так, например. матрица $\mathbf{A}$ с $m$ строками и $n$ столбцами (также обозначаемая как матрица $m\times n$) будет в коде определена как int [][] A = new int[m][n] (при условии, что матрица хранит целые числа). Также вектор $\mathbf{x}$ размера $n$ в коде будет объявлен как int [] x = new int[n] (опять же при условии, что вектор содержит целые числа). {n-1} A[i][j]\cdot x[j].\]
{n-1} A[i][j]\cdot x[j].\]
Упрощение
Обратите внимание, что в приведенном выше определении задачи у нас одинаковое количество строк и столбцов, т. е. $m=n$. Я использую это упрощение, чтобы уменьшить количество переменных, которые нужно держать в голове. Большинство рассуждений в этой заметке можно довольно легко обобщить на случай $m\neq n$.
Если вы еще не видели эту операцию, в этом видео Академии Хана есть несколько примеров (или прочитайте следующий раздел): 9{n-1} х[я]\cdot у[я].\]
Ниже приведена анимация, показывающая скалярное произведение двух случайных векторов размера $n=6$ (нажмите «Далее», чтобы продолжить вычисление внутреннего произведения: анимация начинается с двух новых случайных векторов, если нажать «Далее»). нажата после того, как внутренний продукт уже был вычислен):
Вооружившись определением скалярного произведения, вот эквивалентное определение задачи умножения матрицы на вектор:
Умножение матрицы на вектор (переопределено)
Для матрицы $\mathbf{A}$ размером $n\times n$ и вектора $\mathbf{x}$ длины $n$ их произведение $\mathbf{y }=\mathbf{A}\cdot\mathbf{x}$ также можно определить следующим образом. Его $i$-я запись для $0\le i\lt n$ определяется следующим образом:
\[y_i =\left\langle \mathbf{A}[i],\mathbf{x}\right\rangle,\]
где $\mathbf{A}[i]$ обозначает $i$-ю строку $\mathbf{A}$.
Его $i$-я запись для $0\le i\lt n$ определяется следующим образом:
\[y_i =\left\langle \mathbf{A}[i],\mathbf{x}\right\rangle,\]
где $\mathbf{A}[i]$ обозначает $i$-ю строку $\mathbf{A}$.
Ниже приведен один пример умножения матрицы на вектор: \[ \begin{pматрица} 1 и 2 и -3\\ 2 и 9 &0\\ 6 и -1 и -2 \end{pматрица} \ раз \begin{pматрица} 2\\ 3\\ -1 \end{pматрица} знак равно \begin{pматрица} 1\умножить на 2 + 2\умножить на 3 + (-3)\раз(-1)\\ 2\умножить на 2+ 9\умножить на 3+0\раз (-1)\\ 6\умножить на 2+(-1)\умножить на 3+ (-2)\раз(-1) \end{pматрица} знак равно \begin{pматрица} 11\\ 31\\ 11 \end{pматрица}. \] 92)$ время. Проиллюстрируем этот момент конкретным семейством структурированных матриц:
Внешнее произведение
Для двух векторов $\mathbf{s}$ и $\mathbf{t}$ их внешнее произведение определяется как $n\times n$ матрица $\mathbf{A}$ такая, что для любой записи $(i,j)$ имеем
\[A[i][j]=s[i]\cdot t[j]. {n-1} s[i]\cdot t[j]\cdot x[j].\]
{n-1} s[i]\cdot t[j]\cdot x[j].\]
Детали алгоритма
//Ввод: s[i], t[i], x[i] для 0 сначала
IP=0;
для (j = 0; j < n; j ++)
ip+=t[j]*x[j];
//Теперь вычисляем выходной вектор
у = новый интервал [n];
для (я = 0; я < п; я ++)
y[i] = s[i]*ip;
вернуть у;
Анализ во время выполнения остается в качестве упражнения:
Упражнение 3
Докажите, что приведенный выше алгоритм работает за время $\Theta(n)$.
Дискретное преобразование Фурье
В этом разделе мы рассмотрим, возможно, наиболее широко используемое в мире умножение матрицы на вектор: дискретное преобразование Фурье (или ДПФ). Для приложений и больше математики (чем ниже), посмотрите его страницу Википедии. Вот определение дискретного преобразования Фурье:
Дискретное преобразование Фурье
Сначала определим дискретную матрицу Фурье. $n\times n$ (дискретная) матрица Фурье $\mathbf{F}$ определяется следующим образом. {-2\pi \iota \cdot \frac{i\cdot j}{n}},\]
где $\iota$ — мнимое число. 2
{-2\pi \iota \cdot \frac{i\cdot j}{n}},\]
где $\iota$ — мнимое число. 2
Наконец, для вектора $\mathbf{x}$ длины $n$ его преобразование Фурье задается выражением \[\mathbf{F}\cdot \mathbf{x}.\]
Прежде чем углубиться в математику ДПФ, вот видео, показывающее ДПФ 3 изображения скатерти:
Игра с ДПФ может вызвать привыкание:
Не знаю почему, но мне нравится проводить преобразование Фурье повседневных вещей. Вот крышка слива. pic.twitter.com/31RqNK52bo
— Аатиш Бхатия (@aatishb) 25 августа 2015 г.Комплексное число
Как вы, должно быть, заметили, ДПФ использует комплексные числа. Вот видео о том, почему комплексные числа действительно полезны (и почему «мнимое число» — одна из PR-ошибок математики):
youtube.com/embed/-IJuqR6nz_Q" allowfullscreen="">И, извините, не удержался от этого видео на "воображаемое число Эрдоса" (пропустите, если не хотите отвлекаться):
Итак, получается, что комплексные числа, используемые в дискретной матрице Фурье, являются корнями из единицы 9m$ за время $O(nm)$.
Подсказка: Используйте предложение 1.
В этом разделе мы представим простое наблюдение, которое окажется очень полезным при разработке эффективных алгоритмов (особенно тех, которые включают сложение и умножение чисел). В частности, эту идею (правильно реализованную) можно использовать и для решения упражнения 4, приведенного выше.
Начнем с утверждения распределительного закона:
Распределительный закон
Для трех чисел $a,b,c$ имеем 9{n-1} b_i\право).\]
Вышеизложенное означает, что вместо $n$ умножений в левой части мы можем обойтись одним умножением в правой части. {n-1} s[i]\cdot t[j]\cdot x[j]$ с помощью дистрибутивного закона. Потом мы заметили, что если бы мы сохранили "общий" терм $\left\langle \mathbf{t},\mathbf{x}\right\rangle$, то можно было бы избежать перевычисления этого терма для разных $i$. Мы резюмируем эту стратегию следующим образом:
9{n-1} б_и.\]
В дальнейшем сохраните все промежуточные результаты для возможного использования в будущем.
{n-1} s[i]\cdot t[j]\cdot x[j]$ с помощью дистрибутивного закона. Потом мы заметили, что если бы мы сохранили "общий" терм $\left\langle \mathbf{t},\mathbf{x}\right\rangle$, то можно было бы избежать перевычисления этого терма для разных $i$. Мы резюмируем эту стратегию следующим образом:
9{n-1} б_и.\]
В дальнейшем сохраните все промежуточные результаты для возможного использования в будущем.
Вычисление сумм произведений
Оказывается, стратегия дистрибутивного закона особенно хороша для эффективного вычисления сумм произведений. Вместо более формального определения того, что я имею в виду под суммами произведений, позвольте мне проиллюстрировать мою точку зрения на конкретной задаче: 5
Пример суммы произведения
Даны $n\times n$ матриц $\mathbf{A} ,\mathbf{B},\mathbf{C}$ и вектор $\mathbf{x}$ рассмотрим следующие суммы произведений. В частности, мы хотим вычислить вектор $\mathbf{y}$ такой, что для каждого $0\le i\lt n$:
\[y[i]=\sum_{j=0}^{n-1}\sum_{k=0}^{n-1}\sum_{\ell=0}^{n-1} A[i ][j]\cdot B[j][k]\cdot C[k][\ell]\cdot x[\ell].




 cross(a, b)
array([-16, 9, 1])
cross(a, b)
array([-16, 9, 1])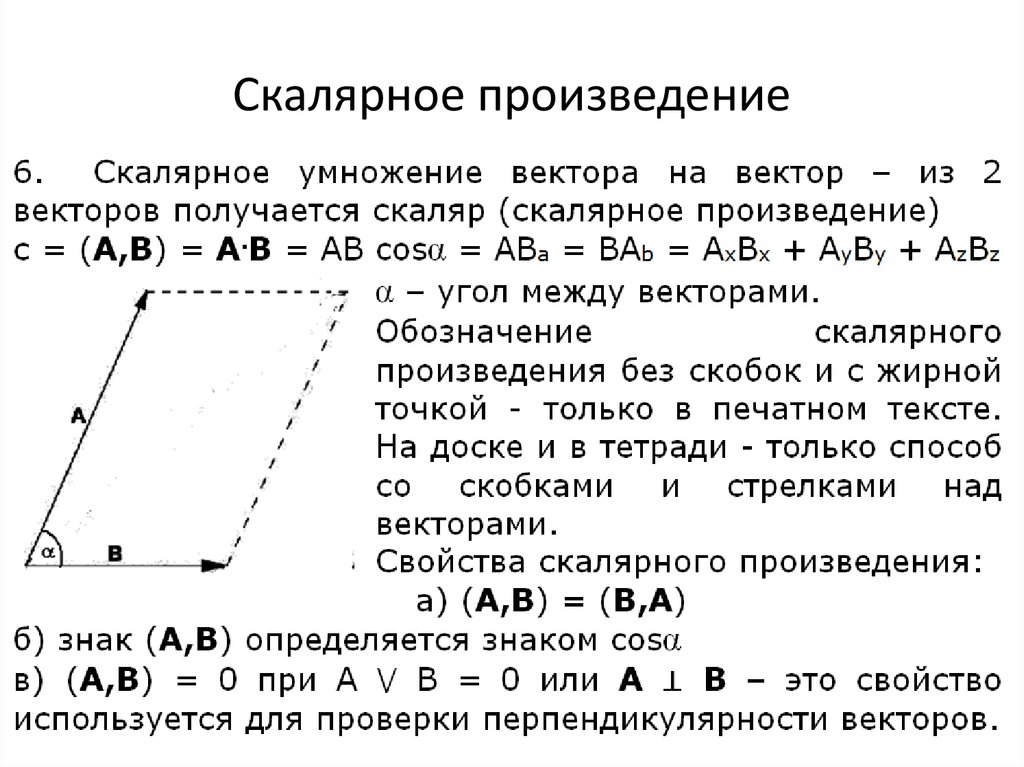
 cross(a, b) # по умолчанию, axisc = 1
array([[-13, 26, -13],
[-13, 26, -13],
[-13, 26, -13],
[-13, 26, -13]])
>>>
>>> np.cross(a, b, axisc = 0)
array([[-13, -13, -13, -13],
[ 26, 26, 26, 26],
[-13, -13, -13, -13]])
>>>
cross(a, b) # по умолчанию, axisc = 1
array([[-13, 26, -13],
[-13, 26, -13],
[-13, 26, -13],
[-13, 26, -13]])
>>>
>>> np.cross(a, b, axisc = 0)
array([[-13, -13, -13, -13],
[ 26, 26, 26, 26],
[-13, -13, -13, -13]])
>>>  cross(a.T, b)
array([[-28, 56, -28],
[-20, 40, -20],
[-12, 24, -12]])
cross(a.T, b)
array([[-28, 56, -28],
[-20, 40, -20],
[-12, 24, -12]])
 Тогда понятно, что если мы просто посмотрим на ту же физическую систему с другой стороны, под другим углом, то от этого скорости, силы, и другие физические величины не изменятся. Раз наши вектора-стрелки изображают эти физические величины, они тоже не должны от этого измениться. И действительно, с чего бы стрелкам в пространстве меняться от того, что на них посмотрели с другой стороны. Это все просто и тривиально. Далее, есть и другой способ посмотреть «по-другому» на физическую систему: посмотреть на ее зеркальное отражение. Зеркальное отражение некоторое векторы оставляет без изменений: я стою перед зеркалом, моя правая рука направлена вправо — ее отражение в зеркале направлено в ту же сторону: для меня-зеркального это «лево», да, но это то же направление. Другие векторы меняет: если я потянусь рукой к зеркалу, мое отражение потянется в обратном направлении. Но так или иначе, логично ожидать, что все физические величины при зеркальном отражении всей системы изменятся одинаковым «зеркальным» способом.
Тогда понятно, что если мы просто посмотрим на ту же физическую систему с другой стороны, под другим углом, то от этого скорости, силы, и другие физические величины не изменятся. Раз наши вектора-стрелки изображают эти физические величины, они тоже не должны от этого измениться. И действительно, с чего бы стрелкам в пространстве меняться от того, что на них посмотрели с другой стороны. Это все просто и тривиально. Далее, есть и другой способ посмотреть «по-другому» на физическую систему: посмотреть на ее зеркальное отражение. Зеркальное отражение некоторое векторы оставляет без изменений: я стою перед зеркалом, моя правая рука направлена вправо — ее отражение в зеркале направлено в ту же сторону: для меня-зеркального это «лево», да, но это то же направление. Другие векторы меняет: если я потянусь рукой к зеркалу, мое отражение потянется в обратном направлении. Но так или иначе, логично ожидать, что все физические величины при зеркальном отражении всей системы изменятся одинаковым «зеркальным» способом.
 е. смотрим под другим углом) или двигаем ее. Но если мы делаем отражение системы координат (т.е. смотрим на зеркальное отражение), то оно меняет знак в сравнении с обычными векторами, и поэтому называется псевдовектором. Это лишний раз подчеркивает странность произвольного выбора правила правой руки, и того, что физические величины, которые ведут себя в соответствии с законами природы, должны почему-то ему подчиняться.
е. смотрим под другим углом) или двигаем ее. Но если мы делаем отражение системы координат (т.е. смотрим на зеркальное отражение), то оно меняет знак в сравнении с обычными векторами, и поэтому называется псевдовектором. Это лишний раз подчеркивает странность произвольного выбора правила правой руки, и того, что физические величины, которые ведут себя в соответствии с законами природы, должны почему-то ему подчиняться. Другой вид, когда мы задаем направление вращения отрезка вокруг своей оси, называется «аксиальное направление».
Другой вид, когда мы задаем направление вращения отрезка вокруг своей оси, называется «аксиальное направление». е. пользуемся их стрелками, и потом соединяем дальние концы. Чтобы сложить два аксиальных вектора, нам нужно понять, как их соединить концами: ведь стрелок нет. Но на самом деле это просто: они соединяются так, чтобы они крутились в одном и том же направлении, если переходить с одного на другой. Можно представить себе такие векторы веревками, которые вращаются в своем направлении; если мы их свяжем двумя концами, то они будут либо мешать друг другу крутиться — и тогда мы связали неправильно — либо крутиться вместе, и это правильный способ. И потом мы соединяем дальние концы и закручиваем то, что получилось, в том же направлении.
е. пользуемся их стрелками, и потом соединяем дальние концы. Чтобы сложить два аксиальных вектора, нам нужно понять, как их соединить концами: ведь стрелок нет. Но на самом деле это просто: они соединяются так, чтобы они крутились в одном и том же направлении, если переходить с одного на другой. Можно представить себе такие векторы веревками, которые вращаются в своем направлении; если мы их свяжем двумя концами, то они будут либо мешать друг другу крутиться — и тогда мы связали неправильно — либо крутиться вместе, и это правильный способ. И потом мы соединяем дальние концы и закручиваем то, что получилось, в том же направлении. При этом, как и требуется, от перестановки мест множителей направление произведение меняется на обратное.
При этом, как и требуется, от перестановки мест множителей направление произведение меняется на обратное. Но это все выходит довольно просто. Скажем, векторное произведение двух полярных векторов дает аксиальный, как мы только что увидели, и двух аксиальных — тоже дает аксиальный (надо разобраться, как соединить их концы и как определить вращение результата). Зато векторное произведение полярного и аксиального векторов дает обычный полярный вектор. Это объясняет, кстати, почему магнитное поле странным образом переворачивается в зеркальном отражении — в обычной формулировке векторного произведения — но у этого нет физических последствий: потому что когда оно действует на движущуюся заряженную частицу, то ее приложение вычисляется через еще одно векторное произведение, и получается обычный вектор, так что частица будет двигаться «правильно» в отражении.
Но это все выходит довольно просто. Скажем, векторное произведение двух полярных векторов дает аксиальный, как мы только что увидели, и двух аксиальных — тоже дает аксиальный (надо разобраться, как соединить их концы и как определить вращение результата). Зато векторное произведение полярного и аксиального векторов дает обычный полярный вектор. Это объясняет, кстати, почему магнитное поле странным образом переворачивается в зеркальном отражении — в обычной формулировке векторного произведения — но у этого нет физических последствий: потому что когда оно действует на движущуюся заряженную частицу, то ее приложение вычисляется через еще одно векторное произведение, и получается обычный вектор, так что частица будет двигаться «правильно» в отражении. А вот если составить скалярное произведение полярного и аксиального векторов, получается такая смешная штука, которую называют псевдоскаляр или аксиальный скаляр. Это число, у которого есть одно из двух направлений, но они не совпадают ни с плюсом, ни с минусом. Само число обязано быть положительным, потому что же это просто длина отрезка, но мы его как бы считаем без знака, не +10 и не -10, а «просто 10», и при этом у него есть одно из двух направлений вращения, которые можно условно назвать, например, правым и левым. То есть это будет «правое 10» или «левое 10».
А вот если составить скалярное произведение полярного и аксиального векторов, получается такая смешная штука, которую называют псевдоскаляр или аксиальный скаляр. Это число, у которого есть одно из двух направлений, но они не совпадают ни с плюсом, ни с минусом. Само число обязано быть положительным, потому что же это просто длина отрезка, но мы его как бы считаем без знака, не +10 и не -10, а «просто 10», и при этом у него есть одно из двух направлений вращения, которые можно условно назвать, например, правым и левым. То есть это будет «правое 10» или «левое 10». Надо выбрать один из двух таких способов: либо правило правой руки, либо правило левой руки (кстати, выбор системы координат — тоже является выбором такого правила: то, как оси x,y,z расположены друг относительно друга, задает либо правую, либо левую руку). Как только мы выбираем одно из них, мы можем все наши аксиальные вектора заменить на сооветствующие полярные, и избавиться от «отрезка с направлением вращения» (а «правое 10» становится соответственно +10 или -10, смотря какое правило мы выбрали). Но тогда мы возвращаемся к старой картине мира, в которой эти вновь полученные вектора начинают вести себя странно в зеркальном отражении, и за это в старой картине мира их называли ‘аксиальными’ или ‘псевдовекторами’. А псевдоскаляры в зеркальном отражении, хоть и выглядят обычными числами, теперь почему-то меняют знак на противоположный. Теперь мы видим, что это странное несимметричное поведение не присутствует в природе, а возникает, когда мы выбираем произвольным образом одно из двух правил для того, чтобы упростить себе жизнь и работать только с одним типом векторов.
Надо выбрать один из двух таких способов: либо правило правой руки, либо правило левой руки (кстати, выбор системы координат — тоже является выбором такого правила: то, как оси x,y,z расположены друг относительно друга, задает либо правую, либо левую руку). Как только мы выбираем одно из них, мы можем все наши аксиальные вектора заменить на сооветствующие полярные, и избавиться от «отрезка с направлением вращения» (а «правое 10» становится соответственно +10 или -10, смотря какое правило мы выбрали). Но тогда мы возвращаемся к старой картине мира, в которой эти вновь полученные вектора начинают вести себя странно в зеркальном отражении, и за это в старой картине мира их называли ‘аксиальными’ или ‘псевдовекторами’. А псевдоскаляры в зеркальном отражении, хоть и выглядят обычными числами, теперь почему-то меняют знак на противоположный. Теперь мы видим, что это странное несимметричное поведение не присутствует в природе, а возникает, когда мы выбираем произвольным образом одно из двух правил для того, чтобы упростить себе жизнь и работать только с одним типом векторов. Но если использовать оба, то законы и движение и все такое происходит логично, отражается в зеркале так, как мы того ожидаем, и не нужно правило правой руки.
Но если использовать оба, то законы и движение и все такое происходит логично, отражается в зеркале так, как мы того ожидаем, и не нужно правило правой руки.





 1 \;\\
\; 30,1 \;
\end{pmatrix}
1 \;\\
\; 30,1 \;
\end{pmatrix} Вектор \textbf{v} равен
Вектор \textbf{v} равен Вот векторное умножение
Вот векторное умножение 0198 .
0198 .