3).вектор направлен в ту сторону, от которого поворот от к на наименьший угол осуществляется против часовой стрелки.
Рис. 1
Алгебраические свойства векторного произведения
Давайте рассмотрим свойства векторного произведения.
Если – произвольные векторы, а – произвольные число, тогда:
- x = x . (Векторное произведение антикоммутативно).
- x = x = x .(Векторное произведение обладает сочетательным свойством относительно скалярного множителя).
- x = x + x .
- x = ||, , . (Два ненулевых вектора коллинеарны только тогда, когда их векторное произведение равно нулевому вектору).
Таблица векторного умножения ортов
x = , x = ;
x = , x = ;
x = , x = .
x = x = x = .
Рис. 2
Векторное произведение одноимённых ортов равняется . При самом коротком повороте от одного орта к другому против часовой стрелки получаем третий орт, а по часовой стрелке – третий орт со знаком .
Формулы векторного произведения в координатной форме
Формулы векторного произведения в координатной форме получаем с учётом таблицы векторного произведения ортов:
x = x = x x x =
x – x + x x =
Примеры нахождения векторного произведения
Чтобы закрепить материал, рассмотрим на примерах, как найти векторное произведение векторов.
Пример 1
Найти векторное произведение векторов = и = . Построить в системе координат векторы и = x .
Обратите внимание, что определитель (1) удобнее вычислять, если применить теорему про разложение за элементами первой строки:
= x = = – + =
Теперь построим векторы по их координатам.
Рис. 3
Из рисунка видно, что положение найденного вектора отвечает определению векторного произведения x .
Пример 2
Найти площадь треугольника , если .
Решение:
Сначала находим векторы:
и и их векторное произведение:
x = = .
Длина полученного вектора по определению численно равняется площади параллелограмма, построенного на данных векторах и поэтому:
пар = x = = .
А площадь треугольника составляет половину найденной площади, то есть:
тр. = пар = x x ,
Средняя оценка 0 / 5. Количество оценок: 0
Поставьте вашу оценку
Сожалеем, что вы поставили низкую оценку!
Позвольте нам стать лучше!
Расскажите, как нам стать лучше?
7328
Закажите помощь с работой
Не отобразилась форма расчета стоимости? Переходи по ссылке
Не отобразилась форма расчета стоимости? Переходи по ссылке
Алгебра свободных и скользящих векторов
Алгебра свободных и скользящих векторов
ОглавлениеПРЕДИСЛОВИЕВВЕДЕНИЕ ГЛАВА I. ВЕКТОРНАЯ АЛГЕБРА 2. Определение вектора.  3. Классификация векторов. 4. Равенство векторов. 5. Перенос вектора. 6. Нуль-вектор. 7. Компланарность и коллинеарность векторов. 8. Прямопротивоположные векторы. § 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ 2. Сумма векторов. 3. Свойства суммы векторов. 4. Правила параллелограмма и параллелепипеда. 5. Разность двух векторов. 6. Свойства модуля суммы векторов. § 3. УМНОЖЕНИЕ И ДЕЛЕНИЕ ВЕКТОРА НА ЧИСЛО 2. Свойства произведения. 3. Деление вектора на число. 4. Единичные векторы. 5. Орт оси. 6. Коллинеарность двух векторов. § 4. РАЗЛОЖЕНИЕ ВЕКТОРОВ 3. Разложение вектора по трем другим векторам. 4. Разложение вектора по ортам базиса. 2. Условие коллинеарности двух векторов. 3. Условие компланарности трех векторов. 4. Линейная зависимость четырех векторов. § 6. ПРОЕКЦИИ ВЕКТОРА 2. Свойства составляющих вектора. 3. Проекция вектора на ось. 4. Свойства проекций.  5. Угол между векторами. 6. Вычисление проекций вектора. 7. Теорема о проекции сумммы векторов. 8. Псевдоскаляры. § 7. СПОСОБЫ ЗАДАНИЯ ВЕКТОРА 2. Естественный способ задания свободного вектора. 3. Задание свободного вектора с помощью его проекций (координатный метод). 4. Связь между естественным и координатным способами задания вектора. 6. Задание скользящего вектора. 7. Некоторые приложения. § 8. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ 2. Свойства скалярного произведения. 3. Выражение скалярного произведения через проекции векторов. 4. Векторные уравнения геометрических мест. 5. Уравнение плоскости. 7. Изменение проекций вектора при преобразовании координат. 8. Другое определение вектора. § 9. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ 2. Примеры из физики. 3. Способ Н. Е. Жуковского построения векторного произведения. 4. Свойства векторного произведения. 5. Разложение вектора-произведения по координатным ортам.  6. Условие коллинеарности двух векторов. 7. Тождество Лагранжа. 8. Полярные и аксиальные векторы. § 10. СЛОЖНЫЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ 2. Двойное векторное произведение. 3. Разложение вектора по трем другим векторам. 4. Скалярное произведение двух векторных произведений. 5. Векторное произведение двух векторных произведений. 6. Произведение двух смешанных произведений. 7. Взаимные реперы. § 11. ВЕКТОРНЫЕ УРАВНЕНИЯ ПРЯМОЙ ЛИНИИ 2. Уравнение прямой, проходящей через две заданные точки. 3. Плюкерово уравнение прямой в пространстве. 4. Прямая как пересечение двух плоскостей. ГЛАВА II. АЛГЕБРА СКОЛЬЗЯЩИХ ВЕКТОРОВ § 13. МОМЕНТ ВЕКТОРА ОТНОСИТЕЛЬНО ТОЧКИ И ОСИ. ЗАДАНИЕ СКОЛЬЗЯЩЕГО ВЕКТОРА 2. Момент вектора относительно точки. 3. Проекции момента. 4. Момент вектора относительно оси. 5. Задание скользящего вектора его проекциями и моментами относительно координатных осей.  § 14. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИСТЕМЫ ВЕКТОРОВ 2. Главный вектор системы векторов. 3. Главный момент системы векторов. 4. Система двух равнопротивоположных векторов. 6. Изменение главного момента с изменением полюса. 7. Инварианты системы векторов. 8. Минимальный момент и центральная ось системы. 9. Распределение главных моментов в пространстве. 10. Понятие о винте. 11. Винт системы векторов. § 15. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ ВЕКТОРОВ 2. Основные определения и аксиомы. § 16. ПРИВЕДЕНИЕ СИСТЕМЫ СВОБОДНЫХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ § 17. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ 2. Приведение произвольной системы скользящих векторов к системе двух векторов (геометрическое решение). § 18. УСЛОВИЯ ЭКВИВАЛЕНТНОСТИ ДВУХ СИСТЕМ СКОЛЬЗЯЩИХ ВЕКТОРОВ 2. Условия эквивалентности двух систем скользящих векторов. 3. Преобразование эквивалентных систем. 1. Пара векторов и ее момент.  2. Свойства пар. 3. Винт § 20. ПРИВЕДЕНИЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ 2. Приведение системы скользящих векторов к системе двух векторов (аналитическое решение). 3. Приведение системы скользящих векторов к вектору и паре. 4. Пример из кинематики. 5. Приведение системы скользящих векторов к винту. 6. Примеры. 7. Уравнения равновесия векторов. 8. Вторая теорема Вариньона. § 21. ИССЛЕДОВАНИЕ ЧАСТНЫХ СЛУЧАЕВ 2. Плоская система скользящих векторов. 3. Система параллельных скользящих векторов. 4. Центр системы параллельных векторов. |
Как применять формулу перекрестного произведения в многомерном исчислении
В векторном исчислении перекрестное произведение двух векторов — это специальная операция, которая дает новый вектор, перпендикулярный обоим исходным векторам. Перекрестное произведение имеет множество приложений в многомерном исчислении и вычислительной геометрии. В этой обзорной статье мы дадим определение векторному произведению и исследуем его свойства. Вы узнаете, как рассчитать перекрестное произведение, как вывести формулу перекрестного произведения и как использовать формулу перекрестного произведения в различных приложениях.
В этой обзорной статье мы дадим определение векторному произведению и исследуем его свойства. Вы узнаете, как рассчитать перекрестное произведение, как вывести формулу перекрестного произведения и как использовать формулу перекрестного произведения в различных приложениях.
Перекрестное произведение двух векторов
Для описания векторов в трехмерном пространстве воспользуемся стандартным ортонормированным базисом в правой системе координат, который образован векторами \vec{i} , \vec {j} и \vec{k} . Здесь \vec{i} = (1,0,0) — единичный вектор вдоль оси x, \vec{j} = (0,1,0) — единичный вектор вдоль оси y, а \ vec{k} = (0,0,1) — единичный вектор вдоль оси z. Любой вектор \vec{a} = (a_x, a_y, a_z) в трех измерениях может быть однозначно выражен как линейная комбинация векторов \vec{i} , \vec{j} и \vec{k} следующим образом :
\vec{a} = a_x \vec{i} + a_y \vec{j} + a_z \vec{k}
На следующем рисунке показано разложение вектора \vec{a} на стандартные базисные векторы:
 Источник изображения: Wikimedia Commons
Источник изображения: Wikimedia Commons Для двух произвольных векторов \vec{a} = (a_x, a_y, a_z) и \vec{b} = (b_x, b_y, b_z) в пространстве векторное произведение \vec{c} = \vec{a} \times \vec{b} — новый вектор, \vec{c} = (c_x, c_y, c_z) , такой, что
\begin{array}{c} c_x = a_y b_z — a_z b_y c_y = a_z b_x — a_x b_z c_z = a_x b_y — a_y b_x \end{array}
Это определение можно запомнить, записав перекрестное произведение в виде определителя:
\vec{c} = \vec{a} \times \vec{b} = \det \left|\begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} a_x & a_y & a_z b_x & b_y & b_z \end{массив} \right| = (a_y b_z — a_z b_y) \vec{i} + (a_z b_x — a_x b_z) \vec{j} + (a_x b_y — a_y b_x) \vec{k}
Следующий пример иллюстрирует это определение.
Пример 1
Пусть \vec{a} = (1,-3,1) и \vec{b} = (-1,-1,1) . Перекрестное произведение двух векторов \vec{a} и \vec{b} в этом случае представляет собой новый вектор, \vec{c}, который можно вычислить следующим образом:
\vec{c} = \ vec{a} \times \vec{b} = \det \left|\begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} 1 & -3 & 1 -1 & -1 & 1 \end{массив} \right| = (-3+1) \vec{i} + (-1-1) \vec{j} + (-1-3) \vec{k} = -2 \vec{i} -2 \vec{j } -4 \vec{к}
В компонентной записи имеем \vec{c} = \vec{a} \times \vec{b} = (-2,-2,-4).
Формула перекрестного произведения
Для двух векторов \vec{a} и \vec{b} удобно выбрать такую систему координат, чтобы оба вектора лежали в плоскости x-y, а ось x была параллельна вектор \vec{a} . В этом случае мы имеем \vec{a} = (|\vec{a}|,0,0) и \vec{b} =(|\vec{b}| cos\theta,|\vec{b} |sin\theta,0) , где |\vec{a}| и |\vec{b}| — нормы векторов \vec{a} и \vec{b} соответственно, а \theta — угол между векторами. По определению векторное произведение векторов \vec{a} и \vec{b} в такой системе координат равно
\vec{a} \times \vec{b} = \det \left|\begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} |\vec{a }| & 0 & 0 |\vec{b}| cos\тета & |\vec{b}| sin\theta & 0 \end{массив} \right| = |\vec{a}|,|\vec{b}| грех\тета,\vec{k}
В компонентной нотации мы можем написать \vec{a} \times \vec{b} =(0,0,|\vec{a}|,|\vec{b}| sin\theta) . Этот результат раскрывает некоторые важные свойства перекрестного произведения:
1. Перекрестное произведение двух векторов, \vec{a} и \vec{b} , есть вектор \vec{a} \times \vec{b} , который перпендикулярен как к \vec{a}, так и к \vec{b}
2. Перекрестное произведение \vec{a} \times \vec{b} указывает направление, из которого поворот от \vec{a} к \vec{b} (через меньший из двух возможных углов) кажется против часовой стрелки
Перекрестное произведение \vec{a} \times \vec{b} указывает направление, из которого поворот от \vec{a} к \vec{b} (через меньший из двух возможных углов) кажется против часовой стрелки
3. В отличие от скалярного произведения, векторное произведение не является коммутативной операцией, и \vec{b} \times \vec{a} = — ,\vec{a} \times \vec{b} . Мы можем легко проверить это свойство прямым вычислением:
\vec{b} \times \vec{a} = \left|\begin{array}{ccc} \vec{i} & \vec{j} & \vec {к} |\vec{b}| cos\тета & |\vec{b}| sin\theta & 0 |\vec{a}| & 0 & 0 \end{массив} \right| = — ,|\vec{a}|,|\vec{b}| sin\theta ,\vec{k} = — ,\vec{a} \times \vec{b} 9{\circ} ), векторным произведением является нулевой вектор: \vec{a} \times \vec{b} = \vec{0} = (0,0,0)
5. Величина векторного произведения двух векторов, | \vec{a} \times \vec{b} | , можно задать следующим соотношением:
| \vec{a} \times \vec{b} | = |\vec{a}|,|\vec{b}| грех\тета
Это последнее равенство известно как формула перекрестного произведения. Формула перекрестного произведения подразумевает, что величина перекрестного произведения |\vec{a} \times \vec{b}| равно площади параллелограмма, стороны которого имеют векторы \vec{a} и \vec{b}, как показано на следующем рисунке:
Формула перекрестного произведения подразумевает, что величина перекрестного произведения |\vec{a} \times \vec{b}| равно площади параллелограмма, стороны которого имеют векторы \vec{a} и \vec{b}, как показано на следующем рисунке:
Давайте продемонстрируем, как использовать векторное произведение на примерах.
Пример 2
Найдем вектор \vec{c}, перпендикулярный обоим векторам \vec{a} = (1,1,-1) и \vec{b} = (1,-1, 1) . Из-за свойств перекрестного произведения любой вектор, перпендикулярный как к \vec{a}, так и к \vec{b}, параллелен \vec{a} \times \vec{b} . Другими словами, \vec{c} = \alpha \left[ \vec{a} \times \vec{b} \right] , где \alpha — некоторое действительное число. Для перекрестного произведения двух векторов, \vec{a} и \vec{b}, мы имеем
\vec{a} \times \vec{b} = \det \left|\begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} 1 & 1 & — 1 1 & -1 & 1 \end{массив} \right| = (1+1) \vec{i} + (-1-1) \vec{j} + (-1-1) \vec{k} = 2 \vec{i} -2 \vec{j} — 2 \vec{k}
В компонентной записи \vec{a} \times \vec{b} = 2(1,-1,-1), и любой вектор, параллельный (1,-1,-1), перпендикулярен обоим \vec {а} и \vec{b} . {,\prime} : 9{,\простое}| = объявление-BC
{,\prime} : 9{,\простое}| = объявление-BC
Скалярное тройное произведение и объем параллелепипеда
Формула векторного произведения имеет множество применений в вычислительной геометрии. Например, с его помощью можно вычислить объем параллелепипеда. Давайте посмотрим, как это можно сделать. Рассмотрим три вектора, \vec{a} , \vec{b} и \vec{c} , представляющие три ребра параллелепипеда, которые встречаются в одной вершине, как показано на рисунке ниже:
Объем параллелепипеда. Источник изображения: ВикискладОбъем параллелепипеда, V , можно рассчитать следующим образом:
V = S \cdot h
Здесь S — площадь основания, а h — высота этого параллелепипеда. Площадь основания по формуле векторного произведения определяется следующим соотношением:
S = |\vec{b} \times \vec{c}|
Высота параллелепипеда равна проекции вектора \vec{a} на направление \vec{b} \times \vec{c} . Таким образом, мы имеем 9{\ круг} . Теперь мы можем использовать определение скалярного произведения двух векторов:
\vec{m} \cdot \vec{n} = m_x n_x + m_y n_y + m_z n_z = |\vec{m}| |\век{п}| cos\phi
Здесь угол \phi — это угол между векторами \vec{m} и \vec{n} . Следовательно, мы можем написать
Следовательно, мы можем написать
V = S \cdot h = |\vec{b} \times \vec{c}| \cdot |\vec{a}| \кдот | кос\фи | = | (\vec{b} \times \vec{c},)\cdot \vec{a} |
Скалярное произведение вектора на векторное произведение двух других векторов известно как скалярное тройное произведение. Используя определения перекрестного произведения и скалярного произведения, мы можем вывести следующее выражение:
(\vec{b} \times \vec{c},)\cdot \vec{a} = (b_y c_z — b_z c_y) a_x + (b_z c_x — b_x c_z) a_y + (b_x c_y — b_y c_x) a_z = \det \left|\begin{array}{ccc} a_x & a_y & a_z b_x & b_y & b_z c_x & c_y & c_z \end{array} \right|
Из известного свойства определителей следует, что скалярное тройное произведение инвариантно относительно циклических перестановок векторов \vec{a} , \vec{b} и \vec{c} :
(\vec{b} \ раз \vec{c})\cdot \vec{a} = (\vec{c} \times \vec{a})\cdot \vec{b} = (\vec{a} \times \vec{b} )\cdot\vec{с}
Более того, скалярное тройное произведение равно нулю, если любые два вектора \vec{a} , \vec{b} и \vec{c} параллельны. Естественно, объем параллелепипеда в этом случае равен нулю. Отсюда следует, что три вектора линейно зависимы тогда и только тогда, когда их скалярное тройное произведение равно нулю:
Естественно, объем параллелепипеда в этом случае равен нулю. Отсюда следует, что три вектора линейно зависимы тогда и только тогда, когда их скалярное тройное произведение равно нулю:
(\vec{a} \times \vec{b})\cdot \vec{c} = \det \left|\begin{ array}{ccc} a_x & a_y & a_z b_x & b_y & b_z c_x & c_y & c_z \end{array} \right| = 0
Если (\vec{a} \times \vec{b})\cdot \vec{c} > 0 , три вектора \vec{a} , \vec{b} и \vec{c} образуют правый Основа в космосе. Базис является левым в противоположном случае, когда (\vec{a} \times \vec{b})\cdot \vec{c} < 0 . Типичный правый базис состоит из трех векторов \vec{i} , \vec{j} и \vec{k} . Это можно продемонстрировать прямым вычислением:
\vec{i} \times \vec{j} = \det \left|\begin{array}{ccc} \vec{i} & \vec{j} & \vec {k} 1 & 0 & 0 0 & 1 & 0 \end{массив} \right| = \vec{k} , \quad (\vec{i} \times \vec{j})\cdot \vec{k} = \vec{k} \cdot \vec{k} = 1
В следующем примере показано, как можно использовать скалярное тройное произведение.
Пример 4
Предположим, что нам даны три вектора: \vec{a} = (1,2,3) , \vec{b} = (4,5,0) и \vec{c} = (3,2,1) . Давайте вычислим скалярное тройное произведение этих трех векторов:
(\vec{a} \times \vec{b},)\cdot \vec{c} = \det \left|\begin{array}{ccc} 1 & 2 & 3 4 & 5 & 0 3 & 2 & 1 \end{массив} \right| = (5-0) + 2(0-4) + 3(8-15) = -,24
Поскольку (\vec{a} \times \vec{b},)\cdot \vec{c} < 0 , три вектора \vec{a} , \vec{b} и \vec{c} равны линейно независимы и образуют левый базис. Объем параллелепипеда, натянутого на векторы \vec{a} , \vec{b} и \vec{c}, определяется следующим выражением:
V = |(\vec{a} \times \vec{ б},)\cdot \vec{c},| = 24
Перекрестное произведение и изгиб векторного поля
Перекрестное произведение играет важную роль в многомерном исчислении. Рассмотрим векторное поле \vec{v}(\vec{r},) = {v_x(x,y,z), v_y(x,y,z), v_z(x,y,z)} . Векторное поле \vec{v}, определенное таким образом, имеет важную дифференциальную характеристику; а именно, завиток \vec{v} , обозначаемый curl \vec{v} . По определению, ротор \vec{v} — это просто векторное произведение дифференциального оператора {\ парциальное} {\ парциальное г}} :
По определению, ротор \vec{v} — это просто векторное произведение дифференциального оператора {\ парциальное} {\ парциальное г}} :
\text{curl}, \vec{v} = \nabla \times \vec{v} = \det \left|\begin{array}{ccc} \vec{i} & \vec{j} & \ vec{k} \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} v_x & v_y & v_z \end{array} \ правильно|
Отсюда следует, что компоненты \text{curl}, \vec{v} определяются следующим образом:
\begin{array}{c} v_x = \dfrac{\partial v_z}{\partial y} — \dfrac{\partial v_y}{\partial z} v_y = \dfrac{\partial v_x}{\partial z} — \dfrac{\partial v_z}{\partial x} v_z = \dfrac{\partial v_y}{ \partial x} — \dfrac{\partial v_x}{\partial y} \end{массив}
Давайте проиллюстрируем этот метод нахождения ротора векторного поля на простом примере.
Пример 5
Рассмотрим векторное поле \vec{v} = (-y,x,0) . Изгиб \vec{v} можно рассчитать следующим образом:
\text{curl}, \vec{v} = \nabla \times \vec{v} = \det \left|\begin{array} {ccc} \vec{i} & \vec{j} & \vec{k} \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial} {\partial z} -y & x & 0 \end{массив} \right| = \vec{i} \left(-,\dfrac{\partial x}{\partial z}\right) + \vec{j} \left(-,\dfrac{\partial y}{\partial z}\ справа) + \vec{k} \left(\dfrac{\partial x}{\partial x} + ,\dfrac{\partial y}{\partial y}\right) = 2 \vec{k}
Следовательно, в этом случае \text{curl}, \vec{v} является постоянным вектором: \text{curl}, \vec{v} = (0,0,2) .
Завершение перекрестного произведения
В этой обзорной статье мы исследовали перекрестное произведение и его свойства. Теперь вы сможете вычислить векторное произведение двух векторов и ротор вектора. Вы также сможете применить формулу векторного произведения, чтобы найти площадь параллелограмма и объем параллелепипеда. Мы надеемся, что эта статья придаст вам большей уверенности в ваших знаниях о векторном произведении и облегчит изучение многомерного исчисления.
Давайте применим все на практике. Попробуйте этот практический вопрос по многомерному исчислению: Ищете больше упражнений по многомерному исчислению? Вы также можете найти тысячи практических вопросов на Albert.io. Albert.io позволяет вам настроить учебный процесс так, чтобы он ориентировался на практику, в которой вам больше всего нужна помощь. Мы дадим вам сложные практические вопросы, которые помогут вам достичь мастерства в многомерном исчислении.
Начните тренироваться здесь .
Вы учитель или администратор, заинтересованный в повышении успеваемости учащихся по многомерному исчислению?
Узнайте больше о наших школьных лицензиях здесь .
Определение, как сделать перекрестное произведение и свойства
В векторной алгебре описываются различные типы векторов, и над этими векторами можно выполнять различные операции, такие как сложение, вычитание, произведение или умножение. Умножение векторов может быть выполнено двумя способами: точечным произведением и перекрестным произведением. Перекрестное произведение векторной алгебры помогает в вычислении ортогональности двух заданных векторов, вычислении крутящего момента и т. д.
В этой статье мы постараемся узнать о перекрестном произведении двух векторов с определением, правилами, решенными примерами и свойствами перекрестного произведения. Перемножение двух векторов — это процесс умножения двух векторов.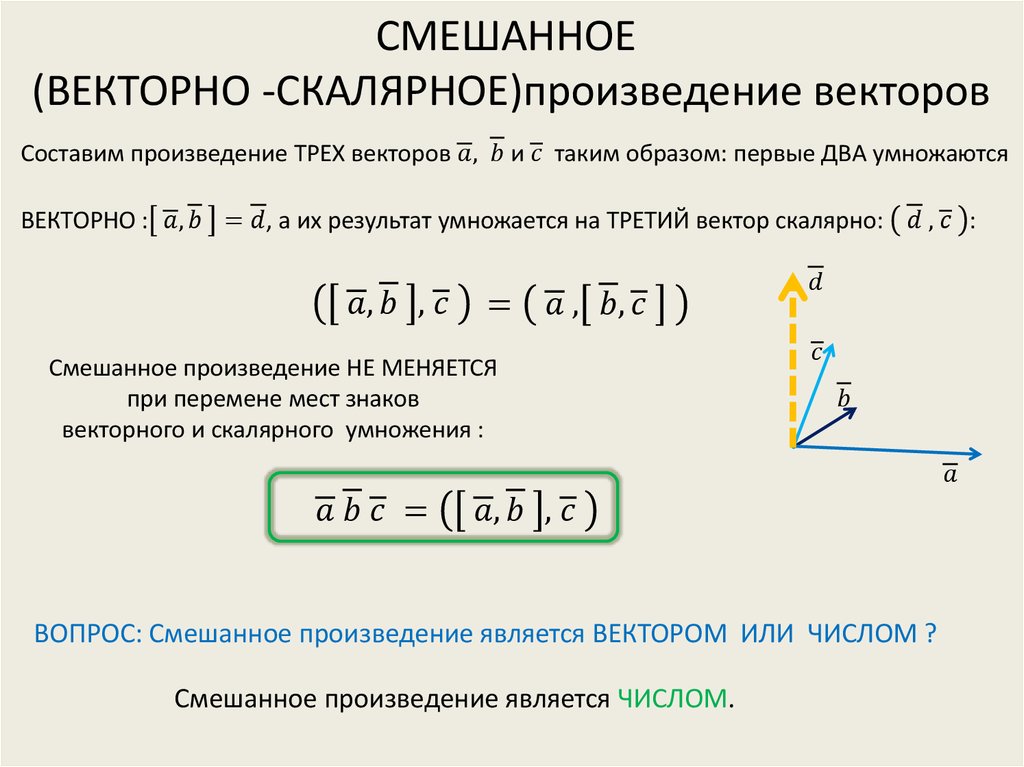 Перекрестное произведение выражается знаком умножения (x) между двумя векторами. Это бинарная векторная операция, проиллюстрированная в трехмерной системе.
Перекрестное произведение выражается знаком умножения (x) между двумя векторами. Это бинарная векторная операция, проиллюстрированная в трехмерной системе.
Перекрестное произведение — это своего рода умножение векторов, выполняемое между двумя векторами различной природы. Вектор обладает как величиной, так и направлением. Мы можем умножать два или более векторов на перекрестное произведение и скалярное произведение.
В результате перекрестного произведения двух векторов третий вектор перпендикулярен двум главным векторам. Его величина представлена площадью параллелограмма среди них, а его направление можно определить по правилу большого пальца правой руки. Перекрестное произведение двух векторов также признается векторным произведением, поскольку результирующая векторного произведения двух векторов является векторной величиной.
Узнайте больше о наборах здесь.
Перекрестное произведение двух векторов Когда два вектора перемножаются друг с другом и конечный продукт данных векторов также является векторной величиной, тогда полученный вектор называется перекрестным произведением двух векторов или векторным произведением. Результирующий вектор перпендикулярен грани, несущей два заданных вектора.
Результирующий вектор перпендикулярен грани, несущей два заданных вектора.
Векторное произведение или перекрестное произведение двух векторов, скажем, вектора «a» и вектора «b», обозначается как a × b , а его результирующий вектор перпендикулярен векторам а и б . Перекрестное произведение в основном применяется для определения вектора, который перпендикулярен плоской поверхности, натянутой на два вектора. Однако скалярное произведение применяется для определения угла между двумя векторами или длины вектора.
Перекрестное произведение двух векторов, скажем, a × b , эквивалентно другому вектору, расположенному под прямым углом к обоим, и появляется в трехмерном пространстве.
Формула перекрестного произведения Формула перекрестного произведения между любыми двумя заданными векторами дает площадь между этими векторами. Формула векторного произведения отражает величину результирующего вектора, который представляет собой площадь параллелограмма, натянутого на два вектора.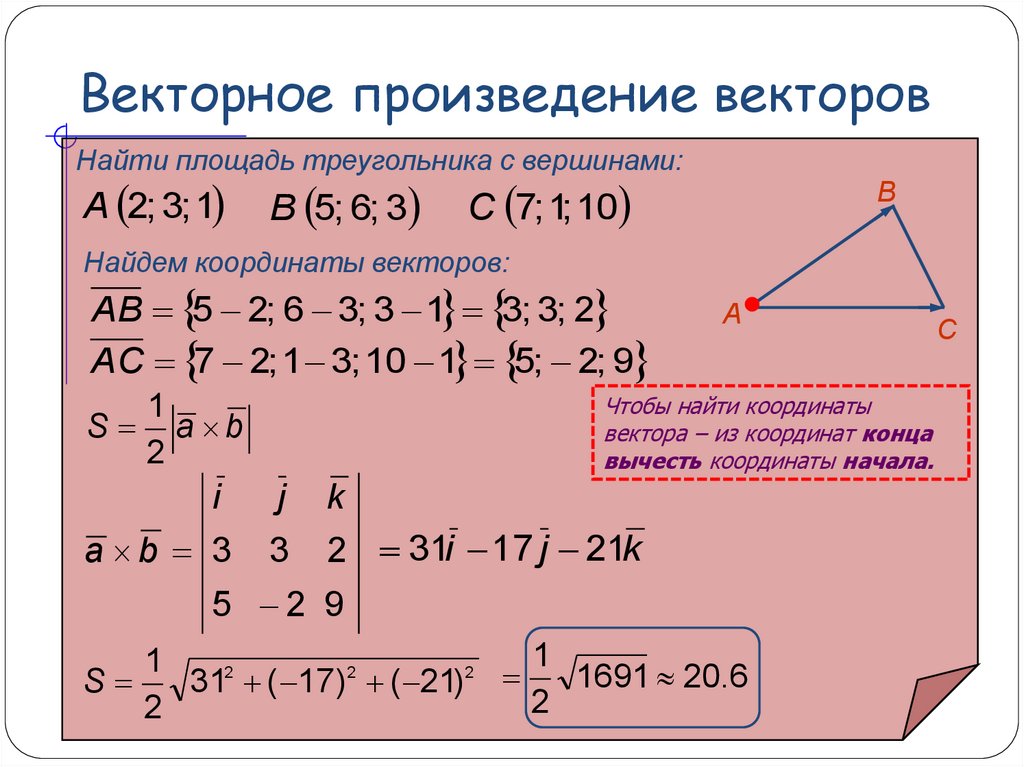
Если \(\theta\) является углом между заданными двумя векторами a и b, , то формула векторного произведения векторов: a вектор b вектор. Математически выражается как:
\(\vec{a}\times\vec{b}=\left|\vec{a}\right|\left|\vec{b}\right|\sinθ\hat{n}\)
Где \(\left|\vec{a}\right|\) и \(\left|\vec{b}\right|\) обозначают величину векторов \(\vec{a}\) и \(\vec{b}\) и \(\theta\) — угол между векторами \(\vec{a}\) и \(\vec{b}\) и \(\hat{n}\ ) — единичный вектор, перпендикулярный обоим векторам \(\vec{a}\) и \(\vec{b}\).
Прочтите эту статью о детерминантах.
- 9{\circ}\) так, чтобы векторное произведение двух векторов было максимальным.
Мы можем предположить это на примере того, что если у нас есть два вектора, простирающиеся в плоскости X-Y, то их векторное произведение даст окончательный результирующий вектор в направлении оси Z, которая перпендикулярна плоскости X-Y. Символ × используется в исходных векторах.
Символ × используется в исходных векторах.
Подробнее о копланарных векторах
Как найти векторное произведение двух векторов? Рассмотрим два вектора \(\vec{a}=a_1\hat{i}+a_2\hat{j}+a_3\hat{k}\) и \(\vec{b}=b_1\hat{i }+b_2\шляпа{j}+b_3\шляпа{k}\). Пусть \(\theta\) — угол, образованный между \(\vec{a}\) и \(\vec{b}\), а \(\hat{n}\) — единичный вектор, перпендикулярный плоскости, содержащей как \(\vec{a}\), так и \(\vec{b}\) . Перекрестное произведение двух векторов можно определить следующим образом:
\(\vec{a}\times\vec{b}=\left(a_1\hat{i}+a_2\hat{j}+a_3\hat{k}\right)\times\left(b_1\hat {i}+b_2\шляпа{j}+b_3\шляпа{k}\право)\)
\(\vec{a}\times\vec{b}=a_1b_1\left(\шляпа{i}\times\ шляпа{i}\правая)+a_1b_2\левая(\шляпа{i}\раз\шляпа{j}\правая)+a_1b_3\левая(\шляпа{i}\раз\шляпа{k}\правая)+a_2b_1\ влево (\ шляпа {j} \ раз \ шляпа {i} \ вправо) \) + \ (a_2b_2 \ влево (\ шляпа {j} \ раз \ шляпа {j} \ вправо) + a_2b_3 \ влево (\ шляпа {j }\times\hat{k}\right)+a_3b_1\left(\hat{k}\times\hat{i}\right)+a_3b_2\left(\hat{k}\times\hat{j}\right )+a_3b_3\влево(\шляпа{к}\раз\шляпа{к}\право)\)
По свойству векторов перекрестного умножения:
\(\hat{i}\times\hat{i}=\hat{j}\times\hat{j}=\hat{k}\times\hat{ k}=0\)
\(\шляпа{i}\times\шляпа{j}=\шляпа{k},\ \шляпа{j}\times\шляпа{k}=\шляпа{i},\ \ шляпа {k} \ раз \ шляпа {i} = \ шляпа {j} \)
\ (\ шляпа {j} \ раз \ шляпа {i} = — \ шляпа {k}, \ \ шляпа {k} \times\hat{j}=-\hat{i},\ \hat{i}\times\hat{k}=-\hat{j}\)
Следовательно, уравнение принимает вид:
\(\vec {a}\times\vec{b}=a_1b_2\шляпа{k}-a_1b_3\шляпа{j}-a_2b_1\шляпа{k}+a_2b_3\шляпа{i}+a_3b_1\шляпа{j}-a_3b_2\шляпа{ я}\)
\(\vec{a}\times\vec{b}=\left(a_2b_3-a_3b_2\right)\hat{i}+\left(a_3b_1-a_1b_3\right)\hat{j}+\left( a_1b_2-a_2b_1\right)\шляпа{k}\)
ИЛИ
\(\vec{a}\times\vec{b}=\left(a_2b_3-a_3b_2\right)\шляпа{i}-\left (a_1b_3-a_3b_1\right)\hat{j}+\left(a_1b_2-a_2b_1\right)\hat{k}\)
Узнать о скалярном тройном произведении
Матрица перекрестного произведения
Тот же полученный результат перекрестного произведения можно сформулировать в матричной форме следующим образом:
\(\vec{a}\times\vec{b}=\left(a_1\hat{i}+a_2\hat{j}+a_3\hat{k}\ вправо)\раз\влево(b_1\шляпа{i}+b_2\шляпа{j}+b_3\шляпа{k}\право)\)
Что эквивалентно:
\(\vec{a}\times\vec{b}=a_1b_2\hat{k}-a_1b_3\hat{j}-a_2b_1\hat{k}+a_2b_3\hat{i }+a_3b_1\шляпа{j}-a_3b_2\шляпа{i}\)
\(\vec{a}\times\vec{b}=\left(a_2b_3-a_3b_2\right)\шляпа{i}+\ влево(a_3b_1-a_1b_3\вправо)\шляпа{j}+\влево(a_1b_2-a_2b_1\вправо)\шляпа{k}\)
ИЛИ
\(\vec{a}\times\vec{b}= \left(a_2b_3-a_3b_2\right)\hat{i}-\left(a_1b_3-a_3b_1\right)\hat{j}+\left(a_1b_2-a_2b_1\right)\hat{k}\)
Матрица представительство:
\(\vec{a}\times\vec{b}=\left[\begin{matrix}\hat{i}&\hat{j}&\hat{k}\\
a_1&a_2&a_3\\
b_1&b_2&b_3\ end{matrix}\right]\)
Также читайте о статистике в этой статье.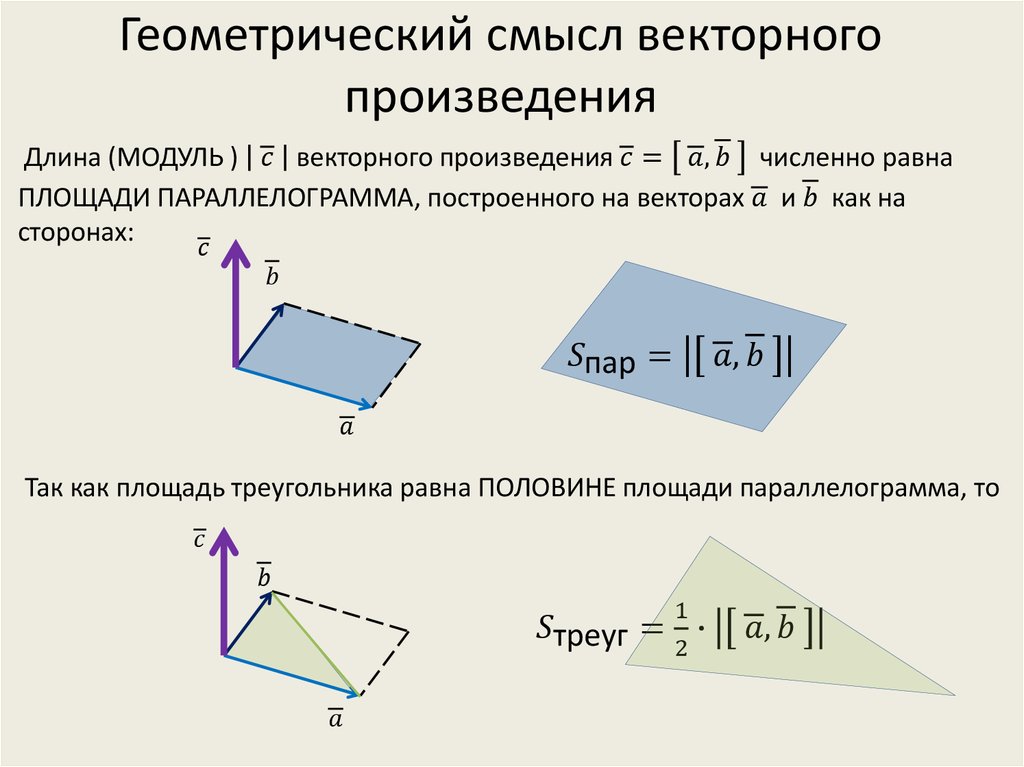
Мы можем определить направление единичного вектора с помощью правила правой руки.
В этом конкретном правиле вытяните правую руку так, чтобы указательный палец правой руки был в направлении первого вектора i,e вектора «A» плюс средний палец был в направлении второго вектора, который является вектором «В». Затем большой палец правой руки показывает направление единичного вектора n.
Это положение большого пальца в направлении векторного произведения двух векторов. Применяя правило правой руки, мы можем просто показать, что векторное произведение векторов не коммутативно. Посмотрите на изображение ниже, чтобы полностью понять этот подход.
Свойства векторного произведения Чтобы получить векторное произведение двух векторов, мы можем применить свойства. Такие свойства, как антикоммутативность, ассоциативность, дистрибутивность, свойство нулевого вектора, играют жизненно важную роль в получении перекрестного произведения двух векторов.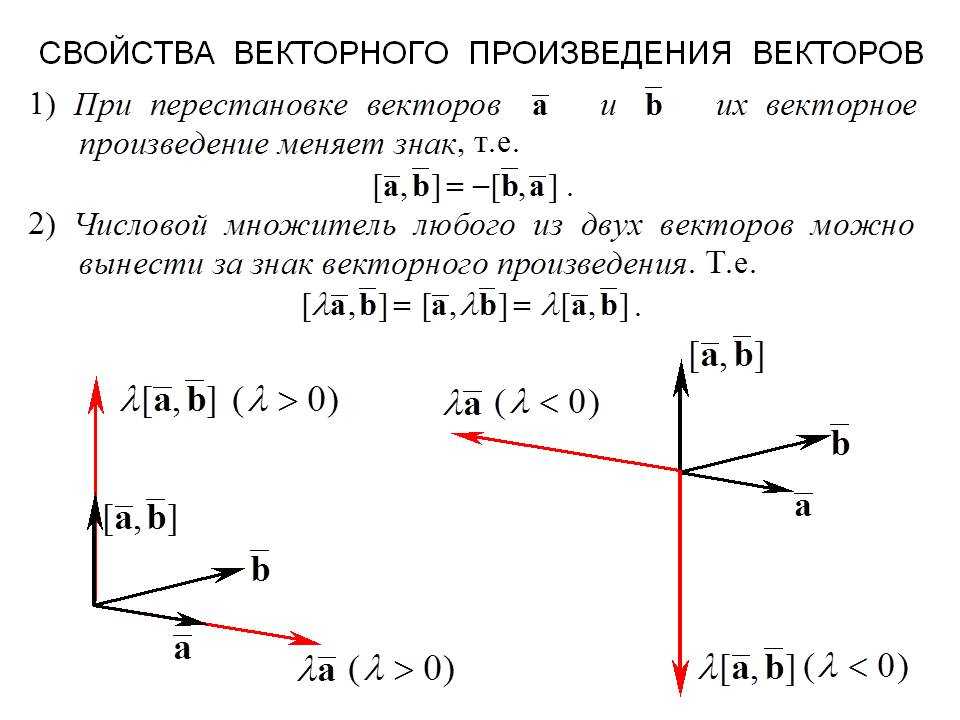 Итак, давайте проверим эти свойства один за другим:
Итак, давайте проверим эти свойства один за другим:
- Длина векторного произведения двух векторов =
- \(\vec{a}\times\vec{b}=\left|\vec{a}\right|\left|\vec{b}\ right|\sinθ\hat{n}\)
- Векторные произведения некоммутативны.
- Если \(\vec{x}\) и \(\vec{y}\) любые два вектора, то:
- \(\vec{x}\times\vec{y}=-\left( \vec{y}\ \times\vec{x}\right)\)
- Векторное произведение ассоциативно относительно скалярного умножения.
- Если \(\vec{x}\) и \(\vec{y}\) — любые два вектора и λ — скаляр, то;
- \(\lambda\left(\vec{x}\times\vec{y}\right)=\left(\lambda\vec{x}\right)\times\vec{y}=\vec{x }\times\left(\lambda\vec{y}\right)\)
- Векторный продукт — это дистрибутив относительно сложения векторов.
- Если \(\vec{x}\), \(\vec{y}\) и \(\vec{z}\) — любые три вектора, то:
- \(\vec{x}\times \left(\vec{y}+\vec{z}\right)=\left(\vec{x}\times\vec{y}\right)+\left(\vec{x}\times\vec{ z}\right)\)
- Перекрестное произведение нулевого вектора или свойства нулевого вектора: \(\vec{a}\times\vec{b}=0\), если a=0 или b=0.

- \(\шляпа{i}\times\шляпа{j}=\шляпа{k},\ \ \шляпа{j}\times\шляпа{k}=\шляпа{i}\ и\ \ \ \ шляпа {k} \ раз \ шляпа {я} = \ шляпа {j} \ \ \)
- \ (\ шляпа {я} \ раз \ шляпа {я} = \ \ шляпа {j} \ раз \ шляпа {j} = \ \ шляпа {k} \ раз \ шляпа {k} = 0 \)
- \ (\ шляпа {j} \ раз \ шляпа {i} = — \ шляпа {k}, \ \ шляпа { k}\times\hat{j}=-\hat{i},\ \hat{i}\times\hat{k}=-\hat{j}\)
- \(\text{If} \vec {x}=x_1\шляпа{i}+x_2\шляпа{j}+x_3\шляпа{k} \text{ и }\vec{y}=y_1\шляпа{i}+y_2\шляпа{j}+y_3 \hat{k}\text{ два вектора, тогда:}\)
- \(\vec{x}\times \vec{y}\left[\begin{matrix}\hat{i}&\hat{j}&\hat{k}\\
x_1&x_2&x_3\\
y_1&y_2&y_3\end {matrix}\right] \) - Тройное перекрестное произведение
Перекрестное произведение вектора с двумя другими векторами означает тройное перекрестное произведение векторов. Конечным результатом тройного векторного произведения является сам вектор. - \(\left(\vec{a}\times\vec{b}\right)\times\vec{c}=\left(\vec{a}⋅\vec{c}\right)\vec{ b}−\left(\vec{b}⋅\vec{c}\right)\vec{a}\) Здесь a, b и c — векторы.

Прочтите эту статью об отношениях и функциях.
Векторы, представляющие собой комбинацию величины и направления, могут применяться для представления физических величин, обычно в физике векторы используются для обозначения смещения, скорости и ускорения, поскольку это становится полезным для анализа физических величин. (включая размер и направление) в виде векторов. Перекрестное произведение векторов находит применение при определении ортогональности двух заданных векторов, вычислении крутящего момента, площади треугольника, параллелограмма и т. д.
- Если \(\vec{x}\) и \(\vec{y}\) две смежные стороны параллелограмма, то площадь параллелограмма:
- \(=\left|\vec{x }\times\vec{y}\right|\)
- Если \(\vec{x}\) и \(\vec{y}\)диагонали параллелограмма, то площадь параллелограмма:
- \(=\left|\vec{x}\times\vec{y}\right|\)
- Если \(\vec{x}\) и \(\vec{y}\) две смежные стороны треугольника, то площадь треугольника:
- \(=\frac{1}{2}\left|\vec{x}\times\vec{y}\right|\)
- Угол между двумя векторами \(\vec{x}\) и \(\vec{y}\) можно определить с помощью векторного произведения по формуле = \(\sinθ=\frac{\left|\vec {a}\times\vec{b}\right|}{\left|\vec{a}\right|\left|\vec{b}\right|}\).

- Поскольку перекрестное произведение двух векторов ортогонально каждому из векторов.
- Перекрестное произведение перпендикулярных векторов =
- \(\vec{a}\times\vec{b}=\left|\vec{a}\right|\left|\vec{b}\right|\sinθ\ шляпа{n}=\left|\vec{a}\right|\left|\vec{b}\right|\sin9{\ circ} \ hat {n} = 0 \)
Проверьте другие темы по математике здесь.
Примеры решения перекрестного произведенияВот некоторые из примеров решения по теме для большей практики:
Пример решения 1: C = 4i + 5j и D = 6i – 4j. Вычислить векторное произведение векторов C и D:
ПОЯСНЕНИЯ:
We C × D = (4i + 5j) × (6i – 4j)
= 24 (i × i ) – 16( i × j ) + 30(j × i) – 20 (j × j)
Мы знаем, что:
\(\шляпа{i}\times\шляпа{j}=\шляпа{k},\ \ \шляпа{j}\times\шляпа{k}=\шляпа{i}\ и \\ \шляпа{k}\times\шляпа{i}=\шляпа{j}\)
\(\шляпа{i}\times\шляпа{i}=\ \шляпа{j}\times\шляпа {j}=\ \шляпа{k}\times\шляпа{k}=0\)
\(\шляпа{j}\times\шляпа{i}=-\шляпа{k},\ \шляпа{k }\times\hat{j}=-\hat{i},\ \\hat{i}\times\hat{k}=-\hat{j}\)
Отсюда получаем:
C × D = -16k -30k = -46 k
, поэтому перекрестное произведение C и D представляет собой вектор величины 46 и в отрицательном направлении z.
Поскольку C и D находятся в плоскости XY, очевидно, что векторное произведение должно быть перпендикулярно этой плоскости, то есть оно должно быть в направлении z.
Решенный Пример 2: Какова величина результирующего перекрестного произведения двух параллельных векторов \(\vec{a}\) и \(\vec{b}\)?
КОНЦЕПЦИЯ:
Векторное произведение: также известно как перекрестное произведение, величина которого равна произведению величины двух векторов и синуса угла между ними, направление которого перпендикулярно плоскости из двух векторов.
Математически это записывается так:
\(\vec{a}\times\vec{b}=\left|\vec{a}\right|\left|\vec{b}\right|\sinθ\ hat{n}\)
Где \(\theta\) — угол между вектором \(\vec{a}\) и \(\vec{b}\). и \(\hat{n}\) — единичный вектор, который перпендикулярен обоим векторам \(\vec{a}\) и \(\vec{b}\).
ОБЪЯСНЕНИЕ:
Математически это записывается так:
\(\vec{a}\times\vec{b}=\left|\vec{a}\right|\left|\vec{b} \right|\sinθ\шляпа{n}\) 9{\ circ} \ шляпа {п} = 0 \).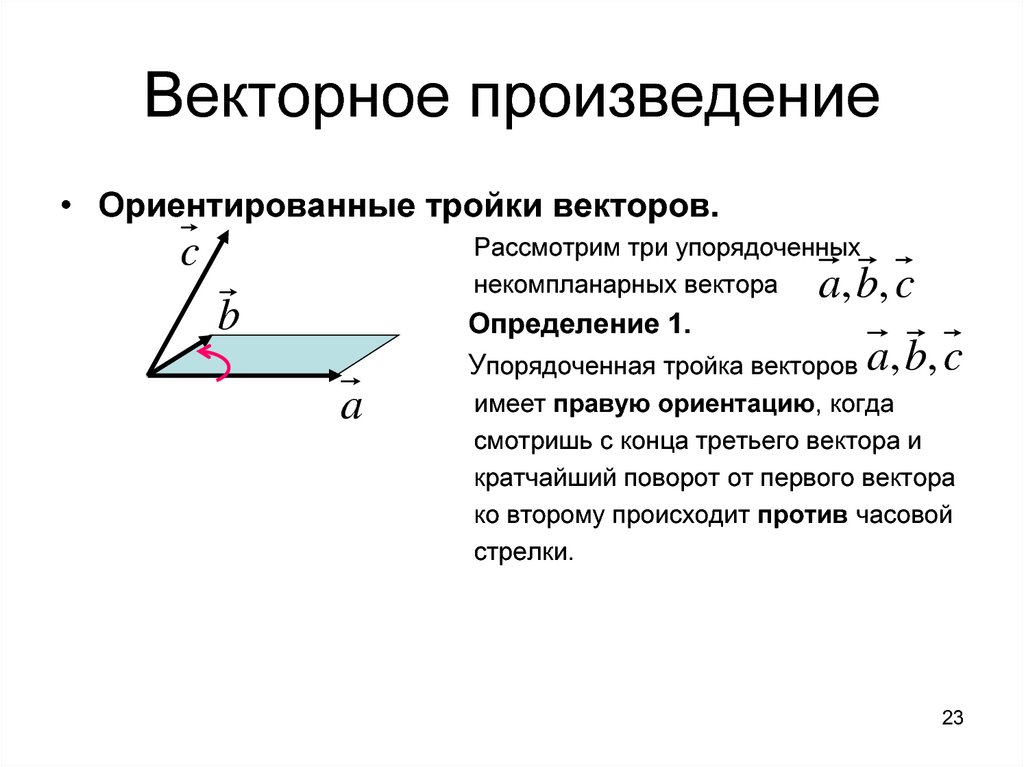
Мы надеемся, что приведенная выше статья о перекрестном произведении поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
Часто задаваемые вопросы о перекрестном произведенииВ.1 Что такое определение перекрестного произведения?
Ответ 1 Когда два вектора перемножаются друг с другом и конечный продукт данных векторов также является векторной величиной, тогда полученный вектор называется перекрестным произведением двух векторов или векторным произведением.
В.2 Как рассчитать перекрестное произведение?
Ans.2 Векторное произведение или перекрестное произведение двух векторов, скажем, вектора «a» и вектора «b», обозначается как a × b, а его результирующий вектор перпендикулярен векторам a и b.
Q.3 Для чего используется перекрестное произведение?
Ответ 3 Перекрестное произведение, используемое для вычисления угла между двумя заданными векторами, для оценки вектора, нормального к плоскости, для вычисления момента силы относительно точки и для определения момента силы о линии.
Q.4 Чему равно векторное произведение двух векторов?
Ответ 4 В результате перекрестного произведения двух векторов получается третий вектор, перпендикулярный двум главным векторам. Его величина представлена площадью параллелограмма среди них, а его направление можно определить по правилу большого пальца правой руки.
В.5 Как работает кросс-произведение?
Ответ 5 Скалярное произведение работает в любом количестве измерений, но перекрестное произведение просто работает в 3D. Скалярное произведение измеряет, насколько два вектора ведут в одном и том же направлении, а векторное произведение измеряет, насколько два вектора указывают в противоположных направлениях.
»
Q.6 Каковы свойства перекрестного произведения?
Ответ 6 Ниже приведены некоторые важные свойства векторных произведений:
- Произведения векторов некоммутативны.
- Векторное произведение ассоциативно относительно скалярного умножения.
- Продукт Vector является дистрибутивным в отношении сложения векторов.
- Перекрестное произведение параллельного вектора = 0.
”
В.7 В чем разница между скалярным произведением и перекрестным произведением?
Ans.7 Основное различие между скалярным произведением и перекрестным произведением заключается в том, что скалярное произведение определяется как произведение величины векторов и cos угла между векторами, с другой стороны, перекрестное Произведение представляет собой произведение величины вектора на синус угла.
Q.8 Каковы типы векторов?
Ответ 8 Различные типы векторов: нулевой вектор, единичный вектор, вектор положения, ко-начальный вектор, похожие и разные векторы, копланарный вектор, коллинеарный вектор, равный вектор, вектор смещения и отрицательные векторы.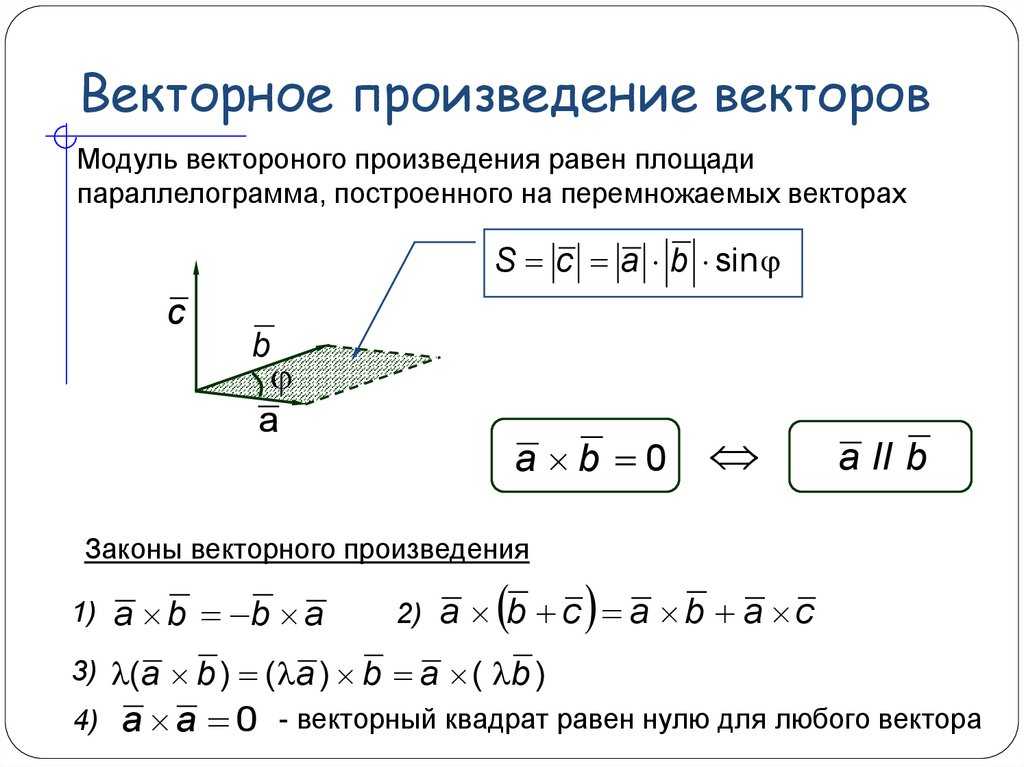


 М: изд-во «Физматгиз», 1962 — 165 с.
М: изд-во «Физматгиз», 1962 — 165 с.


