Скалярное и векторное произведения векторов

Вы можете ознакомиться и скачать презентацию на тему Скалярное и векторное произведения векторов. Доклад-сообщение содержит 25 слайдов. Презентации для любого класса можно скачать бесплатно. Если материал и наш сайт презентаций Mypresentation Вам понравились – поделитесь им с друзьями с помощью социальных кнопок и добавьте в закладки в своем браузере.

Слайды и текст этой презентации

---

Слайд 1

Описание слайда:

Математика. Лекция 3. Скалярное и векторное произведения векторов.

---

Слайд 2

Описание слайда:

В отличие от умножения двух чисел операция умножения вектора на вектор может быть определена двумя различными способами, каждый из которых имеет своё математическое и прикладное значение. В отличие от умножения двух чисел операция умножения вектора на вектор может быть определена двумя различными способами, каждый из которых имеет своё математическое и прикладное значение.

---

Слайд 3

Описание слайда:

Скалярным произведением векторов называют число, равное произведению модулей перемножаемых векторов на косинус угла между ними:

---

Слайд 4

Описание слайда:

---

Слайд 5

Описание слайда:

Свойства скалярного произведения. Скалярное произведение двух векторов обладает переместительным свойством :

---

Слайд 6

Описание слайда:

Свойства скалярного произведения. Скалярное произведение двух векторов равно произведению модуля одного из векторов и проекции другого вектора на направление первого:

---

Слайд 7

Описание слайда:

Свойства скалярного произведения. Проекция вектора на некоторое направление равна скалярному произведению единичного вектора рассматриваемого направления и данного вектора.

---

Слайд 8

Описание слайда:

Свойства скалярного произведения. Скалярное произведение обладает сочетательным свойством относительно скалярного множителя. Скалярное произведение обладает распределительным свойством

---

Слайд 9

Описание слайда:

Свойства скалярного произведения. Скалярное произведение равно нулю, если равен нулю один из перемножаемых векторов или косинус угла между ними (т.е. векторы ортогональны). Это утверждение непосредственно следует из определения. Верно и обратное : если векторы ортогональны, то их скалярное произведение равно нулю. Для того, чтобы два ненулевых вектора были ортогональны, необходимо и достаточно равенство нулю их скалярного произведения.

---

Слайд 10

Описание слайда:

Свойства скалярного произведения. Скалярное произведение вектора самого на себя равно квадрату его модуля. Модуль вектора равен корню квадратному из скалярного квадрата этого вектора.

---

Слайд 11

Описание слайда:

Скалярное произведение в координатной форме Пусть векторы заданы в координатной форме Выразим скалярное произведение векторов через их координаты, для чего воспользуемся разложением векторов по координатным осям и полученными свойствами скалярного произведения

---

Слайд 12

Описание слайда:

Скалярное произведение в координатной форме

---

Слайд 13

Описание слайда:

Скалярное произведение в координатной форме

---

Слайд 14

Описание слайда:

Правые и левые тройки векторов.

Назовём тройку векторов правой, если кратчайший поворот от первого вектора ко второму будет виден с конца третьего вектора происходящим против хода часовой стрелки.

---

Слайд 15

Описание слайда:

Векторное произведение двух векторов. Векторным произведением вектора на вектор назовём вектор , направленный перпендикулярно к обоим векторам, образующим с этими векторами в порядке правую тройку и по модулю равный площади параллелограмма, построенного на векторах и как на сторонах.

---

Слайд 16

Описание слайда:

Векторное произведение двух векторов. Для векторного произведения будем использовать обозначения или . С векторным произведением связаны многие физические величины: момент силы относительно центра; скорость точки при вращательном движении твёрдого тела; сила, действующая на движущийся в магнитном поле заряд.

---

Слайд 17

Описание слайда:

---

Слайд 18

Описание слайда:

Свойства векторного произведения При перестановке сомножителей векторное произведение меняет знак, сохраняя модуль. Векторное произведение обладает распределительным свойством:

---

Слайд 19

Описание слайда:

Свойства векторного произведения Векторное произведение обладает сочетательным свойством относительно скалярного множителя. Если векторное произведение равно нуль-вектору, то либо один из сомножителей равен нуль-вектору, либо синус угла между векторами равен нулю, то есть векторы коллинеарны.

---

Слайд 20

Описание слайда:

Векторное произведение в координатных ортов.

---

Слайд 21

Описание слайда:

Векторное произведение в координатной форме

---

Слайд 22

Описание слайда:

Смешанное произведение трех векторов Рассмотрим три вектора и первые два вектора умножим векторно, а затем полученный вектор умножим скалярно на третий вектор , в итоге получим число. Такое произведение называют смешанным произведением трёх векторов: Для записи смешанного произведения используют также еще одну форму записи:

---

Слайд 23

Описание слайда:

Смешанное произведение трех векторов Пусть векторы заданы в координатной форме. Тогда смешанное произведение через координаты сомножителей выражается как определитель 3-го порядка:

---

Слайд 24

Описание слайда:

Смешанное произведение трех векторов Объём параллелепипеда, построенного на трех некомпланарных векторах, как на сторонах, равен модулю их смешанного произведения.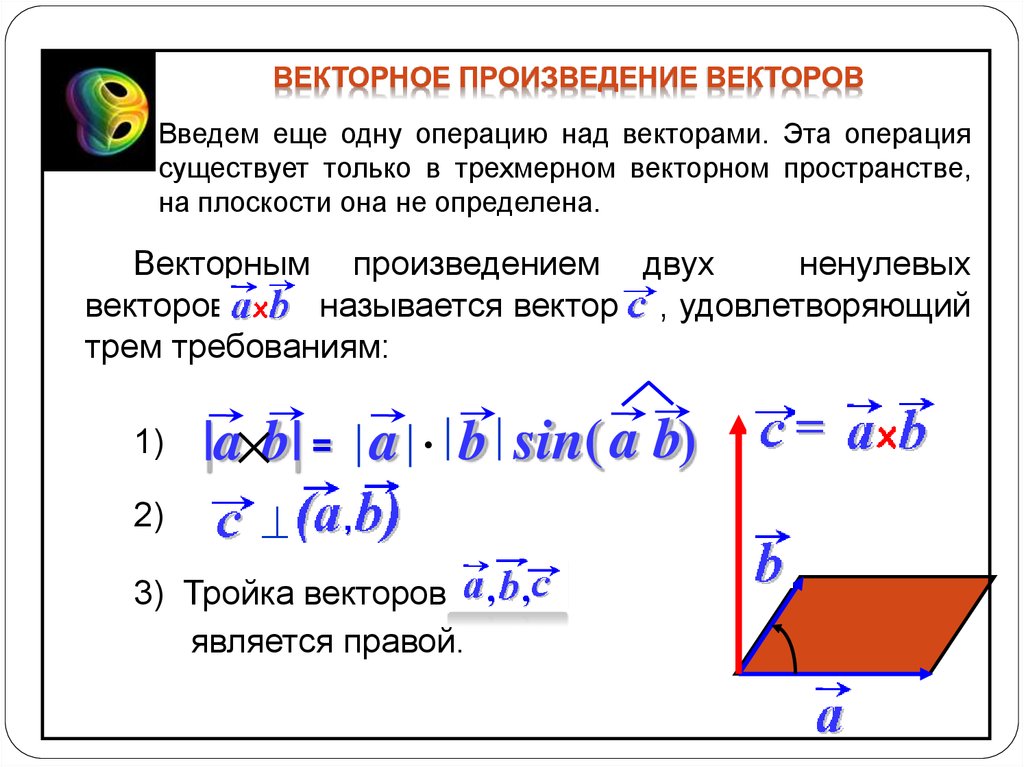 Для компланарности трёх векторов необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.

---

Слайд 25

Описание слайда:

Лекция окончена. Спасибо за внимание.

---

Three.js

.isVector3

Свойство используется для проверки, является ли данный класс и производные от него классы трехмерными векторами (Vector3). Значением по умолчанию является

true

.
Не изменяйте это свойство, так как оно используется для оптимизации внутри three.js.

.x

.y

.z

.add( v )

Метод добавляет к данному вектору вектор

v

.

.addScalar( s )

Метод добавляет скалярное значение

s

к значениям данного вектора

x

,

y

и

z

.

.addScaledVector( v, s )

Добавляет к данному вектору множество из вектора (

v

) и скаляра (

s

).

.addVectors( a, b )

Устанавливает данный вектор как сумму векторов

a + b

.

.angleTo( v )

Метод возвращает угол в радианах между данным вектором и вектором, указанном в параметре

v

.

.applyAxisAngle( axis, angle )

axis — нормализованный вектор Vector3.

angle — угол в радианах.

Метод применяет к данному вектору поворот, определяемый осями (параметр

axis

) и углом (параметр

angle

).

.applyEuler( euler )

Метод конвертирует угол Эйлера, заданный в параметре

euler

, в кватернион и применяет его к данному вектору.

.applyMatrix3( m )

Метод умножает данный вектор на матрицу, указанную в параметре

m

.

.applyMatrix4( m )

Перемножает данный вектор (с подразумеваемой 

1

в четвертом измерении) с матрицей

m

и делит согласно перспективы.

.applyQuaternion( quaternion )

Метод перемножает данный вектор с кватернионом, переданным в аргументе

quaternion

.

.ceil( )

Компоненты вектора

x

,

y

и

z

округляются вверх до ближайшего целочисленного значения.

.clamp( min, max )

min — минимальные значения x, y и z в желаемом диапазоне.

max — максимальные значения x, y и z в желаемом диапазоне.

Если значение

x

,

y

или

z

данного вектора больше значения

x

,

y

или

z

вектора, указанного в параметре

max

, оно заменяется этим соответствующим значением.
Если значение

x

,

y

или

z

данного вектора меньше значения

x

,

y

или

z

вектора, указанного в параметре

min

, оно заменяется этим соответствующим значением.

.clampLength( min, max )

min — минимальное значение длины, на котором она будет зафиксирована (зажата).

max — максимальное значение длины, на котором она будет зафиксирована (зажата).

Если длина данного вектора больше значения, указанного в параметре

max

, она заменяется на значение

max

.
Если длина данного вектора меньше значения, указанного в параметре

min

, она заменяется на значение

min

.

.clampScalar( min, max )

min — минимальное значение компонентов, на котором они будут зафиксированы (зажаты).

max — максимальное значение компонентов, на котором они будут зафиксированы (зажаты).

Если значение

x

,

y

или

z

данного вектора больше значения, указанного в параметре

max

, оно заменяется на значение

max

.
Если значение

x

,

y

или

z

данного вектора меньше значения, указанного в параметре

min

, оно заменяется на значение

min

.

.clone( )

Возвращает новый Vector3 с такими же значениями

x

,

y

и

z

, что и у данного вектора.

.copy( v )

Копирует значения свойств

x

,

y

и

z

из вектора, переданного в параметре

v

, в данный трехмерный вектор.

.cross( v )

Метод устанавливает данный вектор как векторное произведение (в англоязычном варианте это cross product) самого себя и вектора, указанного в параметре

v

.

.crossVectors( a, b )

Устанавливает данный вектор как векторное произведение (в англоязычном варианте это cross product) векторов, указанных в параметрах

a

и

b

.

.distanceTo( v )

Метод вычисляет расстояние от данного вектора до вектора, указанного в параметре

v

.

.distanceToManhattan( v )

Метод вычисляет манхэттенское расстояние (Manhattan length) от данного вектора до вектора, указанного в параметре

v

.

.distanceToSquared( v )

Вычисляет квадрат расстояния от данного вектора до вектора, указанного в параметре

v

. При простом сравнении одного расстояния с другим взамен следует сравнивать именно квадраты расстояний, так как это вычисление несколько более эффективно.

Примечание переводчика: Вычисление расстояния методом distanceTo это вычисление квадратного корня из результата, полученного методом distanceToSquared.

.divide( v )

Метод делит данный вектор на вектор, указанный в параметре 

v

.

.divideScalar( s )

Делит данный вектор на скалярное значение 

s

. Если значение скаляра равно нулю (

s = 0

), вектор устанавливается как 

(0, 0, 0)

.

.dot( v )

Метод вычисляет скалярное произведение (dot product) данного вектора и вектора, переданного в параметре

v

.

.equals( v )

Метод проверяет точное равенство данного вектора и вектора, переданного в параметре

v

.

.floor( )

Этим методом компоненты вектора округляются вниз, до ближайшего целочисленного значения.

.fromArray ( array, offset )

array — исходный массив в виде [x, y, z, w].

offset — смещение массива (дополнительный, необязательный параметр). Значение по умолчанию равно 0.

Метод устанавливает для данного вектора значение

x

равное

array[ offset + 0 ]

, значение

y

равное

array[ offset + 1 ]

и значение

z

равное

array[ offset + 2 ]

.

.fromBufferAttribute( attribute, index )

attribute — исходный атрибут.

index — индекс в атрибуте.

Устанавливает значения

x

,

y

и

z

данного вектора из атрибута, указанного в параметре

attribute

.

.getComponent( index )

index — целочисленное значение, может быть 0, 1 или 2.

Если индекс равен 

0

, возвращается значение 

x

.
Если индекс равен 

1

, возвращается значение 

y

.
Если индекс равен 

2

, возвращается значение 

z

.

.length( )

Вычисляет евклидову длину(Euclidean length), т.е. расстояние по прямой линии, от точки начала координат

(0, 0, 0)

до точки с заданными координатами

(x, y, z)

.

.lengthManhattan( )

Метод вычисляет манхэттенское расстояние (Manhattan length) данного вектора.

.lengthSq( )

Метод вычисляет квадрат евклидовой длины(Euclidean length), т.е. квадрат расстояния по прямой линии, от точки начала координат

(0, 0, 0)

до точки с заданными координатами

(x, y, z)

. При сравнении длин векторов, взамен сравнения длин, следует сравнивать квадраты длины, так как для расчета это несколько более эффективно.

Примечание переводчика: Вычисление длины вектора методом length это вычисление квадратного корня из результата, полученного методом lengthSq.

.lerp( v, alpha )

v — трехмерный вектор (Vector3), до которого будет проводится операция интерполирования.

alpha — коэффициент интерполяции в закрытом интервале [0, 1].

Метод выполняет операцию линейного интерполирования между данным вектором и вектором, переданным в параметре 

v

, с коэффициентом интерполяции 

alpha

, причем 

alpha

можно рассматривать как расстояние вдоль линии соединения этих двух векторов — при

alpha = 0

, он будет равен данному вектору, а при

alpha = 1

— вектору 

v

.

.lerpVectors( v1, v2, alpha )

v1 — начальный трехмерный вектор (Vector3).

v2 — трехмерный вектор (Vector3), до которого будет проводится операция интерполирования.

alpha — коэффициент интерполяции в закрытом интервале [0, 1].

Метод устанавливает данный вектор как линейно интерполированный вектор между векторами 

v1

и 

v2

, и где

alpha

— это расстояние вдоль линии соединения этих двух векторов — при

alpha = 0

, он будет равен вектору 

v1

, при

alpha = 1

— вектору 

v2

.

.max( v )

Если значение

x

,

y

или

z

данного вектора меньше значения

x

,

y

или

z

вектора, переданного в параметре

v

, то это значение заменяется соответствующим значением вектора

v

.

.min( v )

Если значение

x

,

y

или

z

данного вектора больше значения

x

,

y

или 

z

вектора, переданного в параметре 

v

, то это значение заменяется соответствующим значением вектора 

v

.

.multiply( v )

Метод умножает данный вектор на вектор, указанный в параметре 

v

.

.multiplyScalar( s )

Метод умножает данный вектор на скаляр, переданный в параметре 

s

.

.multiplyVectors( a, b )

Устанавливает данный вектор равным произведению

a × b

.

.negate( )

Метод инвертирует данный вектор, т.е. устанавливает

x = -x

,

y = -y

и

z = -z

.

.normalize( )

Метод преобразовывает данный вектор в единичный вектор (unit vector) — то есть, направление его остается тем же самым, а длина вектора (

length

) устанавливается равной 

1

.

.project( camera )

camera — камера, используемая в проекции.

Метод проецирует вектор на камеру.

.projectOnPlane( planeNormal )

planeNormal — вектор, представляющий нормаль к плоскости.

Метод проецирует данный вектор на плоскость путем вычитания из данного вектора проекции данного вектора на нормаль к этой плоскости.

.projectOnVector( Vector3 )

Метод проецирует данный вектор на другой вектор (параметр

Vector3

).

.reflect( normal )

normal — нормаль (перпендикуляр) к плоскости отражения.

Метод отражает вектор от плоскости, перпендикулярной (ортогональной) к нормали (параметр

normal

). Предполагается что нормаль имеет единичную длину.

.round( )

Метод округляет компоненты вектора до ближайшего целочисленного значения.

.roundToZero( )

Метод округляет компоненты вектора к нулю (если значение отрицательно — происходит округление вверх, если положительное — вниз) до целочисленного значения.

.set( x, y, z )

Устанавливает компоненты

x

,

y

и

z

данного вектора.

.setComponent( index, value )

index — целочисленное значение, может быть 0, 1 или 2.

value — число с плавающей запятой.

Если индекс равен 

0

, устанавливается значение 

x

.
Если индекс равен 

1

, устанавливается значение 

y

.
Если индекс равен 

2

, устанавливается значение 

z

.

.setFromCylindrical( c )

Метод устанавливает данный вектор из координат в цилиндрической системе, переданных в 

c

.

.setFromMatrixColumn( matrix, index )

Устанавливает компоненты

x

,

y

и

z

данного вектора равными колонке матрицы (аргумент

matrix

), определяемой по индексу (

index

).

.setFromMatrixPosition( m )

Метод устанавливает данный вектор равным элементам положения матрицы преобразования, переданной в аргументе 

m

.

.setFromMatrixScale( m )

Метод устанавливает данный вектор равным элементам масштабирования матрицы преобразования, переданной в аргументе 

m

.

.setFromSpherical( s )

Метод устанавливает данный вектор из координат в сферической системе, переданных в 

s

.

.setLength( l )

Метод устанавливает данный вектор как вектор с тем же самым направлением, но длиной (

length

) равной значению, переданному в 

l

.

.setScalar( scalar )

Устанавливает значения компонентов

x

,

y

и

z

данного вектора равными скалярному значению, указанному в параметре

scalar

.

.setX( x )

Метод заменяет значение

x

данного вектора на значение, переданное в параметре 

x

.

.setY( y )

Метод заменяет значение

y

данного вектора на значение, переданное в параметре

y

.

.setZ( z )

Метод заменяет значение

z

данного вектора на значение, переданное в параметре

z

.

.sub ( v )

Метод вычитает из данного вектора вектор, указанный в параметре 

v

.

.subScalar( s )

Метод вычитает из компонентов

x

,

y

и

z

данного вектора скалярное значение, указанное в параметре 

s

.

.subVectors( a, b )

Метод устанавливает данный вектор как разность векторов

a — b

.

.toArray( array, offset )

array — дополнительный, необязательный массив для хранения вектора. Если он не предоставлен, создается новый массив.

offset — дополнительное, необязательное смещение в массиве.

Возвращает массив в виде

[x, y, z]

, или копирует

x

,

y

и

z

в предоставленный (

array

) массив.

.transformDirection( m )

Метод изменяет данный вектор на матрицу (набор

3 × 3

вверху слева в матрице, переданной в параметре

m

) и затем нормализует результат.

. unproject( camera )

camera — камера, используемая в проекции.

Отменяет проецирование вектора на проекционную матрицу камеры.

линейная алгебра. Является ли векторное произведение двух единичных векторов единичным вектором?

спросил 11 лет, 10 месяцев назад

Изменено 2 месяца назад

Просмотрено 49 тысяч раз

$\begingroup$

Или, вообще, что означает величина перекрестного произведения? Как бы вы это доказали или опровергли?

• линейная алгебра
• перекрестное произведение

$\endgroup$

2

$\begingroup$

Нет — например, векторное произведение любого единичного вектора на самого себя равно 0.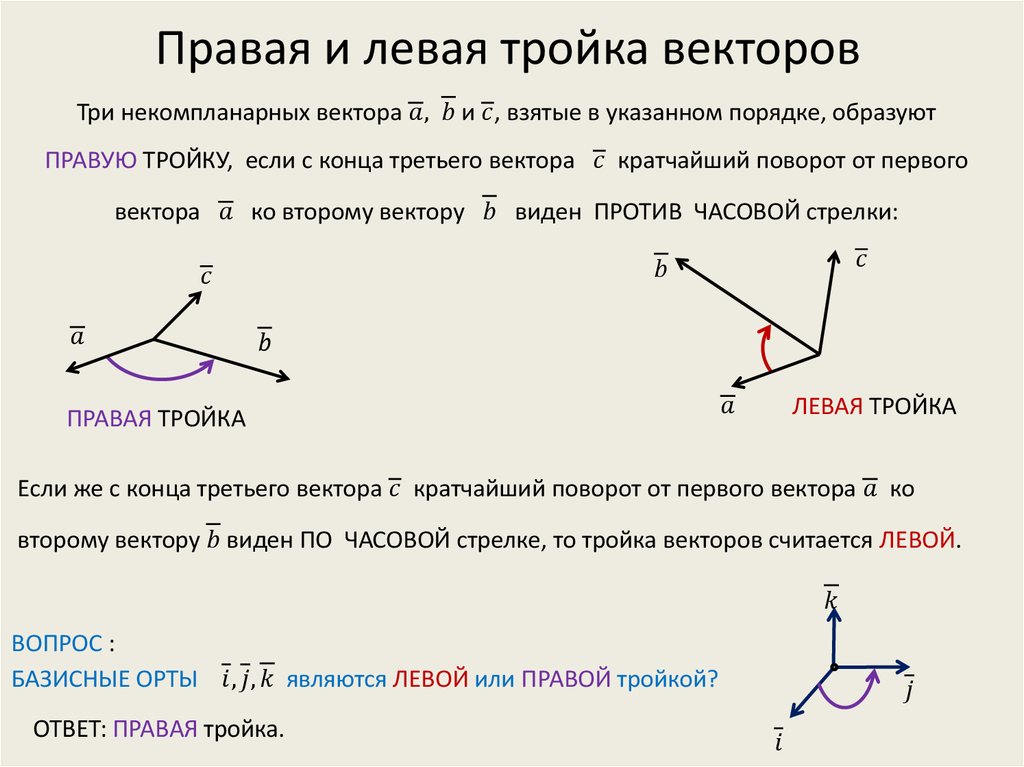 В общем случае величина векторного произведения векторов $\vec{a}$ и $\vec{b}$ равна $$|\ vec{a}\times\vec{b}|=|\vec{a}||\vec{b}|\sin(\theta)$$ где $\theta$ — угол между векторами $\vec{a}$ и $\vec{b}$. Таким образом, векторное произведение двух единичных векторов $\vec{u}$ и $\vec{v}$ само является единичным вектором тогда и только тогда, когда $\vec{u}$ и $\vec{v}$ ортогональны. , т. е. встречаются под прямым углом (это делает $\sin(\theta)=\sin(\frac{\pi}{2})=1$).

Что касается общей интерпретации величины перекрестного произведения, см. Википедию:

Величина векторного произведения может быть интерпретирована как положительная площадь параллелограмма, имеющего стороны $a$ и $b$.

$\endgroup$

0

$\begingroup$

$|\vec{a}\times\vec{b}|=|\vec{a}||\vec{b}||\sin(\theta)|$

Пусть $a,b$ единица векторов, поэтому имеем $|a| = |б| = 1$

$|\vec{a}\times\vec{b}|=|\sin(\theta)| \le 1$ (равенство достигается, когда $|\sin(\theta)| = 1$, т. е. когда a и b перпендикулярны)

Следовательно, в общем случае результат не будет единичным вектором.

$\endgroup$

$\begingroup$

Если вы знаете, что единичные векторы, с которых вы начинаете, перпендикулярны друг другу (скалярное произведение $\vec{a}\cdot\vec{b}$ равно нулю), то векторное произведение $\vec{a}\ times\vec{b}$ будет единичным вектором (длина которого равна единице).

Если у вас нет приведенного выше ограничения для входных единичных векторов, то выход векторного произведения $\vec{a}\times\vec{b}$ не гарантируется единичным вектором, поскольку длина зависит от угла (длина равна $sin(\theta)$, где $\theta$ — угол между входными векторами).

Этот ответ посвящен особым случаям, а обобщения см. в других замечательных ответах.

$\endgroup$

линейная алгебра — Почему перекрестное произведение дает вектор, перпендикулярный плоскости

спросил 9 лет, 7 месяцев назад

Изменено 2 года, 4 месяца назад

Просмотрено 54к раз

$\begingroup$

Мне было интересно, может ли кто-нибудь объяснить мне, что такое перекрестное произведение двух векторов $\textbf{a}$ и $\textbf{b}$. Почему их векторное произведение $\textbf{n} = \textbf{a} \times \textbf{b}$ дает мне вектор, перпендикулярный плоскости?

Я знаю, что могу просто проверить это с помощью скалярного произведения, но я не полностью удовлетворен ответом «это просто работает» =)

Спасибо за любую помощь! =)

• линейная алгебра
• внутренние произведения
• перекрестное произведение

$\endgroup$

2

$\begingroup$

Формула определителя не так загадочна. Рассмотрим перекрестное произведение $\mathbf{v} = \langle a,b,c \rangle \times \langle d,e,f \rangle$ в качестве формального определителя

$$ \det \left(\begin{array}{ccc} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ a & b & c \\ d & e & f \end {массив} \right) $$

где $\mathbf{i}, \mathbf{j}, \mathbf{k}$ — стандартные базисные векторы. Если вместо этого рассматривать $\mathbf{i}, \mathbf{j}, \mathbf{k}$ как неопределенные и заменять их $x, y, z$, этот определитель вычисляет скалярное произведение $\mathbf{v} \ cdot \langle x, y, z \rangle$. Но если $\langle x, y, z \rangle$ равно $\langle a, b, c \rangle$ или $\langle d, e, f \rangle$, то определитель равен нулю, поэтому $\mathbf{v}$ перпендикулярен последним двум векторам, следовательно, плоскости, которую они охватывают, как говорит Омномномном.

$\endgroup$

4

$\begingroup$

По словам профессора Джосайи Уилларда Гиббса, одного из основателей векторного анализа, перекрестное (или косое) произведение определяется следующим образом в его брошюре 1881 г. Определение: косое произведение вектора A на вектор B есть векторная величина C, направление которой нормали к той стороне плоскости А и В, на которой поворот из А в В на угол меньше единицы сто восемьдесят градусов кажется положительным или противоположным по часовой стрелке; и величина которого получается путем умножения произведение величин А и В на синус угол от А до В.

Это определение, как бы исходящее из уст лошади, является геометрическим определением. Почему же тогда мы в 21 в. настаивают на определении его в терминах определителей. Определитель «определения» является прямым следствием геометрического определения и дистрибутивности векторных произведений. $$\vec{\mathbf{w}}\times(\vec{\mathbf{u}}+ \vec{\mathbf{v}}) = \vec{\mathbf{w}}\times\vec{\ mathbf{u}}+\vec{\mathbf{w}}\times\vec{\mathbf{v}}$$ $$(\vec{\mathbf{u}}+\vec{\mathbf{v}})\times\vec{\mathbf{w}} = \vec{\mathbf{u}}\times\vec{\ mathbf{w}}+\vec{\mathbf{v}}\times\vec{\mathbf{w}}$$ теперь попробуй расширить $$(a_1\vec{\mathbf{i}}+a_2\vec{\mathbf{j}}+a_3\vec{\mathbf{k}})\times(b_1\vec{\mathbf{i}}+ b_2\vec{\mathbf{j}}+b_3\vec{\mathbf{k}})$$ чтобы увидеть, что перекрестные произведения на самом деле распределяются по сложению, см. геометрическое доказательство на стр. 9.http://www.math.oregonstate.edu/bridge/papers/dot+cross.pdf

$\endgroup$

0

$\begingroup$

Смотри. Я не математик, но у меня есть перспектива, которая может объяснить, почему векторное произведение двух векторов является другим вектором, перпендикулярным им. Это не доказательство, но оно поможет сделать эту идею фимилярной.

Перекрестное произведение можно понять следующим образом: представьте себе отрезок, оставляющий цветные метки везде, где он перемещается по бумаге. Теперь заставьте его двигаться в том же направлении и на то же расстояние, что и другой сегмент, сохраняя направление первого сегмента. Результатом будет параллелограмм с площадью, подаренной ab sin (θ), где a и b — длины сегментов. Таким образом, мы можем определить перекрестное произведение двух векторов как «площадь параллелограмма, в которой эти векторы являются смежными сторонами».

Первый вопрос: почему это вектор? Представьте себе плоскость, содержащую два вектора a и b, а угол между a и b равен θ, перекрестное произведение a и b равно ||a|| ||б|| грех (θ). Это хорошо работает как скаляр, но проблема возникает, когда вы переворачиваете всю плоскость, содержащую векторы, что равносильно замене a на b и наоборот.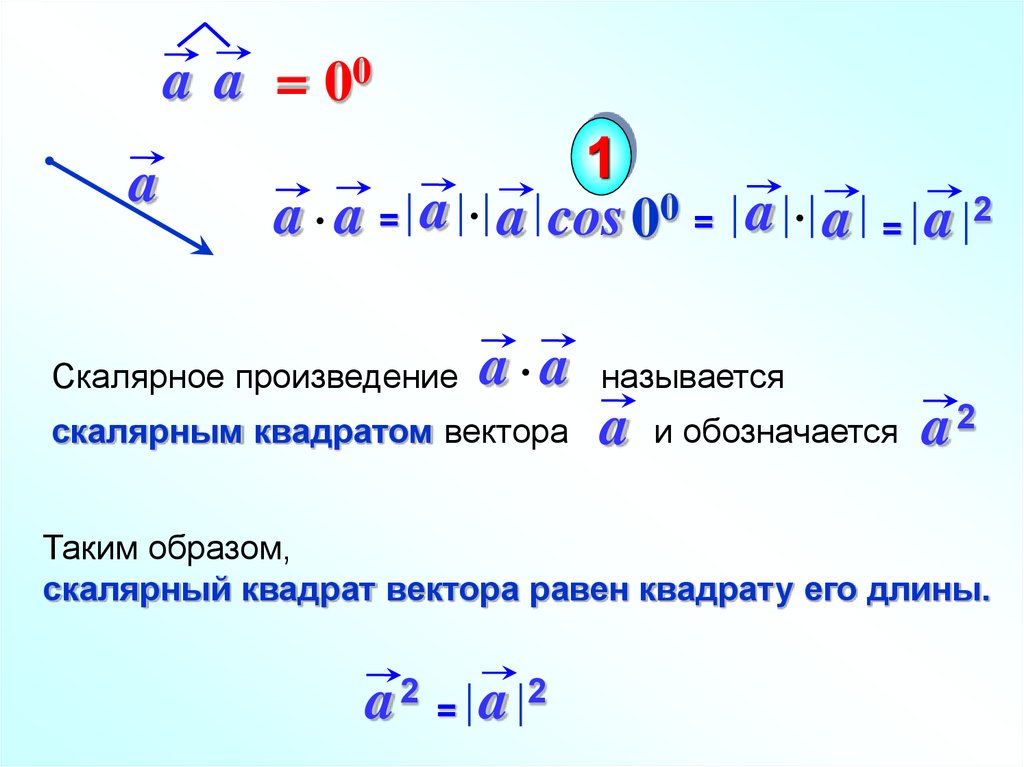 Угол от a до b становится равным -θ, а векторное произведение становится ||a|| ||б|| sin(-θ), что равно -||a|| ||б|| грех (θ). Переворот плоскости меняет результат. Таким образом, векторное произведение можно представить в виде вектора, начальная точка которого лежит на плоскости, указывающей «вверх или вниз». Если этот вектор указывает вверх, он будет указывать вниз, когда вы переворачиваете плоскость, и наоборот.

Второй вопрос: почему векторное произведение перпендикулярно плоскости? Почему он просто не указывает куда-нибудь вверх или вниз? Это потому, что когда вы переворачиваете плоскость, векторное произведение полностью переворачивается, что означает, что оно перпендикулярно плоскости.

$\endgroup$

$\begingroup$

Посмотрите, что происходит, когда вы пытаетесь взять $(a\times b)\cdot a$ или $(a\times b)\cdot b$ (вы должны получить $0$). Если вектор перпендикулярен основанию плоскости, то он перпендикулярен всей этой плоскости.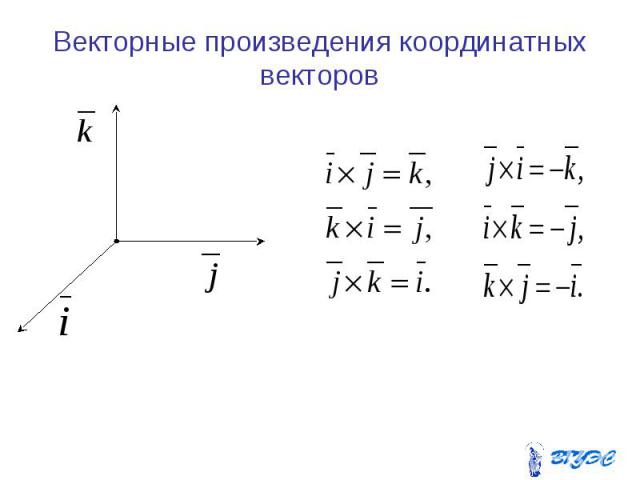 Таким образом, перекрестное произведение двух (линейно независимых) векторов, поскольку оно ортогонально каждому, ортогонально плоскости, которую они охватывают.

Кроме того, пока вы пытаетесь развить интуицию для перекрестных произведений, я настоятельно рекомендую это видео

https://www.khanacademy.org/math/linear-алгебра/vectors_and_spaces/dot_cross_products/v/proof—relationship -between-cross-product-and-sin-of-angle

и, пока мы там, возможно, стоит узнать, как формула углов для скалярных произведений получается из закона косинусов

https://www.khanacademy .org/math/linear-алгебра/vectors_and_spaces/dot_cross_products/v/определение-угла-между-векторами

$\endgroup$

0

$\begingroup$

Вот еще одна перспектива: векторное произведение является своего рода «каррированием» объема из (он же определитель).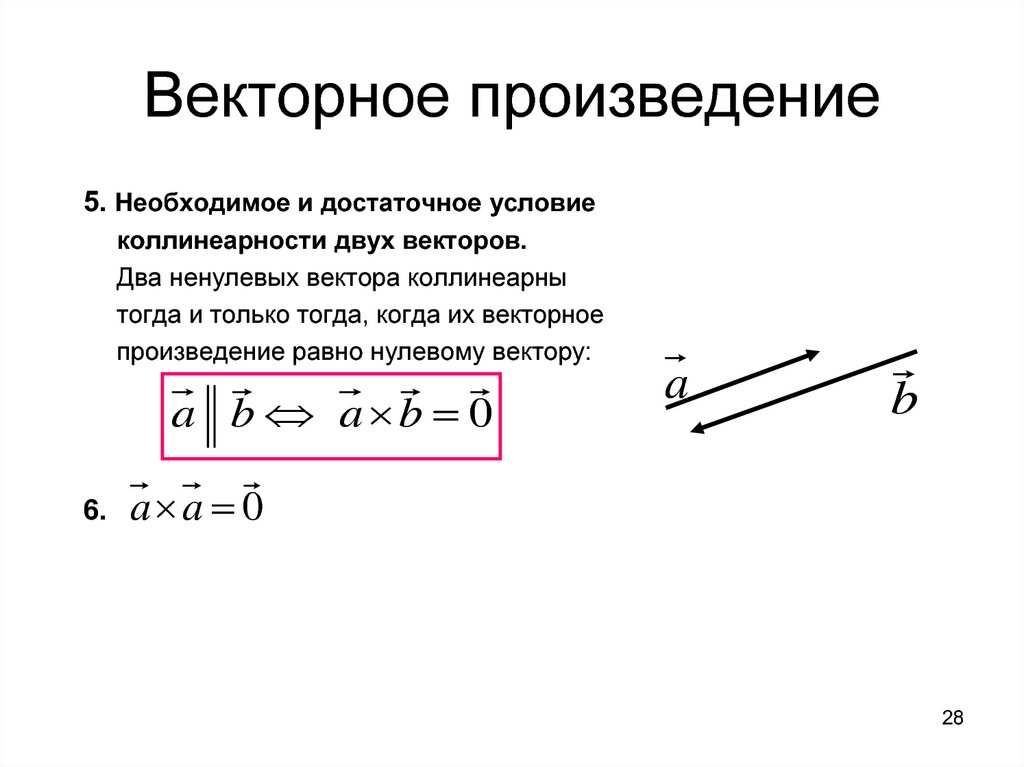 То есть у нас есть функция $V(\mathbf{a}, \mathbf{b}, \mathbf{c})$, определяющая объем, натянутый на три вектора; поскольку эта функция линейна по каждому аргументу, мы можем зафиксировать $\mathbf{a}$ и $\mathbf{b}$ и рассматривать это как линейную функцию $V_{\mathbf{a}\mathbf{b}}(\ mathbf{c})$, переводящий векторы в числа. Но мы знаем, что всякая линейная функция $f(\mathbf{c})$ от векторов к числам имеет вид $\mathbf{v}\cdot\mathbf{c}$ для некоторого вектора $\mathbf{v}$, поэтому мы можем определить перекрестное произведение $\mathbf{a}$ и $\mathbf{b}$ как вектор $\mathbf{v_{\mathbf{a}\mathbf{b}}}$, такой что $ V(\mathbf{a}, \mathbf{b}, \mathbf{c}) = \mathbf{v}_{\mathbf{a}\mathbf{b}}\cdot \mathbf{c}$. Тогда перекрестное произведение будет ортогональным к $\mathbf{a}$ и $\mathbf{b}$, грубо говоря, потому что направление, перпендикулярное обоим векторам, является направлением, которое максимизирует объем. Подробнее об этом подходе см. мой ответ здесь.

$\endgroup$

$\begingroup$

Мой ответ заключается в том, что это так, потому что перекрестное произведение определено как обладающее этим свойством.

$\endgroup$

7

$\begingroup$

У этого вопроса есть два аспекта. Во-первых, определение креста. а точечные произведения следуют непосредственно из произведения введенных кватернионов Гамильтоном, хотя он не дал названий этим изделиям (Гиббс назвал их, хотя он использовал другие имена). Тот факт, что перекрестное произведение перпендикулярно перемножаемым векторам, напрямую связано с теория вращений. Результатом произведения является ось вращения.

Во-вторых, как описано выше, трудно говорить о мотивации определение перекрестного произведения. Это был побочный продукт более общего понятие произведения кватернионов. Благодаря своим свойствам крест продукт стал популярным, когда было показано, что он полезен для решения физических проблема. Однако я случайно нашел мотивацию для перекрестного произведения путем рассмотрения линейной комбинации двух векторов в трехмерном пространстве. Я рассмотрел плоскость, порожденную линейной комбинацией двух векторов u и v. При поиске коэффициентов в линейной комбинации, необходимой для достижения желаемой точки на плоскости, решение предполагает существование вектора нормали n = u × v. Это был неожиданный результат, поскольку понятие линейной комбинации не включает никакого произведения векторов.

Я обсуждаю все вышеперечисленное в статье: Линейная комбинация векторов подразумевает существование перекрестные и точечные произведения, Int. Дж. Матем. Образование наук. Техн., DOI: 10.1080/0020739X.2017.1408149

Полный текст статьи доступен здесь: www.tandfonline.com/eprint/CPN9hQWMMVu7nU2bZebd/full

$\endgroup$

$\begingroup$

Я бы начал с чего-нибудь попроще.

Что такое i x д ?
ответ: к

но почему? Ну, это по определению .