|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья… Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь… История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации… Интересное: Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории… Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным. Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 4 из 4 Найдем формулы вычисления векторного произведения векторов, если векторы заданы координатами: ; . По свойствам векторного произведения = . (2) По свойству 1 векторного произведения , , . Векторы образуют правую тройку, круговая перестановка векторов (рис. 3) ориентации не меняет, поэтому , , . Перестановка соседних векторов меняет ориентацию (рис. 10), поэтому , , . Подставим векторные произведения базисных векторов в равенство (2), получим . Последнее равенство есть не что иное, как разложение определителя по первой строке . Поэтому (3) – формула вычисления векторного произведения в координатах. Найдем формулу вычисления в координатах площади параллелограмма, построенного на векторах и (рис. 5). По формуле (1) , т. е. площадь параллелограмма, построенного на векторах и , равна модулю определителя, первая строка которого – базисные вектора, а вторая и третья – координаты векторов и . Если векторы лежат на плоскости , т.е. , , ; , то площадь параллелограмма, построенного на векторах и равна . Геометрический смысл определителя второго порядка: его модуль равен площади параллелограмма, построенного на векторах, координаты которых расположены в строках определителя. Пример 1. Даны точки , , . Найти площадь треугольника АВС.
Решение. Площадь треугольника АВС равна половине площади параллелограмма, построенного на векторах и (рис. 11). Найдем векторы , . Тогда из геометрического смысла определителя второго порядка площадь параллелограмма . Ответ: 3. Смешанное произведение векторов, его свойства. Признак компланарности векторов. Смешанное произведение в координатах. Определение2. Смешанным произведением трех векторов , и называется число , равное скалярному произведению вектора на векторное произведение векторов и , то есть . Найдем геометрический смысл модуля смешанного произведения 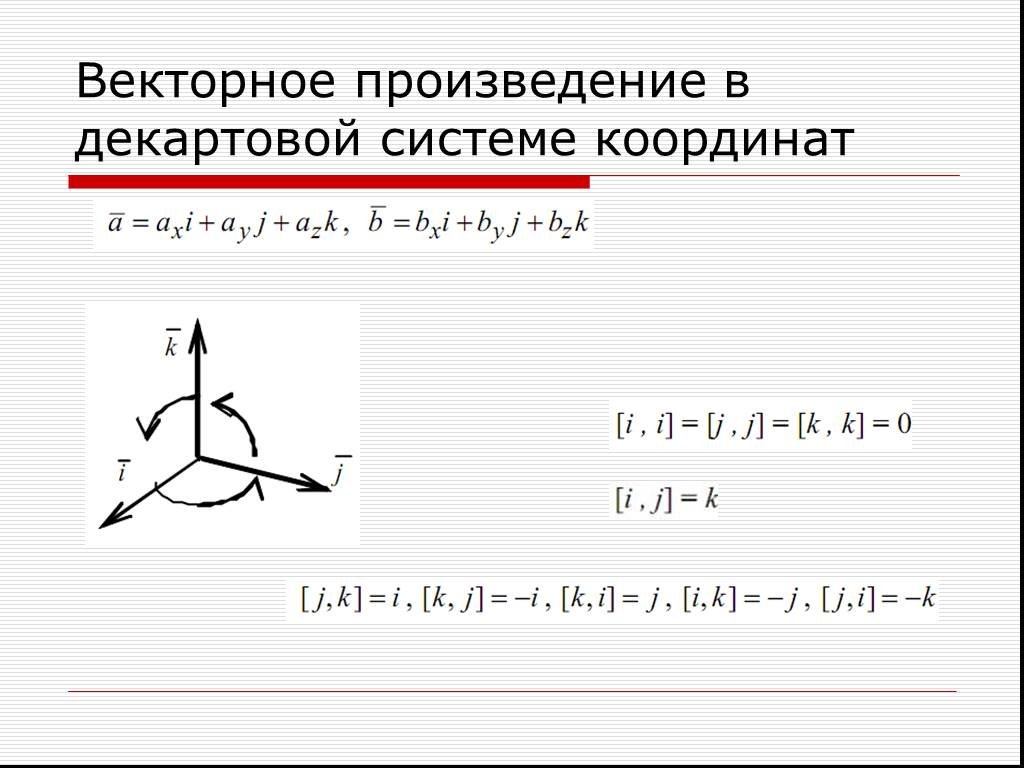 Объем параллелепипеда, построенный на векторах (из рис. 12) Объем параллелепипеда, построенный на векторах (из рис. 12), , , . При этом знак « » необходим, чтобы длина высоты была положительной. Тогда . Таким образом, абсолютная величина смешанного произведения трех векторов равна объему параллелепипеда, построенного на этих векторах, как на сторонах. Найдем формулы для вычисления смешанного произведения векторов, если векторы заданы координатами: , , . Тогда . Скалярное произведение вектора на векторное произведение . – формула вычисления смешанного произведения в координатах. Учитывая формулу для вычисления смешанного произведения в координатах, получаем , (4) модуль определителя равен объему параллелепипеда, построенного на векторах, координаты которых расположены в строках определителя. ⇐ Предыдущая1234 Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства. Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… |
Векторное произведение — презентация онлайн
Похожие презентации:
Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов
Газовая хроматография
Геофизические исследования скважин
Искусственные алмазы
Трансформаторы тока и напряжения
Транзисторы
Воздушные и кабельные линии электропередач
Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса
Магнитные аномалии
Нанотехнологии
Векторное произведение
Подготовил: Хусаинов А.
Закиров А.
студенты 2-го курса «АПТ» группа СТ-201б
Определение векторного
произведения
Система координат — способ определить положение и перемещение точки или тела с
помощью чисел или других символов.
Координаты — это совокупность чисел, которые определяют положение какого-либо
объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки
Скаляр — это величина, которая полностью определяется в любой координатной системе
одним числом или функцией.
Вектор — направленный отрезок прямой, для которого указано, какая точка является
началом, а какая — концом.
Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также
можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот
так: →a.
Коллинеарность — отношение параллельности векторов. Два ненулевых вектора
называются коллинеарными, если они лежат на параллельных прямых или на одной
прямой.

Проще говоря это «параллельные» векторы. Коллинеарные векторы могут быть одинаково
направлены или противоположно направлены.
2
• Посмотрим с конца вектора с⃗ на то, как происходит кратчайший
поворот от вектора a⃗ к b⃗. Если кратчайший поворот происходит
против часовой стрелки, то тройка векторов а⃗, b⃗, c⃗называется
правой, по часовой стрелке — левой.
3
• Векторным произведением двух векторов a ⃗ и b ⃗, которые
заданы в прямоугольной системе координат трехмерного
пространства, называется такой вектор с ⃗, что:
он является нулевым, если векторы a ⃗ и b ⃗ коллинеарные;
он перпендикулярен и вектору a ⃗ и вектору b ⃗;
векторов a ⃗ и b ⃗ на синус угла между ними
тройка векторов a ⃗, b ⃗ , c ⃗ ориентирована так же, как и
заданная система координат.
4
• Векторным произведением
вектора a ⃗ на вектор b ⃗
называется вектор c ⃗, длина
которого численно равна
площади параллелограмма
построенного на векторах a ⃗ и
b ⃗, перпендикулярный к
плоскости этих векторов и
направленный так, чтобы
наименьшее вращение от a ⃗
к (b ) ⃗вокруг вектора c
осуществлялось против
часовой стрелки, если
смотреть с конца вектора с ⃗
5
• Векторное произведение двух векторов a = {ax; ay; az} и
b = {bx; by; bz} в декартовой системе координат — это
формулы вычисления векторного произведения
векторов:
6
Координаты векторного произведения
Рассмотрим векторное произведение векторов в координатах.

Сформулируем второе определение векторного произведения, которое
позволяет находить его координаты по координатам заданных векторов.
В прямоугольной системе координат трехмерного пространства векторное
произведение двух векторов a ⃗= (ax, ay, az) и b ⃗= (bx, by, bz) есть вектор
где i ⃗, j ⃗, k ⃗,— координатные векторы.
Это определение показывает нам векторное произведение в координатной
форме.
Векторное произведение удобно представлять в виде определителя
квадратной матрицы третьего порядка, первая строка которой есть орты i ⃗,
j ⃗, k ⃗, во второй строке находятся координаты вектора a ⃗, а в третьей —
координаты вектора b ⃗ в заданной прямоугольной системе координат:
7
• Если разложим этот определитель по элементам
первой строки, то получим равенство из
определения векторного произведения в
координатах:
8
Свойства векторного произведения
Векторное произведение в координатах представляется в виде
определителя матрицы:
На основании свойств определителя можно легко обосновать свойства
векторного произведения векторов:
3.
 Сочетательное свойство
Сочетательное свойство1. Антикоммутативность
2.Свойство дистрибутивности
9
10
11
12
13
English Русский Правила
координат и векторов в космосе
координат и векторов в космосеКоординатная геометрия даже полезнее в космосе, чем на плоскости, поскольку она намного сложнее рисовать фигуры в 3D для точной визуализации.
Обозначение:
Векторы будут записаны в виде строк или столбцов, если только векторные операции обеспокоены. Если в картину входят матрицы, то есть разница между векторы-строки (матрицы-строки) и векторы-столбцы (матрицы-столбцы).
- Обычно пишут O или иногда 0 для нулевого вектора .
- В 2-местном часто пишут O или 0 для (0, 0), I или i для (1, 0) и J или j для (0, 1).
- В с тремя пробелами часто пишут O или 0 для (0, 0, 0), I или i для (1, 0, 0) и J или j для (0, 1, 0), K или k для (0, 0, 1).
- В n-пространстве даже при n = 1, 2 или 3 записываются векторы e 1 ,
.
 .., е n , где ek — вектор в n-пространстве со всеми элементами = 0
кроме 1 в записи k.
.., е n , где ek — вектор в n-пространстве со всеми элементами = 0
кроме 1 в записи k.
Сложение векторов и скалярное умножение
В этих заметках предполагается, что механика и базовая геометрия векторных сложение и умножение вектора на скаляр (т. е. действительное число) понял.
Центры масс и параметризация линий и Самолеты
Линии и плоскости могут быть описаны в координатной геометрии с помощью параметризации. Эта тема изучалась в Math 444. Дается обзор и несколько упражнений. по ссылке выше.
Уравнения прямых и плоскостей
Линии и плоскости также являются решениями систем линейных уравнений. Эта секция вводит тему.
Основы многоточечного продукта
Здесь приведены основные сведения о скалярном произведении: определение, алгебраические свойства, связь с косинусом и критерий скалярного произведения для ортогональных векторов.
Крест Основные сведения о продукте
Этот сайт Texas A&M определяет векторное произведение и показывает некоторые основные свойства. Вот еще одна ссылка на MathWorld.
Вот еще одна ссылка на MathWorld.
Векторы нормали к плоскостям и линиям
Уравнение плоскости в пространстве или прямой на плоскости имеет векторную форму, А . Х = к. Вектор A является нормальным вектор на плоскость (или прямую). Вектор нормали можно разделить на его длину сделать единицу нормальной. Перекрестное произведение можно использовать для поиска векторов нормалей.
Применение векторных методов к сферической геометрии
Все векторные инструменты для работы с уравнениями плоскостей, нормальных направлений, а также информацию об углах от точечного и перекрестного произведения, можно использовать для ответить на многие вопросы по сфере.
Приложения к компьютерной графике и компьютерным играм
Вот один из многих примеров: объяснение удаления скрытых поверхностей Джеффом Уиксом.
Калькулятор перекрестного произведения
Калькулятор перекрестного произведения используется для нахождения произведения двух векторов с использованием матричного метода. Векторы можно вводить с помощью представления координат или точек.
Векторы можно вводить с помощью представления координат или точек.
Предоставляет возможность выбора размеров. Это означает, что вы можете найти произведение векторов, представленных в измерениях i, j и k, на этом калькуляторе перекрестного произведения, то есть трехмерных векторов.
И последнее, но не менее важное: этот инструмент обеспечивает все этапы вычисления векторного произведения. Нажмите на показать шаги , чтобы увидеть.
Что такое перекрестный продукт?
В векторном произведении перемножаются два вектора. Поскольку векторы имеют размерность и величину, они не перемножаются, как числовые значения.
Известные методы используют формулу перекрестного произведения или расширение кофактора с использованием правила Сарруса.
Письменная форма векторного произведения a x b , который читается как a крест b . При перемножении двух векторов всегда получается вектор. Применение этого продукта включает крутящий момент и магнитную силу.
Применение этого продукта включает крутящий момент и магнитную силу.
Формула векторного произведения:
Формула, используемая для нахождения векторного произведения, использует синусоидальную функцию тригонометрии. Это
A x B = |A||B| Грех????
Здесь;
- |А| величина вектора A .
- |Б| величина вектора B .
- ???? угол между A и B .
Как рассчитать векторное произведение?
Используйте калькулятор перекрестного произведения 2×2, чтобы найти результат. В противном случае есть два варианта найти величину векторного произведения вручную.
Расчет звездной величины:
- Примените вышеупомянутую формулу. Это хорошо работает, если заданы величины и угол.
- Использовать матричный метод. Запишите трехмерные векторы в матрице 3 на 3. Вот так:
Разверните кофакторы, чтобы найти формальные определители и упростить.
Так как вектор должен иметь некоторое направление , необходимо определить его вместе с величиной.
Забавный факт: Величина результирующего вектора такая же, как площадь параллелограмма, построенного с использованием векторов.
Нахождение направления:
Результирующий вектор векторного произведения показывает разницу направлений между исходными векторами. Он присутствует на перпендикулярной оси как A , так и B .
Правило большого пальца правой руки очень эффективно определяет направление. Это правило гласит:
«Раскройте правую руку так, чтобы указательный палец указывал в направлении вектора A . Направьте безымянный или средний палец в направлении вектора B . Прямой большой палец указывает направление результирующего вектора».
Пример:
Найдите векторное произведение следующих векторов.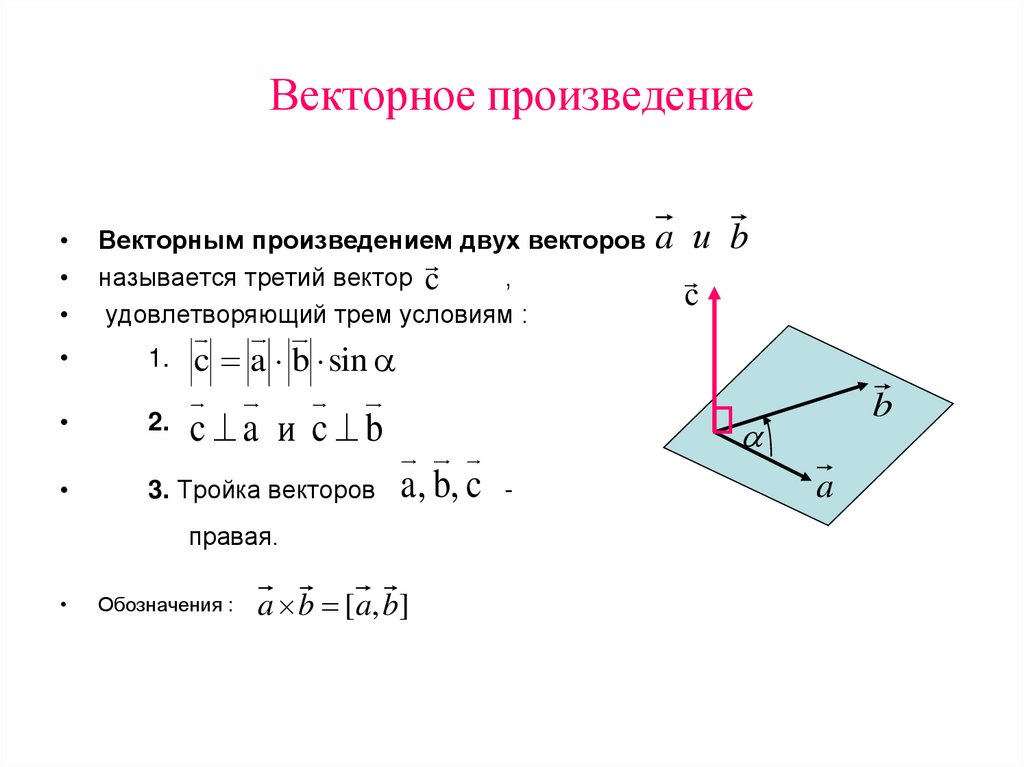





 ..
.. .., е n , где ek — вектор в n-пространстве со всеми элементами = 0
кроме 1 в записи k.
.., е n , где ek — вектор в n-пространстве со всеми элементами = 0
кроме 1 в записи k.