Элементы векторного исчисления

Лаптев Г. Ф. Элементы векторного исчисления. М., 1975 г. — 336 с. Книга представляет собой учебное руководство для студентов втузов. В пен содержится предусмотренный учебными программами материал но векторной алгебре, дифференциальной геометрии и теории поля. Изложение построено с учетом потребностей технических дисциплин, в которых используется векторное исчисление. Книга написана просто и ясно; это делает ее доступной пониманию студентов первого курса, впервые приступающих к изучению высшей математики. Книга окажется полезной и в условиях заочного обучения. Оглавление ВВЕДЕНИЕ ЧАСТЬ ПЕРВАЯ. ВЕКТОРНАЯ АЛГЕБРА Глава I. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ 2. Скаляры и векторы. 3. Равенство векторов. 4. Скользящие и приложенные векторные величины. 5. Модуль вектора. 6. Орт вектора. 7. Угол между двумя векторами. § 2. Сложение векторов 1. Сложение двух векторов. 2. Сложение более чем двух векторов. 3. Модуль суммы. 4. Законы сложения. § 3. Вычитание векторов § 4. Умножение и деление вектора на скаляр 2. Законы умножения вектора на скаляр. 3. Деление вектора на скаляр. 4. Выражение вектора через его модуль и орт. § 5. Линейные зависимости между векторами 2. Коллинеарные векторы. 3. Компланарные векторы. 4. Разложение вектора по трем некомпланарным векторам. 5. Метод координат. Глава II. ТЕОРИЯ ПРОЕКЦИЙ. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ § 1. Проекции векторов на ось § 2. Основные теоремы о скалярных проекциях § 3. Прямоугольная система координат в пространстве 1. Правая и левая прямоугольные системы координат. 2. Разложение вектора по ортам осей 3. Линейные операции над векторами в координатной форме. 4. Радиус-вектор и координаты точки. 5. Определение вектора по его началу и концу. 6. Деление отрезка в данном отношении. Глава III. ПРОИЗВЕДЕНИЯ ДВУХ ВЕКТОРОВ § 1. Скалярное произведение двух векторов 2. Работа силы. 3. Определение. 4. Равенство скалярного произведения нулю. 5. Законы скалярного умножения. 7. Скалярные произведения координатных ортов. 8. Скалярное произведение в координатной форме. 9. Неопределенность действия, обратного скалярному умножению. § 2. Векторное произведение двух векторов 3. Условия равенства нулю векторного произведения. 4. Законы векторного умножения. 5. Векторные произведения координатных ортов. 6. Определители. 7. Векторное произведение в координатной форме. 8. Неопределенность действия, обратного векторному умножению. Глава IV. ПРОИЗВЕДЕНИЯ ТРЕХ ВЕКТОРОВ § 1. Простейшее произведение трех векторов § 2. Векторно-векторное произведение трех векторов 3. Правило разложения векторно-векторного произведения. § 3. Векторно-скалярное произведение трех векторов 2. Законы векторно-скалярного умножения 3. Обращение в нуль векторно-скалярного произведения трех векторов. 4. Векторно-скалярное произведение в координатной форме. § 4. Выражение векторно-скалярного произведения через скалярные произведения Глава V. ФУНКЦИИ ВЕКТОРОВ § 1. Произведения четырех векторов 2. Выражение скалярного произведения двух векторных произведений (а x b), (р x q) через скалярные произведения. 3. Разложение вектора (а, b, с) R по трем векторам a, b, c. 4. Разложение вектора (a, b, c) по векторным произведениям b x с, c x a, а x b § 2. Произведения пяти и шести векторов 2. Разложение вектора (a, b, c) (m x n) по векторам a, b, c. 3. Выражение произведения двух смешанных произведений (a, b, c) (l, m, n) через скалярные произведения. § 3. Основные теоремы о функциях векторов 1. Рациональные функции векторов. 2. Элементарные функции векторов. 3. Произвольные скалярные функции от векторов. 4. Произвольные векторные функции векторов. Глава VI. ОСНОВНЫЕ ЗАДАЧИ § 2. Основные задачи, связанные со скалярным умножением векторов § 3. Основные задачи, связанные с векторным умножением векторов § 4. Основные задачи, связанные с произведениями трех и более векторов § 5. Простейшие векторные уравнения § 6. Геометрические инварианты фигур 2. Треугольник. 3. Полные системы инвариантов треугольника. 4. Тетраэдр. 5. Полные системы инвариантов тетраэдра. 6. Гексаэдр с треугольными гранями. ЧАСТЬ ВТОРАЯ. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ § 1. Векторы, зависящие от скаляра 2. Вектор-функция в координатной форме. 3. Годограф вектора. 4. Предел вектора. § 2. Дифференцирование вектора по скаляру 2. Геометрический смысл производной вектора по скаляру. 3. Механический смысл производной. 5. Дифференциал вектора. 6. Инвариантность дифференциала. 7. Связь дифференциала вектора с его приращением. § 3. Формула Тейлора Глава VIII. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ЛИНИИ В ПРОСТРАНСТВЕ § 1. Основные дифференциально-геометрические понятия, связанные с линией 2. Касательная. 3. Соприкасающаяся плоскость. 4. Главная нормаль и бинормаль. 5. Кривизна. 6. Кручение. 7. Длина дуги. § 2. Основные формулы дифференциальной геометрии линий в пространстве 1. Дуга как параметр. Дифференциал дуги. 2. Орт касательной. Первая основная формула. 3. Инвариантность геометрических понятий. 4. Главная нормаль и кривизна. Вторая основная формула. 5. Бинормаль и кручение. Третья основная формула. 6. Винтовая линия. § 3. Сопровождающий трехгранник 2. Система дифференциальных уравнений движения сопровождающего трехгранника. 3. Расположение линии относительно сопровождающего трехгранника. 4. Линии без кривизны. 5. Линии без кручения. § 4. Инвариантные формулы Глава IX. ПЛОСКИЕ ЛИНИИ § 1. Дифференциальные уравнения плоской линии § 2. Кривизна плоской линии § 3. Круг кривизны § 4. Эволюта § 5. Эвольвента Глава X. ПРИЛОЖЕНИЯ К МЕХАНИКЕ § 1. Скорость и ускорение точки § 2. Движение твердого тела вокруг неподвижной точки 2. Формула Эйлера. 3. Угловая скорость. 4. Доказательстве существования угловой скорости твердого тела. § 3. Относительная производная вектора 2. Абсолютная и относительная производные вектора. 3. Общий случай движения твердого тела. Глава XI. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ § 1. Векторные функции нескольких скалярных аргументов § 2. Параметризованная поверхность 2. Поверхность в декартовых координатах. 3. Параметрическая сеть. 4. Линия на параметризованной поверхности. § 3. Касательная плоскость и нормаль 3. Нормальный вектор. 4. Преобразование параметров. § 4. Площадь области на поверхности 2. Площадь области на поверхности. 3. Формула для вычисления площади поверхности, заданной уравнением z=z(x,y). 4. Элемент площади поверхности. 5. Векторный элемент площади поверхности. § 5. Первая квадратичная форма поверхности 2. Внутренняя геометрия поверхности. 3. Длина дуги линии на поверхности. 4. Угол между линиями на поверхности. 5. Площадь области на поверхности. § 6. Вторая квадратичная форма поверхности 2. Нормальная кривизна линии на поверхности. 3. Теорема Менье. § 7. Главные направления и главные кривизны поверхности 2. Главные направления на поверхности. 3. Перпендикулярность главных направлений. 4. Формула Эйлера. 5. Полная и средняя кривизны поверхности. ЧАСТЬ ТРЕТЬЯ. ТЕОРИЯ ПОЛЯ § 1. Функция поля. Поверхности уровня § 2. Градиент поля 2. Первая теорема о градиенте. § 3. Производная по направлению 2. Выражение производной по направлению через градиент. 3. Вторая теорема о градиенте. § 4. Направляющие косинусы нормали поверхности Глава XIII. КРИВОЛИНЕЙНЫЙ И ПОВЕРХНОСТНЫЙ ИНТЕГРАЛЫ § 1. Криволинейный интеграл как определенный интеграл от сложной функции 2. Криволинейный интеграл от линейной формы по произвольной кривой. 3. Основные свойства криволинейного интеграла. 4. Обобщенный криволинейный интеграл. 5. Примеры. § 2. Криволинейный интеграл как предел криволипейной интегральной суммы § 3. Поверхностный интеграл как двойной интеграл от сложной функции 2. Определение простейшего поверхностного интеграла. 3. Поверхностный интеграл от билинейной формы по произвольной поверхности. § 4. Поверхностный интеграл как предел поверхностной интегральной суммы § 5. Поверхностный интеграл в параметрической форме 2. Параметрический поверхностный интеграл. 3. Поверхностный интеграл как предел суммы. § 6. Кратный интеграл как предел обобщенной интегральной суммы 2. Обобщение основной теоремы о кратном интеграле. Глава XIV. ВЕКТОРНОЕ ПОЛЕ И ЕГО ИНТЕГРАЛЬНЫЕ ИНВАРИАНТЫ § 1. Векторное поле § 2. Векторные линии § 3. Циркуляция поля вдоль линии § 4. Поток поля через поверхность Глава XV. ТЕОРЕМА ОСТРОГРАДСКОГО. ДИВЕРГЕНЦИЯ ПОЛЯ § 1. Формула Остроградского § 2. Дивергенция поля 2. Дивергенция как предел отношения. 3. Гидромеханический смысл дивергенции. 4. Теорема Остроградского. Глава XVI. ТЕОРЕМА СТОКСА. РОТАЦИЯ ПОЛЯ § 1. Формула Стокса § 2. Ротация поля § 3. Оператор Гамильтона Глава XVII. СПЕЦИАЛЬНЫЕ ВЕКТОРНЫЕ ПОЛЯ § 1. Потенциальное поле 3. Циркуляция потенциального поля по замкнутому контуру. 4. Циркуляция потенциального поля между двумя точками. 5. Потенциал. 6. Элемент циркуляции. 7. Характеристические признаки потенциального поля. 8. Вычисление потенциала. 9. Центральное поле. 10. Вихревые шнуры. § 2. Соленоидальное поле 3. Поток соленоидального поля через замкнутую поверхность. 4. Трубчатое строение соленоидального поля. 5. Векторный потенциал. 6. Характеристические признаки соленоидального поля. 7. Источники и стоки. § 3. Потенциальное несжимаемое поле Глава XVIII. ПРОСТЕЙШИЕ ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ § 1. Электростатическое поле точечного заряда 2. Дивергенция поля точечного заряда. 3. Поток поля точечного заряда через замкнутую поверхность. 4. Ротация поля точечного заряда. 5. Потенциал поля точечного заряда. § 2. Электростатическое поле системы точечных зарядов 2. Дивергенция и ротация поля системы точечных зарядов. 3. Поток поля системы точечных зарядов через замкнутую поверхность. 4. Потенциал поля системы точечных зарядов. 5. Непрерывно распределенный заряд. § 3. Магнитное поле тока 2. Напряженность магнитного поля тока, текущего по бесконечному прямолинейному проводу. 3. Векторные линии поля H. 4. Потенциал поля Н. 5. Провод как вихревой шнур. Глава XIX. ВЕКТОРНОЕ ПОЛЕ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ § 1. Криволинейные координаты 3. Координатные поверхности и линии. 4. Линейный элемент. 5. Элемент объема. 6. Подвижной репер. 7. Векторное поле в криволиненных координатах. § 2. Дифференциальные операции в криволинейных координатах 2. Дивергенция в криволинейных координатах. 3. Ротация в криволинейных координатах. § 3. Ортогональные координаты § 4. Цилиндрические координаты 2. Линейный элемент и элемент объема в цилиндрических координатах. 3. Дифференциальные операции в цилиндрических координатах. § 5. Сферические координаты

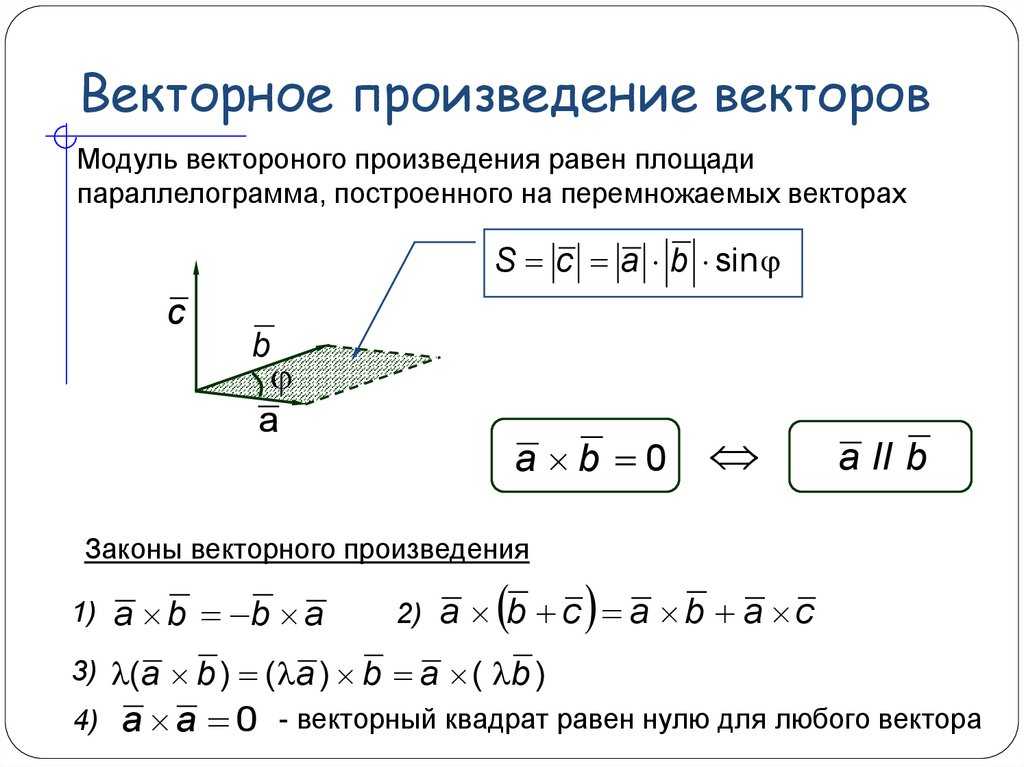
Свойства векторного произведения

1⁰ Векторное произведение равно нулю, если векторы коллинеарны или один из них равен нулю.

следует из определения модуля векторного произведения: .

Модуль равен нулю, если:

1) иливекторыколлинеарны.

2) или.

2⁰, т.е. векторное произведение не коммутативно.

3⁰(сочетательный закон относительно числового множителя).

4⁰. (распределительный закон относительно суммы и произведения).

Векторное произведение векторов, заданных координатами

Пусть заданы векторы и.

Векторное произведение векторов, заданных координатами, равно определителю третьего порядка, первой строкой которого являются единичные векторы и, второй- координаты первого перемножаемого вектора, третьей – координаты второго вектора:

. (4.10)

. (4.11)

Практический способ вычисления векторного произведения

Записать векторы один под другим

и, вычёркивая последовательно столбцы одноимённых координат, получаем определители второго порядка, которые являются координатами векторного произведения. При вычислении второй координаты перед определителем изменить знак.

Составить выражение из координат:

. (4.12)

Для получения координат векторного произведения в выражении (4.12) поочередно вычеркивать столбцы.

Для получения первой координаты x вычеркнуть 1-й столбец:

Для получения y вычеркнуть второй столбец, перед оставшимся минором взять знак « — »:

.

Для z вычеркнуть 3-й столбец:

4.3 Смешанное (векторно-скалярное) произведение векторов, его геометрический смысл

Опр 4 Смешанным произведением векторов называется число, полученное в результате векторного произведения двух векторов, скалярно умноженного на третий.

Обозначается .(4.13)

Геометрический смысл его выражается теоремой.

Теорема. Смешанное произведение представляет собой число, абсолютная величина которого равна объёму параллелепипеда, построенного на векторах как на составляющих, т. е.

. (4.14)

Подставляя эти значения в формулу (*), получим, что и требовалось доказать.

Свойства смешанного произведения

1⁰ Смешанное произведение равно нулю, если векторы — компланарны, один из них нулевой или какие-либо два из них коллинеарные.

2⁰ Можно ли переставлять местами сомножители в смешанном произведении?

Там, где произведение скалярное, там можно, а где векторное– нельзя.

;

;

; ;.

Если расположить векторы по координатным осям, то, делая круговой поворот их против часовой стрелки (рисунок 20), смешанное произведение не меняет знак.

.

Рис. 20

Если вращать векторы по ходу часовой стрелки, то смешанное произведение меняет знак на противоположный (рисунок 21).

.

Рис. 21

Смешанное произведение векторов, заданных координатами

Пусть векторы заданы координатами , ,.

Тогда смешанное произведение их вычисляется с помощью определителя третьего порядка, строками которого являются координаты перемножаемых векторов.

. (4.15)

Все о перекрестном произведении параллельных векторов

Модуль вектора A, умноженный на модуль вектора B, умноженный на синус угла, образованного векторами n, представляет собой единичный вектор, перпендикулярный плоскости, образованной векторами A и B, и направлен в направлении, перпендикулярном плоскости, образованной векторами A и B.

Перекрестное произведение двух векторов является нулевым вектором, перпендикулярным плоскости, образованной двумя векторами, поскольку угол между ними равен нулю. Мы не можем определить плоскость и взять направление вектора, полученного из перекрестного произведения, в соответствии с правым винтом, потому что есть только один вектор. Нулевой вектор, полученный из двух параллельных векторов, не имеет однозначного направления.

Антипараллельные векторы — это параллельные векторы, направленные в противоположном направлении.

Два направленных отрезка, также называемых векторами в прикладной математике, антипараллельны в евклидовом пространстве, если они поддерживаются параллельными прямыми и имеют противоположные направления. В этом случае один из связанных евклидовых векторов является отрицательным произведением другого.

Нахождение вектора w, перпендикулярного и u, и v в пространстве, по двум непараллельным ненулевым векторам u и v очень полезно. Для создания такого вектора можно использовать операцию векторного произведения. В этом разделе определяется векторное произведение, прежде чем углубляться в его свойства и использование.

(Если два вектора указывают в одном направлении, они параллельны; если они указывают в противоположных направлениях, они антипараллельны. )

AB/(|A||B|)=0, если A перпендикулярен B, и наоборот, если AB/(|A||B|)=0 , если A и B перпендикулярны.

Понятие «ортогональность» имеет решающее значение. Быстрое сканирование вашего текущего окружения, несомненно, обнаружит множество перпендикулярных поверхностей и краев (включая края этой страницы). Быстро проверьте ортогональность с помощью скалярного произведения: векторы u и v перпендикулярны тогда и только тогда, когда u.v=0

Скалярное произведение двух ортогональных векторов равно нулю. Матрицы двух столбцов, которые их представляют, имеют нулевой скалярный продукт. Относительная ориентация — это все, что имеет значение. Скалярное произведение будет равно нулю, если векторы ортогональны.

Скалярное произведение ортогональных векторов равно нулю, а скалярное произведение антипараллельных векторов отрицательно. Векторное произведение двух векторов — это вектор, перпендикулярный обоим векторам. Его величина вычисляется путем умножения величин двух углов на синус угла между ними.

Поскольку направление, перпендикулярное обоим векторам, максимизирует объем, векторное произведение примерно ортогонально к a и b.

В этой статье мы делаем вывод, что «Параллельные векторы — это векторы, имеющие одинаковое или прямо противоположное направление. Произведение любых двух параллельных векторов является нулевым вектором. Просто возьмите общий множитель из одного вектора и умножьте его на другой вектор, чтобы увидеть, параллельны ли они. Другой вариант — посмотреть, равно ли их векторное произведение нулю. 92 = 0 Эта сумма квадратов равна нулю, только если каждый член в отдельности ноль, что, конечно, следовало ожидать, потому что два вектора равны параллельны тогда и только тогда, когда их компоненты находятся в одинаковых пропорциях друг к другу, т. x/y = X/Y x/z = X/Z y/z = Y/Z что представляет собой исчезновение трех членов в предыдущем выражение. Это мотивирует определение перекрестного произведения (также известное как векторное произведение) двух векторов (x, y, z) и (X, Y, Z) как состоящий из этих трех компонентов, расположенных симметрично, так что каждый компонент определяется в терминах двух других компонентов аргументы, т. е. [(yZ — Yz), (Xz — xZ), (xY — Xy)] Этот вектор равен нулю тогда и только тогда, когда v и V параллельны. Более того, обратите внимание, что скалярное произведение этого перекрестного произведения и вектора v тождественно равен нулю, т. е. xyZ — xYz + yXz — yxZ + zxY — zXy = 0 и точно так же скалярное произведение перекрестного произведения и V также равно тождественно ноль XyZ — XYz + YXz — YxZ + ZxY — ZXy = 0 Как мы видели ранее, скалярное произведение двух векторов равно 0 тогда и только тогда если векторы перпендикулярны, так что это показывает, что векторное произведение из v и V перпендикулярно к ним обоим. Обобщения на более высокие измерения Также интересно рассмотреть, что происходит более чем за три размеры. 2 = 0 (1) Опять же, этого следовало ожидать, поскольку исчезновение этих терминов соответствует пропорциональности соответствующих компонентов v и V. Например, первый член представляет w/x = W/X. Однако, теперь у нас есть ШЕСТЬ таких условий, поэтому мы не можем использовать их в качестве компоненты четырехмерного вектора. В общем, когда мы образуют такого рода «перекрестное произведение» двух n-мерных векторов, которые мы приходим к C(n,2) терминам. Так получилось, что C(3,2) равно 3, поэтому перекрестное произведение двух трехмерных векторов является трехмерным вектор (пусть и с неоднозначностью знака). С другой стороны, C(4,2) равно 6, поэтому «перекрестное произведение» двух четырехмерных векторов (определяемый таким образом) является ШЕСТЬ мерным вектором. Это не сделало бы хорошо просто расширить нашу область до шести измерений, потому что «Перекрестное произведение» двух 6D-векторов будет иметь C (6,2) = 15 компонентов. Конечно, нам не обязательно нужны все шесть компонентов. перекрестного произведения двух четырехмерных векторов, поскольку только три из них могут служить для обеспечения пропорциональности всем четырем компоненты исходных векторов. Однако мы не можем прийти к симметричный выбор из трех (или четырех) терминов, поэтому такой подход не гарантирует, что векторное произведение ортогонально два заданных вектора. Кроме того, ясно, что ортогональность требование занижено двумя векторами в четырех измерениях, потому что есть целая плоскость направлений, каждая ортогональная любым двум заданным векторам. Это может привести нас к определению перекрестного произведения в четырех измерениях. как операцию на ТРЕХ векторах, а не только на двух. На этом основе мы можем указать, что векторное произведение имеет единственное направление (с точностью до знака), необходимых для того, чтобы сделать его перпендикулярным к каждой из три заданных вектора. Кроме того, мы можем определить величину перекрестного произведения как объема, содержащегося внутри параллельного эпипед, ребра которого (в одной вершине) являются тремя заданными векторами. Это прямо обобщает тот факт, что величина векторное произведение двух векторов в трех измерениях равно площади параллелограмма, порожденного двумя заданными векторами. Четко мы можем обобщить это на любое количество измерений, с понимая, что это «перекрестное произведение» работает с n-1 векторами. С другой стороны, предположим, что мы хотим определить операцию на двух векторах в четырехмерном пространстве, и мы хотим, чтобы он имел свойства, что (1) результат представляет собой четырехмерный вектор, (2) результат перпендикулярен обоим заданным векторам, и (3) величина результата обращается в нуль, если два заданных вектора параллельны. Это может быть достигнуто, но не единственным способом, путем объединения для каждого компонента «перекрестного произведения» трех члены из уравнения (1), которые не включают этот компонент, с правильный выбор знаков. Например, мы можем определить эрзац перекрестное произведение v и V как [ (xY-Xy)+(xZ-Xz)+(yZ-Yz), (Yz-yZ)+(yW-Yw)+(zW-Zw), (xZ-Xz)+(Xw-xW)+(zW-Zw), (Xy-xY)+(Xw-xW)+(Yw-yW)] Мы можем выбрать знаки двенадцати выражений «аб-ба» в любом из них. из восьми различных способов (до общего знака), дающих восемь одинаково подходящие эрзац-перекрестные произведения в 4D-пространстве. Восемь наборов знаки, удовлетворяющие требованиям, где «1» обозначает положительные и «0» обозначают отрицательный, 111 111 111 111 (показано выше) 011 101 101 111 111 011 011 011 011 001 001 011 101 110 111 101 001 100 101 101 101 010 011 001 001 000 001 001 Таким образом, для любых двух заданных четырехмерных векторов v и V суррогатное перекрестное произведение может быть любым из этих восьми (с точностью до знака), которые все лежат на одна двумерная плоскость (перпендикулярная как v, так и V). Например, с v=(19,-29,27,-13) и V=(-5,-11,16,23) показаны результаты ниже Стоит отметить, что хотя каждое из этих восьми перекрестных произведений обращается в нуль, когда v и V параллельны, обратное неверно. В в общем случае условие истинного параллелизма можно выразить как ж/г = ж/г х/у = Х/У г/у = г/у что заставляет все компоненты быть в одинаковой пропорции к друг с другом. Однако необходимым и достаточным условием эрзац-перекрестное произведение для исчезновения состоит в том, что должно существовать постоянная k такая, что w/y = W/Y + k(1 + W/Y) х/у = Х/У + к(1 + Х/У) z/y = Z/Y + k(1 + Z/Y) При k=0 это дает истинный параллелизм, но мы также можем иметь другие значения k, такие как 1/2, что объясняет, почему суррогатное перекрестное произведение из v=(5,2,1,8) и V=(3,1,1,5) равно (0,0,0,0).