XYZ — Векторное произведение двух векторов. Он-лайн калькулятор.
Проект Карла III Ребане и хорошей компании | Раздел недели: Водные растворы и смеси для обработки металлов — мытья, обезжиривания, нанесения покрытий, очистки и т.п. Составы для очистки и обезжиривания поверхности и нанесения покрытий. | ||||||||||
| Техническая информация тут Поиск на сайте DPVA Полезные ссылки О проекте Обратная связь Оглавление | Адрес этой страницы (вложенность) в справочнике DPVA.xyz: главная страница / / Техническая информация/ / Математический справочник / / Линейная алгебра. Вектора, матрицы, определители, миноры, детерминанты… / / Векторное произведение двух векторов.
| ||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | |||||||||||
Коды баннеров проекта DPVA.xyz Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.DPVA.xyz не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. | ||||||||||
Он-лайн калькулятор.
Более того, векторное произведение двух векторов равно нулю тогда и только тогда, когда они коллинеарны. (В случае, если один из них нулевой вектор необходимо вспомнить, что нулевой вектор коллинеарен любому вектору по определению).
5 Модуль вектора
По определению модуль вектора (vector magnitude) равен квадратному корню из суммы квадратов его элементов. Он обозначается тем же символом, что и определитель матрицы.
6 Скалярное произведение векторов
Векторы должны иметь одинаковый
размер. Скалярное произведение двух
векторов и равно
,
где – угол между
векторами. Если векторы ортогональны,
их скалярное произведение равно 0.
Обозначается скалярное произведение
тем же символом умножения. Никогда не
применяйте для обозначения скалярного
произведения символ ×,
который является общеупотребительным
символом векторного произведения.Пример:
7 Векторное произведение
Векторное
произведение (cross product) двух векторов и с углом между ними равно вектору с модулем
,
направленным перпендикулярно плоскости
векторов и
.
Обозначают векторное произведение
символом ×,
который можно ввести нажатием кнопки CrossProduct (Векторное произведение) на панели Matrix (Матрица) или сочетанием клавиш Ctr
+ 8.
8 Сумма элементов вектора и след матрицы
Иногда бывает нужно вычислить сумму всех элементов вектора. Для этого существует вспомогательный оператор, задаваемый кнопкой VectorSum (Сумма вектора) на панели Matrix (Матрица) или сочетанием клавиш Ctrl + 4. Этот оператор чаще оказывается полезным не в векторной алгебре, а при организации циклов с индексированными переменными.
Сумму диагональных элементов квадратной матрицы называют следом (trace) матрицы. След можно найти с помощью функции tr:
tr(A) – след квадратной матрицы
Задание: Найдите след квадратной матрицы A = .
Решение:
9 Обращение квадратной матрицы
Поиск обратной матрицы возможен, если матрица квадратная,
и ее определитель не равен нулю.
. После появления местозаполнителя в
него следует ввести значение степени
.
11 Символьные преобразования
Все матричные и векторные операторы, о которых шла речь выше, допустимо использовать в символьных вычислениях. Мощь символьных операций заключается в возможности проводить их не только над конкретными числами, но и над переменными.
Пример:
12 Генераторы матриц
Самым наглядным способом создания матрицы или вектора является применение первой кнопки панели инструментов Matrix (Матрицы). Однако в большинстве случаев, в частности, при программировании сложных проектов, удобнее бывает создавать массивы с помощью встроенных функций.
12.1 Создание матрицы на основе функции
Matrix(M, N, f) – создание матрицы размера , каждый , элемент которой есть f(i, j), где:
M – количество строк;
N – количество столбцов;
f(i, j) – функция.
12.2 Генерация матриц специального вида
В Mathcad легко создать матрицы определенного вида с помощью одной из встроенных функций:
identity(N) – единичная матрица размера ;
diag(V) – диагональная матрица, на диагонали которой находятся элементы вектора V;
geninv(A) – создание матрицы, обратной матрице А;
rref(A) – преобразование матрицы или вектора A в ступенчатый вид, где:
N – целое число;
V – вектор;
A – матрица из действительных чисел.
Примечание: Размер матрицы A для функции geninv должен быть таким, чтобы .
Векторный калькулятор перекрестного произведения в App Store
Описание
Векторное перекрестное произведение Калькулятор — это простое в использовании и очень полезное приложение для студентов и учителей математики. Это дает вам отличный опыт для поиска векторного произведения векторов с подробными решениями. Аккуратно вставьте значения векторов A и B в пустые поля, нажмите кнопку расчета и получите пошаговые решения с графиками и формулами.
Этот калькулятор создан для того, чтобы сделать его максимально простым для всех. Вот почему мы разработали это приложение с удобным интерфейсом. На экране несколько пустых прямоугольников с векторами A и B. Вам просто нужно ввести правильное значение в правильное поле. После этого нажмите кнопку расчета, и через микросекунды вы получите подробные решения с шагами, чтобы четко понять каждый шаг, чтобы найти перекрестный продукт.
Мы уверены, что вам понравится этот калькулятор.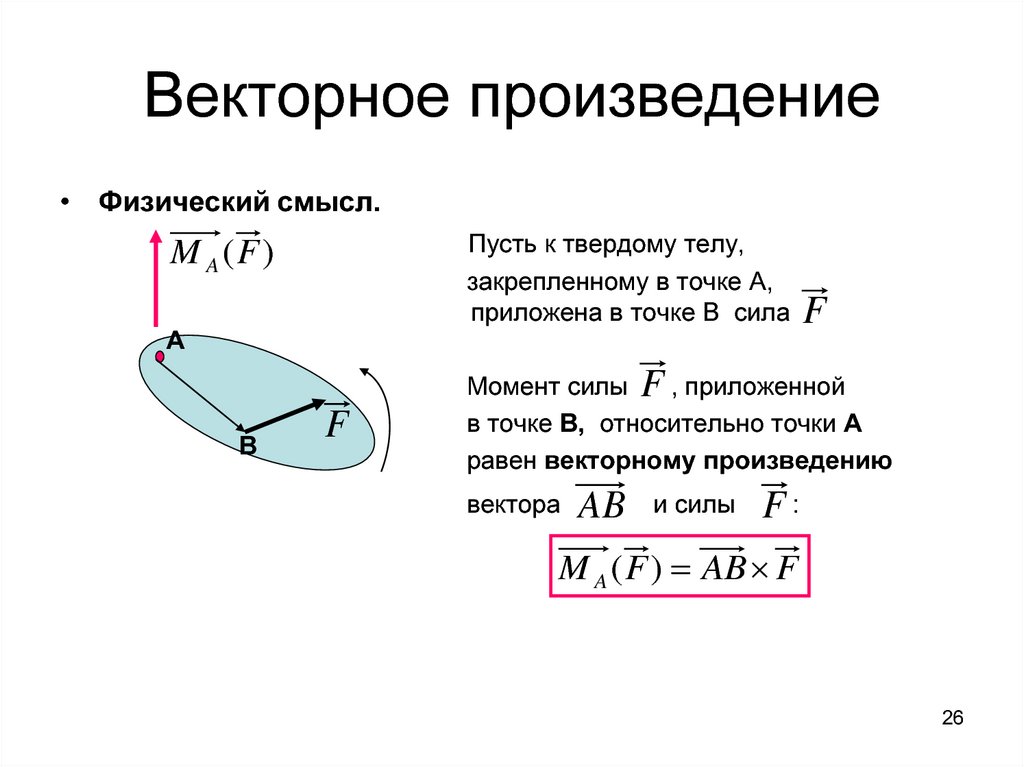
Потому что это приложение экономит много вашего времени от ручного расчета. Кроме того, он также предоставляет вам подробное решение с пошаговыми расчетами, чтобы четко понять обработку и расчет формул перекрестного произведения.
Как использовать
— Запишите значения векторов в пустые поля.
— Нажмите кнопку расчета.
— Получите подробное решение с шагами.
Особенности
— Удобное приложение.
— Легко вычислить векторное произведение.
— Маленький размер.
— Подробные решения.
— Быстрая обработка.
— Пошаговый расчет с графиками.
— Точный ответ.
Это приложение-калькулятор предлагает самые простые способы поиска подробных решений с пошаговыми инструкциями по поиску перекрестных произведений. Это облегчает вашу жизнь и экономит много времени благодаря автоматическому расчету векторных формул. Запишите значения векторов A и B и получите полное решение с шагами с помощью этого приложения.
Получите этот калькулятор векторного перекрестного произведения.
Начните решать неограниченное количество уравнений векторов, чтобы найти векторное произведение с помощью этого простого в использовании калькулятора.
Версия 1.0.1
Обновление пользовательского интерфейса, добавление новых функций, настройка рекламы и повышение производительности
Разработчик Талха Рехман указал, что политика конфиденциальности приложения может включать обработку данных, как описано ниже. Для получения дополнительной информации см. политику конфиденциальности разработчика.
Данные не собираются
Разработчик не собирает никаких данных из этого приложения.
Методы обеспечения конфиденциальности могут различаться в зависимости, например, от используемых вами функций или вашего возраста. Узнать больше
Информация
- Поставщик
- Талха Рехман
- Размер
- Категория
- Образование
- Возрастной рейтинг
- 4+
- Авторское право
- © Баззигейт
- Цена
- Бесплатно
3 megabytes»> 36,3 МБ- Сайт разработчика
- Тех. поддержка
- политика конфиденциальности
Еще от этого разработчика
Вам также может понравиться
Калькулятор векторного произведения — Поиск перекрестных произведений
Поиск инструмента
Найдите инструмент в dCode по ключевым словам:Просмотрите полный список инструментов dCode
Cross Product
Инструмент для вычисления векторного произведения (или векторного произведения) двух векторов в 3D, не коллинеарных (евклидово векторное пространство размерности 3)
Результаты
Кросс-продукт — dCode
Теги: Матрица
Поделиться
dCode и другие
dCode бесплатен, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !
Калькулятор векторного векторного произведения
Вектор 1 Загрузка.
..
(если это сообщение не исчезнет, попробуйте обновить страницу)
Загрузка…
(если это сообщение не исчезнет, попробуйте обновить страницу)
| Используемое обозначение | Крест ⨯ (английское обозначение) Клин ∧ (альтернативное обозначение) |
См. также: Tensor Product
Ответы на вопросы (FAQ)
Что такое векторное перекрестное произведение? (Определение)
Перекрестное произведение (или векторное произведение ) — это операция над двумя векторами $ \vec{u} $ и $ \vec{v} $ трехмерного пространства (не коллинеарная), результат которой отмечен $ \ vec{u} \times \vec{v} = \vec{w} $ (или иногда $ \vec{u} \wedge \vec{v} $) является ортогональным вектором к первым двум векторам.
Как вычислить векторное произведение двух векторов?
Для любой пары векторов $ \vec{u} = (u_1, u_2, u_3) $ и $ \vec{v} = (v_1, v_2, v_3) $ вычисление перекрестного произведения дается формулой : $$ \vec{u} \times \vec{v} = \begin{pmatrix} u_2v_3-u_3v_2 \\ u_3v_1-u_1v_3 \\ u_1v_2-u_2v_1 \end{pmatrix} $$
Пример: Определить вектор перекрестное произведение $ \vec{a} = (1, 2, 3) $ и $ \vec{b} = (4, 5, 6) $ путем вычисления $$ \vec{a} \times \vec{ b} = \begin{pmatrix} 2 \times 6 — 3 \times 5 \\ 3 \times 4 — 1 \times 6 \\ 1 \times 5 — 2 \times 4 \end{pmatrix} = \begin{pmatrix} -3 \6 \\ -3 \end{pmatrix} $$
Зачем вычислять векторное произведение?
Вычисление векторного произведения позволяет:
— проверить, коллинеарны ли 2 вектора (тогда их векторное произведение является нулевым вектором)
— вычислить вектор, ортогональный двум другим, и таким образом создать ортогональный базис с тремя векторами
— проверить, что 2 вектора ортогональны
— вычислить площадь параллелограмма со сторонами $ \vec{u} $ и $ \vec{v} $ (модуль векторное произведение равно площади параллелограмма)
Каковы свойства векторного произведения?
Перекрестное произведение является распределительным с добавлением:
$$ \vec{a} \times ( \vec{b} + \vec{c} ) = \vec{a} \times \vec{b} + \vec{a} \times \
ec{c} $$
Перекрестное произведение является дистрибутивным со скалярным умножением:
$$ \lambda (\vec{a} \times \vec{b} ) = \lambda \vec{a} \times \vec{b} = \vec{a} \times \lambda \vec{b} $$
Перекрестное произведение антисимметрично:
$$ \vec{a} \times \vec{b} = -\vec{b} \times \vec{a} $$
Норма (модуль) векторного произведения определяется по формуле:
$$ \| \vec{u} \times \vec{v} \| = \| \vec{и} \| \| \vec{v} \| \влево| \sin ( \widehat{ \vec{u}, \vec{v} } ) \right| $$
Исходный код
dCode сохраняет за собой право собственности на исходный код Cross Product.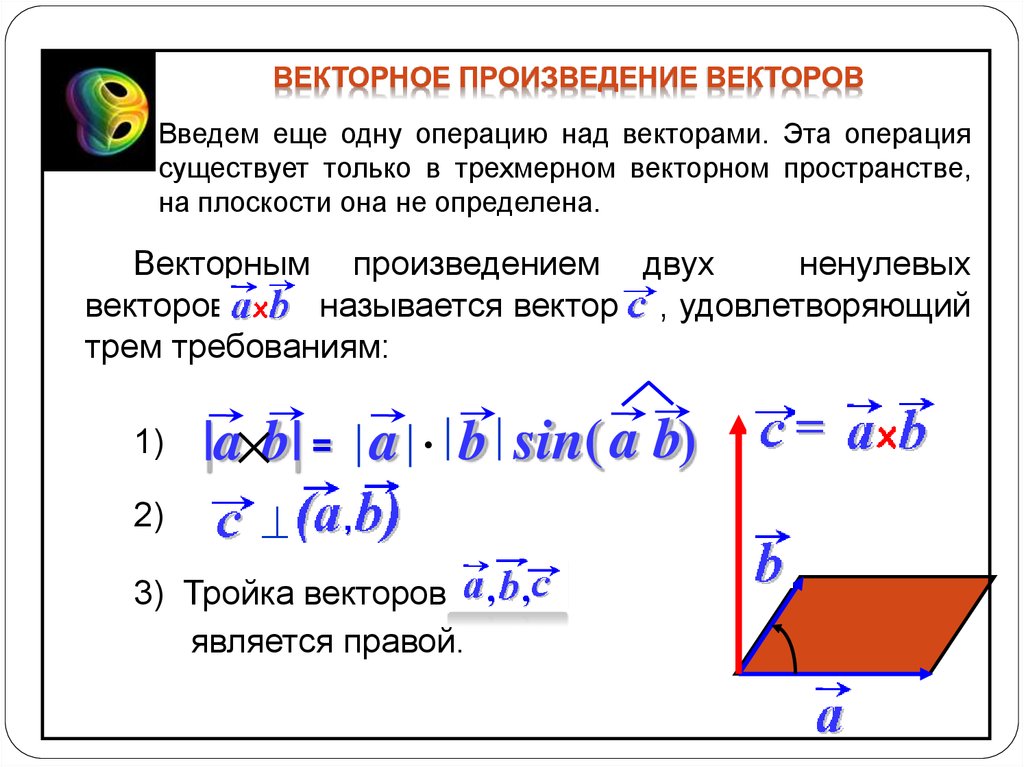
За исключением явной лицензии с открытым исходным кодом (указывается Creative Commons/бесплатно), алгоритма «Кросс-продукт», апплета или фрагмента (конвертер, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Кросс-продукта» функции (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и загрузка всех данных, скрипт, или доступ к API для «Cross Product» не является общедоступным, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
Напоминание: dCode можно использовать бесплатно.
Cite dCode
Копирование и вставка страницы «Cross Product» или любых его результатов разрешено, если вы цитируете dCode!
Ссылка на источник (библиография):
Cross Product на dCode.fr [онлайн-сайт], получено 18 февраля 2023 г.
