Справочник по высшей математике

Выгодский М.Я. Справочник по высшей математике. Изд-во «Наука». М. 1977 г. Справочник включает весь материал, входящий в программу основного курса математики высших учебных заведений. Детальная рубрикация и подробный предметный указатель позволяют быстро получать необходимую информацию. Книга окажет неоценимую помощь студентам, инженерам и научным работникам. Оглавление ПРЕДИСЛОВИЕ АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ § 1. Понятие о предмете аналитической геометрии § 2. Координаты § 3. Прямоугольная система координат § 4. Прямоугольные координаты § 5. Координатные углы § 6. Косоугольная система координат § 7. Уравнение линии § 8. Взаимное расположение линии и точки § 9. Взаимное расположение двух линий § 10. Расстояние между двумя точками § 11. Деление отрезка в данном отношении § 11а. Деление отрезка пополам § 12. Определитель второго порядка § 13. Площадь треугольника § 14. Прямая линия; уравнение, разрешенное относительно ординаты (с угловым коэффициентом) § 15. Прямая, параллельная оси § 16. Общее уравнение прямой § 17. Построение прямой по ее уравнению § 18. Условие параллельности прямых § 19. Пересечение прямых § 20. Условие перпендикулярности двух прямых § 21. Угол между двумя прямыми § 22. Условие, при котором три точки лежат на одной прямой § 23. Уравнение прямой, проходящей через две точки § 24. Пучок прямых § 25. Уравнение прямой, проходящей через данную точку параллельно данной прямой § 26. Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой § 27. Взаимное расположение прямой и пары точек § 28. Расстояние от точки до прямой § 29. Полярные параметры прямой § 30. 2+bx+c § 51. Директрисы эллипса и гиперболы § 52. Общее определение эллипса, гиперболы и параболы § 53. Конические сечения § 54. Диаметры конического сечения § 55. Диаметры эллипса § 56. Диаметры гиперболы § 57. Диаметры параболы § 58. Линии второго порядка § 59. Запись общего уравнения второй степени § 60. Упрощение уравнения второй степени; общие замечания § 61. Предварительное преобразование уравнения второй степени § 62. Завершающее преобразование уравнения второй степени § 63. О приемах, облегчающих упрощение уравнения второй степени § 64. Признак распадения линий второго порядка § 65. Нахождение прямых, составляющих распадающуюся линию второго порядка § 66. Инварианты уравнения второй степени § 67. Три типа линий второго порядка § 68. Центральные и нецентральные линии второго порядка § 69. Нахождение центра центральной линии второго порядка § 70. Упрощение уравнения центральной линии второго порядка § 71. Равносторонняя гипербола как график уравнения y=k/x § 72. Равносторонняя гипербола как график уравнения y=(mx+n)/(px+q) § 73. Полярные координаты § 74. Связь между полярными и прямоугольными координатами § 75. Архимедова спираль § 76. Полярное уравнение прямой § 77. Полярное уравнение конического сечения АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ § 78. Понятие о векторах и скалярах § 79. Вектор в геометрии § 80. Векторная алгебра § 81. Коллинеарные векторы § 82. Нуль-вектор § 83. Равенство векторов § 84. Приведение векторов к общему началу § 85. Противоположные векторы § 86. Сложение векторов § 87. Сумма нескольких векторов § 88. Вычитание векторов § 89. Умножение и деление вектора на число § 90. Взаимная связь коллинеарных векторов (деление вектора на вектор) § 91. Проекция точки на ось § 92. Проекция вектора на ось § 93. Основные теоремы о проекциях вектора § 94. Прямоугольная система координат в пространстве § 95. Координаты точки § 96. Координаты вектора § 97. Выражения вектора через компоненты и через координаты § 98. Действия над векторами, заданными своими координатами § 99. Выражение вектора через радиусы-векторы его начала и конца § 100. Длина вектора. Расстояние между двумя точками § 101. Угол между осью координат и вектором § 102. Признак коллинеарности (параллельности) векторов § 103. Деление отрезка в данном отношении § 104. Скалярное произведение двух векторов § 104а. Физический смысл скалярного произведения § 105. Свойства скалярного произведения § 106. Скалярные произведения основных векторов § 107. Выражение скалярного произведения через координаты сомножителей § 108. Условие перпендикулярности векторов § 109. Угол между векторами § 110. Правая и левая системы трех векторов § 111. Векторное произведение двух векторов § 112. Свойства векторного произведения § 113. Векторные произведения основных векторов § 114. Выражение векторного произведения через координаты сомножителей § 115. Компланарные векторы § 116. Смешанное произведение § 117. Свойства смешанного произведения § 118. Определитель третьего порядка § 119. Выражение смешанного произведения через координаты сомножителей § 120. Признак компланарности в координатной форме § 121. Объем параллелепипеда § 122. Двойное векторное произведение § 123. Уравнение плоскости § 124. Особые случаи положения плоскости относительно системы координат § 125. Условие параллельности плоскостей § 126. Условие перпендикулярности плоскостей § 127. Угол между двумя плоскостями § 128. Плоскость, проходящая через данную точку параллельно данной плоскости § 129. Плоскость, проходящая через три точки § 130. Отрезки на осях § 131. Уравнение плоскости в отрезках § 132. Плоскость, проходящая через две точки перпендикулярно данной плоскости § 133. Плоскость, проходящая через данную точку перпендикулярно двум плоскостям § 134. Точка пересечения трех плоскостей § 135. Взаимное расположение плоскости и пары точек § 136. Расстояние от точки до плоскости § 137. Полярные параметры плоскости § 138. Нормальное уравнение плоскости § 139. Приведение уравнения плоскости к нормальному виду § 140. Уравнения прямой в пространстве § 141. Условие, при котором два уравнения первой степени представляют прямую § 142. Пересечение прямой с плоскостью § 143. Направляющий вектор § 144. Углы между прямой и осями координат § 145. Угол между двумя прямыми § 146. Угол между прямой и плоскостью § 147. Условия параллельности и перпендикулярности прямой и плоскости § 148. Пучок плоскостей § 149. Проекции прямой на координатные плоскости § 150. Симметричные уравнения прямой § 151. Приведение уравнений прямой к симметричному виду § 152. Параметрические уравнения прямой § 153. Пересечение плоскости с прямой, заданной параметрически § 154. Уравнения прямой, проходящей через две данные точки § 155. Уравнение плоскости, проходящей через данную точку перпендикулярно данной прямой § 156. Уравнения прямой, проходящей через данную точку перпендикулярно данной плоскости § 157. Уравнение плоскости, проходящей через данную точку и данную прямую § 158. Уравнение плоскости, проходящей через данную точку и параллельной двум данным прямым § 159. Уравнение плоскости, проходящей через данную прямую и параллельной другой данной прямой § 160. Уравнение плоскости, проходящей через данную прямую и перпендикулярной данной плоскости § 161. Уравнения перпендикуляра, опущенного из данной точки на данную прямую § 162. Длина перпендикуляра, опущенного из данной точки на данную прямую § 163. Условие, при котором две прямые пересекаются или лежат в одной плоскости § 164. Уравнения общего перпендикуляра к двум данным прямым § 165. Кратчайшее расстояние между двумя прямыми § 165а. Правые и левые пары прямых § 166. Преобразование координат § 167. Уравнение поверхности § 168. Цилиндрические поверхности, у которых образующие параллельны одной из осей координат § 169. Уравнения линии § 170. Проекция линии на координатную плоскость § 171. Алгебраические поверхности и их порядок § 172. Сфера § 173. Эллипсоид § 174. Однополостный гиперболоид § 175. Двуполостный гиперболоид § 176. Конус второго порядка § 177. Эллиптический параболоид § 178. Гиперболический параболоид § 179. Перечень поверхностей второго порядка § 180. Прямолинейные образующие поверхностей второго порядка § 181. Поверхности вращения § 182. Определители второго и третьего порядков § 183. Определители высших порядков § 184. Свойства определителей § 185. Практический прием вычисления определителей § 186. Применение определителей к исследованию и решению системы уравнений § 187. Два уравнения с двумя неизвестными § 188. Два уравнения с двумя неизвестными § 189. Однородная система двух уравнений с тремя неизвестными § 190. Два уравнения с двумя неизвестными § 190а. Система n уравнений с n неизвестными ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОГО АНАЛИЗА § 192. Рациональные числа § 193. Действительные (вещественные) числа § 194. Числовая ось § 195. Переменные и постоянные величины § 196. Функция § 197. Способы задания функции § 198. Область определения функции § 199. Промежуток § 200. Классификация функций § 201. Основные элементарные функции § 202. Обозначение функции § 203. Предел последовательности § 204. Предел функции § 205. Определение предела функции § 206. Предел постоянной величины § 207. Бесконечно малая величина § 208. Бесконечно большая величина § 209. Связь между бесконечно большими и бесконечно малыми величинами § 210. Ограниченные величины § 211. Расширение понятия предепа § 212. Основные свойства бесконечно малых величин § 213. Основные теоремы о пределах § 214. Число е § 215. Предел sinx/x при x стремящемся к 0 § 216. Эквивалентные бесконечно малые величины § 217. Сравнение бесконечно малых величин § 217а. Приращение переменной величины § 218. Непрерывность функции в точке § 219. Свойства функций, непрерывных в точке § 219а. Односторонний предел; скачок функции § 220. Непрерывность функции на замкнутом промежутке § 221. Свойства функций, непрерывных на замкнутом промежутке ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ § 223. Скорость § 224. Определение производной функции § 225. Касательная § 226. Производные некоторых простейших функций § 227. Свойства производной § 228. Дифференциал § 229. Механический смысл дифференциала § 230. Геометрический смысл дифференциала § 231. Дифференцируемые функции § 232. Дифференциалы некоторых простейших функций § 233. Свойства дифференциала § 234. Инвариантность выражения f'(x)dx § 235. Выражение производной через дифференциалы § 236. Функция от функции (сложная функция) § 237. Дифференциал сложной функции § 238. Производная сложной функции § 239. Дифференцирование произведения § 240. Дифференцирование частного (дроби) § 241. Обратная функция § 242. Натуральные логарифмы § 243. Дифференцирование логарифмической функции § 244. Логарифмическое дифференцирование § 245. Дифференцирование показательной функции § 246. Дифференцирование тригонометрических функций § 247. Дифференцирование обратных тригонометрических функций § 247а. Некоторые поучительные примеры § 248. Дифференциал в приближенных вычислениях § 249. Применение дифференциала к оценке погрешности формул § 250. Дифференцирование неявных функций § 251. Параметрическое задание линии § 252. Параметрическое задание функции § 253. Циклоида § 254. Уравнение касательной к плоской линии § 254а. Касательные к кривым второго порядка § 255. Уравнение нормали § 256. Производные высших порядков § 257. Механический смысл второй производной § 258. Дифференциалы высших порядков § 259. Выражение высших производных через дифференциалы § 260. Высшие производные функций, заданных параметрически § 261. Высшие производные неявных функций § 262. Правило Лейбница § 263. Теорема Ролля § 264. Теорема Лагранжа о среднем значении § 265. Формула конечных приращений § 266. Обобщенная теорема о среднем значении (Коши) § 267. Раскрытие неопределенности вида 0/0 § 268. Раскрытие неопределенности вида бесконесность на бесконечность § 269. Неопределенные выражения других видов § 270. Исторические сведения о формуле Тейлора § 271. Формула Тейлора § 272. Применение формулы Тейлора к вычислению значений функции § 273. Возрастание и убывание функции § 274. Признаки возрастания и убывания функции в точке § 274а. Признаки возрастания и убывания функции в промежутке § 275. Максимум и минимум § 276. Необходимое условие максимума и минимума § 277. Первое достаточное условие максимума и минимума § 278. Правило нахождения максимумов и минимумов § 279. Второе достаточное условие максимума и минимума § 280. Нахождение наибольшего и наименьшего значений функции § 281. Выпуклость плоских кривых; точка перегиба § 282. Сторона вогнутости § 283. Правило для нахождения точек перегиба § 284. Асимптоты § 285. Нахождение асимптот, параллельных координатным осям § 286. Нахождение асимптот, не параллельных оси ординат § 287. Приемы построения графиков § 288. Решение уравнений. Общие замечания § 289. Решение уравнений. Способ хорд § 290. Решение уравнений. Способ касательных § 291. Комбинированный метод хорд и касательных ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ § 293. Первообразная функция § 294. Неопределенный интеграл § 295. Геометрический смысл интегрирования § 296. Вычисление постоянной интегрирования по начальным данным § 297. Свойства неопределенного интеграла § 298. Таблица интегралов § 299. Непосредственное интегрирование § 300. Способ подстановки (интегрирование через вспомогательную переменную) § 301. Интегрирование по частям § 302. Интегрирование некоторых тригонометрических выражений § 303. Тригонометрические подстановки § 304. Рациональные функции § 304а. Исключение целой части § 305. О приемах интегрирования рациональных дробей § 306. Интегрирование простейших рациональных дробей § 307. Интегрирование рациональных функций (общий метод) § 308. О разложении многочлена на множители § 309. Об интегрируемости в элементарных функциях § 310. Некоторые интегралы, зависящие от радикалов § 311. Интеграл от биномиального дифференциала § 312. Интегралы вида … § 313. Интегралы вида S R(sinx, cosx)dx § 314. Определенный интеграл § 315. Свойства определенного интеграла § 316. Геометрический смысл определенного интеграла § 317. Механический смысл определенного интеграла § 318. Оценка определенного интеграла § 318а. Неравенство Буняковского § 319. Теорема о среднем интегрального исчисления § 320. Определенный интеграл как функция верхнего предела § 321. Дифференциал интеграла § 322. Интеграл дифференциала. Формула Ньютона — Лейбница § 323. Вычисление определенного интеграла с помощью неопределенного § 324. Определенное интегрирование по частям § 325. Способ подстановки в определенном интеграле § 326. О несобственных интегралах § 327. Интегралы с бесконечными пределами § 328. Интеграл функции, имеющей разрыв § 329. О приближенном вычислении интеграла § 330. Формулы прямоугольников § 331. Формула трапеций § 332. Формула Симпсона (параболических трапеций) § 333. Площади фигур, отнесенных к прямоугольным координатам § 334. Схема применения определенного интеграла § 335. Площади фигур, отнесенных к полярным координатам § 336. Объем тела по поперечным сечениям § 337. Объем тела вращения § 338. Длина дуги плоской линии § 339. Дифференциал дуги § 340. Длина дуги и ее дифференциал в полярных координатах § 341. Площадь поверхности вращения ОСНОВНЫЕ СВЕДЕНИЯ О ПЛОСКИХ И ПРОСТРАНСТВЕННЫХ ЛИНИЯХ § 342. Кривизна § 343. Центр, радиус и круг кривизны плоской линии § 344. Формулы для кривизны, радиуса и центра кривизны плоской линии § 345. Эволюта плоской линии § 346. Свойства эволюты плоской линии § 347. Развертка (эвольвента) плоской линии § 348. Параметрическое задание пространственной линии § 349. Винтовая линия § 350. Длина дуги пространственной линии § 351. Касательная к пространственной линии § 352. Нормальная плоскость § 353. Вектор-функция скалярного аргумента § 354. Предел вектор-функции § 355. Производная вектор-функции § 356. Дифференциал вектор-функции § 357. Свойства производной и дифференциала вектор-функции § 358. Соприкасающаяся плоскость § 359. Главная нормаль. Сопутствующий трехгранник § 360. Взаимное расположение линии и плоскости § 361. Основные векторы сопутствующего трехгранника § 362. Центр, ось и радиус кривизны пространственной линии § 363. Формулы для кривизны, радиуса и центра кривизны пространственной линии § 364. О знаке кривизны § 365. Кручение РЯДЫ § 367. Определение ряда § 368. Сходящиеся и расходящиеся ряды § 369. Необходимое условие сходимости ряда § 370. Остаток ряда § 371. Простейшие действия над рядами § 372. Положительные ряды § 373. Сравнение положительных рядов § 374. Признак Даламбера для положительного ряда § 375. Интегральный признак сходимости § 376. Знакопеременный ряд. Признак Лейбница § 377. Абсолютная и условная сходимость § 378. Признак Даламбера для произвольного ряда § 379. Перестановка членов ряда § 380. Группировка членов ряда § 381. Умножение рядов § 382. Деление рядов § 383. Функциональный ряд § 384. Область сходимости функционального ряда § 385. О равномерной и неравномерной сходимости § 386. Определение равномерной и неравномерной сходимости § 387. Геометрический смысл равномерной и неравномерной сходимости § 388. Признак равномерной сходимости; правильные ряды § 389. Непрерывность суммы ряда § 390. Интегрирование рядов § 391. Дифференцирование рядов § 392. Степенной ряд § 393. Промежуток и радиус сходимости степенного ряда § 394. Нахождение радиуса сходимости § 395. Область сходимости ряда, расположенного по степеням х – х0 § 396. Теорема Абеля § 397. Действия со степенными рядами § 398. Дифференцирование и интегрирование степенного ряда § 399. Ряд Тейлора § 400. Разложение функции в степенной ряд § 401. Разложение элементарных функций в степенные ряды § 402. Применение рядов к вычислению интегралов § 403. Гиперболические функции § 404. Обратные гиперболические функции § 405. Происхождение наименований гиперболических функций § 406. О комплексных числах § 407. Комплексная функция действительного аргумента § 408. Производная комплексной функции § 409. Возведение положительного числа в комплексную степень § 410. Формула Эйлера § 411. Тригонометрический ряд § 412. Исторические сведения о тригонометрических рядах § 413. Ортогональность системы функций cos nx, sin nx § 414. Формулы Эйлера-Фурье § 415. Ряд Фурье § 416. Ряд Фурье для непрерывной функции § 417. Ряд Фурье для четной и нечетной функции § 418. Ряд Фурье для разрывной функции ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ АРГУМЕНТОВ § 420. Функция трех и большего числа аргументов § 421. Способы задания функций нескольких аргументов § 422. Предел функции нескольких аргументов § 424. Непрерывность функции нескольких аргументов § 425. Частные производные § 426. Геометрический смысл частных производных для случая двух аргументов § 427. Полное и частное приращения § 428. Частный дифференциал § 429. О выражении частной производной через дифференциал § 430. Полный дифференциал § 431. Геометрический смысл полного дифференциала (случай двух аргументов) § 432. Инвариантность выражения … полного дифференциала § 433. Техника дифференцирования § 434. Дифференцируемые функции § 435. Касательная плоскость и нормаль к поверхности § 436. Уравнение касательной плоскости § 437. Уравнения нормали § 438. Дифференцирование сложной функции § 439. Замена прямоугольных координат полярными § 440. Формулы для производных сложной функции § 441. Полная производная § 442. Дифференцирование неявной функции нескольких переменных § 443. Частные производные высших порядков § 444. Полные дифференциалы высших порядков § 445. Техника повторного дифференцирования § 446. Условное обозначение дифференциалов § 447. Формула Тейлора для функции нескольких аргументов § 448. Экстремум (максимум и минимум) функции нескольких аргументов § 449. Правило нахождения экстремума § 450. Достаточные условия экстремума (случай двух аргументов) § 451. Двойной интеграл § 452. Геометрический смысл двойного интеграла § 453. Свойства двойного интеграла § 454. Оценка двойного интеграла § 455. Вычисление двойного интеграла (простейший случай) § 456. Вычисление двойного интеграла (общий случай) § 457. Функция точки § 458. Выражение двойного интеграла через полярные координаты § 459. Площадь куска поверхности § 460. Тройной интеграл § 461. Вычисление тройного интеграла (простейший случай) § 462. Вычисление тройного интеграла (общий случай) § 463. Цилиндрические координаты § 464. Выражение тройного интеграла через цилиндрические координаты § 465. Сферические координаты § 466. Выражение тройного интеграла через сферические координаты § 467. Схема применения двойного и тройного интегралов § 468. Момент инерции § 471. Криволинейный интеграл § 472. Механический смысл криволинейного интеграла § 473. Вычисление криволинейного интеграла § 474. Формула Грина § 475. Условие, при котором криволинейный интеграл не зависит от пути § 476. Другая форма условия предыдущего параграфа ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ § 478. Уравнение первого порядка § 479. Геометрический смысл уравнения первого порядка § 480. Изоклины § 481. Частное и общее решения уравнения первого порядка § 482. Уравнения с разделенными переменными § 483. Разделение переменных. Особое решение § 484. Уравнение в полных дифференциалах § 484а. Интегрирующий множитель § 485. Однородное уравнение § 486. Линейное уравнение первого порядка § 487. Уравнение Клеро § 488. Огибающая § 489. Об интегрируемости дифференциальных уравнений § 490. Приближенное интегрирование уравнений первого порядка по методу Эйлера § 491. Интегрирование дифференциальных уравнений с помощью рядов § 492. О составлении дифференциальных уравнений § 493. Уравнение второго порядка § 494. Уравнение n-го порядка § 495. Случаи понижения порядка § 496. Линейное уравнение второго порядка § 497. Линейное уравнение второго порядка с постоянными коэффициентами § 498. Линейное уравнение второго порядка с постоянными коэффициентами без правой части § 498а. Связь между случаями 1 и 3 § 498 § 499. Линейное уравнение второго порядка с постоянными коэффициентами с правой частью § 500. Линейные уравнения любого порядка § 501. Метод вариации постоянных § 502. Системы дифференциальных уравнений. Линейные системы НЕКОТОРЫЕ ЗАМЕЧАТЕЛЬНЫЕ КРИВЫЕ § 503. Строфоида § 504. Циссоида Диокла § 505. Декартов лист § 506. Верзьера Аньези § 507. Конхоида Никомеда § 508. Улитка Паскаля; кардиоида § 509. Линия Кассини § 510. Лемниската Бернулли § 511. Архимедова спираль § 512. Эвольвента (развертка) круга § 513. Логарифмическая спираль § 514. Циклоиды § 515. Эпициклоиды и гипоциклоиды § 516. Трактриса § 517. Цепная линия

20. Векторное произведение

Векторным произведением вектора на вектор называется вектор , длина и направление которого определяется условиями:

1. , где ‑ угол между и ;

2. перпендикулярен каждому из векторов и ;

3. направлен так, что кратчайший поворот от к виден из его конца совершающимся против часовой стрелки.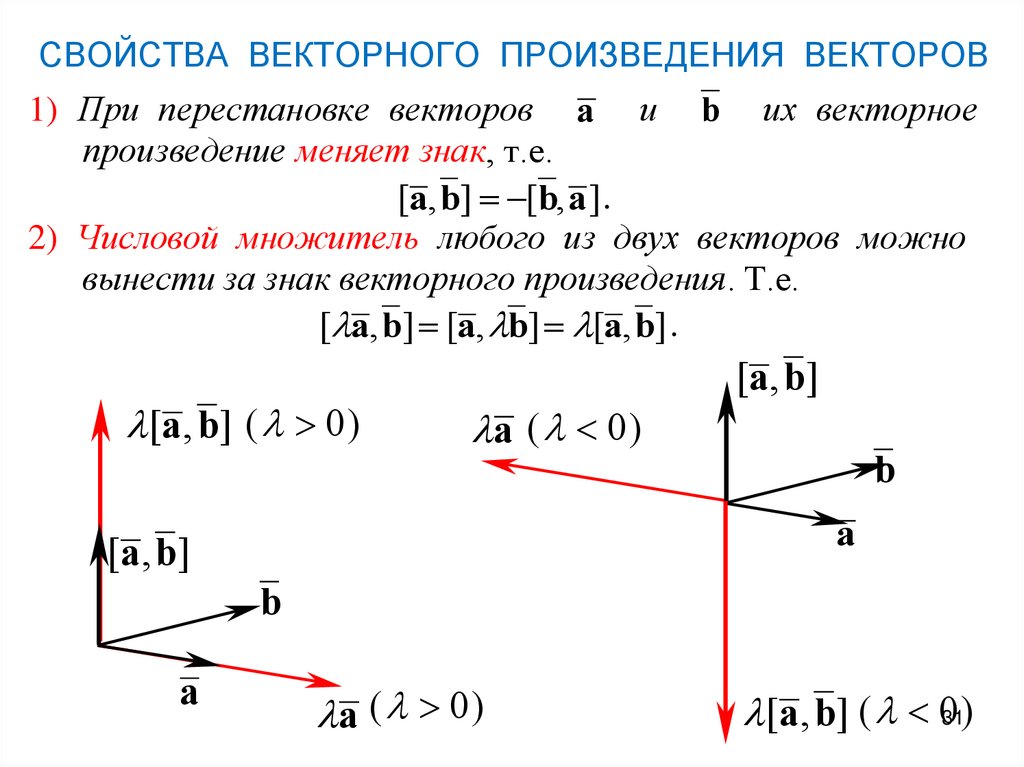

Векторное произведение обладает следующими свойствами:

1. ;

2. ;

3. ;

4. Векторное произведение равно нулю (нуль вектору) тогда и только тогда, когда и коллинеарны. В частности, для любого вектора ;

5. Если и неколлинеарны, то модуль векторного произведения равен площади параллелограмма построенного на этих векторах, как на сторонах.

Из первых трех свойств следует, что векторное умножение суммы векторов на сумму векторов подчиняется обычным правилам перемножения многочленов. Надо только следить за тем, чтобы порядок следования множителей не менялся.

Основные орты перемножаются следующим образом:

.

Если и , то c учетом свойств векторного произведения векторов, можно вывести правило вычисления координат векторного произведения по координатам векторов-сомножителей:

.

Если принять во внимание полученные выше правила перемножения ортов, то:

(4. 11)

Более компактную форму записи выражения для вычисления координат векторного произведения двух векторов можно построить, если ввести понятие определителя матрицы.

Рассмотрим частный случай, когда вектора и принадлежат плоскости , т. е. их можно представить как и .

Если координаты векторов записать в виде таблицы следующим образом: , то можно сказать, что из них сформирована квадратная матрица второго порядка, т. е. размером , состоящая из двух строк и двух столбцов. Каждой квадратной матрице ставится в соответствие число, которое вычисляется из элементов матрицы по определенным правилам и называется определителем. Определитель матрицы второго порядка равен разности произведений элементов главной диагонали и побочной диагонали:

.

В таком случае:

Абсолютная величина определителя, таким образом, равна площади параллелограмма, построенного на векторах и , как на сторонах.

Если сравнить это выражение с формулой векторного произведения (4. 7), то:

(4.12)

Это выражение представляет собой формулу для вычисления определителя матрицы третьего порядка по первой строке.

Таким образом:

Определитель матрицы третьего порядка вычисляется следующим образом:

И представляет собой алгебраическую сумму шести слагаемых.

Формулу для вычисления определителя матрицы третьего порядка легко запомнить, если воспользоваться Правилом Саррюса, которое формулируется следующим образом:

· Каждое слагаемое является произведением трех элементов, расположенных в разных столбцах и разных строках матрицы;

· Знак “плюс” имеют произведения элементов, образующих треугольники со стороной, параллельной главной диагонали;

· Знак “минус” имеют произведения элементов, принадлежащих побочной диагонали, и два произведения элементов, образующих треугольники со стороной, параллельной побочной диагонали.

< Предыдущая		Следующая >

Выразите перекрестное и скалярное произведение двух векторов в декартовой системе координат.

ПУБЛИКАЦИЯ СУРЫ-КИНЕМАТИКА-Числовые задачи

20 видео

РЕКЛАМА

Аб Падхай каро бина адс ке

Хариэдо Д.Н. Про и дехо сари видео бина киси ад ки рукаават ке!

Войти, если уже приобретено

Обновлено: 27-06-2022

Текст Решение

Решение

Пусть →Aи→B два вектора.
→A=→Axˆi+→Asˆj+→Azˆk,→B=→Bxˆi+→Byˆj+→Bzˆk
Перекрестное произведение →Aи→B.
→A×→B=(→Axˆi+→Ayˆj+→Azˆk)×(→Bxˆi+→Byˆj+→Bzˆk)
=→Ax→Bxˆi׈i+→Ax→Byˆi׈j+→Ax→Bzˆi׈k
+→Ay→Byˆj ׈i+→Ay→Bzˆj׈j+→AzBzatk׈k
→A×→B=→Ax→By(k)+AxBz(−ˆj)+→Ay→Bx(−ˆk)+→Ay→By(0)
+→Ay→Bz(ˆi)+→Az→Bx(ˆj)+→Az→Bz(0)
(→A×→B)=(→Ay→Bz−→Az→By)ˆi+(→Az→Bx −→Ax→Bz)ˆj+(→Ax→By−→Ay→Bx)ˆk
[∵ˆi׈i=ˆj׈j=ˆk׈k=0
ˆi׈j=k,ˆi׈k=−ˆj,ˆj ׈i=−k,ˆj׈k=ˆi,ˆk׈i=+ˆj׈j=−ˆk]
Это может быть в детерминантной форме как,
→A×→B=∣∣ ∣ ∣∣ˆiˆjˆjkAxAyAzBxByBz∣∣ ∣ ∣∣
=ˆi(AyBz−ByAz)−ˆj(AxBz−ByAz)+ˆk(AxBy−BxAy)
Скалярное произведение →Aи→B.
→A=→Axˆi+→Ayˆj+→Azˆk,→B=→Bxˆi+→Bxˆj→B_(z)ˆk
→A.→B=(→Axˆi+→Ayˆj+→Azˆk).(→Bxˆi+→Byˆj+→Bzˆk)
( →Ax→Bx(ˆi.ˆj)+→Ax→By(ˆi.ˆj)
+→Ax→Bz(ˆi.ˆk)+→Ay→Bx(ˆj.ˆk)+→Ay→By(ˆi.ˆj)
+→Ay→Bz(ˆj.ˆk)+→Az→Bx(ˆk.ˆi)+→Az→By(ˆk.ˆj)
+AzBz(ˆk.ˆk)
→A.→B=−→Ax− →Bx(1)+−→Ax−→By(0)+→Ax−→Bz(0)+−→Ay−→Bz(0)+−→Ay−→By(1)
+−→Ay− →Bz(0)+−→Az−→Bx(0)+−→Azvy(0)+AzBz(1)
→A.→B=→Ax→Bx+−→Ay−→By+→Az→Bz
[ ∵ˆi.ˆi=ˆj.ˆj=ˆk.ˆk=1
ˆi.ˆj=ˆi.ˆk=0,ˆj.ˆi=ˆj.ˆk=0,ˆk.ˆi=ˆk.ˆj=0]

Ответ

Пошаговое решение от экспертов, которое поможет вам в устранении сомнений и подсчете очков отличные оценки на экзаменах.

---

Похожие видео

Утверждение: Скалярное произведение одного вектора на другой вектор может быть скалярным или векторным.
Причина: Если произведение двух векторов является векторной величиной, то произведение называется скалярным произведением.

34887732

Если отношение скалярного произведения двух векторов к векторному произведению тех же двух векторов равно √3, два вектора образуют угол

141174130

দুটি ক্রস ক্রস গুণফল ও গুনফলের মানের অনুপাত 1√3, ভেক্টর দুটির মধ্যবর্তী কোণ হবে

371084256

Магнитуда поперечного продукта двух векторов (→ B) два . Величина их равнодействующей может быть записана как

435636826

Векторы | Скалярное произведение двух векторов

510394015

Скалярное скалярное произведение|Векторное перекрестное произведение

612893365

Если скалярное произведение двух векторов равно величине перекрестного произведения тех же векторов, то угол между векторами равен

642708657

Если скалярное произведение двух векторов равно величине векторного произведения этих же векторов, то угол между векторами равен

642845818

Если отношение скалярного произведения двух векторов и перекрестного произведение тех же двух векторов равно √3, два вектора составляют угол

642978036

Получите выражение для векторного произведения двух векторов через их прямоугольную форму.

643068622

Объясните скалярное произведение и векторное произведение единичных векторов.

643080976

Точка || Перекрестное произведение векторов

643454618

выражает магнитный поток как скалярное произведение двух векторов.

644568581

Выразите магнитный поток как скалярное произведение двух векторов.

644989170

Текст Решение

Утверждение: Скалярное произведение одного вектора на другой вектор может быть скалярным или векторным.
Причина: Если произведение двух векторов является векторной величиной, то произведение называется скалярным произведением.

645862288

Векторная геометрия – линейная алгебра с приложениями

Перейти к содержимому

В этой главе мы изучаем геометрию трехмерного пространства. Мы рассматриваем точку в трехмерном пространстве как стрелку из начала координат в эту точку. Это дает «картину» сути дела, которая действительно стоит тысячи слов.

Векторов в

Ввести систему координат в трехмерном пространстве обычным способом. Сначала выберите точку, называемую , затем выберите три взаимно перпендикулярные линии, проходящие через , называемые , и , и установите числовую шкалу на каждой оси с нулем в начале координат. Данной точке в -пространстве мы связываем три числа , и с , как показано на рисунке 4.1.1.

Эти числа называются числом , и мы обозначаем точку как , или, чтобы подчеркнуть метку . Результат называется системой координат для трехмерного пространства, а результирующее описание трехмерного пространства называется .

Как и на плоскости, мы вводим векторы, отождествляя каждую точку с вектором
в , представленном от начала до, как на рисунке 4.1.1. Неформально мы говорим, что точка имеет вектор , а этот вектор имеет точку . Таким образом, 3-пространство отождествляется с , и это отождествление будет проводиться на протяжении всей главы, часто без комментариев. В частности, термины «вектор» и «точка» взаимозаменяемы. Полученное описание трехмерного пространства называется . Обратите внимание, что происхождение .

 

Длина и направление

Мы собираемся обсудить два фундаментальных геометрических свойства векторов в : длину и направление. Во-первых, если это вектор с точкой , вектор определяется как расстояние от начала координат до , то есть длина стрелки, представляющей . Следующие свойства длины будут часто использоваться.

Позвольте быть вектором.

1. .
2. тогда и только тогда, когда
3. для всех скаляров.

Доказательство:

Пусть есть точка .

1. На рис. 4.1.2 — гипотенуза прямоугольного треугольника , и, следовательно, по теореме Пифагора. Но есть гипотенуза прямоугольного треугольника, значит. Теперь (1) следует путем исключения и извлечения положительных квадратных корней.
2. Если = 0, то по (1). Поскольку квадраты действительных чисел неотрицательны, отсюда следует, что и, следовательно, что . Обратное потому что.
3. У нас так (1) дает

      

   Следовательно, и мы закончили, потому что для любого действительного числа.

Если
, то . Точно так же, если
в двойном пространстве, то .

Когда мы рассматриваем два ненулевых вектора как стрелки, исходящие из начала координат, геометрически ясно, что мы имеем в виду, говоря, что они имеют одинаковые или противоположные . Это приводит к принципиально новому описанию векторов.

 

 

 

Позвольте и быть векторами в . Тогда как матрицы тогда и только тогда, когда и имеют одинаковое направление и одинаковую длину.

Доказательство:

Если , они явно имеют одинаковое направление и длину. Обратно, пусть и — векторы с точками и соответственно. Если и имеют одинаковую длину и направление, то геометрически и должны быть одной и той же точкой.

Отсюда , и , то есть .

Обратите внимание, что длина и направление вектора зависят от выбора системы координат в . Такие описания важны в приложениях, потому что физические законы часто формулируются в терминах векторов, и эти законы не могут зависеть от конкретной системы координат, используемой для описания ситуации.

Геометрические векторы

Если и являются различными точками в пространстве, стрелка от до имеет длину и направление.

Следовательно,

Предположим, что и любые две точки в . На рис. 4.1.4 отрезок от до обозначен и называется от до . Точка называется из , называется и обозначается .

Обратите внимание, что если любой вектор находится в точке с точкой, то он сам является геометрическим вектором, где находится начало координат. Обращение к «вектору» представляется оправданным в силу теоремы 4.1.2, поскольку он имеет направление (от к ) и длину . Однако возникает проблема, поскольку два геометрических вектора могут иметь одинаковую длину и направление, даже если кончики и хвосты различны.

Например, и на рис. 4.1.5 имеют одинаковую длину и одинаковое направление (1 единица влево и 2 единицы вверх), поэтому по теореме 4.1.2 это один и тот же вектор! Наилучший способ понять этот кажущийся парадокс — это увидеть различия в одном и том же основном векторе. Как только это прояснено, это явление становится большим преимуществом, потому что, благодаря теореме 4.1.2, оно означает, что один и тот же геометрический вектор может быть расположен в любом месте в пространстве; важна длина и направление, а не расположение кончика и хвоста. Эта возможность перемещать геометрические векторы очень полезна.

Закон параллелограмма

Теперь мы даем внутреннее описание суммы двух векторов и в , то есть описание, которое зависит только от длин и направлений, а не от выбора системы координат. Используя теорему 4.1.2, мы можем думать, что эти векторы имеют общий хвост. Если их кончики и соответственно, то они оба лежат в плоскости, содержащей , и , как показано на рисунке 4.1.6. Векторы и создают параллелограмм в , заштрихованный на рис. 4.1.6, называемый параллелограммом через и .

 

Если мы теперь выберем систему координат на плоскости с началом, то закон параллелограмма на плоскости показывает, что их сумма является диагональю параллелограмма, который они определяют с хвостом . Это внутреннее описание суммы, поскольку оно не ссылается на координаты. Это обсуждение доказывает:

В параллелограмме, определяемом двумя векторами и , вектором является диагональ с таким же хвостом, как и .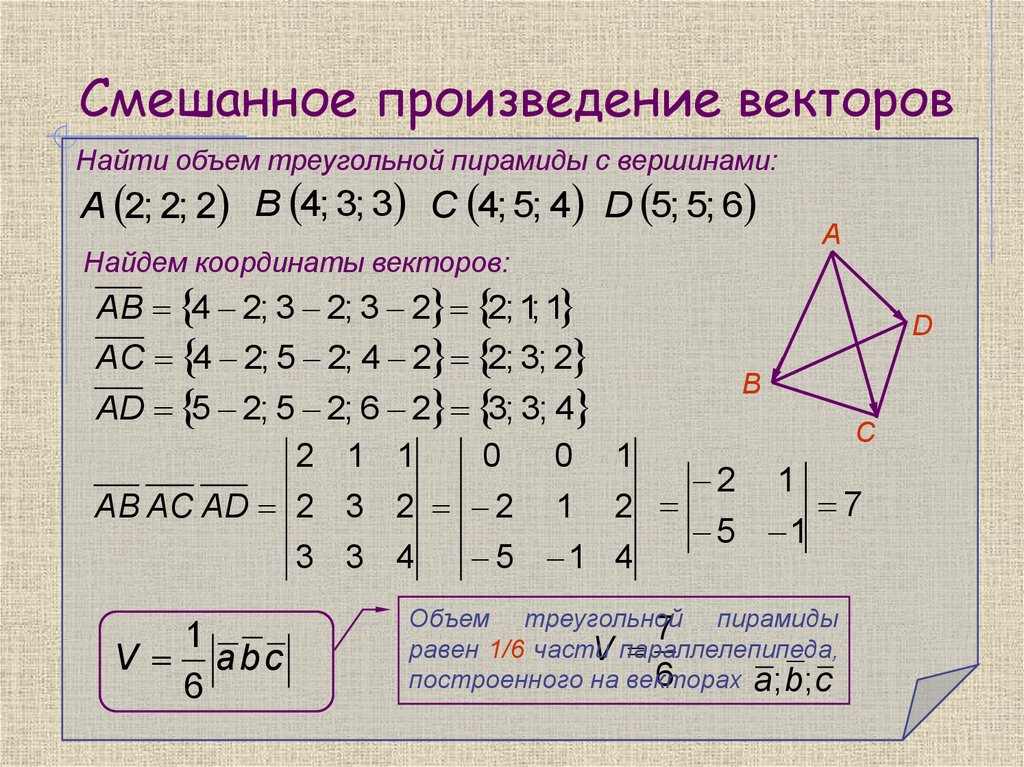

Поскольку хвост вектора можно расположить в любой точке, закон параллелограмма приводит к другому способу рассмотрения сложения векторов. На рис. 4.1.7 (а) сумма двух векторов и показана как заданная законом параллелограмма. Если его переместить так, чтобы его хвост совпал с кончиком (показан на (b)), то сумма видится как «сначала, а затем . Точно так же перемещение хвоста к кончику показывает в (с), что это «сначала, а затем». Это будет называться , и это дает наглядную иллюстрацию того, почему .

Так как обозначает вектор из точки в точку , правило от кончика к хвосту принимает легко запоминающуюся форму

   

для любых точек , и .

 

 

 

Одна из причин важности правила «кончик к хвосту» заключается в том, что оно означает, что два или более вектора могут быть добавлены путем последовательного размещения их кончиком к хвосту. Это дает полезную «картину» суммы нескольких векторов и проиллюстрировано для трех векторов на рис. 4.1.8, где сначала рассматривается как , затем , затем .

 

 

 

Существует простой геометрический способ визуализации (матрицы) двух векторов. Если и расположены так, что у них есть общий хвост , и если и являются их соответствующими концами, то правило от кончика к хвосту дает . Следовательно, это вектор от кончика к кончику . Таким образом, оба и появляются как диагонали в параллелограмме, определяемом и (см. рис. 4.1.9.

).

 

Если и имеют общий хвост, то это вектор от вершины к вершине .

Одним из наиболее полезных применений вычитания векторов является то, что оно дает простую формулу для вектора из одной точки в другую и для расстояния между точками.

Пусть и две точки. Затем:

1. .
2. Расстояние между и равно

Вы можете доказать эти результаты?

 

 

Расстояние между и равно , а вектор от до равен
.

Следующая теорема говорит нам, что происходит с длиной и направлением скаляра, кратного данному вектору.

Если a — действительное число и вектор, то:

• Длина .
• Если , то направление такое же, как если бы ; напротив if

Доказательство:

Первое утверждение верно в силу теоремы 4.1.1.

Чтобы доказать второе утверждение, позвольте обозначить начало координат в Позвольте иметь точку и выбрать любую плоскость, содержащую и . Если мы установим систему координат на этой плоскости с началом, то такой результат следует из скалярного кратного закона на плоскости.

Вектор называется a if . Тогда
,   и
являются единичными векторами, называемыми векторами.

Если показать, что это уникальный единичный вектор в том же направлении, что и

Решение:
Векторы в том же направлении, что и скалярные кратные, где . Но когда , то единичный вектор тогда и только тогда, когда .

 

 

 

Два ненулевых вектора вызываются, если они имеют одинаковое или противоположное направление.

Два ненулевых вектора и параллельны тогда и только тогда, когда один из них кратен другому.

 

 

Учитывая точки , , , и , определить, являются ли и параллельными.

Решение:

По теореме 4.1.3 и . Если
то , значит и , что невозможно. Следовательно, кратно , поэтому эти векторы не параллельны по теореме 4.1.5.

 

Линии в космосе

С помощью этих векторных методов можно очень просто описать прямые линии в пространстве. Для того, чтобы сделать это, нам сначала нужен путь к
укажите ориентацию такой линии.

Мы называем ненулевой вектор вектором направления для прямой, если он параллелен для некоторой пары различных точек и на прямой.

Обратите внимание, что любой ненулевой скаляр, кратный , также будет служить вектором направления линии.

Мы используем тот факт, что существует ровно одна линия, которая проходит через конкретную точку и имеет заданный вектор направления
. Мы хотим описать эту линию, задав условие на , и то, что точка лежит на этой линии. Пусть

и обозначают векторы и соответственно.

Рисунок 4.1.10

Затем

   

Следовательно, лежит на прямой тогда и только тогда, когда параллелен ей, т. е. тогда и только тогда, когда для некоторого скаляра по теореме 4.1.5. Таким образом, вектор точки на линии тогда и только тогда, когда для некоторого скаляра .

 

 

 

Прямая, параллельная точке с вектором, задается как

   

Другими словами, точка с вектором находится на этой прямой тогда и только тогда, когда существует действительное число t такое, что .

 

В компонентной форме векторное уравнение становится

   

Приравнивание компонентов дает другое описание линии.

Прямая с вектором направления
задается как

   

Другими словами, точка находится на этой прямой тогда и только тогда, когда существует действительное число такое, что , , и .

 

 

Найдите уравнения прямой через точки и .

Решение:

Пусть

обозначает вектор от до . Тогда параллелен прямой (и на линии), поэтому служит вектором направления для линии. Использование в качестве точки на линии приводит к параметрическим уравнениям

   

Обратите внимание, что если используется (а не ), уравнения равны

   

Они отличаются от предыдущих уравнений, но это просто результат изменения параметра. Фактически, .

Определить, пересекаются ли следующие прямые, и если да, то найти точку пересечения.

   

Решение:
Предположим, что вектор лежит на обеих линиях. Затем

   

где первое (второе) уравнение потому что лежит на первой (второй) строке. Следовательно, прямые пересекаются тогда и только тогда, когда три уравнения

   

есть решение. В этом случае и удовлетворяются все три уравнения, поэтому прямые 90 365 и 90 366 пересекаются, а точка пересечения равна 90 003.

   

с использованием . Конечно, эту точку можно найти и от
с помощью .

 

 

 

Предположим, что даны точка и плоскость, и требуется найти точку, лежащую на плоскости и ближайшую к , как показано на рис. 4.2.1.

Рисунок 4.2.1

 

Понятно, что требуется найти прямую, проходящую через нее, перпендикулярную плоскости, а затем получить как точку пересечения этой прямой с плоскостью. Для нахождения линии 90 365, перпендикулярной 90 366 плоскости, требуется способ определить, когда два вектора перпендикулярны. Это можно сделать, используя идею скалярного произведения двух векторов.

 

Скалярное произведение и углы

Для векторов
и
их скалярное произведение является числом, определенным

   

Поскольку это число, его иногда называют скалярным произведением и

.

Если
и , то .

Пусть , и обозначают векторы в (или ).

1. — действительное число.
2. .
3. .
4. .
5. для всех скаляров.

Читателям предлагается доказать эти свойства, используя определение скалярных произведений.

Убедитесь, что при , и .

Решение:

Применим теорему 4.2.1 несколько раз:

   

Существует внутреннее описание скалярного произведения двух ненулевых векторов в . Чтобы понять это, нам потребуется следующий результат из тригонометрии.

Если треугольник имеет стороны , , и , и если внутренний угол напротив, то

   

Рисунок 4.2.2

Доказательство:

Мы доказываем это, когда остро, то есть ; тупой случай аналогичен. На рис. 4.2.2 у нас есть и .

Следовательно, теорема Пифагора дает

   

Закон косинусов следует, потому что для любого угла .

 

Обратите внимание, что закон косинусов сводится к теореме Пифагора, если угол прямой (потому что ).

Теперь пусть и ненулевые векторы, расположенные с общим хвостом. Затем они определяют уникальный угол в диапазоне

   

Этот угол будет называться углом между и . Ясно и параллельны, если есть или или . Обратите внимание, что мы не определяем угол между и, если один из этих векторов равен .

Следующий результат дает простой способ вычислить угол между двумя ненулевыми векторами с помощью скалярного произведения.

Пусть и ненулевые векторы. Если угол между и , то

   

Рисунок 4.2.4

Доказательство:

Мы рассчитываем двумя способами. Сначала примените закон косинусов к треугольнику на рис. 4.2.4, чтобы получить:

   

 

С другой стороны, мы используем теорему 4.2.1:

   

Сравнивая их, мы видим, что и результат следует.

Если и ненулевые векторы, теорема 4.2.2 дает внутреннее описание, поскольку , и угол между и не зависят от выбора системы координат. Более того, поскольку и ненулевые ( и ненулевые векторы), это дает формулу для косинуса угла:

   

Поскольку , это можно использовать для поиска .

 

Вычислите угол между
  и
.

Решение:

Вычислить . Теперь вспомним, что и определены так, что (, ) — точка на единичной окружности, определяемая углом (нарисованным против часовой стрелки, начиная с положительной оси). В данном случае мы знаем то и это. Потому что из этого следует.

Если и отличны от нуля, предыдущий пример показывает, что имеет тот же знак, что и , поэтому

   

В этом последнем случае (ненулевые) векторы перпендикулярны. В линейной алгебре используется следующая терминология:

 

 

 

Два вектора и называются \textbf{ортогональными}\index{ортогональными векторами}\index{векторами!ортогональными векторами}, если или или угол между ними равен .

Так как если либо или , то мы имеем следующую теорему:

Два вектора и ортогональны тогда и только тогда, когда .

 

 

Докажите, что точки , и являются вершинами прямоугольного треугольника.

Решение:

Векторы вдоль сторон треугольника равны

   

Очевидно, что и являются ортогональными векторами. Это означает, что стороны и перпендикулярны, то есть угол в является прямым углом.

 

 

Выступы

В приложениях к векторам часто полезно записывать вектор как сумму двух ортогональных векторов.

Рисунок 4.2.5

Если задан ненулевой вектор, основная идея состоит в том, чтобы иметь возможность записать произвольный вектор в виде суммы двух векторов,

   

где параллелен и ортогонален . Предположим, что и исходят из общего хвоста (см. рис. 4.2.5). Позвольте быть наконечником, и позвольте обозначать основание перпендикуляра от к линии через параллель к.

Тогда имеет необходимые свойства:

1. параллельно .

2. ортогонален .

3. .

Вектор на рис. 4.2.6 называется проекцией на .

Обозначается

   

На рис. 4.2.5 (а) вектор имеет то же направление, что и ; однако и иметь противоположные направления, если угол между и больше (см. рис. 4.2.5 (b)). Обратите внимание, что проекция равна нулю тогда и только тогда, когда и ортогональны.

Вычислить проекцию on очень просто.

Позвольте и быть векторами.

1. Проекция на задается .
2. Вектор ортогонален .

Доказательство:

Вектор параллелен и поэтому имеет форму для некоторого скаляра . Требование ортогональности и определяет . Фактически это означает, что по теореме 4.2.3. Если здесь подставляется, то условие равно

   

Отсюда следует, что , где допущение, гарантирующее, что .

Найти проекцию

на
и выразить, где параллельно и ортогонально .

Решение:

Проекция на

   

Следовательно, и это ортогонально по теореме 4. 2.4 (в качестве альтернативы заметим, что ). Так как мы закончили.

 

Обратите внимание, что идею проекций можно использовать для нахождения кратчайшего расстояния от точки до прямой линии, в которой длина вектора ортогональна вектору направления линии.

 

 

Самолеты

Ненулевой вектор называется нормалью к плоскости, если он ортогонален каждому вектору на плоскости.

Например, единичный вектор является вектором нормали к плоскости.

Рисунок 4.2.6

Для данной точки и ненулевого вектора существует единственная плоскость, проходящая через нормаль , заштрихованная на рисунке 4.2.6. Точка лежит на этой плоскости тогда и только тогда, когда вектор ортогонален ей, т. е. тогда и только тогда, когда . Потому что это дает следующий результат:

 

Плоскость, проходящая через нормаль
в качестве вектора нормали, определяется как

   

Другими словами, точка находится на этой плоскости тогда и только тогда, когда , , и удовлетворяют этому уравнению.

Найдите уравнение плоскости через
как обычно.

Решение:

Здесь общее скалярное уравнение принимает вид

   

Это упрощается до .

Если мы напишем , скалярное уравнение показывает, что каждая плоскость с нормальным
имеет линейное уравнение вида

(4.2)  

для некоторой константы . И наоборот, график этого уравнения представляет собой плоскость с нормальным вектором (при условии, что , и не все равны нулю).

 

Найдите уравнение плоскости, через которую проходит параллельная плоскости с уравнением .

Решение:

Плоскость с уравнением имеет нормаль. Поскольку две плоскости параллельны, она служит нормалью к плоскости, которую мы ищем, поэтому уравнение для некоторых соответствует (4.2). Настаивая на том, что лежит на плоскости определяет ; то есть, . Следовательно, уравнение .

Рассмотрим точки и с векторами
и
.
Для вектора, отличного от нуля, скалярное уравнение плоскости с нормалью принимает векторную форму:

Плоскость с нормалью, проходящей через точку с вектором, определяется как

   

Другими словами, точка с вектором находится на плоскости тогда и только тогда, когда удовлетворяет этому условию.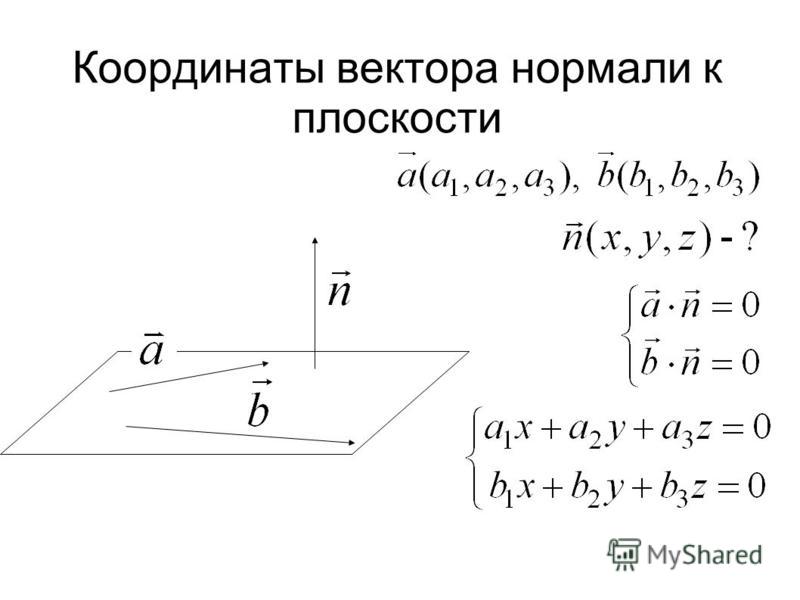

Кроме того, уравнение (4.2) переводится следующим образом:

Каждая плоскость с нормалью имеет векторное уравнение для некоторого числа.

Найдите кратчайшее расстояние от точки до плоскости с помощью уравнения . Также найдите точку на этой плоскости, ближайшую к .

Решение:

У рассматриваемого самолета нормальный . Выберите любую точку на плоскости, скажем, и пусть это будет ближайшая к ней точка на плоскости (см. схему). Вектор от к равен . Теперь прямо с хвостом в . Тогда и проекция на :

   

Следовательно, расстояние равно . Для расчета точки пусть
и

— векторы и . Затем

   

Это дает координаты .

 

 

Перекрестное произведение

Если , , и являются тремя различными точками, которые не все находятся на некоторой прямой, геометрически ясно, что существует единственная плоскость, содержащая все три. Векторы и оба лежат в этой плоскости, поэтому поиск нормали сводится к нахождению ненулевого вектора, ортогонального обоим и . Перекрестное произведение обеспечивает систематический способ сделать это.

Учитывая векторы и  , определите векторное произведение на

   

 

Поскольку это вектор, его часто называют векторным произведением . Существует простой способ запомнить это определение, используя векторы координат :

   

Это векторы длины, направленные вдоль положительных осей , и . Причина названия в том, что любой вектор можно записать как

.

   

При этом векторное произведение можно описать следующим образом:

Если и два вектора, то

   

где определитель разложен по первому столбцу.

Если и , то

   

Обратите внимание, что это ортогонально обоим и в примере 4.2.11. В общем случае это верно, как можно проверить непосредственно вычислением и , и записано как первая часть следующей теоремы. Оно будет следовать из более общего результата, который вместе со второй частью будет доказан позже.

Позвольте и быть векторами в :

1.   является вектором, ортогональным обоим и .
2. Если и отличны от нуля, то тогда и только тогда, когда и параллельны.

Напомним, что

   

Найдите уравнение плоскости через , и .

Решение:

Векторы
и
лежат в плоскости
, поэтому

   

— нормаль к плоскости (ортогональная к обоим и ). Следовательно, плоскость имеет уравнение

   

Так как лежит в плоскости у нас есть . Отсюда и уравнение. Можете ли вы проверить, что то же самое уравнение может быть получено, если и , или и , используются в качестве векторов на плоскости?

 

 

 

 

 

Перекрестное произведение двух -векторов и
было определено в разделе 4.2, где мы заметили, что его лучше всего запоминать с помощью определителя:

(4.3)  

Здесь ,  и
— векторы координат, а определитель разложен по первому столбцу. Мы заметили (но не доказали) в теореме 4.2.5, что она ортогональна обоим и . Это легко следует из следующего результата.

Если , и  , то  .

Доказательство:

Напомним, что вычисляется путем умножения соответствующих компонентов и последующего сложения. Используя уравнение (4.3), получаем результат:

   

, где последний определитель расширен по столбцу 1.

Результат теоремы 4.3.1 можно кратко сформулировать следующим образом: если , , и три вектора из , то

   

где обозначает матрицу с , и в качестве ее столбцов. Теперь ясно, что ортогонален обоим и потому, что определитель матрицы равен нулю, если два столбца идентичны.

 

 

 

В силу (4.3) и теоремы 4.3.1 некоторые из следующих свойств векторного произведения следуют из
свойств определителей (их можно проверить и непосредственно).

Пусть , и обозначают произвольные векторы в .

1.   — это вектор.
2.   ортогонален обоим и .
3. .
4. .
5. .
6. для любого скаляра.
7. .
8. .

 

Мы видели некоторые из этих результатов в прошлом; Вы можете доказать 6,7 и 8?

 

 

Теперь мы подошли к фундаментальному соотношению между точечным и перекрестным произведениями.

Если и любые два вектора в , то

   

Доказательство:

Даны и , ввести систему координат и записать
и
в компонентной форме. Тогда все члены тождества могут быть вычислены с точки зрения компонентов.

Выражение для модуля вектора легко получить из тождества Лагранжа. Если угол между и , подстановка в тождество Лагранжа дает

   

, используя тот факт, что . Но неотрицательна в диапазоне , поэтому извлечение положительного квадратного корня из обеих сторон дает

   

Рисунок 4.3.1

Это выражение для не имеет отношения к системе координат и, кроме того, имеет хорошую геометрическую интерпретацию. Параллелограмм определяется векторами и имеет длину основания и высоту. Следовательно, площадь параллелограмма, образованного и равна

   

 

Если и два ненулевых вектора и угол между и , то:

1.   площадь параллелограмма определяется и .
2. и параллельны тогда и только тогда, когда .

Доказательство 2:

По (1) тогда и только тогда, когда площадь параллелограмма равна нулю. Площадь исчезает тогда и только тогда, когда и имеют одинаковое или противоположное направление, то есть тогда и только тогда, когда они параллельны.

 

 

Найдите площадь треугольника с вершинами , и .

Решение:

У нас есть
и . Площадь треугольника равна половине площади параллелограмма, образованного этими векторами, и поэтому равна . У нас есть

   

значит площадь треугольника

Рис. 4.3.2

Если даны три вектора , и , они определяют «сжатое» прямоугольное тело, называемое параллелепипедом (рис. 4.3.2), и часто бывает полезно найти объем такого тела . Основанием твердого тела является параллелограмм, определяемый и , поэтому он имеет площадь . Высота тела — это длина проекции на . Отсюда

   

 

 

Таким образом, объем параллелепипеда равен . Это доказывает

Объем параллелепипеда определяется тремя векторами , и определяется как .

 

 

Найдите объем параллелепипеда, заданного векторами

   

Решение:

По теореме 4.3.1, .
Следовательно, объем по теореме 4.3.5.

Теперь мы можем дать внутреннее описание перекрестного произведения.

 

 

Если вектор взять в правую руку и пальцы сгибаются от угла к углу, большой палец указывает в направлении

Чтобы показать, почему это так, введите координаты в следующим образом: Пусть и имеют общий хвост , выберите начало координат в точке , выберите ось так, чтобы она указывала в положительном направлении, а затем выберите ось так, чтобы она находилась в плоскости – и положительная ось находится на той же стороне оси, что и .