Обозначения Дирака — Azure Quantum
- Статья
- Чтение занимает 10 мин
Нотация Дирака — это язык, который разработан для точного выражения состояния в квантовой механике. Примеры в этой статье можно рассматривать как предложения и использовать их для краткого выражения идей в квантовых вычислениях.
Ограничения нотации для вектора-столбца
Хотя нотация для векторов-столбцов широко используется в линейной алгебре, она часто может иметь громоздкий вид в квантовых вычислениях, особенно при работе с несколькими кубитами. Например, когда вы определяете $\psi$ как вектор, то не всегда очевидно, является ли $\psi$ вектором-строкой или вектором-столбцом. Таким образом, если $\phi$ и $\psi$ — векторы, то опять-таки непонятно, задан ли $\phi\psi$, поскольку в определенном контексте формы $\phi$ и $\psi$ могут быть не совсем ясны. Помимо неоднозначности в формах векторов, выражение даже простых векторов с использованием линейной алгебраические нотации может иметь громоздкий вид. Например, если вам нужно описать $n$-кубитное состояние, в котором каждый кубит принимает значение $0$, то формально выразите состояние как
Таким образом, если $\phi$ и $\psi$ — векторы, то опять-таки непонятно, задан ли $\phi\psi$, поскольку в определенном контексте формы $\phi$ и $\psi$ могут быть не совсем ясны. Помимо неоднозначности в формах векторов, выражение даже простых векторов с использованием линейной алгебраические нотации может иметь громоздкий вид. Например, если вам нужно описать $n$-кубитное состояние, в котором каждый кубит принимает значение $0$, то формально выразите состояние как
$$\begin{bmatrix}1 \\ 0 \end{bmatrix}\otimes\cdots\otimes\begin{bmatrix}1 \\ 0 \end{bmatrix}. $$
Оценка этого тензорного произведения непрактична, поскольку вектор находится в экспоненциально большом пространстве. Таким образом, эта нотация фактически является лучшим описанием состояния, которое может быть задано с помощью предыдущей нотации.
Типы векторов в нотации Дирака
В нотации Дирака существует два типа векторов: вектор bra и вектор ket, которые при объединении образуют название braket или внутреннее произведение. 2$.
2$.
$$\begin{bmatrix} 1 \\ 0 \end{bmatrix}=\ket{{0},\qquad\begin{bmatrix} 0 \\ 1 \end{bmatrix}=\ket{{1}. $$
Пример. Представление операции Адамара с помощью нотации Дирака
Следующую нотацию часто используют для описания состояний, возникающих в результате применения вентиля Адамара к $\ket{0}$ и $\ket{1}$. Эти состояния соответствуют единичным векторам в направлениях $+x$ и $-x$ в сфере Блоха:
$$\frac{1}{\sqrt{{2}}\begin{bmatrix} 1 \\ 1 \end{bmatrix}=H\ket{0}=\ket{+},\qquad\frac{1}{\sqrt{{2}}\begin{bmatrix} 1 \\ -1 \end{bmatrix}=H\ket{{1}=\ket{{-} . $$
С помощью нотации Дирака эти состояния также можно развернуть в виде сумм $\ket{0}$ и $\ket{1}$:
$$\ket{+}=\frac{{1}{\sqrt{2}}(\ket{0} + \ket{1}),\qquad\ket{{-}=\frac{{1}{\sqrt{{2}}(\ket{{0} — \ket{1}). $$
Векторы вычислительной базы
Эти состояния часто называют вычислительной базой по следующей причине: каждое квантовое состояние всегда можно выразить в виде сумм векторов вычислительной базы, и такие суммы можно легко выразить с помощью нотации Дирака. Обратное утверждение также верно в том смысле, что состояния $\ket{+}$ и $\ket{-}$ также образуют базис для квантовых состояний. Это подтверждается тем фактом, что
Обратное утверждение также верно в том смысле, что состояния $\ket{+}$ и $\ket{-}$ также образуют базис для квантовых состояний. Это подтверждается тем фактом, что
$$\ket{{0}=\frac{1}{\sqrt{2}}(\ket{+} + \ket{-}),\qquad\ket{{1}=\frac{{1}{\sqrt{{2}}(\ket{+} — \ket{-}). $$
В качестве примера нотации Дирака рассмотрим braket $\braket{0 | 1}$, который является внутренним произведением $0$ и $1$. Это можно записать как
$$\braket{0 | 1}=\begin{bmatrix} 1 & 0 \end{bmatrix}\begin{bmatrix}0\\ 1\end{bmatrix}=0. $$
Этот пример говорит о том, что $\ket{{0}$ и $\ket{{1}$ являются ортогональными векторами, т. е. $\braket{0 | 1}=\braket{1 | 0}=0$. Кроме того, по определению $\braket{0 | 0}=\braket{1 | 1}=1$, что означает, что два вектора вычислительной базы также можно назвать ортонормальными.
Эти ортонормальные свойства пригодятся в следующем примере. Если у вас есть состояние $\ket{\psi}={\frac{3}{5}}\ket{{1} + {\frac{{4}{5}}\ket{0}$, то так как $\braket{1 | 0}=0$ вероятность измерения $1$ составляет
$$\big|\braket{1 |\psi}\big|^2=\left|\frac{{3}{5}\braket{1 | 1} +\frac{{4}{5}\braket{1 | 0}\right|^2=\frac{{9}{{25}. $$
$$
Нотация тензорного произведения
Нотация Дирака также включает неявную структуру тензорного произведения. Эта структура важна, поскольку в квантовых вычислениях вектор состояния, описанный двумя некоррелированными квантовыми регистрами, является тензорным произведением двух векторов состояния. Сжатое описание структуры тензорного произведения или его отсутствие имеет критически важное значение, если необходимо разъяснить квантовые вычисления. Структура тензорного произведения подразумевает, что вы можете записать $\psi\otimes\phi$ для любых двух векторов квантового состояния $\phi$ и $\psi$ как $\ket{\psi}\otimes\ket{\phi}$. Но, как правило, запись $\otimes$ между векторами не требуется, и вы можете просто записать $\ket{\psi}\ket{\phi}=\ket{\psi\phi}$. Дополнительные сведения о векторах и тензорных произведениях см. в статье Векторы и матрицы в квантовых вычислениях. Например, состояние с двумя кубитами, инициализированное в нулевом состоянии, задано как
$$\ket{0}\otimes\ket{0}=\ket{{0}\ket{{0}=\ket{{00}=\begin{bmatrix} 1 \\ 0 \end{bmatrix}\otimes\begin{bmatrix} 1 \\ 0 \end{bmatrix}=\begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix}. \dagger$ для векторов квантовых состояний $\psi$ и $\phi$. Самый простой и, вероятно, наиболее распространенный пример этой нотации
\dagger$ для векторов квантовых состояний $\psi$ и $\phi$. Самый простой и, вероятно, наиболее распространенный пример этой нотации
$$\ket{{0}\bra{0}=\begin{bmatrix}1\\ 0 \end{bmatrix}\begin{bmatrix}1&0 \end{bmatrix}=\begin{bmatrix}1 &0\\ 0 &0\end{bmatrix}\qquad\ket{1}\bra{1}=\begin{bmatrix}0\\ 1 \end{bmatrix}\begin{bmatrix}0&1 \end{bmatrix}=\begin{bmatrix}0 &0\\ 0 &1\end{bmatrix}. $$
Ketbra часто называют проекторами, так как они проецируют квантовое состояние на зафиксированное значение. Так как эти операции не являются унитарными (и даже не сохраняют норму вектора), то квантовый компьютер не может детерминированно применить проектор. Однако проекторы выполняют полезную задачу, описывая воздействие, которое оказывает измерение на квантовое состояние. Например, если вы измеряете состояние $\ket{\psi}$ и получаете значение $0$, тогда результирующее преобразование состояния в результате измерения будет
$$\ket{\psi}\rightстрелка \frac{(\ket{{0}\bra{{0})\ket{\psi}}{|\braket{0 |\psi}|}=\ket{{0},$$
что и ожидалось, когда в результате измерения состояния получено значение $\ket{0}$.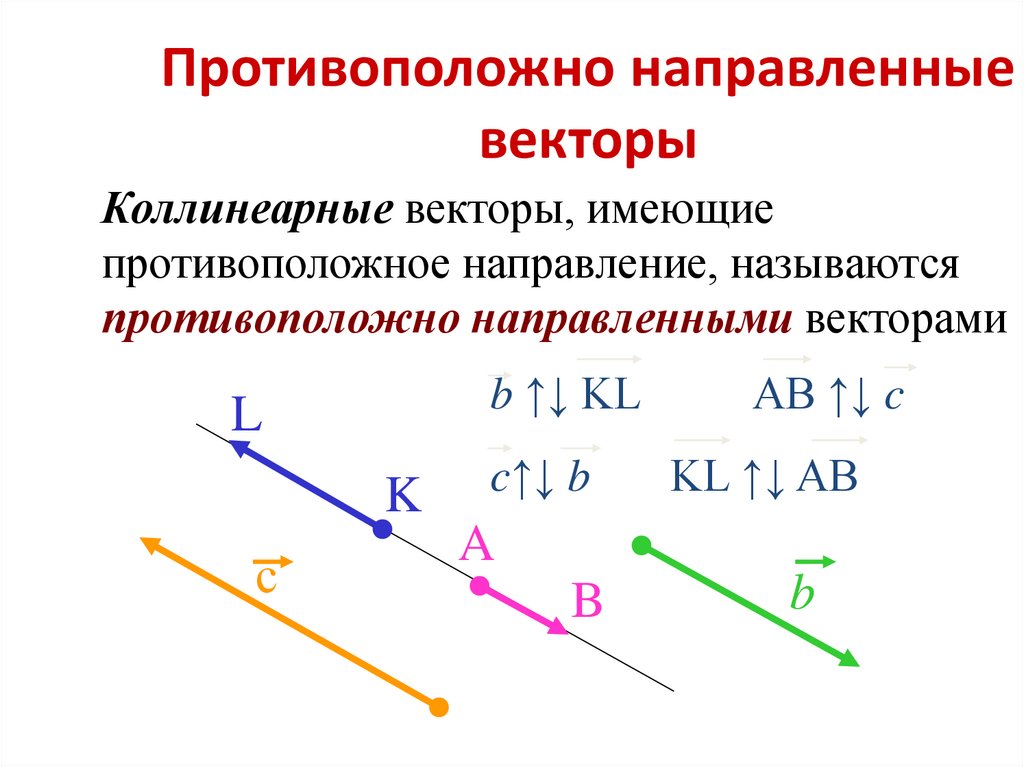 {\dagger}$ (то есть $\rho$ — это эрмитова матрица).
{\dagger}$ (то есть $\rho$ — это эрмитова матрица).
В совокупности эти условия гарантируют, что матрицу $\rho$ можно рассматривать как ансамбль. Оператор плотности для вектора квантового состояния $\ket{\psi}$ имеет вид $\rho =\sum_i p_i \ket{\psi_i}\bra{\psi_i}$, то есть разложение собственного значения $\rho$. В этом случае $\rho$ описывает ансамбль $\rho ={\ket{\psi_i}\text{ с вероятностью }p_i}$.
Чистые квантовые состояния — это такие состояния, которые характеризуются одним кет-вектором или волновой функцией и не могут быть записаны в виде статистического сочетания (или выпуклой комбинации) других квантовых состояний. Смешанное квантовое состояние — это статистический ансамбль чистых состояний.
На сфере Блоха чистые состояния представлены точкой на поверхности сферы, тогда как смешанные состояния представлены внутренней точкой.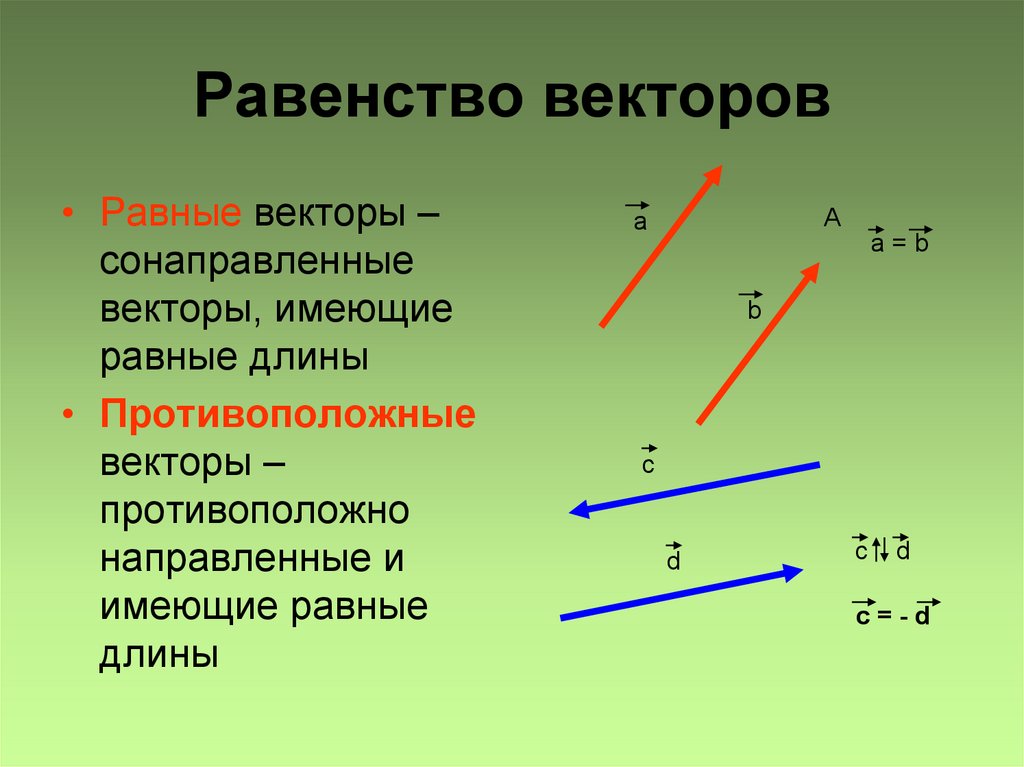 Полностью смешанное состояние одного кубита представлено центром сферы, симметрией. Чистоту состояния можно визуализировать как степень, в которой оно близко к поверхности сферы.
Полностью смешанное состояние одного кубита представлено центром сферы, симметрией. Чистоту состояния можно визуализировать как степень, в которой оно близко к поверхности сферы.
Эта концепция представления состояния в виде матрицы, а не вектора зачастую удобна тем, что она позволяет удобный способ представления вычислений вероятности, а также позволяет описать как статистическую неопределенность, так и квантовую неопределенность в рамках одно и той же математической модели.
Совет
Библиотека Python QuTiP полезна при работе с квантовыми состояниями. Вы можете записывать квантовые состояния в нотации QuTiP, используя qt.basis(2, i) для представления $\ket{i}$ одного кубита. Дополнительные сведения о методах и функциях QuTiP см. в руководстве пользователя QuTiP.
Оператор плотности $\rho$ представляет чистое состояние в том и только в том случае, если выполняются следующие условия:
- $\rho$ можно записать как внешнее произведение вектора состояния $\rho=\ket{\psi}\bra{\psi}$.
 2$ можно получить так:
2$ можно получить так:print((rho_pure ** 2).tr())
0.9999999999999996
Для однокубитных систем смешанные состояния могут отображаться на сфере Блоха так же, как векторы состояния. Чистые состояния — это те состояния, которые находятся на поверхности сферы Блоха, а смешанные состояния в общем случае могут находиться «внутри» нее.
import matplotlib.pyplot as plt plt.figure(figsize=(6, 6)) bloch = qt.bloch.Bloch() bloch.add_states([rho_pure], kind='point') print(bloch.show())
plt.figure(figsize=(6, 6)) bloch = qt.bloch.Bloch() bloch.add_states([rho_mixed], kind='point') bloch.show()
Состояние в центре сферы Блоха является максимально смешанным. В отличие от чистых состояний максимально смешанное состояние возвращает результаты 50/50 для любого идеального измерения Паули.
Дополнительные сведения об операторах плотности и чистых и смешанных состояниях можно получить в одной из справочных книг, представленных в разделе Рекомендуемое содержимое.
 {\otimes n}\ket{0}$. Это экспоненциально более короткое описание состояния не только имеет то преимущество, что можно аргументировать его в рамках классической модели, но оно также четко определяет операции, которые необходимо распространить через программный стек для реализации алгоритма. По этой причине Q# предназначен для создания последовательностей ворот, а не квантовых состояний, однако на теоретическом уровне эти две перспективы эквивалентны.
{\otimes n}\ket{0}$. Это экспоненциально более короткое описание состояния не только имеет то преимущество, что можно аргументировать его в рамках классической модели, но оно также четко определяет операции, которые необходимо распространить через программный стек для реализации алгоритма. По этой причине Q# предназначен для создания последовательностей ворот, а не квантовых состояний, однако на теоретическом уровне эти две перспективы эквивалентны.примеры и решения, формулы и теоремы
Основные понятия вектораДля того чтобы приступить к разбору формул нахождения длины вектора, необходимо разобраться в основных понятиях и определениях векторов.
Понятие вектора получило широкое распространение в 19 веке, в математических науках, особенно в таком её разделе, как «Комплексные числа».
Определение
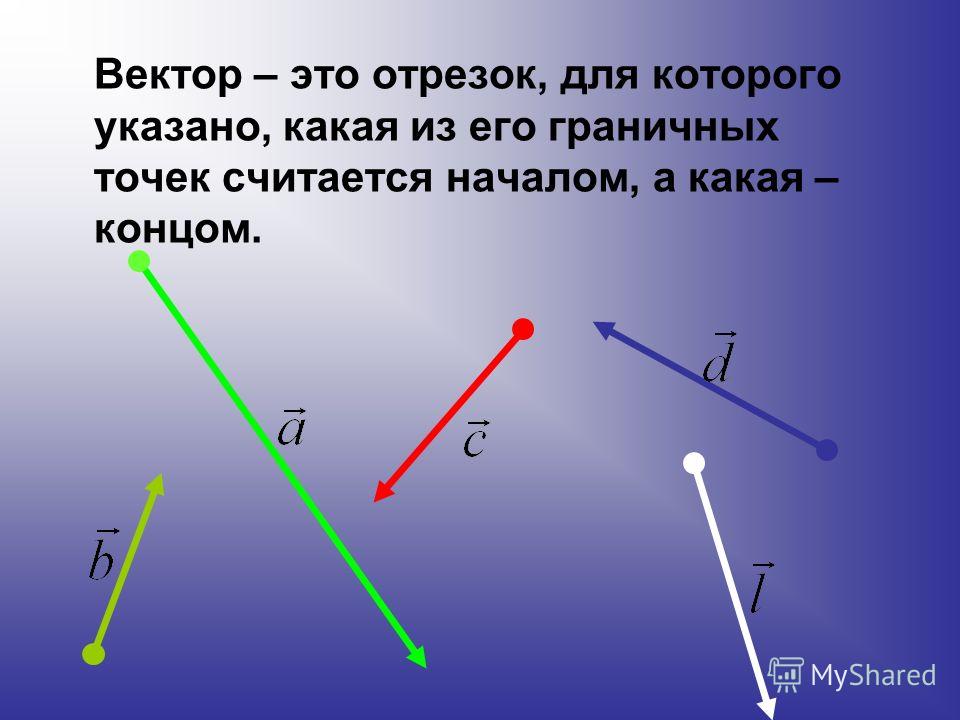
Вектор — это отрезок с определённой длиной и направлением.
Графическое изображение вектора — отрезок который имеет указание направления в виде стрелки.

Вектор, который будет иметь начальную точку Х и конец в точке А, правильно обозначать ХА, с верхним подчёркиванием или стрелочкой, а также допустимо прописывать одной прописной буквой.
Длину вектора (модуль), определяет числовое значение длины отрезка, имеющего направление. Обозначается длинна двумя вертикальными отрезками |ХА|.
- Понятие нулевого вектора. Такое название получил вектор, у которого и начало, и конец находятся в одной точке. Обозначение он имеет в виде цифры ноль с верхним подчёркивание, а длина равна нулю.
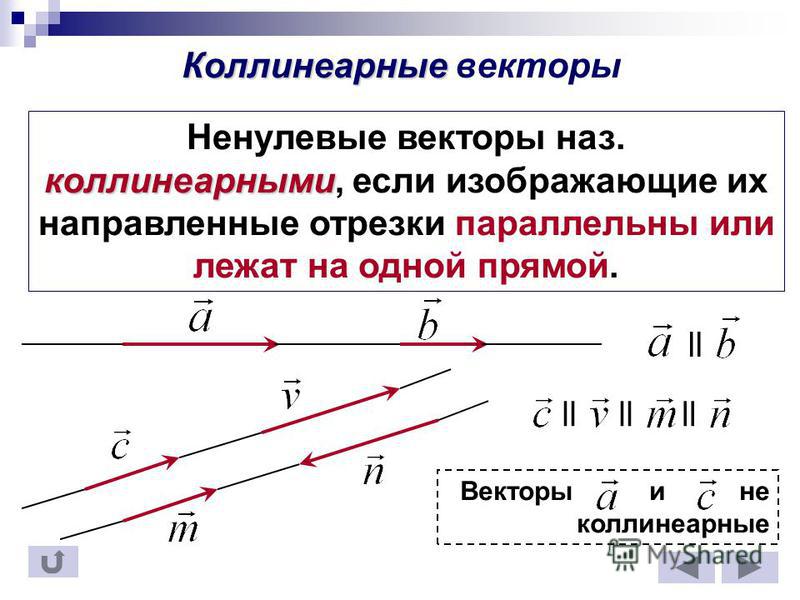
- Коллинеарные вектора. Одна прямая может содержать несколько векторов, такие векторы получили название коллинеарных. Также коллинеарными считаются векторы на параллельных прямых.
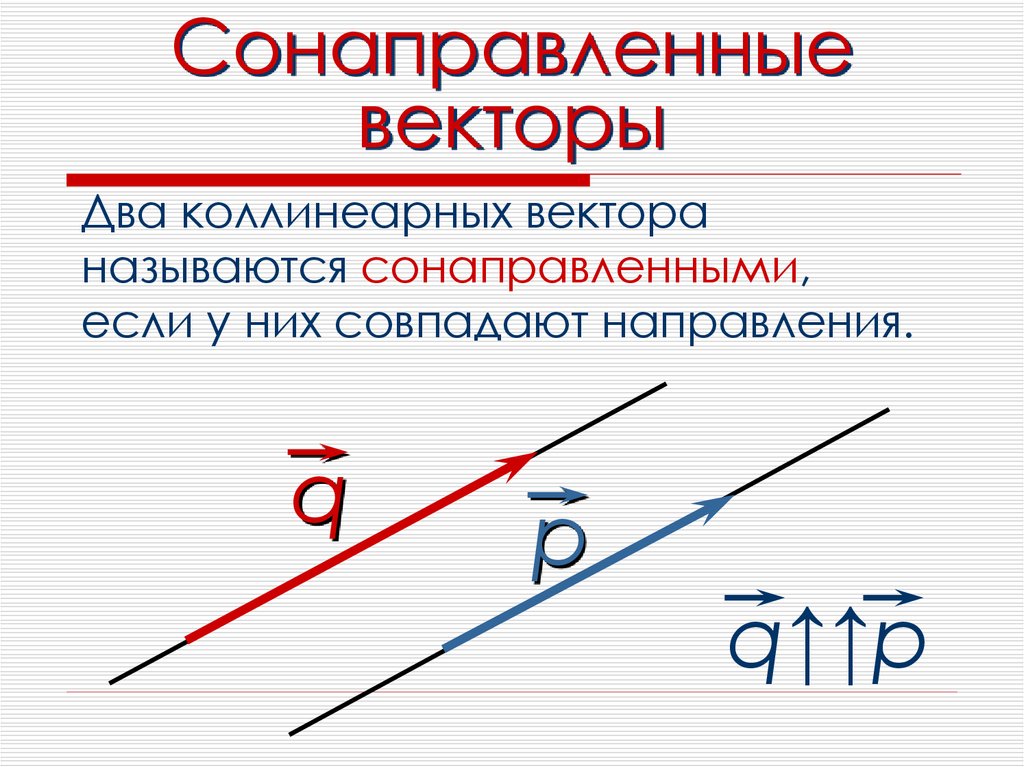
- Сонаправленные. Два коллинеарных вектора считаются сонаправленными, если имеют одно направление.
- Противоположно направленные. Вектора, с направлениями в разные стороны, и являются коллинеарными, называют противоположно направленными.

- Компланарные вектора. Такими векторами называют, те что лежат в одной плоскости
Так как, всегда можно отыскать плоскость, которая будет параллельной двум векторам, то любые два вектора всегда копланарные.
Так как, всегда можно отыскать плоскость, которая будет параллельной двум векторам, то любые два вектора всегда копланарные.
Вектора могут находится не только на плоскости, но и в пространстве, от этого расположения будет зависеть какую формулу необходимо использовать для нахождения их длины или модуля. Стоит также отметить, что вектора могут быть равными, при этом они должны иметь одно направление, одинаковые длины и быть коллинеарными. Существует понятие единичного вектора, таким он будет являться если равен единице измерения.
Как найти длину вектора
Модуль вектора а будем обозначать .
Для того чтобы найти модуль вектора или его длину, на плоскости по координатам, необходимо рассмотреть вектор используя прямоугольную декартову систему координат Оxy.
 Допустим в данной системе будет задан, так вектор имеющий координаты (aₓ ; aᵧ). Получим формулу, которая поможет найти длину вектора , через известные нам координаты aₓ и aᵧ.
Допустим в данной системе будет задан, так вектор имеющий координаты (aₓ ; aᵧ). Получим формулу, которая поможет найти длину вектора , через известные нам координаты aₓ и aᵧ.На взятой системе координат, от её начала отложим вектор В соответствии с проекцией точки А возьмём и определим Aₓ и Aᵧ на оси координат. Рассмотрим полученный прямоугольник ОAₓ и АAᵧ с диагональю ОА.
Далее используя теорему Пифагора мы получим равенство АО² = ОAₓ² и OAᵧ², отсюда следует
Теперь в соответствии с определением вектора относительно прямоугольной оси координат выходит, что ОAₓ² = aₓ² и также для OAᵧ² = aᵧ² , а так как на построенном прямоугольнике мы видим, что ОА равна длине вектора получаем
Из вышесказанного выходит, что для того чтобы найти длину вектора с точками (aₓ ; aᵧ), выводим следующую формулу:
Когда вектор дан в формате разложения по координатным векторам , то вычислить его можно по той же формуле , в таком варианте коэффициент aₓ и aᵧ будут выражать в роли координат , в данной системе координат.

из определения получаются равенства ОAₓ=aₓ; OAᵧ=aᵧ; OA=a , а значение длины ОА совпадает с длиной вектора, которую необходимо найти. Из этого следует:
Пример
Необходимо узнать длину вектора \( \left|\vec{a}\right|=2*\vec{i}+3*\vec{j}+4*\vec{k} \), в котором \( \vec{i}, \vec{j}, \vec{k} \), орты.
Решение
Получается, что дан вектор \( \left|\vec{a}\right| \) с координатами (2; 3; 4)
Применив выведенную ранее формулу получим
Ответ:
Длина вектора через координаты точек начала и конца
Ранее мы рассмотрели формулы, которые позволят находить длину вектора используя при этом координаты. Рассматривались примеры в трёхмерном пространстве на плоскости. Используя данные формулы можно найти длину вектора, если известны координаты точек его начала и конца.
Возьмём точки с обозначенными координатами начала A(aₓ ; aᵧ) и конца В(bₓ ; bᵧ), из чего следует, что вектор имеет координаты (bₓ-aₓ ; bᵧ-aᵧ), поэтому его длину мы выразим в формуле
При этом формула вычисления длины вектора для трёхмерного пространства, с координатами и ), будет следующей:
Пример
Для прямой системы координат, найти длину вектора \( \overrightarrow{AB}\) , где A(1,√3) B(-3,1)
Решение
Применив формулу, для нахождения длины вектора, с известными координатами точек начала и конца, в плоской системе координат, выходит:
Существует второй вариант решения, где формулы применяются по очереди:
Ответ:
Пример
Найти, решения, при подстановке которых, длина вектора будет равна корню из тридцати, при координатах точек А (0,1,2) и В (5,2,\(λ^2\))
Решение
В первую очередь представим длину вектора в виде формулы.
 2-2=-2
2-2=-2
\)
\(
\lambda_1=-2, \lambda_2=2, \lambda_3=0.
\)Ответ: \(
\lambda_1=-2, \lambda_2=2, \lambda_3=0.
\)Длина вектора по теореме косинусов
Так как бывают случаи, когда не известны координаты точек вектора, необходимо искать другие варианты, при помощи которых можно найти длину вектора. Таким способов может стать применение теоремы косинусов.
К примеру, нам известны длины двух векторов \(\overrightarrow{AB}\) и \(\overrightarrow{AC}\) , а также угол между ними, или его косинус. При этом необходимо найти длину вектора \( \overrightarrow{BC} \) , в таком варианте задания необходимо воспользоваться теоремой косинусов, представив треугольник АВС. В данном треугольнике мы будем искать сторону ВС, она и будет равна длине искомого вектора. Подробнее рассмотрим на примере.
Пример
Даны длины двух векторов \( \overrightarrow{AK}\) и \( \overrightarrow{AM}\) 2 и 4 соответственно, а угол между ними равен \( \frac{\pi}{3} \) . необходимо найти длину \( \overrightarrow{KM}\).
 2}\) чаще такая формула применима в физике, для того чтобы узнать длину пути материальной точки.
2}\) чаще такая формула применима в физике, для того чтобы узнать длину пути материальной точки.В случае если известен угол, между двумя векторами, можно использовать теорему Пифагора.
Применение векторов в других сферах
Понятие и вычисление вектора важно не только в математике, но и других науках:
- в физике. Для визуального изображения таких понятий как скорость, сила, ускорение и т.д. А также векторы помогают моделировать физические процессы;
- в химии. Для изображения химических процессор. При помощи векторов изображают движение электронов и других частиц;
- в биологии. Биологические процессы, также имеют графическое изображение при помощи векторов. К примеру перенос паразитов;
- географии. Вектором обозначается движение воздушных масс, или течение реки;
Векторы используются не только в науках, но и различных отраслях и профессиях. В судоходстве и аэрофлоте, архитектуре и конструировании, а также многих других областях. Для того чтобы найти длину вектора, мы можем использовать одну из формул, в зависимости от того, что нам о нём известно, и в каком пространстве или плоскости находится неизвестный вектор.

Что такое вектор? — PMC
1. Гусман М.Г., Харрис Э. 2015. Денге. Ланцет 385, 453–465. ( 10.1016/S0140-6736(14)60572-9) [PubMed] [CrossRef] [Google Scholar]
2. Гублер Д.Дж. 2007. Продолжающееся распространение вируса западного нила в западном полушарии. клин. Заразить. Дис. 45, 1039–1046. ( 10.1086/521911) [PubMed] [CrossRef] [Google Scholar]
3. Sambri V, et al. 2013. Вирус Западного Нила в Европе: возникновение, эпидемиология, диагностика, лечение и профилактика. клин. микробиол. Заразить. 19, 699–704. ( 10.1111/1469-0691.12211) [PubMed] [CrossRef] [Google Scholar]
4. Maltezou HC, et al. 2010. Конго-крымская геморрагическая лихорадка в Европе: текущая ситуация требует готовности. евронаблюдение 15, 48–51. [PubMed] [Google Scholar]
5. Reusken C, Heyman P. 2013. Факторы, способствующие появлению хантавируса в Европе. Курс. мнение Вирол. 3, 92–99. ( 10.1016/j.coviro.2013.01.002) [PubMed] [CrossRef] [Google Scholar]
6. Wilson AJ, Mellor PS.
 2009.
Синий язык в Европе: прошлое, настоящее и будущее. Фил. Транс. Р. Соц. Б
364, 2669–2681. ( 10.1098/rstb.2009.0091) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
2009.
Синий язык в Европе: прошлое, настоящее и будущее. Фил. Транс. Р. Соц. Б
364, 2669–2681. ( 10.1098/rstb.2009.0091) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]7. Gatherer D, Kohl A. 2016. Вирус Зика: ранее медленная пандемия быстро распространяется по Америке. Дж. Генерал Вирол. 97, 269–273. ( 10.1099/jgv.0.000381) [PubMed] [CrossRef] [Google Scholar]
8. Rizzoli A, Hauffe HC, Carpi G, Vourc’h GI, Neteler M, Rosa R. 2011. Боррелиоз Лайма в Европе. евронаблюдение 16, 2–9. [Google Scholar]
9. Weaver SC, Lecuit M. 2015. Вирус чикунгунья и глобальное распространение болезни, переносимой комарами. Н. англ. Дж. Мед. 372, 1231–1239 гг.. ( 10.1056/NEJMra1406035) [PubMed] [CrossRef] [Google Scholar]
10. Европейский центр профилактики и контроля заболеваний. 2014. Ежегодный эпидемиологический отчет за 2014 г. — новые и трансмиссивные болезни. Стокгольм, Швеция: ECDC. [Google Scholar]
11. Хотез П.Дж. 2016. Грядущие бедствия Южной Европы: трансмиссивные забытые тропические болезни.
 PLoS Негл. Троп. Дис.
10, e0004243 ( 10.1371/journal.pntd.0004243) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
PLoS Негл. Троп. Дис.
10, e0004243 ( 10.1371/journal.pntd.0004243) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]12. 2009. Ищу руководство по ТБ. Вет. Рек. 164, 477 (10.1136/vr.164.16.477) [CrossRef] [Google Scholar]
13. Леонард Д. 2014. Контроль туберкулёза крупного рогатого скота. Вет. Рек. 174, 535–536. ( 10.1136/vr.g3414) [PubMed] [CrossRef] [Google Scholar]
14. Roberts T, O’Connor C, Nuñez-Garcia J, de la Rua-Domenech R, Smith NH. 2014. Необычный кластер инфекции Mycobacterium bovis у кошек. Вет. Рек. 174, 326 ( 10.1136/vr.102457) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
15. Центры по контролю и профилактике заболеваний. 2016. Бешенство: домашние животные. Атланта, Джорджия: Центры по контролю и профилактике заболеваний (CDC). [Google Scholar]
16. Pinaud S, et al. 2016. Переход от клеточных к гуморальным реакциям способствует врожденной иммунной памяти у улитки-переносчика Biomphalaria glabrata .
 PLoS Патог.
12, e1005361 ( 10.1371/journal.ppat.1005361) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
PLoS Патог.
12, e1005361 ( 10.1371/journal.ppat.1005361) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]17. Barbosa FS, Olivier L. 1958. Исследования улиток-переносчиков бильгарциоза мансони в северо-восточной Бразилии. Бык. Всемирный орган здравоохранения. 18, 895–908. [Бесплатная статья PMC] [PubMed] [Google Scholar]
18. 2015. Трансмиссивные болезни в Канаде. Может. коммун. Дис. Респ. 41, 117–154. См. http://www.phac-aspc.gc.ca/publicat/ccdr-rmtc/15vol41/dr-rm41-06/assets/pdf/15vol41_06-eng.pdf. [Бесплатная статья PMC] [PubMed] [Google Scholar]
19. Kuno G, Chang G-JJ. 2005. Биологическая передача арбовирусов: пересмотр и новое понимание компонентов, механизмов и уникальных признаков, а также тенденций их эволюции. клин. микробиол. преп. 18, 608–637. ( 10.1128/cmr.18.4.608-637.2005) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
20. Гибсон Д.Р., Флинн Н.М., Пералес Д. 2001. Эффективность программ обмена шприцев в снижении поведения, связанного с риском заражения ВИЧ, и сероконверсии ВИЧ среди потребителей инъекционных наркотиков.
 СПИД
15, 1329–1341. ( 10.1097/00002030-200107270-00002) [PubMed] [CrossRef] [Google Scholar]
СПИД
15, 1329–1341. ( 10.1097/00002030-200107270-00002) [PubMed] [CrossRef] [Google Scholar]21. Ангелакис Э., Ажар Э.И., Биби Ф., Ясир М., Аль-Гамди А.К., Ашши А.М., Эльшеми А.Г., Рауль Д. 2014. Бумажные деньги и монеты как потенциальные переносчики инфекционных заболеваний. Фут. микробиол. 9, 249–261. ( 10.2217/fmb.13.161) [PubMed] [CrossRef] [Google Scholar]
22. Всемирная организация здравоохранения. 2016. Трансмиссивные болезни. В информационных бюллетенях ВОЗ. Женева, Швейцария: ВОЗ; См. http://www.who.int/mediacentre/factsheets/fs387/en/. [Google Scholar]
23. Центры по контролю и профилактике заболеваний. 2016. Словарь терминов. Атланта, Джорджия, США: CDC. [Google Scholar]
24. Лафферти К.Д., Курис А.М. 2002. Трофические стратегии, разнообразие животных и размер тела. Тенденции Экол. Эвол. 17, 507–513. ( 10.1016/s0169-5347(02)02615-0) [CrossRef] [Google Scholar]
25. Semenza JC, Menne B. 2009. Изменение климата и инфекционные заболевания в Европе.
 Ланцет Инфекция. Дис.
9, 365–375. ( 10.1016/S1473-3099(09)70104-5) [PubMed] [CrossRef] [Google Scholar]
Ланцет Инфекция. Дис.
9, 365–375. ( 10.1016/S1473-3099(09)70104-5) [PubMed] [CrossRef] [Google Scholar]26. Европейский центр профилактики и контроля заболеваний. 2016. Трансмиссивные болезни. В темах Здоровье. Сольна, Швеция: Европейский центр профилактики и контроля заболеваний; См. http://ecdc.europa.eu/en/healthtopics/climate_change/health_effects/Pages/vector_borne_diseases.aspx. [Академия Google]
27. Межправительственная группа экспертов по изменению климата. 2007. Изменение климата 2007: воздействия, адаптация и уязвимость. Вклад Рабочей группы II в Четвертый оценочный отчет Межправительственной группы экспертов по изменению климата (редакторы М.Л. Парри, О.Ф. Канзиани, Дж.П. Палутикоф, П.Дж. ван дер Линден, К.Э. Хэнсон). Кембридж, Великобритания: Издательство Кембриджского университета. См. http://www.ipcc.ch/publications_and_data/publications_ipcc_fourth_assessment_report_wg2_report_impacts_adaptation_and_vulnerability.htm.
28. Молинье Д.Х. 2003. Общие темы в меняющихся сценариях трансмиссивных болезней.
-6) [PubMed] [CrossRef] [Google Scholar] Транс. R Соц. Троп. Мед. Гиг.
97, 129–132. ( 10.1016/S0035-9203(03)
Транс. R Соц. Троп. Мед. Гиг.
97, 129–132. ( 10.1016/S0035-9203(03)29. Гублер Д.Дж. 1998. Возрождение трансмиссивных болезней как глобальная проблема здравоохранения. Эмердж. Заразить. Дис Дж. 4, 442 (10.3201/eid0403.980326) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
30. Центры по контролю и профилактике заболеваний. 2016. Отдел трансмиссивных болезней (DVBD). Атланта, Джорджия, США: CDC. [Академия Google]
31. Hu C, et al. 2008. Инфекции иммуногенными трипаносомами снижают репродуктивную способность цеце: потенциальное влияние различных штаммов паразитов на структуру популяции переносчиков. PLoS Негл. Троп. Дис. 2, e192 ( 10.1371/journal.pntd.0000192) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
32. Cator LJ, George J, Blanford S, Murdock CC, Baker TC, Read AF, Thomas МБ. 2013. «Манипуляция» без паразита: измененное пищевое поведение комаров не зависит от заражения малярийными паразитами.
 проц. Р. Соц. Б
280, 20130711 ( 10.1098/rspb.2013.0711) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
проц. Р. Соц. Б
280, 20130711 ( 10.1098/rspb.2013.0711) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]33. Cator LJ, Pietri JE, Murdock CC, Ohm JR, Lewis EE, Read AF, Luckhart S, Thomas MB. 2015. Иммунный ответ и передача сигналов инсулина изменяют пищевое поведение комаров, повышая потенциал передачи малярии. науч. Респ. 5 (10.1038/srep11947) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
34. Sanders CJ, Selby R, Carpenter S, Reynolds DR. 2011. Высотный полет Culicoides мокрецы. Вет. Рек. 169, 208 (10.1136/vr.d4245) [PubMed] [CrossRef] [Google Scholar]
35. Randolph SE. 1998. Клещи не насекомые: последствия противопоставления биологии переносчиков для потенциала передачи. Паразитол. Сегодня 14, 186–192. ( 10.1016/S0169-4758(98)01224-1) [PubMed] [CrossRef] [Google Scholar]
36. Diekmann O, Heesterbeek JAP, Roberts MG. 2010. Построение матриц нового поколения для сегментарных моделей эпидемий. Дж. Р. Соц. Интерфейс 7, 873–885.
 ( 10.1098/rsif.2009.0386) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
( 10.1098/rsif.2009.0386) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]37. Hartemink NA, Randolph SE, Davis SA, Heesterbeek JAP. 2008. Базовый репродуктивный номер для сложных систем заболеваний: определение R 0 для клещевых инфекций. Являюсь. Нац. 171, 743–754. ( 10.1086/587530) [PubMed] [CrossRef] [Google Scholar]
38. Добсон А., Фуфопулос Дж. 2001. Новые инфекционные патогены диких животных. Фил. Транс. Р. Соц. Лонд. Б 356, 1001–1012. ( 10.1098/rstb.2001.0900) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
39. Добсон А. 2004. Динамика популяций возбудителей с несколькими видами хозяев. Являюсь. Нац. 164, С64–С78. ( 10.1086/424681) [PubMed] [CrossRef] [Google Scholar]
40. Fenton A, Streicker DG, Petchey OL, Pedersen AB. 2015. Все хосты созданы равными? Разделение вклада видов-хозяев в устойчивость паразитов в сообществах с несколькими хозяевами. Являюсь. Нац. 186, 610–622. ( 10.1086/683173) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
41.
 Гандон С.
2004.
Эволюция многохозяинных паразитов. Эволюция
58, 455–469. ( 10.1111/j.0014-3820.2004.tb01669.x) [PubMed] [CrossRef] [Google Scholar]
Гандон С.
2004.
Эволюция многохозяинных паразитов. Эволюция
58, 455–469. ( 10.1111/j.0014-3820.2004.tb01669.x) [PubMed] [CrossRef] [Google Scholar]42. Холт Р.Д., Добсон А.П., Бегон М., Бауэрс Р.Г., Шаубер Э.М. 2003. Расселение паразитов в принимающих сообществах. Экол. лат. 6, 837–842. ( 10.1046/j.1461-0248.2003.00501.x) [CrossRef] [Google Scholar]
43. Андерсон Р.М., Мэй Р.М. 1991. Инфекционные болезни человека: динамика и борьба. Оксфорд, Великобритания: Издательство Оксфордского университета. [Академия Google]
44. Ализон С., ван Баален М. 2008. Компромисс между передачей и вирулентностью при трансмиссивных болезнях. Теор. Народ. биол. 74, 6–15. (10.1016/j.tpb.2008.04.003) [PubMed] [CrossRef] [Google Scholar]
45. Андерсон Р.М., Мэй Р.М. 1978 год. Регуляция и стабильность популяционных взаимодействий хозяина и паразита: I. Регуляторные процессы. Дж. Аним. Экол. 47, 219–247. ( 10.2307/3933) [CrossRef] [Google Scholar]
46. Макдональд Г. 1957.
 Эпидемиология и борьба с малярией. Лондон, Великобритания: Издательство Оксфордского университета. [Академия Google]
Эпидемиология и борьба с малярией. Лондон, Великобритания: Издательство Оксфордского университета. [Академия Google]47. Шаубер Э.М., Остфельд Р.С. 2002. Моделирование последствий снижения компетентности резервуара и демографического оборота в экологии болезни Лайма. Экол. заявл. 12, 1142–1162. ( 10.2307/3061042) [CrossRef] [Google Scholar]
48. Шмидт К.А., Остфельд Р.С. 2001. Биоразнообразие и эффект разбавления в экологии болезней. Экология 82, 609–619. ( 10.2307/2680183) [CrossRef] [Google Scholar]
49. Dubey JP. 2008. История Toxoplasma gondii — первые 100 лет. Дж. Юкар. микробиол. 55, 467–475. ( 10.1111/j.1550-7408.2008.00345.x) [PubMed] [CrossRef] [Google Scholar]
50. Бегон М., Беннетт М., Бауэрс Р.Г., Френч Н.П., Хейзел С.М., Тернер Дж. 2002. Уточнение условий передачи в моделях хозяин-микропаразит: количество, плотность и площадь. Эпидемиол. Заразить. 129, 147–153. ( 10.1017/s0950268802007148) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
51.
 Fenton A, Fairbairn JP, Norman R, Hudson PJ.
2002.
Паразитарная передача: примирение теории и реальности. Дж. Аним. Экол.
71, 893–905. ( 10.1046/j.1365-2656.2002.00656.x) [CrossRef] [Google Scholar]
Fenton A, Fairbairn JP, Norman R, Hudson PJ.
2002.
Паразитарная передача: примирение теории и реальности. Дж. Аним. Экол.
71, 893–905. ( 10.1046/j.1365-2656.2002.00656.x) [CrossRef] [Google Scholar]52. Маккаллум Х., Барлоу Н., Хоун Дж. 2001. Как следует моделировать передачу патогена? Тенденции Экол. Эвол. 16, 295–300. ( 10.1016/S0169-5347(01)02144-9) [PubMed] [CrossRef] [Google Scholar]
53. Вайшер Б., Браун Д. 2000. Введение в нематоды: общая нематология. София, Болгария: Издательство Pensoft. [Google Scholar]
54. Перкинс С.Е., Фентон А. 2006. Гельминты как переносчики возбудителей у позвоночных хозяев: теоретический подход. Междунар. Дж. Паразитол. 36, 887–894. (10.1016/j.ijpara.2006.04.001) [PubMed] [CrossRef] [Google Scholar]
55. Lund EE, Burtner RH. 1957. Инфекционность яиц Heterakis gallinae с яиц Histomonas meleagridis . Эксп. Паразитол. 6, 189–193. ( 10.1016/0014-4894(57)
-0) [PubMed] [CrossRef] [Google Scholar]
56.
 Лунд Э.Э., Вер Э.Э., Эллис Д.Дж.
1966 год.
Передача дождевыми червями Heterakis и Histomonas индейкам и курам. Дж. Паразитол.
52, 899–902. ( 10.2307/3276528) [PubMed] [CrossRef] [Google Scholar]
Лунд Э.Э., Вер Э.Э., Эллис Д.Дж.
1966 год.
Передача дождевыми червями Heterakis и Histomonas индейкам и курам. Дж. Паразитол.
52, 899–902. ( 10.2307/3276528) [PubMed] [CrossRef] [Google Scholar]57. André AvS, et al. 2002. Роль эндосимбиотических бактерий Wolbachia в патогенезе речной слепоты. Наука 295, 1892–1895 гг. ( 10.1126/science.1068732) [PubMed] [CrossRef] [Google Scholar]
58. Aitken MM, Jones PW, Hall GA, Hughes DL, Brown GTH. 1981. Реакции крупного рогатого скота, инфицированного и свободного от трематод, на экспериментальное повторное заражение Salmonella dublin . Рез. Вет. науч. 31, 120–126. [PubMed] [Google Scholar]
59. Brady MT, O’Neill SM, Dalton JP, Mills KHG. 1999. Фасциола hepatica подавляет защитный ответ Th2 против Bordetella pertussis . Заразить. Иммун. 67, 5372–5378. [Бесплатная статья PMC] [PubMed] [Google Scholar]
60. Randolph SE, Miklisová D, Lysy J, Rogers DJ, Labuda M.
 1999.
Заболеваемость по совпадению: модели заражения клещами грызунов способствуют передаче вируса клещевого энцефалита. Паразитология
118, 177–186. ( 10.1017/s0031182098003643) [PubMed] [CrossRef] [Google Scholar]
1999.
Заболеваемость по совпадению: модели заражения клещами грызунов способствуют передаче вируса клещевого энцефалита. Паразитология
118, 177–186. ( 10.1017/s0031182098003643) [PubMed] [CrossRef] [Google Scholar]61. Лашарм-Лора Л., Солсбери В., Хамфри Т.Дж., Стаффорд К., Перкинс С.Е. 2009. Бактерии, выделенные из паразитических нематод, — потенциальный новый переносчик патогенов? Окружающая среда. Здоровье 8, S17 (10.1186/1476-069x-8-s1-s17) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
62. Lacharme-Lora L, Perkins SE, Humphrey TJ, Hudson PJ, Salisbury В. 2009. Использование биолюминесцентных бактериальных биосенсоров для изучения роли свободноживущих гельминтов как резервуаров и переносчиков Salmonella . Окружающая среда. микробиол. 1, 198–207. ( 10.1111/j.1758-2229.2009.00031.x) [PubMed] [CrossRef] [Google Scholar]
63. Kaplan EH, Khoshnood K, Heimer R. 1994. Сокращение количества игл, инфицированных ВИЧ, возвращено в программу обмена игл в Нью-Хейвене: смена клиентов или обмен игл? Являюсь.
 Дж. Общественное здравоохранение
84, 1991–1994. (10.2105/ajph.84.12.1991) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
Дж. Общественное здравоохранение
84, 1991–1994. (10.2105/ajph.84.12.1991) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]64. Anderson RM, May RM. 1982. Коэволюция хозяев и паразитов. Паразитология 85, 411–426. ( 10.1017/S0031182000055360) [PubMed] [CrossRef] [Google Scholar]
65. Франк С.А. 1996. Модели вирулентности паразитов. Q. Преподобный Биол. 71, 37–78. ( 10.1086/419267) [PubMed] [CrossRef] [Google Scholar]
66. Choisy M, Brown SP, Lafferty KD, Thomas F. 2003. Эволюция трофической передачи у паразитов: зачем добавлять промежуточных хозяев? Являюсь. Нац. 162, 172–181. ( 10.1086/375681) [PubMed] [CrossRef] [Google Scholar]
67. Пулин Р. 1994. Эволюция паразитарных манипуляций поведением хозяина — теоретический анализ. Паразитология 109, С109–С118. ( 10.1017/S0031182000085127) [PubMed] [CrossRef] [Google Scholar]
68. Mideo N, Alizon S, Day T. 2008. Связь динамики внутри и между хозяевами в эволюционной эпидемиологии инфекционных заболеваний.
 Тенденции Экол. Эвол.
23, 511–517. ( 10.1016/j.tree.2008.05.009) [PubMed] [CrossRef] [Google Scholar]
Тенденции Экол. Эвол.
23, 511–517. ( 10.1016/j.tree.2008.05.009) [PubMed] [CrossRef] [Google Scholar]69. Mideo N, Day T. 2008. Об эволюции репродуктивной сдержанности при малярии. проц. Р. Соц. Б 275, 1217–1224. ( 10.1098/rspb.2007.1545) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
70. McKenzie FE, Bossert WH. 1998. Оптимальная продукция гаметоцитов Plasmodium falciparum . Дж. Теор. биол. 193, 419–428. ( 10.1006/jtbi.1998.0710) [PubMed] [CrossRef] [Google Scholar]
71. Koella JC, Antia R. 1995. Оптимальная схема репликации и передачи паразитов с двумя стадиями жизненного цикла. Теор. Народ. биол. 47, 277–291. ( 10.1006/tpbi.1995.1012) [CrossRef] [Google Scholar]
72. Bell AS, Huijben S, Paaijmans KP, Sim DG, Chan BHK, Nelson WA, Read AF, Borrmann S. 2012. Повышенная передача лекарственно-устойчивых паразитов комарам после медикаментозного лечения малярии грызунов. ПЛОС ОДИН 7, e37172 ( 10.1371/journal.pone.0037172) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
73.
 Huijben S, Nelson WA, Wargo AR, Sim DG, Drew DR, Read AF.
2010.
Химиотерапия, экология внутри хозяина и приспособленность лекарственно-устойчивых малярийных паразитов. Эволюция
64, 2952–2968. ( 10.1111/j.1558-5646.2010.01068.x) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
Huijben S, Nelson WA, Wargo AR, Sim DG, Drew DR, Read AF.
2010.
Химиотерапия, экология внутри хозяина и приспособленность лекарственно-устойчивых малярийных паразитов. Эволюция
64, 2952–2968. ( 10.1111/j.1558-5646.2010.01068.x) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]74. Paul REL, Bonnet S, Boudin C, Tchuinkam T, Robert V. 2007. Агрегация малярийных паразитов ограничивает уровень заражения комарами. Заразить. Жене. Эвол. 7, 577–586. ( 10.1016/j.meegid.2007.04.004) [PubMed] [CrossRef] [Google Scholar]
75. Грейшар М., Мидео Н., Рид А., Бьорнстад О. 2016. Прогнозирование оптимальных инвестиций в передачу малярийных паразитов. Эволюция 70, 1542–1558. ( 10.1111/evo.12969) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
76. Pollitt LC, Churcher TS, Dawes EJ, Khan SM, Sajid M, Basáñez MG, Colegrave N, Reece SE. 2013. Затраты на скученность при передаче малярийных паразитов. Эвол. заявл. 6, 617–629. ( 10.1111/eva.12048) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
77.
 Ари Ф. и др.
2014.
Молекулярный маркер резистентной к артемизинину малярии Plasmodium falciparum . Природа
505, 50–55. ( 10.1038/nature12876) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
Ари Ф. и др.
2014.
Молекулярный маркер резистентной к артемизинину малярии Plasmodium falciparum . Природа
505, 50–55. ( 10.1038/nature12876) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]78. Straimer J, et al. 2015. Мутации K13-пропеллера придают устойчивость к артемизинину клиническим изолятам Plasmodium falciparum . Наука 347, 428–431. ( 10.1126/science.1260867) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
79. Миотто О и др. 2015. Генетическая архитектура резистентного к артемизинину Plasmodium falciparum . Нац. Жене. 47, 226–234. (10.1038/ng.3189) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
80. Molina-Cruz A, et al. 2013. Ген малярийного паразита человека Pfs47 опосредует уклонение от иммунной системы комаров. Наука 340, 984–987. ( 10.1126/science.1235264) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
81. Mideo N, et al. 2016. Инструмент глубокого секвенирования для разделения показателей элиминации после противомалярийного лечения при поликлональных инфекциях.
 Эвол. Мед. Здравоохранение
2016, 21–36. ( 10.1093/emph/eov036) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
Эвол. Мед. Здравоохранение
2016, 21–36. ( 10.1093/emph/eov036) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]82. St Laurent B, et al. 2015. Клинические изоляты Plasmodium falciparum , устойчивые к артемизинину, могут инфицировать различных комаров-переносчиков в Юго-Восточной Азии и Африке. Нац. коммун. 6, 8614 (10.1038/ncomms9614) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
83. Mellor PS, Boorman J. 1980. Размножение вируса блютанга у Culicoides nubeculosus (meigen), одновременно инфицированных вирусом и микрофиляриями Onchocercacercais (Райе и Генри). Энн. Троп. Мед. Паразитол. 74, 463–469. ( 10.1080/00034983.1980.11687368) [PubMed] [CrossRef] [Google Scholar]
84. Turell M, Rossignol P, Spielman A, Rossi C, Bailey CL. 1984. Усиленная передача арбовирусов комарами, которые одновременно проглатывают микрофилярии. Наука 225, 1039–1041. ( 10.1126/science.6474165) [PubMed] [CrossRef] [Google Scholar]
85.
 Shaw AE, et al.
2012. Дрозофила меланогастр в качестве модельного организма для репликации и тропизма вируса блутанга. Дж. Вирол. 86, 9015–9024. ( 10.1128/jvi.00131-12) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
Shaw AE, et al.
2012. Дрозофила меланогастр в качестве модельного организма для репликации и тропизма вируса блутанга. Дж. Вирол. 86, 9015–9024. ( 10.1128/jvi.00131-12) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]86. Antonovics J, Wilson AJ, Forbes MR, Hauffe HC, Kallio ER, Leggett HC, Longdon B, Okamura Б., Саит С.М., Вебстер Дж.П. 2017. Эволюция режима передачи. Фил. Транс. Р. Соц. Б 372, 20160083 (10.1098/rstb.2016.0083) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
87. Barnett HC. 1962. Инкриминация членистоногих как переносчиков болезней. В проц. XI межд. Конгресс энтомологов , стр. 341–345. Вена.
88. Ламбрехтс Л., Скотт Т.В. 2009. Способ передачи и эволюция вирулентности арбовирусов у комаров-переносчиков. проц. Р. Соц. Б 276, 1369–1378. ( 10.1098/rspb.2008.1709) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
89. Box GEP. 1979. Надежность в стратегии построения научной модели.
 В книге «Надежность в статистике» (редакторы Лаунер Р.Л., Уилкинсон Г.Н.), стр. 201–236. Лондон, Великобритания: Академическая пресса. [Академия Google]
В книге «Надежность в статистике» (редакторы Лаунер Р.Л., Уилкинсон Г.Н.), стр. 201–236. Лондон, Великобритания: Академическая пресса. [Академия Google]Набор стерильных чернил MarginMarker | Тканевые чернила
Глобальный стандарт ориентации тканей
В онкологической хирургии единственным наиболее важным предиктором местного рецидива являются края ткани. Стерильные чернила MarginMarker обеспечивают надежное и точное обозначение краев образца. Патология получает ткань, четко обозначенную стандартной цветовой схемой, чтобы полностью определить каждую из шести краевых плоскостей. Неровности или трещины на поверхности четко идентифицируются. MarginMarker является одним из элементов векторной системы ориентации хирургических тканей; второй компонент — рентгенографические маркеры CorrectClips™ для интраоперационного анализа. Система обеспечивает безопасное, полное и точное обозначение границ образца ткани.
Используемые чернила MarginMarker Tissue
Демонстрация для хирурга с использованием стерильных чернил MarginMarker
“
“MarginMarker позволил мне отправить патологоанатому образец молочной железы с точными границами.



 2$ можно получить так:
2$ можно получить так: {\otimes n}\ket{0}$. Это экспоненциально более короткое описание состояния не только имеет то преимущество, что можно аргументировать его в рамках классической модели, но оно также четко определяет операции, которые необходимо распространить через программный стек для реализации алгоритма. По этой причине Q# предназначен для создания последовательностей ворот, а не квантовых состояний, однако на теоретическом уровне эти две перспективы эквивалентны.
{\otimes n}\ket{0}$. Это экспоненциально более короткое описание состояния не только имеет то преимущество, что можно аргументировать его в рамках классической модели, но оно также четко определяет операции, которые необходимо распространить через программный стек для реализации алгоритма. По этой причине Q# предназначен для создания последовательностей ворот, а не квантовых состояний, однако на теоретическом уровне эти две перспективы эквивалентны.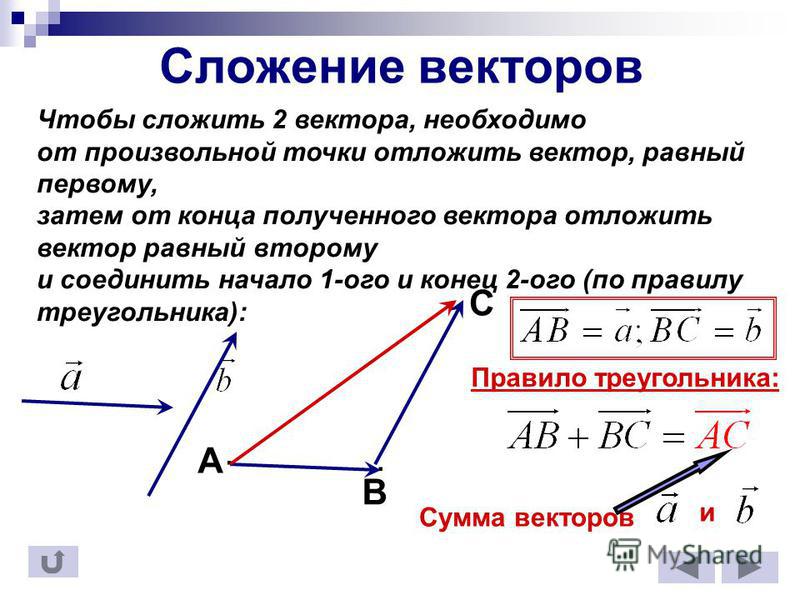
 Допустим в данной системе будет задан, так вектор имеющий координаты (aₓ ; aᵧ). Получим формулу, которая поможет найти длину вектора , через известные нам координаты aₓ и aᵧ.
Допустим в данной системе будет задан, так вектор имеющий координаты (aₓ ; aᵧ). Получим формулу, которая поможет найти длину вектора , через известные нам координаты aₓ и aᵧ.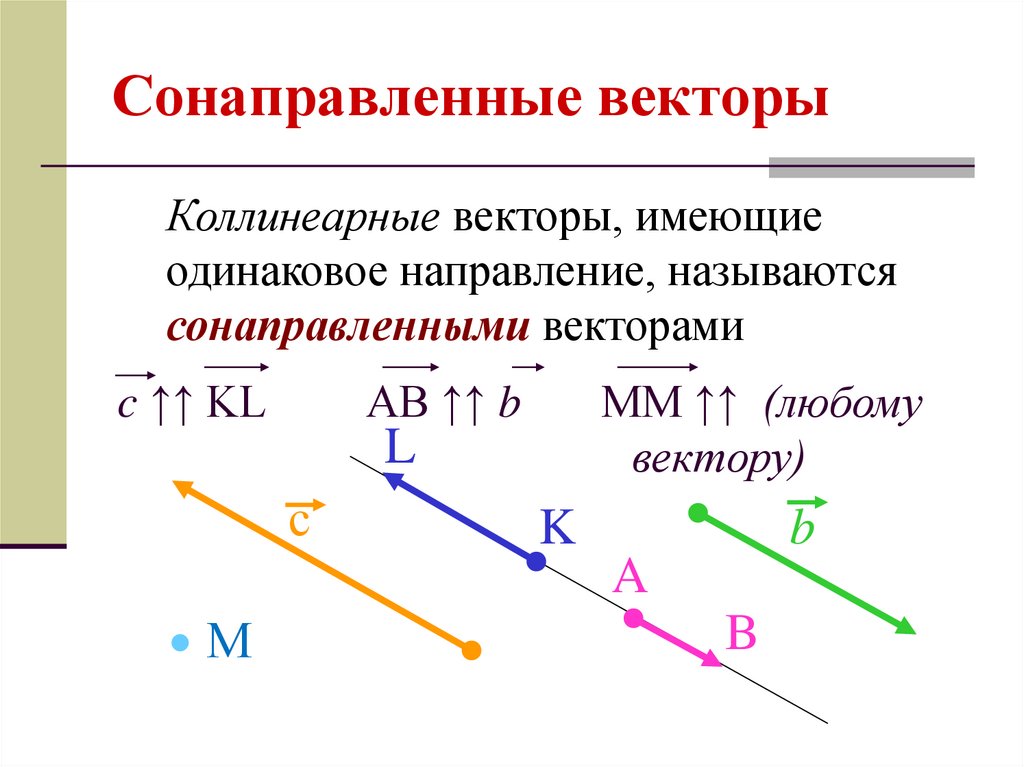
 2-2=-2
2-2=-2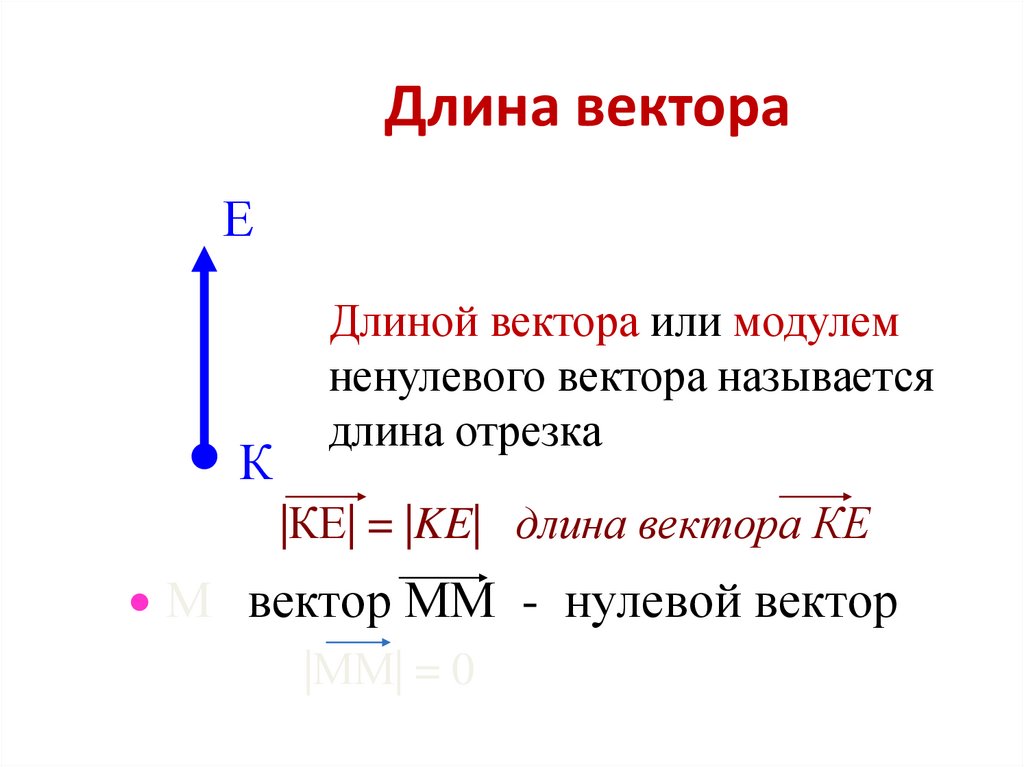 2}\) чаще такая формула применима в физике, для того чтобы узнать длину пути материальной точки.
2}\) чаще такая формула применима в физике, для того чтобы узнать длину пути материальной точки.
 2009.
Синий язык в Европе: прошлое, настоящее и будущее. Фил. Транс. Р. Соц. Б
364, 2669–2681. ( 10.1098/rstb.2009.0091) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
2009.
Синий язык в Европе: прошлое, настоящее и будущее. Фил. Транс. Р. Соц. Б
364, 2669–2681. ( 10.1098/rstb.2009.0091) [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar] PLoS Негл. Троп. Дис.
10, e0004243 ( 10.1371/journal.pntd.0004243) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
PLoS Негл. Троп. Дис.
10, e0004243 ( 10.1371/journal.pntd.0004243) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar] PLoS Патог.
12, e1005361 ( 10.1371/journal.ppat.1005361) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
PLoS Патог.
12, e1005361 ( 10.1371/journal.ppat.1005361) [бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]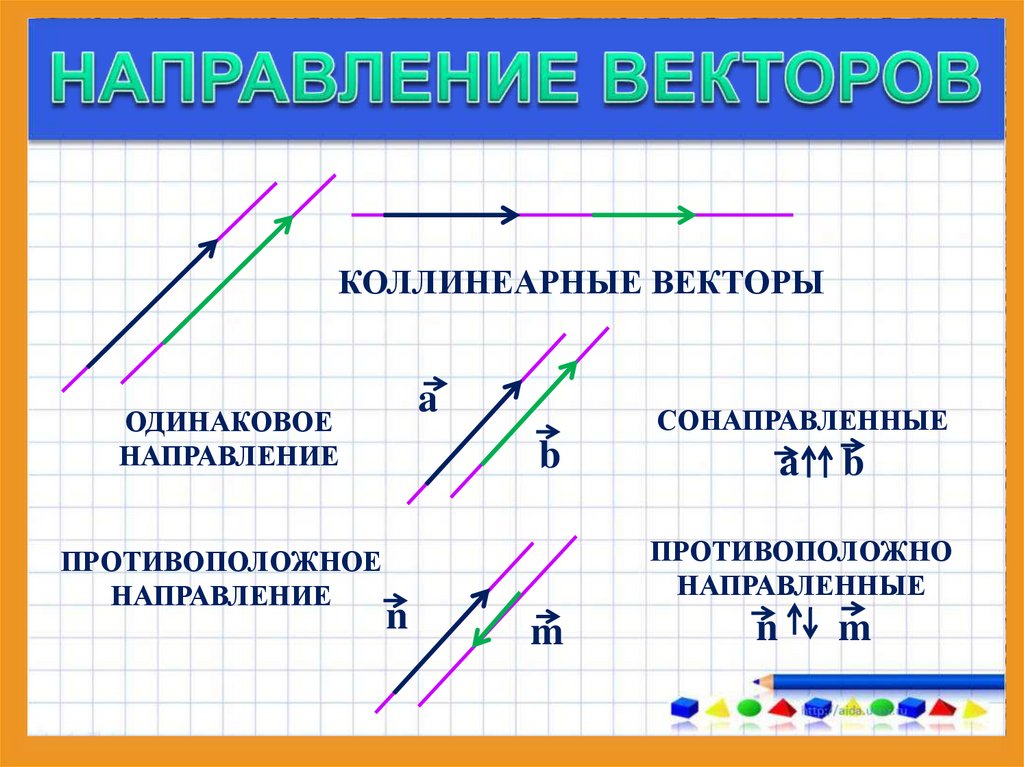 СПИД
15, 1329–1341. ( 10.1097/00002030-200107270-00002) [PubMed] [CrossRef] [Google Scholar]
СПИД
15, 1329–1341. ( 10.1097/00002030-200107270-00002) [PubMed] [CrossRef] [Google Scholar]