Как определяются координаты вектора в пространстве. Координаты вектора. Направляющие косинусы. Свойства скалярного произведения векторов

Нахождение координат вектора довольно часто встречаемое условие многих задач в математике. Умение находить координаты вектора поможет вам в других, более сложных задачах со схожей тематикой. В данной статье мы рассмотрим формулу нахождения координат вектора и несколько задач.

Нахождение координат вектора в плоскости

Что такое плоскость? Плоскостью считается двухмерное пространство, пространство с двумя измерениями (измерение x и измерение y). К примеру, бумага – плоскость. Поверхность стола – плоскость. Какая-нибудь необъемная фигура (квадрат, треугольник, трапеция) тоже является плоскостью. Таким образом, если в условии задачи нужно найти координаты вектора, который лежит на плоскости, сразу вспоминаем про x и y. Найти координаты такого вектора можно следующим образом: Координаты AB вектора = (xB – xA; yB – xA). Из формулы видно, что от координат конечной точки нужно отнять координаты начальной точки.

Пример:

• Вектор CD имеет начальные (5; 6) и конечные (7; 8) координаты.
• Найти координаты самого вектора.
• Используя вышеупомянутую формулу, получим следующее выражение: CD = (7-5; 8-6) = (2; 2).
• Таким образом, координаты CD вектора = (2; 2).
• Соответственно, x координата равна двум, y координата – тоже двум.

Нахождение координат вектора в пространстве

Что такое пространство? Пространство это уже трехмерное измерение, где даны 3 координаты: x, y, z. В случае, если нужно найти вектор, который лежит в пространстве, формула практически не меняется. Добавляется только одна координата. Для нахождения вектора нужно от координат конца отнять координаты начала. AB = (xB – xA; yB – yA; zB – zA)

Пример:

• Вектор DF имеет начальные (2; 3; 1) и конечные (1; 5; 2).
• Применяя вышеупомянутую формулу, получим: Координаты вектора DF = (1-2; 5-3; 2-1) = (-1; 2; 1).
• Помните, значение координат может быть и отрицательным, в этом нет никакой проблемы.

Как найти координаты вектора онлайн?

Если по каким-то причинам вам не хочется находить координаты самостоятельно, можно воспользоваться онлайн калькулятором . Для начала, выберите размерность вектора. Размерность вектора отвечает за его измерения. Размерность 3 означает, что вектор находится в пространстве, размерность 2 – что на плоскости. Далее вставьте координаты точек в соответствующие поля и программа определит вам координаты самого вектора. Все очень просто.

Нажав на кнопку, страница автоматически прокрутится вниз и выдаст вам правильный ответ вместе с этапами решения.

Рекомендовано хорошо изучить данную тему, потому что понятие вектора встречается не только в математике, но и в физике. Студенты факультета Информационных Технологий тоже изучают тему векторов, но на более сложном уровне.

Необходимо определить вектор на плоскости или в пространстве, то есть дать информацию о его направлении и длине.

Координаты вектора

Пусть задана прямоугольная декартова система координат (ПДСК) $x O y$ и произвольный вектор $\overline{a}$, начало которого совпадает с началом системы координат (рис.

1).

Определение

Координатами вектора $\overline{a}$ называются проекции $a_{x}$ и $a_{y}$ данного вектора на оси $O x$ и $O y$ соответственно:

Величина $a_{x}$ называется абсциссой вектора $\overline{a}$, а число $a_{y}$ — его ординатой . То, что вектор $\overline{a}$ имеет координаты $a_{x}$ и $a_{y}$, записывается следующим образом: $\overline{a}=\left(a_{x} ; a_{y}\right)$.

Пример

Запись $\overline{a}=(5 ;-2)$ означает, что вектор $\overline{a}$ имеет следующие координаты: абсцисса равна 5, ордината равна -2.

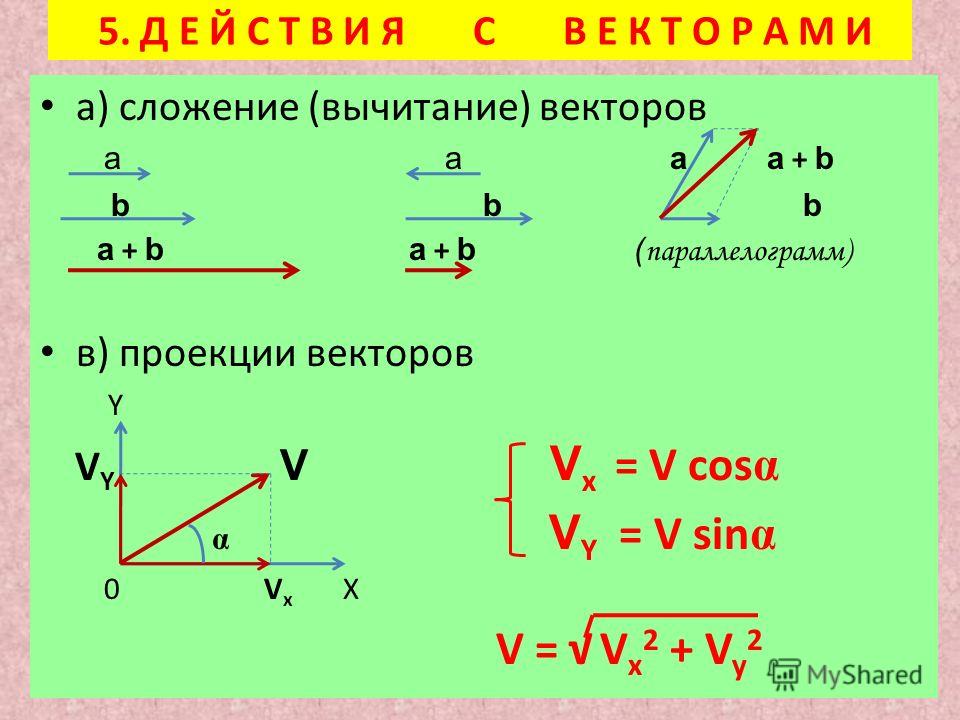
Сумма двух векторов, заданных координатами

Пусть заданы $\overline{a}=\left(a_{x} ; a_{y}\right)$ и $\overline{b}=\left(b_{x} ; b_{y}\right)$, тогда вектор $\overline{c}=\overline{a}+\overline{b}$ имеет координаты $\left(a_{x}+b_{x} ; a_{y}+b_{y}\right)$ (рис. 2).

Определение

Чтобы найти сумму двух векторов , заданных своими координатами, надо сложить их соответствующие координаты.

Пример

Задание. Заданы $\overline{a}=(-3 ; 5)$ и $\overline{b}=(0 ;-1)$. Найти координаты вектора $\overline{c}=\overline{a}+\overline{b}$

Решение. $\overline{c}=\overline{a}+\overline{b}=(-3 ; 5)+(0 ;-1)=(-3+0 ; 5+(-1))=(-3 ; 4)$

Умножение вектора на число

Если задан $\overline{a}=\left(a_{x} ; a_{y}\right)$, то тогда вектор $m \overline{a}$ имеет координаты $m \overline{a}=\left(m a_{x} ; m a_{y}\right)$, здесь $m$ — некоторое число (рис. 3).

Пример

Задание. Вектор $\overline{a}=(3 ;-2)$. Найти координаты вектора 2$\overline{a}$

Решение. $2 \overline{a}=2 \cdot(3 ;-2)=(2 \cdot 3 ; 2 \cdot(-2))=(6 ;-4)$

Рассмотрим далее случай, когда начало вектора не совпадает с началом системы координат. Предположим, что в ПДСК заданы две точки $A\left(a_{x} ; a_{y}\right)$ и $B\left(b_{x} ; b_{y}\right)$. Тогда координаты вектора $\overline{A B}=\left(x_{1} ; y_{1}\right)$ находятся по формулам (рис.

{2}}}$

Здесь $\alpha$, $\beta$ и $\gamma$ — углы, которые составляет вектор с положительными направлениями осей $O x$, $O y$ и $O z$ соответственно.

На оси абсцисс и ординат называются координатами вектора . Координаты вектора общепринято указывать в виде (х, у) , а сам вектор как: =(х, у).

Формула определения координат вектора для двухмерных задач.

В случае двухмерной задачи вектор с известными координатами точек A(х 1 ;у 1) и B(x 2 ; y 2 ) можно вычислить:

= (x 2 — x 1 ; y 2 — y 1).

Формула определения координат вектора для пространственных задач.

В случае пространственной задачи вектор с известными координатами точек A(х 1 ;у 1 ; z 1 ) и B(x 2 ; y 2 ; z 2 ) можно вычислить применив формулу:

= (x 2 — x 1 ; y 2 — y 1 ; z 2 — z 1 ).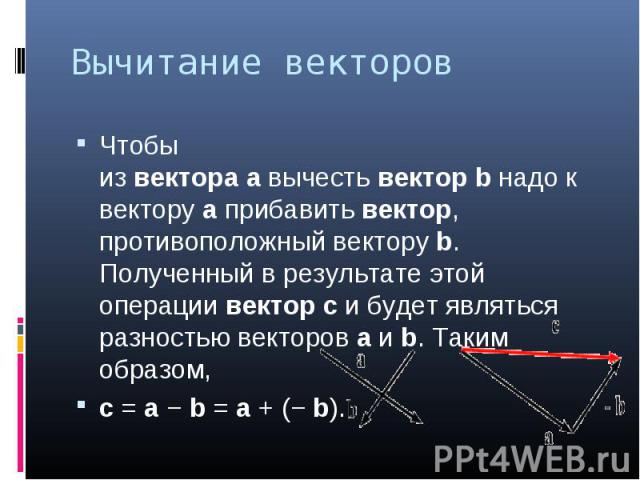

Координаты дают всеобъемлющую характеристику вектора, поскольку по координатам есть возможность построить и сам вектор. Зная координаты, легко вычислить и

длину вектора . (Свойство 3, приведенное ниже).

Свойства координат вектора.

1. Любые равные векторы в единой системе координат имеют равные координаты .

2. Координаты коллинеарных векторов пропорциональны. При условии, что ни один из векторов не равен нулю.

3. Квадрат длины любого вектора равен сумме квадратов его координат .

4.При операции умножения вектора на действительное число каждая его координата умножается на это число.

5. При операции сложения векторов вычисляем сумму соответствующие координаты векторов .

6. Скалярное произведение двух векторов равняется сумме произведений их соответствующих координат.

Для начала дадим определение координат вектора в заданной системе координат. Чтобы ввести данное понятие, определим что мы называем прямоугольной или декартовой системой координат.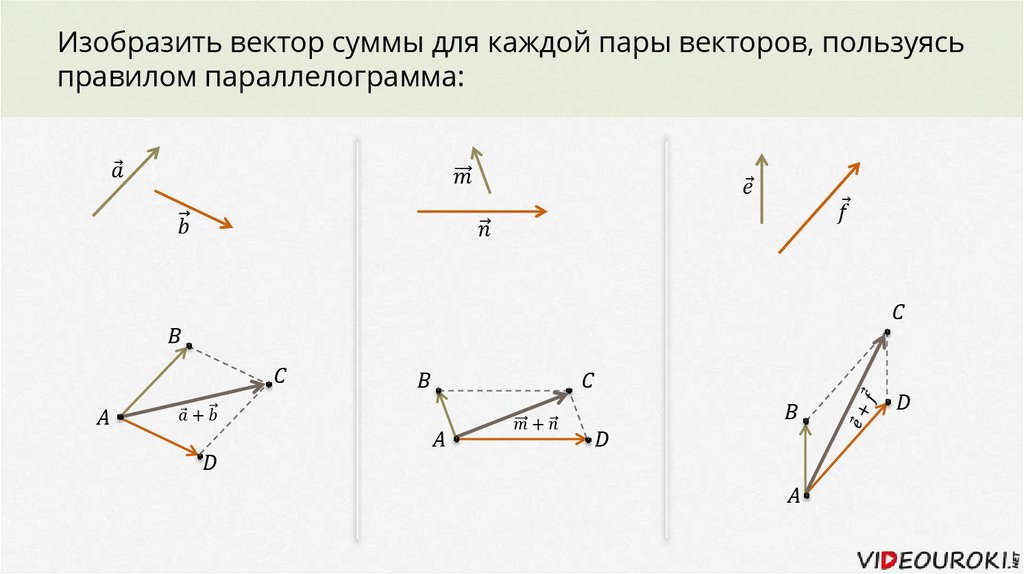

Определение 1

Прямоугольная система координат представляет из себя прямолинейную систему координат с взаимно перпендикулярными осями на плоскости или в пространстве.

С помощью введения прямоугольной системы координат на плоскости или в трехмерном пространстве становится возможным описывание геометрических фигур вместе с их свойствами при помощи уравнений и неравенств, то есть использовать алгебраические методы при решении геометрических задач.

Тем самым, мы можем привязать к заданной системе координат векторы. Это значительно расширит наши возможности при решении определенных задач

Прямоугольная система координат на плоскости обычно обозначается O x y , где O x и O y – оси коорднат. Ось O x называют осью абсцисс, а ось O y – осью ординат (в пространстве появляется ещё одна ось O z , которая перпендикулярна и O x и O y).

Пример 1

Итак, нам дана прямоугольная декартова система координат O x y на плоскости если мы отложим от начала координат векторы i → и j → , направление которых соответственно совпадет с положительными направлениями осей O x и O y , и их длина будет равна условной единице, мы получим координатные векторы.

То есть в данном случае i → и j → являются координатными векторами.

Координатные векторы

Определение 2

Векторы i → и j → называются координатными векторами для заданной системы координат.

Пример 2

Откладываем от начала координат произвольный вектор a → . Опираясь на геометрическое определение операций над векторами, вектор a → может быть представлен в виде a → = a x · i → + a y · j → , где коэффициенты a x и a y — единственные в своем роде, их единственность достаточно просто доказать методом от противного.

Разложение вектора

Определение 3

Разложением вектора a → по координатным векторам i → и j → на плоскости называется представление вида a → = a x · i → + a y · j → .

Определение 4

Коэффициенты a x и a y называются координатами вектора в данной системе координат на плоскости.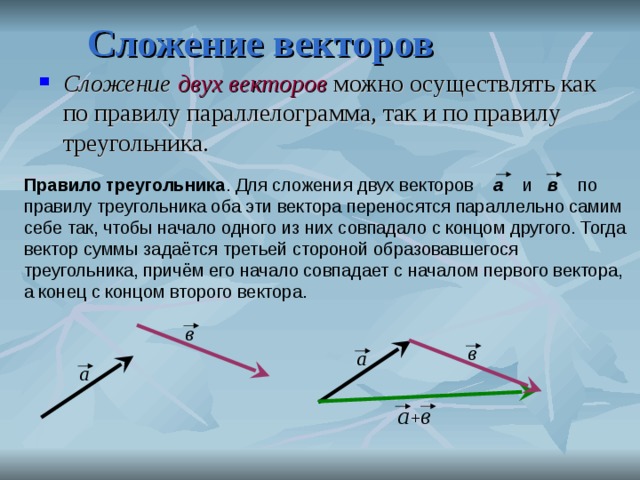

Координаты вектора в данной системе координат принято записывать в круглых скобках, через запятую, при этом заданные координаты следует отделять от обозначения вектора знаком равенства. К примеру, запись a → = (2 ; — 3) означает, что вектор a → имеет координаты (2 ; — 3) в данной системе координат и может быть представлен в виде разложения по координатным векторам i → и j → как a → = 2 · i → — 3 · j → .

Замечание

Следует обратить внимание, что порядок записи координат, имеет важное значение, если вы запишите координаты вектора в другом порядке, вы получите совершенно другой вектор.

Опираясь на определения координат вектора и их разложения становится очевидным, что единичные векторы i → и j → имеют координаты (1 ; 0) и (0 ; 1) соответственно, и они могут быть представлены в виде следующих разложений i → = 1 · i → + 0 · j → ; j → = 0 · i → + 1 · j → .

Также имеет место быть нулевой вектор 0 → с координатами (0 ; 0) и разложением 0 → = 0 · i → + 0 · j → .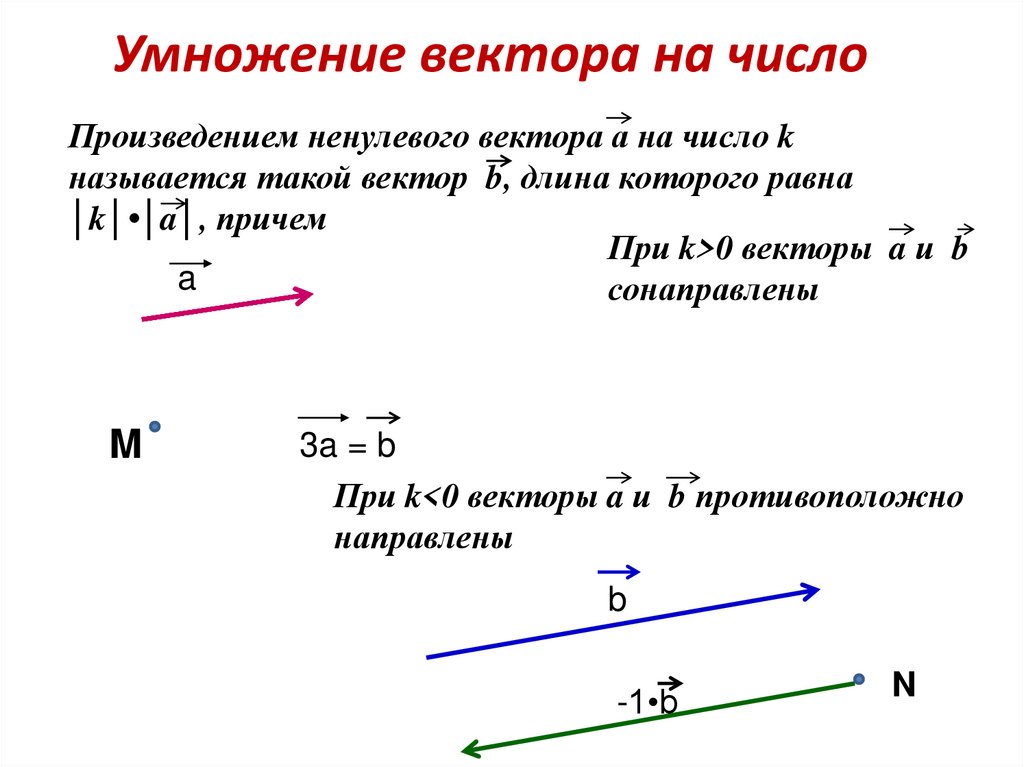

Равные и противоположные векторы

Определение 5

Векторы a → и b → равны тогда, когда их соответствующие координаты равны.

Определение 6

Противоположным вектором называется вектор противоположный данному.

Отсюда следует, что координаты такого вектора будут противоположны координатам данного вектора, то есть, — a → = (- a x ; — a y) .

Все вышеизложенное можно аналогично определить и для прямоугольной системы координат, заданной в трехмерном пространстве. В такой системе координат имеет место быть тройка координатных векторов i → , j → , k → , а произвольный вектор a → раскладывается не по двум, а уже по трем координатам, причем единственным образом и имеет вид a → = a x · i → + a y · j → + a z · k → , а коэффициенты этого разложения (a x ; a y ; a z) называются координатами вектора в данной (трехмерной) системе координат.

Следовательно, координатные векторы в трехмерном пространстве принимают также значение 1 и имеют координаты i → = (1 ; 0 ; 0) , j → = (0 ; 1 ; 0) , k → = (0 ; 0 ; 1) , координаты нулевого вектора также равны нулю 0 → = (0 ; 0 ; 0) , и в таком случае два вектора будут считаться равными, если все три соответствующие координаты векторов между собой равны a → = b → ⇔ a x = b x , a y = b y , a z = b z , и координаты противоположного вектора a → противоположны соответствующим координатам вектора a → , то есть, — a → = (- a x ; — a y ; — a z) .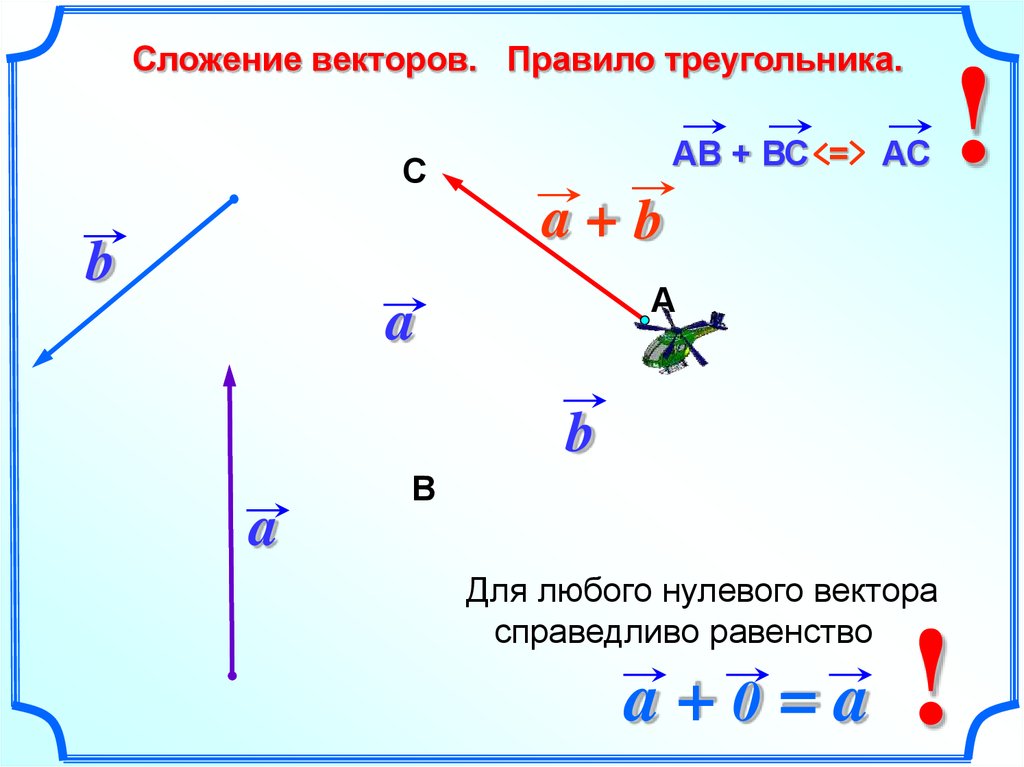

Чтобы ввести данное определение, требуется показать в данной системе координат связь координат точки и координат вектора.

Пусть нам дана некоторая прямоугольная декартова система координат O x y и на ней задана произвольная точка M с координатами M (x M ; y M) .

Определение 7

Вектор O M → называется радиус-вектором точки M .

Определим, какие координаты в данной системе координат имеет радиус-вектор точки

Вектор O M → имеет вид суммы O M → = O M x → + O M y → = x M · i → + y M · j → , где точки M x и M y это проекции точки М на координатные прямые Ox и Oy соответственно (данные рассуждения следуют из определения проекция точки на прямую), а i → и j → — координатные векторы, следовательно, вектор O M → имеет координаты (x M ; y M) в данной системе координат.

Иначе говоря, координаты радиус-вектора точки М равны соответствующим координатам точки М в прямоугольной декартовой системе координат.

Аналогично в трехмерном пространстве радиус-вектор точки M (x M ; y M ; z M) разлагается по координатным векторам как O M → = O M x → + O M y → + O M z → = x M · i → + y M · j → + z M · k → , следовательно, O M → = (x M ; y M ; z M) .

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

До сих пор считалось, что векторы рассматриваются в пространстве. Начиная с этого момента будим считать, что все векторы рассматриваются на плоскости. Будем также полагать, что на плоскости задана Декартова система координат (даже если об этом не говорится), представляющая две взаимно перпендикулярные числовые оси – горизонтальная ось и вертикальная ось. Тогда каждой точке
на плоскости ставится в соответствие пара чисел
, которые являются ее координатами. Обратно, каждой паре чисел
соответствует точка плоскости такая, что пара чисел
являются ее координатами.

Из элементарной геометрии известно, что если на плоскости имеются две точки
и
, то расстояние
между этими точками выражается через их координаты по формуле

Пусть на плоскости задана Декартова система координат.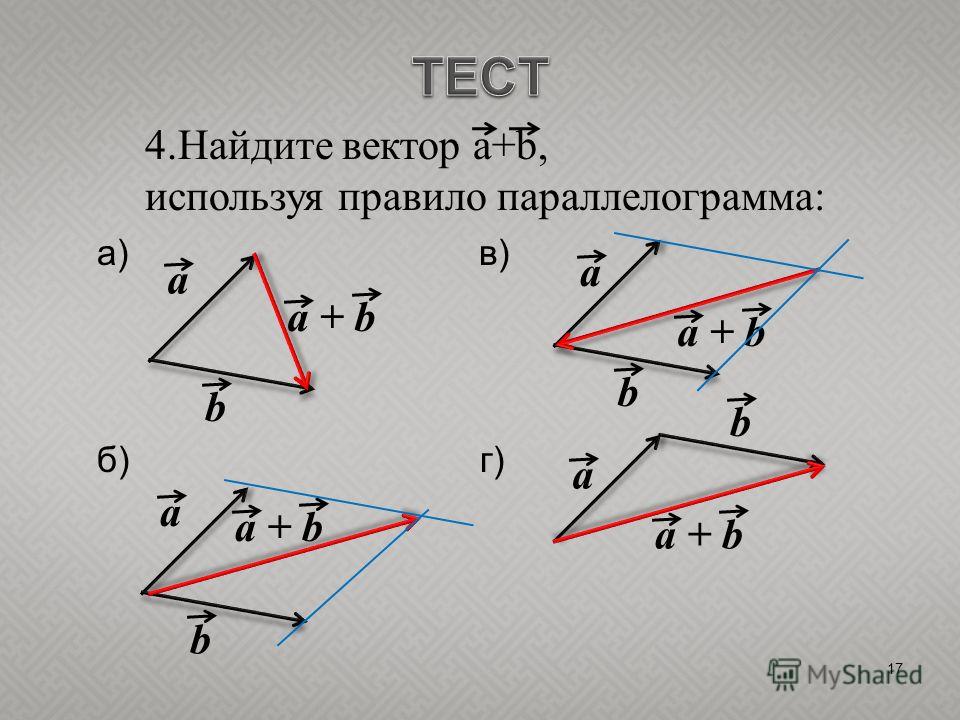 Орт оси будем обозначать символом, а орт осисимволом. Проекцию произвольноговекторана осьбудем обозначать символом
, а проекцию на осьсимволом
.

Пусть — произвольный вектор на плоскости. Имеет место следующая теорема.

Теорема 22.

Для любого вектора на плоскости существует пара чисел

.

При этом
,
.

Доказательство.

Пусть дан вектор. Отложим векторот начала координат. Обозначим черезвектор-проекцию векторана ось, а черезвектор-проекцию векторана ось. Тогда, как видно из рисунка 21, имеет место равенство

.

Согласно теореме 9,

,

.

Обозначим
,
. Тогда получаем

.

Итак, доказано, что для любого вектора существует пара чисел
таких, что справедливо равенство

,

,

.

При другом расположении вектора относительно осей доказательство аналогично.

Определение.

Пара чисел итаких, что
, называются координатами вектора. Числоназывается иксовой координатой, а числоигрековой координатой.

Определение.

Пара ортов осей координат
называется ортонормированным базисом на плоскости. Представление любого векторав виде
называется разложением векторапо базису
.

Непосредственно из определения координат вектора следует, что если координаты векторов равны, то равны и сами векторы. Справедливо также и обратное утверждение.

Теорема.

Равные векторы имеют равные координаты.

Доказательство.

,

и
. Докажем, что
,
.

Из равенства векторов следует, что

.

Допустим, что
, а
.

Тогда
и значит
, что не верно. Аналогично, если
, но
, то
. Отсюда
, что не верно. Наконец, если допустить, что
и
, то получаем, что

.

Это означает, что векторы иколлинеареы. Но это не верно, так как они перпендикулярны. Следовательно, остается, что
,
, что и требовалось доказать.

Таким образом, координаты вектора полностью определяют сам вектор. Зная координаты ивектораможно построить сам вектор, построив векторы
и
и сложив их. Поэтому часто сам векторобозначают в виде пары его координат и пишут
. Такая запись означает, что
.

Непосредственно из определения координат вектора следует следующая теорема.

Теорема.

При сложении векторов их координаты складываются а при умножении вектора на число его координаты умножаются на это число. Записываются эти утверждения в виде

.

Доказательство.

,

Теорема.

Пусть
, причем начало вектора точкаимеет координаты
, а конец вектора есть точка
. Тогда координаты вектора связаны с координатами его концов следующими соотношениями

,

.

Доказательство.

Пусть
и пусть вектор-проекция векторана осьсонаправлен с осью(см. рис. 22). Тогда

так как длина отрезка на числовой осиравна координате правого конца минус координата левого конца. Если вектор

противонаправлен оси(как на Рис. 23), то

Рис. 23.

Если
, то в этом случае
и тогда получаем

.

Таким образом, при любом расположении вектора
относительно осей координат его координатаравна

.

Аналогично доказывается, что

.

Пример.

Даны координаты концов вектора
:
. Найти координаты вектора
.

Решение.

В следующей теореме приводится выражение длины вектора через его координаты.

Теорема 15.

Пусть
.Тогда

.

Доказательство.

Пусть и- вектор-проекции векторана осии, соответственно. Тогда, как показано при доказательстве теоремы 9, имеет место равенство

.

При этом, векторы ивзаимно перпендикулярны. При сложении этих векторов по правилу треугольника получаем прямоугольный треугольник (см. Рис. 24).

По теореме Пифагора имеем

.

,

.

Следовательно

,

.

.

.

Пример.

.Найти.

Введем понятие направляющих косинусов вектора.

Определение.

Пусть вектор
составляет с осьюугол, а с осьюугол(см. Рис. 25).

,

.

Следовательно,

Так как для любого вектора имеет место равенство

,

Где — орт вектора, то есть вектор единичной длины, сонаправленный с вектором, то

Вектор определяет направление вектора. Его координаты
и
называются направляющими косинусами вектора. Направляющие косинусы вектора можно выразить через его координаты по формулам

,

.

Имеет место соотношение

.

До настоящего момента в этом параграфе считалось, что все векторы располагаются в одной и той же плоскости. Теперь сделаем обобщение для векторов в пространстве.

Будем считать, что в пространстве задана Декартова система координат с осями ,и.

Орты осей ,ибудем обозначать символами,и, соответственно (Рис. 26).

Можно показать, что все понятия и формулы, которые были получены для векторов на плоскости, обобщаются для

Рис. 26.

векторов в пространстве. Тройка векторов
называется ортонормированным базисом в пространстве.

Пусть ,и- вектор-проекции векторана оси,и, соответственно. Тогда

.

В свою очередь

,

,

.

Если обозначить

,

,

,

То получаем равенство

.

Коэффициенты перед базисными векторами ,иназываются координатами вектора. Таким образом, для любого векторав пространстве существует тройка чисел,,, называемых координатами векторатаких, что для этого вектора справедливо представление

.

Вектор в этом случае также обозначают в виде
. При этом, координаты вектора равны проекциям этого вектора на координатные оси

,

,

,

где — угол между вектороми осью,- угол между вектороми осью,- угол между вектороми осью.

Длина вектора выражается через его координаты по формуле

.

Справедливы утверждения о том, что равные векторы имеют равные координаты, при сложении векторов их координаты складываются, а при умножении вектора на число его координаты умножаются на это число.
,
и
называются направляющими косинусами вектора. Они связаны с координатами вектора формулами

,
,
.

Отсюда следует соотношение

Если концы вектора
имеют координаты
,
, то координаты вектора
связаны с координатами концов вектора соотношениями

,

,

.

Пример.

Даны точки
и
. Найти координаты вектора
.

vector — Translation into Russian — examples English

Premium History Favourites

Advertising

Download for Windows It’s free

Download our free app

Advertising

Advertising

No ads with Premium

Suggestions: vector control

These examples may contain rude words based on your search.

These examples may contain colloquial words based on your search.

вектор m переносчик m направление n

курс m

переносчик инфекции m

векторный

векторизовать

Vector борьбы с переносчиками болезней

радиус-вектор

Suggestions

660

vector space 294

vector graphics 546

multi-vector 474

vector of development 354

vector-borne 338

vector-borne diseases 242

interrupt vector table

vector flux

There are disclosed expression vector and cloning vector containing this polynucleotide, and host cells containing the above expression vector.

Раскрыты вектор экспрессии и клонирующий вектор, содержащие этот полинуклеотид, и клетки-хозяева, содержащие указанный вектор экспрессии.

When a message vector is received, the syndrome vector is calculated.

После того как получен вектор, вычисляется его синдром.

This vector represents the initial vector, which displays the resting potential in the measurement and is used as the base vector for calibration of the measuring device.

Этот вектор представляет собой начальный вектор, который отображает потенциал покоя при измерении и применяется в качестве базисного вектора для калибровки измерительного устройства.

A vector can be of any type, for example a recombinant vector such as an expression vector.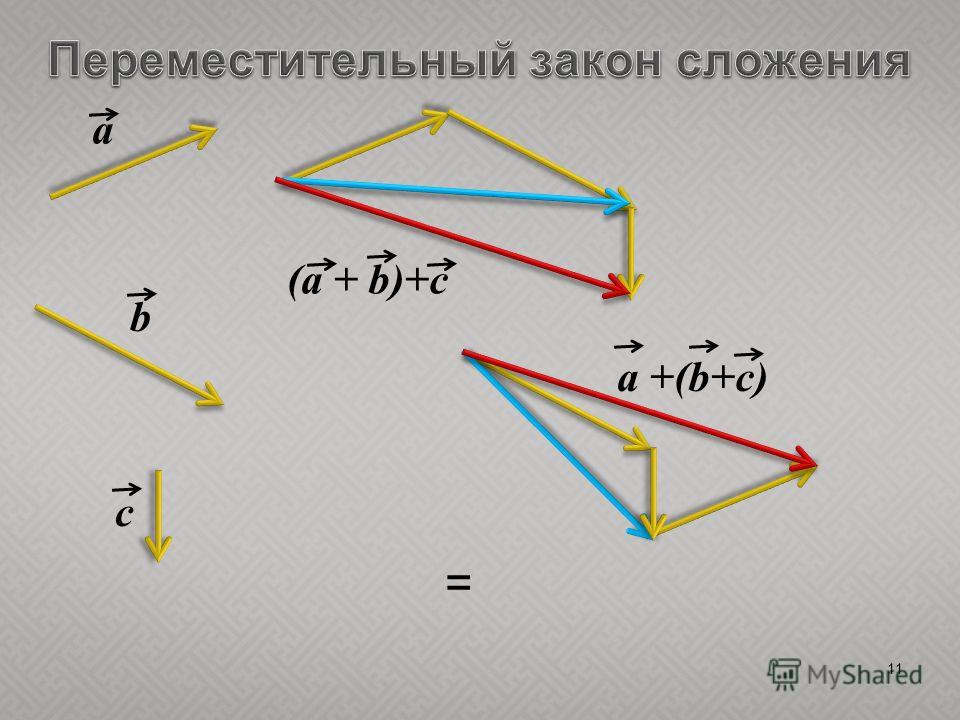

Вектор может быть любого типа, например рекомбинантный вектор, такой как вектор экспрессии.

Each sender has a different, unique vector v chosen from that set, but the construction method of the transmitted vector is identical.

Каждый отправитель имеет другой, уникальный вектор V выбран из этого набора, но метод строительства переданного вектора совпадает.

So they need a vector — and this vector, it’s normally an animal.

Поэтому им нужен вектор, и этим вектором обычно выступает животное.

Let’s say someone gives you a vector v that isn’t a unit vector.

Допустим вам дан вектор v, который не является единичным вектором.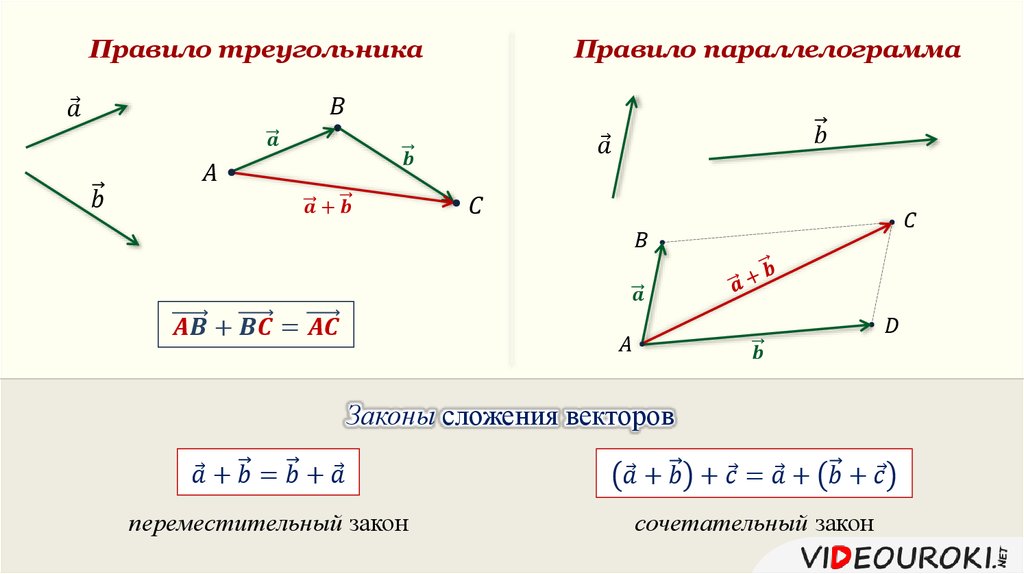

Note that a null vector is not the same as a zero vector.

Заметим, что светоподобный вектор не совпадает с нулевым вектором.

In pattern recognition and machine learning, a feature vector is an n-dimensional vector of numerical features that represent some object.

В распознавании образов и обучении машин вектор признаков является n-мерным вектором числовых признаков, который представляет некоторый объект.

After expiration of such a time interval, any newly detected vector may be considered a new initial vector.

По истечении такого интервала времени любой вновь обнаруженный вектор можно рассматривать в качестве нового исходного вектора.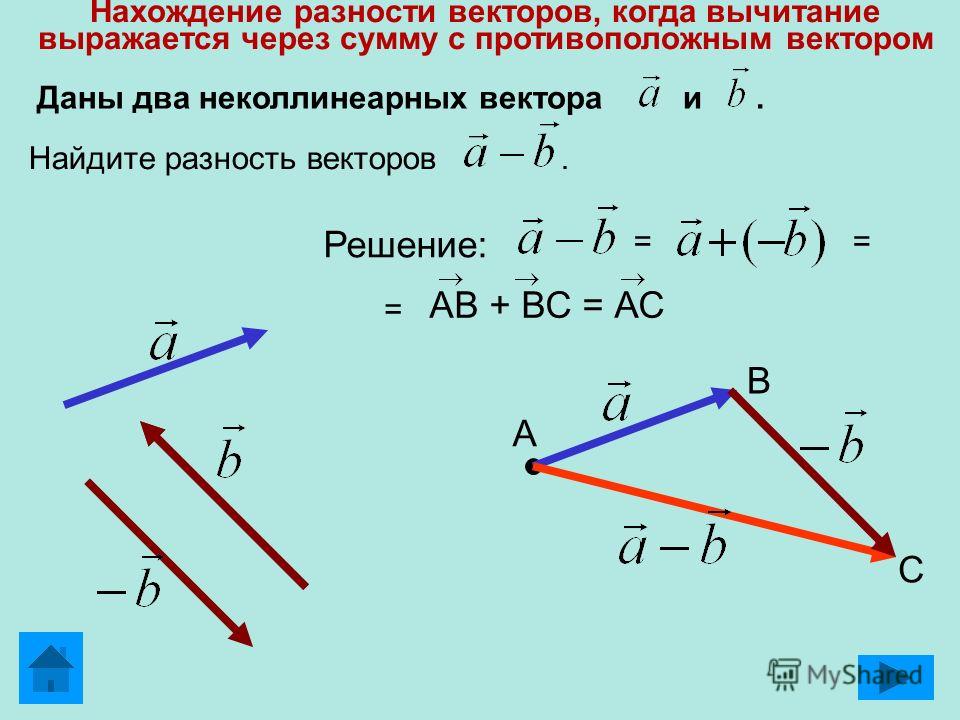

Described are: an isolated coding nucleic acid, and expression vector and a method for producing the antibody with the use of the above vector.

Описаны: изолированная кодирующая нуклеиновая кислота, вектор экспрессии и способ получения антитела с использованием указанного вектора.

Supervised learning assumes that for each input vector there is a target vector representing the required output.

Обучение с учителем предполагает, что для каждого входного вектора существует целевой вектор, представляющий собой требуемый вы-ход.

Any plane is uniquely defined by vector perpendicular to it, called a normal vector.

Любой ненулевой вектор, перпендикулярный плоскости, называется ее нормальным вектором.

According to our hypothesis, the conversion of electrons and positrons into each other occurs by replacing the charge motion vector with the opposite vector.

По нашей гипотезе превращение электронов и позитронов друг в друга происходит посредством замены вектора движения электрона на противоположный вектор.

For any vector there is an opposite vector:.

Для любого вектора существует противоположный ему вектор:.

Subtracts the second vector from the first vector.

То есть из второго вектора импульса отнять первый вектор.

The zero vector has no specific direction, but it is considered collinear with any other vector.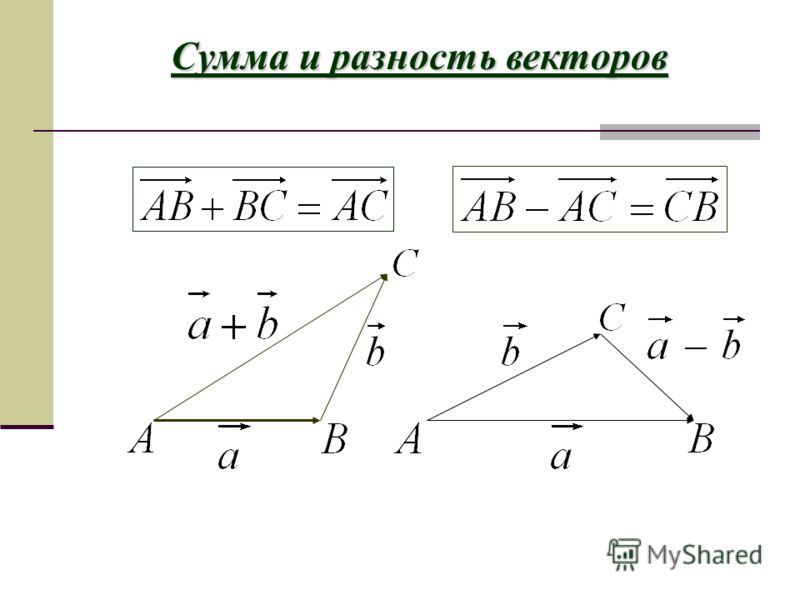

Так как нулевой вектор не имеет определённого направления, его можно считать ортогональным к любому другому вектору.

The vector representing that tap may be stored as a reference vector.

Вектор, представляющий это постукивание, можно хранить в качестве контрольного вектора.

The average vector in the interval of rest is defined as a vector basis for calibration of the measuring device.

Средний вектор в интервале покоя определяется как базисный вектор для калибровки измерительного устройства.

The vector having unit magnitude is called unit vector.

Вектор единичной длины называют единичным вектором.

Possibly inappropriate content

Examples are used only to help you translate the word or expression searched in various contexts. They are not selected or validated by us and can contain inappropriate terms or ideas. Please report examples to be edited or not to be displayed. Rude or colloquial translations are usually marked in red or orange.

Register to see more examples It’s simple and it’s free

Register Connect

No results found for this meaning.

vector control 660

vector space 294

vector graphics 546

multi-vector 474

vector of development 354

vector-borne 338

vector-borne diseases 242

interrupt vector table

vector flux

More features with our free app

Voice and photo translation, offline features, synonyms, conjugation, learning games

Results: 10873.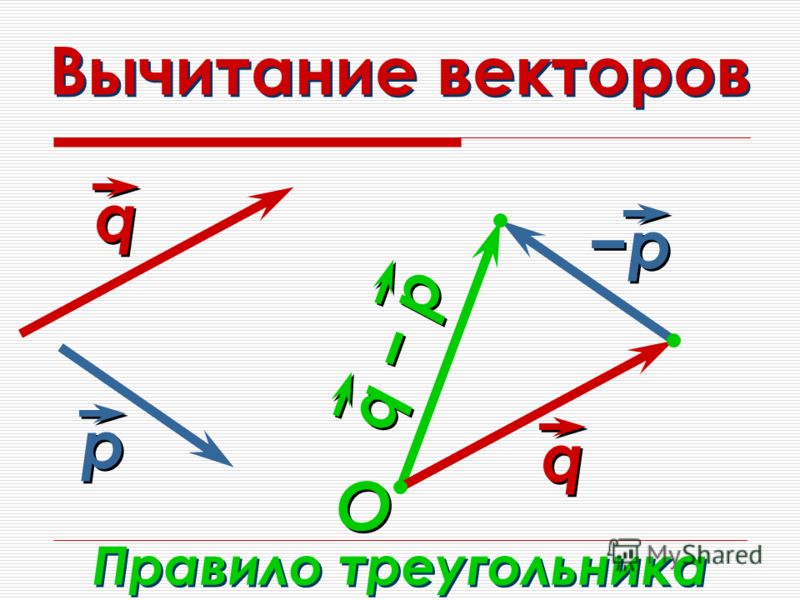 Exact: 10873. Elapsed time: 219 ms.

Documents Corporate solutions Conjugation Synonyms Grammar Check Help & about

Word index: 1-300, 301-600, 601-900

Expression index: 1-400, 401-800, 801-1200

Phrase index: 1-400, 401-800, 801-1200

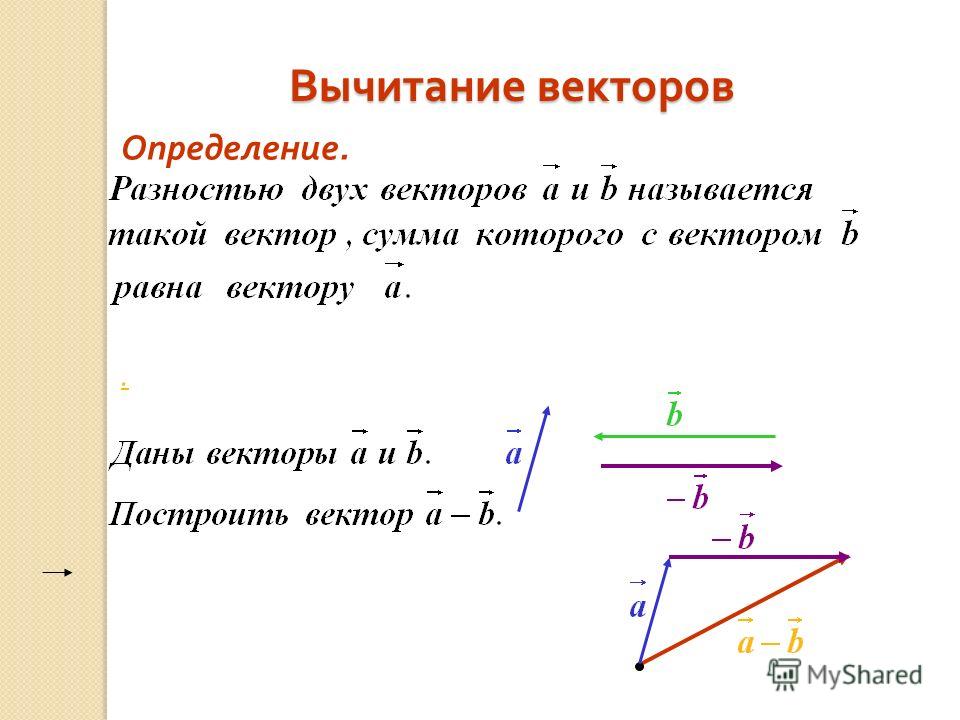
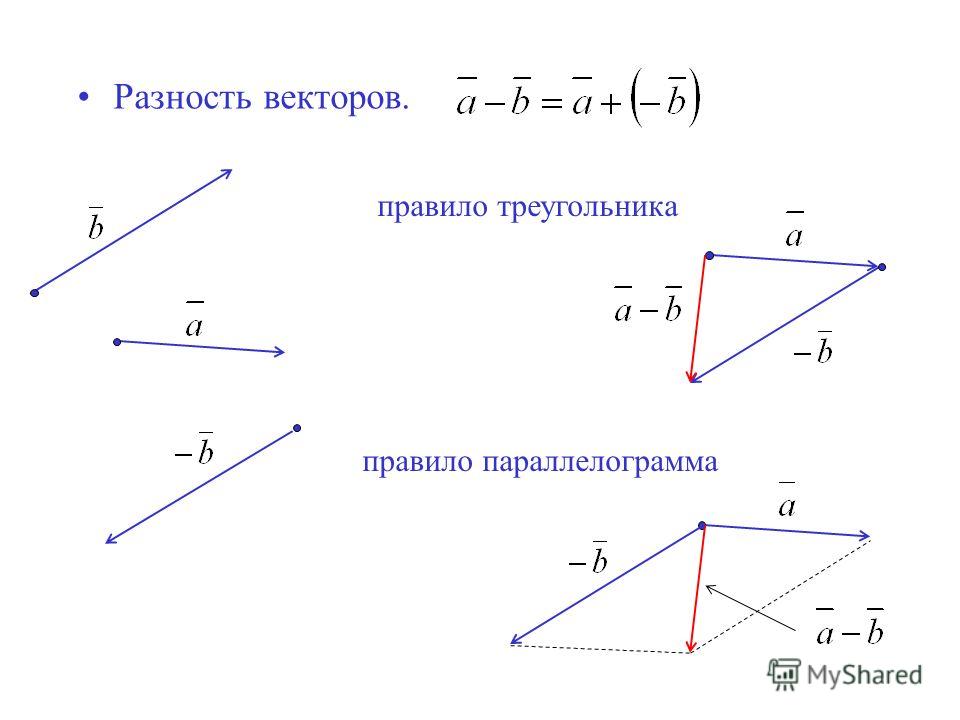
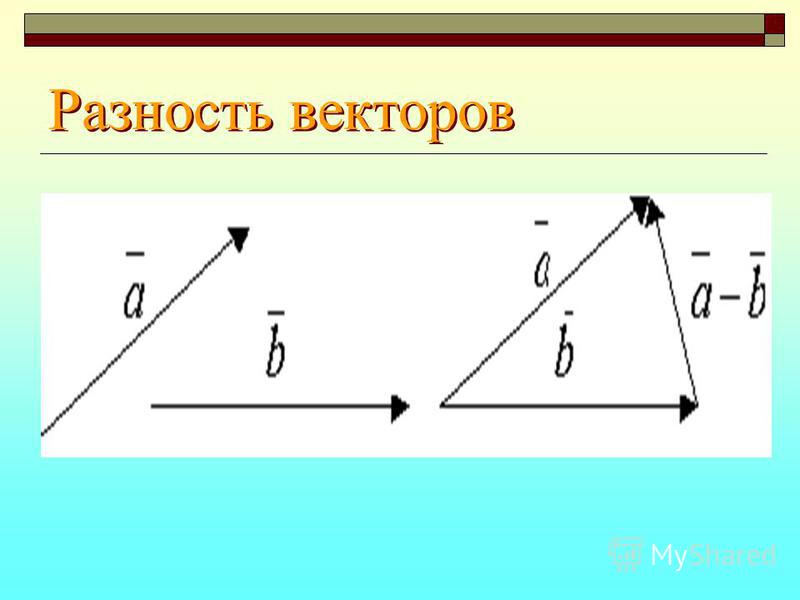
Вычитание векторов Важные понятия и советы по подготовке к экзамену JEE

Вектор можно определить как величину, измерение или объект, который имеет как величину, так и направление. Это одно из самых важных и основных понятий в физике, которое находит свое применение почти во всех разделах предмета. Вектор можно представить геометрически как направленный отрезок. Длина сегмента линии соответствует величине вектора, а наконечник стрелки соответствует направлению вектора. Направление любого вектора определяется от его хвоста к его голове, где находится стрелка.

Наиболее распространенные примеры векторных величин включают силу, скорость, ускорение, перемещение, импульс, электрическое поле и т.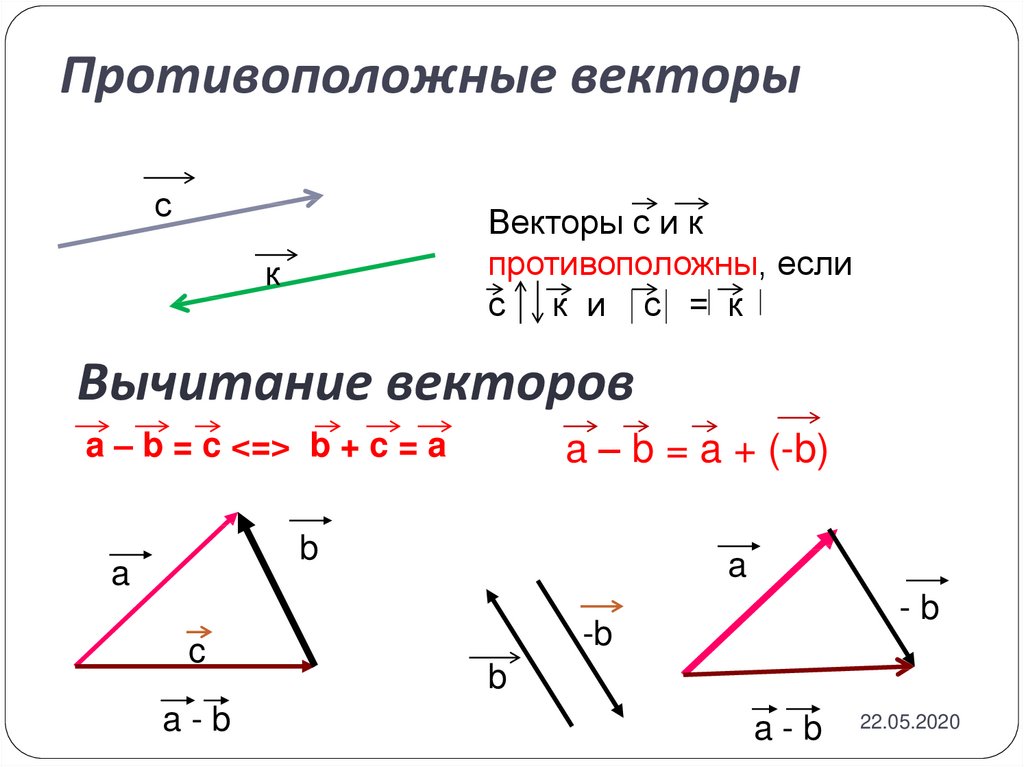 д. К векторам можно применять основные алгебраические операции, но для этих операций существуют свои правила. Мы не можем складывать или вычитать векторы, как мы складываем или вычитаем числа. У векторов тоже есть направления, так что это нужно учитывать. В этой статье мы подробно рассмотрим, как вычитать векторы.

Изображение: геометрическое представление вектора

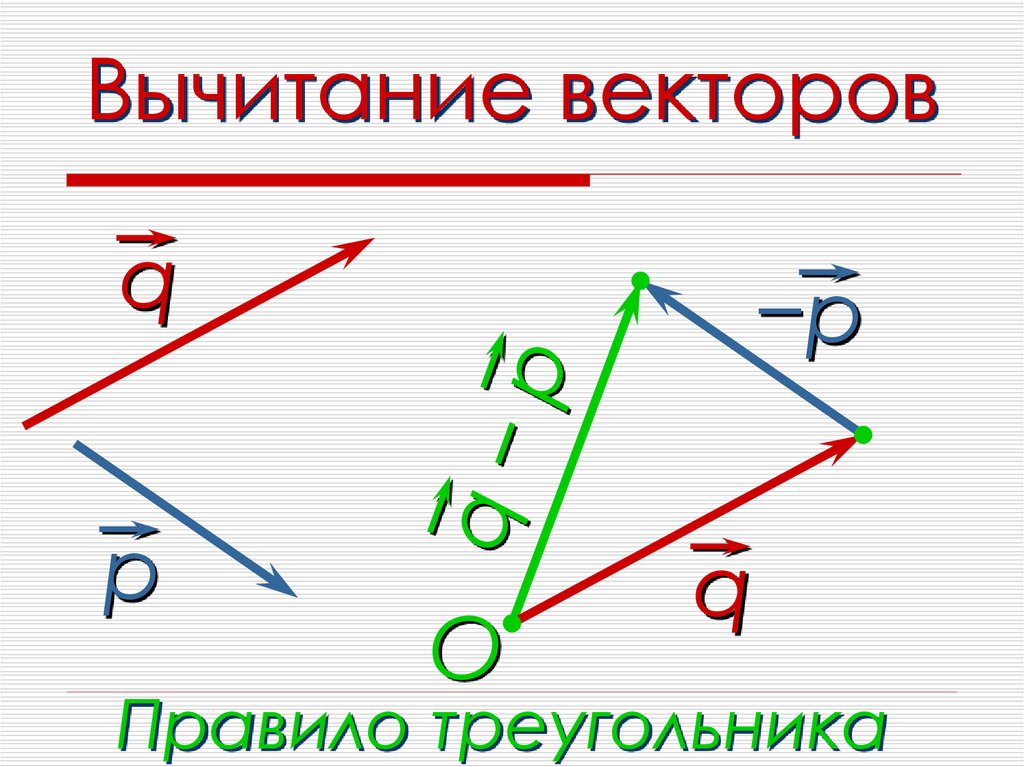
Что такое вычитание векторов?

Предположим, что есть векторы a и b. Вычитание этих векторов представлено как, a-b. Простыми словами, это просто добавление вектора -b к вектору a. Его можно записать как

a-b=a+(-b)

Вычитание векторов можно представить как добавление вектора к другому вектору после поворота его на 180° в пространстве. Вычитание векторов включает в себя сложение векторов и отрицание любого вектора. Очевидно, что вычитание двух векторов даст в результате вектор. Можно выделить два правила вычитания векторов.

• Вычитание векторов может выполняться только между двумя векторами.

• Вычитаемые векторы должны представлять одну и ту же физическую величину, иначе их нельзя вычесть.

Параллелограмм Закон вычитания векторов

Продолжим с теми же векторами a и b. Эти векторы можно визуализировать в пространстве, как показано на диаграмме, приведенной ниже. Чтобы применить закон параллелограмма, векторы должны быть котерминальными или их начальные точки должны совпадать.

 

 Изображение: параллелограммный закон вычитания векторов

Основной вопрос перед началом вычитания: как понять, что означает вычитание этих векторов. Вычитание представляет собой a-b, и когда к этому вычитанию добавляется b, ответ должен быть a. Это можно представить как

(a-b)+b=a

На приведенном выше рисунке показаны векторы a и b. Теперь вычитание в основном означает добавление -b к a. Если мы повернем вектор b на 180°, а затем добавим его к a, мы получим ответ. Рисунок ниже помогает визуализировать этот процесс.

Теперь, образуя параллелограмм путем построения линий вокруг двух векторов, мы получим параллелограмм, как показано на рисунке выше. Тогда диагональ, проведенная из начальной точки векторов в противоположную вершину, даст равнодействующую, в данном случае, вычитание. Таким образом, у нас есть результирующая, a-b по закону параллелограмма.

Треугольный закон вычитания векторов

Чтобы использовать треугольный закон вычитания векторов, векторы не обязательно должны иметь одну и ту же начальную точку. Начальная точка одного вектора должна быть в конечной точке предыдущего вектора. Затем результирующая векторов или сумма этих векторов будет проведена от начальной точки первого вектора до конечной точки последнего вектора. Для вычитания второй вектор следует повернуть на 180°, а затем можно применить закон треугольника, чтобы получить результат или вычитание этих векторов.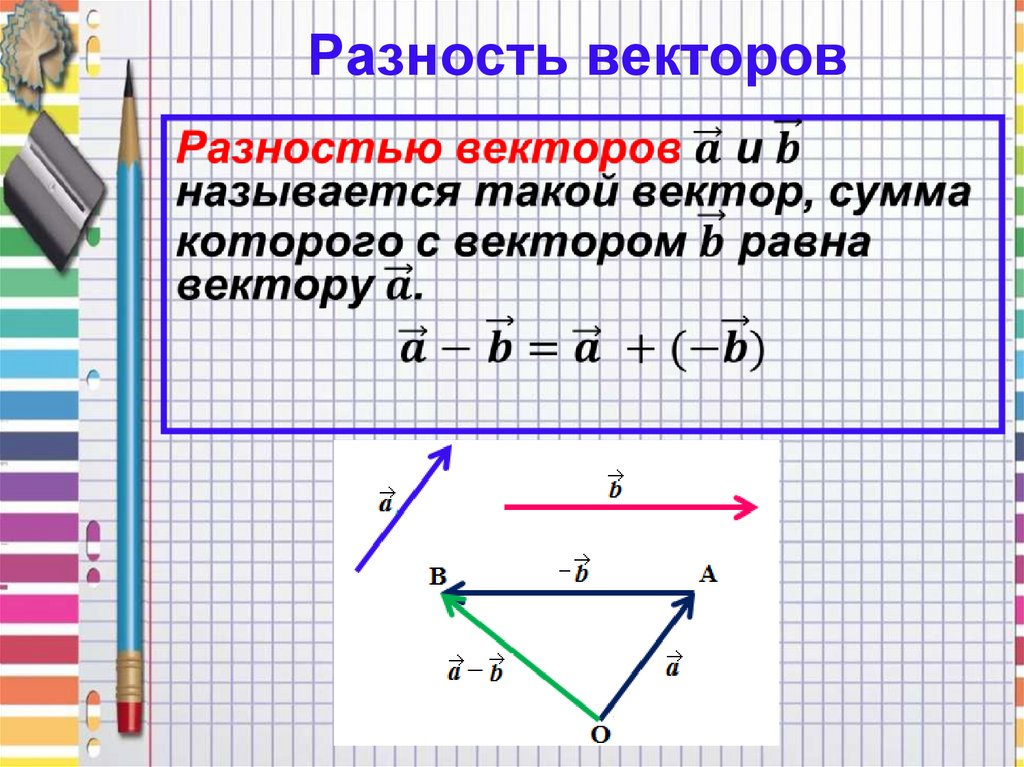

Его можно визуализировать с помощью рисунка ниже.

Изображение: Закон треугольника для векторного вычитания

Здесь вектор b был повернут на 180°, а затем результирующая проведена от начальной точки a до вершины -b, чтобы получить a-b.

Формула вычитания векторов

Продолжим работу с векторами a и b. Помимо графических способов вычитания векторов, их также можно вычитать, вычитая их соответствующие компоненты друг из друга. Пусть,

a={a1, a2} 

b={b1, b2}

Соответствующие компоненты можно вычесть, чтобы получить a-b.

a-b=a+(-b) 

a-b={(a1-b1), (a2-b2)}

Это формула вычитания векторов. Это может быть распространено на любое количество компонентов, которые имеет вектор.

Давайте рассмотрим пример вычитания векторов, чтобы лучше понять ситуацию.

Предположим, что a={3,5}, а b={2,6}.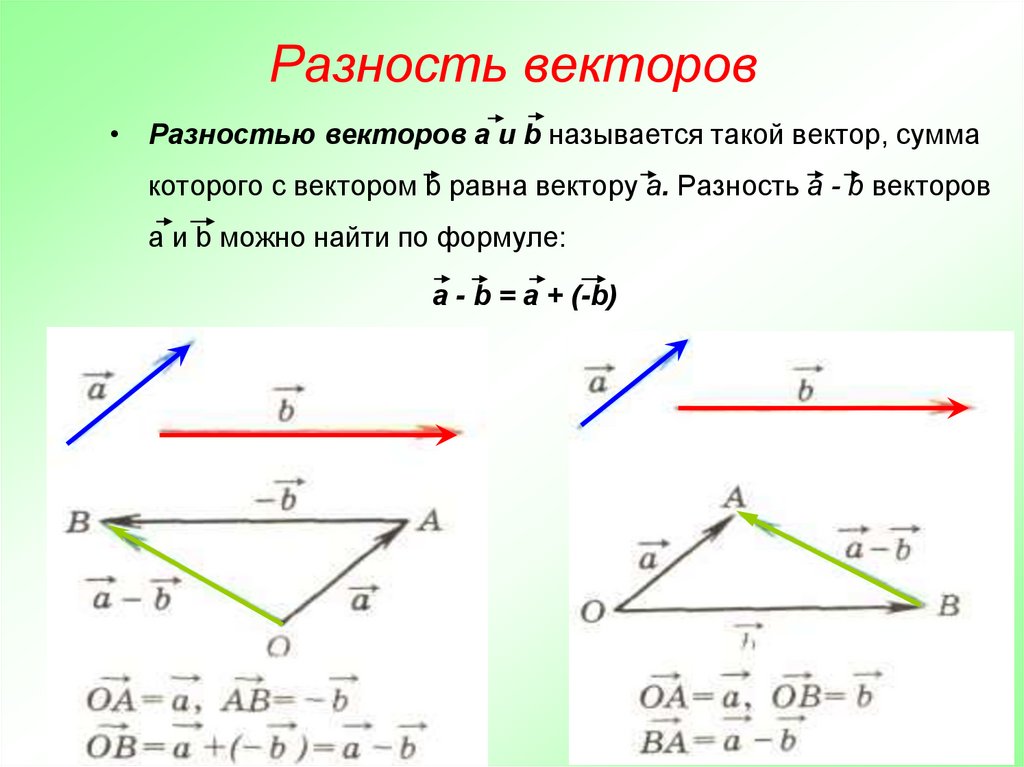

Вычитание будет дано как

a-b={(3-2), (5-6)} 

a-b={1, -1}

Важно знать, каким законам подчиняется вычитание векторов. Вычитание векторов подчиняется закону распределения, то есть

a(b-c)=ab-ac

Здесь a, b и c – векторы.

Заключение

Вычитание векторов аналогично прибавлению реверса или инверсии одного вектора к другому вектору. Закон вычитания параллелограмма можно использовать для вычисления вычитания векторов, нарисовав параллелограмм, взяв два вектора с одной и той же начальной точкой. Тогда равнодействующую можно провести как диагональ из начальной точки в противоположную вершину.

Точно так же закон треугольника можно использовать для нахождения вычитания векторов. Векторы должны быть расположены таким образом, чтобы начальная точка второго вектора находилась на вершине первого вектора, а затем проводилась результирующая от начальной точки первого вектора к вершине второго вектора.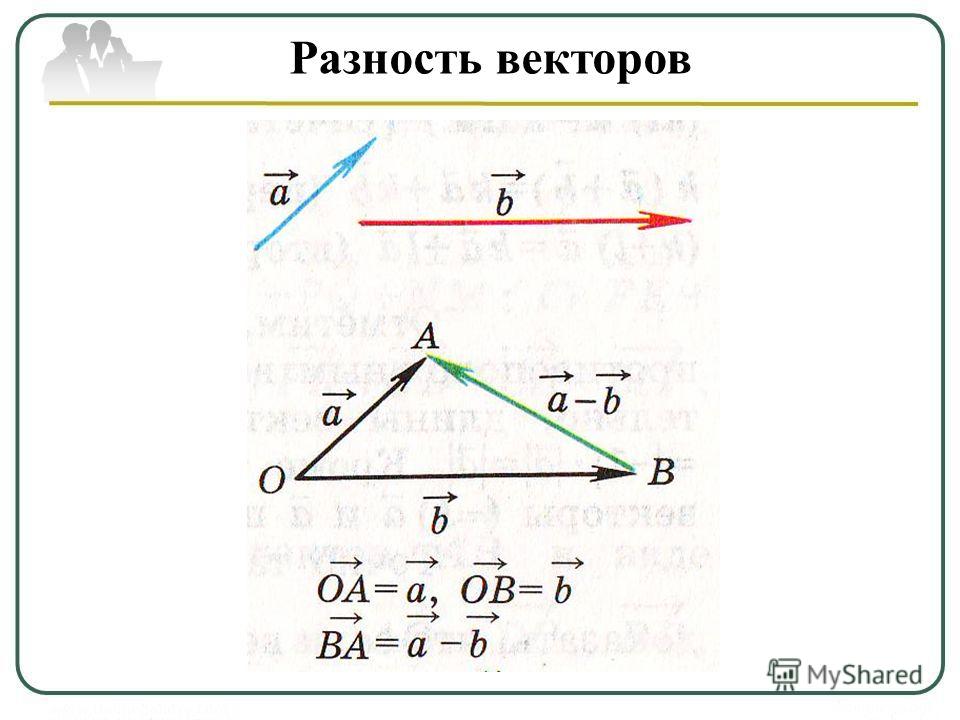 Кроме того, отдельные компоненты могут быть вычтены, чтобы получить вычитание.

Сложение и вычитание векторов: графические методы

Векторы в двух измерениях

Вектор — это величина, которая имеет величину и направление. Например, перемещение, скорость, ускорение и сила — все это векторы. В одномерном или прямолинейном движении направление вектора может быть задано просто знаком плюс или минус. Однако в двух измерениях (2-d) мы указываем направление вектора относительно некоторой системы отсчета (т. е. системы координат), используя стрелку, длина которой пропорциональна величине вектора и указывает направление вектора.

На рисунке 2 показано графическое представление вектора на примере полного перемещения человека, идущего по городу, рассматриваемого в книге «Кинематика в двух измерениях: введение». Мы будем использовать обозначение, что жирный символ, такой как D , обозначает вектор. Его величина представлена ​​выделенным курсивом символом D , а его направление — θ .

Векторы в этом тексте

В этом тексте мы будем представлять вектор с переменной, выделенной жирным шрифтом. Например, мы представим количественную силу вектором F , который имеет как величину, так и направление. Величина вектора будет представлена ​​переменной, выделенной курсивом, например, F , а направление переменной будет задано углом θ .

Рисунок 2. Человек проходит 9 кварталов на восток и 5 кварталов на север. Смещение 10,3 блока под углом 29,1º к северу от востока.

Рис. 3. Для графического описания результирующего вектора пешехода, идущего по городу, изображенному на рис. 2, нарисуйте стрелку, обозначающую вектор полного перемещения Д . Используя транспортир, нарисуйте линию под углом θ  относительно оси восток-запад. Длина D  стрелки пропорциональна модулю вектора и измеряется вдоль линии с помощью линейки. В этом примере величина D вектора составляет 10,3 единицы, а направление θ составляет 29,1º к северу от востока.

Сложение векторов: метод «голова к хвосту»

Метод «голова к хвосту» представляет собой графический способ добавления векторов, описанный на Рисунке 4 ниже и в следующих шагах. хвост вектора является начальной точкой вектора, а наконечник (или кончик) вектора является конечным заостренным концом стрелки.

Рис. 4. Метод «голова к хвосту». Метод графического сложения векторов «голова к хвосту» проиллюстрирован для двух перемещений человека, идущего по городу, показанного на рисунке 2. (a) Нарисуйте вектор, представляющий перемещение на восток. (b) Нарисуйте вектор, представляющий смещение на север. Хвост этого вектора должен исходить из головы первого вектора, указывающего на восток. (c) Проведите линию от хвоста вектора, указывающего на восток, до начала вектора, указывающего на север, чтобы получить сумму или результирующий вектор D . Длина стрелки D пропорциональна модулю вектора и составляет 10,3 единицы. Его направление, описываемое как угол относительно востока (или горизонтальной оси) θ, измеренное с помощью транспортира, равно 29,1º.

Шаг 1. Нарисуйте стрелку, представляющую первый вектор (9 блоков на восток), используя линейку и транспортир .

Рисунок 5

Шаг 2. Теперь нарисуйте стрелку, обозначающую второй вектор (5 кварталов на север). Поместите конец второго вектора в начало первого вектора .

Рисунок 6

Шаг 3. Если имеется более двух векторов, продолжайте этот процесс для каждого добавляемого вектора. Обратите внимание, что в нашем примере у нас есть только два вектора, поэтому мы закончили размещать стрелки от начала до конца .

Шаг 4. Проведите стрелку от хвоста первого вектора к началу последнего вектора . Это равнодействующее или сумма других векторов.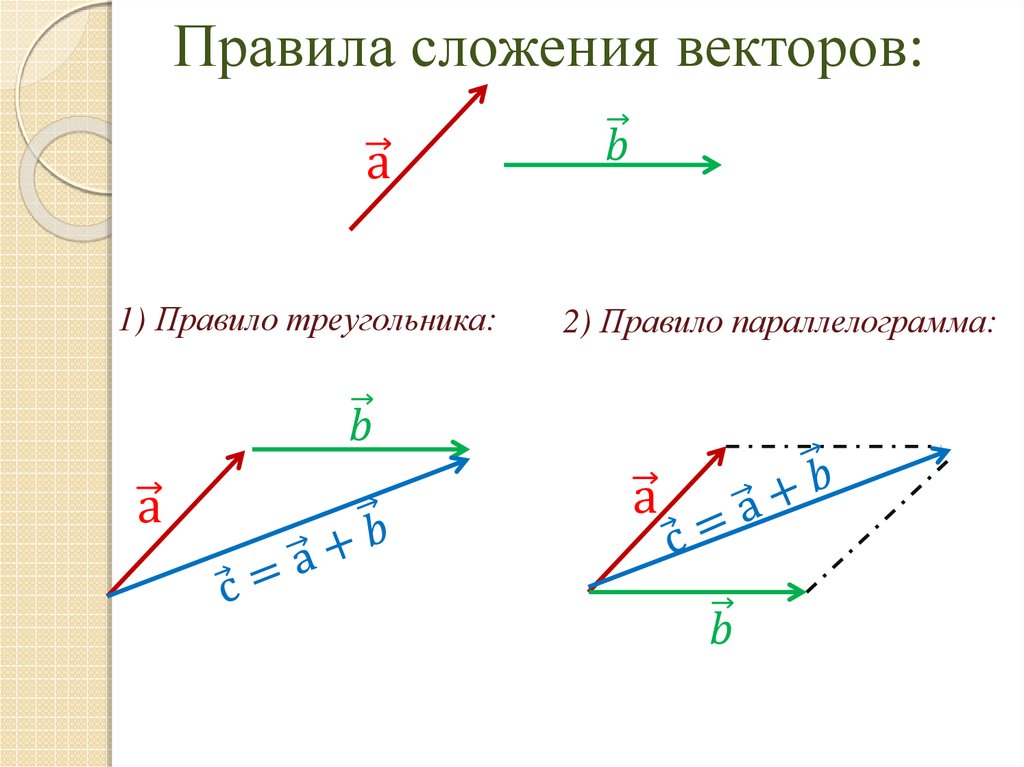

Рисунок 7

 

Шаг 5. Чтобы получить величину равнодействующей , измерьте ее длину линейкой. (Обратите внимание, что в большинстве расчетов мы будем использовать теорему Пифагора для определения этой длины.)

Шаг 6. Чтобы получить направление равнодействующей, измерьте угол, который она образует с системой отсчета. с помощью транспортира. (Обратите внимание, что в большинстве расчетов мы будем использовать тригонометрические отношения для определения этого угла.)

Точность графического сложения векторов ограничена только точностью, с которой могут быть выполнены чертежи, и точностью измерительных инструментов. Это справедливо для любого количества векторов.

Пример 1. Графическое сложение векторов с использованием метода «голова к хвосту»: прогулка женщины ровное поле. Сначала она проходит 25,0 м в направлении 49..0º к северу от востока.

Затем она проходит 23,0 м в направлении 15,0º к северо-востоку. Наконец, она поворачивается и проходит 32,0 м в направлении 68,0° к югу от востока.

Стратегия

Представьте каждый вектор смещения графически стрелкой, обозначив первый A , второй B и третий C , делая длины пропорциональными расстоянию и направлениям, указанным относительно линия восток-запад. Описанный выше метод «голова к хвосту» позволит определить величину и направление результирующего смещения, обозначенного цифрой 9.0105 Р .

Решение

(1) Нарисуйте три вектора смещения.

Рис. 8.

(2) Разместите векторы от начала до конца, сохранив их первоначальную величину и направление.

Рис. 9.

(3) Нарисуйте результирующий вектор R .

Рисунок 10.

(4) Используйте линейку для измерения величины R и транспортир для измерения направления R .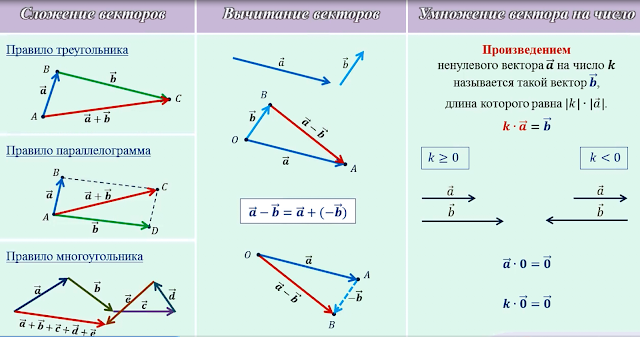 Хотя направление вектора можно указать разными способами, проще всего измерить угол между вектором и ближайшей горизонтальной или вертикальной осью. Поскольку результирующий вектор находится к югу от оси, направленной на восток, мы переворачиваем транспортир вверх ногами и измеряем угол между осью, направленной на восток, и вектором.

Рисунок 11

 

В этом случае видно, что полное смещение R имеет величину 50,0 м и направлено на 7,0º к югу от востока. Используя его величину и направление, этот вектор можно выразить как R = 50,0 м и θ = 7,0º к югу от востока.

Обсуждение

Графический метод сложения векторов «голова к хвосту» работает для любого количества векторов. Также важно отметить, что результирующая не зависит от порядка добавления векторов. Таким образом, мы можем добавлять векторы в любом порядке, как показано на рисунке 12, и все равно получим то же решение.

Рисунок 12.

Здесь мы видим, что при сложении одних и тех же векторов в другом порядке результат будет тот же. Эта характеристика верна в любом случае и является важной характеристикой векторов. Сложение векторов коммутативно . Векторы можно добавлять в любом порядке.

A + B = B + A

.

Это видео можно использовать для просмотра. Он включает в себя основы работы с векторами — рисование векторов/добавление векторов. Вы узнаете об основном понятии вектора, о том, как графически складывать векторы, а также о том, что графически означает умножение вектора на скаляр.

Вычитание векторов

Вычитание векторов является прямым расширением сложения векторов. Чтобы определить вычитание (скажем, мы хотим вычесть B из A, записанного A – B), мы должны сначала определить, что мы подразумеваем под вычитанием.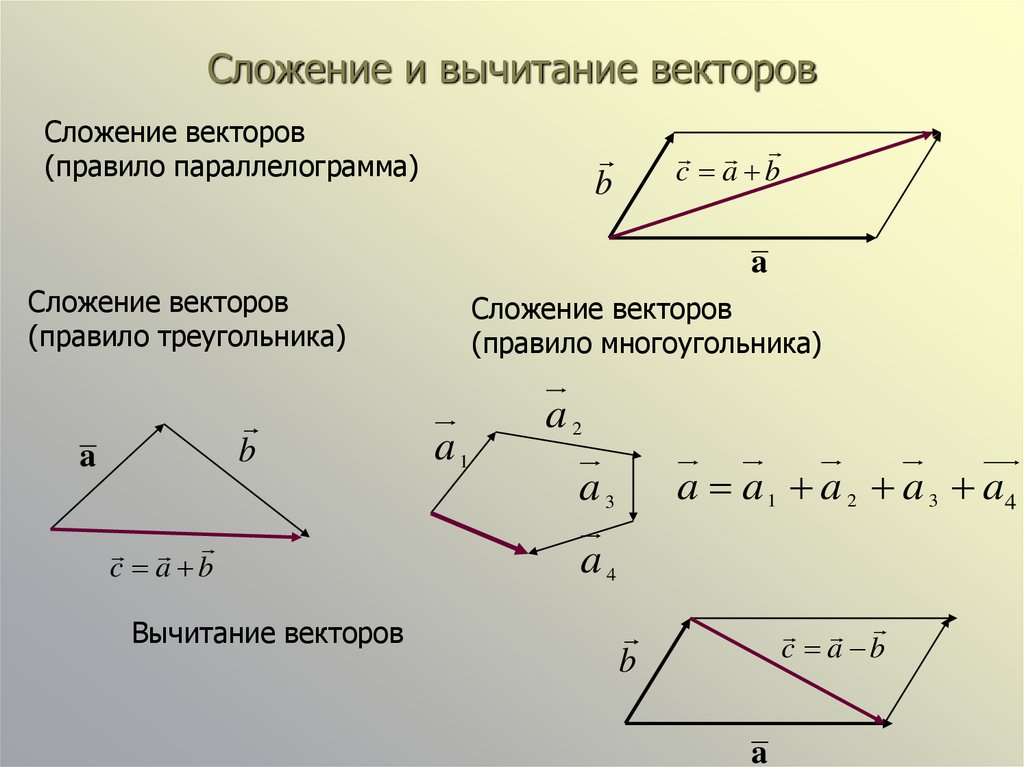 0099 минус вектора B определяется как –B; то есть графически отрицательный вектор любого вектора имеет ту же величину, но противоположное направление , как показано на рисунке 13. Другими словами, B имеет ту же длину, что и -B, но указывает в противоположном направлении. По сути, мы просто переворачиваем вектор так, чтобы он указывал в противоположном направлении.

Рис. 13. Отрицательное значение вектора — это просто другой вектор той же величины, но направленный в противоположном направлении. Итак, B — это минус 9.0105 –В ; он имеет ту же длину, но противоположное направление.

Вычитание вектора B из вектора A определяется как сложение –B с A . Обратите внимание, что вычитание вектора — это добавление отрицательного вектора. Порядок вычитания не влияет на результат.

A – B = A + (-B)

Это аналогично вычитанию скаляров (где, например, 5 – 2 = 5 + (–2)).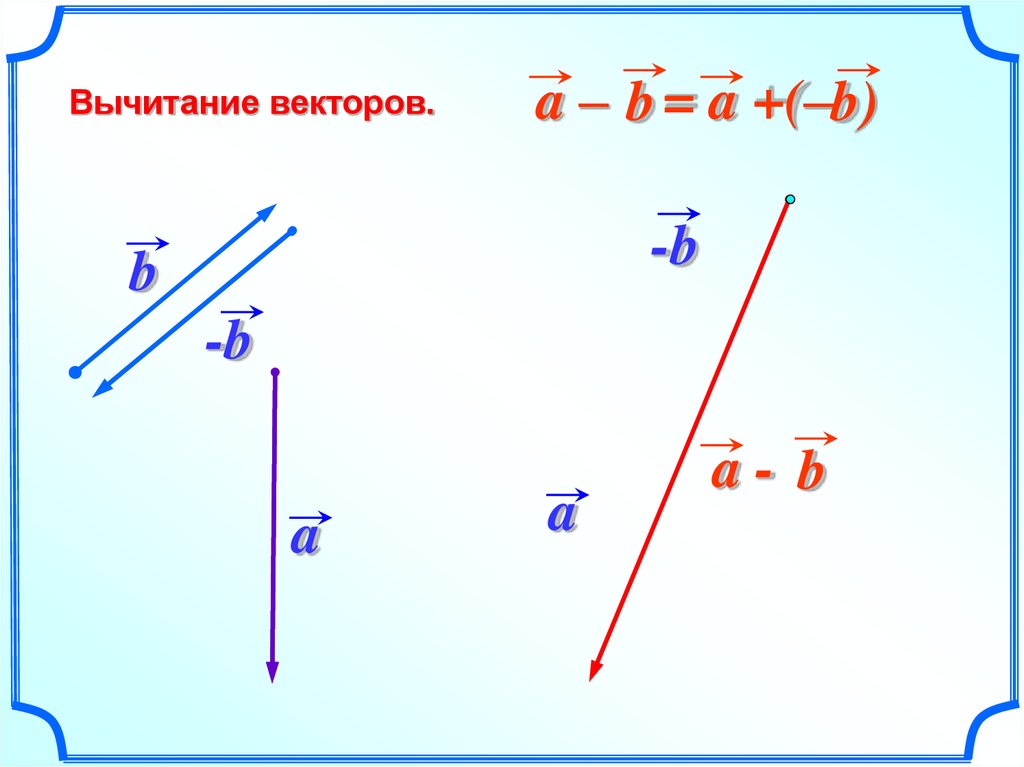 Опять же, результат не зависит от порядка, в котором производится вычитание. Когда векторы вычитаются графически, используются описанные выше методы, как показано в следующем примере.

Пример 2. Графическое вычитание векторов: женщина, плывущая на лодке

Женщина, плывущая на лодке ночью, следует указаниям к пристани. Инструкции гласили: сначала пройти 27,5 м в направлении 66,0° к северу от востока от ее текущего местоположения, а затем пройти 30,0 м в направлении 112° к северу от востока (или 22,0° к западу от севера). Если женщина совершит ошибку и поедет в направлении , противоположном , на второй этап поездки, где она окажется? Сравните это место с расположением дока.

Рисунок 14.

Стратегия

Мы можем представить первый этап поездки вектором A , а второй этап поездки вектором B . Док расположен по адресу A+B . Если женщина по ошибке едет в направлении , противоположном , для второго этапа путешествия, она проедет расстояние B (30,0 м) в направлении 180º–112º=68º к югу от востока.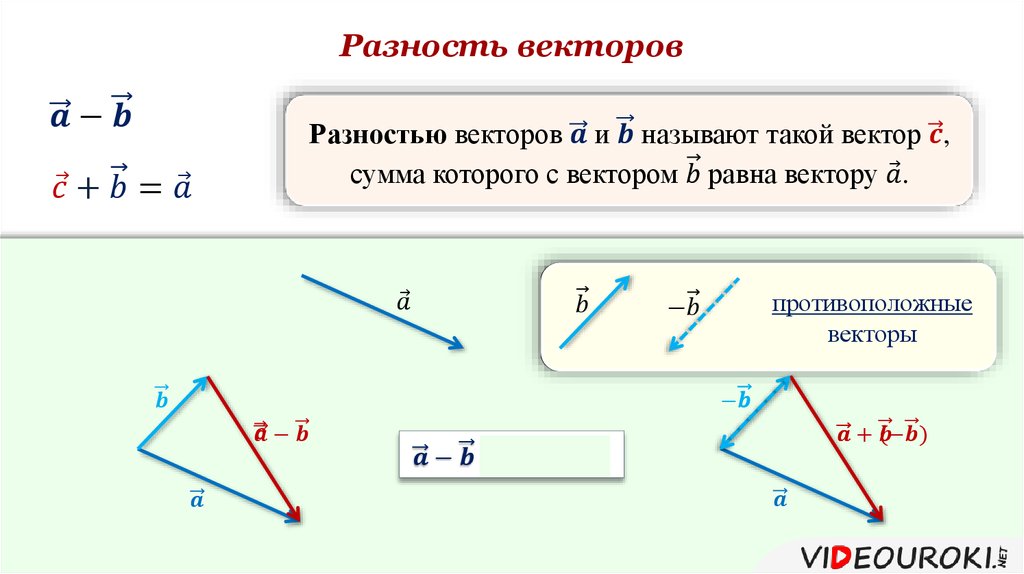 Мы представляем это как –B , как показано ниже. Вектор –B имеет ту же величину, что и B, но в противоположном направлении. Таким образом, она окажется в локации A + (–B) , или A – B .

Рисунок 15

 

Выполним сложение векторов, чтобы сравнить положение причала A + B с местом, куда по ошибке прибыла женщина, A + (-B) .

Решение

(1) Чтобы определить место, куда случайно попала женщина, нарисуйте векторы А и –В .

(2) Разместите векторы лицом к хвосту.

(3) Нарисуйте результирующий вектор R .

(4) С помощью линейки и транспортира измерьте величину и направление R .

Рисунок 16

В этом случае R = 23 . 0 м и θ = 7 . 5º к югу от востока.

(5) Чтобы определить местоположение дока, мы повторяем этот метод, чтобы добавить векторы A и B . Получаем результирующий вектор 9Рисунок 17

Мы видим, что женщина окажется на значительном расстоянии от пристани, если она отправится в противоположном направлении на второй этап поездки.

Обсуждение

Поскольку вычитание вектора аналогично сложению вектора с противоположным направлением, графический метод вычитания векторов работает так же, как и сложение.

Умножение векторов и скаляров

Если бы мы решили пройти в три раза больше расстояния на первом этапе пути, рассматриваемого в предыдущем примере, то мы бы прошли 3 × 27,5 м, или 82,5 м, в направлении 66,0 º к северу от востока. Это пример умножения вектора на положительный скаляр . Обратите внимание, что величина меняется, но направление остается прежним.

Если скаляр отрицательный, то умножение вектора на него изменяет величину вектора и дает новому вектору в противоположном направлении . Например, если умножить на -2, величина удвоится, но изменится направление.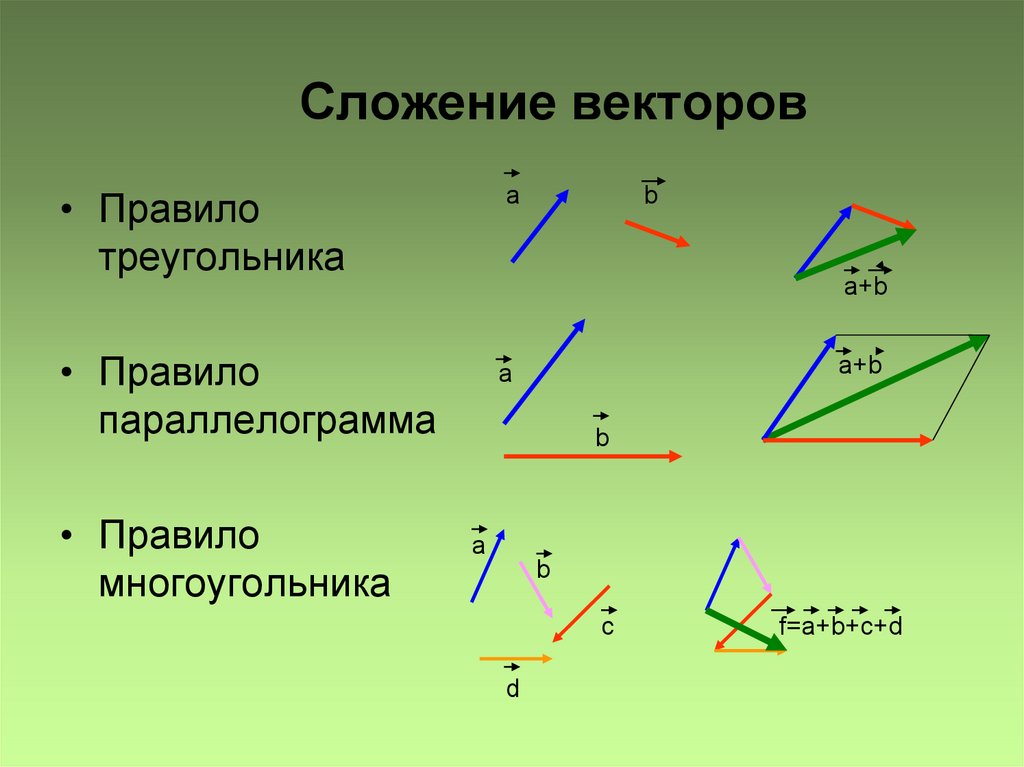 Мы можем обобщить эти правила следующим образом: когда вектор A умножается на скаляр c ,

• , величина вектора становится абсолютной величиной c A ,
• если c положительно, направление вектора не меняется,
• , если c отрицательно, направление меняется на противоположное.

В нашем случае c = 3 и A = 27,5 м. Векторы умножаются на скаляры во многих ситуациях. Обратите внимание, что деление является обратным умножению. Например, деление на 2 равносильно умножению на значение (1/2). Правила умножения векторов на скаляры такие же, как и при делении; просто рассматривайте делитель как скаляр от 0 до 1.

Разложение вектора на компоненты

В приведенных выше примерах мы добавляли векторы для определения результирующего вектора. Однако во многих случаях нам нужно будет сделать обратное. Нам нужно будет взять один вектор и найти, какие другие векторы, сложенные вместе, дают его.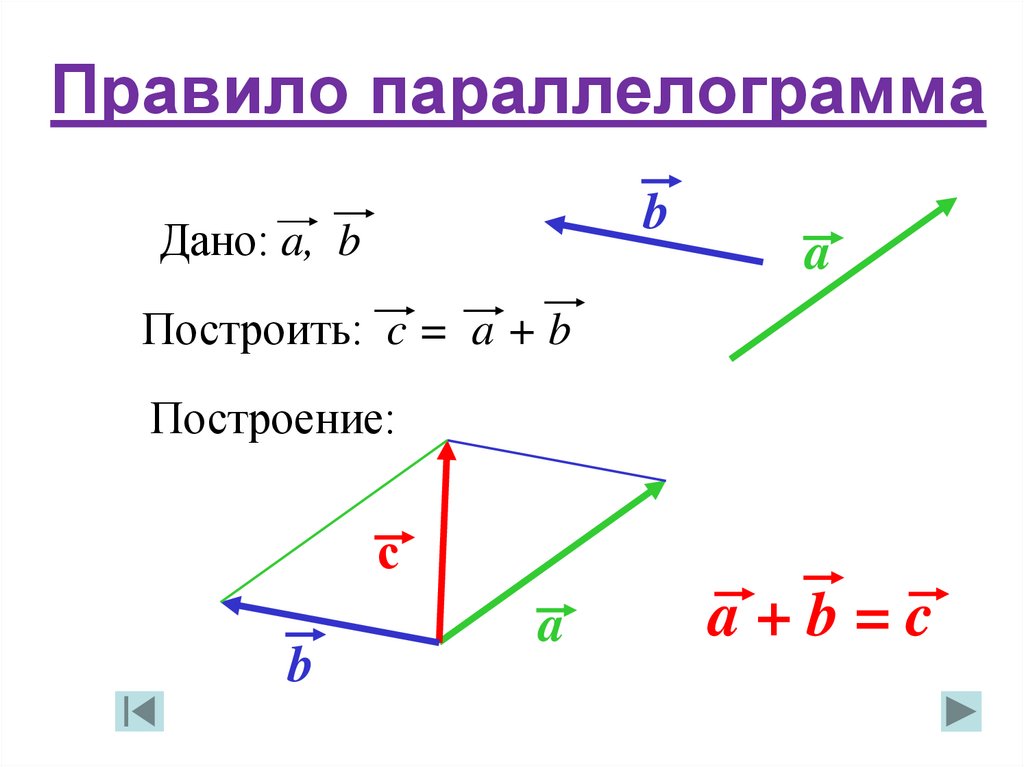 В большинстве случаев это связано с определением перпендикуляра компоненты одного вектора, например компоненты x – и y , или компоненты север-юг и восток-запад.

Например, мы можем знать, что общее перемещение человека, идущего по городу, составляет 10,3 квартала в направлении 29,0º к северу от востока, и мы хотим узнать, сколько кварталов ему пришлось пройти на восток и север. Этот метод называется нахождением компонентов (или частей) смещения в восточном и северном направлениях, и он является обратным процессу, используемому для нахождения полного смещения. Это один из примеров нахождения компонентов вектора. В физике есть много приложений, где это может оказаться полезным. Мы скоро увидим это в Projectile Motion и многое другое, когда рассмотрим заставляет в динамике: законы движения Ньютона. Большинство из них включают поиск компонентов вдоль перпендикулярных осей (например, север и восток), так что задействованы прямоугольные треугольники. Аналитические методы, представленные в разделе «Сложение и вычитание векторов: аналитические методы», идеально подходят для поиска компонентов вектора.

PhET Explorations: Maze Game

Узнайте о положении, скорости и ускорении на «Арене боли». Используйте зеленую стрелку, чтобы переместить мяч. Добавьте больше стен на арену, чтобы усложнить игру. Постарайтесь достичь цели как можно быстрее.

Нажмите, чтобы скачать. Запуск с использованием Java.

Резюме

• Графический метод сложения векторов   A и B включает в себя рисование векторов на графике и их сложение методом «голова к хвосту». Результирующий вектор R определяется так, что A + B = R . Величина и направление R затем определяются с помощью линейки и транспортира соответственно.
• Графический метод вычитания вектора B  из A включает добавление вектора, противоположного вектору B , который определяется как -B . В этом случае А – В = А + (-В) = R . Затем обычным образом применяется метод сложения головы к хвосту для получения результирующего вектора R .
• Сложение векторов коммутативно, так что A + B = B + A .
• Метод сложения векторов «голова к хвосту» включает в себя рисование первого вектора на графике, а затем размещение хвоста каждого последующего вектора в начале предыдущего вектора. Затем результирующий вектор рисуется из хвоста первого вектора в начало конечного вектора.
• Если вектор A  умножить на скалярную величину c , величина произведения будет равна cA . Если c положительно, направление произведения указывает на то же направление, что и A ; если c отрицательно, направление произведения указывает на направление, противоположное A .

Концептуальные вопросы

1. Что из следующего является вектором: рост человека, высота над уровнем моря на Эвересте, возраст Земли, температура кипения воды, стоимость этой книги, население Земли, ускорение свободного падения?

2. Приведите конкретный пример вектора, указав его величину, единицы измерения и направление.

3. Что общего между векторами и скалярами? Чем они отличаются?

4. Два отдыхающих в национальном парке отправляются из своей хижины в одно и то же место на озере, каждый по своему пути, как показано ниже. Общее расстояние, пройденное по Пути 1, составляет 7,5 км, а по Пути 2 — 8,2 км. Каково конечное перемещение каждого туриста?

Рисунок 18.

5. Если пилоту самолета велят пролететь 123 км по прямой, чтобы добраться из Сан-Франциско в Сакраменто, объясните, почему он может оказаться в любом месте круга, показанного на рисунке 19.. Какая еще информация ему понадобится, чтобы добраться до Сакраменто?

Рисунок 19.

6. Предположим, вы делаете два шага A и B (то есть два ненулевых перемещения). При каких обстоятельствах вы можете оказаться в исходной точке? В более общем смысле, при каких обстоятельствах два ненулевых вектора могут сложиться, чтобы получить ноль? Является ли максимальное расстояние, которое вы можете пройти от начальной точки A + B суммой длин двух шагов?

7. Объясните, почему нельзя добавить скаляр к вектору.

8. Если вы сделаете два шага разной длины, сможете ли вы оказаться в исходной точке? В более общем смысле, могут ли два вектора с разными величинами дать в сумме ноль? Можно три или больше?

Задачи и упражнения

Используйте графические методы для решения этих задач. Вы можете предположить, что данные, взятые из графиков, имеют точность до трех цифр.

1. Найдите следующее для пути A на рис. 20: (a) общее пройденное расстояние и (b) величину и направление смещения от начала до конца.

Рис. 20. Различные линии обозначают пути, по которым идут разные люди, идущие по городу. Все блоки со стороной 120 м.

2. Найдите следующее для пути B на рисунке 20: (a) общее пройденное расстояние и (b) величину и направление смещения от начала до конца.

3. Найдите северную и восточную составляющие смещения для туристов, показанных на Рисунке 20.

4. Предположим, вы прошли 18,0 м прямо на запад, а затем 25,0 м прямо на север. Как далеко вы находитесь от своей начальной точки и каково направление по компасу линии, соединяющей вашу начальную точку с вашим конечным положением? (Если вы представляете два этапа ходьбы как векторные смещения A и B , как на рисунке 21, то эта задача требует от вас найти их сумму R = A + B .

Рисунок 21. Два смещения A и B складываются, чтобы получить общее перемещение R , имеющее величину R и направление θ .

5. Предположим, вы сначала прошли 12,0 м в направлении 20° к западу от севера, а затем 20,0 м в направлении 40,0° к югу от запада. Как далеко вы находитесь от своей начальной точки и каково направление по компасу линии, соединяющей вашу начальную точку с вашим конечным положением? (Если вы представляете два этапа ходьбы как векторные смещения A и B , как на рисунке 22, то эта задача находит их сумму R = A + B . )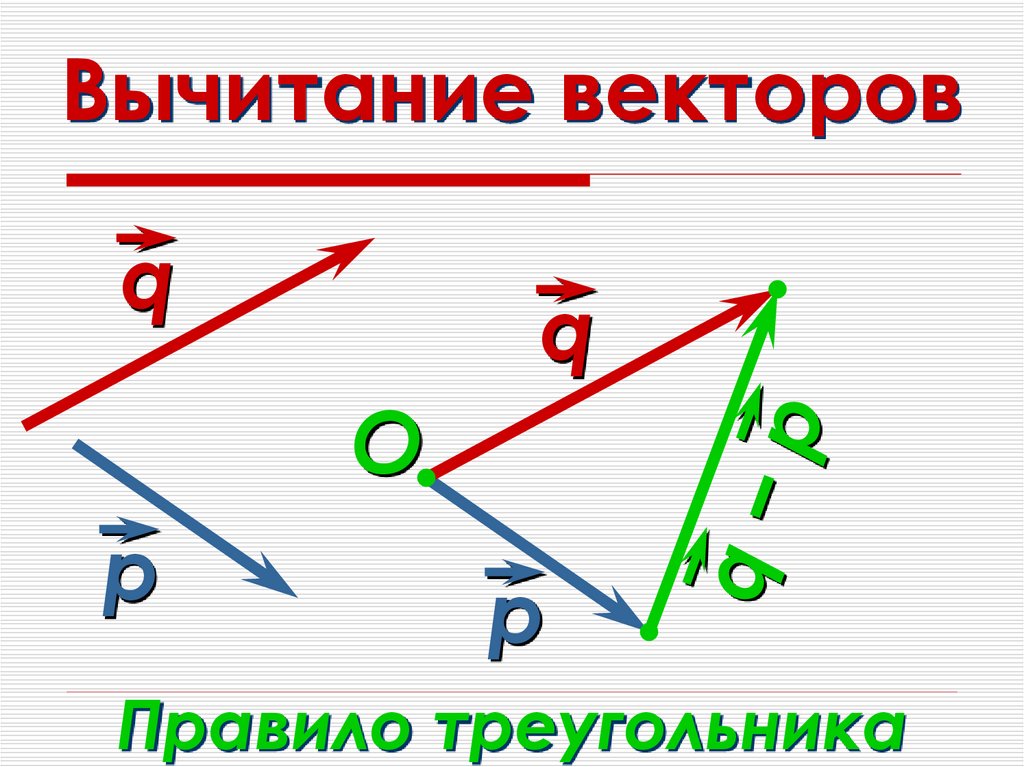

Рисунок 22.

6. Повторите задачу выше, но поменяйте порядок двух шагов ходьбы; показать, что вы получаете тот же конечный результат. То есть сначала вы проходите участок B , который составляет 20,0 м в направлении точно на 40º к югу от запада, а затем участок A , который составляет 12,0 м в направлении ровно на 12,0 к западу от севера. (Эта задача показывает, что A + B = B + A .)

7. (a) Повторите задачу двумя предыдущими задачами, но на втором этапе вы пройдете 20,0 м в направлении 40° к северу от востока (что эквивалентно вычитанию B из A , т. е. к нахождению R’ = A – B ). (b) Повторите задачу двумя предыдущими задачами, но теперь вы сначала проходите 20,0 м в направлении 40° к югу от запада, а затем 12,0 м в направлении 20° к востоку от юга (что эквивалентно вычитанию A из B — это есть, чтобы найти R” = B – A = R’  Покажите, что это так.

8. Покажите, что порядок сложения трех векторов не влияет на их сумму. Покажите это свойство, выбрав любые три вектора  A , B и C , а также [latex]\mathbf{C}[/latex] , имеющие разную длину и направление. Найдите сумму 90 105 A + B + C , затем найдите их сумму при сложении в другом порядке и покажите, что результат тот же. (Есть еще пять порядков, в которых A , B и C  можно добавить; выберите только один.)

9. Покажите, что сумма векторов, рассмотренных в примере 2, дает результат, показанный на рисунке 17.

10. Найдите модули скоростей на рисунке 23.

Рисунок 23. Две скорости V _A  и V _B складываются, чтобы получить общее значение V _к .

11. Найдите компоненты V _TOT вдоль x -и y -Оси на рисунке 23.

12. Найдите компоненты V _Total . тем, что на рис. 23.

Глоссарий

компонент (двумерного вектора):

часть вектора, указывающая либо в вертикальном, либо в горизонтальном направлении; каждый двумерный вектор может быть выражен как сумма двух компонент вертикального и горизонтального векторов

коммутативный:

относится к взаимозаменяемости порядка в функции; сложение векторов является коммутативным, потому что порядок сложения векторов не влияет на окончательную сумму

направление (вектора):

ориентация вектора в пространстве

голова (вектора):

конечная точка вектора; расположение кончика стрелки вектора; также называется «наконечник»

метод «голова к хвосту»:

метод сложения векторов, при котором конец каждого вектора помещается в начало предыдущего вектора

величина (вектора):

длина или размер вектора; величина является скалярной величиной

результат:

сумма двух или более векторов

Результирующий вектор:

векторная сумма двух или более векторов

скаляр:

количество с величиной, но без направления

хвост:

начальная точка вектора; напротив наконечника или наконечника стрелки

Избранные решения задач и упражнений

1.