Site Loader
Posted on 29.01.1993

Для того, чтобы задать вектор, необходимо указать:

1) прямую, на которой лежит вектор или которой он параллелен;

2) направление (ориентацию) вектора на этой прямой;

3) длину вектора.

Один и тот же вектор может быть отложен от любой точки пространства при помощи параллельного переноса, при этом сохраняются все три указанные характеристики этого вектора.

  • Вектор называется нулевым, если его начало и конец совпадают:

  • Векторы называются коллинеарными, если они лежат на параллельных или совпадающих прямых, обозначают  .

  • Векторы называются сонаправленными, если они коллинеарны и одинаково направлены.

  • Векторы называются равными, если они сонаправлены и имеют одинаковую длину, обозначают .

Заметим, что от любой точки пространства можно отложить вектор , равный данному, и при этом только один.

5.2. Операции над векторами

Из правила треугольника сложения векторов следует правило их вычитания: действительно, если , то .

  • Произведением вектора на число  называется вектор , коллинеарный вектору , длиной , который сонаправлен с вектором , если >0 и противоположно направлен, если <0.

  • Любому ненулевому вектору можно поставить в соответствие орт , имеющий единичную длину и направление которого совпадает с направлением вектора .

Свойства

:

1)

2)

3)

4)

5)

Теорема 5.1. Векторы коллинеарны тогда и только тогда, когда для некоторого .

Пример. В треугольнике АВС точки M, N, K – середины сторон АВ, АС, ВС соответственно. Найти векторы , если .

Р ешение: По условию, . Применяя правило вычитания, находим:

, .

Далее, AK — половина диагонали параллелограмма, сторонами которого являются отрезки АВ и АС (так как диагонали параллелограмма точкой пересечения делятся пополам). Следовательно, по правилу параллелограмма сложения векторов, имеем .

5 .3. Координаты векторов

Рассмотрим трехмерное пространство.

  • О

    y

    y

    ртонормированным репером в трехмерном пространстве называется совокупность начальной точки О и векторов , таких, что:

1) (единичные векторы),

2) (попарно перпендикулярные),

3) векторы образуют правую тройку векторов, то есть из конца вектора поворот от вектора к вектору виден в положительном направлении – против часовой стрелки.

В таком случае обычная декартова система координат соответствует заданному ортонормированному реперу, так что направления осей Ох, Оу, Oz совпадают с направлениями базисных векторов .

Р ассмотрим теперь произвольный вектор в трехмерном пространстве.

Отметим, что если вектор отложен от начала координат, то его координаты совпадают с координатами конца этого вектора.

Применив дважды правило параллелограмма, замечаем, что

.

Свойства:

Пусть , . Тогда

1)

2)

3)

4 )

Теорема 5.2. Пусть точка А имеет координаты (xA, yA, zA), точка В(xВ, yВ, zВ).

Тогда

.

Для доказательства достаточно заметить, что , причем .

Замечание. Координаты вектора не изменятся, если этот вектор отложить от любой другой точки пространства.

Доказательство этого факта предоставим читателю.

Многие геометрические задачи на плоскости и в пространстве легко решаются с помощью векторов. При этом надо все условия задачи, сформулированные для точек и отрезков (а в дальнейшем – и углов) переформулировать для векторов, а затем перевести в координатную форму. Если рассматривается задача на плоскости, то и точки, и векторы имеют 2 координаты, и все сформулированные выше свойства имеют место для первых двух координат.

Пример 1: Точка М делит пополам отрезок АВ, где А(xA, yA, zA),

В(xВ, yВ, zВ).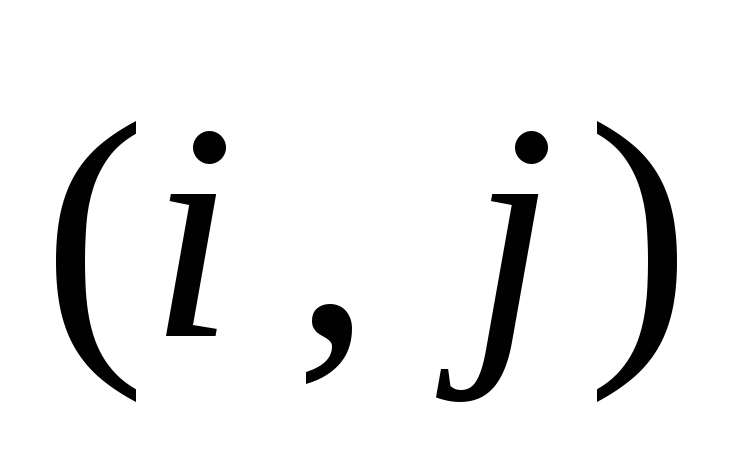 Найти координаты точки М.

Решение: Для решения этой задачи используем векторы.

Точка М лежит на отрезке АВ   , причем эти векторы сонаправлены.

Кроме того, по условию, . Следовательно, .

Обозначим координаты точки М (xМ, yМ, zМ). Тогда , .

Используя свойство 2) координат, имеем:

, откуда выражаем

.

Пример 2. Даны точки: A(1; 0), B(4; 2), C(2; 5). Найти точку пересечения медиан треугольника АВС.

Р ешение: Как известно, все медианы треугольника пересекаются в одной точке. Обозначим эту искомую точку К(xK, yK) и рассмотрим две медианы: BN и CM.

Найдем сначала координаты точек N и M как середин сторон АВ и АС (см. Пример 1).

Точка М – середина отрезка АВ  . Аналогично, .

Следовательно, можем найти координаты векторов:

Точка КСМ    (свойство 4). Аналогично,

точка КBN    .

Таким образом, мы получили два линейных уравнения с двумя неизвестными – координатами точки К. Решаем полученную систему:

 .

Таким образом, искомая точка .

Как найти вектор по точкам? Ответ на webmath.ru

Содержание:

  • Формула
  • Примеры нахождения координат вектора по точкам

Формула

Чтобы найти координаты вектора $\overline{A B}$ на плоскости, если он задан координатами своих начала $A\left(x_{1} ; y_{1}\right)$ и конца $B\left(x_{2} ; y_{2}\right)$, необходимо от координат конца отнять соответствующие координаты начала, то есть

$$\overline{A B}=\left(x_{2}-x_{1} ; y_{2}-y_{1}\right)$$

Чтобы найти координаты вектора $\overline{A B}$, заданного в пространстве координатами $A\left(x_{1} ; y_{1} ; z_{1}\right)$ и $B\left(x_{2} ; y_{2} ; z_{2}\right)$, необходимо, по аналогии с плоским случаем, из координат конца вычесть координаты начала:

$$\overline{A B}=\left(x_{2}-x_{1} ; y_{2}-y_{1} ; z_{2}-z_{1}\right)$$

Примеры нахождения координат вектора по точкам

Пример

Задание. Даны точки $A(4;-1)$ и $B(2;1)$. Найти координаты векторов $\overline{A B}$ и $\overline{B A}$

Решение. Для вектора $\overline{A B}$ точка $A$ является началом, а точка $B$ — концом. Тогда координаты вектора $\overline{A B}$ равны

$$\overline{A B}=(2-4 ; 1-(-1))=(-2 ; 2)$$

Для вектора точка $B$ является началом, а точка $A$ — концом. Тогда координаты вектора $\overline{B A}$ равны

$$\overline{B A}=(4-2 ;-1-1)=(2 ;-2)$$

Ответ.

$\overline{A B}=(-2 ; 2), \overline{B A}=(2 ;-2)$

Пример

Задание. Даны три точки в пространстве точки $A(1;-2;0,5)$, $B(3;2;1,5)$ и $C(0;-1;1)$. Найти координаты векторов $\overline{A B}$, $\overline{A C}$, $\overline{B C}$

Решение. Для искомого вектора $\overline{A B}$ точка $A$ является началом, а точка $B$ — концом. Тогда координаты вектора $\overline{A B}$ соответственно равны:

$$\overline{A B}=(3-1 ; 2-(-2) ; 1,5-0,5)=(2 ; 4 ; 1)$$

Для вектора $\overline{A C}$ точка $A$ является началом, а точка $C$ — концом.

Тогда его координаты соответственно равны

$$\overline{A C}=(0-1 ;-1-(-2) ; 1-0,5)=(-1 ; 1 ; 0,5)$$

Для вектора $\overline{B C}$ точка $B$ является началом, а точка $C$ — концом. Его координаты равны

$$\overline{B C}=(0-3 ;-1-2 ; 1-1,5)=(-3 ;-3 ;-0,5)$$

Ответ. $\overline{A B}=(2 ; 4 ; 1), \overline{A C}=(-1 ; 1 ; 0,5), \overline{B C}=(-3 ;-3 ;-0,5)$

Читать дальше: как найти сумму векторов.

  • Как найти сумму векторов
  • Как найти скалярное произведение векторов
  • Как найти векторное произведение векторов
  • Как найти смешанное произведение векторов
  • Как найти вектор коллинеарный вектору
  • Как найти вектор перпендикулярный вектору
  • Как найти орт вектора
  • Как найти разность векторов
  • Как найти проекцию вектора
  • Как найти длину вектора
  • Как найти модуль вектора
  • Как найти координаты вектора
  • Как найти направляющие косинусы вектора
  • Как найти угол между векторами
  • Как найти косинус угла между векторами

В чем разница между набором, вектором и векторным пространством?

спросил

Изменено 4 года, 7 месяцев назад

Просмотрено 14 тысяч раз

$\begingroup$

В чем разница между набором, вектором и векторным пространством?

Объясните, пожалуйста, без использования формальных математических обозначений. Потому что, если вы будете использовать формальные математические обозначения, я ничего не пойму.

  • векторные пространства

$\endgroup$

1

$\begingroup$

Набор — это то, что называется примитивным понятием . Это означает, что мы на самом деле не определяем его, мы просто предполагаем, что все имеют в виду примерно одну и ту же идею, когда мы это произносим. Подумайте, что означает набор объектов вне математики. Здесь должно работать то же определение. Набор — это группа (/коллекция/ассортимент/сборка/… стайка — может быть, это работает только для гусей) предметов. Эти объекты называются членами или элементами множества.

Вектор является элементом векторного пространства.

Векторное пространство представляет собой набор объектов, которые можно умножать на обычные числа и складывать вместе с помощью некоторых правил, называемых аксиомами векторного пространства.

Примером набора является $\{1,2,3\}$. Это просто набор из трех чисел. Другой пример: $\{банан, апельсин, тако, овсянка\}$. Этот набор содержит продукты на 4$. Ни в одном из этих наборов нет никаких предустановленных понятий сложения или умножения — это просто группы объектов.

Примером векторного пространства является множество всех действительных чисел, $\Bbb R$, наряду с обычными видами умножения и сложения. Это набор чисел, но мы также можем говорить о их сложении и умножении на другие числа. Вы можете проверить, что они удовлетворяют всем тем правилам, которым должны удовлетворять сложения и умножения, и, таким образом, это множество также является векторным пространством.
Число $3$ является примером вектора в приведенном выше векторном пространстве. Так и $\pi$. То же самое и с $\dots$

Менее тривиальным (и более типичным) примером векторного пространства является множество всех непрерывных функций, определенных на интервале $[0,1] \subset \Bbb R$. Сложение двух функций $f$ и $g$ определяется как $(f+g)(x) = f(x)+g(x)$, а умножение определяется как $(af)(x) = a\cdot f(x)$ для $a\in \Bbb R$. Вы можете убедиться, что это тоже векторное пространство. 92-2$ — это вектор, это векторное пространство.

$\endgroup$

2

$\begingroup$

Векторное пространство — это множество, в котором вы можете складывать его элементы друг с другом и в котором вы можете «растягивать» его элементы, другими словами, умножать их на действительное число. Элементами векторного пространства являются векторы. Некоторые люди сказали бы, что векторные пространства — это наборы с «более структурированными».

С другой стороны, векторные пространства отличаются от большинства множеств в том смысле, что их элементы могут быть произвольными и их нельзя складывать друг с другом.

$\endgroup$

$\begingroup$

Набор — это набор объектов. Например, набор целых чисел от $1$ до $5$.

Векторное пространство — это набор элементов (называемых векторами), который определен «над полем» в том смысле, что если вы умножаете на число в поле (представьте, что это действительные числа), вы все равно получаете элемент в векторном пространстве . Также можно складывать элементы в векторном пространстве, и существует специальный элемент под названием ‘$0$’, обладающий тем свойством, что $\vec{v}+0=\vec{v}=0+\vec{v }$ для каждого элемента (то же самое, что и вектор) $\vec{v}$ в векторном пространстве.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

alexxlab

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *