Векторы. Метод координат. Угол между прямыми, плоскостями. Расстояние от точки до плоскости, между скрещивающимися прямыми
\({\color{red}{\textbf{Факт 1. Про векторы}}}\)
\(\bullet\) Если в пространстве заданы две точки \(A(x_1;y_1;z_1)\) и \(B(x_2;y_2;z_2)\), то вектор \(\overrightarrow{AB}\) имеет координаты \[\overrightarrow{AB} = \{x_2-x_1;y_2-y_1;z_2-z_1\}\]
\(\bullet\) Если в пространстве заданы два вектора \(\vec{a}
=\{x_1;y_1;z_1\}\) и \(\vec{b}=
\{x_2;y_2;z_2\}\), то:
\(\qquad \blacktriangleright\) сумма этих векторов \(\vec{a}+\vec{b}=\{x_1+x_2;y_1+y_2;z_1+z_2\}\)
\(\qquad \blacktriangleright\) разность этих векторов \(\vec{a}-\vec{b}=\{x_1-x_2;y_1-y_2;z_1-z_2\}\)
\(\qquad \blacktriangleright\) произведение вектора на число \(\lambda
\vec{a}=\{\lambda x_1;\lambda
y_1;\lambda z_1\}\)
\(\bullet\) Если в пространстве заданы две точки \(A(x_1;y_1;z_1)\) и \(B(x_2;y_2;z_2)\), а точка \(O\) — середина отрезка \(AB\), то \(O\) имеет координаты \[O\left(\dfrac{x_1+x_2}2;\dfrac{y_1+y_2}2;\dfrac{z_1+z_2}2\right)\]
\(\bullet\) Длина вектора \(\vec{a}=\{x;y;z\}\) обозначается \(|\vec{a}|\) и вычисляется по формуле \[|\vec{a}|=\sqrt{x^2+y^2+z^2}\]
\({\color{red}{\textbf{Факт 2. Про скалярное произведение}}}\)
\(\bullet\) Скалярным произведением двух векторов называется произведение длин этих векторов на косинус угла между ними: \[{\large{(\vec{a},
\vec{b})=|\vec{a}|\cdot|\vec{b}|\cdot\cos \angle (\vec{a},
\vec{b})}}\] На рисунке показано, что такое угол между векторами:
\(\bullet\) Справедливы следующие утверждения:
I. Скалярное произведение ненулевых векторов (их длины не равны нулю) равно нулю тогда и только тогда, когда они перпендикулярны: \[(\vec{a}, \vec{b})=0 \quad\Leftrightarrow\quad \vec{a}\perp \vec{b}\]
II. Длина вектора равна квадратному корню из скалярного произведения вектора на себя: \[|\vec{a}|=\sqrt{(\vec{a}, \vec{a})}\]
III. Переместительный закон: \[(\vec{a}, \vec{b})=(\vec{b}, \vec{a})\]
IV. Распределительный закон: \[(\vec{a}+\vec{b}, \vec{c})=(\vec{a}, \vec{c})+(\vec{b}, \vec{c})\]
V.
2_2}}}}\]
\({\color{red}{\textbf{Факт 3. Про уравнение плоскости}}}\)
\(\bullet\) Если \(\vec{n}=\{a;b;c\}\) – нормаль к плоскости, то уравнение плоскости имеет вид \[ax+by+cz+d=0\] Для того, чтобы найти \(d\), нужно подставить в уравнение плоскости вместо \(x, y, z\) координаты любой точки, лежащей в этой плоскости.
Пример: если \(\vec{n}=\{1;2;3\}\) – нормаль к плоскости, \(O(4;5;6)\) – точка из плоскости, то справедливо: \(1\cdot 4+2\cdot 5+3\cdot
6+d=0\), откуда \(d=-32\), следовательно, уравнение плоскости имеет вид \(x+2y+3z-32=0\).
\(\bullet\) Уравнение плоскости можно составить, используя три точки из плоскости, не лежащие на одной прямой.
\({\color{red}{\textbf{Факт 4.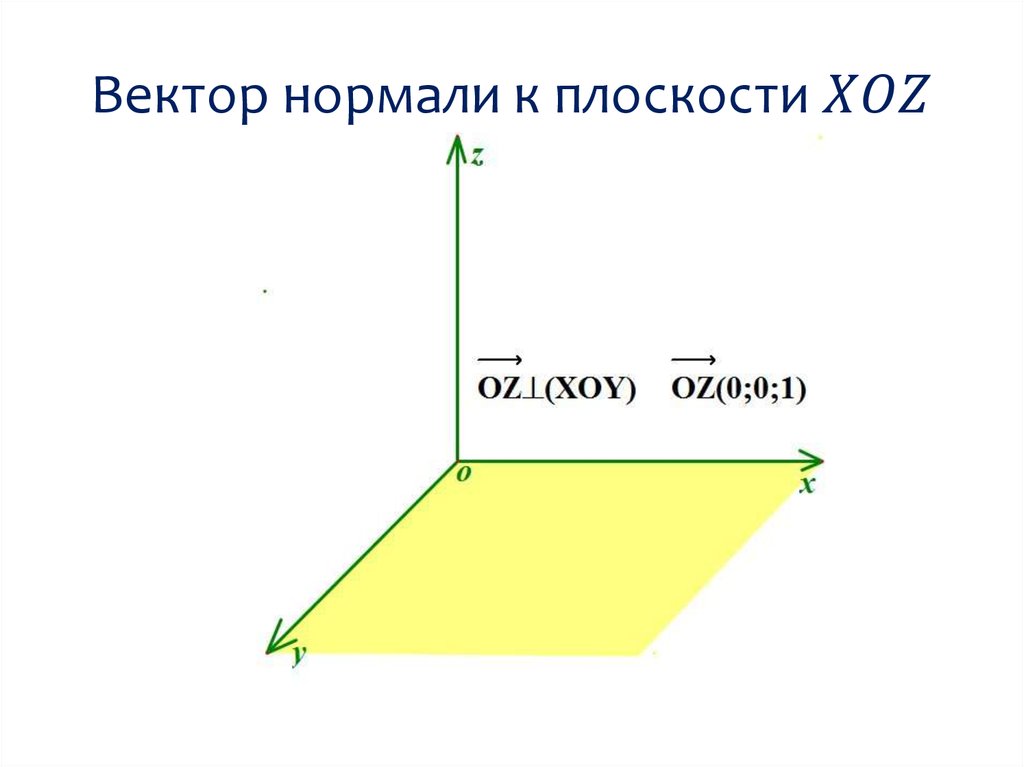
2}}\]
\(\bullet\) Для того, чтобы найти расстояние между скрещивающимися прямыми, нужно
— построить плоскость, проходящую через одну из них и параллельную другой;
— найти уравнение этой плоскости;
— найти расстояние от любой точки первой прямой до этой плоскости.
Создание, изменение и доступ к векторным элементам
В этой статье вы узнаете о векторах в программировании на R. Вы научитесь создавать их, получать доступ к их элементам с помощью различных методов и изменять их в своей программе.
Вектор — это базовая структура данных в R. Она содержит элементы того же типа. Типы данных могут быть логическими, целочисленными, двойными, символьными, сложными или необработанными.
Тип вектора можно проверить с помощью функции typeof() .
Еще одним важным свойством вектора является его длина. Это количество элементов в векторе, и его можно проверить с помощью функции 9.0007 длина() .
Как создать вектор в R?
Векторы обычно создаются с помощью функции c() .
Так как вектор должен иметь элементы одного типа, эта функция попытается привести элементы к одному типу, если они разные.
Приведение от младших к более высоким типам от логического к целому к двойному к символьному.
> х <- с(1, 5, 4, 9, 0) > тип(х) [1] «двойной» > длина (х) [1] 5 > x <- c(1, 5.4, ИСТИНА, "привет") > х [1] «1» «5.4» «ИСТИНА» «привет» > тип(х) [1] "персонаж"
Если мы хотим создать вектор последовательных чисел, очень полезен оператор : .
Пример 1: Создание вектора с помощью: оператора
> х <- 1:7; Икс [1] 1 2 3 4 5 6 7 > у <- 2:-2; у [1] 2 1 0 -1 -2
Более сложные последовательности могут быть созданы с помощью функции seq()
Пример 2. Создание вектора с помощью функции seq()
> seq(1, 3, by=0.2) # указать размер шага [1] 1,0 1,2 1,4 1,6 1,8 2,0 2,2 2,4 2,6 2,8 3,0 > seq(1, 5, length.out=4) # указать длину вектора [1] 1,000000 2,333333 3,666667 5,000000
out=4) # указать длину вектора
[1] 1,000000 2,333333 3,666667 5,000000
Как получить доступ к элементам вектора?
Доступ к элементам вектора можно получить с помощью векторной индексации. Вектор, используемый для индексации, может быть логическим, целочисленным или вектором символов.
Использование целочисленного вектора в качестве индекса
Индекс вектора в R начинается с 1, в отличие от большинства языков программирования, где индекс начинается с 0.
Мы можем использовать вектор целых чисел в качестве индекса для доступа к определенным элементам.
Мы также можем использовать отрицательные целые числа, чтобы вернуть все элементы, кроме указанных.
Но мы не можем смешивать положительные и отрицательные целые числа, в то время как индексация и действительные числа, если они используются, усекаются до целых чисел.
> х [1] 0 2 4 6 8 10 > x[3] # доступ к третьему элементу [1] 4 > x[c(2, 4)] # доступ ко 2-му и 4-му элементам [1] 2 6 > x[-1] # доступ ко всем элементам, кроме 1-го [1] 2 4 6 8 10 > x[c(2, -4)] # нельзя смешивать положительные и отрицательные целые числа Ошибка в x[c(2, -4)]: только 0 могут быть смешаны с отрицательными нижними индексами >x[c(2.
4, 3.54)] # действительные числа усекаются до целых
[1] 2 4
Использование логического вектора в качестве индекса
Когда мы используем логический вектор для индексации, возвращается позиция, где логический вектор равен TRUE .
Эта полезная функция помогает нам фильтровать вектор, как показано ниже.
> х[с(ИСТИНА, ЛОЖЬ, ЛОЖЬ, ИСТИНА)] [1] -3 3 > x[x < 0] # фильтрация векторов по условиям [1] -3 -1 > х [х > 0] [1] 3
В приведенном выше примере выражение x>0 даст логический вектор (ЛОЖЬ, ЛОЖЬ, ЛОЖЬ, ИСТИНА) , который затем используется для индексации.
Использование вектора символов в качестве индекса
Этот тип индексации полезен при работе с именованными векторами. Мы можем назвать каждый элемент вектора.
> x <- c("первый"=3, "второй"=0, "третий"=9)
> имена(х)
[1] "первый" "второй" "третий"
> х["секунда"]
второй
0
> х[с("первый", "третий")]
первая треть
3 9
Как изменить вектор в R?
Мы можем изменить вектор с помощью оператора присваивания.
Мы можем использовать методы, описанные выше, для доступа к определенным элементам и их модификации.
Если мы хотим обрезать элементы, мы можем использовать переназначения.
> х [1] -3 -2 -1 0 1 2 >х[2] <- 0; x # изменить 2-й элемент [1] -3 0 -1 0 1 2 > х[х<0] <- 5; x # изменить элементы меньше 0 [1] 5 0 5 0 1 2 > х <- х[1:4]; x # обрезать x до первых 4 элементов [1] 5 0 5 0
Как удалить вектор?
Мы можем удалить вектор, просто назначив NULL к нему.
> х [1] -3 -2 -1 0 1 2 > х <- NULL > х НУЛЕВОЙ > х[4] НУЛЕВОЙ
- ПРЕДЫДУЩИЙ
Функция R switch() - СЛЕДУЮЩИЙ
R Матрица
Stan Справочное руководство
Это старая версия, посмотреть текущую версию.
Stan поддерживает массивы произвольной размерности. Значения в массиве
может быть любого типа, так что массивы могут содержать значения, которые являются простыми
вещественные или целые числа, векторы, матрицы или другие массивы.
Двумерный массив — это просто массив массивов, оба концептуально
и с точки зрения текущей реализации. Когда индекс передается
массив, он возвращает значение по этому индексу. Когда более одного
index предоставляется, эта операция индексации цепочка. Например, если a — двумерный массив, тогда a[m, n] — это просто
удобное сокращение для a[m][n] .
Векторы, матрицы и массивы нельзя присваивать друг другу, даже если их размеры совпадают.
Объявление переменных массива
Массивы объявляются путем заключения размеров в квадратные скобки после имени переменной.
Переменная n объявляется как массив из пяти целых чисел следующим образом.
инт п[5];
Двумерный массив действительных значений с тремя строками и четырьмя столбцами.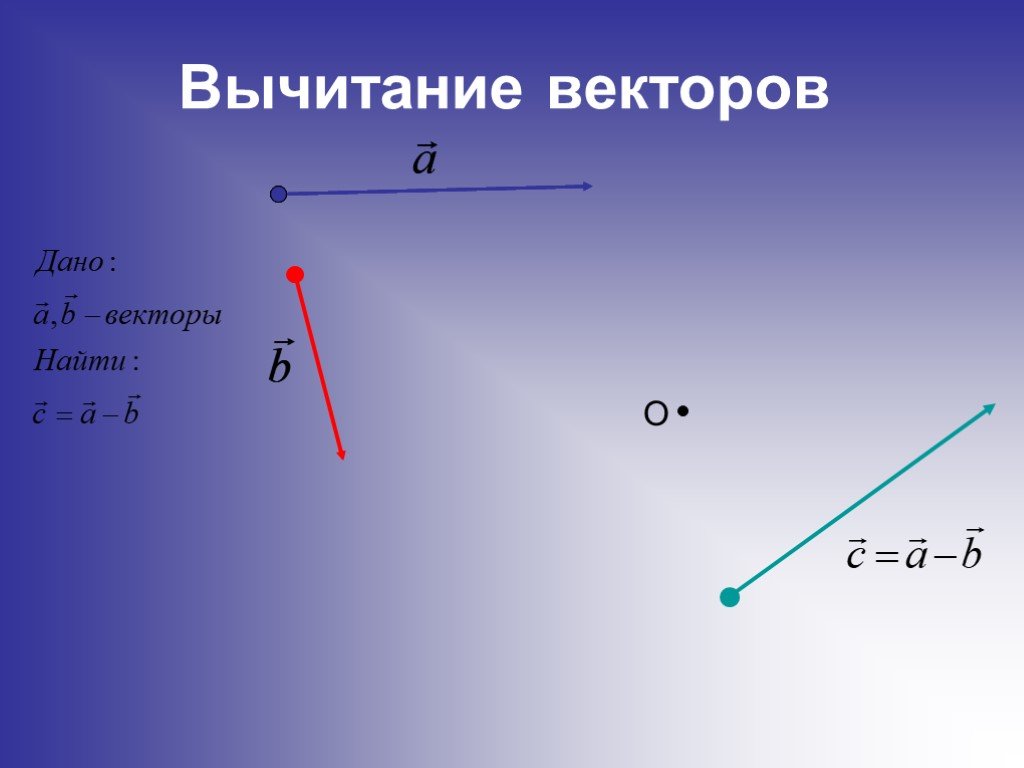
объявлено следующим.
реальный а[3, 4];
Трехмерный массив z положительных вещественных чисел с пятью строками, четырьмя
колонны и две полки можно объявить следующим образом.
реальное<нижний=0> z[5, 4, 2];
Массивы также могут быть объявлены содержащими векторы. Например,
вектор[7] мю[3];
объявляет mu массивом размера 3, содержащим векторы с 7
элементы. Массивы также могут содержать матрицы. Пример
matrix[7, 2] mu[15, 12];
объявляет массив 15 на 12 матриц \(7 \times 2\). Любой из ограниченные типы также могут использоваться в массивах, как в объявлении
cholesky_factor_cov[5, 6] mu[2, 3, 4];
массива \(2 \times 3 \times 4\) из \(5 \times 6\) коэффициентов Холецкого ковариационные матрицы.
Доступ к элементам массива и подмассивам
Если x — это одномерный массив длины 5, то x[1] — это
первый элемент массива, а x[5] — последний.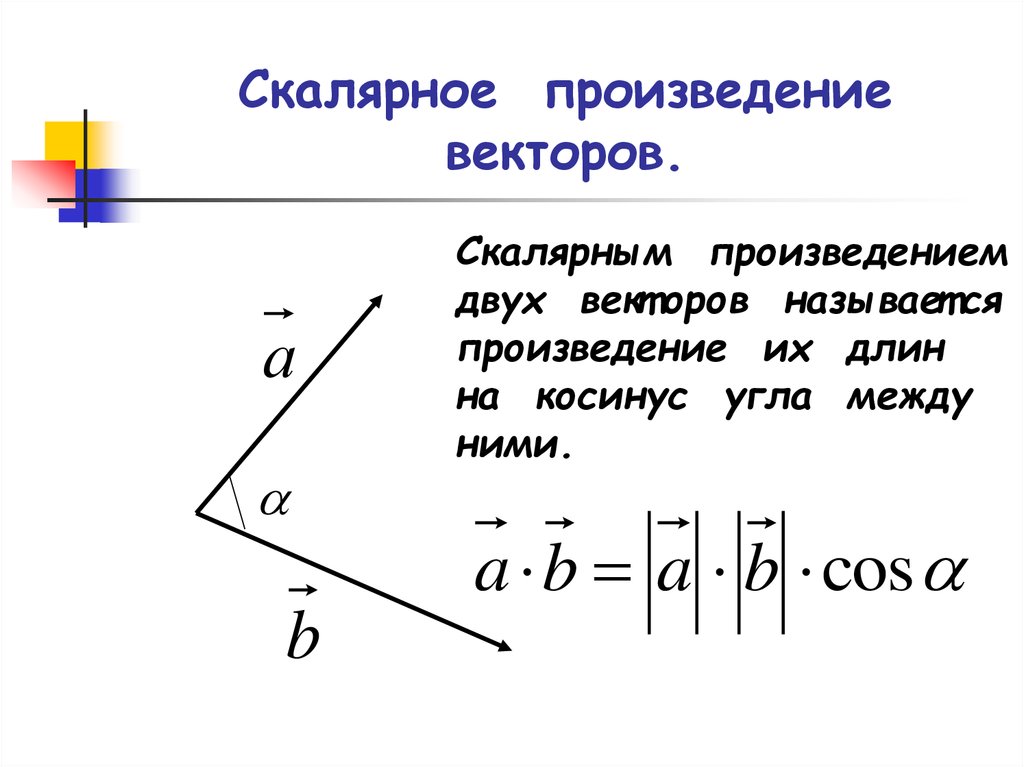
Для массива \(3 \times 4\) y из двух измерений y[1, 1] является первым
элемент и y[3, 4] последний элемент. Для трехмерного
массив z , первый элемент — z[1, 1, 1] и так далее.
Доступ к подмассивам массивов можно получить, предоставив меньше, чем полный
количество индексов. Например, предположим, что y — это двумерное число.
массив с тремя строками и четырьмя столбцами. Тогда y[3] одномерный массив длины четыре. Это означает, что y[3][1] можно использовать вместо y[3, 1] для доступа к значению первого
столбец третьей строки y . Форма y[3, 1] — это
предпочтительная форма (см. примечание в этой главе).
Массивы матриц и векторов
Доступ к массивам векторов и матриц осуществляется так же, как к массивам двойников. Рассмотрим следующие векторные и скалярные объявления.
вектор[5] а[3, 4]; вектор[5] б[4]; вектор[5] с; реальный х;
С этими объявлениями допустимы следующие присвоения.
б = а[1]; // результат - массив векторов с = а[1, 3]; // результат вектор с = б[3]; // тот же результат, что и выше х = а[1, 3, 5]; // результат скалярный х = Ь[3, 5]; // тот же результат, что и выше х = с[5]; // тот же результат, что и выше
Векторы-строки и другие производные типы векторов (простые и упорядоченные) вести себя одинаково с точки зрения индексации.
Рассмотрим следующие объявления матрицы, вектора и скаляра.
матрица[6, 5] d[3, 4]; матрица[6, 5] e[4]; матрица[6, 5] f; строка_вектор[5] г; реальный х;
С этими объявлениями следующие определения являются законными.
е = д[1]; // результат - массив матриц е = д[1,3]; // результат - матрица е = е[3]; // тот же результат, что и выше г = д[1,3,2]; // результат - вектор-строка г = е[3,2]; // тот же результат, что и выше г = f[2]; // тот же результат, что и выше х = д[1,3,5,2]; // результат скалярный х = е[3,5,2]; // тот же результат, что и выше х = f[5,2]; // тот же результат, что и выше х = г[2]; // тот же результат, что и выше
Как показано, результат f[2] предоставления одного индекса в
матрица — индексированная строка, здесь строка 2 матрицы f .
Смешивание типов массивов, векторов и матриц
Массивы, векторы-строки, векторы-столбцы и матрицы не взаимозаменяемы в Стэне. Таким образом, переменная любого из этих фундаментальные типы не могут быть присвоены никаким другим и не могут использоваться в качестве аргумента там, где требуется другой (использовать в качестве аргументов следует правилам назначения).
Смешивание векторов и массивов
Например, векторы нельзя назначать массивам и наоборот.
реальный а[4]; вектор[4] б; строка_вектор с[4]; // ... а = б; // недопустимое присвоение вектора массиву б = а; // недопустимое присвоение массива вектору а = с; // недопустимое присвоение вектора-строки массиву с = а; // незаконное присвоение массива вектору-строке
Смешивание векторов-строк и векторов-столбцов
Недопустимо даже назначать векторы-строки векторам-столбцам или наоборот наоборот
вектор b[4]; строка_вектор с[4]; // ... б = с; // недопустимое присвоение вектора-строки вектору-столбцу с = б; // недопустимое присвоение вектора-столбца вектору-строке
Смешивание матриц и массивов
То же самое верно для матриц, где двумерные массивы не могут быть
присваивается матрицам или наоборот.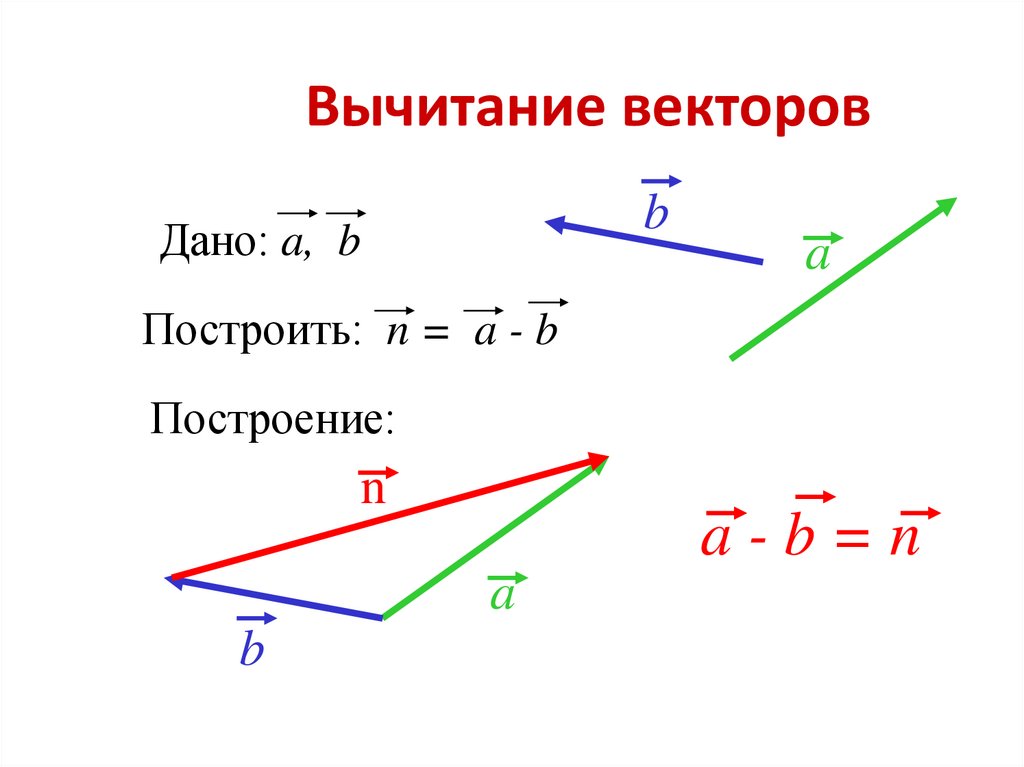
реальное а[3,4]; матрица[3,4] б; // ... а = б; // недопустимое присвоение матрицы массиву б = а; // недопустимое присвоение массива матрице
Смешивание матриц и векторов
Матрице \(1 \times N\) нельзя присвоить вектор-строку или наоборот.
матрица[1,4] а; строка_вектор[4] б; // ... а = б; // недопустимое присвоение вектора-строки матрице б = а; // недопустимое присвоение матрицы вектору-строке
Точно так же матрица \(M \times 1\) не может быть назначена вектору-столбцу.
матрица[4,1] а; вектор[4] б; // ... а = б; // недопустимое присвоение вектор-столбца матрице б = а; // недопустимое присвоение матрицы вектору-столбцу
Ограничения объявления размера
Целочисленное выражение используется для выбора размеров массивов.
применяются те же ограничения, что и для размеров векторов и матриц, а именно
размер объявляется целочисленным выражением, которое не
содержать любые параметры, преобразованные параметры или сгенерированные величины.
