ОглавлениеВВЕДЕНИЕЧАСТЬ ПЕРВАЯ. ВЕКТОРНАЯ АЛГЕБРА Глава I. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ 2. Скаляры и векторы. 3. Равенство векторов. 4.  Скользящие и приложенные векторные величины.6. Орт вектора. 7. Угол между двумя векторами. § 2. Сложение векторов 1. Сложение двух векторов. 2. Сложение более чем двух векторов. 3. Модуль суммы. 4. Законы сложения. § 3. Вычитание векторов § 4. Умножение и деление вектора на скаляр 2. Законы умножения вектора на скаляр. 3. Деление вектора на скаляр. 4. Выражение вектора через его модуль и орт. § 5. Линейные зависимости между векторами 2. Коллинеарные векторы. 3. Компланарные векторы. 4. Разложение вектора по трем некомпланарным векторам. 5. Метод координат. Глава II. ТЕОРИЯ ПРОЕКЦИЙ. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ § 1. Проекции векторов на ось § 3. Прямоугольная система координат в пространстве 1. Правая и левая прямоугольные системы координат. 2. Разложение вектора по ортам осей 3. Линейные операции над векторами в координатной форме.  4. Радиус-вектор и координаты точки. 5. Определение вектора по его началу и концу. 6. Деление отрезка в данном отношении. Глава III. ПРОИЗВЕДЕНИЯ ДВУХ ВЕКТОРОВ § 1. Скалярное произведение двух векторов 2. Работа силы. 3. Определение. 4. Равенство скалярного произведения нулю. 5. Законы скалярного умножения. 8. Скалярное произведение в координатной форме. 9. Неопределенность действия, обратного скалярному умножению. § 2. Векторное произведение двух векторов 3. Условия равенства нулю векторного произведения. 4. Законы векторного умножения. 5. Векторные произведения координатных ортов. 6. Определители. 7. Векторное произведение в координатной форме. 8. Неопределенность действия, обратного векторному умножению. Глава IV. ПРОИЗВЕДЕНИЯ ТРЕХ ВЕКТОРОВ § 1. Простейшее произведение трех векторов § 2. Векторно-векторное произведение трех векторов 3. Правило разложения векторно-векторного произведения.  § 3. Векторно-скалярное произведение трех векторов 2. Законы векторно-скалярного умножения 3. Обращение в нуль векторно-скалярного произведения трех векторов. 4. Векторно-скалярное произведение в координатной форме. § 4. Выражение векторно-скалярного произведения через скалярные произведения Глава V. ФУНКЦИИ ВЕКТОРОВ § 1. Произведения четырех векторов 2. Выражение скалярного произведения двух векторных произведений (а x b), (р x q) через скалярные произведения. 3. Разложение вектора (а, b, с) R по трем векторам a, b, c. 4. Разложение вектора (a, b, c) по векторным произведениям b x с, c x a, а x b 2. Разложение вектора (a, b, c) (m x n) по векторам a, b, c. 3. Выражение произведения двух смешанных произведений (a, b, c) (l, m, n) через скалярные произведения. § 3. Основные теоремы о функциях векторов 1. Рациональные функции векторов. 2. Элементарные функции векторов. 3. Произвольные скалярные функции от векторов.  4. Произвольные векторные функции векторов. Глава VI. ОСНОВНЫЕ ЗАДАЧИ § 2. Основные задачи, связанные со скалярным умножением векторов § 3. Основные задачи, связанные с векторным умножением векторов § 5. Простейшие векторные уравнения § 6. Геометрические инварианты фигур 2. Треугольник. 3. Полные системы инвариантов треугольника. 4. Тетраэдр. 5. Полные системы инвариантов тетраэдра. 6. Гексаэдр с треугольными гранями. ЧАСТЬ ВТОРАЯ. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ § 1. Векторы, зависящие от скаляра 2. Вектор-функция в координатной форме. 3. Годограф вектора. 4. Предел вектора. § 2. Дифференцирование вектора по скаляру 2. Геометрический смысл производной вектора по скаляру. 3. Механический смысл производной. 5. Дифференциал вектора. 6. Инвариантность дифференциала. § 3. Формула Тейлора Глава VIII.  ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ЛИНИИ В ПРОСТРАНСТВЕ§ 1. Основные дифференциально-геометрические понятия, связанные с линией 2. Касательная. 3. Соприкасающаяся плоскость. 4. Главная нормаль и бинормаль. 5. Кривизна. 6. Кручение. 7. Длина дуги. § 2. Основные формулы дифференциальной геометрии линий в пространстве 1. Дуга как параметр. Дифференциал дуги. 2. Орт касательной. Первая основная формула. 3. Инвариантность геометрических понятий. 4. Главная нормаль и кривизна. Вторая основная формула. 6. Винтовая линия. § 3. Сопровождающий трехгранник 2. Система дифференциальных уравнений движения сопровождающего трехгранника. 3. Расположение линии относительно сопровождающего трехгранника. 4. Линии без кривизны. 5. Линии без кручения. § 4. Инвариантные формулы Глава IX. ПЛОСКИЕ ЛИНИИ § 1. Дифференциальные уравнения плоской линии § 2. Кривизна плоской линии § 3.  Круг кривизны§ 4. Эволюта § 5. Эвольвента Глава X. ПРИЛОЖЕНИЯ К МЕХАНИКЕ § 1. Скорость и ускорение точки § 2. Движение твердого тела вокруг неподвижной точки 3. Угловая скорость. 4. Доказательстве существования угловой скорости твердого тела. § 3. Относительная производная вектора 2. Абсолютная и относительная производные вектора. 3. Общий случай движения твердого тела. Глава XI. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ § 1. Векторные функции нескольких скалярных аргументов § 2. Параметризованная поверхность 2. Поверхность в декартовых координатах. 3. Параметрическая сеть. 4. Линия на параметризованной поверхности. § 3. Касательная плоскость и нормаль 3. Нормальный вектор. 4. Преобразование параметров. § 4. Площадь области на поверхности 3. Формула для вычисления площади поверхности, заданной уравнением z=z(x,y). 4. Элемент площади поверхности.  5. Векторный элемент площади поверхности. § 5. Первая квадратичная форма поверхности 2. Внутренняя геометрия поверхности. 3. Длина дуги линии на поверхности. 4. Угол между линиями на поверхности. 5. Площадь области на поверхности. § 6. Вторая квадратичная форма поверхности 2. Нормальная кривизна линии на поверхности. 3. Теорема Менье. § 7. Главные направления и главные кривизны поверхности 2. Главные направления на поверхности. 4. Формула Эйлера. 5. Полная и средняя кривизны поверхности. ЧАСТЬ ТРЕТЬЯ. ТЕОРИЯ ПОЛЯ § 1. Функция поля. Поверхности уровня § 2. Градиент поля 2. Первая теорема о градиенте. § 3. Производная по направлению 2. Выражение производной по направлению через градиент. 3. Вторая теорема о градиенте. § 4. Направляющие косинусы нормали поверхности Глава XIII. КРИВОЛИНЕЙНЫЙ И ПОВЕРХНОСТНЫЙ ИНТЕГРАЛЫ § 1. Криволинейный интеграл как определенный интеграл от сложной функции 2.  Криволинейный интеграл от линейной формы по произвольной кривой.4. Обобщенный криволинейный интеграл. 5. Примеры. § 2. Криволинейный интеграл как предел криволипейной интегральной суммы § 3. Поверхностный интеграл как двойной интеграл от сложной функции 2. Определение простейшего поверхностного интеграла. 3. Поверхностный интеграл от билинейной формы по произвольной поверхности. § 4. Поверхностный интеграл как предел поверхностной интегральной суммы § 5. Поверхностный интеграл в параметрической форме 2. Параметрический поверхностный интеграл. 3. Поверхностный интеграл как предел суммы. § 6. Кратный интеграл как предел обобщенной интегральной суммы Глава XIV. ВЕКТОРНОЕ ПОЛЕ И ЕГО ИНТЕГРАЛЬНЫЕ ИНВАРИАНТЫ § 1. Векторное поле § 2. Векторные линии § 3. Циркуляция поля вдоль линии § 4. Поток поля через поверхность Глава XV.  ТЕОРЕМА ОСТРОГРАДСКОГО. ДИВЕРГЕНЦИЯ ПОЛЯ§ 1. Формула Остроградского § 2. Дивергенция поля 2. Дивергенция как предел отношения. 3. Гидромеханический смысл дивергенции. 4. Теорема Остроградского. Глава XVI. ТЕОРЕМА СТОКСА. РОТАЦИЯ ПОЛЯ § 1. Формула Стокса § 2. Ротация поля § 3. Оператор Гамильтона Глава XVII. СПЕЦИАЛЬНЫЕ ВЕКТОРНЫЕ ПОЛЯ § 1. Потенциальное поле 3. Циркуляция потенциального поля по замкнутому контуру. 4. Циркуляция потенциального поля между двумя точками. 5. Потенциал. 6. Элемент циркуляции. 7. Характеристические признаки потенциального поля. 8. Вычисление потенциала. 9. Центральное поле. 10. Вихревые шнуры. § 2. Соленоидальное поле 3. Поток соленоидального поля через замкнутую поверхность. 4. Трубчатое строение соленоидального поля. 5. Векторный потенциал. 6. Характеристические признаки соленоидального поля. 7. Источники и стоки. § 3. Потенциальное несжимаемое поле Глава XVIII.  ПРОСТЕЙШИЕ ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ§ 1. Электростатическое поле точечного заряда 2. Дивергенция поля точечного заряда. 3. Поток поля точечного заряда через замкнутую поверхность. 4. Ротация поля точечного заряда. 5. Потенциал поля точечного заряда. § 2. Электростатическое поле системы точечных зарядов 2. Дивергенция и ротация поля системы точечных зарядов. 3. Поток поля системы точечных зарядов через замкнутую поверхность. 4. Потенциал поля системы точечных зарядов. 5. Непрерывно распределенный заряд. § 3. Магнитное поле тока 2. Напряженность магнитного поля тока, текущего по бесконечному прямолинейному проводу. 3. Векторные линии поля H. 4. Потенциал поля Н. 5. Провод как вихревой шнур. Глава XIX. ВЕКТОРНОЕ ПОЛЕ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ § 1. Криволинейные координаты 3. Координатные поверхности и линии. 4. Линейный элемент. 5. Элемент объема. 6. Подвижной репер. 7. Векторное поле в криволиненных координатах.  § 2. Дифференциальные операции в криволинейных координатах 2. Дивергенция в криволинейных координатах. 3. Ротация в криволинейных координатах. § 3. Ортогональные координаты § 4. Цилиндрические координаты 2. Линейный элемент и элемент объема в цилиндрических координатах. 3. Дифференциальные операции в цилиндрических координатах. § 5. Сферические координаты |
Урок 4. Произведение векторов | Уроки математики и физики для школьников и родителей
Умножение вектора на число.
В геометрии часто возникает потребность в сложении двух, трёх или более одинаковых векторов:
и так далее.
Такие суммы, как в алгебре, удобно записывать
и так далее.
Эта
процедура подсказывает определение операции умножения
вектора на число.
Произведение ненулевого
вектора
на число k – вектор
который сонаправлен с
если k > 0 и противоположно направлен с
если k < 0.
Длина вектора
равна
В результате произведения вектора на число всегда получается векторная величина.
Произведение нулевого вектора на любое число – нулевой вектор.
Произведение вектора
на число k обозначают так:
Произведение числа нуль на любой вектор есть нулевой вектор.
ПРИМЕР:
На рисунке
изображены:
Основные законы умножения
вектора на число.
Для операции умножения вектора на число выполняются следующие законы.
– сочетательный закон:
– первый распределительный закон:
– второй распределительный закон:
Здесь k, l, – любые числа;
– любые векторы.
Если
Умножение вектора на число с помощью координат вектора.
При умножении вектора на число его координаты умножаются на это число, а именно, если
то есть
Или другими словами:
Координаты
вектораравняются произведению
числа k на соответствующие координаты вектораВекторы часто
помогают изучать геометрические факты: для этого нужно научиться переводить
геометрические факты на векторный язык, и наоборот, уметь векторное выражение
перевести на язык геометрии.
Предположим, что нам
нужно доказать, что прямые а и b параллельны.
Рассмотрим векторы
принадлежащие соответственно прямым а и b.
Векторы
могут иметь и
противоположные направления.
Можно доказать, что если
векторы
коллинеарны, то по
определению коллинеарности векторов получим, что прямые а и b параллельны.
Вектор
коллинеарен ненулевому вектору
тогда и только тогда, когда
Два вектора,
отложенные от одной и той же точки, лежат на одной прямой тогда и только тогда,
когда один из них получается из другого умножением на число.
Другими
словами, точка Х лежит на прямой АВ тогда и только тогда, когда
Скалярное произведение двух векторов.
Угол между двумя векторами с общим началом определяется, как обычный угол.
Если есть два произвольных вектора
то углом между ними называется угол между равными векторами с общим началом.
При этом рассматривают так называемый выпуклый угол (угол, имеющий меньшую величину). Иногда угол между векторами
обозначают так:
Читают: угол между векторами
равен 30°.
Углом между двумя ненулевыми векторами называют угол между соответствующими им направленными отрезками, исходящими из одной точки.
Угол между противоположно направленными векторами равен 180°, а между сонаправленными – 0°.
Скалярное произведение двух ненулевых векторов равняется произведению длин этих векторов на косинус угла между ними.
Если угол между векторами
равен φ,
то их скалярное произведение
Если хотя бы один из
двух векторов нулевой, то скалярное произведение равно 0.
Если
векторы
равны, то есть
то пишут
и говорят о скалярном квадрате вектора.
В этом случае cos φ = 1, то есть
Итак, скалярный квадрат вектора совпадает с квадратом его длины:
Если
и при этом, если
то следует, что
Скалярное умножение связано со сложением векторов (распределительный закон):
Скалярным произведением двух векторов называется число, которое равняется сумме произведений соответствующих координат этих векторов.
Обозначение таково же, как и для произведения чисел.
Если есть векторы
то
Признак перпендикулярности
векторов.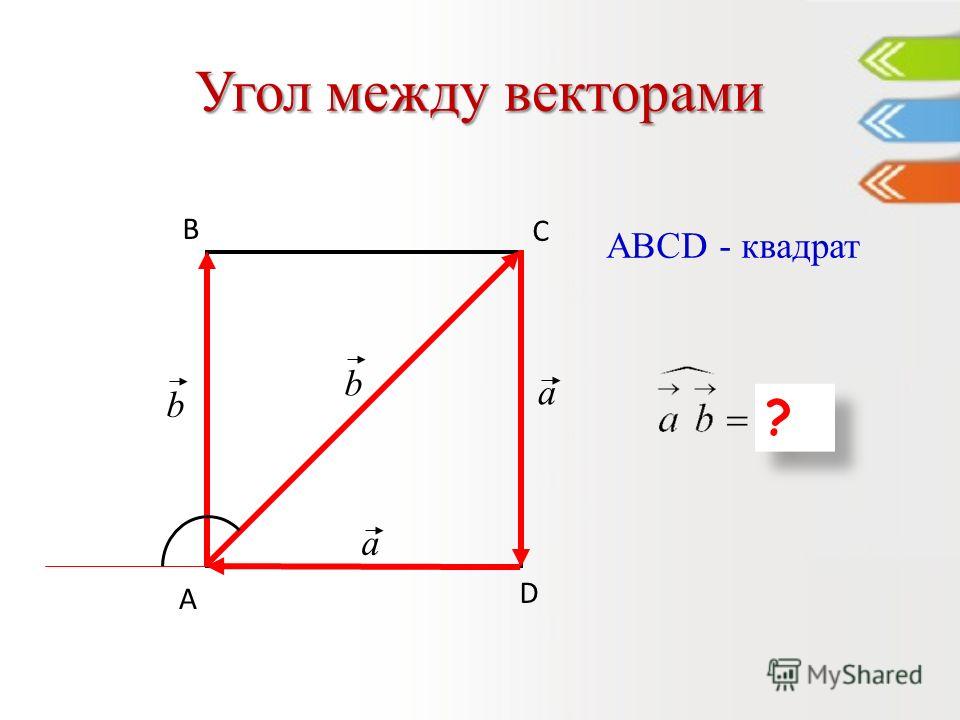
Если векторы перпендикулярны,
то их скалярное произведение равняется нулю
И наоборот, если скалярное произведение отличающихся от нуля векторов равняется нулю, то векторы перпендикулярны.
ПРИМЕР:
Необходимо выяснить, будут ли перпендикулярными отрезки KL и MN, если
К(3; 5), L(–2; 0),
M(8; –1), N(1; 4).
РЕШЕНИЕ:
Здесь речь идёт об обычных отрезках плоскости. Хотя речь идёт об обычных отрезках, а задача всё равно решается через векторы. Найдём векторы:
Вычислим их скалярное произведение:
Значит, отрезки KL и MN не перпендикулярны.
ПРИМЕР:
Пусть
Найти вектор:
РЕШЕНИЕ: ОТВЕТ: ПРИМЕР:
Пусть
Найти вектор:
РЕШЕНИЕ:
ОТВЕТ:
ПРИМЕР:
Найдите угол α между векторами:
РЕШЕНИЕ:
По определению скалярного произведения
где α – искомый угол, a и b – модули векторовсоответственно.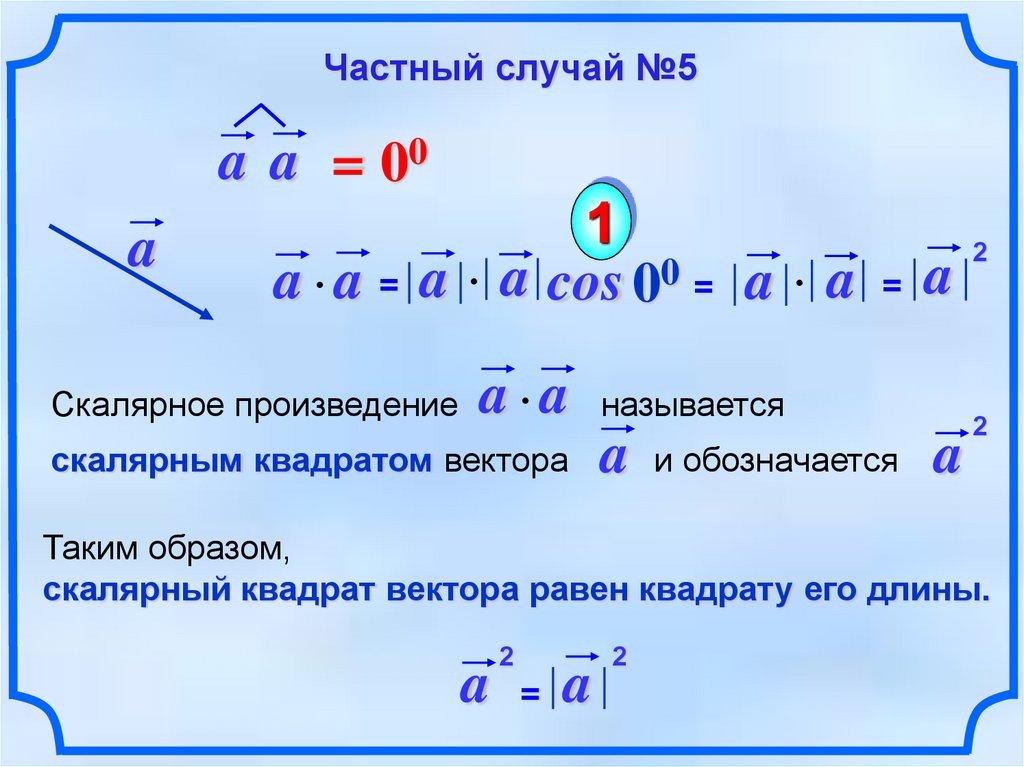
Отсюда
В свою очередь,
тогдаОтсюда α ≈ 173°.
Задания к уроку 4
линейная алгебра — Какова геометрическая интерпретация квадрата вектора?
Задавать вопрос
спросил
Изменено 8 лет, 1 месяц назад
Просмотрено 5к раз
$\begingroup$ 92, c = \vec{a} + \vec{b}$
Здесь я застрял, так как не смог найти, как обрабатывать вектор, умноженный сам на себя. Информация в одном месте гласит, что вектор, умноженный сам на себя, равен точечному произведению вектора на самого себя: $\vec{c}\cdot\vec{c}$.
В других местах я нашел информацию, которая заставляет меня думать, что умножение вектора на другой вектор в том смысле, что скаляр умножается на скаляр, не является допустимой операцией для выполнения.
Что из этих двух верно, или это третий случай, который я не рассматривал? Я неправильно подхожу к проблеме? 92$.
Пусть $\vec{c}=(2,1)$. Затем $$\vec{c} \cdot \vec{c} = (2,1) \cdot (2,1) = 2 \cdot 2 + 1 \cdot 1 = 5 \;,$$ который является квадратом длины вектора $(2,1)$, т. е. этот вектор имеет длину $\sqrt{5}$. Умножение скалярного произведения является «покомпонентным», т. е. произведением $x$-координат, плюс произведение $y$-координат. Итак, геометрическая интерпретация: квадрат длины вектора.
(Существует еще одно известное векторное умножение, векторное произведение.)
$\endgroup$
2
Четыре вектора в теории относительности
Четыре вектора в теории относительности В литературе по теории относительности пространственно-временные координаты и энергия/импульс частицы часто выражаются в четырехвекторной форме.
| Index Reference | |||||||||||||
| ||||||||||||||
Они определены так, что длина четырехмерного вектора не меняется при преобразовании координат. Эта инвариантность связана с физическими представлениями. Инвариантность пространственно-временного четырехвектора связана с тем, что скорость света постоянна. Инвариантность четырехвектора энергии-импульса связана с тем, что масса покоя частицы инвариантна относительно преобразований координат.
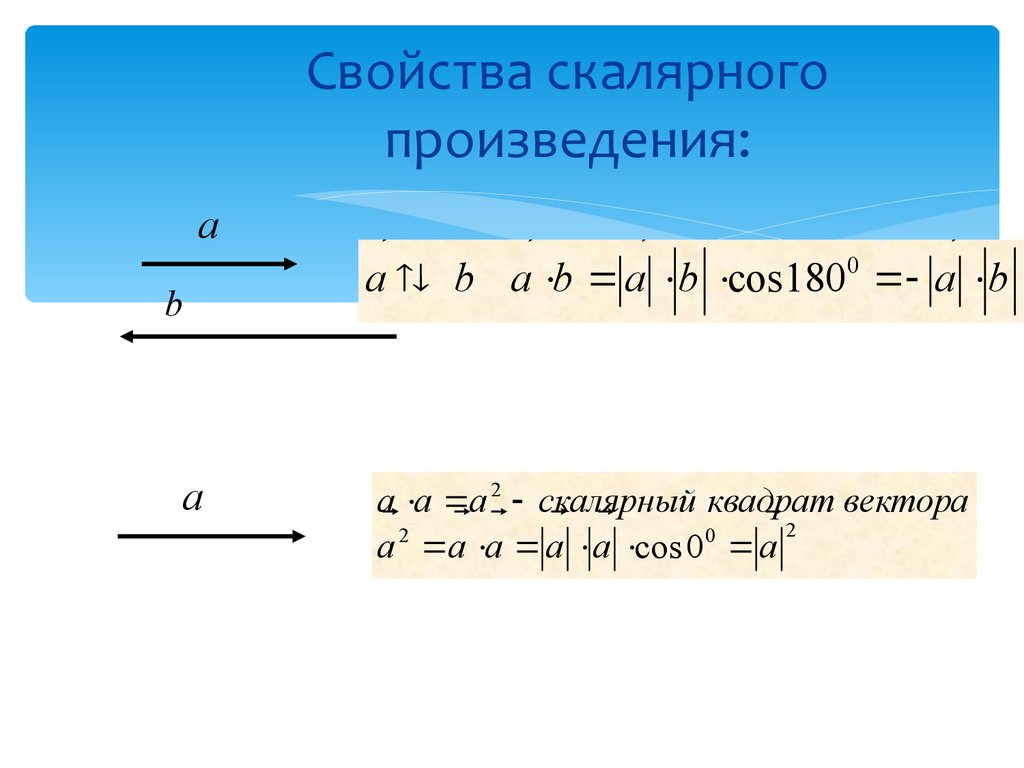
Для двух частиц можно определить длину 4-вектора энергии-импульса, который является инвариантом относительно преобразования Лоренца. Практическое преимущество этого для столкновений с высокой энергией состоит в том, что он позволяет вычислить импульс каждой частицы в системе отсчета с нулевым импульсом. Один из подходов к этому для системы из двух частиц включает добавление импульсов и энергии для двух частиц:
