ОглавлениеВВЕДЕНИЕЧАСТЬ ПЕРВАЯ. ВЕКТОРНАЯ АЛГЕБРА Глава I. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ 2. Скаляры и векторы. 3. Равенство векторов. 4.  Скользящие и приложенные векторные величины.6. Орт вектора. 7. Угол между двумя векторами. § 2. Сложение векторов 1. Сложение двух векторов. 2. Сложение более чем двух векторов. 3. Модуль суммы. 4. Законы сложения. § 3. Вычитание векторов § 4. Умножение и деление вектора на скаляр 2. Законы умножения вектора на скаляр. 3. Деление вектора на скаляр. 4. Выражение вектора через его модуль и орт. § 5. Линейные зависимости между векторами 2. Коллинеарные векторы. 3. Компланарные векторы. 4. Разложение вектора по трем некомпланарным векторам. 5. Метод координат. Глава II. ТЕОРИЯ ПРОЕКЦИЙ. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ § 1. Проекции векторов на ось § 3. Прямоугольная система координат в пространстве 1. Правая и левая прямоугольные системы координат. 2. Разложение вектора по ортам осей 3. Линейные операции над векторами в координатной форме.  4. Радиус-вектор и координаты точки. 5. Определение вектора по его началу и концу. 6. Деление отрезка в данном отношении. Глава III. ПРОИЗВЕДЕНИЯ ДВУХ ВЕКТОРОВ § 1. Скалярное произведение двух векторов 2. Работа силы. 3. Определение. 4. Равенство скалярного произведения нулю. 5. Законы скалярного умножения. 7. Скалярные произведения координатных ортов. 9. Неопределенность действия, обратного скалярному умножению. § 2. Векторное произведение двух векторов 3. Условия равенства нулю векторного произведения. 4. Законы векторного умножения. 5. Векторные произведения координатных ортов. 6. Определители. 7. Векторное произведение в координатной форме. 8. Неопределенность действия, обратного векторному умножению. Глава IV. ПРОИЗВЕДЕНИЯ ТРЕХ ВЕКТОРОВ § 1. Простейшее произведение трех векторов § 2. Векторно-векторное произведение трех векторов 3. Правило разложения векторно-векторного произведения.  § 3. Векторно-скалярное произведение трех векторов 2. Законы векторно-скалярного умножения 3. Обращение в нуль векторно-скалярного произведения трех векторов. 4. Векторно-скалярное произведение в координатной форме. § 4. Выражение векторно-скалярного произведения через скалярные произведения Глава V. ФУНКЦИИ ВЕКТОРОВ § 1. Произведения четырех векторов 2. Выражение скалярного произведения двух векторных произведений (а x b), (р x q) через скалярные произведения. 3. Разложение вектора (а, b, с) R по трем векторам a, b, c. 4. Разложение вектора (a, b, c) по векторным произведениям b x с, c x a, а x b 2. Разложение вектора (a, b, c) (m x n) по векторам a, b, c. 3. Выражение произведения двух смешанных произведений (a, b, c) (l, m, n) через скалярные произведения. § 3. Основные теоремы о функциях векторов 1. Рациональные функции векторов. 2. Элементарные функции векторов. 3. Произвольные скалярные функции от векторов.  4. Произвольные векторные функции векторов. Глава VI. ОСНОВНЫЕ ЗАДАЧИ § 2. Основные задачи, связанные со скалярным умножением векторов § 3. Основные задачи, связанные с векторным умножением векторов § 4. Основные задачи, связанные с произведениями трех и более векторов § 6. Геометрические инварианты фигур 2. Треугольник. 3. Полные системы инвариантов треугольника. 4. Тетраэдр. 5. Полные системы инвариантов тетраэдра. 6. Гексаэдр с треугольными гранями. ЧАСТЬ ВТОРАЯ. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ § 1. Векторы, зависящие от скаляра 2. Вектор-функция в координатной форме. 3. Годограф вектора. 4. Предел вектора. § 2. Дифференцирование вектора по скаляру 2. Геометрический смысл производной вектора по скаляру. 3. Механический смысл производной. 5. Дифференциал вектора. 6. Инвариантность дифференциала. 7. Связь дифференциала вектора с его приращением. Глава VIII.  ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ЛИНИИ В ПРОСТРАНСТВЕ§ 1. Основные дифференциально-геометрические понятия, связанные с линией 2. Касательная. 3. Соприкасающаяся плоскость. 4. Главная нормаль и бинормаль. 5. Кривизна. 6. Кручение. 7. Длина дуги. § 2. Основные формулы дифференциальной геометрии линий в пространстве 1. Дуга как параметр. Дифференциал дуги. 2. Орт касательной. Первая основная формула. 3. Инвариантность геометрических понятий. 4. Главная нормаль и кривизна. Вторая основная формула. 5. Бинормаль и кручение. Третья основная формула. § 3. Сопровождающий трехгранник 2. Система дифференциальных уравнений движения сопровождающего трехгранника. 3. Расположение линии относительно сопровождающего трехгранника. 4. Линии без кривизны. 5. Линии без кручения. § 4. Инвариантные формулы Глава IX. ПЛОСКИЕ ЛИНИИ § 1. Дифференциальные уравнения плоской линии § 2. Кривизна плоской линии § 3.  Круг кривизны§ 4. Эволюта § 5. Эвольвента Глава X. ПРИЛОЖЕНИЯ К МЕХАНИКЕ § 1. Скорость и ускорение точки § 2. Движение твердого тела вокруг неподвижной точки 3. Угловая скорость. 4. Доказательстве существования угловой скорости твердого тела. § 3. Относительная производная вектора 2. Абсолютная и относительная производные вектора. 3. Общий случай движения твердого тела. Глава XI. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ § 1. Векторные функции нескольких скалярных аргументов § 2. Параметризованная поверхность 2. Поверхность в декартовых координатах. 3. Параметрическая сеть. 4. Линия на параметризованной поверхности. § 3. Касательная плоскость и нормаль 3. Нормальный вектор. 4. Преобразование параметров. § 4. Площадь области на поверхности 2. Площадь области на поверхности. 4. Элемент площади поверхности.  5. Векторный элемент площади поверхности. § 5. Первая квадратичная форма поверхности 2. Внутренняя геометрия поверхности. 3. Длина дуги линии на поверхности. 4. Угол между линиями на поверхности. 5. Площадь области на поверхности. § 6. Вторая квадратичная форма поверхности 2. Нормальная кривизна линии на поверхности. 3. Теорема Менье. § 7. Главные направления и главные кривизны поверхности 2. Главные направления на поверхности. 3. Перпендикулярность главных направлений. 4. Формула Эйлера. ЧАСТЬ ТРЕТЬЯ. ТЕОРИЯ ПОЛЯ § 1. Функция поля. Поверхности уровня § 2. Градиент поля 2. Первая теорема о градиенте. § 3. Производная по направлению 2. Выражение производной по направлению через градиент. 3. Вторая теорема о градиенте. § 4. Направляющие косинусы нормали поверхности Глава XIII. КРИВОЛИНЕЙНЫЙ И ПОВЕРХНОСТНЫЙ ИНТЕГРАЛЫ § 1. Криволинейный интеграл как определенный интеграл от сложной функции 2.  Криволинейный интеграл от линейной формы по произвольной кривой.3. Основные свойства криволинейного интеграла. 4. Обобщенный криволинейный интеграл. § 2. Криволинейный интеграл как предел криволипейной интегральной суммы § 3. Поверхностный интеграл как двойной интеграл от сложной функции 2. Определение простейшего поверхностного интеграла. 3. Поверхностный интеграл от билинейной формы по произвольной поверхности. § 4. Поверхностный интеграл как предел поверхностной интегральной суммы § 5. Поверхностный интеграл в параметрической форме 2. Параметрический поверхностный интеграл. 3. Поверхностный интеграл как предел суммы. § 6. Кратный интеграл как предел обобщенной интегральной суммы 2. Обобщение основной теоремы о кратном интеграле. Глава XIV. ВЕКТОРНОЕ ПОЛЕ И ЕГО ИНТЕГРАЛЬНЫЕ ИНВАРИАНТЫ § 2. Векторные линии § 3. Циркуляция поля вдоль линии § 4. Поток поля через поверхность Глава XV.  ТЕОРЕМА ОСТРОГРАДСКОГО. ДИВЕРГЕНЦИЯ ПОЛЯ§ 1. Формула Остроградского § 2. Дивергенция поля 2. Дивергенция как предел отношения. 3. Гидромеханический смысл дивергенции. 4. Теорема Остроградского. Глава XVI. ТЕОРЕМА СТОКСА. РОТАЦИЯ ПОЛЯ § 1. Формула Стокса § 2. Ротация поля § 3. Оператор Гамильтона Глава XVII. СПЕЦИАЛЬНЫЕ ВЕКТОРНЫЕ ПОЛЯ § 1. Потенциальное поле 3. Циркуляция потенциального поля по замкнутому контуру. 4. Циркуляция потенциального поля между двумя точками. 5. Потенциал. 6. Элемент циркуляции. 7. Характеристические признаки потенциального поля. 8. Вычисление потенциала. 9. Центральное поле. 10. Вихревые шнуры. § 2. Соленоидальное поле 3. Поток соленоидального поля через замкнутую поверхность. 4. Трубчатое строение соленоидального поля. 5. Векторный потенциал. 6. Характеристические признаки соленоидального поля. 7. Источники и стоки. § 3. Потенциальное несжимаемое поле Глава XVIII.  ПРОСТЕЙШИЕ ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ§ 1. Электростатическое поле точечного заряда 2. Дивергенция поля точечного заряда. 3. Поток поля точечного заряда через замкнутую поверхность. 4. Ротация поля точечного заряда. 5. Потенциал поля точечного заряда. § 2. Электростатическое поле системы точечных зарядов 2. Дивергенция и ротация поля системы точечных зарядов. 3. Поток поля системы точечных зарядов через замкнутую поверхность. 4. Потенциал поля системы точечных зарядов. 5. Непрерывно распределенный заряд. § 3. Магнитное поле тока 2. Напряженность магнитного поля тока, текущего по бесконечному прямолинейному проводу. 3. Векторные линии поля H. 4. Потенциал поля Н. 5. Провод как вихревой шнур. Глава XIX. ВЕКТОРНОЕ ПОЛЕ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ § 1. Криволинейные координаты 3. Координатные поверхности и линии. 4. Линейный элемент. 5. Элемент объема. 6. Подвижной репер. 7. Векторное поле в криволиненных координатах.  § 2. Дифференциальные операции в криволинейных координатах 2. Дивергенция в криволинейных координатах. 3. Ротация в криволинейных координатах. § 3. Ортогональные координаты § 4. Цилиндрические координаты 2. Линейный элемент и элемент объема в цилиндрических координатах. 3. Дифференциальные операции в цилиндрических координатах. § 5. Сферические координаты |
Является ли расстояние вектором или скаляром: 7 важных пояснений
Расстояние — вектор или скаляр? Чтобы ответить на этот конкретный вопрос, мы должны понимать концепции расстояния, скаляра и вектора.
Можно сказать, что расстояние — это скалярная величина поскольку скаляры — это физические величины, которые имеют только величину, а векторы контраста имеют как величину, так и направление, а расстояние — это физическая величина, которая говорит нам только о протяженности пути, пройденного телом во время его движения.
Теперь давайте обсудим несколько аспектов, чтобы узнать подробнее о том, как расстояние является скаляром.
Прежде чем понять, как расстояние может быть скалярной величиной, мы должны подробно понять концепцию как скалярных, так и векторных величин.
Скаляр относится к физической величине, которая имеет только величину.Изображение: Скалярная физическая величина
Вектор относится к величинам, имеющим как величину, так и направление.
Изображение: Физическая величина вектораОбъяснение заключается в том, что расстояние всегда является скалярной величиной, что означает, что общая длина, пройденная телом, не зависит от направления пути, по которому оно проходит во время своего движения.Изображение: Общая длина, которую фургон преодолевает во время движения.
Исходя из объяснения, мы можем рассматривать расстояние как скалярную величину.
Расстояние: скалярная величина.
Расстояние показывает единственную величину пути, т. Е. Числовое значение того, сколько длины прошло тело.
Расстояние — это числовое измерение того, сколько жира тело прошло из одной точки в другую, игнорируя направление. Расстояние дает нам числовое значение, которое в физике считается величиной, а скалярные величины имеют только величину.
Таким образом, расстояние — это скалярная величина.Изображение: Расстояние по изогнутому курсу
Как расстояние является скалярнымнтити?Давайте разберемся с расстоянием с помощью примера и изображения, показанных ниже.
- На изображении, показанном ниже, обратите внимание на длину изогнутого пути, соединяющего две точки 1 и 2 (фиолетовая линия).
- На изображении ниже обратите внимание на прямые точки соединения 3 и 4 (зеленая линия)..
- Первое изображение указывает расстояние, потому что мы можем вычислить величину тела, не учитывая движение.
- Напротив, второе изображение говорит о смещении, потому что расстояние между любыми двумя точками меньше.
Таким образом, мы можем сказать, что расстояние — это скалярная величина.
Формула для расчетае расстояниеANCE.Математически мы можем рассчитать расстояние между двумя ссылками, используя формулу, показанную ниже.
Поскольку мы знаем, что расстояние — это скаляр, формула для расчета расстояния должна состоять из физических величин, таких как скорость и время, которые являются скалярами.
Формула для скорости определяется следующим образом:Скорость = пройденное расстояние * затраченное время
S = d * t ——— Уравнение 1
Формула для времени определяется следующим образом:Время = скорость / расстояние
Время = с / день ———- Уравнение 2
Из уравнения 1 и Уравнение 2,
Формула для расчета расстоянияРасстояние = скорость × время
д = с × т
Где,
- d = расстояние, пройденное телом в метрах.
- s = скорость тела метр в секунду (м / с)
- t = время, затраченное телом на преодоление дистанции в секундах.
Здесь скорость, расстояние и время взаимосвязаны.
Некоторые задачи, которые нужно решить с помощью формулы расстояния.Может подробно понять понятие расстояния, решая задачи по формуле.
Проблема 1
Ребенок переходит дорогу, и скорость ребенка, переходящего дорогу, составляет примерно 6 м / с. Однако ребенку требуется 30.0 секунд, чтобы перейти улицу. Рассчитать расстояние дороги от одного конца до другого?
Решения: Как показано выше, формула для расчета расстояния имеет вид
Расстояние = скорость * время.
д = с * т
d = (6 * 30)
d = 180 метров.
Таким образом, расстояние между двумя концами дороги составляет 180 метров.
Проблема 2В марафоне спортсмен бежит со скоростью 4 км / ч, чтобы преодолеть расстояние, равное 15 км. Посчитать, что ему нужно для завершения марафона?Изображение кредита: https://cdn.pixabay.com/photo/2019/03/27/13/48/marathon-4085048_1280.jpg
Решение: Здесь они дали
Скорость = s = 4 км / ч
Расстояние = d = 15 км
Формула скорости = s = d * t
т = с / д
т = 4 / 15
t = 15.6 мин
Таким образом, время, затрачиваемое спортсменом на преодоление марафона, составляет 15.6 минуты.
Проблема 3Рассмотрим пример велосипеда, который первоначально едет на запад на 7 км и поворачивает на юг еще на 10 км.
Какое общее расстояние преодолевает велосипед?
Решение: Общее расстояние, пройденное велосипедом, можно рассчитать как
д = д1 + д2
г = 7 + 10
d = 10 км.
Таким образом, общее расстояние, пройденное велосипедом, составляет 10 км.
Некоторые существенные характеристики расстояния как скалярной величины.Ниже приведены основные характеристики, которые дают ответ на определение расстояния в виде скаляра или вектора.
- Единица расстояния в системе СИ для макроскопических объектов обычно выражается в метрах.
- Для расчета расстояния необходимы ссылка и конечная точка.
- Формула для расчета расстояния состоит из скорости и времени.
- Расстояние и скорость скалярны.
- Расстояние от 1 до 2 или от 2 до 1 можно изменить.
Это некоторые важные особенности, позволяющие доказать расстояние как скаляр.
Некоторые примеры расстояния как скалярной величины.В нашей повседневной жизни бывают ситуации, когда необходимо рассчитать расстояние.
Путешествуя в школьном автобусе.
Путешествие в школьном автобусе приносит детям азарт. Школьный автобус перемещается в разные места, чтобы забрать учеников из разных мест и принять множество отклонений в своем движении, так что он движется на восток на 4 км и поворачивает на юг на 2 км. Общее расстояние, пройденное автобусом, составляет 6 км.Изображение Фото: https://cdn.pixabay.com/photo/2020/01/17/20/03/school-bus-4773905__480.jpg
Обычно повар аккуратно нарезает овощи и фрукты. В больших ресторанах для этой цели требуется красиво подать блюдо, и шеф-повар нарезает фрукты одинакового размера, сохраняя положение нарезки, чтобы получить нарезанные кусочки одинакового размера.
- Расстояние требуется для планирования поездки.
- Мы оцениваем расстояние, которое нам нужно преодолеть, чтобы перевезти тяжеловесный багаж, и можно ли перевезти багаж.
- Расстояние необходимо, чтобы забронировать автомобиль через приложение, чтобы снизить стоимость проезда.
- Расстояние между нашим домом и местом работы.
Из этих примеров повседневной жизни мы можем сделать вывод, что расстояние — это скаляр.
Часто задаваемые вопросы о расстоянии | FAQsЧто такое расстояние?Расстояние — это физическая величина, используемая для измерения длины между двумя контрольными точками.
Расстояние, как правило, определяется как общее числовое значение длины пути, пройденного человеком или телом при их движении, т. Е. Оно показывает единственную величину пройденного пути.
Следовательно, это скалярный характер.
Скаляр — это тип измеримой физической величины.
Скаляр — это одна из физических величин, используемых для измерения размера и длины тела, когда оно находится в движении. Скаляр определяется как величины, которые сосредоточены только на величине тела, т. Е. Говорят только о числовом значении пройденного пути. Мгновенная скорость, расстояние, масса являются примерами скаляра.
Что такое величина?Величина — один из специальных терминов, используемых в физической науке.
Величина обычно указывает числовое значение определенных количеств тела, основанных на размере, длине, скорости и т. Д. Она говорит о том, сколько времени тело прошло во время своего движения.
В каком направлении?Направление в физике используется для обозначения конкретных точек путешествия.
Направление — это термин, который мы используем для обозначения пути, по которому движется тело во время своего движения.
Это также называется особыми ориентациями, которые тело принимает во время движения, чтобы добраться до места назначения. Он дает точную точку, в которой происходит действие.
Вектор — это одна из физических величин, используемых для измерения величины и направления.
Векторы обычно определяются как величины, которые концентрируются на величине, такой как размер, длина и т. Д., И направлении тела при его движении. Угловая скорость, ускорение, смещение — вот некоторые примеры твердого тела. Символ v обычно обозначает его.
Почему расстояние не может быть отрицательным?Расстояние — это измеримая физическая величина, которая не может быть отрицательной.
В общем, расстояние — это сумма числового значения длины пути тела во время его движения. Расстояние аддитивно; он не может иметь отрицательных значений. Следовательно, расстояние — это физическая величина, состоящая только из положительных значений.
Расстояние — это измеримая величина, и она не может быть нулевой.
Мы знаем, что расстояние — это общая сумма длины пути, который проходит тело, когда оно движется между двумя контрольными точками. Расстояние может быть нулевым только тогда, когда тело остается в покое, и оно не может уменьшаться.
Узнайте больше о Может ли расстояние быть кривой?
2.2 Векторы, скаляры и системы координат – Колледж физики, главы 1-17
2 Кинематика
РезюмеОпределение и различие между скалярными и векторными величинами.
Назначьте систему координат для сценария с одномерным движением. Рисунок 1. Движение этого самолета Eclipse Concept может быть описано в терминах пройденного им расстояния (скалярная величина) или его смещения в определенном направлении (векторная величина). Чтобы указать направление движения, его перемещение должно быть описано на основе системы координат.
В этом случае может быть удобно выбрать движение влево как положительное движение (для плоскости это направление вперед), хотя во многих случаях x -координата идет слева направо, движение вправо считается положительным, а движение влево — отрицательным. (кредит: кресло «Авиатор», Flickr).В чем разница между расстоянием и перемещением? В то время как смещение определяется как направлением, так и величиной, расстояние определяется только величиной. Перемещение является примером векторной величины. Расстояние является примером скалярной величины. Вектор — это любая величина с величиной и направлением . Другие примеры векторов включают скорость 90 км/ч на восток и силу 500 ньютонов прямо вниз.
Направление вектора в одномерном движении задается просто знаком плюс (+) или минус (-). Векторы представлены графически стрелками. Стрелка, используемая для представления вектора, имеет длину, пропорциональную величине вектора (например, чем больше величина, тем больше длина вектора) и указывает в том же направлении, что и вектор.
Некоторые физические величины, такие как расстояние, либо не имеют направления, либо не указаны. А 9o\textbf{C}}[/latex]температура. В этом случае знак минус указывает точку на шкале, а не направление. Скаляры никогда не изображаются стрелками.
Чтобы описать направление векторной величины, вы должны указать систему координат в системе отсчета. Для одномерного движения это простая система координат, состоящая из одномерной координатной линии. В общем, при описании горизонтального движения движение вправо обычно считается положительным, а движение влево считается отрицательным. При вертикальном движении движение вверх обычно положительное, а движение вниз отрицательное. Однако в некоторых случаях, как в случае со струей на рис. 1, может быть удобнее поменять местами положительное и отрицательное направления. Например, если вы анализируете движение падающих объектов, может быть полезно определить положительное направление вниз. Если люди в гонке бегут налево, полезно определить лево как положительное направление.
Это не имеет значения, пока система ясна и последовательна. Как только вы задаете положительное направление и начинаете решать проблему, вы не можете изменить его.
- Вектор — это любая величина, имеющая величину и направление.
- Скаляром является любая величина, имеющая величину, но не имеющую направления.
- Перемещение и скорость являются векторами, тогда как расстояние и скорость являются скалярами.
- В одномерном движении направление задается знаком плюс или минус для обозначения влево или вправо, вверх или вниз и т.п.
- скаляр
- количество, описываемое величиной, но не направлением
- вектор
- количество, описываемое как величиной, так и направлением
Как найти скалярную и векторную проекции одного вектора на другой — Криста Кинг Математика
Что такое скалярная и векторная проекции?
Скалярные проекции
Скалярная проекция одного вектора на другой (также называемая компонентой одного вектора вдоль другого) равна
???\text{comp}_a{b}=\frac{a\cdot{b}}{ |а|}???
где ???a\cdot{b}??? скалярное произведение векторов ???a??? и ???б???, и ???|а|??? длина ???a??? (также называется величиной ???a???).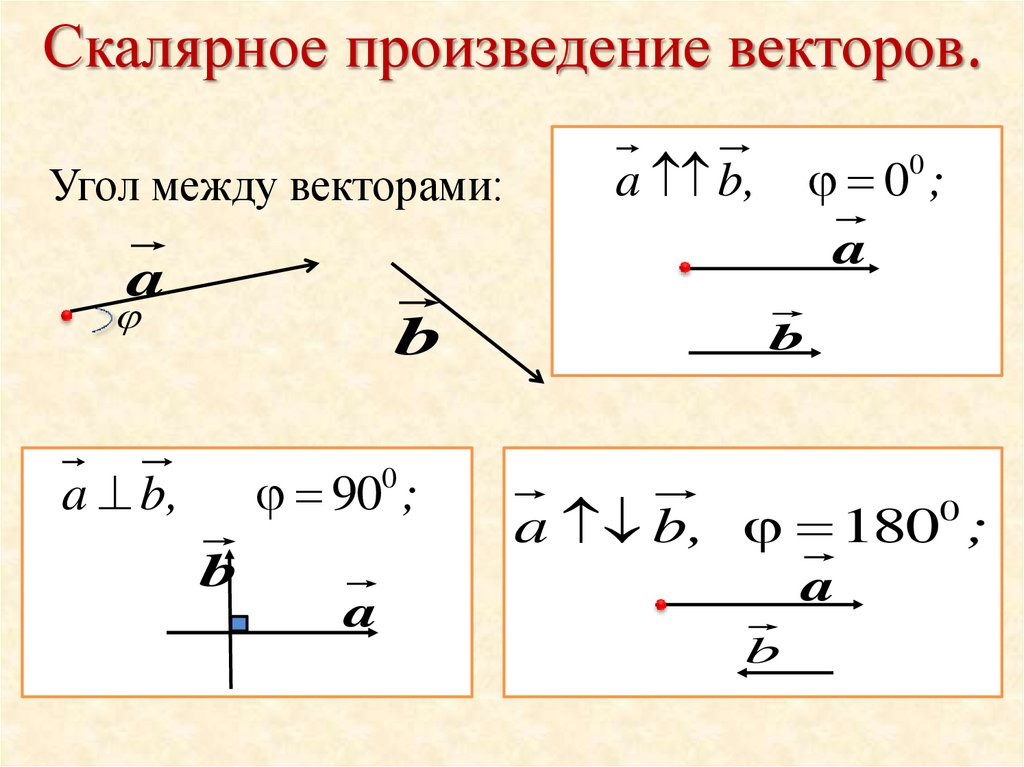
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Векторные проекции
Векторная проекция одного вектора на другой подобна тени, которую один вектор отбрасывает на другой вектор. Например, проекция зеленого на оранжевый будет синей:
.???\text{proj}_a{b}=\left(\frac{a\cdot{b}}{|a|}\right)\frac{a}{|a|}???
где ???a\cdot{b}??? скалярное произведение векторов ???a??? и ???б???, и ???|а|??? длина ???a??? (также называется величиной ???a???).
Как найти скалярную и векторную проекции одного вектора на другой
Пройти курс
Хотите узнать больше об исчислении 3? У меня есть пошаговый курс для этого. :). на ???а???.
???a=i+2j-3k???
???b=6i+j???
Поскольку мы используем значение скалярной проекции в формуле для векторной проекции, мы начнем с нахождения скалярной проекции.
