Радиус-вектор — Википедия

Материал из Википедии — свободной энциклопедии

Ра́диус-ве́ктор (обычно обозначается r→{\displaystyle {\vec {r}}} или просто r{\displaystyle \mathbf {r} }) — вектор, задающий положения точки в пространстве (например, евклидовом) относительно некоторой заранее фиксированной точки, называемой началом координат.

Для произвольной точки в пространстве радиус-вектор — это вектор, идущий из начала координат в эту точку.

Длина, или модуль радиус-вектора — расстояние, на котором точка находится от начала координат, стрелка вектора — указывает направление на эту точку пространства.

На плоскости углом радиус-вектора называется угол, на который радиус-вектор повёрнут относительно оси абсцисс в направлении против часовой стрелки.

Радиус-вектор в различных системах координат[править | править код]

Двумерное пространство[править | править код]

r→=xe→x+ye→y={x,y}{\displaystyle {\vec {r}}=x{\vec {e}}_{x}+y{\vec {e}}_{y}=\left\{x,y\right\}}

r→=ρe→ρ={ρ,0}{\displaystyle {\vec {r}}=\rho {\vec {e}}_{\rho }=\left\{\rho ,0\right\}}

Трёхмерное пространство[править | править код]

r→=xe→x+ye→y+ze→z={x,y,z}{\displaystyle {\vec {r}}=x{\vec {e}}_{x}+y{\vec {e}}_{y}+z{\vec {e}}_{z}=\left\{x,y,z\right\}}

r→=ρe→ρ+ze→z={ρ,0,z}{\displaystyle {\vec {r}}=\rho {\vec {e}}_{\rho }+z{\vec {e}}_{z}=\left\{\rho ,0,z\right\}}

r→=ρe→ρ={ρ,0,0}{\displaystyle {\vec {r}}=\rho {\vec {e}}_{\rho }=\left\{\rho ,0,0\right\}}

n-мерное пространство[править | править код]

r→=x1e→1+x2e→2+…+xne→n={x1,x2,…,xn}{\displaystyle {\vec {r}}=x_{1}{\vec {e}}_{1}+x_{2}{\vec {e}}_{2}+…+x_{n}{\vec {e}}_{n}=\left\{x_{1},x_{2},…,x_{n}\right\}}

Волновой вектор — Википедия

Материал из Википедии — свободной энциклопедии

Волновой вектор — вектор, направление которого перпендикулярно фазовому фронту бегущей волны, а абсолютное значение равно волновому числу.

Волновой вектор обычно обозначается латинской буквой k{\displaystyle \mathbf {k} } и величина его измеряется в обратных метрах (Международная система единиц (СИ)) или в обратных сантиметрах (система СГС) (т. е. радианах на метр или радианах на сантиметр). Следует быть внимательным, т. к. иногда может использоваться определение в оборотах, отличающееся множителем 2π{\displaystyle 2\pi }, но дающее ту же физическую размерность.

Волновое число связано с длиной волны λ{\displaystyle \lambda } соотношением:

k=2πλ{\displaystyle k={\frac {2\pi }{\lambda }}}.

Связь между волновым вектором и частотой задаётся законом дисперсии. Все возможные значения волновых векторов образуют обратное пространство, или k-пространство.

Наиболее общим определением волнового вектора можно считать такое: волновой вектор есть градиент фазы волны:

k=gradϕ.{\displaystyle \mathbf {k} =\mathbf {grad} \phi .}

Для строго монохроматической плоской волны в однородной среде распространения волновой вектор строго фиксирован (не зависит от координат и времени). Любая строго монохроматическая волна в однородной среде может быть представлена как сумма (интеграл) плоских волн с волновыми векторами, имеющими одинаковую абсолютную величину (но разное направление, если волна отличается от плоской).

Как правило, использование волнового вектора подразумевает, что речь идет о монохроматических или близких к монохроматичности квазимонохроматических волнах, в случае же существенно немонохроматических волн речь идет как правило о том, что они представлены (см. Преобразование Фурье) в виде суммы монохроматических, к каждой из которых понятие волнового вектора применяется отдельно, и у каждой из которых он отличается.

Однако в отдельных случаях (например, при использовании интеграла по траекториям, а также иногда при использовании определенных других математических приёмов) волновой вектор может достаточно быстро меняться в пространстве и со временем.

Кроме того, в задачах с существенно немонохроматическими, но периодическими или близкими к периодичности, плоскими волнами волновой вектор в принципе может быть определен прямо через длину волны (как в начале статьи), не используя понятия фазы; в таком виде он может оказаться полезным, но надо осознавать, что такое понимание существенно отличается от обычного (хотя и сходное).

В квантовой механике волновой вектор волновой функции есть импульс, с точностью до универсальной константы (т. е. с точностью до выбора единиц измерения физических величин):

p=ℏk,{\displaystyle \mathbf {p} =\hbar \mathbf {k} ,}

где p{\displaystyle \mathbf {p} } — вектор импульса, ℏ{\displaystyle \hbar } — постоянная Планка, или, при выборе системы единиц так, чтобы ℏ=1{\displaystyle \hbar =1}, просто:

p=k.{\displaystyle \mathbf {p} =\mathbf {k} .}

Это соотношение определяет фундаментальный смысл импульса с точки зрения квантовой механики и современной физики вообще: с этой точки зрения импульс есть волновой вектор (с отличием разве что на постоянный множитель).

Вектор Пойнтинга — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 10 апреля 2019; проверки требуют 14 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 10 апреля 2019; проверки требуют 14 правок.

Вектор Пойнтинга (также вектор Умова — Пойнтинга) — вектор плотности потока энергии электромагнитного поля, компоненты которого входят в состав компонент тензора энергии-импульса электромагнитного поля^[1].

Вектор Пойнтинга S можно определить через векторное произведение двух векторов:

S=c4π[E×H]{\displaystyle \mathbf {S} ={\frac {c}{4\pi }}[\mathbf {E} \times \mathbf {H} ]} (в системе СГС),

S=[E×H]{\displaystyle \mathbf {S} =[\mathbf {E} \times \mathbf {H} ]} (в Международной системе единиц (СИ)),

где

E и H — векторы напряжённости электрического и магнитного полей соответственно.

цепь постоянного тока i, соединяющая батарею V с резистором R
вектор Пойнтинга S в пространстве, окружающем цепь
напряжённость электрического поля Е
напряжённость магнитного поля H
Вокруг батареи вектор Пойнтинга направлен от батареи, что свидетельствует о переносе энергии из батареи; вокруг резистора вектор Пойнтинга направлен к резистору, что говорит о переносе энергии в резистор; поток вектора Пойнтинга через любую плоскость Р между батареей и резистором — направлен от батареи к резистору.

В случае квазимонохроматических электромагнитных полей, справедливы следующие формулы для усреднённой по периоду комплексной плотности потока энергии^[2]:

S¯=c8π[E×H∗]{\displaystyle {\overline {\mathbf {S} }}={\frac {c}{8\pi }}[\mathbf {E} \times \mathbf {H^{\ast }} ]} (в системе СГС),

S¯=12[E×H∗]{\displaystyle {\overline {\mathbf {S} }}={\frac {1}{2}}[\mathbf {E} \times \mathbf {H^{\ast }} ]} (в системе СИ),

где E и H — векторы комплексной амплитуды электрического и магнитного полей соответственно. В этом случае чёткий физический смысл имеет только действительная часть комплексного вектора S — это вектор усреднённой за период плотности потока энергии. Физический смысл мнимой части зависит от конкретной задачи.

Модуль вектора Пойнтинга равен количеству энергии, переносимой через единичную площадь, нормальную к S, в единицу времени. Своим направлением вектор определяет направление переноса энергии.

Поскольку тангенциальные к границе раздела двух сред компоненты E и H непрерывны (см. граничные условия), то нормальная составляющая вектора S непрерывна на границе двух сред.

Вектор Пойнтинга и импульс электромагнитного поля[править | править код]

В силу симметричности тензора энергии-импульса, все три компоненты вектора пространственной плотности импульса электромагнитного поля равны соответствующим компонентам вектора Пойнтинга, делённым на квадрат скорости света:

dpdV=1c2S=1c2[E×H]{\displaystyle {\frac {d\mathbf {p} }{dV}}={\frac {1}{c^{2}}}\mathbf {S} ={\frac {1}{c^{2}}}[\mathbf {E} \times \mathbf {H} ]} (в системе СИ)

В этом соотношении проявляется материальность электромагнитного поля.

Поэтому, чтобы узнать импульс электромагнитного поля в той или иной области пространства, достаточно проинтегрировать вектор Пойнтинга по объёму.

Общее представление о потоке механической энергии в пространстве впервые было введено Н. А. Умовым в 1874 году для упругих сред и вязких жидкостей. На этом основании в более старых русскоязычных публикациях вектор плотности потока энергии любой физической природы называется вектором Умова^[3]. В 1884 году Д. Г. Пойнтингом^[4] были разработаны представления о плотности потока электромагнитной энергии. Поэтому вектор плотности потока электромагнитной энергии называется вектором Пойнтинга.

Сами же законы сохранения и превращения энергии, где присутствует понятие плотности потока какого-либо вида энергии, используются, как правило, без указания имен первооткрывателей, поскольку законы сохранения являются следствием других уравнений и дополнительных условий.

Теорема Пойнтинга

1. ↑ Пойнтинга вектор // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1992. — Т. 3: Магнитоплазменный — Пойнтинга теорема. — С. 671. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
2. ↑ Марков Г.Т., Сазонов Д.М. Глава 1 Электродинамические основы теории антенн, § 1-1. Уравнения Максвелла // Антенны. — М.: Энергия, 1975. — С. 16-17. — 528 с.
3. ↑ Сивухин Д. В. Общий курс физики. Т III. Электричество. 1975
4. ↑ Фейнман Р. Глава 27. Энергия поля и его импульс. § 3. Плотность энергии и поток энергии в электромагнитном поле // Лекции по физике. — Вып. 4. — М.: Мир, 1965. — Т. 6. Электродинамика. — С. 286-290. — 340 с.

Вектор электрической поляризации — Википедия

Материал из Википедии — свободной энциклопедии

Вектор поляризации — векторная физическая величина, равная дипольному моменту единицы объёма вещества, возникающему при его поляризации, количественная характеристика диэлектрической поляризации^[1].

Обозначается буквой P{\displaystyle \mathbf {P} }, в Международной системе единиц (СИ) измеряется в Кл/м².

Диэлектрическая поляризация обусловлена смещением связанных зарядов вещества во внешнем электрическом поле относительно их расположения при отсутствии внешнего электрического поля. Если выделить какой-либо объём в диэлектрике, то в результате приложения поля на его поверхности могут возникнуть поверхностные электрические заряды σsur{\displaystyle \sigma _{sur}}. Такие заряды могут возникнуть или благодаря смещению электронной оболочки относительно ядра атома, или же в результате переориентации молекул, которые имеют собственный дипольный момент.

Нормальную к поверхности составляющую вектора поляризации определяют как

Pn=P⋅n=σsur,{\displaystyle P_{n}=\mathbf {P} \cdot \mathbf {n} =\sigma _{sur},}

где n{\displaystyle \mathbf {n} } — орт нормали к поверхности.

Можно ввести вектор электрической индукции D{\displaystyle \mathbf {D} }, который удобен при описании электрического поля в сплошной среде:

D=ε0E+P{\displaystyle \mathbf {D} =\varepsilon _{0}\mathbf {E} +\mathbf {P} } (СИ)

D=E+4πP{\displaystyle \mathbf {D} =\mathbf {E} +4\pi \mathbf {P} } (СГС)

В основном зависимость между вектором поляризации и электрическим полем, которое обусловило поляризацию, линейна и задается тензором поляризуемости.

P=α^E{\displaystyle \mathbf {P} ={\hat {\alpha }}\mathbf {E} }.

Определённые вещества могут быть поляризованными при отсутствии электрического поля. К таким веществам относятся пироэлектрики — кристаллические вещества со спонтанной поляризацией и электреты — аморфные вещества, в которых наведённая полем поляризация может сохраняться на протяжении длительного времени.

В случае переменного электрического поля среда может реагировать на изменение поля с некоторым запозданием. В этом случае вектор поляризации в данный момент зависит от напряжённости приложенного электрического поля в предыдущие моменты времени. В таких случаях говорят о временно́й дисперсии и соотношения между вектором поляризации и электромагнитным полем выглядят как

P(t)=∫0∞α^(t′)E(t−t′)dt′{\displaystyle \mathbf {P} (t)=\int \limits _{0}^{\infty }{\hat {\alpha }}(t^{\prime })\mathbf {E} (t-t^{\prime })dt^{\prime }}.

Фурье-образы вектора поляризации и напряжённости электрического поля в таком случае связаны линейным соотношением: (P)ω=α^(ω)Eω{\displaystyle \mathbf {(} P)_{\omega }={\hat {\alpha }}(\omega )\mathbf {E} _{\omega }}, где

α^(ω)=∫0∞α^(t)eiωtdt{\displaystyle {\hat {\alpha }}(\omega )=\int \limits _{0}^{\infty }{\hat {\alpha }}(t)e^{i\omega t}dt}.

Если электромагнитное поле неоднородно в пространстве, как, например, в случае распространения электромагнитных волн, и взаимодействует с возбуждениями в веществе, которые имеют длину волны порядка длины электромагнитной волны, то значение поляризации в определённой точке пространства зависит от значения напряжённости электрического поля в соседних точках пространства. В таких случаях говорят о пространственной дисперсии (укр.)русск..

P(t,r)=∫d3r′∫0∞α^(t′,r′)E(t−t′,r−r′)dt′{\displaystyle \mathbf {P} (t,\mathbf {r} )=\int d^{3}r^{\prime }\int \limits _{0}^{\infty }{\hat {\alpha }}(t^{\prime },\mathbf {r} ^{\prime })\mathbf {E} (t-t^{\prime },\mathbf {r} -\mathbf {r} ^{\prime })dt^{\prime }}.

В сильных электрических полях зависимость между поляризацией и электрическим полем может отличаться от линейной. Явления, которые при этом возникают, изучаются, например, в нелинейной оптике.

Вектор скорости — это… Что такое Вектор скорости?

Ско́рость (часто обозначается 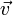, от англ. velocity или фр. vitesse) — векторная величина, характеризующая быстроту перемещения и направление движения материальной точки в пространстве относительно выбранной системы отсчёта. Этим же словом может называться скалярная величина, точнее модуль производной радиус-вектора.

В науке повсеместно используется также скорость в широком смысле, то есть как скорость изменения какой-либо величины (не обязательно радиус-вектора). Так, например, говорят об угловой скорости, скорости роста температуры, скорости химической реакции и т. д. Математически находится с помощью производной от данной величины (обычно по времени, либо от другого аргумента).

Скорость тела в механике

Вектор скорости материальной точки в каждый момент времени определяется производной по времени радиус-вектора 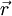этой точки:

Здесь v — модуль скорости, 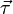 — направленный вдоль скорости единичный вектор касательной к траектории в точке .

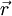Говорят, что тело совершает мгновенно-поступательное движение, если в данный момент времени скорости всех составляющих его точек равны. Так, например, равны скорости всех точек кабинки колеса обозрения (если, конечно, пренебречь колебаниями кабинки).

В общем случае, скорости точек, образующих твёрдое тело, не равны между собой. Так, например, для катящегося без проскальзывания колеса величина скорости точек на ободе относительно дороги принимает значения от нуля (в точке касания с дорогой) до удвоенного значения скорости автомобиля (в точке, диаметрально противоположной точке касания). Распределение скоростей в твёрдом теле определяется с помощью кинематической формулы Эйлера.

Если скорость тела (как векторная величина) не меняется во времени, то движение тела — равномерное (ускорение равно нулю).

Полезно отличать понятие средней скорости перемещения от понятия средней скорости пути, равной отношению пройденного точкой пути ко времени, за которое этот путь был пройден. В отличие от скорости перемещения, средняя скорость пути — скаляр.

Мгновенная и средняя скорость

Когда говорят о средней скорости , для различения, скорость согласно выше приведённому определению называют мгновенной скоростью. Так, хотя мгновенная скорость бегуна, кружащего по стадиону, в каждый момент времени отлична от нуля, его средняя скорость (перемещения) от старта до финиша оказывается равной нулю, если точки старта и финиша совпадают. Заметим, что при этом, средняя путевая скорость остаётся отличной от нуля.

Преобразование скорости

В классической механике Ньютона скорости преобразуются при переходе из одной инерциальной системы отсчёта в другую согласно преобразованиям Галилея. Если скорость тела в системе отсчёта S была равна 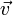, а скорость системы отсчёта S’ относительно системы отсчёта S равна 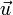, то скорость тела в при переходе в систему отсчёта S’ будет равна .

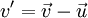Для скоростей, близких к скорости света преобразования Галилея становятся несправедливы. При переходе из системы S в систему S’ необходимо использовать преобразования Лоренца для скоростей:

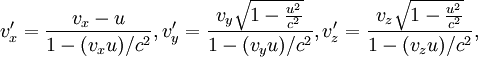
в предположении, что скорость направлена вдоль оси х системы S. Легко убедиться, что в пределе нерелятивистских скоростей преобразования Лоренца сводятся к преобразованиям Галилея.

Единицы измерения скорости

Соотношение между единицами скорости

• 1 м/с = 3,6 км/ч
• 1 узел = 1,852 км/ч = 0,514 м/c
• Мах 1 ~ 330 м/c ~ 1200 км/ч (зависит от условий, в которых находится воздух)
• c = 299 792 458 м/c

См. также

Wikimedia Foundation. 2010.