Разница между скалярным и векторным количеством

• 2019

Без майонеза!Салат …

Please enable JavaScript

Без майонеза!Салат с пекинской капустой и кукурузой

Скалярное количество относится к количеству, которое имеет только величину и не имеет направления. С другой стороны, векторная величина подразумевает физическую величину, которая включает в себя как величину, так и направление.

Физика — это наука, основанная на математике. Изучая физику, мы проходим через ряд понятий и понятий, которые опираются на математику. Математические величины, объясняющие движение тела, делятся на две группы: скалярная величина и векторная величина.

Для непрофессионала оба термина одинаковы, но в мире физики существует огромная разница между скалярной и векторной величиной. Итак, взгляните на статью, предоставленную вам, для лучшего понимания.

Сравнительная таблица

Основа для сравнения	Скалярная величина	Количество векторов
Имея в виду	Любая физическая величина, которая не включает в себя направление, называется скалярной величиной.	Количество векторов равно единице, которая имеет величину и направление.
Количества	Одномерные величины	Многомерные величины
+ Изменить	Это изменяется с изменением их величины.	Это изменяется с изменением их направления или величины или обоих.
операции	Следуйте обычным правилам алгебры.	Следуйте правилам векторной алгебры.
Сравнение двух величин	просто	Сложный
разделение	Скаляр может делить еще один скаляр.	Два вектора никогда не могут делиться.

Определение скалярного количества

Термин «скалярная величина» определяется как величина, имеющая только один элемент числового поля, связанный с единицей измерения, например градусами или метрами. Это величина, которая демонстрирует только величину или размер, то есть она определяется числовым значением вместе с единицей измерения. Например, скорость автомобиля, температура тела, расстояние между двумя точками и т. Д.

Правила обычной алгебры могут применяться для объединения скалярных величин, так что скаляры можно складывать, вычитать или умножать так же, как числа. Однако работа скаляра возможна только для величин с одинаковыми единицами измерения.

Определение количества векторов

Математическая величина, которая нуждается в двух независимых характеристиках, чтобы полностью ее описать, а именно: величина и направление. Здесь величина представляет размер величины, которая также является ее абсолютным значением, а направление представляет сторону, то есть восток, запад, север, юг и т. Д. Например, смещение между двумя точками, скорость и ускорение движущегося тела, сила, вес и т. д.

Величина вектора следует закону сложения треугольника. Стрелка используется для указания количества вектора, расположенного над или рядом с символом, который обозначает вектор.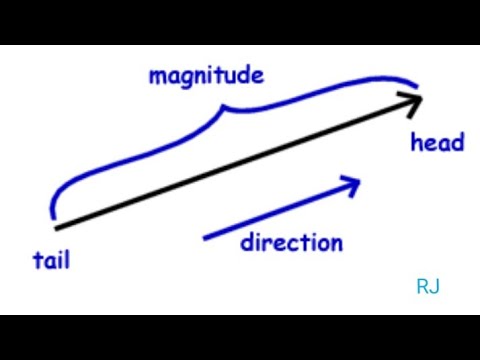

Следующие пункты заслуживают внимания, поскольку речь идет о разнице между скалярной и векторной величиной:

1. Скалярная величина описывается как величина, имеющая только одну характеристику, т.е. величину. Векторная величина — это физическая величина, для определения которой необходимы величина и направление.
2. Скалярные величины объясняют одномерные величины. С другой стороны, многомерные величины объясняются векторной величиной.
3. Скалярное количество изменяется только тогда, когда происходит изменение их величины. В противоположность этому, величина вектора изменяется с изменением их величины, направления или того и другого.
4. За обычными правилами алгебры следуют скалярные величины для выполнения таких операций, как сложение, вычитание и умножение, в то время как для выполнения операций векторные величины следуют правилам векторной алгебры.
5. При сравнении двух скалярных величин необходимо учитывать только величину, тогда как при сравнении двух векторных величин необходимо учитывать как величину, так и направление. Таким образом, с векторными величинами работать сложнее, чем со скалярными.
6. Наконец, что не менее важно, скалярная величина может разделить другой скаляр, но это не может быть сделано в случае векторной величины.

Заключение

Короче говоря, скалярное количество дает вам представление о том, сколько существует объекта, но векторное количество дает вам представление о том, сколько существует объекта и что также в каком направлении. Таким образом, основное различие между этими двумя величинами связано с направлением, то есть скаляры не имеют направления, а векторы.

Что такое векторное количество? (С примерами) / математика | Thpanorama

Он определяет векторное количество, или вектор, как тот, для которого необходимо указать как его величину или модуль (с соответствующими единицами), так и его адрес.

В отличие от векторной величины, скалярная величина имеет только величину (и единицы измерения), но не имеет направления. Некоторыми примерами скалярных величин являются температура, объем объекта, длина, масса и время, среди прочих.

Разница между вектором и скалярной величиной

В следующем примере вы можете научиться отличать скалярную величину от векторной величины:

Скорость 10 км / ч является скалярной величиной, а скорость 10 км / ч к северу является векторной величиной. Разница в том, что во втором случае указывается адрес, помимо величины.

Векторные величины имеют бесконечное множество применений, особенно в мире физики.

Графики и обозначения векторной величины

Чтобы обозначить векторную величину, поместите стрелку (→) на букву, которая будет использоваться, или написав ее жирным шрифтом (в).

Чтобы отобразить векторное количество, необходима система отсчета. В этом случае декартовой план будет использоваться в качестве системы отсчета.

График вектора представляет собой линию, длина которой представляет величину; и угол между этой линией и осью X, измеренный против часовой стрелки, представляет ее направление.

Вы должны указать, что является отправной точкой вектора и какова точка прибытия. В конце линии также указана стрелка, указывающая на точку прибытия, которая указывает направление вектора..

После задания системы отсчета вектор можно записать в виде упорядоченной пары: первая координата представляет его величину, а вторая — его направление..

примеров

1- Гравитация, воздействующая на объект

Если объект находится на высоте 2 метра над землей и он выпущен, сила тяжести воздействует на него с величиной 9,8 м / с² и направлением, перпендикулярным земле, в направлении вниз.

2- Движение самолета

Самолет, который переместился из точки A = (2,3) в точку B = (5,6) декартовой плоскости со скоростью 650 км / ч (величина). Направление траектории 45 ° к северо-востоку (направление).

Следует отметить, что если точки поменялись местами, то вектор имеет одинаковую величину и одинаковое направление, но разное направление, которое будет на юго-запад.

3- Сила, приложенная к объекту

Хуан решает подтолкнуть кресло силой 10 фунтов в направлении, параллельном земле. Возможные значения приложенной силы: слева или справа (в случае декартовой плоскости).

Как и в предыдущем примере, значение, которое Хуан решает придать силе, даст другой результат.

Это говорит нам о том, что два вектора могут иметь одинаковую величину и направление, но быть разными (они дают разные результаты).

Два или более векторов могут быть добавлены и вычтены, для которых есть очень полезные результаты, такие как, например, закон параллелограмма. Вы также можете умножить вектор на скаляр.

ссылки

1. Барраган А., Серпа Г., Родригес М. и Нуньес Х. (2006). Физика для бакалавриата Cinematica. Пирсон Образование.
2. Форд, К. В. (2016). Основная физика: решения для упражнений. Всемирная научная издательская компания.
3. Джанколи, доктор философии (2006). Физика: принципы с приложениями. Пирсон Образование.
4. Гомес, А. Л., & Трехо, Х. Н. (2006). Физика л, Конструктивистский подход. Пирсон Образование.
5. Serway, R.A. & Faughn, J.S. (2001). физика. Пирсон Образование.
6. Страуд, К. А. и Бут, Д. Дж. (2005). Векторный анализ (Иллюстрированный ред.). Индустриал Пресс Инк.
7. Wilson, J.D. & Buffa, A.J. (2003). физика. Пирсон Образование.

Разница между скалярными и векторными величинами | Физика Фургон

Категория Выберите категориюО фургоне физикиЭлектричество и магнитыВсе остальноеСвет и звукДвижение вещейНовая и захватывающая физикаСостояния материи и энергииКосмосПод водой и в воздухе

Подкатегория

Поиск

Задайте вопрос

Последний ответ: 16.05.2009

В:

в чем разница между скалярными и векторными величинами?
— Фатима (16 лет)
Пакистан

A:

Скалярная величина – это одномерное измерение величины, такой как температура или масса.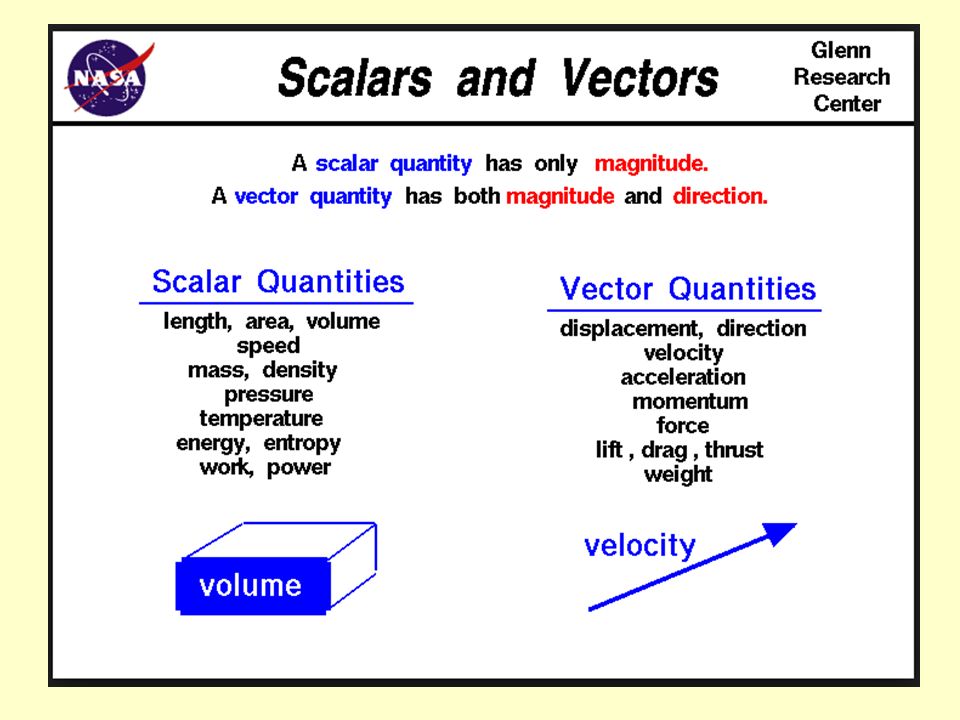 С вектором связано более одного числа. Простой пример — скорость. У него есть величина, называемая скоростью, а также направление, такое как север или юго-запад или 10 градусов к западу от севера. С вектором может быть связано более двух чисел. Например, вы можете добавить измерение высоты к скорости и сказать, например, «Я иду в гору с уклоном 5 градусов в северо-восточном направлении». Векторы часто разбиваются на компоненты по ортогональной системе координат, например по осям x и y. Таким образом, вы можете сказать, что y-компонент моей скорости равен 3 км/сек, а x-компонент моей скорости равен 4 км/сек. Величина или скорость представляет собой квадратный корень из суммы отдельных компонентов, в данном случае 5. Направление по отношению к оси х задается арктангенсом V

y /Vx или 36,9 градусов.

LeeH

(опубликовано 16.05.2009)

Дополнение №1: Комплексные числа — скаляры или векторы?

Q:

Является ли «комплексное число (представленное a+bi и т. д.)» скаляром или вектором? Я читал раньше, что это скалярное число. но кажется, что комплексное число (внутренне? по своей сути?) содержит больше информации, чем информация о реальном скалярном числе (и содержит векторную и пространственную информацию?), потому что комплексное число может быть выражено (находится в виде одной точки) в комплексной плоскости ( с действительными и мнимыми частями). Комплексные числа часто появляются в QM («Вероятно, единственное наиболее полное использование векторных пространств — в квантовой механике»: http://van.physics.illinois.edu/qa/listing.php?id=16247), почему они появляются ? просто для удобства выражения/вычисления/представления/соединения вектора, пространства, волн и т. д. математически? или в использовании комплексных чисел есть более внутренний и глубокий «физический (в отличие от чистой математики)» смысл? т. е. является ли комплексное число неотъемлемым свойством/частью физического мира/природы/фундаментальных составляющих (неотъемлемо ли оно встроено в природу?)? или просто вычислительный инструмент, или просто проявление/грань физической природы (строительная составляющая вселенной)? Возвращаясь к первому вопросу: Итак, является ли комплексное число скаляром или вектором в физике (как науке) и в природе (что физический мир делает спонтанно)? или комплексное число является (может быть?) и скалярным, и векторным числом при изучении физики/математики, а также? в природе? Как мы можем наблюдать/измерять комплексные числа/величины в физике с помощью прямых/косвенных экспериментов? есть примеры? Спасибо.
— Anonymous

A:

Это хорошее продолжение.

Набор комплексных чисел действительно является двумерным векторным пространством, если вы обращаете внимание только на то, что происходит при сложении чисел. Однако особенными комплексные числа делает их правило умножения:

(a+bi)*(c+di)=ac-bd+(ad+bc)i.

Это сильно отличается от общего векторного скалярного произведения 2D, ac+bd, которое дает число, а не другой вектор. Это правило сложного умножения заставляет комплексные числа формировать математическое поле (), на которое затем можно умножать векторы, чтобы получить тот же тип вектора, с которого вы начали. Другими словами, он позволяет использовать комплексные числа в качестве скаляров точно так же, как вы используете действительные числа. В физике мы обычно используем их как скаляры, поскольку они не меняются при пространственном вращении, в отличие, скажем, от стандартных 3-векторов или 4-векторов.

Вы можете измерять такие вещи, как магнитная восприимчивость к переменному току, которую мы не без оснований представляем в виде комплексных чисел. Нет необходимости использовать это представление, но оно очень удобно. Я думаю, вас больше интересует сложная квантовая волновая функция. С некоторой неловкостью его можно было бы представить без явных комплексных чисел, но какое бы математическое выражение не использовалось, оно в конечном итоге было бы точно эквивалентным. Волновая функция не совсем измерима, поскольку всегда существует произвольный абсолютный комплексный фазовый коэффициент. (Относительные фазы определены.)

Роль векторных пространств в квантовой механике гораздо глубже, чем простое использование комплексных чисел. Сами квантовые состояния образуют (обычно бесконечномерное) векторное пространство. Физические измеримые величины, такие как энергия, представлены линейными операторами в этом векторном пространстве, подобно матрицам в конечномерных векторных пространствах. Оператор зависимости от времени сохраняет длину, поэтому это просто поворот в абстрактном векторном пространстве. Как только вы начнете думать о квантовой механике с точки зрения этих векторов состояния, вы попадетесь на крючок.

Что касается философских вопросов о внутренней реальности и т. д., нам нечего сказать.

Майк В.

(опубликовано 07.06.2013)

Дополнение №2: какие числа?

Q:

Включают ли комплексные числа все числа? Или могут быть числа, которые нельзя выразить комплексными числами (или которые не лежат в комплексной плоскости)? Если это так, то почему разумно предполагать/подозревать, что такие числа могут существовать? Если не может быть таких чисел помимо комплексных чисел (=любое число может быть выражено комплексным числом?), то почему? Не могли бы вы привести примеры (в физике и математике) чисел или величин, которые не могут быть частью комплексных чисел, если вообще могут быть?
— Anonymous

A:

Если вы начинаете с простого подсчета чисел, есть веские причины добавить больше типов. Например, вы хотите, чтобы отрицательные значения позволяли решать уравнения вида x+5=4. Эти негативы имеют интуитивное значение. То же самое касается дробей, необходимых для решения уравнений типа 5x=4. Продолжая этот процесс изобретения новых чисел для решения уравнений, вы получите различные иррациональные числа, такие как Sqrt (2), а затем комплексные числа, такие как Sqrt (-1). Включение всех пределов последовательностей этих чисел дает вам полный набор комплексных чисел. Затем оказывается, что все готово — у вас есть все решения всех ваших уравнений. Традиционно для обозначения всех этих расширений наших счетных чисел используется слово «числа».

Однако существует множество других математических объектов. К ним относятся, например, матрицы и кватернионы. Однако эти другие объекты не называются числами.

Mike W.

(опубликовано 04.09.2014)

Дополнение к этому ответу

Связанные вопросы

• что в числе пи?

• значение деления

• математика

• скорость убегания и интегрированное ускорение

• генерация простых чисел

• сколько картинок на экране?

• Что такое жизнь без векторов?

• Группа Вейля

• Расчет толщины океана

• Нейпир, логарифмы и исчисление

Все еще любопытно?

Вопросы и ответы по Expore в смежных категориях

• Математика

Разница между скалярной и векторной величиной (со сравнительной таблицей)

Скалярная величина относится к величине, которая имеет только величину и не имеет направления. С другой стороны, векторная величина подразумевает физическую величину, которая включает в себя как величину, так и направление.

Физика — наука, основанная на математике. Изучая физику, мы проходим через ряд понятий и понятий, которые опираются на математику. Математические величины, объясняющие движение тела, делятся на две группы: скалярные величины и векторные величины.

Для неспециалиста эти два термина одинаковы, но в мире физики существует огромная разница между скалярной и векторной величиной. Итак, взгляните на статью, предоставленную вам, для лучшего понимания.

Содержание: Скалярное количество против векторного количества

1. Сравнительная таблица
2. Определение
3. Ключевые отличия
4. Заключение

Сравнительная таблица

База для сравнения	Скаляр Количество	Количество векторов
Значение	Любая физическая величина, не включающая направление, называется скалярной величиной.	Векторная величина — это единица, имеющая как величину, так и направление.
Величины	Одномерные величины	Многомерные величины
Изменение	Изменяется с изменением их величины.	Он изменяется с изменением их направления или величины, или того и другого.
Операции	Следуйте обычным правилам алгебры.	Следуйте правилам векторной алгебры.
Сравнение двух величин	Простой	Сложный
Деление	Скаляр может делить другой скаляр.	Два вектора не могут делиться.

Определение скалярной величины

Термин «скалярная величина» определяется как величина, которая имеет только один элемент числового поля, присоединенного к единице измерения, такой как градусы или метры. Это величина, которая показывает только величину или размер, т. е. определяется числовым значением вместе с единицей измерения. Например, скорость автомобиля, температура тела, расстояние между двумя точками и т. д.

Правила обычной алгебры могут применяться для комбинирования скалярных величин, так что скаляры можно складывать, вычитать или умножать точно так же, как и числа. Однако операция скаляра возможна только для величин с одной и той же единицей измерения.

Определение векторной величины

Математическая величина, для полного описания которой требуются две независимые характеристики, т. е. величина и направление. Здесь величина представляет величину величины, которая также является ее абсолютной величиной, а направление представляет собой сторону, то есть восток, запад, север, юг и т. д. Например, перемещение между двумя точками, скорость и ускорение движущегося тела, сила, вес и т.д.

Векторная величина подчиняется треугольному закону сложения. Стрелка используется для обозначения векторной величины, расположенной над или рядом с символом, обозначающим вектор.

Ключевые различия между скалярной и векторной величиной

Следующие пункты заслуживают внимания, поскольку речь идет о различии между скалярной и векторной величиной:

1. . Скалярная величина описывается как величина, которая имеет только одну характеристику, т.е. величина. Векторная величина — это физическая величина, для определения которой нужны как величина, так и направление.
2. Скалярные величины объясняют одномерные величины. С другой стороны, многомерные величины объясняются векторной величиной.
3. Скалярные величины изменяются только при изменении их величины. В отличие от этого, векторная величина изменяется с изменением их величины, направления или того и другого.
4. Обычные правила алгебры следуют скалярным величинам для выполнения таких операций, как сложение, вычитание и умножение, в то время как для выполнения операций векторные величины следуют правилам векторной алгебры.
5. При сравнении двух скалярных величин необходимо учитывать только величину, тогда как при сравнении двух векторных величин необходимо учитывать и величину, и направление. Таким образом, с векторными величинами работать немного сложнее, чем со скалярными.