Конспект открытого урока «Векторы. Действия над векторами»
Характеристика урока:
Данный урок является вторым в разделе «Векторы».
Теме «Векторы в пространстве» в примерной программе ФИРО отводится 12 часов.
Темы разбиты следующим образом:
Понятие вектора. Действия над векторами
1.Скалярные и векторные величины. Угол между векторами. Сумма векторов
2.Противоположные векторы. Разность векторов. Умножение вектора на число
3.Коллинеарные векторы. Разложение вектора
Прямоугольная декартова система координат
4.Прямоугольная декартова система координат. Координаты вектора. Длина вектора
5.Скалярное произведение векторов. Свойства скалярного произведения
6.Угол между векторами
Для гуманитарного и естественно-научного
профилей профессионального образования более характерным является усиление
общекультурной составляющей учебной дисциплины с ориентацией на
визуально-образный и логический стили учебной работы.
Использование компьютерных технологий в образовательном процессе вообще и на уроках математики в частности, позволяет придти к следующим выводам:
Мультимедийная система обеспечивает:
· Наглядность материала, в том числе, за счет звука, цвета, движения;
· Ускорение темпа урока;
· Свободу постоянного экспериментирования с целью улучшения методики преподавания;
·
Последовательный
характер обучения за счет планомерного накапливания наглядных электронных
пособий, позволяющих с легкостью в любой момент вернуться к уже знакомым,
эмоционально окрашенным образам пройденного материала, которые могут быть
гораздо экспрессивнее всем известных опорных сигналов.
Компьютер на уроке — это педагогическая реальность, которая твердо вошла в нашу жизнь; при этом компьютер можно рассматривать как еще одно дополнение к процессу обучения, а не заменяющее учителя и учебник средство обучения.
В этой теме основной акцент делается на формирование наглядных представлений. Для каждого из рассматриваемых случаев даются определения и некоторые признаки. При изучении определений и свойств векторов основное внимание необходимо уделить усвоению формулировок и умению применять их к решению задач.
Основное
внимание направлено на задачи вычисления суммы и разности векторов, нахождения
координат вектора, через начало и конец вектора , умножения вектора на число, а
также признака коллинеарности векторов. При повторении определений равных и сонаправленых, противоположных и противоположнонаправленных векторов особое внимание следует уделить “реальному” изображению этих векторов.
С этой целью различные векторы иллюстрирую на отдельных слайдах и на
прямоугольном параллелепипеде.
Работая на уроке, учащиеся овладевают:
1. Учебно-интеллектуальными умениями и навыками:
— по формулам вычисляют координаты вектора, длину вектора, сумму и разность векторов, умножают вектор на число.
2. Учебно-исследовательским:
— анализируют учебный материал 9 класса , сравнивают коллинеарные векторы, равные, сонаправленные, противоположные и противоположнонаправленные векторы по их координатам и представляя их графически.
3. Учебно-организационными:
— планируют работу, осуществляют самоконтроль.
Чтобы урок для учащихся был активным и максимально индивидуализированным, чтобы реализовались особенности каждого учащегося, применяю технологию интерактивного обучения с опорными конспектами.
Тема урока: Векторы в пространстве. Действия с векторами
Цели урока:
образовательные:
·
Ввести
понятие вектора в пространстве, его длины, понятие коллинеарных и равных
векторов; действия над векторами в пространстве.
развивающие:
· Развитие пространственного воображения учащихся.
· Развивать умения строить логическую цепочку рассуждений, анализировать, выделять главное, сравнивать, строить аналогии, обобщать и систематизировать, делать выводы.
· Развивать умение работать в должном темпе.
воспитательные:
· Воспитание умения слушать, умения работать в малых группах.
· Воспитание познавательного интереса к предмету.
методические:
· Активизация мыслительно-познавательной деятельности учащихся.
· Создание условий для формирования знаний, умений и навыков
Вид урока: урок с компьютерным сопровождением.
Интерактивная технология: работа с опорным конспектом, во время компьютерного сопровождения
Учебный предмет: геометрия
Уровень
образования школьников: урок проводился с учащимися 1 курса колледжа «Подмосковье».
Метод обучения: наглядный; демонстрация мультимедийной презентации.
Дидактическое обеспечение:
· тесты;
· опорные конспекты “Векторы на плоскости и в пространстве”.
Материально-техническое обеспечение:
· Компьютер.
· Экран.
· Мультимедийный проектор.
· Мультимедийная презентация.
Межпредметные связи:
Алгебра: «Действия над действительными числами»
Физика: «Сила», «Скорость», «Движение», «Давление»
А так же биология, химия, экономика, психология, литература
Структура урока:
I. Организационный момент.
II. Мотивация учебной деятельности.
III. Изучение нового материала и применение знаний при решении типовых задач.
IV.
Самостоятельное применение знаний, умений
и навыков.
V. Задание на дом.
VI. Рефлексия.
VII. Итог урока.
Ход урока:
I. Организационный момент.
Преподаватель приветствует учащихся и отмечает в журнале отсутствующих.
II. Мотивация учебной деятельности.
Вступительное слово преподавателя:
(слайд 1)
Эпиграфом к нашему уроку я взяла высказывание американского физика Юджина Пола Вигнера: “Математика — это наука о хитроумных операциях, производимых по специально разработанным правилам над специально придуманными понятиями“. Сегодня как раз мы и будем заниматься такими хитроумными операциями над специально разработанными понятиями.
(слайд 2) Шарада:
Мой первый слог — почтенный срок,
Коль прожит он недаром;
Модель второго на столе,
Румяна, с пылу с жару.
Меня вы встретите везде –
Такой
я вездесущий.
А имя громкое мое –
Латинское «несущий».
(Век-тор)
Слайд(3-4)
Преподаватель сообщает тему урока и ставит задачу совместного сотрудничества с учащимися на период урока,
Слайд(5-8)
В наши дни понятие «вектор» постоянно встречается в газетных и журнальных публикациях, в выступлениях политиков, ученых, педагогов. Обсуждая важнейшие процессы в жизни общества, говорят о векторе реформ и его социальной составляющей, о векторе экономических преобразований и его изменении, о направлении вектора развития системы образования.
С уверенностью можно сказать, что мало кто из людей задумывается о том, что векторы окружают нас повсюду и помогают нам в повседневной жизни. Рассмотрим ситуацию: парень назначил девушке свидание в двухстах метрах от своего дома. Найдут ли они друг друга? Конечно, нет, так как юноша забыл указать главное: направление, то есть по-научному – вектор.
Понятие о векторе как направленном отрезке
вошло в сознание и речь современного образованного человека.
Зачатки векторного исчисления появились вместе с геометрической моделью комплексных чисел (Гаусс, 1831).
А окончательный вид оно приняло в трудах американского физика и математика Джозайи Уилларда Гиббса (1839 – 1903), который в 1901 году опубликовал обширный учебник по векторному анализу
Гибсс — американский физик, физикохимик, математик и механик, один из создателей векторного анализа, статистической физики, математической теории термодинамики, что во многом предопределило развитие современных точных наук и естествознания в целом.
Образ Гиббса запечатлён в «Галерее славы великих американцев». Его имя присвоено многим величинам и понятиям химической термодинамики: энергия Гиббса, парадокс Гиббса, правило фаз Гиббса, уравнения Гиббса — Гельмгольца, уравнения Гиббса — Дюгема, лемма Гиббса, треугольник Гиббса — Розебома и др.
(Слайд 6)
Сам термин
«вектор» впервые появился в 1845 году у ирландского математика и астронома
Уильяма Гамильтона (1805 – 1865) в работах по построению числовых систем,
обобщающих комплексные числа.
Слайд(7)
Почти одновременно с ним исследованиями в том же направлении занимался
английский математик — Уильям Кингдон Клиффорд (1845–1879)
Конец прошлого и начало текущего столетия ознаменовались широким развитием векторного исчисления и его приложений. Были созданы векторная алгебра и векторный анализ, общая теория векторного пространства. Эти теории были использованы при построении специальной и общей теории относительности, которые играют исключительно важную роль в современной физике.
( Слайд 8) Коши
Слайд(9)
Векторы всюду.
Предлагается учащимся сделать небольшие выступления по заданной теме
1-ый учащийся
Вектор используются везде, даже там, где мы их не замечаем, например в литературе:
Маргарита
Алигер, биография которой вызывает искренний интерес у поклонников ее творчества,
– знаменитая советская поэтесса, удостоившаяся Сталинской премии второй степени
за поэму «Зоя» о бесстрашном подвиге советской девушки Зои Космодемьянской. После
семилетки училась в химическом техникуме. С детства писала стихи.
После
семилетки училась в химическом техникуме. С детства писала стихи.
Векторы в физике.
О,
физика, наука из наук!
Все впереди!
Как мало за плечами!
Пусть химия нам будет вместо рук,
Пусть станет математика очами.
Не разлучайте этих трех сестер,
Познания всего в подлунном мире.
Тогда лишь будет ум и глаз остер,
И знанье человеческое шире.
Вспомним басню Ивана Андреевича Крылова о том, как «лебедь, рак да щука везти с поклажей воз взялись». Басня утверждает, что «воз и ныне там», другими словами, что равнодействующая всех сил приложенных к возу равна нулю. А сила, как известно, векторная величина.
2 –ой учащийся
В химии. Нередко даже
великими учеными высказывалась мысль, что химическая реакция является вектором.
Вообще-то, под понятие «вектор» можно подвести любое явление. Вектором выражают
действие или явление, имеющее четкую направленность в пространстве и в
конкретных условиях, отражаемое его величиной.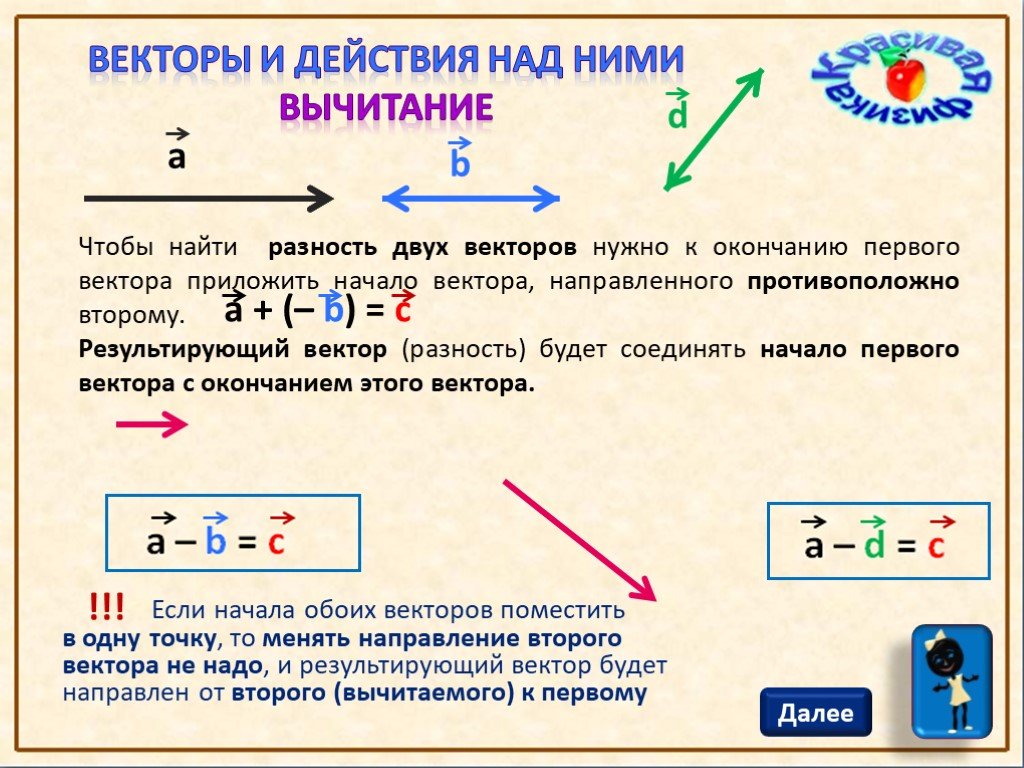 Направление вектора в
пространстве определяется углами, образующимися между вектором и координатными
осями, а длина (величина) вектора – координатами его начала и конца. Однако
утверждение, что химическая реакция является вектором, до сих пор было неточно.
Тем не менее, основой этого утверждения служит следующее правило: «Любой
химической реакции отвечает симметричное уравнение прямой в пространстве с
текущими координатами в виде количеств веществ (молей), масс или объемов».
Направление вектора в
пространстве определяется углами, образующимися между вектором и координатными
осями, а длина (величина) вектора – координатами его начала и конца. Однако
утверждение, что химическая реакция является вектором, до сих пор было неточно.
Тем не менее, основой этого утверждения служит следующее правило: «Любой
химической реакции отвечает симметричное уравнение прямой в пространстве с
текущими координатами в виде количеств веществ (молей), масс или объемов».
3 –ий учащийся
Вектором (в биологии) называется организм, переносящий паразита от одного организма-хозяина к другому. Например, вши переносят возбудителей сыпного тифа, крысы – чумы. Вектор (в генетике) — молекула нуклеиновой кислоты, чаще всего ДНК, используемая в генетической инженерии для передачи генетического материала другой клетке.
4-ый учащийся
Векторы в экономике
Одним из разделов
высшей математики является линейная алгебра. Ее элементы широко применяются при
решении разнообразных задач экономического характера. Среди них важное место
занимает понятие вектора. Вектор представляет собой упорядоченную
последовательность чисел. Числа в векторе с учетом их расположения по номеру в
последовательности называются компонентами вектора. Отметим, векторы можно
рассматривать в качестве элементов любой природы, в том числе и экономической.
Предположим, что некоторая текстильная фабрика должна выпустить в одну смену 30
комплектов постельного белья, 150 полотенец, 100 домашних халатов, тогда
производственную программу данной фабрики можно представить в виде вектора, где
всё, что должна выпустить фабрика – это трехмерный вектор.
Среди них важное место
занимает понятие вектора. Вектор представляет собой упорядоченную
последовательность чисел. Числа в векторе с учетом их расположения по номеру в
последовательности называются компонентами вектора. Отметим, векторы можно
рассматривать в качестве элементов любой природы, в том числе и экономической.
Предположим, что некоторая текстильная фабрика должна выпустить в одну смену 30
комплектов постельного белья, 150 полотенец, 100 домашних халатов, тогда
производственную программу данной фабрики можно представить в виде вектора, где
всё, что должна выпустить фабрика – это трехмерный вектор.
5-ый учащийся
Векторы в психологии
На сегодняшний день
имеется огромное количество информационных источников для самопознания,
направлений психологии и саморазвития. И не трудно заметить, что все больше
обретает популярность такое необычное направление, как системно-векторная
психология, в ней существует 8 векторов. Системно-векторная психология позиционируется
не как отрасль классической психологии или определенное течение, а
как отдельная наука изучения типологии личности.
Вектор – это симбиоз физиологических и психологических качеств человека. Это — характер, темперамент, здоровье, привычки индивида.
Векторы в повседневной жизни
Мы обратили внимание, что векторы, помимо точных наук, встречаются нам каждый день, т.е. повседневно. Векторы – указатели, которые помогают нам быстро найти тот или иной объект, отдел и сэкономить время, или стрелки дорожных знаков.
Слайд(10)
В курсе 9 класса вы изучали векторы на плоскости
Перед нами стоит задача – дать определение вектора в пространстве, научиться находить его длину по координатам начала и конца вектора и рассмотреть основные действия над векторами: сложение, вычитание, умножение на число, а также рассмотреть коллинеарные и компланарные векторы.
Поставленную перед нами задачу мы будем решать
на основе сравнительного анализа и установления закономерностей: как давались
определения вектора и операций над векторами на плоскости и как они
формулируются для векторов в пространстве. На каждой парте лежат опорные
конспекты, правую часть которых необходимо заполнить учащимся, пользуясь материалом
учебника.
На каждой парте лежат опорные
конспекты, правую часть которых необходимо заполнить учащимся, пользуясь материалом
учебника.
III. Изучение нового материала и применение знаний при решении типовых задач.
На прошлом уроке вы составляли опорные конспекты. где отмечали основные определения и действия с векторами на плоскости. Теперь я предлагаю вам в этих же конспектах заполнить вторую часть их
На плоскости | В пространстве | ||||||||||||||||
Определение. Вектором называется направленный отрезок Длина этого отрезка называется длиной (модулем, абсолютной величиной) вектора. = || = АВ | Определение. | ||||||||||||||||
Координаты вектора.
(х2 – х1; у2 – у1) | Координаты вектора. А1(х1; у1; z1) А2 (х2; у2; z2)
(________;_________;__________) | ||||||||||||||||
Длина вектора. (х; у) = + у2 | Длина вектора. (х; у; z) = √ | ||||||||||||||||
Коллинеарные векторы Векторы .лежащие на одной прямой или на парраллельных прямых | Коллинеарные векторы
| ||||||||||||||||
Сонаправленные векторы
|
. | ||||||||||||||||
Противоположнонаправленные векторы
| |||||||||||||||||
Признак коллинеарности векторов (х1; у1) (x2; y2)
=
| Признак коллинеарности векторов (х1; у1; z1) (x2; y2; z2)
| ||||||||||||||||
Равные векторы. (х1; у1) х1 = х2 (х2; у2) у1 = у2
Векторы равны, если: 1. Равны длины векторов 2. Векторы сонаправлены | Равные векторы.
(х1; у1; z1) (х2; у2; z2)
Векторы равны, если: 1.
2. | ||||||||||||||||
Противоположные векторы.
(х1; у1) x1 = — x2
(x2; y2) y1 = — y2
| Противоположные векторы.
(х1; у1; z1)
(x2; y2; z2)
| ||||||||||||||||
Сумма векторов
(х1; у1) и (x2; y2)
+ = (x1 + y1; x2 + y2) |
Сумма векторов (х1; у1; z1) и (x2; y2; z2)
+ = (______; ______;_______) | ||||||||||||||||
Разность векторов (х1; у1) и (x2; y2)
— = (x1 — y1; x2 — y2) |
Разность векторов (х1; у1; z1) и (x2; y2; z2)
— = (______; _______;________) | ||||||||||||||||
Умножение вектора на число λ (х; у) = (λх; λу)
| Умножение вектора на число λ (х; у; z) = (λх; λу; λz)
|
Вопросы:
(слайд12)
Дайте определение вектора в пространстве и запишите его в таблицу.
(слайд 13)
Как найти координаты вектора, зная координаты точек начала и конца вектора., запишите в таблицу
(слайд 14)
Задача Найдите координаты вектора , если М(10; -4; 2) и К(16; 2 -5).
Ответ: (6; 6; -7)
(слайд 15)
Как вычислить длину вектора, зная его координаты, запишите в таблицу
(слайд 16)
Задача 2. Найдите модуль вектора ( — 5; 1; 2).
Ответ:
(слайд 17)
Любая точка пространства является нулевым вектором. Длина нулевого вектора равна 0.
(слайды 18 -20 )
Коллинеарные вектора, сонаправленные, противоположнонаправленные, признак коллинеарности , записать в таблицу
(слайд21)
(слайд 22)
Устно
решить задачу. Какие векторы на рисунке сонаправлены, противоположнонаправлены. Найти длины векторов
Найти длины векторов
(слайд23,24)
Равенство векторов, противоположные векторы, записать в таблицу
(слайд25)
Могут быть ли равными векторы?
( слайд26)
Сколько равных векторов изображено на рисунках?
(слайд 27)
При каком значении n векторы (4; 2n — 1; -1) и (4; 9 – 3n; -1) равны?
Ответ: при n = 2
(слайд 28)
Лови ошибку.
(слайд 29)
Назовите векторы.
( слайды30-36)
Дайте определение суммы векторов. А если сложить несколько векторов в пространстве, какая фигура получится?
Заметили ли вы, что многоугольник, который получается при построении суммы нескольких векторов, может оказаться пространственным, т. е. не все его вершины лежат в одной плоскости?
(слайд 37)
Задача
5. Найдите
сумму векторов и
,
если А(2; 3; -1), С(3; -2; 0), а В – произвольная точка пространства
Найдите
сумму векторов и
,
если А(2; 3; -1), С(3; -2; 0), а В – произвольная точка пространства
Ответ: (1; -5; 1)
(слайды 38-39)
Дайте определение разности векторов.,запишите в таблицу
(слайд 40)
Задача 6. Найдите разность векторов и , если В(3; 7; 10), С(1; 9; -6), а А – произвольная точка пространства.
Ответ: (2; -2; 16)
(слайды 41-43)
Как умножается вектор на число?,запишите в таблицу
(слайд 44)
Задача 7. Найдите координаты вектора с = 2а -3b, если а(7; -3; 0) и b(4; 1; -2)
Ответ: (2; -9; 6)
(слайд 45)
Задача 8. Найдите абсолютную величину вектора 3, если (4; -4; 2) Рассмотреть 2 способа решения.
Ответ: = 18
IV. Самостоятельное
применение знаний, умений и навыков.
(слайд 50)
Устный тест:
1.Что называется вектором?
а)любой отрезок
б)отрезок, обозначенный двумя заглавными латинскими буквами
в) отрезок с выбранным направлением
2. Какой вектор является нулевым?
а)длина вектора равна 0
б)вектор лежит на прямой
в)вектор обозначен одной буквой
3. Векторы коллинеарны, если…
а)лежат на прямых
б)лежат на параллельных прямых
в)один из векторов нулевой
5. Векторы называются равными, если …
а)их длины равны
б)их модули равны и векторы направлены в одну сторону
в)они отложены от одной точки
(слайд 52)
Даны векторы (-3; 0; 4) и (2; 4; -4)
Запишите:
1. Длину вектора .
2. При каких значениях k и m вектор (k; -3; m) коллинеарен вектору ?
3. Из
векторов (1; 1; -2), (-1;
-2; 2), (2;
-4; 4), (-4;
-4; 2) укажите векторы противоположнонаправленные с вектором .
Из
векторов (1; 1; -2), (-1;
-2; 2), (2;
-4; 4), (-4;
-4; 2) укажите векторы противоположнонаправленные с вектором .
(Слайд53)
Дано:
Решение
1) Находим координаты вектора
;
2) Затем находим координаты вектора
3) Теперь находим аналогично координаты вектора
4) Теперь находим сумму данных векторов, складывая соответствующие координаты:
Ответ:
С учетом познавательных и когнитивных способностей необходимо учащимся раздать разноуровневые задания на применение навыков и умений действий над векторами (работа в тетрадях).
Вариант А
1. Найдите координаты вектора , если
2. Даны векторы и Найдите координаты и длину вектора .
Вариант В
1. Даны векторы и Найдите координаты и длину вектора .
2. Даны векторы Найдите координаты вектора
3. Найдите длину вектора ,
если
Найдите длину вектора ,
если
Вариант С
1. Даны векторы Найдите координаты вектора
2. Найдите длину вектора , если
3. Из точки построен вектор . Найдите координаты точки , если:
4. Даны векторы и Найдите координаты и длину вектора .
Данный вид работы учащиеся выполняют в тетрадях, после чего учитель собирает тетради для проверки.
V. Задание на дом. (слайд 54)
VI. Рефлексия. (слад 55)
Закончи предложение: Я умею …, я могу …, я знаю ….
VII. Итог урока. Оценивание учащихся.
Действия над векторами и свойства векторов
В этом разделе мы обобщим раздел векторов, опишем все действия, которые можно выполнять над векторами, и какие у них свойства.
Действия по векторам
Определение
Вектор — это направленный сегмент \(\
\overline{A B}
\), где точка \(\
A
\) — это начало, а точка \(\
B
\) — конец вектора.
Сумма \(\ \overline{a}+\overline{b} \) векторов \(\ \overline{a} {и} \overline{b} \) называется таким третьим вектором \(\ \overline{c} \), начало которого совпадает с началом \(\ \overline{a} \) , а конец с концом \(\ \overline{b} \), при условии, что конец вектора \(\ \overline{a} \) и начало вектора \(\ \overline{b} \) совпадают.
Свойства операции сложения:
1. – \(\ \overline{a}+\overline{b}=\overline{b}+\overline{a} \)коммутативность
2. – \(\ (\overline{a}+\overline{b})+\overline{c}=\overline{a}+(\overline{b}+\overline{c}) \) ассоциативность
3. \(\ \overline{a}+\overline{0}=\overline{a} \)
4. \(\ \overline{a}+(-\overline{a})=\overline{0} \)
Определение
Разница \(\ \overline{a}-\overline{b} \) векторов \(\ \overline{a} и \overline{b} \) называется вектором \(\ \overline{c} \) таким, что условие: \(\ \overline{b}+\overline{c}=\overline{a} \)
Произведение \(\ \alpha \overline{a} \) вектора \(\ \overline{a} \) на число \(\ \alpha \) представляет собой вектор \(\ \overline{b} \) , удовлетворяющий условиям:
1. \(\
\overline{b}\|\overline{a}
\)
\(\
\overline{b}\|\overline{a}
\)
2. \(\ |\overline{b}|=|\alpha||\overline{a}| \)
3.\(\ \overline{a} \uparrow \uparrow \overline{b}, \operatorname{если} \alpha>0, \overline{a} \uparrow \rfloor \overline{b}, \operatorname{если} \alphaСвойства умножения вектора на число:
1. \(\ (\alpha \pm \beta) \overline{a}=\alpha \overline{a} \pm \beta \overline{a} \)
2. \(\ \alpha(\overline{a} \pm \overline{b})=\alpha \overline{a} \pm \alpha \overline{b} \)
3. \(\ \alpha(\beta \overline{a})=(\alpha \beta) \overline{a}=\beta(\alpha \overline{a}) \)
4. \(\ 1 \cdot \overline{a}=\overline{a} \)
5.\(\ -1 \cdot \overline{a}=-\overline{a} \)
6. \(\ 0 \cdot \overline{a}=\overline{0} \)
Определение
Скалярное произведение двух ненулевых векторов \(\ \overline{a} {и} \overline{b} \) представляет собой число, равное произведению длин этих векторов и косинуса угла между ними: \(\ \overline{a} \overline{b}=\overline{a} \cdot \overline{b}=(\overline{a}, \overline{b})=|\overline{a}||\overline{b}| \cos (\overline{a}, \overline{b}) \)
Свойства точечного продукта:
1. {2}
\) и называется скалярным квадратом.
{2}
\) и называется скалярным квадратом.
3. Если \(\ \overline{a} \neq \overline{0} \), то \(\ (\overline{a}, \overline{b})=|\overline{a}| \cdot \Pi p_{\overline{a}} \overline{b} \)
4. Если \(\ \overline{a} \neq \overline{0} \quad{и}\quad \overline{b} \neq \overline{0} \quad{и}\quad(\overline{a}, \overline{b})=0 \) Обратное также верно.
5. \(\ (\overline{a}+\overline{b}, \overline{c})=(\overline{a}, \overline{c})+(\overline{b}, \overline{c}) \)
6. \(\ (\lambda \overline{a}, \overline{b})=\lambda(\overline{a}, \overline{b}) \)
7. \(\ (\alpha \overline{a}+\beta \overline{b}, \gamma \overline{c}+\delta \overline{d})=\alpha \gamma(\overline{a}, \overline{c})+\alpha \delta(\overline{a}, \overline{d})+\beta \gamma(\overline{b}, \overline{c})+\beta \delta(\overline{b}, \overline{d}) \)
Определение
Векторное произведение ненулевых векторов \(\ \overline{a} и \overline{b} \) представляет собой вектор \(\ \overline{c} \), обозначаемый символом \(\ [\overline{a}, \overline{b}] \) или \(\ \overline{a} \times \overline{b} \), длина которого равна \(\ |\overline{c}|=|\overline{a}||\overline{b}| \sin (\overline{a}, \overline{b}) \)
Свойства векторного произведения:
1. \(\
[\overline{a}, \overline{b}]=\overline{0}
\) если и только если \(\
\overline{a}\|\overline{b}
\)
\(\
[\overline{a}, \overline{b}]=\overline{0}
\) если и только если \(\
\overline{a}\|\overline{b}
\)
2. \(\ [\overline{a}, \overline{b}]=-[\overline{b}, \overline{a}] \)
3. Модуль векторного произведения \(\ |[\tilde{a}, \overline{b}]| \) равен площади параллелограмма, построенного на указанных векторах \(\ \overline{a} {и} \overline{b} \) (рис. 2), т.е.
\(\ S=|[\overline{a}, \overline{b}]|=|\overline{a}||\overline{b}| \sin (\overline{a}, \overline{b}) \)
4. \(\ [\lambda \overline{a}, \overline{b}]=[\overline{a}, \lambda \overline{b}]=\lambda[\overline{a}, \overline{b}] \)
5. \(\ \left[\tilde{a}_{1}+\overline{a}_{2}, \overline{b}\right]=\left[\overline{a}_{1}, \overline{b}\right]+\left[\overline{a}_{2}, \overline{b}\right] ;\left[\overline{a}, \overline{b}_{1}+\overline{b}_{2}\right]=\left[\overline{a}, \overline{b}_{1}\right]+\left[\overline{a}, \overline{b}_{2}\right] \)
Определение
Смешанное произведение трех векторов \(\ \overline{a}, \overline{b}, \overline{c} \) , это число, равное скалярному произведению вектора \(\ \overline{a} \times \overline{b} \) на вектор \(\ (\overline{a}, \overline{b}, \overline{c})=([\overline{a}, \overline{b}], \overline{c}) \):
Свойства смешанного продукта:
1. \(\
(\overline{a}, \overline{b}, \overline{c})=(\overline{a},[\overline{b}, \overline{c}])
\)
\(\
(\overline{a}, \overline{b}, \overline{c})=(\overline{a},[\overline{b}, \overline{c}])
\)
2. \(\ (\overline{a}, \overline{b}, \overline{c})=(\overline{b}, \overline{c}, \overline{a})=(\overline{c}, \overline{a}, \overline{b})=-(\overline{b}, \overline{a}, \overline{c})=-(\overline{c}, \overline{b}, \overline{a})=-(\overline{a}, \overline{c}, \overline{b}) \)
3. Три вектора копланарны тогда и только тогда, когда \(\ (\overline{a}, \overline{b}, \overline{c})=0 \)
4. Три вектора правильны тогда и только тогда, когда \(\ (\overline{a}, \overline{b}, \overline{c})>0 \). Если \(\ (\overline{a}, \overline{b}, \overline{c})5. \(\ (\lambda \overline{a}, \overline{b}, \overline{c})=(\overline{a}, \lambda \overline{b}, \overline{c})=(\overline{a}, \overline{b}, \lambda \vec{c})=\lambda(\overline{a}, \overline{b}, \overline{c}) \)
6. \(\ \left(\overline{a}_{1}+\overline{a}_{2}, \overline{b}, \overline{c}\right)=\left(\overline{a}_{1}, \overline{b}, \overline{c}\right)+\left(\overline{a}_{2}, \overline{b}, \overline{c}\right) \)
7. \(\
\left(\overline{a}, \overline{b}_{1}+\overline{b}_{2}, \overline{c}\right)=\left(\overline{a}, \overline{b}_{1}, \overline{c}\right)+\left(\overline{a}, \overline{b}_{2}, \overline{c}\right)
\)
\(\
\left(\overline{a}, \overline{b}_{1}+\overline{b}_{2}, \overline{c}\right)=\left(\overline{a}, \overline{b}_{1}, \overline{c}\right)+\left(\overline{a}, \overline{b}_{2}, \overline{c}\right)
\)
8. \(\ \left(\overline{a}, \overline{b}, \overline{c}_{1}+\overline{c}_{2}\right)=\left(\overline{a}, \overline{b}, \overline{c}_{1}\right)+\left(\overline{a}, \overline{b}, \overline{c}_{2}\right) \)
9. \(\ ([\overline{a}, \overline{b}], \overline{c})=\overline{b}(\overline{a}, \overline{c})-\overline{a}(\overline{b}, \overline{c}) ;(\overline{a},[\overline{b}, \overline{c}])=\overline{b}(\overline{a}, \overline{c})-\overline{c}(\overline{a}, \overline{b}) \)
10. Личность Якоби: \(\ (\overline{a},[\overline{b}, \overline{c}])+(\overline{b},[\overline{c}, \overline{a}])+(\overline{c},[\overline{a}, \overline{b}])=0 \)
Векторы действия: сила скорости над скоростью
Анн-Лора Ле Кунф
• Время чтения: 4 минуты. Мы живем в обществе, где скорость стала мерилом производительности. Мы стараемся быстро просматривать наши списки дел, не отставать от быстро меняющихся требований рынка и оперативно выпускать обновления продуктов.
Мы стараемся быстро просматривать наши списки дел, не отставать от быстро меняющихся требований рынка и оперативно выпускать обновления продуктов.
Конечно, мы продуктивны, в старейшем смысле этого слова — от латинского productre , что означает «производить». Но как-то не чувствуется, что мы идем дальше. Мы с ужасом чувствуем, что, несмотря на всю работу, которую мы делаем, мы на самом деле не растем.
Мы застряли в бессмысленной погоне, пытаясь обогнать друг друга и, в конечном счете, обогнать самих себя. В результате головокружительный темп слепой продуктивности заставляет многих людей выгорать.
В статье 1953 года известный физик Сэмюэл Гоудсмит уже задавался вопросом, «не сыграли ли [все] приспособления, которые физики недавно приспособили для создания энергии путем ускорения частиц материи, злую шутку над своими изобретателями. «Они ускоряют и нас», — говорит он. Протестуя против ускорения, Гоудсмит может говорить авторитетно, поскольку всего за несколько лет он, как и многие другие современные физики, увидел, как его образ жизни изменился от спокойного созерцания к крысиным бегам».
Можно утверждать, что скорость сама по себе не является проблемой. На самом деле, многие из нас обнаруживают, что могут довольно быстро работать над проектом, когда мы увлечены им — как будто ветер дует сквозь наши паруса и легко толкает нас вперед. Но это потому, что такие проекты идут с чувством направления.
Ментальная модель направленного роста
Скорость сама по себе не имеет направления. Когда вы говорите, что движетесь с определенной скоростью («Я еду со скоростью 80 миль в час»), это ничего не говорит вам о том, куда вы направляетесь.
Это то, что математики называют «скаляром» — величиной, которая может быть полностью описана только ее величиной. Скорость является скаляром, как и объем, масса и время. Когда вы говорите о том, насколько быстро или насколько велико что-то, вы описываете это как скаляр.
Напротив, вектор описывается как его величиной, так и его направлением. Скорость — это пример вектора: он не только сообщает вам , как быстро вы едете , но также , где вы едете — например, «Я еду на юг со скоростью 80 миль в час».
Думать о своих действиях как о векторах, а не как о скалярах — это полезная ментальная модель для управления вашими целями. Вы много работаете (величина), но учитесь ли вы (направление)? Ваша команда выпускает обновления продуктов быстро (величина), но улучшается ли обратная связь с клиентами (направление)?
Как спроектировать эффективные векторы действия
Как только вы поймете эту ментальную модель, вы сможете рассмотреть свои векторы действий, чтобы вам было легче объективно оценивать свой прогресс, свое влияние и свое благополучие.
- Скорость важнее скорости. Не забывайте учитывать не только масштабы действий — то есть, как быстро вы движетесь, сколько работы вы производите, — но и направление ваших действий. Обдумывая свои действия, подумайте о своей траектории, например о целях обучения, личном росте, возможностях самопознания и более широком влиянии.
- Подумайте о своем чувстве направления. Вам кажется, что вас тянет в разные стороны? Что вы не понимаете, куда именно вы или ваша команда направляетесь? А может, вы идете в правильном направлении, но в ущерб своему благополучию.
 Выделите время, чтобы регулярно анализировать как ваш прогресс, так и его влияние на ваше эмоциональное и психическое здоровье. Нет смысла прогрессировать, если вы выгораете в процессе. Анализ вашего внешнего успеха и вашего внутреннего опыта поможет вам использовать более устойчивые методы работы.
Выделите время, чтобы регулярно анализировать как ваш прогресс, так и его влияние на ваше эмоциональное и психическое здоровье. Нет смысла прогрессировать, если вы выгораете в процессе. Анализ вашего внешнего успеха и вашего внутреннего опыта поможет вам использовать более устойчивые методы работы. - Продолжайте корректировать траекторию. Если вы заметили, что никуда не идете или идете не в правильном направлении, внесите изменения, чтобы выбрать путь, который имеет для вас смысл. Эти изменения могут быть небольшими, такими как настройка рабочего процесса или внедрение новой рутины, или большими, такими как изучение новой карьеры или начало дополнительного проекта. Опять же, важно то, что эти изменения улучшают направление ваших действий.
Векторы действия предлагают более целостное представление о вашем прогрессе и о том, движетесь ли вы в правильном направлении. Восприятие своих действий как вектора, а не как скаляра, — это простая ментальная модель, которую можно отразить и внести коррективы в то, как вы работаете, чтобы вы могли максимизировать личностный рост, не жертвуя своим психическим здоровьем. По словам доктора Скотта Барри Кауфмана: «Рост — это направление, а не пункт назначения».
По словам доктора Скотта Барри Кауфмана: «Рост — это направление, а не пункт назначения».
Присоединяйтесь к 50 000 осознанных творцов!
Maker Mind — это еженедельный информационный бюллетень с научно обоснованными идеями о творчестве, осознанной продуктивности, лучшем мышлении и обучении на протяжении всей жизни.
Одно письмо в неделю, никакого спама. Ознакомьтесь с нашей Политикой конфиденциальности.
2. Векторы: определения, алгебра
2. Векторы: определения, алгебрапринтер Дружественный Копия
Статика частиц имеет дело с эффектами концентрированных силы на частицы, сложение таких сил, их разложение на компонентов, определение равнодействующей системы сил, действующих на частицу, а также связь между силами, действующими на частица в состоянии равновесия.
 Для их выполнения мы будем
необходимо применить правила векторной алгебры.
Для их выполнения мы будем
необходимо применить правила векторной алгебры. Силы, действующие на частицу
Сила – это действие/следствие, стремящееся изменить состояние покоя или равномерное движение тела. Сила полностью характеризуется своим величину и направление. Направление силы задается ее точкой приложения и линии действия, которая представляет собой прямую линию, лежащую на одной прямой с вектором силы.
Обратите внимание, что, поскольку частицы идеализируются как точечные массы, система
все силы, действующие на частицу, проходят через точку, занимаемую
частица. Система сил, проходящая через общую точку,
говорят, что они одновременны.
Скаляры и векторы
Механика имеет дело с двумя видами величин
— скаляры и векторы. Скалярные величины – это величины, величина которых
только напр. расстояние, время, объем, плотность, скорость, энергия, масса, длина,
температура и т. д. С другой стороны, векторные величины имеют как
величина и направление (линия действия и смысл) и должны подчиняться параллелограмму
закон сложения. Примеры векторов включают скорость, смещение,
ускорение, сила, момент и количество движения.
д. С другой стороны, векторные величины имеют как
величина и направление (линия действия и смысл) и должны подчиняться параллелограмму
закон сложения. Примеры векторов включают скорость, смещение,
ускорение, сила, момент и количество движения.
Вектор представлен графически стрелкой
который определяет величину и направление вектора. Величина
вектора обозначается длиной стрелки, направление
определяется углом между базовой осью и линией действия стрелки
а смысл указан стрелкой. В учебниках векторы
представлены полужирными буквами , но в классе мы будем использовать
подчеркивание для представления векторов, например. вектор A будет записан как А .
Классификация векторов
Векторы можно сгруппировать в три класса — бесплатно
векторы, скользящие векторы и фиксированные векторы. Физические величины, которые
векторы попадают в одну из этих трех категорий. Бесплатные векторы ар
векторы, которые могут свободно перемещаться в пространстве, т. е. их линии действия
не ограничен или не связан с уникальной линией в пространстве, например. пары, смещение
вектор тела, движущегося в пространстве без вращения. Наоборот, скользящий вектор — это тот, для которого единственная линия в пространстве, вдоль которой
векторные действия должны поддерживаться, например. внешнее действие силы на
твердое тело (сила может быть приложена в любой точке вдоль его линии действия
без изменения его действия на организм в целом — принцип трансмиссивности).
Фиксированный вектор — это вектор, для которого определена уникальная точка приложения.
указан, и поэтому вектор занимает определенную позицию в пространстве
например действие силы на деформируемое или нежесткое тело или силы
действует на данную частицу. Фиксированный вектор полностью характеризуется
по его точке приложения, его величине и направлению (где направление
определяется линией действия и смыслом). Потому что частица
бесконечно мала, силы, действующие на него, имеют одну и ту же точку приложения,
следовательно, силы, действующие на частицу, полностью характеризуются своей величиной
и направление.
е. их линии действия
не ограничен или не связан с уникальной линией в пространстве, например. пары, смещение
вектор тела, движущегося в пространстве без вращения. Наоборот, скользящий вектор — это тот, для которого единственная линия в пространстве, вдоль которой
векторные действия должны поддерживаться, например. внешнее действие силы на
твердое тело (сила может быть приложена в любой точке вдоль его линии действия
без изменения его действия на организм в целом — принцип трансмиссивности).
Фиксированный вектор — это вектор, для которого определена уникальная точка приложения.
указан, и поэтому вектор занимает определенную позицию в пространстве
например действие силы на деформируемое или нежесткое тело или силы
действует на данную частицу. Фиксированный вектор полностью характеризуется
по его точке приложения, его величине и направлению (где направление
определяется линией действия и смыслом). Потому что частица
бесконечно мала, силы, действующие на него, имеют одну и ту же точку приложения,
следовательно, силы, действующие на частицу, полностью характеризуются своей величиной
и направление.
Два вектора называются равными, если они имеют
той же величины, направления и точки приложения. Если векторы
являются свободными векторами, они могут не иметь одинаковой точки приложения или
одна и та же линия действия, но их величина и направление должны быть одинаковыми,
например рассмотрим векторы A , B и C , которые имеют
одинаковая величина, но разные точки приложения.
А = В = С тогда и только тогда, когда А , В , С являются
бесплатные векторы
А нет = Б нет = С если А , Б , С являются фиксированными векторами
А не = Б а А = С если А , Б , С скользящие векторы
Два вектора равны и противоположны , если они
имеют одинаковую величину, но имеют противоположные направления. (т.е. их
линии действия коллинеарны или параллельны, но их смысл противоположен). Нулевой вектор — это вектор с нулевой величиной в любом произвольном направлении.
Нулевой вектор — это вектор с нулевой величиной в любом произвольном направлении.
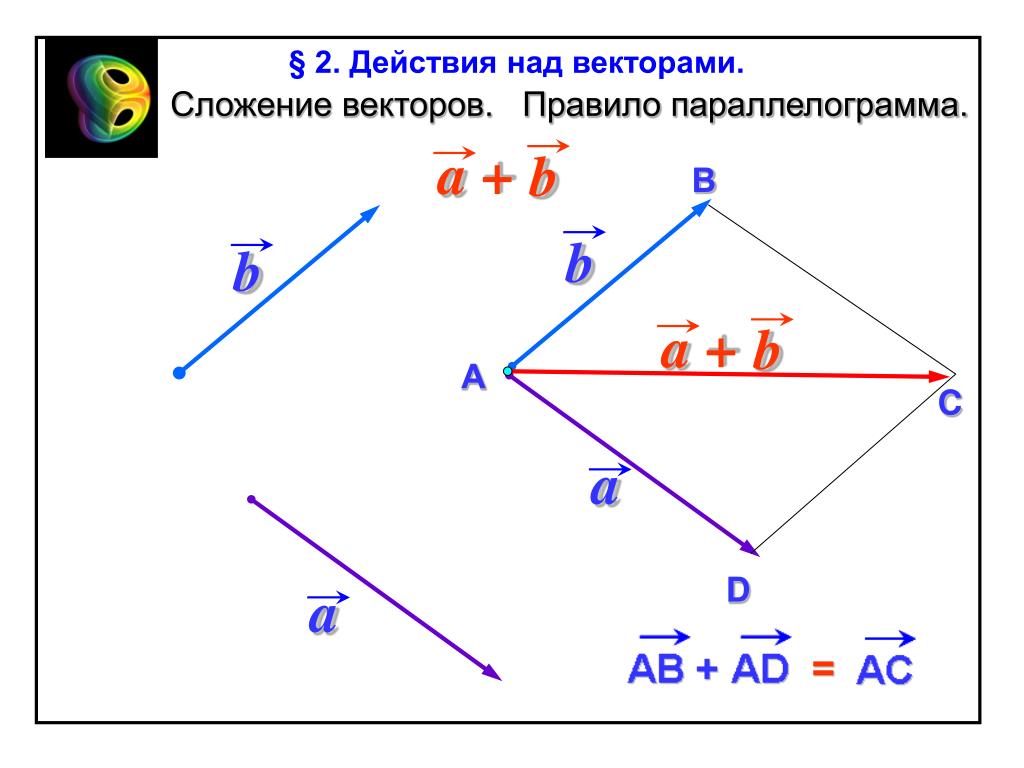
Сложение двух векторов : Закон параллелограмма
Напомним из определения векторов, которые они добавляют по закону параллелограмма. Сумма двух векторов получается построив параллелограмм с векторами по обеим сторонам параллелограмм. Диагональ параллелограмма представляет собой сумму векторного сложения двух векторов. например
Обратите внимание, что сложение векторов является коммутативным , т.е.
P + О = О + Р
Свойство коммутативности становится очевидным, если использовать треугольник . Правило сложения векторов.
Вычитание вектора следует рассматривать как сложение соответствующих
отрицательный вектор. Следовательно,
P — Q = P + (- Q )
Чтобы получить сумму трех или более векторов, примените
закон параллелограмма многократно к последовательным парам векторов, пока все
векторы заменяются одним вектором, результирующим .
Правило треугольника/многоугольника для сложения двух и более Векторы
Это означает, что сумма (т.е. результирующая)
два или более векторов, действующих на тело, можно получить графически, расположив
заданные векторы в форме кончик-к-хвосту и соединяющие хвост
первый вектор с вершиной последнего при условии, что все векторы компланарны (т.е. все они лежат в одной плоскости). Результирующий
из нескольких одновременных копланарных сил также можно получить в этом
способ. Система сил называется совпадающей, если все силы
действовать через одну точку. Обратите внимание, что система сил должна быть компланарной.
тоже потому, что рисунок должен быть на плоскости.
Используя правило многоугольника, легко увидеть, что вектор
сложение является одновременно коммутативным и ассоциативным ; то есть
P + Q = Q + P (коммутативный закон)
P + Q + R = ( P + Q ) + R = P + ( Q + Р ) (ассоциативный закон)
Произведение скаляра на вектор
Произведение скаляра k на вектор P это
вектор k P , имеющий то же направление, что и P (если k положительное)
или направление, противоположное направлению P (если k отрицательное),
и величина которого равна произведению | Р | (и абсолютное
значение k, где | Р | величина вектора P
Результат двух сил
Равнодействующая двух сил, действующих на частицу
единая сила, которая действует на частицу так же, как
две силы объединились. Такой результат можно получить из
Закон параллелограмма сложения двух сил. Обратите внимание, что параллелограмм
Закон основан на экспериментальных данных и не может быть доказан или выведен математически.
Такой результат можно получить из
Закон параллелограмма сложения двух сил. Обратите внимание, что параллелограмм
Закон основан на экспериментальных данных и не может быть доказан или выведен математически.
Разложение вектора на компоненты
Так же, как две или более сил, действующих на частицу, могут
заменить одной силой (равнодействующей), которая имеет тот же эффект
на частицу можно также заменить одну силу двумя или
больше сил (называемых составляющими одной силы).
процесс называется разложением единой силы на составные части .
Обратите внимание, что существует бесконечное количество компонентов для любого отдельного
сила F . Однако практическое значение имеет определение
двух составляющих силы, когда (1) известна одна из двух составляющих
и (2) известна линия действия каждого компонента. В этих и
В других случаях необходимые компоненты могут быть получены с помощью треугольника
правило или закон параллелограмма.
Рассмотрим силу F , компоненты которой P и Q
- (a) F – заданная сила. P известен и только линия действия Q известна; Получите величину Q
- Нарисуйте линию от кончика P до кончика F
- Перенести Q в место применения P и Ф
- Получите величину Q либо графически, либо с помощью тригонометрии 90 040
- (b) Учитывая F и линии действий
оба компонента P и Q известны. Получить величины Р и Q
Использует правила синуса и косинуса
| a / sin A = b / sin B = c / sin C (правило синусов) | |
| а 2 = б 2 +
c 2 — 2bc Cos A \ b 2 = a 2 + c 2 — 2ac Cos B (Правило косинуса) c 2 = a 2 + b 2 — 2ab Cos C / |
— Когда проблема затрагивает только три силы ,
используйте силовой треугольник и правила синуса и / или косинуса, чтобы решить его.
— Когда проблема включает в себя более трех сил ,
разложите силы на их прямоугольные компоненты и решите с помощью вектора
алгебра.
Пример 2-1
Кабели AB и AC на рис. ниже помогают поддерживать консольный крыша спортивного стадиона. Силы, с которыми тросы действуют на опору, к которой они прикреплены представлены векторами F AB и F AC , которые имеют величины 100 кН и 60 кН соответственно. Определить величину и направление суммы приложенных сил. (1) на пилоне за тросы (2) на стадионе за тросы. Получать ваше решение (а) графически и (б) с помощью тригонометрии.
Учитывая :
| F аб | = 100 кН
| F ак | = 60 кН
Требуется : Величина и направление
сумма сил, действующих на трос
а) на пилоне
Используйте (1) графическое решение
б) на стадионе
(2) Тригонометрическое решение
Пример задачи 2. 1
1
Учитывая :
Две силы с величиной и направлением, как показано на диаграмме
Требуется : Величина и направление
результирующая сила
Пример задачи 2.2
Дано : Две силы с величиной и направлением как показано на схеме
Требуется : Величина и направление
результирующая сила
Пример задачи 2.10
Дано : Автомобиль-инвалид, протянутый мимо две веревки АВ и АС. Напряжение в АВ = 4000 Н·а = 20 градусов Результирующая сила действует вдоль оси автомобиля.
Требуется :
а) Натяжение троса AC
b) Величина равнодействующей силы
приложены две силы
c) Стоимость такого
что напряжение в переменном токе минимально, а R по-прежнему действует по оси
автомобиля.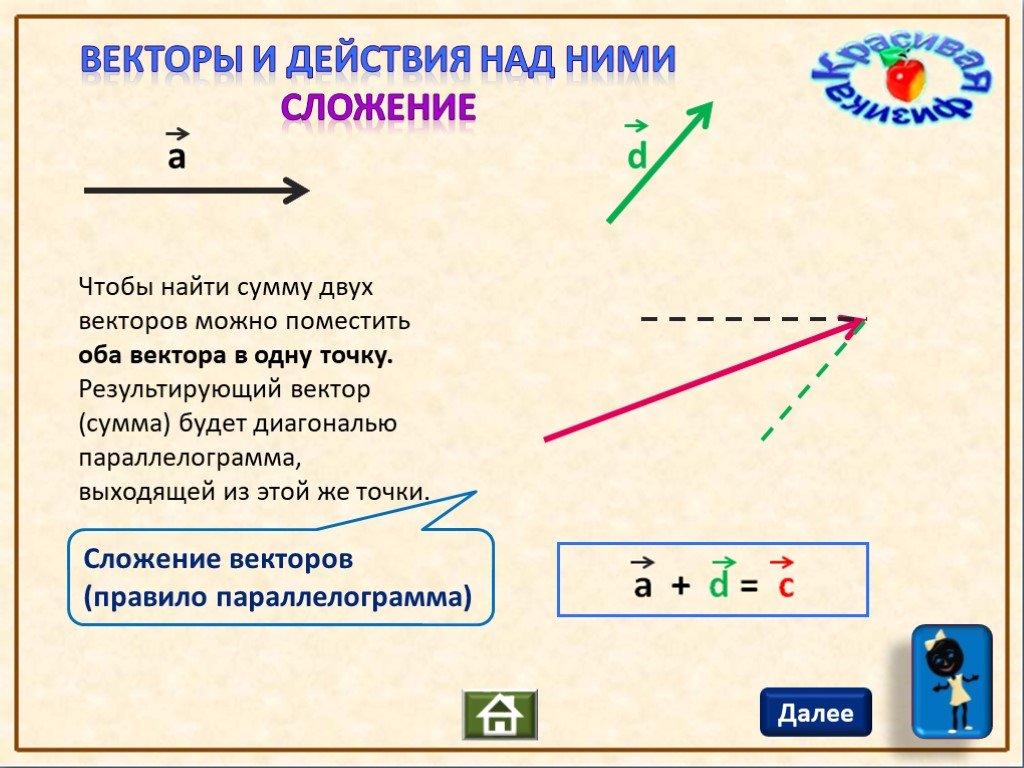 Какова величина Т ак а так же
результирующая сила, которая все еще действует вдоль оси автомобиля.
Какова величина Т ак а так же
результирующая сила, которая все еще действует вдоль оси автомобиля.
Прямоугольные компоненты силы в плоскости и в космосе
— Компоненты силы, параллельные к прямоугольным/декартовым координатным осям. Такие компоненты перпендикулярны друг другу.
Любая сила F в трехмерном пространстве может разложить на прямоугольные компоненты F x , F y и F z , которые параллельны осям x и z соответственно. Следовательно, F является суммой или равнодействующей прямоугольных составляющих F x , Ф у и F z , т.е.
Единичный вектор — это вектор который имеет величину один (1).
 Этот вектор очень важен, потому что
он устанавливает направление любого заданного вектора. Чтобы получить направление
вектора, вычислить единичный вектор, который действует в том же направлении, что и
вектор. Это делается путем деления заданного вектора на его величину.
направление единичного вектора обычно задается указанием направления
углы, которые представляют собой углы, которые вектор образует с положительным x-,
оси координат y и z.
Этот вектор очень важен, потому что
он устанавливает направление любого заданного вектора. Чтобы получить направление
вектора, вычислить единичный вектор, который действует в том же направлении, что и
вектор. Это делается путем деления заданного вектора на его величину.
направление единичного вектора обычно задается указанием направления
углы, которые представляют собой углы, которые вектор образует с положительным x-,
оси координат y и z. Если i, j и k являются единичными векторами в x, y,
направления и z и F x , F y и F z ортогональных скалярных компонентов F , где F x , Ф у и F z являются ортогональными компонентами вектора F и F x = | F x | ; Ф и =| Ф у | и F г = | Ф з | ,
F x = F x i F y = F y j F z = F z k
Тогда уравнение 1 может быть выражено как
 . . (2)
. . (2) Сложение сил (вычисление равнодействующей)
Использование прямоугольных компонентов
Обратите внимание, что и закон параллелограмма, и треугольник
правило позволяет добавить две силы с использованием графического подхода, в то время как
Правило многоугольника позволяет добавить три или более сил.
Силовой треугольник и тригонометрическое решение могут
использоваться, когда задействованы только три силы . Когда больше чем
задействованы три силы, подход все еще может быть использован последовательным
одновременно рассматривая тео сил и находя их равнодействующую. Однако,
такой подход обычно утомителен. Когда сложение векторов включает
более трех векторов, сложение лучше всего выполнять путем разрешения
каждый вектор на его прямоугольные компоненты и сложение этих компонентов
для получения прямоугольных составляющих результирующей силы, например. если Р есть равнодействующая сил А , В , С и D , т.е.
если Р есть равнодействующая сил А , В , С и D , т.е.
Р = А + В + С + D
Где A =
B =
C =
D =
R =
Тогда R = где
Обратите внимание, что скалярная составляющая R x , R y и
R z результирующего R определяется алгебраической суммой
соответствующие скалярные компоненты заданных векторов. Величина
равнодействующей силы находится из выражения:
Углы направления и косинусы направления
Углы q x , q y и q z , которые вектор составляет с
положительные концы осей x, y и z соответственно называются
углы направления. Эти углы важны, потому что их косинусы
— прямоугольные скалярные компоненты единичного вектора, действующие в одном и том же
направление. Для любого вектора R = ,
направляющие косинусы связаны с его прямоугольными скалярными компонентами
и величина следующим образом:
Для любого вектора R = ,
направляющие косинусы связаны с его прямоугольными скалярными компонентами
и величина следующим образом:
Обратите внимание на соотношение выше, что
, ,
но R =
и
, где должна быть единица
вектор, поскольку величина вектора
равно 1. Используя отношение
R =
У нас есть
Следовательно,
Заметим, что направляющие косинусы вектора равны прямоугольные скалярные компоненты (по трем координатным осям) единичный вектор, действующий в том же направлении, что и вектор.
Обратите внимание, что скалярные компоненты единичного вектора вдоль трех декартовых
системы координат равны направляющим косинусам вектора с
отношение к осям. Также три угла направления q x ,
д д и q z не все независимы.
Если известны два дирекционных угла, то третий можно определить из
уравнение выше. Также
Также
Пример (см. пример задачи 2.7, стр. 44)
Дано : Вектор известной величины | В | но
линия действия которого определяется двумя точками (x 1 , y 1 ,
z 1 ) и (x 2 , y 2 , z 2 ).
Требуется : для определения компонентов вектора В в трех ортогональных направлениях. Что такое направляющие косинусы?
Пример задачи 2.59
Дано : Пружина AB и стойка DA, с углом 30 градусов между стойкой и пружиной. Напряжение | Т | = 250 Н
Требуется : (a) компоненты x, y, z
сила, действующая на пластину в точке B
(б) q x , кв г и q z , определяющие направление
сила в точке В
Пример задачи 2. 61
61
Дано : F = (240Н)i — (270Н)j + (680Н)k
Требуется : Величина и направление F
Равновесие частиц
Говорят, что частица находится в равновесии, если равнодействующая всех силы, действующие на него, равны нулю. Это означает, что если силовой многоугольник для всех сил, действующих на частицу, находящуюся в равновесии, силовой многоугольник замкнется, как показано ниже (см. учебник стр. 32, рис. 2.27 и 2.28). Алгебраически условие равновесия представляется как
Ч = å Ф = 0
==>
==>
Задачи на равновесие лучше всего решать с помощью бесплатных схемы тела. Вы должны нарисовать свободные диаграммы тела для своих решений.
Бесплатные схемы корпуса
Диаграмма свободного тела — это диаграмма, на которой показано тело (или частица) и все
силы, как известные, так и неизвестные, действующие на него.
Обратите внимание, что все соответствующие размеры, величины и направления должны показать на диаграмме свободного тела. Все уравнения должны быть написаны на основе на применимых диаграммах свободного тела
Примеры
Для каждой из приведенных ниже задач нарисуйте диаграмму свободного тела, которую можно решить. используется для решения проблемы.
Вопрос 1
Определите силы натяжения канатов AB и AC.
Вопрос 2
Определите горизонтальную силу «P», которую рабочий должен приложить к
канат для размещения 50-килограммового ящика непосредственно над транспортным средством?
Вопрос 3
Определить натяжение тросов AC и BC.
Вопрос 4
Две веревки связаны вместе в точке С. Если максимально допустимое натяжение в
каждая веревка 2,5 кН, что такое Fmax и соответствующий ей угол наклона,
альфа?
Вопрос 5
Определите натяжение кабелей AB, AC и AD, необходимое для
удерживайте 60-фунтовый ящик в равновесии.
Вопрос 6
Вышка со срезными опорами используется для буксировки 200-килограммовой сети.
рыбы на причал. Определить сжатие
усилие в каждой из опор AB и CB и напряжение в
кабель БД. Предположим, что сила каждой ноги действует вдоль ее
ось.
Вопрос 7
Хомут А может свободно скользить по горизонтальному гладкому стержню. Весна прикреплен к
муфта имеет константу 10 фунтов/дюйм и не деформируется, когда муфта находится прямо под
опора Б. Определить величину силы Р, необходимой для поддержания
равновесие, когда (а) c = 9 дюймов; (б) с = 16 дюймов.
ОБЗОР
Учитывая систему сил в пространстве, действующих на частицу, определить величину и направление равнодействующей силы.
Учитывая значение силы и две точки вдоль его линии действия, выразите силу через ее прямоугольные компоненты.
- Получите прямоугольные компоненты каждой силы
- Отдельно добавьте все x-, y- и z-компоненты, чтобы получить компоненты равнодействующей силы вдоль координатных направлений
- Получите величину равнодействующей силы, используя ее прямоугольные компоненты
- Вычислите направляющие косинусы и, следовательно, получите направляющие углы




 У равных векторов равны
соответствующие координаты.
У равных векторов равны
соответствующие координаты.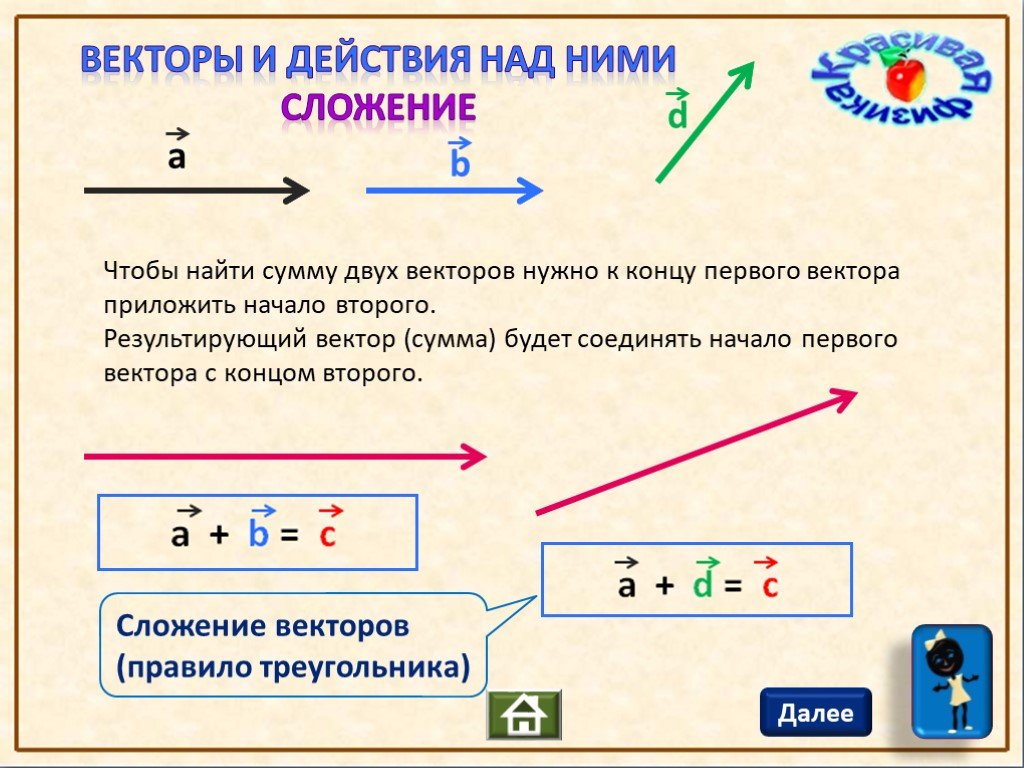
 Выделите время, чтобы регулярно анализировать как ваш прогресс, так и его влияние на ваше эмоциональное и психическое здоровье. Нет смысла прогрессировать, если вы выгораете в процессе. Анализ вашего внешнего успеха и вашего внутреннего опыта поможет вам использовать более устойчивые методы работы.
Выделите время, чтобы регулярно анализировать как ваш прогресс, так и его влияние на ваше эмоциональное и психическое здоровье. Нет смысла прогрессировать, если вы выгораете в процессе. Анализ вашего внешнего успеха и вашего внутреннего опыта поможет вам использовать более устойчивые методы работы.