Координаты вектора / Метод координат / Справочник по геометрии 7-9 класс

Прямоугольная система координат (декаротова система координат) — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Для задания прямоугольной системы координат нужно провести две взаимно перпендикулярные прямые, на каждой из них выбрать направление (оно обозначается стрелкой) и выбрать единицу измерения отрезков.

На рисунке выше оси и перпендикулярны. При выбранной единице измерения отрезков длина каждого отрезка выражается положительным числом. В дальнейшем под длиной отрезка мы будем понимать это число. Так, единичный вектор — это вектор, длина которого равна 1.

Отложим от начала координат О единичные векторы и так, чтобы их направления совпадали с направлениями осей и соответственно.

Векторы и называют координатными векторами.

Координатные векторы не коллинеарны, поэтому любой вектор можно разложить по координатным векторам, т.е. представить в виде , причем коэффициенты разложения и определяются единственным образом. Коэффициенты разложения вектора по координатным векторам называются координатами вектора в данной системе координат.

Координаты вектора записывают в фигурных скобках после обозначения вектора: .

На рисунке выше .

Нулевой вектор можно представить в виде , следовательно, его координаты равны нулю: .

Если векторы и

равны, то и . Значит, координаты равных векторов соответственно равны.

Правила, позволяющие по координатам векторов находить координаты их суммы, разности и произведения вектора на число:

10. Каждая координата суммы двух и более векторов равна сумме соответствующих координат этих векторов.

Доказательство

Дано: , , .

Доказать: .

Доказательство:

По условию и , тогда и .

Сложим последние два равенства и применим свойства сложения векторов и умножения вектора на число, получим: , следовательно, координаты вектора равны , т.е. .

Что и требовалось доказать.

20. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.

Доказательство

Дано: , , .

Доказать: .

Доказательство:

По условию и , тогда (1)  и .  (2) 

Вычтем из равенства (1) равенство (2) и применим свойства сложения векторов и умножения вектора на число, получим: , следовательно, координаты вектора равны , т.

е. . Что и требовалось доказать.

30. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.

Доказательство

Дано: , — число, .

Доказать: .

Доказательство:

По условию , значит, .

Умножим последнее равенство на число и используя свойства умножения вектора на число, получим: , следовательно, координаты вектора равны , т.е. . Что и требовалось доказать.

Данные правила позволяют определить координаты любого вектора, представленного в виде алгебраической суммы данных векторов с известными координатами.

Пример

Найти координаты вектора , если известно, что .

Решение:

По правилу 3⁰ вектор будет иметь координаты , т. е. , вектор координаты , т.е. .

Так как , то координаты вектора можно найти по правилу 1⁰: , т.е. .

Ответ: .

Зачем нужна нормализация вектора? — CodeRoad

Чтение документации Godot Game Engine о единичном векторе, нормализации и точечном продукте действительно имеет большой смысл. Вот эта статья:

Единичные векторы

Итак, мы знаем, что такое вектор. У него есть направление и величина. Мы также знаем, как использовать их в Годо. Следующий шаг-изучение единичных векторов. Любой вектор с величиной длины 1 считается единичным вектором. В 2D представьте себе, что вы рисуете круг радиусом один. Этот круг содержит все единичные векторы, существующие для 2 измерений:

Итак, что же такого особенного в единичных векторах? Единичные векторы удивительны. Другими словами, единичные векторы обладают несколькими очень полезными свойствами.

Не могу дождаться, чтобы узнать больше о фантастических свойствах единичных векторов, но шаг за шагом.

Итак, как создается единичный вектор из обычного вектора?

Нормализация

Взятие любого вектора и уменьшение его величины до 1.0 при сохранении его направления называется нормализацией. Нормализация выполняется путем деления компонент X и y (и z в 3D) вектора на его величину:

var a = Vector2(2,4)
var m = sqrt(a.x*a.x + a.y*a.y)
a.x /= m
a.y /= m

Как вы могли догадаться, если вектор имеет величину 0 (то есть это не вектор, а начало координат, также называемое вектором null), происходит деление на ноль, и Вселенная проходит через второй Большой взрыв, за исключением обратной полярности, а затем обратно. В результате человечество в безопасности, но Годо напечатает ошибку. Помни! Вектор (0,0) не может быть нормализован!.

Конечно, Vector2 и метода Vector3 уже предусматривает способ, чтобы сделать это:

a = a.normalized()

Скалярное произведение

OK, точечное произведение является наиболее важной частью векторной математики. Без скалярное произведение, землетрясение, никогда бы не сделал. Это самый важный раздел учебника, поэтому убедитесь, что вы поняли его правильно. Большинство людей, пытающихся понять векторную математику, сдаются здесь, потому что, несмотря на то, насколько она проста, они не могут сделать из нее голову или хвост. Почему? Вот почему, это потому…

Скалярное произведение принимает два вектора и возвращает scalar:

var s = a.x*b.x + a.y*b.y

Да, в значительной степени. Умножьте x из вектора a на x из вектора b. Сделайте то же самое с y и сложите его вместе. В 3D году почти то же самое:

var s = a.x*b.x + a.y*b.y + a.z*b.z

Я знаю, это совершенно бессмысленно! Вы даже можете сделать это с помощью встроенной функции:

var s = a.dot(b)

Порядок двух векторов не имеет значения, a.dot(b) возвращает то же значение, что и b.dot(a) .

Именно здесь начинается отчаяние и книги и учебники показывают вам эту формулу:

И вы понимаете, что пришло время отказаться от создания 3D игр или сложных 2D игр. Как может что-то такое простое быть таким сложным? Кто-то другой должен будет сделать следующую Zelda или Call of Duty. Сверху вниз RPGs все-таки не так уж плохо выглядят. Да, я слышал, что кто-то сделал довольно Уилл с одним из них в Steam…

Так что это ваш момент, это ваше время сиять. не сдавайтесь! На этом этапе этот учебник сделает резкий поворот и сосредоточится на том, что делает продукт dot полезным. Вот почему это полезно. Мы сосредоточимся один за другим на примерах использования продукта dot с реальными приложениями. Больше никаких формул, которые не имеют никакого смысла. Формулы обретут смысл, как только вы узнаете, для чего они полезны.

Сайдинг Первое полезное и самое важное свойство точечного продукта-проверять, на какую сторону смотрит материал. Давайте представим, что у нас есть любые два вектора, a и b. Любое направление или величина (ни происхождение). Не имеет значения, что это такое, но давайте представим, что мы вычисляем точечное произведение между ними.

var s = a.dot(b)

Операция вернет одно число с плавающей запятой (но так как мы находимся в векторном мире, мы называем их scalar, будем продолжать использовать этот термин с этого момента). Это число скажет нам следующее:

Если число больше нуля, то оба смотрят в одном направлении (угол между ними равен < 90 ° градусов). Если число меньше нуля, то оба смотрят в противоположном направлении (угол между ними > 90° градусов). Если число равно нулю, то векторы имеют форму L (угол между ними равен 90° градусов).

Итак, давайте подумаем о реальном сценарии использования. Представьте себе, что змея идет через лес, а рядом с ней враг. Как мы можем быстро определить, видел ли враг обнаруженную змею? Чтобы обнаружить его, враг должен уметь видеть змея. Допустим, тогда это:

Змея находится в позиции А. Противник находится на позиции Б. Противник стоит лицом к вектору направления F.

Итак, давайте создадим новый вектор BA, который идет от охранника (B) к змее (A), вычитая эти два:

var BA = A - B

В идеале, если бы охранник смотрел прямо на змею, чтобы установить зрительный контакт, он сделал бы это в том же направлении, что и вектор BA.

Если точечное произведение между F и BA больше 0, то будет обнаружена змея. Это происходит потому, что мы сможем сказать, что охранник стоит лицом к нему:

if (BA.dot(F) > 0):
    print("!")

Похоже, Снейк пока в безопасности.

Сайдинг с единичными векторами Итак, теперь мы знаем, что точечное произведение между двумя векторами даст нам знать, смотрят ли они в одну и ту же сторону, противоположные стороны или просто перпендикулярны друг другу.

Это работает одинаково со всеми векторами, независимо от величины, поэтому единичные векторы не являются исключением. Однако использование того же свойства с единичными векторами дает еще более интересный результат, так как добавляется дополнительное свойство:

Если оба вектора направлены в одном и том же направлении (параллельны друг другу, угол между ними равен 0°), то результирующая scalar равна 1. Если оба вектора направлены в прямо противоположном направлении (параллельны друг другу, но угол между ними равен 180°), то результирующий scalar равен -1. Это означает, что точечное произведение между единичными векторами всегда находится в диапазоне от 1 до -1. Итак, Еще Раз…

Если их угол равен 0°, то точечное произведение равно 1. Если их угол равен 90°, то точечное произведение равно 0. Если их угол равен 180°, то точечное произведение равно -1. Э-э … это странно знакомо… я уже видел такое раньше… — куда?

Возьмем два единичных вектора. Первый из них направлен вверх, второй тоже, но мы будем вращать его полностью от вверх (0°) до вниз (180° градусов)…

При построении графика полученного scalar!

Ага! Теперь все это имеет смысл, это Косинусная функция!

Так можно сказать, как правило…

Точечное произведение между двумя единичными векторами — это косинус угла между этими двумя векторами. Итак, чтобы получить угол между двумя векторами, мы должны сделать:

var angle_in_radians = acos( a.dot(b) )

Для чего это полезно? Ну, прямое получение угла, вероятно, не так полезно, но просто возможность определить угол полезна для справки. Один из примеров-демонстрация кинематического персонажа, когда персонаж движется в определенном направлении, а затем мы ударяем по объекту. Как определить, что мы ударились об пол?

Сравнивая Нормаль точки столкновения с ранее вычисленным углом.

Прелесть этого заключается в том, что один и тот же код работает точно так же и без изменений в 3D. Векторная математика в значительной степени dimension-amount-independent, поэтому добавление или удаление оси добавляет очень мало сложности.

Единичный вектор — касательная — Большая Энциклопедия Нефти и Газа, статья, страница 2

Единичный вектор — касательная

Cтраница 2

Тогда перемещение точки А совпадает с вектором, образованным векторным произведением единичного вектора касательной к кривой Г в точке А и единичного вектора нормали к поверхности S в этой же точке.  [16]

Определим вектор-функцию Я т, где R — натяжение нити, а т — единичный вектор касательной в точке А.  [18]

Тогда выполняются равенства ( 28) и ( 31), где г — единичный вектор касательной, is — единичный вектор нормали к кривой Г в данной ее точке.  [19]

Из ( 2) следует, что V сопз1, V VI, где т — единичный вектор касательной к траектории.  [20]

Имея в виду дальнейшие обобщения, представим вектор скорости в виде v vs, где s — единичный вектор касательной к окружности. Первый множитель v есть модуль вектора скорости, второй множитель s указывает направление.  [21]

Имея в виду дальнейшие обобщения, представим вектор скорости в виде v vs, где s — единичный вектор касательной к окружности. Первый множитель v дает численную величину скорости, второй множитель s указывает ее направление.  [22]

Обозначим через k единичный вектор оси Oz, направленный перпендикулярно к плоскости чертежа в сторону читателя, а через t — единичный вектор касательной к контуру Ст, направленный так, чтобы система t, n, h была, сонаправлена с системой координат Охуг.  [23]

Введем в рассмотрение трехгранник единичных взаимно ортогональных векторов er, е, ez, образующих правую систему; ег является единичным вектором радиуса, е — единичным вектором касательной к окружности, ez — единичным вектором образующей.  [24]

Здесь VT — разрыв касательной составляющей скорости перемещений к поверхности разрыва, G — скорость распространения поверхности разрыва, Vn — нормальная к поверхности разрыва составляющая скорости перемещений частиц, т, щ — единичные векторы касательной и нормали к поверхности разрыва.  [25]

Какие из перечисленных величин совпадают между собой в случае свободного падения тела с нулевой начальной скоростью: dv / dt, dv / dt, dv / dt, dv / dt, ( dv / dt) t, dv / dt т, где v — скорость тела в момент t, т — единичный вектор касательной к траектории.  [26]

Мч там видели, что при переходе какой-либо точки по поверхности из положения М в смежное положение AJlt отстоящее от начального на бесконечно малое расстояние 8а, плоскость, касательная к поверхности, повертывается на бесконечно малый угол 8ф 68о вокруг так называемой оси полного изгиба поверхности, соответствующей точке М и направлению и; при этом о есть единичный вектор касательной к дуге MMlt а 0 — так называемый полный изгиб.  [27]

Мм там видели, что при переходе какой-либо точки по поверхности из положения М в смежное положение Ж, отстоящее от начального на бесконечно малое расстояние из, плоскость, касательная к поверхности, повертывается на бесконечно малый угол 8ф 68о вокруг так называемой оси полного изгиба поверхности, соответствующей точке М и направлению и; при этом о есть единичный вектор касательной к дуге / И / VJj, а в — так называемый полный изгиб. Полный изгиб определяется формулами ( 10 3) на стр.  [28]

Первой естественной осью является касательная / Ит. Ее положительное направление совпадает с направлением единичного вектора касательной т, направленного в сторону возрастающих расстояний.  [29]

Первой естественной осью является касательная Mi. Ее положительное направление совпадает с направлением единичного вектора касательной т, направленного в сторону возрастающих расстояний.  [30]

Страницы:      1    2    3    4

Определение вектора, простейшие алгебраические операции с векторами, единичный вектор. Базисные единичные векторы i, j, k и система координат.

⇐ ПредыдущаяСтр 3 из 9Следующая ⇒

Вектор — это направленный отрезок, то есть отрезок, имеющий длину и определенное направление.

Сложение векторов (правило треугольника):

Для того чтобы сложить два вектора и  нужно переместить вектор  параллельно самому себе так, чтобы его начало совпадало с концом вектора . Тогда их суммой будет вектор , начало которого совпадает с началом вектора , а конец — с концом вектора .

             

 

Вычитание векторов:

Чтобы из  вычесть  надо к  прибавить (- ). Полученный в результате этой операции вектор  и будет являться разностью векторов   и . Таким образом:   =  −   =  + (- ).

                                                                                                                                  

 

Умножение вектора на число:

Произведением вектора   на число x называется вектор =x . Например, если x=2:  

                                                                              

 

Единичный вектор или орт – вектор, длина которого равна единице.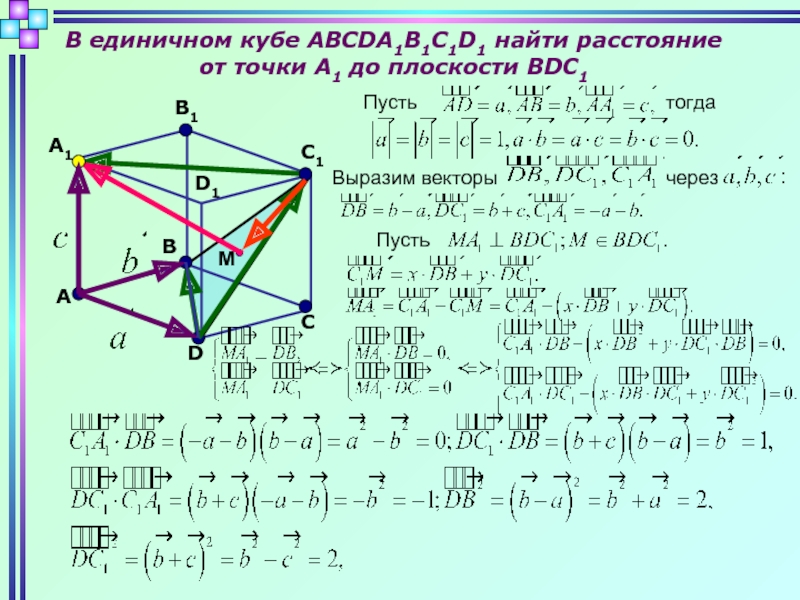

Единичный вектор , направленный вдоль оси Х, обозначается i, единичный вектор , направленный вдоль оси Y , обозначается j, а единичный вектор, направленный вдоль оси Z, обозначается k . i = 1, j = 1, k = 1.

Радиус-вектор r, вектор перемещения r, вектор мгновенной скорости v.

Радиус-вектор точки — это вектор, начало которого совпадает с началом системы координат, а конец — с данной точкой.

 

                                

Вектор перемещения (или просто перемещение) – это направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. = t

Мгновенная скорость — скорость в каждое мгновение в каждой точке траектории.

Вектор мгновенной скорости всегда направлен по касательной к траектории движения.

Вектор ускорения, нормальная составляющая и тангенциальная составляющая вектора ускорения.

Ускорение – физическая величина, равная отношению очень малого изменения вектора скорости  к малому промежутку времени , за которое это изменение произошло. Ускорение – величина векторная.

Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.

Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой _n. Вектор нормального ускорения направлен по радиусу кривизны траектории.

Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:

Рекомендуемые страницы:

перевод на русский, синонимы, антонимы, произношение, примеры предложений, транскрипция, значение, словосочетания

If x, y, and z are the components of the unit vector representing the axis, and.	Если x, y и z-компоненты единичного вектора, представляющего ось, и.
Moreover, since k is a unit vector, K has unit 2-norm.	Кроме того, поскольку k-единичный вектор, K имеет единичную 2-норму.
Because uρ is a unit vector, its magnitude is fixed, and it can change only in direction, that is, its change duρ has a component only perpendicular to uρ.	Поскольку up-единичный вектор, его величина фиксирована, и он может изменяться только в направлении, то есть его изменение dup имеет компонент только перпендикулярный up.
When each component of the vector is divided by that length, the new vector will be a unit vector pointing in the same direction.	Когда каждая составляющая вектора делится на эту длину, новый вектор будет единичным вектором, указывающим в том же направлении.
If the hill height function H is differentiable, then the gradient of H dotted with a unit vector gives the slope of the hill in the direction of the vector.	Если функция высоты холма H дифференцируема, то градиент H, усеянный единичным вектором, дает наклон холма в направлении вектора.
The boosts along the Cartesian directions can be readily obtained, for example the unit vector in the x direction has components nx = 1 and ny = nz = 0.	Ускорения вдоль декартовых направлений могут быть легко получены, например единичный вектор в направлении x имеет компоненты nx = 1 и ny = nz = 0.
Here a is the position of a point on the line, and n is a unit vector in the direction of the line.	Здесь a-положение точки На прямой, а n-единичный вектор в направлении прямой.
The magnitude of the radial velocity is the dot product of the velocity vector and the unit vector in the direction of the displacement.	Величина радиальной скорости является точечным произведением вектора скорости и единичного вектора в направлении перемещения.
In the context of a function on a Euclidean space, some texts restrict the vector v to being a unit vector.	В контексте функции на евклидовом пространстве некоторые тексты ограничивают вектор v единичным вектором.
Whether, therefore, the unit vector of the system is to correspond in reality to one meter or an Ångström depends on the application.	Поэтому, должен ли единичный вектор системы соответствовать в действительности одному метру или Ангстрему, зависит от приложения.
Polar coordinates in the plane employ a radial unit vector uρ and an angular unit vector uθ, as shown above.	Полярные координаты в плоскости используют радиальный единичный вектор вверх и угловой единичный вектор uθ, как показано выше.
Unit vector uθ also travels with the particle and stays orthogonal to uρ.	Единичный вектор uθ также перемещается вместе с частицей и остается ортогональным вверх.
To evaluate the velocity, the derivative of the unit vector uρ is needed.	Для оценки скорости необходима производная от единичного вектора вверх.
As with uρ, uθ is a unit vector and can only rotate without changing size.	Как и в случае с up, uθ является единичным вектором и может вращаться только без изменения размера.
As mentioned above, a state of a quantum system is given by a unit vector in a Hilbert space.	Как уже упоминалось выше, состояние квантовой системы задается единичным вектором в гильбертовом пространстве.
The direction of ur is described by θ, the angle between the x-axis and the unit vector, measured counterclockwise from the x-axis.	Направление ur описывается θ, углом между осью x и единичным вектором, измеренным против часовой стрелки от оси X.
The normalized vector or versor û of a non-zero vector u is the unit vector in the direction of u, i.e.,.	Нормированный вектор или версор-ненулевого вектора u является единичным вектором в направлении u, т. е.
The value of each component is equal to the cosine of the angle formed by the unit vector with the respective basis vector.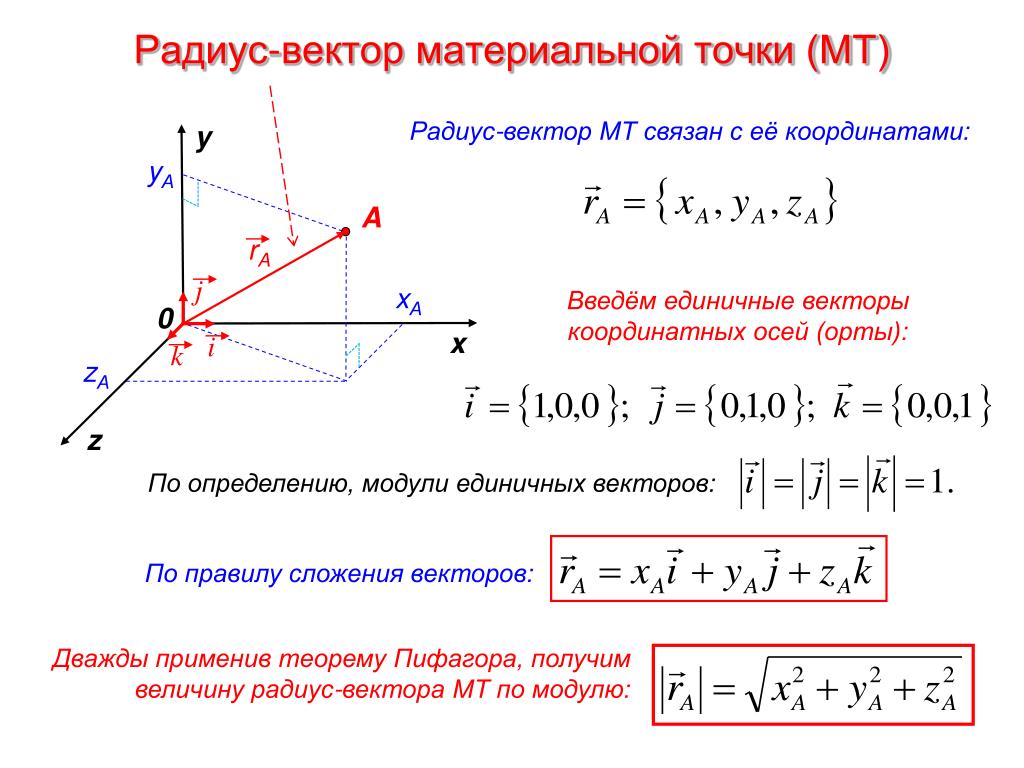	Значение каждой составляющей равно Косинусу угла, образованного единичным вектором с соответствующим базисным вектором.
Другие результаты
The gravitational field is a vector field that describes the gravitational force which would be applied on an object in any given point in space, per unit mass.	Гравитационное поле-это векторное поле, которое описывает гравитационную силу, приложенную к объекту в любой заданной точке пространства, на единицу массы.
Then the unit axis vector can be written.	Тогда вектор единичной оси может быть записан.
In the United States, cities or special districts are responsible for vector control.	В Соединенных Штатах ответственность за борьбу с переносчиками инфекции несут города или специальные районы.
The vector 1/rx is uniformly distributed over the surface of the unit n-ball.	Вектор 1 / rx равномерно распределен по поверхности единичного n-шара.
The unit tangent vector determines the orientation of the curve, or the forward direction, corresponding to the increasing values of the parameter.	Единичный вектор тангенса определяет ориентацию кривой или направление движения вперед, соответствующее возрастающим значениям параметра.
Unit vectors are often chosen to form the basis of a vector space.	Единичные векторы часто выбираются для формирования основы векторного пространства.
Every vector in the space may be written as a linear combination of unit vectors.	Каждый вектор в пространстве может быть записан как линейная комбинация единичных векторов.
But more than that, a vector processor may have multiple functional units adding those numbers in parallel.	Но более того, векторный процессор может иметь несколько функциональных блоков, добавляющих эти числа параллельно.
However, in the case of torque, the unit is assigned to a vector, whereas for energy, it is assigned to a scalar.	Однако в случае крутящего момента единица измерения присваивается вектору, тогда как для энергии она присваивается скаляру.
This vector mode was therefore removed shortly after its introduction, to be replaced with the much more powerful Neon Advanced SIMD unit.	Поэтому этот векторный режим был удален вскоре после его введения, чтобы быть замененным на гораздо более мощный Neon Advanced SIMD unit.
A thrust vector control unit fitted to the rocket motor increases the missile’s agility.	Блок управления вектором тяги, установленный на ракетном двигателе, повышает маневренность ракеты.
The minimal gated unit is similar to the fully gated unit, except the update and reset gate vector is merged into a forget gate.	Минимальный блок стробирования аналогичен полностью стробируемому блоку, за исключением того, что вектор ворот обновления и сброса объединен в ворота забвения.
This coordinate system sometimes is referred to as intrinsic or path coordinates or nt-coordinates, for normal-tangential, referring to these unit vectors.	Эта система координат иногда называется внутренними или путевыми координатами или nt-координатами, для нормальных-тангенциальными, относящимися к этим единичным векторам.
Given a rotating frame of three unit coordinate vectors, all the three must have the same angular speed at each instant.	Учитывая вращающуюся рамку из трех единичных векторов координат, все три должны иметь одинаковую угловую скорость в каждый момент времени.
Consider a unit sphere with three unit vectors OA, OB and OC drawn from the origin to the vertices of the triangle.	Рассмотрим единичную сферу с тремя единичными векторами OA, OB и OC, проведенными от начала координат до вершин треугольника.
More specifically, the formulas describe the derivatives of the so-called tangent, normal, and binormal unit vectors in terms of each other.	Более конкретно, формулы описывают производные так называемых касательных, нормальных и бинормальных единичных векторов в терминах друг друга.
By definition, in a Euclidean space the dot product of two unit vectors is a scalar value amounting to the cosine of the smaller subtended angle.	По определению, в евклидовом пространстве точечное произведение двух единичных векторов представляет собой скалярное значение, равное Косинусу меньшего вложенного угла.
Unit vectors may be used to represent the axes of a Cartesian coordinate system.	Единичные векторы могут быть использованы для представления осей декартовой системы координат.
For instance, the unit vectors in the direction of the x, y, and z axes of a three dimensional Cartesian coordinate system are.	Например, единичные векторы в направлении осей x, y и z трехмерной декартовой системы координат являются.
They form a set of mutually orthogonal unit vectors, typically referred to as a standard basis in linear algebra.	Они образуют набор взаимно ортогональных единичных векторов, обычно называемых стандартным базисом в линейной алгебре.
The vectors ei are an orthonormal basis, which means that they have unit length and are at right angles to each other.	Векторы ei являются ортонормированным базисом, что означает, что они имеют единичную длину и находятся под прямым углом друг к другу.
Hence since these vectors have unit length.	Следовательно, поскольку эти векторы имеют единичную длину.
The unit magnitude of these vectors is a consequence of Eq. 1.	Единичная величина этих векторов является следствием эквалайзера. 1.
All it means is that we are using unit vectors that vary with s to describe the path, but still observe the motion from the inertial frame.	Все это означает, что мы используем единичные векторы, которые изменяются с s для описания траектории, но все же наблюдаем движение из инерциальной системы отсчета.

Единичные взаимно перпендикулярные векторы

Данная статья раскрывает смысл перпендикулярности двух векторов на плоскости в трехмерном пространстве и нахождение координат вектора, перпендикулярному одному или целой паре векторов. Тема применима для задач, связанных с уравнениями прямых и плоскостей.

Мы рассмотрим необходимое и достаточное условие перпендикулярности двух векторов, решим по методу нахождения вектора, перпендикулярному заданному, затронем ситуации по отысканию вектора, который перпендикулярен двум векторам.

Необходимое и достаточное условие перпендикулярности двух векторов

Применим правило о перпендикулярных векторах на плоскости и в трехмерном пространстве.

При условии значения угла между двумя ненулевыми векторами равным 90 ° ( π 2 радиан) называют перпендикулярными.

Что это значит, и в каких ситуациях необходимо знать про их перпендикулярность?

Установление перпендикулярности возможно через чертеж. При отложении вектора на плоскости от заданных точек можно геометрически измерить угол между ними. Перпендикулярность векторов если и будет установлена, то не совсем точно. Чаще всего данные задачи не позволяют делать это при помощи транспортира, поэтому данный метод применим только в случае, когда ничего больше о векторах неизвестно. векторов a → и b → равен 90 ° . По определению это и есть необходимое и достаточное свойство.

Условие перпендикулярности на координатной плоскости

Раздел скалярного произведения в координатах демонстрирует неравенство ( a → , b → ) = a x · b x + a y · b y , справедливое для векторов с координатами a → = ( a x , a y ) и b → = ( b x , b y ) , на плоскости и ( a → , b → ) = a x · b x + a y · b y для векторов a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) в пространстве. Необходимым и достаточным условием перпендикулярности двух векторов в координатной плоскости имеет вид a x · b x + a y · b y = 0 , для трехмерного пространства a x · b x + a y · b y + a z · b z = 0 .

Применим на практике и рассмотрим на примерах.

Проверить свойство перпендикулярности двух векторов a → = ( 2 , – 3 ) , b → = ( – 6 , – 4 ) .

Для решения данной задачи необходимо найти скалярное произведение. Если по условию оно будет равным нулю, значит, они перпендикулярны.

( a → , b → ) = a x · b x + a y · b y = 2 · ( – 6 ) + ( – 3 ) · ( – 4 ) = 0 . Условие выполнено, значит, заданные векторы перпендикулярны на плоскости.

Ответ: да, заданные векторы a → и b → перпендикулярны.

Даны координатные векторы i → , j → , k → . Проверить, могут ли векторы i → – j → и i → + 2 · j → + 2 · k → быть перпендикулярными.

Для того, чтобы вспомнить, как определяются координаты вектора, нужно прочитать статью про координаты вектора в прямоугольной системе координат. Таким образом получаем, что у заданных векторов i → – j → и i → + 2 · j → + 2 · k → имеются соответствующие координаты ( 1 , – 1 , 0 ) и ( 1 , 2 , 2 ) . Подставляем числовые значения и получаем: i → + 2 · j → + 2 · k → , i → – j → = 1 · 1 + ( – 1 ) · 2 + 0 · 2 = – 1 .

Выражение не равно нулю, ( i → + 2 · j → + 2 · k → , i → – j → ) ≠ 0 , а это означает, что векторы i → – j → и i → + 2 · j → + 2 · k → не перпендикулярны, так как условие не выполнилось.

Ответ: нет, векторы i → – j → и i → + 2 · j → + 2 · k → не перпендикулярны.

Даны векторы a → = ( 1 , 0 , – 2 ) и b → = ( λ , 5 , 1 ) . Найти значение λ , при котором данные векторы перпендикулярны.

Используем условие перпендикулярности двух векторов в пространстве в квадратной форме, тогда получим

a x · b x + a y · b y + a z · b z = 0 ⇔ 1 · λ + 0 · 5 + ( – 2 ) · 1 = 0 ⇔ λ = 2

Ответ: векторы перпендикулярны при значении λ = 2 .

Имеются случаи, когда вопрос о перпендикулярности невозможен даже при необходимом и достаточном условии. При известных данных о трех сторонах треугольника на двух векторах, возможно, найти угол между векторами и проверить его.

Дан треугольник А В С со сторонами А В = 8 , А С = 6 , В С = 10 см. проверить на перпендикулярность векторы A B → и A C → .

При перпендикулярности векторов A B → и A C → треугольник A B C считается прямоугольным. Тогда применим теорему Пифагора, где В С – гипотенуза треугольника. Равенство B C 2 = A B 2 + A C 2 должно выполниться. Отсюда следует, что 10 2 = 8 2 + 6 2 ⇔ 100 = 100 . Значит, А В и А С являются катетами треугольника А В С , следовательно, A B → и A C → перпендикулярны.

Нахождение вектора, перпендикулярного данному

Важно научиться находить координаты вектора, перпендикулярного заданному. Это возможно как на плоскости, так и в пространстве при условии перпендикулярности векторов.

Нахождение вектора, перпендикулярного данному в плоскости.

Ненулевой вектор a → может иметь бесконечное количество перпендикулярных векторов на плоскости. Изобразим это на координатной прямой.

Задан ненулевой вектор a → , лежащий на прямой а. Тогда заданный b → , расположенный на любой прямой, перпендикулярной прямой а, становится перпендикулярным и a → . Если вектору i → перпендикулярен вектор j → или любой из векторов λ · j → при λ равной любому действительному числу кроме нуля, то нахождение координат вектора b → , перпендикулярному a → = ( a x , a y ) , сводится к бесконечному множеству решений. Но необходимо найти координаты вектора, перпендикулярного a → = ( a x , a y ) . Для этого необходимо записать условие перпендикулярности векторов в такой форме a x · b x + a y · b y = 0 . Имеем b x и b y , являющиеся искомыми координатами перпендикулярного вектора. Когда a x ≠ 0 , значение b y является ненулевым, а b x вычислим из неравенства a x · b x + a y · b y = 0 ⇔ b x = – a y · b y a x . При a x = 0 и a y ≠ 0 присваиваем b x любое значение кроме нуля, а b y находим из выражения b y = – a x · b x a y .

Дан вектор с координатами a → = ( – 2 , 2 ) . Найти перпендикулярный данному вектор.

Обозначим искомый вектор как b → ( b x , b y ) . Найти его координаты можно из условия перпендикулярности векторов a → и b → . Тогда получим: ( a → , b → ) = a x · b x + a y · b y = – 2 · b x + 2 · b y = 0 . Присвоим b y = 1 и подставим: – 2 · b x + 2 · b y = 0 ⇔ – 2 · b x + 2 = 0 . Отсюда из формулы получим b x = – 2 – 2 = 1 2 . Значит, вектор b → = ( 1 2 , 1 ) является вектором, перпендикулярным a → .

Если ставится вопрос о трехмерном пространстве, задача решается по такому же принципу. При заданном векторе a → = ( a x , a y , a z ) существует бесконечное множество перпендикулярных векторов. Зафиксирует это на координатной трехмерной плоскости. Дана a → , лежащая на прямой a . Перпендикулярную прямой a плоскость обозначаем α . В этом случае любой ненулевой вектор b → из плоскости α перпендикулярен a → .

Необходимо найти координаты b → , перпендикулярного ненулевому вектору a → = ( a x , a y , a z ) .

Пусть задан b → с координатами b x , b y и b z . Чтобы найти их, необходимо применить определение условия перпендикулярности двух векторов. Равенство a x · b x + a y · b y + a z · b z = 0 должно выполняться. Из условия a → – ненулевой, значит, одна из координат имеет значение не равное нулю. Предположим, что a x ≠ 0 , ( a y ≠ 0 или a z ≠ 0 ). Следовательно, имеем право разделить на эту координату все неравенство a x · b x + a y · b y + a z · b z = 0 , получим выражение b x + a y · b y + a z · b z a x = 0 ⇔ b x = – a y · b y + a z · b z a x . Присваиваем координатам b y и b x любое значение, вычисляем значение b x , исходя из формулы, b x = – a y · b y + a z · b z a x . Искомый перпендикулярный вектор будет иметь значение a → = ( a x , a y , a z ) .

Рассмотрим доказательство на примере.

Дан вектор с координатами a → = ( 1 , 2 , 3 ) . Найти вектор, перпендикулярный данному.

Обозначим искомый вектор за b → = ( b x , b y , b z ) . Исходя из условия о перпендикулярности векторов, скалярное произведение должно быть равным нулю.

a ⇀ , b ⇀ = 0 ⇔ a x · b x + a y · b y + a z · b z = 0 ⇔ 1 · b x + 2 · b y + 3 · b z = 0 ⇔ b x = – ( 2 · b y + 3 · b z )

Если значение b y = 1 , b z = 1 , тогда b x = – 2 · b y – 3 · b z = – ( 2 · 1 + 3 · 1 ) = – 5 . Отсюда следует, что координаты вектора b → ( – 5 , 1 , 1 ) . Вектор b → является одним из перпендикулярных векторов заданному.

Ответ: b → = ( – 5 , 1 , 1 ) .

Нахождение координат вектора, перпендикулярного двум заданным векторам

Нужно найти координаты вектора в трехмерном пространстве. Он перпендикулярен не коллинеаренным векторам a → ( a x , a y , a z ) и b → = ( b x , b y , b z ) . При условии коллинеарности векторов a → и b → в задаче достаточно будет найти вектор, перпендикулярный a → или b → .

При решении применяется понятие векторного произведения векторов.

Векторным произведением векторов a → и b → называют вектор, одновременно перпендикулярный и a → и b → . Для решения данной задачи применяется векторное произведение a → × b → . Для трехмерного пространства имеет вид a → × b → = a → j → k → a x a y a z b x b y b z

Разберем подробнее векторное произведение на примере задачи.

Заданы векторы b → = ( 0 , 2 , 3 ) и a → = ( 2 , 1 , 0 ) . Найти координаты любого перпендикулярного вектора данным одновременно.

Для решения необходимо найти векторное произведение векторов. (Необходимо обратиться к пункту вычисления определителя матрицы для нахождения вектора). Получим :

a → × b → = i → j → k → 2 1 0 0 2 3 = i → · 1 · 3 + j → · 0 · 0 + k → · 2 · 2 – k → · 1 · 0 – j → · 2 · 3 – i → · 0 · 2 = 3 · i → + ( – 6 ) · j → + 4 · k →

Ответ: ( 3 , – 6 , 4 ) – координаты вектора, одновременно перпендикулярного заданным a → и b → .2 =
= 1 + 10*0 + 25*1 = 26,
/q/ = V26
5) cosA = p*q / [/p/*/q/*] = 13/V[13*26] =V13/V26= 1/V2 =[V2]/2
6) A = arccos <[V2]/2>+,-2pi*n
n = 0, 1, 2, 3.. б 2pi*n- период;

Единичный вектор — объяснение и примеры

Как и в физике, у каждой измеряемой величины есть единица измерения. Точно так же в векторной геометрии каждый вектор также имеет единицу измерения, которую можно назвать единичным вектором . Проще говоря, единичный вектор можно определить как:

«Любой вектор с величиной 1 может быть описан как единичный вектор».

В теме единичных векторов мы рассмотрим следующие темы:

• Что такое единичный вектор?
• Как найти единичный вектор?
• Как найти единичный вектор в том же направлении?
• Какова формула для единичных векторов?
• Каковы свойства единичного вектора?
• Примеры
• Практические задачи

Что такое единичный вектор?

Единичный вектор — это вектор, величина которого равна 1, или, говоря математическим языком, единице..

В математике и физике мы часто встречаем слово «единица». Но что именно оно означает? Если погрузиться в элементарную математику, то слово «единица» было определено в самом начале математики. Слово «единица» обозначает «1 » . Слово «единица»; впервые был обнаружен в математической системе разметки. В основе системы лежали единицы, так как они символизируют «единичное» место.

Точно так же в области векторной геометрии единичный вектор также обозначает «1».Для масштабирования вектора требуется единичный вектор. На языке физики мы можем описать это масштабирование как измерение.

Единичные векторы — это в основном элементы вектора, и любой вектор может быть представлен в терминах единичного вектора.

Поскольку единичные векторы имеют величину 1, единственная информация, которую они предоставляют относительно вектора, — это его направление. По этой причине единичные векторы также называют «векторами направления». Когда единичные векторы используются для масштабирования вектора, они предоставляют нам направление этого конкретного вектора.

Например, вектор v , показанный ниже, имеет величину 3, но этот вектор также может быть представлен в терминах единичного вектора a , величина которого равна 1, но его направление — северо-восток.

Единичные векторы используются для масштабирования векторов как в двух, так и в трехмерном пространстве

Направление единичных векторов

Единичный вектор любого вектора v обязательно должен существовать в том же направлении, что и вектор v .Это потому, что единичный вектор любого вектора действует как единица измерения вектора. Поскольку величина единичного вектора уже равна 1, то учитывается только направление вектора v.

Вот почему единичный вектор любого вектора v существует в том же направлении, что и вектор v. Так же, как компоненты вектора не являются действительными векторами, которые существуют в определенном месте. Точно так же единичный вектор физически не существует на плоскости. Его единственная цель — предоставить единицу измерения любому вектору и задать ему определенное направление.

Независимо от того, существует ли вектор в двумерной или трехмерной плоскости, вектор должен иметь соответствующий единичный вектор. Та же самая формула применяется для нахождения единичных векторов как в двух, так и в трех измерениях.

Направление единичных векторов в двух измерениях

В случае двумерной плоскости один компонент, единичный вектор, направлен вдоль оси x, а другой — вдоль оси y.

Нам хорошо известно, что только две оси, x и y, существуют в двух измерениях.2)

| v | = 3,6

Итак, вектор (ii) не является единичным вектором.

Как найти единичный вектор?

Поскольку единичные векторы известны только для определения направления любого вектора v, единичный вектор любого вектора v имеет то же направление, что и вектор v. После выполнения необходимых вычислений величины для определенного единичного вектора, он может быть Очевидно, что величина равна 1.

Мы уже обсуждали, что любой вектор может быть представлен в терминах его единичных векторов.Точно так же мы можем найти единичный вектор любого заданного вектора, имеющий то же направление, что и данный вектор.

Примеры могут усилить эту концепцию.

Итак, проще говоря, мы можем заключить, что каждый вектор в двухмерной или трехмерной плоскости обязательно должен сопровождаться своим единичным вектором, отвечающим за отображение направления вектора.

Векторы могут существовать как в двухмерной, так и в трехмерной плоскости. Точно так же их единичные векторы также могут существовать в этих плоскостях.Каждый единичный вектор существует вдоль определенной оси, будь то x, y или z, и перпендикулярен остальным осям.

Формула для поиска векторов единиц

Для любого вектора v его соответствующая единица измерения, которая является его единичным вектором, существует в направлении, параллельном вектору v, и имеет величину 1. Этот единичный вектор можно найти, применив следующую формулу:

Единичный вектор = вектор / величина вектора

u = v / | v |

Единичный вектор также может быть обозначен u.

Мы можем суммировать нахождение единичного вектора в 4 основных шага:

1. Обратите внимание на вектор v с заданными компонентами по каждой оси.
2. Найти звездную величину вектора v.
3. Разделите два параметра.
4. Проверьте величину полученного единичного вектора для подтверждения.

Эта формула включает два параметра, оба основанные на векторе v . В числителе формула показывает вектор v , существующий либо в двухмерной, либо в трехмерной плоскости.Знаменатель показывает величину вектора v . При делении двух параметров получается единичный вектор и вектора v .

Эту формулу можно распространить как на двумерные, так и на трехмерные задачи. 2)

u = (2, 4, 1) / √21

u = (2 / √21, 4 / √21, 1 / √21)

Итак, и — это требуемый единичный вектор.2)

| u | = √0,99

| u | = 1

Следовательно, доказано, что вектор u является единичным вектором v.

Свойства единичного вектора

Содержание этого раздела можно резюмировать в свойствах единичного вектора следующим образом:

1. Единичный вектор имеет величину 1.
2. Единичные векторы используются только для определения направления вектора.
3. Единичные векторы существуют как в двух, так и в трехмерной плоскости.
4. Каждый вектор имеет единичный вектор в виде его компонентов.
5. Ортопедические векторы вектора направлены по осям.
6. Единичные векторы вектора перпендикулярны соответствующим единичным векторам того же вектора.

Практические задачи

1. Для данного вектора v проверьте, существует ли его единичный вектор: v = (1, 3) v = (2, -1, 4)
2. Найдите единичный вектор следующего вектора: v = (-2, -4, -4)
3. Найдите и покажите доказательством единичный вектор следующего вектора: v = (2, -5)
4. Найдите и покажите доказательством единичный вектор следующего вектора: v = (1, -1)
5. Найдите и покажите доказательством единичный вектор следующего вектора: v = (0, -4)

Ответы

1. да, да
2. (-2/6, -4/6, -4/6)
3. Нет
4. Есть
5. Есть

Предыдущий урок | Главная страница | Следующий урок

Единичные векторы | Brilliant Math & Science Wiki

Векторные величины имеют направление и величину.Однако иногда интересует только направление вектора, а не его величина. В таких случаях для удобства векторы часто «нормализуются», чтобы иметь единичную длину. Эти единичные векторы обычно используются для указания направления со скалярным коэффициентом, определяющим величину. Затем векторное разложение можно записать как сумму единичных векторов и скалярных коэффициентов.

Для вектора V⃗ \ vec {V} V можно рассмотреть задачу поиска вектора, параллельного V⃗ \ vec {V} V, с единичной длиной.= vx wx + vy wy + vz wz,

, как и ожидалось.

Можно ли ⟨6,8⟩ \ langle 6, 8 \ rangle⟨6,8⟩ выразить как сумму девяти единичных векторов?

я + j + ки + j + ки + j + k 2i + 3j + k2i + 3j + k2i + 3j + к 3i + j + k3i + j + k3i + j + k 4k4k4k

Какой вектор самый длинный?

5i + j − 2k5 i + j — 2 k5i + j − 2k 530i + 130j − 230k \ frac {5} {30} i + \ frac {1} {30} j- \ frac {2} {30} k305 i + 301 j − 302 k 530i + 130j − 230k \ frac {5} {\ sqrt {30}} i + \ frac {1} {\ sqrt {30}} j- \ frac {2} {\ sqrt {30}} k30 5 i + 30 1 к − 30 2 к Ни один из вышеперечисленных

Найдите единичный вектор в направлении 5i + j − 2k.5 i + j — 2 k. 5i + j − 2k.

Единичные векторы

Вектор имеет как величину, так и направление. Единичный вектор — это вектор с величиной 1. В некоторых ситуациях полезно найти единичный вектор, который имеет то же направление, что и данный вектор.

Единичный вектор v в том же направлении, что и v , можно найти, разделив v на его величину ∥v∥.

ВЕКТОР ЕДИНИЦЫ:

Если v ≠ 0 и ∥v∥ представляет величину вектора v, то его единичный вектор u равен:

u = v∥v∥ = 1∥v∥v

Единица измерения вектор u имеет длину 1 в том же направлении, что и v.

Единичные векторы 〈1,0〉 и 〈0,1〉 являются специальными единичными векторами, называемыми стандартными единичными векторами , и представлены векторами i и j следующим образом:

i = 〈1,0〉 j = 〈0,1〉

Любой вектор на плоскости может быть записан с использованием этих стандартных единичных векторов. V = 〈v1, v2〉 = v1i + v2j → Линейная комбинация

Эта векторная сумма называется линейной комбинацией . Например, вектор v = 〈3,11〉 = 3i + 11j.

Давайте рассмотрим несколько примеров.

Для работы этих примеров требуется использование различных правил дифференциации. Если вы не знакомы с правилом, перейдите к соответствующей теме для обзора.

Пример 1. Найдите единичный вектор u в том же направлении, что и v = 〈12, −9〉, и покажите, что он имеет величину 1.

Шаг 1. Найдите величину v. Величина вектора вычисляется путем извлечения квадратного корня из суммы квадратов его компонентов. v = 〈x, y〉 ∥v∥ = x2 + y2	v = 〈12, −9〉 || v || = 122 + (- 9) 2 ∥v∥ = 225 = 15
Шаг 2: Рассчитайте единичный вектор. u = v∥v∥ = 1∥v∥v	u = v∥v∥ = 1∥v∥v u = 〈12, −9〉 15 = 115 〈12, −9〉 u = 〈1215, −915〉 = 〈45, −35〉
Шаг 3: Покажите, что вектор u имеет величину 1. Величина вектора вычисляется путем извлечения квадратного корня из суммы квадратов его компонентов. v = 〈x, y〉 ∥v∥ = x2 + y2	u = 〈45, −35〉 || u || = (45) 2 + (- 35) 2 || u || = 1625 + 925 = 2525 ∥u∥ = 1 = 1

Пример 2: Если u = -3i + 2j и v = -i + 6j, найти 2u + 4v.

Шаг 1. Найдите векторы 2u и 4v, используя скалярное умножение. kv = kv1, v2 = kv1, kv2 → Скалярное умножение	2u = 2 (−3i + 2j) = [2 · (−3i) +2 · 2j] 2u = −6i + 4j 4v = 4 (−i + 6j) = [4 · (−i) +4 · 6j] 4v = −4i + 24j
Шаг 2: Складываем векторы 2u и 4v, используя сложение векторов. u + v = u1 + v1, u2 + v2 → Сложение векторов	2u + 4v (-6i + 4j) + (-4i + 24j) (-6i — 4i) + (4j + 24j) (-10i + 28j)

Найти единичный вектор в том же направлении, что и данный вектор

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или несколько ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Unit Vector — обзор

1 Предварительные сведения

Сначала мы вспомним несколько ключевых свойств L _p и ℓ _p , которые обсуждаются на протяжении всей главы, посвященной основным концепциям.

Базис единичного вектора для ℓ _p является 1-симметричным базисом [49, раздел 3]. Базис Хаара ( h _i ) ₀ ^∞ является безусловным базисом L _p для 1 < p <∞ [49, раздел 3], [24]. Это также монотонная основа для L _p для 1 ≤ p <∞. Функции Радемахера (rn) n = 1∞, [49, раздел 4], эквивалентны базису единичного вектора ₂ для p <∞, (и базису единичного вектора ℓ ₁ для p = ∞).

Таким образом, для 0 < p <∞ существуют константы A _p , B _p с

(1.1) Ap (∑ | an | 2) 1 / 2≤ (∫01 | ∑anrn (t) | pdt) 1 / p≤Bp (∑ | an | 2) 1/2

для всех скаляров ( a _n ). A _p = 1, если 2 ≤ p <∞ и B _p = 1, если p ≤ 2.

Если (xi) 1∞ — это нормализованная последовательность функций с дизъюнктными опорами на [0, 1] в L _p с (1 ≤ p <∞), тогда ( x _i ) эквивалентно 1 базис единичного вектора ℓ _p и [( x _i )] дополняется 1 через проекцию

P (x) = ∑i = 1∞ (∫01sign xi (t) | xi (t) | p − 1x (t) dt) xi.

При 1 < p <∞, L _p равномерно выпуклая и равномерно гладкая с модулем выпуклости (соответственно гладкости) степенного типа p (соответственно степенного типа q с 1p + 1q = 1), [49, раздел 6], L _p относится к типу min (2, p ) и котиру max (2, p ) для 1 ≤ p <∞ [ 49, Раздел 8].

Для (xi) 1n⊆Lp

(1.2) Ap (∑1n || xi || p2) 1 / 2≤ (∫01 || ∑1nri (t) xi || ppdt) 1 / p≤ (∑1n || xi || pp) 1 / p

, если 1 ≤ p <2, и

(1.3) (∑1n || xi || pp) 1 / p≤ (∫01 || ∑1nri (t) xi || ppdt) 1 / p≤Bp (∑1n || xi || p2) 1/2

, если 2 < p <∞.

Например, чтобы увидеть (1.2), воспользуемся теоремой Фубини, || ⋅ || Lp≤ || ⋅ || L2, (1.1) при p = 2 и || ⋅ || ℓp≥ || ⋅ || ℓ2, чтобы получить

(1.4) ∫01 || ∑1nri (t) xi || ppdt = ∫01∫01 | ∑1nri (t) xi (s) | pdt ds≤∫01 [∫01 | ∑1nri (t) xi ( s) | 2dt] p / 2ds = ∫01 (∑1n | xi (s) | 2) p / 2ds≤∫01∑1n | xi (s) | pds

, что дает правое неравенство (1.2). Также согласно (1.1)

∫01∫01 | ∑1nri (t) xi (s) | pdt ds ≥ App∫01 (∑1n | xi (s) | 2) p / 2ds.

Сейчас

(∑1n || xi || p2) p / 2 = || (|| xi || pp) 1n || ℓ2 / p = ∑1n || xi || ppai | для некоторого (ai) 1n∈ℓ2 / (2 − p) нормы 1≤∫01 (∑1n | xi (s) | 2) p / 2 (∑1n | ai | 2 / (2 − p)) (2 − p) / 2ds по неравенству Хёдера = ∫01 (∑1n | xi (s) | 2) p / 2ds,

, что завершает доказательство (1.2).

(1.2) и (1.3) можно рассматривать как обобщения неравенств Кларксона [29]. С || ⋅ || Lp≤ || ⋅ || L2 для p ≤ 2 мы также имеем, используя (1.2) для p = 2, что

(1.5) (∫01 || ∑1nri (t) xi || ppdt) 1 / p≤ (∑1n || xi || 22) 1/2 для 1 ≤ p <2,

и аналогично

(1.6) (∫01 || ∑1nri (t) xi || ppdt) 1 / p≤ (∑1n || xi || 22) 1/2 для 2

Техника интегрирования против Радемахера дает некоторые полезные неравенства для безусловных основных последовательностей в L _p . Если ( x _n ) является λ-безусловной базовой последовательностью в L _p , то

(1,7) λ − 1 [∫01 (∑ | an | 2 | xn (s) | 2) p / 2ds] 1 / 2≤ || ∑anxn || p ≤λBp [∫01 (∑ | an | 2 | xn (s) | 2) p / 2ds], если 2≤p <∞,

(1.8) (λ, Ap) −1 [∫01 (∑ | an | 2 | xn (s) | 2) p / 2ds] 1 / p≤ || ∑anxn || p ≤λ [∫01 (∑ | an | 2 | xn (s) | 2) p / 2] 1 / p, если 1≤p≤2,

откуда следует, что ( x _n ) и (| xn |) эквивалентны.

Если ( x _n ) также нормализовано,

(1.9) λ − 1 (∑ | an | p) 1 / p≤ || ∑anxn || p≤λBp (∑ | an | 2) 1/2, если 2≤p <∞.

(1,10) (λAp) −1 (∑ | an | 2) 1 / 2≤ || ∑anxn || p≤λ (∑ | an | p) 1 / p, если 2 ≤ p ≤2.

Последние два неравенства являются непосредственными следствиями (1.2) и (1.3).

Любая разностная последовательность мартингалов в L _p является безусловной [25], что обобщает тот факт, что базис Хаара безусловен. В частности, любая последовательность независимых случайных величин со средним нулевым значением в L _p является безусловной.Неравенство Розенталя [91] дает нам некоторую информацию о таких последовательностях. Пусть 2 < p <∞. Существует K _p <∞, так что если ( x _i ) ⁿ ₁ являются независимыми средними нулевыми случайными величинами в L _p , то

(1.11) 12max {(∑i = 1n || xi || pp) 1 / p, (∑i = 1n || xi || 22)} ≤ || ∑i = 1nxi || p≤Kpmax {( ∑i = 1n || xi || pp) 1 / p, (∑i = 1n || xi || 22) 1/2}.

В [55] показано, что K _p ~ p / ln p .

Банахово пространство X — это L _{p , λ} -пространство, если для всех конечномерных пространств F ⊆ X существует конечномерное E с F⊆E⊆X так что d (E, ℓpdim E) ≤λ. В конечном итоге оказывается (см. Раздел 5), что разделимый X L _{p , λ} для некоторого λ и 1 < p <∞ тогда и только тогда, когда X изоморфно дополненному подпространству L _p , которое не изоморфно гильбертову пространству [66,68].

Ситуация с L ₁ сложнее. Предполагается, что каждое бесконечномерное дополняемое подпространство X из L ₁ изоморфно L ₁ или ℓ ₁ . Известно, что если X содержит изоморф L ₁ , то X изоморфен L ₁ [36], и если X встраивается в ℓ ₁ , то X является изоморфна ℓ ₁ [65].Различные характеристики L ₁ — (и L _∞ ) приведены в [68]. Была проделана большая работа по изучению и попыткам классификации L _p -пространство с точностью до изоморфизма, и это обсуждается в разделе 5 ниже.

Мы начнем с некоторых результатов по глобальной структуре L _p и, в частности, тех, которые связаны с базисом Хаара. Все банаховы пространства считаются сепарабельными, если не указано иное.

Основы работы с векторной графикой

Вектор — это то, что имеет как величину, так и направление.То, что имеет только величину, является скаляром. В этих заметках вектор выделен жирным шрифтом. буква, например A или B . В учебнике или при написании от руки вектор показан стрелкой вверху. Запись A или B (не жирным шрифтом, без стрелки) означает просто величину вектора.

Какие примеры векторов?

Какие примеры скаляров?

• Примеры векторов: скорость, ускорение, сила
• Примеры скаляров: масса, расстояние, температура

На рисунке вектор показан в виде стрелки, указывающей в направлении вектора.сверху, вот так:. Это произносится как «р-хат».

Три очень особых единичных вектора:,,.

— единичный вектор в направлении x.

— единичный вектор в направлении y.

— единичный вектор в направлении z.

Нахождение компонент вектора

Разделение вектора на компоненты выполняется с использованием геометрии прямоугольного треугольника. Компонент x вектора сообщает нам, какая часть этого вектора находится в направлении x. Соответствующее утверждение применяется к y-компоненту.

Положительные направления: + x = вправо и + y = вверх. Вектор v указывает вниз и вправо. Сделайте v гипотенузой прямоугольного треугольника с двумя другими сторонами, параллельными осям координат.

• Используйте геометрию, чтобы найти величину каждого компонента
• Используйте схему, чтобы обозначить знак

cos (θ) = v _x / v, поэтому v _x = v cos (θ)

Включая положительное направление из диаграммы, v _x = + v cos (θ)

sin (θ) = v _y / v, поэтому v _y = v sin (θ)

Включая отрицательное направление из диаграммы, v _y = -v sin (θ)

Если v = 3.5 м / с и θ = 25 градусов, тогда:

v _x = 3,5 cos (25) = 3,2 м / с

v _y = -3,5 sin (25) = -1,5 м / с

Тогда весь вектор v можно записать в нотации единичного вектора:

v = 3,2 -1,5 м / с

Помните, что составляющая на стороне треугольника, примыкающей к углу, идет с косинусом; составляющая напротив угла идет с синусом.

Скалярное произведение

Один из способов умножения двух векторов — использовать скалярное произведение, что дает скаляр.Точечные произведения важны в таком случае, как работа, когда работа, выполняемая силой при перемещении объекта, зависит от составляющей силы в направлении смещения.

W = F _y мболь «> · d = F d cos (θ)

Обратите внимание, что скалярное произведение — это …

• ноль, когда векторы перпендикулярны друг другу
• максимум, когда они параллельны
• положительный, когда угол между векторами отрицательный, когда угол между ними> 90

c = a _y mbol «> · b = a _x b _x + a _y b _y + a _z b _z

Перекрестное произведение

Второй способ умножения векторов — это использовать перекрестное произведение, в результате чего получается вектор, перпендикулярный двум векторам в перекрестном произведении.Примером может служить крутящий момент:

τ = r × F

Величина результирующего вектора равна r F sin (θ).

Направление задается правилом правой руки. Правой рукой укажите пальцами в направлении первого вектора ( r ), закрутите их в направлении второго вектора ( F ), а большой палец, торчащий наружу, будет указывать в направлении вектора. результирующий вектор.

Обратите внимание, что перекрестное произведение …

• ноль, когда векторы параллельны
• максимум, когда векторы перпендикулярны друг другу

Отметим также, что a × b = — б × а .

c = a × b = (a _y b _z — b _y a _z ) + (a _z b _x — b _z a _x ) + (a _x b _y — b _x a _y )

Единичные векторы — Задача 2

Одна проблема, которую вы, вероятно, заметите в своей домашней работе в какой-то момент, — это найти единичный вектор с тем же направлением, что и v, который равен <-4, 3> или какому-либо другому вектору.Единичный вектор, определение единичного вектора состоит в том, что единичный вектор имеет длину 1. Любой вектор, имеющий длину 1, является единичным вектором, но какова длина v? Это квадратный корень из -4² плюс 3², что составляет 16 плюс 9, что равно 25. Корень 25 равен 5. Длина v равна 5.

Чтобы получить единичный вектор, мне нужен вектор, который указывает на то же самое. направление как v, но имеет 1/5 длины. Мой единичный вектор, я назову его u-hat, будет 1/5 от v. 1/5 от <-4, 3>. Это <-4/5, 3/5>.Это предлагает общий метод определения единичного вектора. Для любого вектора v единичный вектор u с тем же направлением равен u, который равен 1 по величине v, умноженной на вектор v. Итак, это скалярное кратное, которое дает вам длину 1, но в том же направлении, что и вектор v. Давайте попробуем это на некоторых задачах.

Я хочу найти единичный вектор с тем же направлением, что и все эти векторы, начиная с <3, 3>. Какова длина этого вектора? Это квадратный корень из 3² плюс –3².Итак, 9 плюс 9, корень 18 равен 3 корню 2. Это длина. И тогда единичный вектор будет иметь значение 1, 3 корня, 2 раза больше этого вектора. Вы вытягиваете этот скаляр внутрь, и вы получаете 3 больше 3 корня 2, -3 больше 3 корня 2. Если вы упростите это, вы получите корень 2 больше 2, отрицательный корень 2 больше 2. Это единичный вектор с тем же направлением, что и <3, -3>.

Что насчет этого парня? V равно <-1, -2>. Сначала находим длину. Длина v — это квадратный корень из -1² или 1 плюс -2², 4. Итак, это корень 5.Единичный вектор u-hat будет равен 1 корню 5, длина которого равна единице, умноженной на этот вектор. Это будет <-1 над корнем 5 и затем -2 над корнем 5>. Ваш учитель, вероятно, захочет, чтобы вы рационализировали знаменатель. Вы получите отрицательный корень 5 вместо 5 и -2 корень 5 вместо 5.

Наконец, давайте попробуем это. V <-5, 12>, какая величина? Какая длина? Это квадратный корень из -5², 25 плюс 12², 144. 25 и 144 равны 169, а корень 169 равен 13. Единичный вектор будет u-hat равным 1 более 13 раз <-5, 12>.