Site Loader
Posted on 17.04.1986

Содержание

PhysBook:Электронный учебник физики — PhysBook

Содержание

  • 1 Учебники
  • 2 Механика
    • 2.1 Кинематика
    • 2.2 Динамика
    • 2.3 Законы сохранения
    • 2.4 Статика
    • 2.5 Механические колебания и волны
  • 3 Термодинамика и МКТ
    • 3.1 МКТ
    • 3.2 Термодинамика
  • 4 Электродинамика
    • 4. 1 Электростатика
    • 4.2 Электрический ток
    • 4.3 Магнетизм
    • 4.4 Электромагнитные колебания и волны
  • 5 Оптика. СТО
    • 5.1 Геометрическая оптика
    • 5.2 Волновая оптика
    • 5.3 Фотометрия
    • 5.4 Квантовая оптика
    • 5.5 Излучение и спектры
    • 5. 6 СТО
  • 6 Атомная и ядерная
    • 6.1 Атомная физика. Квантовая теория
    • 6.2 Ядерная физика
  • 7 Общие темы
  • 8 Новые страницы

Здесь размещена информация по школьной физике:

  1. материалы из учебников, лекций, рефератов, журналов;
  2. разработки уроков, тем;
  3. flash-анимации, фотографии, рисунки различных физических процессов;
  4. ссылки на другие сайты

и многое другое.

Каждый зарегистрированный

пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.

Учебники

Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –

Механика

Кинематика

Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве

Динамика

Законы Ньютона – Силы в механике – Движение под действием нескольких сил

Законы сохранения

Закон сохранения импульса – Закон сохранения энергии

Статика

Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика

Механические колебания и волны

Механические колебания – Механические волны

Термодинамика и МКТ

МКТ

Основы МКТ – Газовые законы – МКТ идеального газа

Термодинамика

Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение

Электродинамика

Электростатика

Электрическое поле и его параметры – Электроемкость

Электрический ток

Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках

Магнетизм

Магнитное поле – Электромагнитная индукция

Электромагнитные колебания и волны

Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны

Оптика.

СТО

Геометрическая оптика

Прямолинейное распространение света. Отражение света – Преломление света – Линзы

Волновая оптика

Свет как электромагнитная волна – Интерференция света – Дифракция света

Фотометрия

Фотометрия

Квантовая оптика

Квантовая оптика

Излучение и спектры

Излучение и спектры

СТО

СТО

Атомная и ядерная

Атомная физика. Квантовая теория

Строение атома – Квантовая теория – Излучение атома

Ядерная физика

Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы

Общие темы

Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике

Новые страницы

Запрос не дал результатов.

Скалярное произведение векторов через координаты. Онлайн калькулятор.


Укажите размерность пространства 23
Укажите форму представления первого вектора Координаты точек начала и конца первого вектораКоординаты первого вектора
Укажите форму представления второго вектора Координаты точек начала и конца второго вектораКоординаты второго вектора

Задайте координаты первого вектора
a̅ = { ; }

Задайте координаты вектора b
b̅ = { ; }

Как вычислить скалярное произведение векторов через координаты

Скалярным произведением двух векторов a и b – называется сумма произведений координат данных векторов:

Если a = {ax; ay} и b = {bx; by}, тогда:
a ⋅ b = axbx + ayby

Если

a = {ax; ay; az} и b = {bx; by; bz}, тогда:
a ⋅ b = axbx + ayby + azbz

Если координаты векторов a и b заданы точками, а именно:

Вектор a задан точками A и B, где
A = {Ax; Ay}
B = {Bx; By}
Вектор b задан точками C и D, где
C = {Cx; Cy}
D = {Dx

; Dy}
то скалярное произведение определяется как:
a ⋅ b = (Bx — Ax)(Dx — Cx) + (By — Ay)(Dy — Cy)

Если координаты векторов a и b заданы точками, а именно:

Вектор a задан точками A и B, где
A = {Ax; Ay; Az}
B = {Bx; By; Bz}
Вектор b задан точками C и D, где
C = {Cx

; Cy; Cz}
D = {Dx; Dy; Dz}
то скалярное произведение определяется как:
a ⋅ b = (Bx — Ax)(Dx — Cx) + (By — Ay)(Dy — Cy) + (Bz — Az)(Dz — Cz)

Примеры вычисления скалярного произведения векторов по координатам

Пример 1. Найдем скалярное произведение векторов плоскости.

Координаты вектора a: (-2; 6)Координаты вектора b: (3; 5)

a ⋅ b = axbx + ayby = -2 ⋅ 3 + 6 ⋅ 5 = -6 + 30 = 24
a ⋅ b = 24

Пример 2. Найдем скалярное произведение векторов пространства.

Координаты вектора a: (5; 1; 7)
Координаты вектора b: (2; 4; 6)

a ⋅ b = axbx + ayby + azbz = 5 ⋅ 2 + 1 ⋅ 4 + 7 ⋅ 6 = 10 + 4 + 42 = 56
a ⋅ b = 56

Пример 3. Найдем скалярное произведение векторов плоскости, координаты которых заданы точками.

Координаты точки А вектора AB: (5 ; 9)
Координаты точки B вектора AB: (-2 ; 11)
Координаты точки C вектора CD: (0 ; 12)
Координаты точки D вектора CD: (-3 ; 1)

Точки A, B, C, D

Воспользуемся формулой: a ⋅ b = (Bx — Ax)(Dx — Cx) + (By — Ay)(Dy — Cy) тогда,

AB ⋅ CD = (-2 — 5) ⋅ (-3 — 0) + (11 — 9) ⋅ (1 — 12) = -1

Этот пример можно решить по-другому, вычислив сначала координаты векторов по точкам, а затем зная координаты вычислить скалярное произведение:

Вычислим координаты первого вектора по двум точкам A и B:

AB = {Bx— Ax; By— Ay} = {-2 — 5 ; 11 — 9} = {-7 ; 2}

Вектор AB

Вычислим координаты второго вектора по двум точкам C и D:

CD = {Dx— Cx; Dy— Cy} = {-3 — 0 ; 1 — 12} = {-3 ; -11}

Вектор CD

Найдем скалярное произведение векторов: AB и CD, воспользуемся формулой a ⋅ b = axbx + ayby

AB

⋅ CD = ABxCDx + AByCDy = -7 ⋅ (-3) + 2 ⋅ (-11) = 21 + (-22) = -1

Пример 4. Найдем скалярное произведение векторов пространства. Координаты обоих векторов заданны точками.

Координаты точки А вектора AB: (7; 0.2 ; 69)
Координаты точки B вектора AB: (-1 ; 0 ; 2/8)
Координаты точки C вектора CD: (-4 ; -6 ; 2)
Координаты точки D вектора CD: (3 ; 0 ; 9)

Воспользуемся формулой: a ⋅ b = (Bx — A

x)(Dx — Cx) + (By — Ay)(Dy — Cy) + (Bz — Az)(Dz — Cz) тогда,

AB ⋅ CD = (-1 — 7) ⋅ (3 — (-4)) + (0 — 0.2) ⋅ (0 — (-6)) + ((2/8) — 69) ⋅ (9 — 2) = -538.45

Как в предыдущем примере решим пример иначе, сначала вычислив координаты векторов по точкам:

Вычислим координаты первого вектора по двум точкам A и B:

AB = {Bx— Ax;By— Ay;Bz— Az} = {-1 — 7 ; 0 — 0. 2 ; 2/8 — 69} = {-8 ; -1/5 ; -275/4}

Вычислим координаты второго вектора по двум точкам C и D:

CD = {Dx— Cx;Dy— Cy;Dz— Cz} = {3 — (-4) ; 0 — (-6) ; 9 — 2} = {7 ; 6 ; 7}

Найдем скалярное произведение векторов: AB и CD

AB ⋅ CD = ABxCDx + AByCDy + ABzCDz = -8 ⋅ 7 + (-1/5) ⋅ 6 + (-275/4) ⋅ 7 = -56 + (-6/5) + (-1925/4) = -10769/20 = -538.45

#11. Произведение матриц и векторов, элементы линейной алгебры

Смотреть материал на видео

Пришло время познакомиться с одной из фундаментальных возможностей пакета NumPy–матричных и векторных вычислений. На одном из прошлых занятий мы с вами уже видели, как можно поэлементно умножать один вектор на другой или одну матрицу на другую: 

a = np.arange(1, 10). reshape(3, 3)
b = np.arange(10, 19).reshape(3, 3)
a*b

В консоли увидим результат:

array([[ 10,  22,  36],
       [ 52,  70,  90],
[112, 136, 162]])

Матричное умножение

Но если нам нужно выполнить именно матричное умножение, то есть, строки одной матрицы умножать на столбцы другой и результаты складывать:

то для этого следует использовать специальные функции и операторы. Начнем с функций. Итак, чтобы перемножить две матрицы a иbпо всем правилам математики, запишем следующую команду: 

np.dot(a, b)

Эта функция возвращает новую матрицу (двумерный массив) с результатом умножения:

array([[ 84,  90,  96],
[201, 216, 231],
[318, 342, 366]])

Тот же результат можно получить и с помощью функции: 

np. matmul(a, b)

Считается, что этот вариант предпочтительнее использовать при умножении матриц.

Векторное умножение

Аналогичные операции можно выполнять и с векторами. Математически, если у нас имеются два вектора:

то их умножение можно реализовать в двух видах:

и

Первое умножение реализуется либо через функцию: 

a = np.arange(1, 10)
b = np.ones(9)
np.dot(a, b) # значение 45

Либо, более предпочтительной функцией для внутреннего умножения векторов: 

np.inner(a, b) # 45

Второй вариант умножения (внешнее умножение векторов) реализуется с помощью функции: 

np.outer(a, b)

получим результат в виде следующей матрицы:

array([[1., 1., 1., 1., 1., 1., 1., 1., 1.],
       [2., 2., 2., 2. , 2., 2., 2., 2., 2.],
       [3., 3., 3., 3., 3., 3., 3., 3., 3.],
       [4., 4., 4., 4., 4., 4., 4., 4., 4.],
       [5., 5., 5., 5., 5., 5., 5., 5., 5.],
       [6., 6., 6., 6., 6., 6., 6., 6., 6.],
       [7., 7., 7., 7., 7., 7., 7., 7., 7.],
       [8., 8., 8., 8., 8., 8., 8., 8., 8.],
[9., 9., 9., 9., 9., 9., 9., 9., 9.]])

Операция умножения матриц и векторов используется довольно часто, поэтому в пакете NumPy имеется весьма полезный перегруженный оператор, заменяющий функцию matmul: 

a @ b # значение 45

или, с использованием матриц: 

a.resize(3, 3)
b.resize(3, 3)
a @ b # аналог np.matmul(a, b)

Умножение вектора на матрицу

Наконец, рассмотрим умножение вектора на матрицу. Это также можно записать двумя способами:

или

Для реализации первого способа, зададим одномерный вектор и двумерную матрицу: 

a = np. array([1,2,3])
b = np.arange(4,10).reshape(3,2) # матрица 3x2

И, затем, воспользуемся уже знакомой нам функцией dot: 

np.dot(a, b) # array([40, 46])

При такой записи, когда одномерный массив записан первым аргументом, а матрица – вторым, получаем умножение вектора-строки на матрицу, то есть, первый способ.

Для реализации второго способа аргументы нужно поменять местами: сначала указать матрицу, а затем, вектор. Но, если мы сейчас это сделаем с нашими массивами, то получим ошибку: 

np.dot(b, a) # несогласованность размеров

Дело в том, что массив a должен представлять вектор длиной два элемента, так как матрица b имеет размер в 3 строки и 2 столбца:

Определим массивa в два элемента и умножим на матрицу b: 

a = np.array([1, 2])
np.dot(b, a) # array([14, 20, 26])

Получаем вектор-строку (одномерный массив) как результат умножения. Обратите внимание, по правилам математики вектор aдолжен быть вектором-столбцом, то есть, быть представленным в виде: 

a.shape = -1, 1 # вектор-столбец 2x1

Но мы использовали вектор-строку. В NumPyтак тоже можно делать и это не приведет к ошибке. Результат будет именно умножение матрицы как бы на вектор-столбец. Ну а если использовать вектор-столбец, то и на выходе получим вектор-столбец: 

np.dot(b, a) # вектор-столбец 3x1

Этого же результат можно достичь, используя оператор @ (перегрузка функции matmul): 

a @ b # вектор-столбец 3x1

Результат будет тем же. Вот так в NumPyвыполняется умножение матриц, векторов и вектора на матрицу.

Элементы линейной алгебры

Из высшей математики хорошо известно, что матрицы можно использовать для решения систем линейных уравнений. Для этого в NumPyсуществует модуль linalg. Давайте рассмотрим некоторые из его функций.

Предположим, имеется квадратная матрица 3×3: 

a = np.array([(1, 2, 3), (1, 4, 9), (1, 8, 27)])

Первым делом вычислим ранг этой матрицы, чтобы быть уверенным, что она состоит из линейно независимых строк и столбцов: 

np.linalg.matrix_rank(a) # рангравен 3

Если ранг матрицы совпадает с ее размерностью, значит, она способна описывать систему из трех независимых линейных уравнений. В нашем случае, система уравнений будет иметь вид:

Здесь  - некие числа линейного уравнения. Например, возьмем их равными: 

y = np.array([10, 20, 30])

Тогда корни уравнения можно вычислить с помощью функции solve: 

np.linalg.solve(a, y) # array([-5.  , 10.   , -1.66666667])

Другой способ решения этой же системы линейных уравнений возможен через вычисление обратной матрицы. Изначально, уравнение можно записать в векторно-матричном виде:

Откуда получаем решения :

На уровне пакета NumPy это делается так: 

invA = np. linalg.inv(a) # вычисление обратной матрицы
invA @ y # вычисление корней

Конечно, я здесь представил лишь примеры использования модуля linalg. Приводить все функции нет смысла, так как они имеют довольно специализированное назначение и специалисты в своих областях без труда смогут ими воспользоваться. Для полноты картины я лишь приведу список наиболее характерных функций, чтобы вы знали возможности расширения linalg.

Функция

Описание

linalg.cholesky()

Разложение Холецкого

linalg.qr()

QR-разложение матрицы

linalg.svd()

Сингулярное (SVD) разложение матрицы

linalg. norm()

Норма матрицы или вектора

linalg.cond()

Число обусловленности матрицы

linalg.det()

Определитель (детерминант) матрицы

linalg.matrix_rank()

Вычисление ранга матрицы по алгоритму SVD

np.trace()

Сумма диагональных элементов массива

linalg.eig()

Вычисление собственных значений и правых собственных векторов

linalg. eigvals()

Вычисление собственных значений матрицы

linalg.solve()

Решение линейного матричного уравнения

linalg.tensorsolve()

Решение линейного тензорного уравнения

linalg.lstsq()

Решает задачу поиска наименьших квадратов для линейного матричного уравнения

linalg.inv()

Вычисление обратной матрицы

linalg.pinv()

Вычисление псевдообратной (Мура-Пенроуза) матрицы

linalg. tensorinv()

Вычисление обратного тензора (N-мерного массива)

Конечно, это не все математические функции пакета NumPy. Полное описание смотрите на сайте с официальной документацией:

https://numpy.org/doc/stable/

Видео по теме

#1. Пакет numpy — установка и первое знакомство | NumPy уроки

#2. Основные типы данных. Создание массивов функцией array() | NumPy уроки

#3. Функции автозаполнения, создания матриц и числовых диапазонов | NumPy уроки

#4. Свойства и представления массивов, создание их копий | NumPy уроки

#5. Изменение формы массивов, добавление и удаление осей | NumPy уроки

#6. Объединение и разделение массивов | NumPy уроки

#7. Индексация, срезы, итерирование массивов | NumPy уроки

#8. Базовые математические операции над массивами | NumPy уроки

#9. Булевы операции и функции, значения inf и nan | NumPy уроки

#10. Базовые математические функции | NumPy уроки

#11. Произведение матриц и векторов, элементы линейной алгебры | NumPy уроки

#12. Множества (unique) и операции над ними | NumPy уроки

#13. Транслирование массивов | NumPy уроки

Умножение векторов — определение, формула, примеры

Умножение векторов бывает двух типов. Вектор имеет как величину, так и направление, и, исходя из этого, двумя способами умножения векторов являются скалярное произведение двух векторов и перекрестное произведение двух векторов. Скалярное произведение двух векторов также называется скалярным произведением, поскольку результирующее значение является скалярной величиной. Перекрестное произведение называется векторным произведением, так как в результате получается вектор, перпендикулярный этим двум векторам.

Давайте узнаем о двух умножениях векторов, рабочем правиле, свойствах, использовании, примерах этого умножения векторов.

1. Как сделать умножение векторов?
2. Рабочее правило умножения векторов
3. Свойства умножения векторов
4.Применение умножения векторов
5. Примеры умножения векторов
6. Практические вопросы по умножению векторов
7. Часто задаваемые вопросы об умножении векторов

Как сделать умножение векторов?

Вектор имеет как величину, так и направление. Мы можем умножать два или более векторов на скалярное произведение и перекрестное произведение. Давайте разберемся подробнее о каждом умножении векторов.

Скалярное произведение

Скалярное произведение векторов также называется скалярным произведением векторов. Результат скалярного произведения векторов является скалярным значением. Скалярное произведение векторов равно произведению величин двух векторов и косинуса угла между двумя векторами. Результат скалярного произведения двух векторов лежит в одной плоскости двух векторов. Скалярный продукт может быть положительным действительным числом или отрицательным действительным числом.

Пусть a и b — два ненулевых вектора, а θ — угол между векторами. Тогда скалярное произведение или скалярное произведение обозначается буквой a.b, которая определяется как:

\(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a||\overrightarrow b|\) cos θ .

Здесь \(|\overrightarrow a|\) — величина \(\overrightarrow a\), \(|\overrightarrow b|\) — величина \(\overrightarrow b\), а θ — величина угол между ними.

Перекрестное произведение

Перекрестное произведение также называется векторным произведением. Перекрестное произведение — это форма умножения векторов, выполняемая между двумя векторами разной природы или вида. Когда два вектора перемножаются друг с другом, и умножение также является векторной величиной, то результирующий вектор называется перекрестным произведением двух векторов или векторным произведением. Результирующий вектор перпендикулярен плоскости, содержащей два заданных вектора.

Понять это можно на примере: если у нас есть два вектора, лежащих в плоскости X-Y, то их векторное произведение даст результирующий вектор в направлении оси Z, которая перпендикулярна плоскости XY. Символ × используется между исходными векторами. Умножение векторов или перекрестное произведение двух векторов показано следующим образом.

\(\overrightarrow{a} \times \overrightarrow{b} = \overrightarrow{c}\)

Здесь \(\overrightarrow{a}\) и \(\overrightarrow{b}\) — два вектора, и \(\overrightarrow{c}\) — результирующий вектор. Пусть θ — угол, образованный между \(\overrightarrow{a}\) и \(\overrightarrow{b}\), а \(\hat n\) — единичный вектор, перпендикулярный плоскости, содержащей обе \(\overrightarrow{a }\) и \(\overrightarrow{b}\). Перекрестное произведение двух векторов определяется следующей формулой:

\(\overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta) \hat n\)

Рабочее правило умножения векторов

Рабочее правило умножения векторов, которое включает скалярное произведение и векторное произведение, можно понять из приведенных ниже предложений.

Скалярное произведение

Для скалярного умножения векторов два вектора выражаются через единичные векторы i, j, k вдоль осей x, y, z, затем скалярное произведение получается следующим образом:

Если \(\overrightarrow a = a_1\hat i + b_1 \hat j + c_1 \hat k\) и \(\overrightarrow b = a_2 \hat i + b_2 \hat j + c_2\hat k\), то

\(\overrightarrow a. \overrightarrow b\) = \((a_1 \hat i + b_1 \hat j + c_1 \hat k)(a_2 \hat i + b_2 \hat j + c_2 \hat k)\)

= \((a_1a_2) (\hat i. \hat i) + (a_1b_2) (\hat i.\hat j)+ (a_1c_2) (\hat i. \hat k) + \\(b_1a_2) ( \hat j. \hat i) + (b_1b_2)(\hat j. \hat j) + (b_1c_2 (\hat j. \hat k) + \\(c_1a_2)(\hat k. \hat i) + ( c_1b_2)(\шляпа k.\шляпа j) + (c_1c_2)(\шляпа k.\шляпа k)\)

\(\overrightarrow a. \overrightarrow b\) = \(a_1a_2 + b_1b_2+ c_1c_2\)

Перекрестное произведение

Предположим, что \(\overrightarrow{a}\) и \(\overrightarrow{b}\ ) — два вектора, такие, что \(\overrightarrow{a}\)= \(a_1\hat i+b_1 \hat j+c_1 \hat k\) и \(\overrightarrow{b}\) = \(a_2 \ шляпа i+b_2 \ шляпа j+c_2 \ шляпа k\), то с помощью определителей мы могли бы найти векторное произведение векторов, используя следующую матричную запись.

Перемножение векторов также представляется с помощью формулы перекрестного произведения как:

\(\overrightarrow{a} \times \overrightarrow{b} = \hat i (b_1c_2-b_2c_1) — \hat j (a_1c_2-a_2c_1) + \hat k (a_1b_2-a_2b_1)\)

Примечание: \ ( \hat i, \hat j, \text{ и } \hat k \) — единичные векторы в направлении оси x, оси y и оси z соответственно.

Свойства умножения векторов

Скалярное произведение единичного вектора изучается путем взятия единичных векторов \(\hat i\) вдоль оси x, \(\hat j\) вдоль оси y и \(\hat k\) по оси Z соответственно. Скалярное произведение единичных векторов \(\hat i\), \(\hat j\), \(\hat k\) подчиняется тем же правилам, что и скалярное произведение векторов. Угол между одинаковыми векторами равен 0º, а значит, их скалярное произведение равно 1. А угол между двумя перпендикулярными векторами равен 90º, а их скалярное произведение равно 0.

  • \(\hat i.\hat i\) = \(\hat j.\hat j\) = \(\hat k.\hat k\)= 1
  • \(\шляпа i.\шляпа j\) = \(\шляпа j.\шляпа k\) = \(\шляпа k.\шляпа i\)= 0

Перекрестное произведение единичных векторов \(\hat i\), \(\hat j\), \(\hat k\) подчиняется тем же правилам, что и перекрестное произведение векторов. Угол между одинаковыми векторами равен 0º, а значит, их векторное произведение равно 0. А угол между двумя перпендикулярными векторами равен 90º, и их векторное произведение дает вектор, который перпендикулярен двум заданным векторам.

  • \(\overrightarrow{i}\times \overrightarrow{i} =\overrightarrow{j}\times \overrightarrow{j} = \overrightarrow{k}\times \overrightarrow{k} = 0\)

Перекрестное произведение двух векторов следует циклическому порядку, как показано на изображении ниже. Перекрестное произведение двух векторов в циклической последовательности дает третий вектор в последовательности.

  • \(\overrightarrow{i}\times \overrightarrow{j} = \overrightarrow{k}; \overrightarrow{j}\times \overrightarrow{k}= \overrightarrow{i}; \overrightarrow{k} \times \overrightarrow{i} = \overrightarrow{j}\)
  • \(\overrightarrow{j}\times \overrightarrow{i} = \overrightarrow{-k}; \overrightarrow{k}\times \overrightarrow{j}= \overrightarrow{-i}; \overrightarrow{i}\times \overrightarrow{k} = \overrightarrow{-j}\)

Свойства умножения векторов помогают получить детальное представление об умножении векторов, а также выполнять многочисленные вычисления с использованием векторов. Здесь перечислены несколько важных свойств умножения векторов.

  1. Перекрестное произведение двух векторов определяется формулой \( \overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta)\).
  2. Скалярное произведение двух векторов определяется формулой \( \overrightarrow{a} . \overrightarrow{b} = |a| |b| \cos(\theta)\).
  3. Скалярное произведение двух векторов подчиняется свойству коммутативности. \(\vec a. \vec b = \vec b. \vec a \)
  4. Перекрестное произведение двух векторов не соответствует свойству коммутативности. \( \vec a \times \vec b\neq \vec b \times \vec a \)
  5. Антикоммутативное свойство: \(\overrightarrow{a} \times \overrightarrow{b} = — \overrightarrow{b} \times \overrightarrow{a}\)
  6. Распределительное свойство: \(\overrightarrow{a} \times (\overrightarrow{b} + \overrightarrow{c}) = (\overrightarrow{a}\times \overrightarrow{b} )+ (\overrightarrow{a}\times \overrightarrow{с})\)
  7. Перемножение нулевого вектора: \(\overrightarrow{a}\times \overrightarrow{0} = \overrightarrow{0}\)
  8. Перемножение вектора с самим собой: \(\overrightarrow{a}\times \overrightarrow{a} = \overrightarrow{0}\)
  9. Умножить на скалярную величину: \(c(\overrightarrow{a}\times \overrightarrow{b}) = c\overrightarrow{a}\times \overrightarrow{b} = \overrightarrow{a}\times c\overrightarrow{ б}\)
  10. Скалярное произведение двух векторов является скаляром и лежит в плоскости двух векторов.
  11. Перекрестное произведение двух векторов — это вектор, который перпендикулярен плоскости, содержащей эти два вектора.

Применение умножения векторов

Ниже приведены некоторые из важных применений умножения векторов. Давайте разберемся с каждым из этих применений в следующих параграфах.

  • Проекция вектора
  • Угол между двумя векторами
  • Продукт тройного креста
  • Площадь параллелограмма
  • Объем параллелепипеда

Проекция вектора

Скалярное произведение полезно для нахождения компонента одного вектора в направлении другого. Проекция вектора одного вектора на другой вектор — это длина тени данного вектора на другой вектор. Он получается путем умножения величины данных векторов на косеканс угла между двумя векторами. Результатом формулы векторной проекции является скалярное значение.

Здесь \(\overrightarrow a\) и \(\overrightarrow b\) — два вектора, а θ — угол между двумя векторами. 2}}\)

Тройное перекрестное произведение

Перекрестное произведение вектора на произведение двух других векторов представляет собой тройное перекрестное произведение векторов. Результатом тройного перекрестного произведения является вектор. Равнодействующий вектора тройного пересечения лежит в плоскости данных трех векторов. Если a, b и c — векторы, то векторное тройное произведение этих векторов будет иметь вид:

\((\overrightarrow{a}\times \overrightarrow{b}) \times \overrightarrow{c} = (\overrightarrow{a}\cdot \overrightarrow{c})\overrightarrow{b} -(\overrightarrow{b}\cdot \overrightarrow{c}) \overrightarrow{a}\)

Площадь параллелограмма

Две смежные стороны параллелограмма могут быть представлены векторами \(\overrightarrow a\) и \(\overrightarrow b\). Площадь параллелограмма равна произведению основания и высоты параллелограмма. Рассмотрим основание параллелограмма как \(|\overrightarrow a|\), а высоту параллелограмма как \(|\overrightarrow b|\)sin θ.

Здесь Основание = \(|\overrightarrow a|\), Высота = \(|\overrightarrow b|\)sin θ, а Площадь параллелограмма = Основание x Высота

Площадь параллелограмма = \(|\overrightarrow a|.|\overrightarrow b|\)sin θ = \(\overrightarrow a \times \overrightarrow b \)

Объем параллелепипеда

Параллелепипед равен шести двусторонняя фигура, каждая из сторон которой является параллелограммом. Здесь параллелограммы противоположных сторон одинаковы. Объем V параллелепипеда можно получить со стороны ребер a, b, c. Объем параллелепипеда можно получить из произведения площади основания на высоту параллелепипеда. Площадь основания параллелепипеда равна |b x c| а высота параллелепипеда равна |a|. Формула расчета объема параллелепипеда выглядит следующим образом.

V = a.(b x c)

Связанные темы

Следующие темы помогают лучше понять умножение векторов.

  • Коллинеарные векторы
  • Векторы
  • Типы векторов
  • Добавление векторов
  • Перекрестное произведение двух векторов

Часто задаваемые вопросы по умножению векторов

Что такое скалярное умножение векторов?

Скалярное умножение векторов также называется скалярным произведением двух векторов и имеет два определения. Алгебраически скалярное произведение двух векторов равно сумме произведений отдельных компонентов двух векторов. a.b = \(a_1b_1\) + \(a_2b_2\)+ \(a_3b_3\). Геометрически скалярное произведение двух векторов есть произведение величины векторов и косинуса угла между двумя векторами. ( \(\overrightarrow a. \overrightarrow b\) = \(|\overrightarrow a||\overrightarrow b|\) cos θ). Результат скалярного умножения векторов является скалярным значением.

Как вычислить скалярное произведение векторов?

Скалярное умножение векторов можно вычислить в три простых шага. Сначала найдите величину двух векторов a и b, т.е. |a| и |б|. Во-вторых, найдите косеканс угла θ между двумя векторами. Наконец, возьмите произведение величины двух векторов и косеканса угла между двумя векторами, чтобы получить скалярное произведение двух векторов. (a.b = |a|.|b|.Cosθ). Также проверьте калькулятор скалярного произведения, чтобы легко найти векторное скалярное произведение.

Почему скалярное произведение называется скалярным умножением векторов?

Скалярное произведение называется скалярным умножением векторов, поскольку все отдельные составляющие ответа являются скалярными величинами. В a.b = |a|.|b|.Cosθ, |a|, |b| и Cosθ — скалярные значения. Следовательно, скалярное произведение также называют скалярным умножением векторов.

Почему мы используем косинус в скалярном умножении векторов?

Чтобы найти скалярное произведение векторов, нам нужно, чтобы два вектора a, b были направлены в одном направлении. Поскольку векторы a и b расположены под углом друг к другу, значение acosθ является компонентом вектора a в направлении вектора b. Следовательно, мы находим cosθ в скалярном произведении или скалярном умножении двух векторов.

Что такое векторное умножение векторов?

Перемножение двух векторов при умножении приводит к третьему вектору, перпендикулярному двум исходным векторам. Величина результирующего вектора определяется площадью параллелограмма между ними, а его направление можно определить по правилу большого пальца правой руки. a × b = c, где c — перекрестное произведение или векторное произведение двух векторов a и b.

Что такое скалярное умножение и векторное умножение векторов?

Векторы можно умножать двумя разными способами: точечным произведением и перекрестным произведением.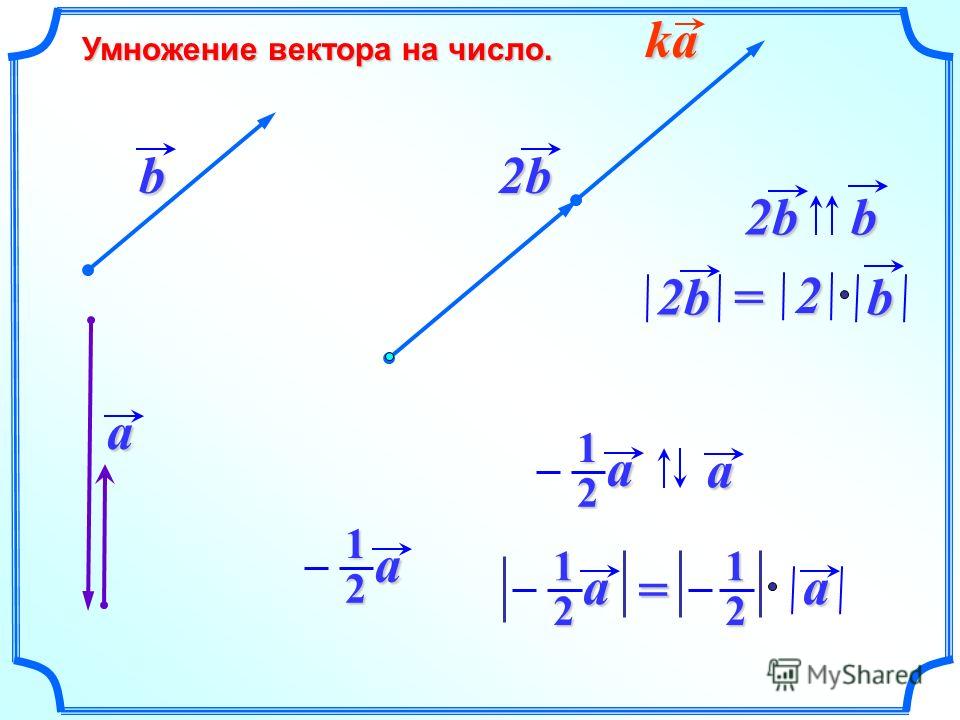 Результаты обоих этих умножений векторов различны. Скалярное умножение векторов или скалярное произведение дает в результате скалярную величину, тогда как векторное умножение векторов или перекрестное произведение дает векторную величину. Векторное произведение двух векторов задается как: \(\overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta) \hat n\) и формула скалярного произведения двух векторов задается как: \(\overrightarrow{a}. \overrightarrow{b} = |a| |b| \cos(\theta)\).

В чем разница между скалярным умножением и векторным умножением векторов?

При умножении векторов скалярное умножение векторов или скалярное произведение исходных векторов дает скалярную величину, тогда как векторное умножение двух векторов или перекрестное произведение двух векторов дает векторную величину. Скалярное произведение — это произведение величины векторов на косинус угла между ними. а . б = |а| |б| cosθ. Векторное произведение — это произведение величины векторов на синус угла между ними.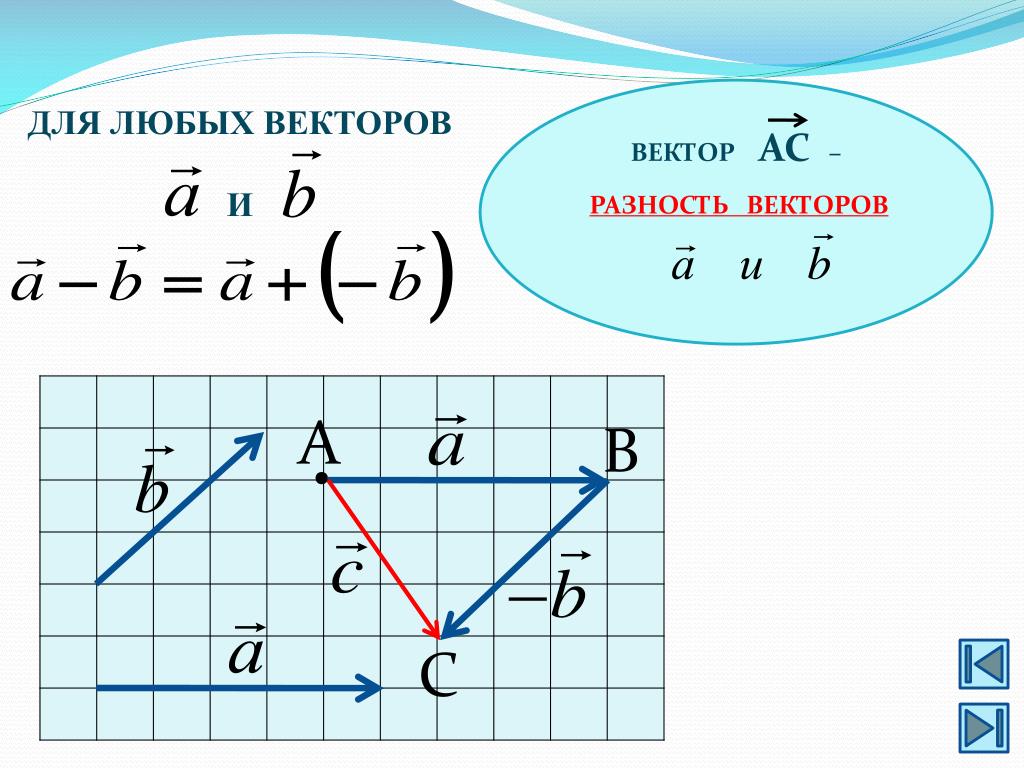 а × б = | а | |б| грех θ.

Что такое правило большого пальца правой руки для перекрестного произведения векторов?

Правило правой руки для векторного произведения двух векторов помогает определить направление результирующего вектора. Если мы направим правую руку в направлении первой стрелки, а пальцы согнем в направлении второй, то наш большой палец окажется в направлении векторного произведения двух векторов. Правило большого пальца правой руки дает формулу векторного произведения для нахождения направления результирующего вектора.

Видео-урок: Векторное произведение двух векторов

Стенограмма видео

В этом видео мы говорим о векторное произведение двух векторов. Как мы увидим, это способ взяв два вектора, лежащих в 𝑥- и 𝑦-плоскостях, и объединив их, чтобы получить третий вектор в 𝑧-измерении.

Для начала можно вспомнить, что существует несколько способов объединения векторов.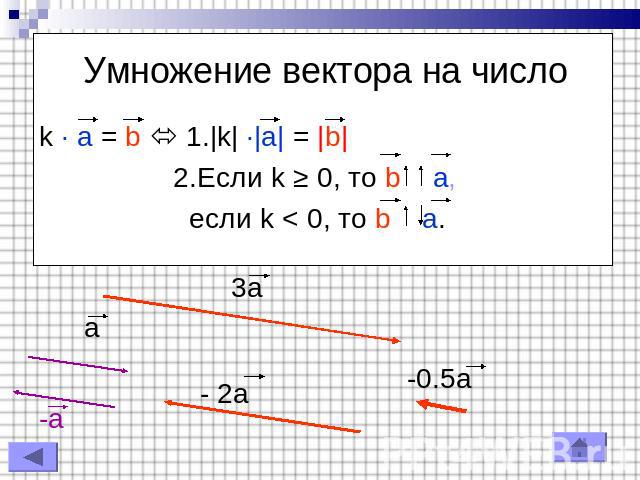 Можно добавить векторы вместе или вычесть одно из другого. И мы также можем комбинировать векторы используя то, что называется скалярным или скалярным произведением. В этом уроке мы говорим о векторные произведения, которые уникальны тем, что векторное произведение является способом умножения два вектора вместе, так что вектор, величина с величиной и направлением, полученные результаты. Другими словами, векторное произведение создает другой вектор.

Чтобы посмотреть, как это работает математически, давайте дадим имена этим двум векторам. Допустим, вектор синего цвета вектор 𝐀, а красный — вектор 𝐁. Не зная больше ничего о 𝐀 и 𝐁 мы можем записать общее правило для их векторного произведения. Мы можем представить векторное произведение из 𝐀 с 𝐁 таким образом, используя × или крестик между двумя векторными символами.

Теперь уравнение, которое мы собираемся write применяется конкретно к векторам, лежащим в 𝑥𝑦-плоскости. Это означает, что мы можем написать вектор 𝐀 и вектор 𝐁 математически похожи на это. Мы можем представить 𝐀 как сумму компонент в 𝑥-направлении и компонент в 𝑦-направлении. И мы можем представить вектор 𝐁 в виде Подобный способ. И обратите внимание на эти векторные символы, которые применяются в наших определениях для векторов 𝐀 и 𝐁. В обоих случаях имеем вектор называется 𝐢 и вектор называется 𝐣.

Мы можем вспомнить, что это единичные векторы для 𝑥- и 𝑦-осей соответственно. Заметим, кстати, что когда мы включите третье измерение и назовите его 𝑧, единичный вектор для этого измерения равен обычно обозначается буквой 𝐤. В любом случае, когда мы пишем 𝐀 и 𝐁 в с точки зрения их компонентов таким образом, мы можем сделать следующий шаг и заполнить из правой части этого уравнения векторного произведения. Мы делаем это, используя 𝑥- и 𝑦-компоненты 𝐀 и 𝐁.

Если взять 𝑥-компоненту 𝐀, вот этот компонент, и умножьте его на 𝑦-компонент 𝐁, вот это компонент здесь. А потом вычесть из этого 𝑦-компонент 𝐀 здесь, умноженный на 𝑥-компонент 𝐁 здесь. Тогда у нас будет правильный выражение для величины нашего векторного произведения. Но помните, мы говорили, что вектор произведение приводит к другому вектору. И вот где этот 𝐤 блок входит вектор. Это дает величину 𝐀 𝑥 раз 𝐁 𝑦 минус 𝐀 𝑦 раз 𝐁 𝑥 направление.

Действительно, мы вычисляем вектор. И заметьте что-то об этом направление. В то время как 𝐀 и 𝐁 были полностью в 𝑥𝑦-плоскости и, следовательно, имел только 𝐢- и 𝐣-компоненты, векторное произведение 𝐀 и 𝐁 совершенно в другом измерении. Это в 𝐤-направлении. Всегда бывает так, что вектор произведение двух векторов перпендикулярно этим двум исходным векторам. Теперь давайте потренируемся применяя это уравнение, используя эти два вектора здесь.

Скажем, мы находим 𝐀 и 𝐁 на набор координатных осей. И мы обозначаем 𝑥- и 𝑦-оси используя эти числа, но мы не указываем единицы, которые они представляют. Для наших целей эти единицы не важны, поэтому мы оставим их неопределенными. Изучая эти оси, мы видим что вектор 𝐀 имеет расширение на одну единицу в 𝑥-направлении. И затем, он расширяется на пять единиц в положительное 𝑦-направление. Это означает, что мы можем записать 𝐀 как 𝐢 плюс пять раз 𝐣. Аналогично, с вектором 𝐁 мы видим что это расширяет четыре единицы в положительном 𝑥-направлении и две единицы в позитив 𝑦. Итак, 𝐁 равно четырем 𝐢 плюс два раза 𝐣.

Теперь, когда мы знаем 𝑥- и 𝑦-компоненты 𝐀 и 𝐁, мы можем вычислить их векторное произведение. В частности, давайте посчитаем 𝐀 крест 𝐁.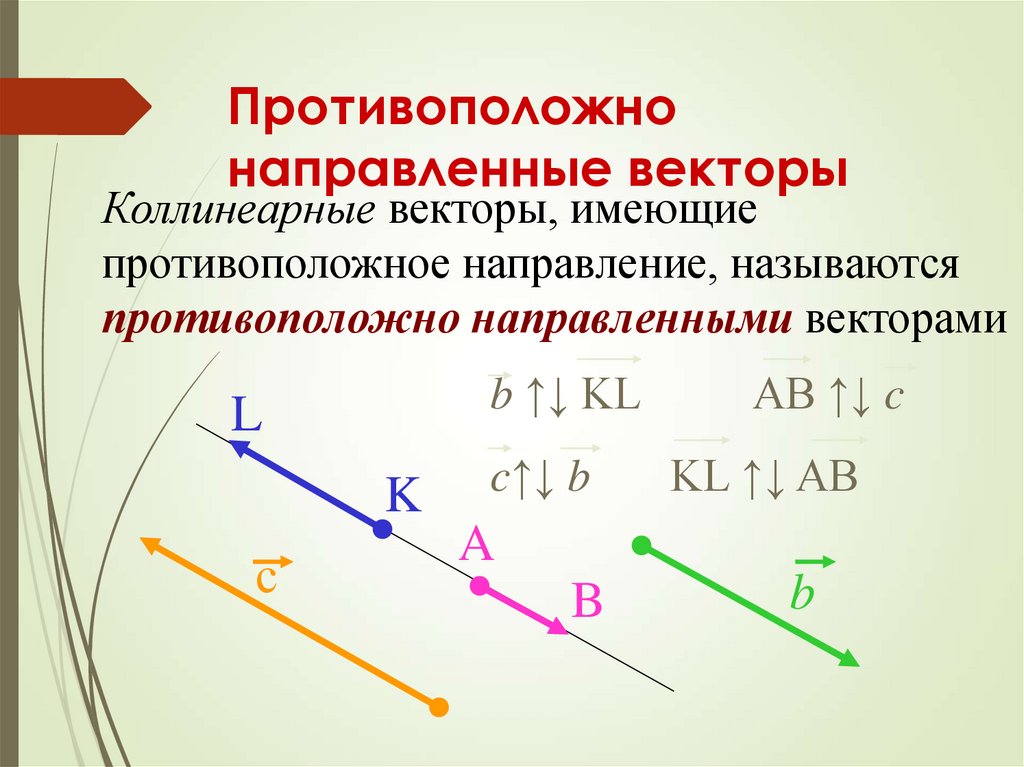 Мы видим, исходя из нашего векторного произведения уравнение, что оно равно 𝑥-компоненте 𝐀, в нашем случае это единица, умножить на 𝑦-компоненту 𝐁, что равно двум на основе нашего определения вектора 𝐁. А потом из этого вычитаем 𝑦-компонента 𝐀, равная пяти, умноженная на 𝑥-компонента 𝐁, и это равно четырем.

И так же, как мы видели для нашего генерала векторов, лежащих в плоскости 𝑥𝑦, поэтому эти конкретные векторы 𝐀 и 𝐁, компоненты, которые мы знаем, в соответствии с этим набором координатных осей дадут вектор произведение, которое указывает либо в положительном, либо в отрицательном 𝐤-направлении. Другими словами, это векторное произведение будет указывать куда-то вдоль 𝑧-измерения. И у него не будет компонента в 𝑥- или 𝑦-размеры.

Итак, глядя на это уравнение, теперь мы можем вычислить, что находится внутри круглых скобок, выделенных синим цветом. Один раз два два. И пять раз четыре равно 20. Итак, у нас есть два минус 20 или отрицательный 18𝐤 в качестве результирующего вектора. Тогда на наших осях координат, если мы представляет отрицательное 𝑧-направление с помощью этой пунктирной линии, тогда вектор Произведение 𝐀 и 𝐁 указывало бы на 18 единиц вдоль этой линии.

А вот и кое-что очень важно помнить всякий раз, когда мы вычисляем векторное произведение. И это то, что приказ векторы, которые мы используем, очень важны. Обратите внимание на то, что в этом уравнении, когда мы скрещиваем 𝐀 с 𝐁, 𝐀 идет первым, тогда это 𝑥-компонента этого первого вектор, который умножает 𝑦-компоненту второго. А затем, в следующем семестре, 𝑦-компонента первого вектора, умноженная на 𝑥-компонента второго. Если бы мы поменяли местами эти два векторов в начале — вместо 𝐀 креста 𝐁 мы берем 𝐁 креста 𝐀 — тогда мы будет вычислять другой результат в правой части.

Чтобы убедиться, что это так, давайте сделаем это. Мы уже рассчитали 𝐀 крест 𝐁 используя эти конкретные примеры векторов 𝐀 и 𝐁. Теперь обратим порядок. Возьмем векторное произведение 𝐁 и 𝐀. Когда мы это сделаем, будет немного сбивает с толку обращение к нашему эталонному уравнению здесь, потому что это уравнение имеет вектор с именем 𝐀 идет первым, а вектор с именем 𝐁 идет вторым. Но если мы будем осторожны в этом, мы сможем разобраться и рассчитать 𝐁 крест 𝐀.

Хорошо, первый термин в вычисление векторного произведения — это 𝑥-компонента первого вектора. В случае нашего конкретного вычисления, этот первый вектор равен 𝐁, а его 𝑥-компонента равна четырем. Затем это значение умножается на 𝑦-компонента второго вектора. Опять же, в нашем случае эта секунда вектор равен 𝐀, а его 𝑦-компонента равна пяти. Итак, у нас есть четыре раза по пять.

И из этого вычитаем 𝑦-компонента нашего первого вектора. 𝑦-компонента вектора 𝐁 над здесь в два раза больше 𝑥-компонента нашего второго вектора. Наш второй вектор в этом вычисление является вектором 𝐀 и его 𝑥-компонента равна единице. И теперь, когда мы вычисляем значение внутри синих скобок, у нас есть четыре раза по пять, или 20, минус два раза один или два. А 20 минус два равно 18.

Сравнивая этот результат с нашим результат вычисления 𝐀 cross 𝐁, мы можем заметить две вещи. Во-первых, эти результаты не такой же. И как оказалось, это в целом верно. То есть в общем так что 𝐀 крест 𝐁 не равен 𝐁 крест 𝐀. Но обратите внимание на кое-что еще о эти результаты. Эти два векторных произведения имеют той же величины, 18 единиц, и они направлены в противоположные стороны. Это также верно в целом.

И мы можем написать это так. Можно сказать, что векторное произведение 𝐀 и 𝐁 равно отрицательному векторному произведению 𝐁 и 𝐀. Как следствие этого, кстати, мы можем написать, что величина 𝐀 креста 𝐁 равна величине 𝐁 креста 𝐀. Итак, есть много уравнений здесь, но мы обнаруживаем важные соотношения для векторных произведений. Теперь, когда мы вычислили векторные произведения наших двух векторов 𝐀 и 𝐁 на этом графике, давайте расчистим место для нового расчета.

Что произойдет, если мы вычислить векторное произведение двух единичных векторов? То есть, что если бы мы взяли единичный вектор 𝐢, а затем скрестить 𝐢 с единичным вектором 𝐣? Мы знаем, что технически оба это векторы, так что это должно работать. А на самом деле так же, как векторы 𝐀 и 𝐁, мы можем выписать 𝑥- и 𝑦-компоненты этих единичных векторов 𝐢 и 𝐣.

Глядя на нашу диаграмму в внизу слева мы можем записать единичный вектор 𝐢 таким образом. Единичный вектор 𝐢 имеет одну единицу величина в 𝐢-направлении, 𝑥-измерении. А то вообще не показатель в 𝐣-направлении вдоль 𝑦-оси. Тогда мы могли бы сказать, что 𝐢 равно к единице 𝐢 плюс ноль 𝐣, и аналогично с единичным вектором 𝐣. Этот вектор имеет нулевую величину в 𝐢-направление или 𝑥-размерность. И имеет величину один в 𝐣-направление.

С выписанными 𝐢 и 𝐣 по их 𝑥- и 𝑦-компонентам теперь мы можем вычислить 𝐢 крест 𝐣. Он равен 𝑥-компоненте первый вектор, это 𝐢. И эта 𝑥-компонента одна умножается на 𝑦-компоненту второго вектора. Этот второй вектор равен 𝐣, и его 𝑦-компонента тоже одна. А потом из этого продукта мы вычтите 𝑦-компоненту первого вектора. Это вектор 𝐢. Мы видим, что 𝑦-компонента нуль. И умножаем это на 𝑥-компонента второго вектора. Этот второй вектор равен 𝐣. И эта 𝑥-компонента равна нулю, поскольку Что ж.

Теперь вычисляем результат у нас есть один раз один или один минус ноль умножить на ноль, что равно нулю. И когда все это выражение упрощает, мы находим, что 𝐢 крест 𝐣 равен единичному вектору 𝐤. И мы можем записать это уравнение в зеленый, потому что в целом это правда. Зная это, что, если бы мы захотели изменить порядок и вычислить векторное произведение 𝐣 и 𝐢?

Для этого мы могли бы еще раз пойти через этот расчет. Но не будем забывать о отношения векторного произведения, которые мы обнаружили, в частности это, которое говорит векторное произведение 𝐀 и 𝐁 равно отрицательному значению векторного произведения 𝐁 и 𝐀. Это избавляет нас от некоторых вычислений Работа. Зная, что 𝐢 крест 𝐣 равно к 𝐤, мы знаем, что 𝐣 крест 𝐢 равен минусу этого, минуса 𝐤. Итак, как ни странно, действительно, мы можем вычислить векторное произведение единичных векторов, и результатом будет вектор это перпендикулярно как 𝐢, так и 𝐣.

А теперь еще кое-что, что мы хочу отметить о векторных продуктах. И это связано с величиной этих продуктов. Скажем, мы возвращаемся к нашему графику векторы 𝐀 и 𝐁 и что пока мы игнорируем 𝑧-размерность. Итак, у нас есть эти два вектора в 𝑥𝑦-плоскость, 𝐀 и 𝐁. И скажем, что мы хотим вычислить величина их векторного произведения. Оказывается, мы можем что дало три части информации. Во-первых, нам нужно знать, величина 𝐀. Во-вторых, нам нужно знать величина 𝐁. И в-третьих, нам нужно знать угол между этими двумя векторами. И мы можем назвать этот угол 𝜃.

Итак, вот как это работает. Величина векторного произведения 𝐀 и 𝐁 равно величине 𝐀, умноженной на величину 𝐁, умноженной на грех угла между этими двумя векторами. Эти отношения могут быть очень полезно, когда мы знаем величины наших двух векторов, но не знаем их компонент части. Нам не нужно знать эти составные части для вычисления величины векторного произведения, если мы также знать угол между двумя векторами. Мы можем немного больше понять о это уравнение, рассматривая этот коэффициент греха 𝜃 здесь.

Мы знаем, что если угол 𝜃 равен ноль градусов, и это будет означать, что 𝐀 и 𝐁 параллельны, то, поскольку грех нуля равен нулю, мы знаем, что это приведет к этому всему векторному произведению быть нулем. Другими словами, для параллельного векторов, их векторное произведение равно нулю. Но что, если вместо того, чтобы быть угол 0 градусов, 𝜃 угол 90 градусов? Ну, мы знаем, что грех 90 градус равен единице. И это приведет к максимальному возможное значение величины 𝐀 умноженной на величину 𝐁 умноженной на грех угол между ними.

Это говорит нам о том, что векторы, перпендикулярны друг другу под углом 90 градусов имеют максимально возможное векторное произведение величина, учитывая их индивидуальные величины. Итак, просто зная, как sin of 𝜃, мы можем немного больше понять об этом уравнении. Зная все это о векторе продукты, давайте попробуем пример упражнения.

Рассмотрим два вектора 𝐑 равны три 𝐢 плюс два 𝐣 и 𝐒 равно пяти 𝐢 плюс восемь 𝐣. Вычислить 𝐑 крест 𝐒.

Итак, мы видим, что это упражнение примерно вычисление векторного произведения между этими двумя векторами 𝐑 и 𝐒. Нам даны эти два вектора в компонентной форме. И мы видим, что у каждого есть 𝐢-компонента, то есть компонента вдоль оси 𝑥, а также 𝐣-компонента, некоторая компонента по 𝑦-размерности. Мы видим тогда, что оба эти векторы 𝐑 и 𝐒 лежат в 𝑥𝑦-плоскости. В самом деле, если бы мы набросали 𝑥- и 𝑦-оси, то мы можем нарисовать на этом графике векторы 𝐑 и 𝐒.

Вектор 𝐑 расширяется на три единицы в положительное 𝑥-направление и две единицы в положительном 𝑦, что дает вектор вида это. В то время как вектор 𝐒 расширяется на пять единиц в положительном 𝑥-направлении, а затем восемь единиц в положительном 𝑦-направлении. И этот вектор выглядит так это. Теперь, чтобы вычислить этот вектор произведения, 𝐑 через 𝐒, мы хотим вспомнить математическую форму вектора произведение двух векторов, которые целиком лежат в плоскости 𝑥𝑦, как это делают 𝐑 и 𝐒.

Если мы назовем два общих вектора, которые оба обязаны лежать в 𝑥𝑦-плоскости 𝐀 и 𝐁. Тогда векторное произведение 𝐀 и 𝐁, также называемое векторным произведением 𝐀 и 𝐁, равно 𝑥-компоненте 𝐀 умножить на 𝑦-компоненту 𝐁 минус 𝑦-компоненту 𝐀 умножить на 𝑥-компоненту 𝐁. Обратите внимание, что векторное произведение двух vectors приводит к вектору. То есть он имеет как величину, так и ну и направление. А так как наши векторы 𝐀 и 𝐁 оба лежат в 𝑥𝑦-плоскости, их векторное произведение указывает перпендикулярно к ней, в 𝐤-направление.

Теперь воспользуемся этим соотношением вместе с 𝐑 и 𝐒, записанными в их компонентной форме, для вычисления 𝐑 пересечения 𝐒. Это векторное произведение равно 𝑥-компонента 𝐑 раз 𝑦-компонента 𝐒 минус 𝑦-компонента 𝐑 раз 𝑥-компонента 𝐒. И это также укажет на 𝐤-направление, как положительное, так и отрицательное. Глядя на эти разные термины в скобки, мы видим, что 𝑥-компонента 𝐑 равна трем, что 𝑦-компонента 𝐒 равна восьми, тогда 𝑦-компонента 𝐑 равна двум и 𝑥-компонента 𝐒 равна пяти.

Когда мы подставляем эти значения, нашей следующей задачей является вычисление их результата. Трижды восемь будет 24, а два умножить на пять будет 10. И тогда 24 минус 10 равно 14. Итак, наше векторное произведение точек 14 единиц в положительном 𝐤-направлении. Итак, если мы нарисовали ось 𝑧 на нашем график, где та ось указывала на нас из экрана, то это векторное произведение укажет на нас 14 единиц в этом направлении. Это векторное произведение 𝐑 и 𝐒.

Подведем итог тому, что у нас есть узнали о векторном произведении двух векторов. На этом уроке мы узнали, что векторное произведение двух векторов является другим вектором. Вместе с тем мы видели, что если есть два вектора 𝐀 и 𝐁, целиком лежащие в 𝑥𝑦-плоскости. Тогда векторное произведение 𝐀 и 𝐁 равно 𝑥-компоненте 𝐀, умноженной на 𝑦-компоненту 𝐁 минус 𝑦-компонента 𝐀, умноженная на 𝑥-компонента 𝐁. И что это векторное произведение указывает в направлении 𝐤-единичного вектора.

Мы также узнали, что заказ в какие два вектора появляются в векторном произведении, имеет значение. Векторное произведение, также называемое векторное произведение 𝐀 и 𝐁 равно отрицательному векторному произведению 𝐁 и 𝐀. Наряду с этим мы обнаружили отношения между самими единичными векторами. Что векторное произведение 𝐢 и 𝐣 равно единичному вектору 𝐤, а векторное произведение 𝐣 и 𝐢 равно отрицательный этот вектор.

И, наконец, мы увидели, что если у нас есть два вектора 𝐀 и 𝐁 в 𝑥𝑦-плоскости, разделенные углом 𝜃, то величина их векторного произведения равна величине индивидуального векторов, умноженных на грех 𝜃.

Векторное умножение: скалярное произведение

С технической точки зрения скалярное произведение является своего рода скалярным произведением. Это означает, что это операция, которая берет два вектора и «умножает» их. вместе, и производит скаляр. Однако нам не нужен скалярный продукт двух векторы для получения любого скаляра. Было бы хорошо, если бы продукт мог предоставить значимая информация о векторах в терминах скаляров.

Что мы подразумеваем под «значимым»? Рад, что вы спросили. Для начала поищем скалярные величины, которые могут характеризовать вектор. Одним из простых примеров этого является длина , или величина вектора v , обычно обозначаемая | против |. Каждый из 2- и 3-мерных векторов, которые мы обсуждали, имеет длина, а длина является скалярной величиной. Например, чтобы найти длину вектор ( a , b , c ), нам просто нужно вычислить расстояние между началом координат и точка ( a , b , c ). (Идея та же самая в двух измерениях). Наше измерение даст скалярное значение величины без направления — не еще один вектор! Этот тип скаляры звучит как вид значимой информации, точечный продукт может предоставить нам.

Компонентный метод

Теорема Пифагора говорит нам, что длина вектора ( а , б , в ) есть данный . Это дает нам представление о том, как мы можем определить скалярное произведение. Например, если нам нужно скалярное произведение вектора v = ( v 1 , v 2 , v 3 ) с собой ( v · v ) чтобы дать информацию о нас v , имеет смысл потребовать, чтобы это выглядело так:

в · v = v 1 v 1 + v 2 v 2 + v 3 v 3


Следовательно, скалярное произведение вектора на самого себя дает величину вектора в квадрате.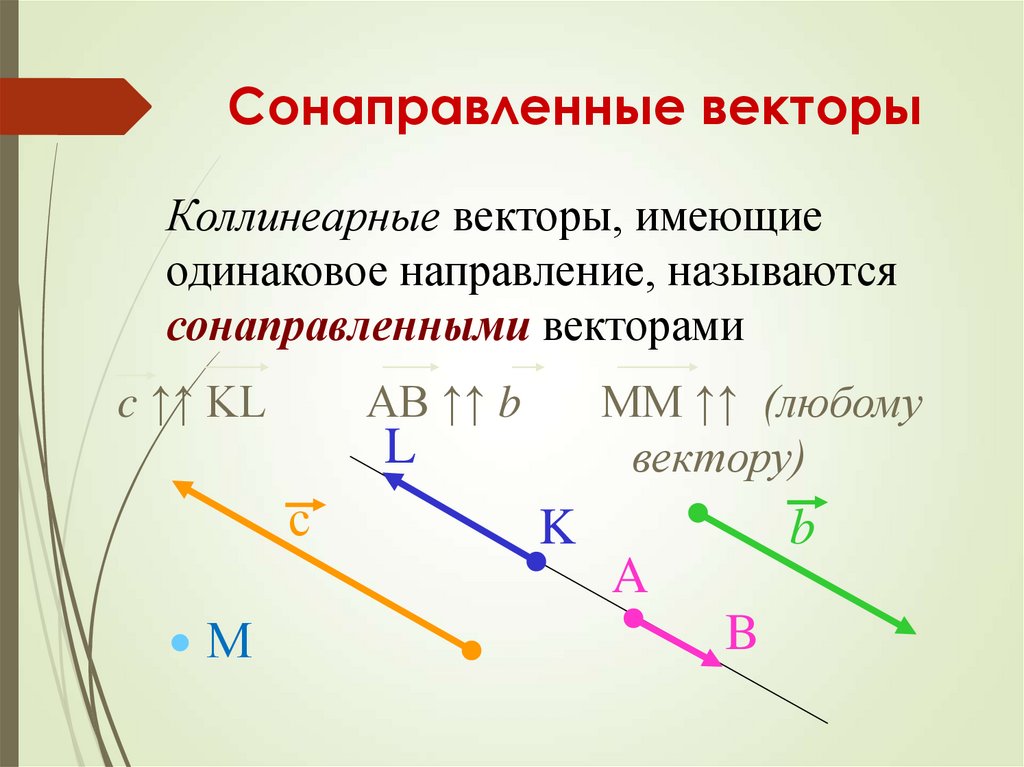

Хорошо, это то, что мы хотели, но теперь царит новый вопрос: что такое точка произведение между двумя разными векторами? Важно помнить, что как бы мы ни определяли общее правило, оно должно сводиться к тому, когда мы подключаем два одинаковых вектора. На самом деле, @@Equation @@ уже написано наводя на размышления, чтобы указать, что общее правило для скалярного произведения между двумя векторов u = ( u 1 , u 2 , u 3 ) and v = ( v 1 , v 2 , v 3 ) может быть:

u · v = u 1 v 1 + u 2 v 2 + u 3 v 3


Это уравнение точно соответствует формуле скалярного произведения двух Трехмерные векторы. (Обратите внимание, что количество, полученное справа, является скаляр, , хотя мы больше не можем сказать, что это представляет собой длину either vector.) For 2-dimensional vectors, u = ( u 1 , u 2 ) and v = ( v 1 , v 2 ), мы есть:

U · V = U 1 V 1 + U 2 1 + U 2 2 + .


Снова подставив u = v , мы восстановим квадрат длины вектора в двух измерениях.

Геометрический метод

Так что же дает скаляр, полученный при скалярном произведении u . в представляете? Мы можем получить представление о том, что происходит, взглянув на скалярное произведение вектора. с единичными векторами. В Unit Vectors мы определили единицу векторы i , j и k для трехмерного случая. В двух измерениях мы имеем только i = (1, 0) и j = (0, 1). (Пока мы будем работать в двух измерениях, так как такие векторы легче представить графически.) Скалярные произведения вектора v = ( v 1 , v 2 ) с единичными векторами i и j определяются по формуле:

v · i = v 1 1 + v 2 0 = v 1
v · j = v 1 0 + v 5 5 v 5 3 6 5 3 1 9093 2


Другими словами, скалярное произведение v с i выделяет компонент v в направлении x , и точно так же скалярное произведение на с на выделяет компонент на , лежащий в направлении на . Это так же, как вычисление величины проекции v на оси x и y соответственно.

Это может показаться не слишком захватывающим, поскольку в некотором смысле мы уже знали об этом, как только как мы записали наш вектор с точки зрения компонентов. Но что было бы, если бы вместо компонентов нам были даны только направление и величина вектора v , как на следующем рисунке?

Рисунок %: Вектор v с длиной l и направлением, заданным углом θ .

В этом случае, заметив образовавшиеся два прямоугольных треугольника и вспомнив правила из тригонометрии находим, что v · i и v · j можно вычислить по-другому. А именно:

v · i = | против | cos θ
v · j = | против | sin θ = l cos(90 — θ )


Что произойдет, если мы возьмем скалярное произведение v с общим вектором, лежащим чисто в направлении x (т. е. не обязательно единичный вектор)? Мы можем написать такой вектор, как w = ( w 1 , 0) = w 1 (1, 0) = w 1 i , а величина w | с | = ш 1 . Следовательно, w = | с | я . Используя приведенное выше правило для скалярного произведения между v и i , находим, что:

v · w = | против || с | cos θ


На самом деле, это уравнение выполняется в общем случае: если мы возьмем v и w произвольными векторы в двух или трех измерениях, и пусть θ будет углом между их, мы находим, что эта версия формулы скалярного произведения точно согласуется с формула компонента, которую мы нашли ранее.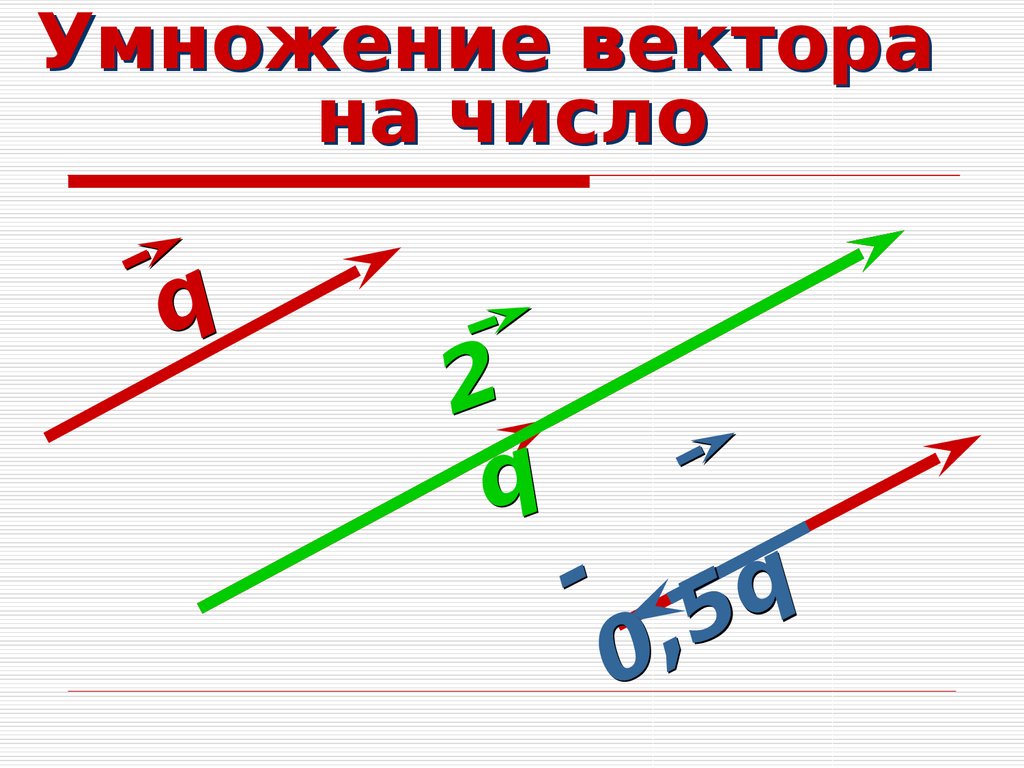

Геометрически скалярное произведение v · w равно | против || с | cos θ .

Обратите внимание, что когда векторы лежат в одном направлении, θ = 0 и cos θ достигает своего максимального значения 1. (В частности, это случай то два вектора совпадают, что восстанавливает наше первоначальное требование для скалярный продукт: v · v = | против | 2 .) Фактически, для векторов равной величины чем меньше угол между ними, тем больше будет их скалярное произведение. это в этом смысле мы можем сказать, что скалярное произведение дает информацию о том, как во многом два вектора «перекрываются». Например, если два вектора перпендикулярны друг друга (т.е. они вообще не «перекрываются»), угол между ними равен 90 градусов. Поскольку cos 90 o = 0, их скалярное произведение равно нулю.

Краткое изложение правил скалярного произведения

Таким образом, правила скалярных произведений 2- и 3-мерных векторов по компонентам это:

U · V = U 1 V 1 + U 2 1 + U 2 2 + .


u · v = u 1 v 1 + u 2 v 2 + u 3 v 3


Правило для векторов, заданных с точки зрения величины и направления (либо в 2 или 3 измерения), где θ обозначает угол между ними, составляет:

в · в = | против || с | cos θ


Как обозначить перекрестное произведение (a ⨯ b) в LaTeX?

Вы все умеете письменно представлять перекрестные произведения. Вам нужно использовать символы умножения для записи перекрестных произведений в векторах. Для этого вам нужно использовать команду \times в латексе.

Предположим, здесь a и b — два вектора, тогда их векторное произведение будет равно

 \documentclass{статья}
\начать{документ}
  $$\vec{a}\times\vec{b}$$
\конец{документ}

Вывод:

Две команды используются для представления векторного векторного произведения в латексе. Первый — это \vec{} , в котором, если один символ передается в качестве аргумента , он возвращает стрелку на этом единственном символе. И второй \times в которому нет необходимости передавать какой-либо аргумент, который вернет вам символ умножения.

Результат перекрестного произведения всегда представляет собой вектор. И этот результат записывается в виде единичного вектора и матрицы.

Перекрестное произведение в виде единичного вектора

В этом случае перекрестное произведение выражается в единичных векторах с величиной.

Чтобы представить персонажа модом, вы должны использовать \left| и \право| команд и пропустите персонажа через оба.

 \documentclass{статья}
\начать{документ}
  $$\vec{a}\times\vec{b} =\left| \vec{a}\times\vec{b} \right |\hat{n}$$
\конец{документ}

Вывод:

Также, когда записывается единичный вектор, вам нужно использовать команду \hat{} , которая вернет заглавную букву символа.

Во-вторых, вы можете записать значение перекрестного произведения в виде sinθ . Например,

Здесь для sinθ, вам нужно использовать две латексные команды \sin и \theta . Команда и \theta вернет вам символ тета. 

 \documentclass{статья}
\начать{документ}
   $$\vec{a}\times\vec{b} =|\vec{a}||\vec{b}|\sin\theta\hat{n}$$
\конец{документ}

Вывод:

Кросс-произведение в виде матрицы

Прежде чем писать кросс-произведение в виде матрицы, нужно знать, как матрица определяется в латексе. Существуют разные типы матриц, , но в этом уроке мы обсудим один тип матрицы, элементы которого будут заключены в круглые скобки.

Базовый синтаксис матрицы без каких-либо скобок

 $\begin{matrix}
  ....
  ....
\end{matrix}$

И поскольку здесь я буду использовать матрицу в скобках, вам нужно ввести pmatrix вместо matrix в командах \begin{} и \end{} .

 $\begin{pmatrix}
  ....
  ....
\end{pmatrix}$

Вы создаете базовый синтаксис матрицы. Опять же, вы должны указать элемент в матрице. Для этого нужно использовать два символа и и \ . Символ и создаст промежуток между двумя элементами, а символ и создаст новую линию.

 \documentclass{статья}
\usepackage{аммат}
\начать{документ}
  $$\begin{pматрица}
    а и б \\
    CD
  \end{pmatrix}$$
\end{document}

Вывод:

Вы заметили вывод выше, где символы и создали пробелы между (а, б) и (в, г) и символ \ создал новые линии между расположенными в ряду элементами.

Надеюсь, на этот раз, если я запишу векторное произведение двухпозиционных векторов в виде матрицы, то у вас не возникнет проблем с пониманием. Итак,

 \documentclass{статья}
\usepackage{аммат}
\начать{документ}
  $$\vec{a}\times\vec{b}=\begin{pmatrix}
      \ шляпа {я} и \ шляпа {j} & \ шляпа {к} \\
      х_{1} и у_{1} и z_{1} \\
      х_{2} и у_{2} и z_{2}
   \end{pmatrix}$$
\конец{документ}

Вывод:

Вопросы и ответы

1. Как записать единичный вектор в виде перекрестного вектора? 

 \documentclass{статья}
\начать{документ}
   $$\шляпа{n}=\frac{\vec{a}\times\vec{b}}{\left | \vec{a}\times\vec{b}\right |}$$
\end{document}

Вывод:

Обратите внимание на латексный код выше. Команда \frac{}{} используется для дробей, и вам всегда нужно передавать два аргумента для числителя и знаменателя в этой команде.

2. Как вы определяете тройной продукт с латексом?

Тройные произведения всегда записываются комбинацией векторных точечных и перекрестных произведений.

 \documentclass{статья}
\начать{документ}
   $$\vec{a}\cdot \left(\vec{b}\times\vec{c}\right )$$
\конец{документ}

Вывод:

Вам нужно использовать команду \cdot для символа точки. А для скобок нужно передать аргументы между \влево ( и \вправо ) команд.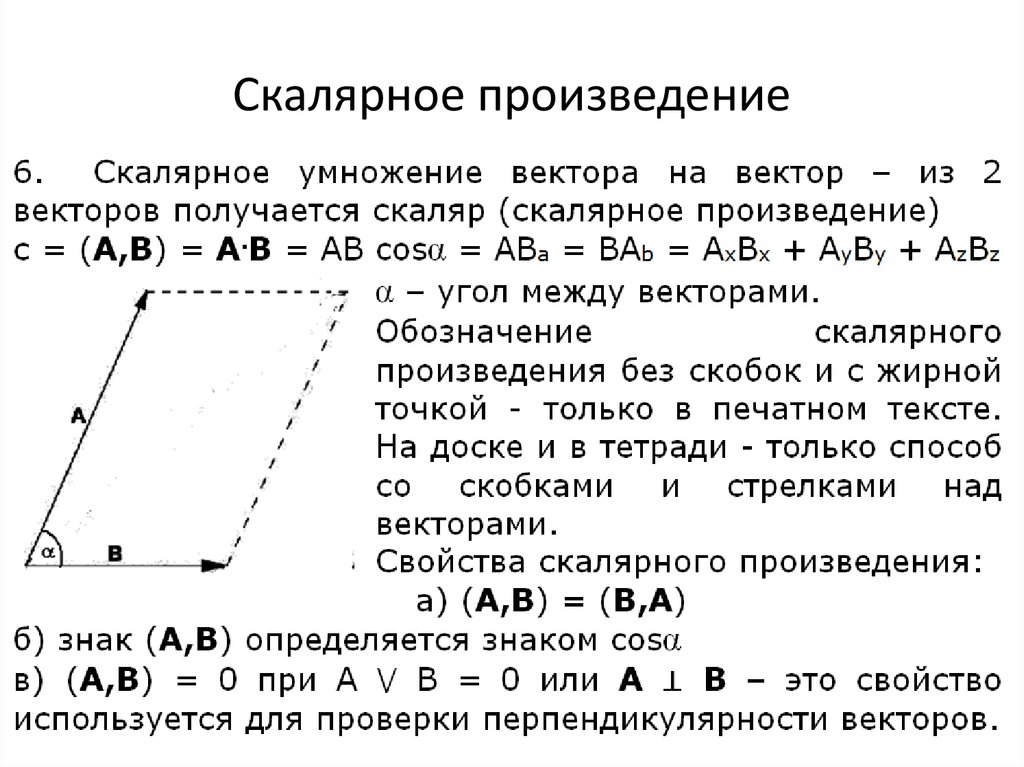

Заключение

В этом руководстве подробно рассматриваются изделия из латекса. Вы можете определить эти латексные уравнения, вызвав другие внешние пакеты. Но здесь с вами делится подлинным методом.

И поскольку Latex имеет множество команд, не путайтесь. Есть много команд, в которых вам не нужно передавать ни один аргумент, и есть много команд, в которых вам нужно передать более одного аргумента. Спасибо

Предстоящие учебные пособия
  • Подчеркнуть
  • Надпись
  • Параграф
  • Стол
  • Точка пули
  • Выравнивание уравнения
  • Новая команда
  • Подзаголовок
  • Пакет
  • Использовать пакет
  • Авторское право
  • Рекомендация
Подписаться на уроки

Векторная математика — документация Godot Engine (stable) на английском языке

Введение

Этот учебник представляет собой краткое и практическое введение в линейную алгебру. это относится к разработке игр. Линейная алгебра — это изучение векторов и их использование. Векторы имеют множество применений как в 2D-, так и в 3D-разработке. и Годо широко их использует. Развитие хорошего понимания вектора математика необходима, чтобы стать сильным разработчиком игр.

Примечание

Это руководство , а не формальный учебник по линейной алгебре. Мы будет только смотреть на то, как это применяется к разработке игр. Для более широкого взгляда на математику, см. https://www.khanacademy.org/math/linear-алгебра

Системы координат (2D)

В двухмерном пространстве координаты определяются с помощью горизонтальной оси ( x ) и вертикальная ось ( y ). Определенная позиция в 2D-пространстве записывается в виде пары значений, таких как (4, 3) .

Примечание

Если вы новичок в компьютерной графике, может показаться странным, что положительный y ось указывает вниз вместо вверх, как вы, вероятно, узнали на уроке математики. Однако это обычное в большинстве приложений компьютерной графики.

Любая позиция в 2D-плоскости может быть идентифицирована парой чисел в этом путь. Однако мы также можем думать о позиции (4, 3) как о смещении . из точки (0, 0) или начала . Нарисуйте стрелку, указывающую от от начала до точки:

Это вектор . Вектор представляет много полезной информации. В качестве а также говоря нам, что точка находится на (4, 3) , мы также можем думать о это как угол θ и длиной (или звездной величиной) м . В этом случае стрелка — это вектор положения — он обозначает позицию в пространстве, относительную к происхождению.

Очень важный момент, который следует учитывать в отношении векторов, заключается в том, что они представляют относительных направлений и величин. Нет понятия о положение вектора. Следующие два вектора идентичны:

Оба вектора представляют точку на 4 единицы правее и на 3 единицы ниже некоторой отправная точка. Неважно, где на плоскости ты рисуешь вектор, он всегда представляет относительное направление и величину.

Векторные операции

Вы можете использовать любой метод (координаты x и y или угол и величина) для относятся к вектору, но для удобства программисты обычно используют обозначение координат. Например, в Godot начало координат находится в верхнем левом углу. углу экрана, чтобы разместить 2D-узел с именем Node2D на 400 пикселей вправо и 300 пикселей вниз, используйте следующий код:

 $Node2D.position = Vector2(400, 300)

Godot поддерживает как Vector2, так и Vector3 для использования в 2D и 3D соответственно. Одинаковый математические правила, обсуждаемые в этой статье, применимы к обоим типам.

Доступ для участников

Доступ к отдельным компонентам вектора можно получить непосредственно по имени.

 # создать вектор с координатами (2, 5)
переменная a = Vector2 (2, 5)
# создаем вектор и назначаем x и y вручную
переменная b = Vector2()
б. х = 3
б.у = 1

Добавление векторов

При сложении или вычитании двух векторов добавляются соответствующие компоненты:

 var c = a + b # (2, 5) + (3, 1) = (5, 6)

Мы также можем увидеть это визуально, добавив второй вектор в конце первый:

Обратите внимание, что сложение a + b дает тот же результат, что и b + a .

Скалярное умножение

Примечание

Векторы представляют как направление, так и величину. Ценность представляющий только величину, называется скаляром .

Вектор можно умножить на скаляр :

 вар с = а * 2 # (2, 5) * 2 = (4, 10)
var d = b / 3 # (3, 6) / 3 = (1, 2)

Примечание

Умножение вектора на скаляр не меняет его направление, только его величина. Вот как ты масштаб вектор.

Практическое применение

Давайте рассмотрим два распространенных способа сложения и вычитания векторов.

Механизм

Вектор может представлять любую величину с величиной и направлением. Типичными примерами являются: положение, скорость, ускорение и сила. В На этом изображении космический корабль на шаге 1 имеет вектор положения (1,3) и вектор скорости (2,1) . Вектор скорости показывает, насколько далеко корабль движется каждый шаг. Мы можем найти позицию для шага 2, добавив скорость до текущего положения.

Совет

Скорость измеряет изменение положения в единицу времени. новое положение находится путем прибавления скорости к предыдущему положению.

Указание на цель

В этом сценарии у вас есть танк, который хочет направить свою башню на робот. Вычитание положения танка из положения робота дает вектор, указывающий от танка к роботу.

Подсказка

Чтобы найти вектор, указывающий от A до B используйте B-A .

Единичные векторы

Вектор с величиной из 1 называется единичным вектором . Они есть также иногда упоминается как векторов направления или нормалей . Ед. изм векторы полезны, когда вам нужно отслеживать направление.

Нормализация

Нормализация вектора означает уменьшение его длины до 1 при сохраняя свое направление. Это делается путем деления каждой из его составляющих по своей величине. Поскольку это такая распространенная операция, Vector2 и Vector3 предоставляют метод нормализации:

 а = а.нормализованный()

Предупреждение

Поскольку нормализация включает деление на длину вектора, вы не можете нормализовать вектор длины 0 . Пытаться это приведет к ошибке.

Отражение

Обычно единичные векторы используются для обозначения нормалей . Обычный векторы — это единичные векторы, выровненные перпендикулярно поверхности, определяющие его направление. Они обычно используются для освещения, столкновений и других операции с поверхностями.

Например, представьте, что у нас есть движущийся мяч, который мы хотим отскочить от стена или другой объект:

Нормаль поверхности имеет значение (0, -1) , потому что это горизонтальная поверхность. Когда мяч сталкивается, мы берем его остаточное движение (количество оставшийся после удара о поверхность) и отразите его с помощью нормали. В Годо, класс Vector2 имеет метод bounce() справиться с этим. Вот пример GDScript диаграммы выше с использованием Кинематическое тело2D:

 # объект "столкновение" содержит информацию о столкновении
переменная коллизия = move_and_collide(скорость * дельта)
если столкновение:
    переменная отражения = столкновение.остаток.отскок(столкновение.нормальный)
    скорость = скорость.отскок(столкновение.норма)
    move_and_collide (отражать)

Скалярный продукт

Скалярное произведение — одно из самых важных понятий в векторной математике. но часто неправильно понимают. Скалярное произведение — это операция над двумя векторами, возвращает скаляр . В отличие от вектора, который содержит как величину, так и направление, скалярное значение имеет только величину.

Формула скалярного произведения принимает две распространенные формы:

и

Однако в большинстве случаев проще всего использовать встроенный метод. Обратите внимание, что порядок двух векторов не имеет значения:

 переменная c = a.dot(b)
var d = b.dot(a) # Они эквивалентны.

Скалярное произведение наиболее полезно при использовании с единичными векторами, что делает первая формула уменьшите до cosθ . Это означает, что мы можем использовать точку произведение, чтобы сообщить нам что-то об угле между двумя векторами:

При использовании единичных векторов результат всегда будет между -1 (180°) и 1 (0°).

Облицовка

Мы можем использовать этот факт, чтобы определить, обращен ли объект к другому объект.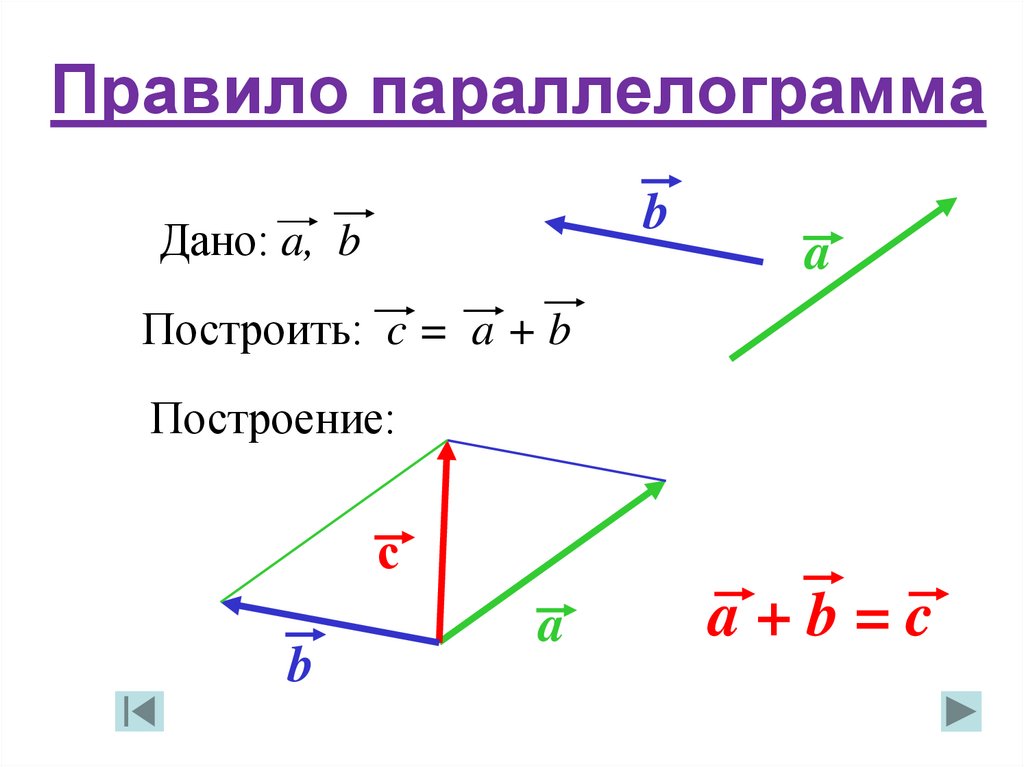 На диаграмме ниже игрок P пытается избежать зомби A и B . Предположим, что поле зрения зомби равно 9.0067 180° , они видят игрока?

Зеленые стрелки fA и fB представляют собой единичных векторов , представляющих направления зомби, а синий полукруг представляет его поле Посмотреть. Для зомби A мы находим вектор направления AP , указывающий на игрок использует P - A и нормализует его, однако у Годо есть помощник метод для этого называется direction_to . Если угол между этим вектор и обращенный вектор меньше 90°, то зомби может видеть игрок.

В коде это будет выглядеть так:

 вар AP = A.direction_to(P)
если AP.dot(fA) > 0:
    print("А видит Р!")

Перекрестное произведение

Как и скалярное произведение, перекрестное произведение представляет собой операцию над двумя векторами. Однако результатом векторного произведения является вектор с направлением что перпендикулярно обоим. Его величина зависит от их относительного угла. Если два вектора параллельны, результатом их перекрестного произведения будет нулевой вектор.

Перекрестное произведение вычисляется следующим образом:

 переменная c = Vector3()
c.x = (a.y * b.z) - (a.z * b.y)
су = (а.з * б.х) - (а.х * б.з)
c.z = (a.x * b.y) - (a.y * b.x)

С Godot вы можете использовать встроенный метод:

 переменная c = a.cross(b)

Примечание

В векторном произведении важен порядок. а.крест(б) нет дают тот же результат, что и b.cross(a) . Результирующие векторы точка в противоположных направлениях.

Расчет нормалей

Одним из распространенных применений векторных произведений является нахождение нормали к поверхности плоскости. или поверхность в трехмерном пространстве. Если у нас есть треугольник ABC , мы можем использовать вектор вычитание, чтобы найти два ребра AB и AC . Используя перекрестное произведение, AB x AC дает вектор, перпендикулярный обеим сторонам: нормали к поверхности.

Вот функция для вычисления нормали треугольника:

 функция get_triangle_normal(a, b, c):
    # найти нормаль к поверхности по трем вершинам
    переменная сторона1 = б - а
    переменная сторона2 = с - а
    переменная нормальная = сторона1.кросс(сторона2)
    вернуться в нормальное состояние

Наведение на цель

В разделе скалярного произведения выше мы увидели, как его можно использовать для нахождения угол между двумя векторами. Однако в 3D этой информации недостаточно. Нам также нужно знать, вокруг какой оси вращаться. Мы можем найти это по вычисление векторного произведения текущего направления взгляда и целевое направление. Результирующий перпендикулярный вектор является осью вращение.

Дополнительная информация

Дополнительные сведения об использовании векторной математики в Godot см. в следующих статьях:

  • Расширенная векторная математика

  • Матрицы и преобразования

Символ перекрестного произведения в LaTeX

Написано администратором в математических символах


Узнайте, как написать символ векторного произведения в LaTeX, также известный как векторное произведение, самым простым и понятным способом

  1. Команда векторного произведения в LaTeX
  2. Пример единичного вектора
  3. Пример матрицы
  4. Символ больших чисел

В математике перекрестное произведение используется для представления векторного произведения, которое представляет собой бинарную операцию между векторами в трехмерном пространстве. Проще говоря, перекрестное произведение — это произведение двух векторов, которое порождает третий вектор, ортогональный первым двум. Обозначается (x), символом умножения.

\times — это команда перекрестного произведения в LaTeX

Предположим, что a и b являются векторами, тогда их векторное произведение определяется в LaTeX как 

 % Перекрестное произведение в LaTeX
\documentclass{статья}
\usepackage{аммат}
\начать{документ}
$\vec{a} \times \vec{b}$
\ end {Document}

Выход:

Комментарии:

  • \ USEPACKAGE {AMSMATH} : он находится в нашей Preamble (Amsmath} : он находится в нашей Preamble (область до . Он принимает аргумент ammath , который способен интерпретировать и облегчать написание математических символов, формул и улучшает качество математического вывода в нашем документе.
  • \times команда, которая возвращает x, символ перекрестного произведения.
  • \vec{} Команда принимает один символ в качестве аргумента и возвращает символ со стрелкой над ним.

Определение перекрестного (векторного) произведения

1. Перекрестное произведение в виде единичного вектора

Перекрестное произведение двух векторов, a и b , определяется следующим образом:

и

3 в Латексе: 

 % Векторный продукт LaTeX
\documentclass{статья}
\usepackage{аммат}
\начать{документ}
$\vec{a} \times \vec{b} = |a||b|\sin\theta\hat{n}$
\end{document}

Где θ — угол между двумя векторами, а n — единичный вектор, перпендикулярный a и b .

Команды LaTeX для sin: \sin , а для θ мы используем \theta . \шляпа{ } Команда принимает один символ в качестве аргумента и возвращает его с символом вставки (circumflex) поверх него.

2. Перекрестное произведение в виде матрицы

Для того, чтобы определить перекрестное произведение в виде матрицы, вам нужно знать, как набирать матрицы в LaTeX. Существует несколько различных типов матриц, но в этом уроке мы сосредоточимся на 2 типах:

  • Матрица в скобках (матрица со скобками).
  • Матрица с вертикальной полосой (часто используется для представления определителей).

Матрица в скобках получается в LaTeX с помощью среды pmatrix , а матрица вертикальной полосы — с помощью среды vmatrix . Взгляните на два синтаксиса ниже:

 $\begin{pmatrix}
.  . . \\
. . .
\end{pmatrix}$ 
 $\begin{vmatrix}
. . . \\
. . .
\end{vmatrix}$

Если имеется несколько записей , то строки-записи разделяются (разносятся) с помощью ( и ) и записи столбцов с помощью ( \\ ) команды разрыва строки, как вы увидите в наших различных определениях ниже.

Пример 1:

и вот соответствующий код LaTeX:

 Учитывая $\vec{a} = \begin{pmatrix} a_1\\a_2\\a_3 \end{pmatrix}$ и
$\vec{b} = \begin{pmatrix} b_1\\b_2\\b_3 \end{pmatrix}$.\\
Тогда определяется их перекрестное произведение $\vec{a} \times \vec{b}$
$\vec{a} \times \vec{b} = (a_2b_3-a_3b_2)i + (a_3b_1-a_1b_3)j+(a_1b_2-a_2b_1)k$

Пример 2:

Это получается с помощью следующего кода LaTeX:

 % детерминантная форма
\начать{выравнивать*}
\vec{a} \times \vec{b} =\begin{vmatrix}
я & j & k \\
а_1 и а_2 и а_3\\
б_1 и б_2 и б_3
\end{vmatrix} = (a_2b_3-a_3b_2)i + (a_3b_1-a_1b_3)j+(a_1b_2-a_2b_1)k
\end{align*}

Символ большого умножения в LaTeX

Символ большого перекрестного произведения можно получить в LaTeX с помощью команды \bigtimes , предоставленной пакет mathabx . Вот пример:

 % Большой символ умножения
\documentclass{статья}
\usepackage{mathabx}
\начать{документ}
$\vec{a} \bigtimes \vec{b}$
\end{document}

Заключение

Этот учебник дает краткое описание концепции перекрестного (векторного) произведения и в то же время дает глубокие знания LaTeX; в основном, знания о том, как генерировать математику, связанную с работой с перекрестными произведениями. Чаще всего в LaTeX есть несколько способов достижения одинаковых результатов, и этот учебник научит вас самому простому и ясному методу набора перекрестных произведений.

Последние сообщения

ссылка на набор вопросов с несколькими вариантами ответов в LaTeX

Набор вопросов с несколькими вариантами ответов в LaTeX

В этом руководстве мы увидим, как написать экзамен с несколькими вариантами ответов в LaTeX, используя класс документа экзамена.

alexxlab

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *