Векторы примеры решения задач, формулы и онлайн калькуляторы
Содержание:
Вектора применяются во многих науках, таких как: математика, физика, геометрия и многих других прикладных науках. На практике, они позволяют не делать лишних операций и сократить время выполнения задач. Поэтому, будущим специалистам очень важно понять теорию векторов и научиться решать задачи с ними.
Перед изучением примеров решения задач советуем изучить теоретический материал по векторам, прочитать все определения и свойства. Список тем находится в правом меню.
Координаты вектора
Теоретический материал по теме — координаты вектора.
Пример
Запись $\overline{a}=(5 ;-2)$ означает, что вектор $\overline{a}$ имеет следующие координаты: абсцисса равна 5, ордината равна -2.
Слишком сложно?
Примеры решения задач с векторами не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Теоретический материал по теме — разложение вектора по ортам. Пример Задание. Зная разложения вектора $\overline{a}$
по базисной системе векторов: $\overline{a}=3 \overline{i}-\overline{k}$, записать координаты этого вектора в пространстве. Решение. Коэффициенты при ортах и есть координатами вектора, поэтому из того, что $\overline{a}=3 \overline{i}-0 \cdot \overline{j}-\overline{k}$,
получаем, что $\overline{a}=(3 ; 0 ;-1)$ Пример Задание. Вектор $\overline{a}$ задан
своими координатами: $\overline{a}=(2 ;-1 ; 5)$. Записать разложение данного вектора по ортам осей координат. Решение. Координаты вектора — это коэффициенты при ортах координатных осей в разложении вектора
по базисной системе векторов, поэтому искомое разложение: $\overline{a}=2 \overline{i}-\overline{j}+5 \overline{k}$ Теоретический материал по теме — скалярное произведение векторов. Пример Задание. Найти скалярное произведение векторов $\overline{a}=(3 ;-1)$ и
$\overline{b}=(-2 ; 7)$ Решение.
Разложение вектора по ортам координатных осей
Скалярное произведение векторов
 {\circ}=6 \cdot \frac{1}{2}=3$
{\circ}=6 \cdot \frac{1}{2}=3$
$\overline{a} \overline{b}=3 \cdot(-2)+(-1) \cdot 7=-6-7=-13$
Векторное произведение векторов
Теоретический материал по теме — векторное произведение векторов.
Пример
Задание. Найти векторное произведение векторов $\overline{a}=(6 ; 7 ; 10)$ и $\overline{b}=(8 ; 5 ; 9)$
Решение. Составляем определитель и вычисляем его:
$\overline{a} \times \overline{b}=\left| \begin{array}{ccc}{\overline{i}} & {\overline{j}} & {\overline{k}} \\ {6} & {7} & {10} \\ {8} & {5} & {9}\end{array}\right|=\overline{i} \left| \begin{array}{cc}{7} & {10} \\ {5} & {9}\end{array}\right|-\overline{j} \left| \begin{array}{cc}{6} & {10} \\ {8} & {9}\end{array}\right|+\overline{k} \left| \begin{array}{cc}{6} & {7} \\ {8} & {5}\end{array}\right|=$
$=\overline{i}(7 \cdot 9-5 \cdot 10)-\overline{j}(6 \cdot 9-8 \cdot 10)+\overline{k}(6 \cdot 5-8 \cdot 7)=$
$=13 \overline{i}+26 \overline{j}-26 \overline{k}=(13 ; 26 ;-26)$
Смешанное произведение векторов
Теоретический материал по теме — смешанное произведение векторов.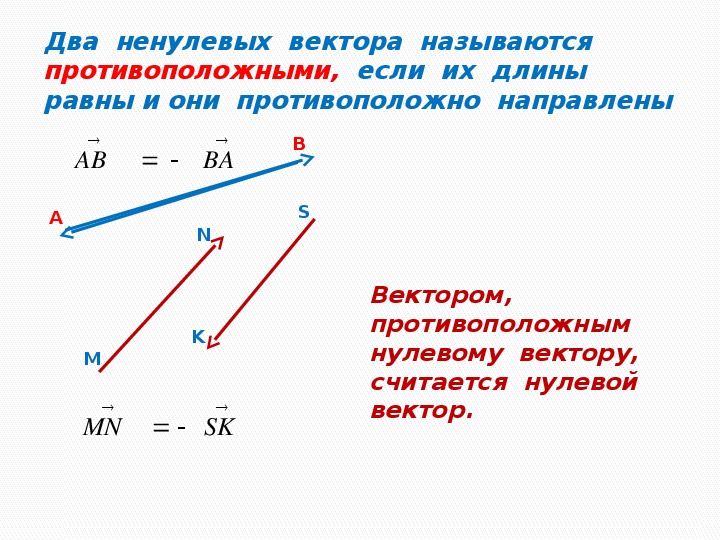
Пример
Задание. Вычислить объем пирамиды, построенной на векторах $\overline{a}=(2 ; 3 ; 5)$, $\overline{b}=(1 ; 4 ; 4)$, $\overline{c}=(3 ; 5 ; 7)$
Решение. Найдем смешанное произведение заданных векторов, для это составим определитель, по строкам которого запишем координаты векторов $\overline{a}$, $\overline{b}$ и $\overline{c}$:
$(\overline{a}, \overline{b}, \overline{c})=\left| \begin{array}{lll}{2} & {3} & {5} \\ {1} & {4} & {4} \\ {3} & {5} & {7}\end{array}\right|=2 \cdot 4 \cdot 7+1 \cdot 5 \cdot 5+3 \cdot 4 \cdot 3-$
$-3 \cdot 4 \cdot 5-5 \cdot 4 \cdot 2-1 \cdot 3 \cdot 7=-4$
$$V_{пир}=\frac{1}{6}|(\overline{a}, \overline{b}, \overline{c})|=\frac{1}{6} \cdot 4=\frac{2}{3}$$
Читать первую тему — операции над векторами, раздела векторы.
Вектор: определение и основные понятия.
Определение вектора
Определение. Вектор — это направленный отрезок, то есть отрезок, имеющий длину и определенное направление.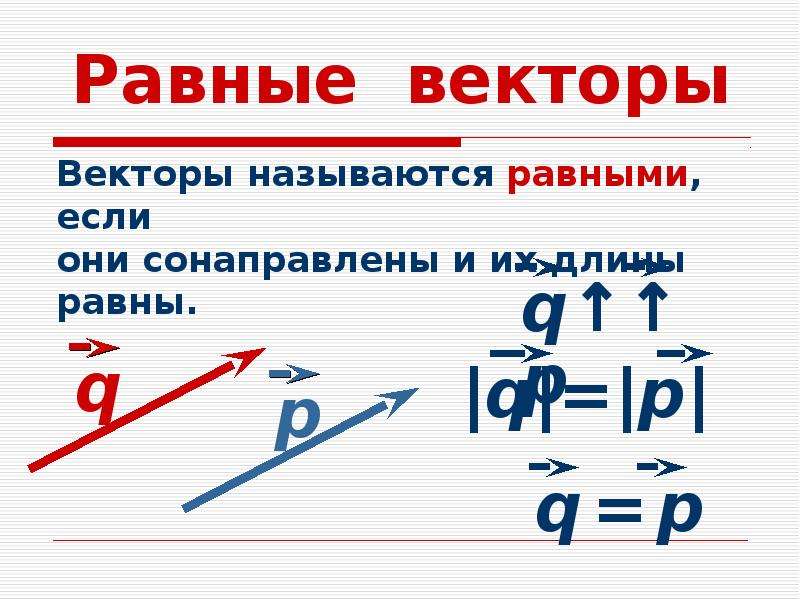 Графически вектора изображаются в виде направленных отрезков прямой определенной длины. (рис.1)
Графически вектора изображаются в виде направленных отрезков прямой определенной длины. (рис.1)
| рис. 1 |
Обозначение вектора
Вектор началом которого есть точка А, а концом — точка В, обозначается AB (рис.1). Также вектора обозначают одной маленькой буквой, например a.
Длина вектора
Для обозначения длины вектора используются две вертикальные линии слева и справа |AB|.
Нулевой вектор
Определение. Нулевым вектором называется вектор, у которого начальная и конечная точка совпадают.
Нулевой вектор обычно обозначается как 0.
Длина нулевого вектора равна нулю.
Коллинеарные вектора
| рис. 2 |
Сонаправленные вектора
Определение. Два коллинеарных вектора a и b называются сонаправленными векторами, если их направления совпадают: a↑↑b (рис.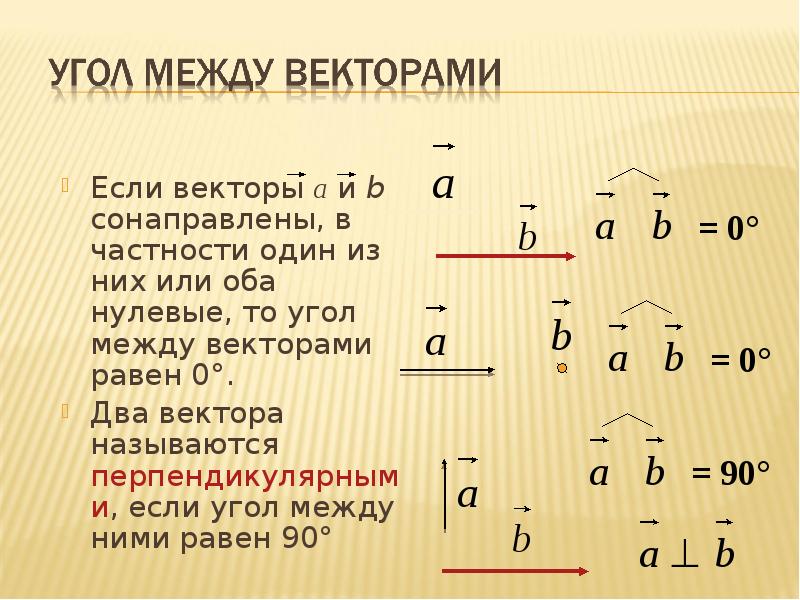 3).
3).
| рис. 3 |
Противоположно направленные вектора
Определение. Два коллинеарных вектора a и b называются
| рис. 4 |
Компланарные вектора
Определение. Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами. (рис. 5).| рис. 5 |
Всегда возможно найти плоскости параллельную двум произвольным векторам, по-этому любые два вектора всегда компланарные.
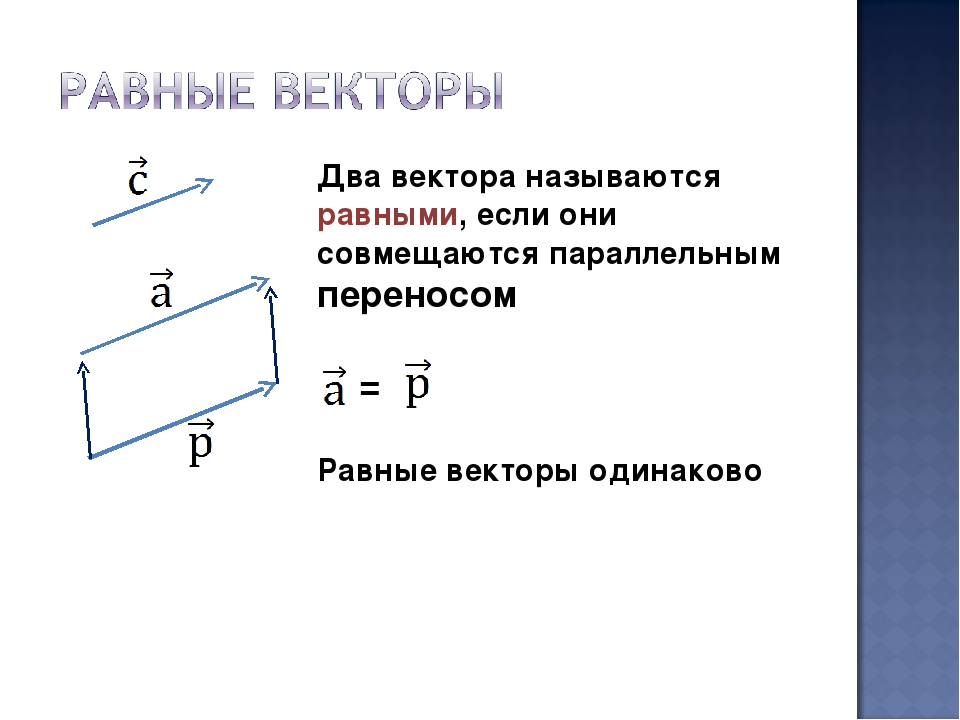
Равные вектора
Определение. Вектора a и b называются равными, если они лежат на одной или параллельных прямых, их направления совпадают, а длины равны (рис. 6).
| рис. 6 |
То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:
a = b, если a↑↑b и |a| = |b|.
Единичный вектор
Определение. Единичным вектором или ортом — называется вектор, длина которого равна единице.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Векторы. Действия с векторами
Векторы. Действия с векторами. В этой статье мы поговорим о том, что такое вектор, как находить его длину, и как умножать вектор на число, а также как находить сумму, разность и скалярное произведение двух векторов.
Как обычно, немного самой необходимой теории.
Вектор — это направленный отрезок, то есть такой отрезок, у которого есть начало и конец:
Здесь точка А — начало вектора, а точка В — его конец.
У вектора есть два параметра: его длина и направление.
Длина вектора — это длина отрезка, соединяющего начало и конец вектора. Длина вектора обозначается
Два вектора называются равными, если они имеют одинаковую длину и сонаправлены.
Два вектора называются сонаправленными, если они лежат на параллельных прямых и направлены в одну сторону: вектора и сонаправлены:
Два вектора называются противоположно направленными, если они лежат на параллельных прямых и направлены в противоположные стороны: вектора и , а также и направлены в противоположные стороны:
Вектора, лежащие на параллельных прямых называются коллинеарными: вектора , и — коллинеарны.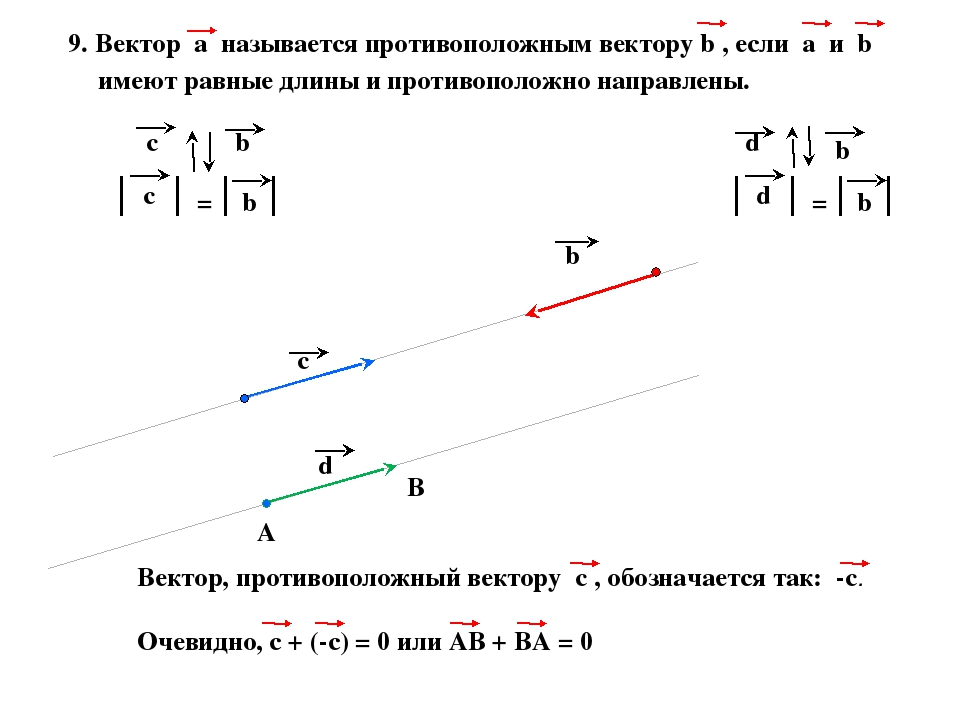
Произведением вектора на число называется вектор, сонаправленный вектору , если , и направленный в противоположную сторону, если , и длина которого равна длине вектора , умноженной на :
=k:
Чтобы сложить два вектора и , нужно начало вектора соединить с концом вектора . Вектор суммы соединяет начало вектора с концом вектора :
Это правило сложения векторов называется правилом треугольника.
Чтобы сложить два вектора по правилу параллелограмма, нужно отложить вектора от одной точки и достроить до параллелограмма. Вектор суммы соединяет точку начала векторов с противоположным углом параллелограмма:
Разность двух векторов определяется через сумму: разностью векторов и называется такой вектор , который в сумме с вектором даст вектор :
:
Отсюда вытекает правило нахождения разности двух векторов: чтобы из вектора вычесть вектор , нужно отложить эти вектора от одной точки. Вектор разности соединяет конец вектора с концом вектора ( то есть конец вычитаемого с концом уменьшаемого):
Чтобы найти угол между вектором и вектором , нужно отложить эти вектора от одной точки.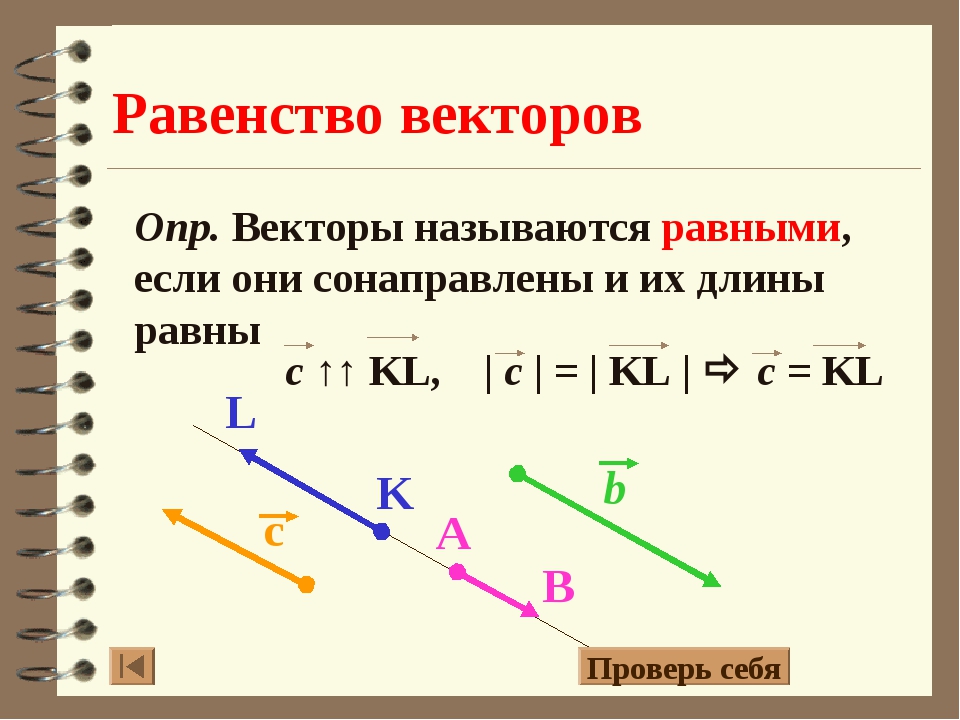
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними:
Предлагаю вам решить задачи из Открытого банка заданий для подготовки к ЕГЭ по математике, а затем сверить све решение с ВИДЕОУРОКАМИ:
1. Задание 4 (№ 27709)
Две стороны прямоугольника ABCD равны 6 и 8. Найдите длину разности векторов и .
2. Задание 4 (№ 27710)
Две стороны прямоугольника ABCD равны 6 и 8. Найдите скалярное произведение векторов и . (чертеж из предыдущей задачи).
3. Задание 4 (№ 27711)
Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке O. Найдите длину суммы векторов и .
4. Задание 4 (№ 27712)
Две стороны прямоугольника ABCD равны 6 и 8. Диагонали пересекаются в точке O. Найдите длину разности векторов и . (чертеж из предыдущей задачи).
Найдите длину разности векторов и . (чертеж из предыдущей задачи).
5. Задание 4 (№ 27713)
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора .
6. Задание 4 (№ 27714)
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора + .
7.Задание 4 (№ 27715)
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора — .(чертеж из предыдущей задачи).
8.Задание 4 (№ 27716)
Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора — .
9. Задание 4 (№ 27717)
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора + .
10. Задание 4 (№ 27718)
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора — . (чертеж из предыдущей задачи).
(чертеж из предыдущей задачи).
11.Задание 4 (№ 27719)
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите скалярное произведение векторов и .(чертеж из предыдущей задачи).
12. Задание 4 (№ 27720)
Стороны правильного треугольника ABC равны Найдите длину вектора +.
13. Задание 4 (№ 27721)
Стороны правильного треугольника ABC равны 3. Найдите длину вектора -.(чертеж из предыдущей задачи).
14. Задание 4 (№ 27722)
Стороны правильного треугольника ABC равны 3. Найдите скалярное произведение векторов и . (чертеж из предыдущей задачи).
Вероятно, Ваш браузер не поддерживается.
 Чтобы использовать тренажёр «Час ЕГЭ», попробуйте скачать
Чтобы использовать тренажёр «Час ЕГЭ», попробуйте скачатьFirefox
И.В. Фельдман, репетитор по математике.
| 795 | Векторы и образуют угол , зная, что =3, =4, вычислить: | |
| 795.1 | ; | |
| 795.2 | ; | |
| 795.3 | ; | |
| 795.4 | ; | |
795. 5 5 | ; | |
| 795.6 | ; | |
| 795.7 | ; | |
| 796 | Векторы и взаимно перпендикулярны; вектор образует с ними углы, равные ; зная, что =3, =5, =8, вычислить: | |
| 796.1 | ; | |
| 796.2 | ; | |
| 796.3 | . | |
| 797 | Доказать
справедливость тождества и
выяснить его геометрический смысл.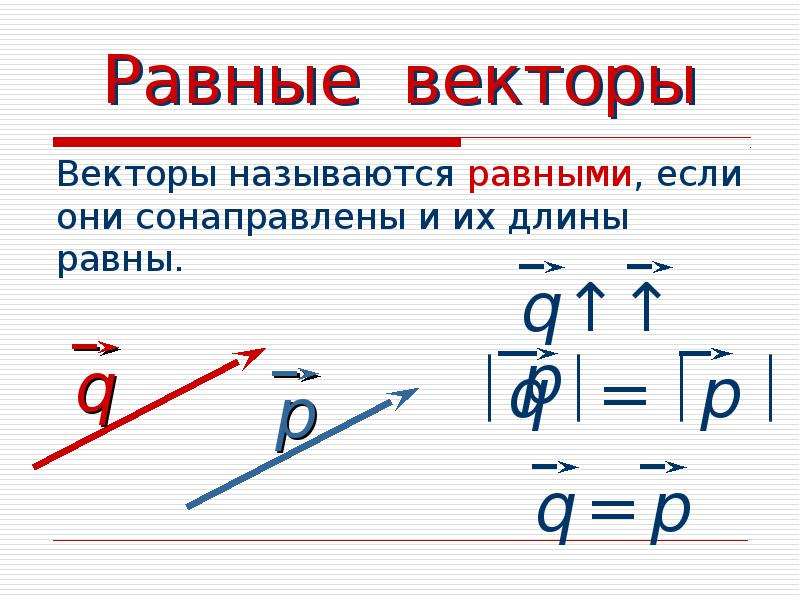 | |
| 798 | Доказать, что ; в каких случаях здесь может иметь место знак равенства? | |
| 799 | Считая, что каждый из векторов , , отличен от нуля, установить, при каком их взаимном расположении справедливо равенство . | |
| 800 | Даны единичные вектторы , , , удовлетворяющие условию . Вычислить . | |
| 801 | Даны векторы , , , удовлетворяющие условию . Зная, что =3, =1, =4, вычислить . | |
| 802 | Векторы , , попарно образуют друг с другом углы,
каждый из которых равен 600. Зная, что =2, =2, =6, определить
модуль вектора . Зная, что =2, =2, =6, определить
модуль вектора . | |
| 803 | Дано, что =3, =5. Определить, при каком значении векторы , будут взаимно перпендикулярны. | |
| 804 | Какому условию должны удовлетворять векторы и , чтобы вектор был перпендикулярен к вектору . | |
| 805 | Доказать, что вектор перпендикулярен к вектору . | |
| 806 | Доказать, что вектор перпендикулярен к вектору . | |
| 807 | Даны векторы и ,
совпадающие со сторонами
треугольника АВС. Найти разложение вектора,
приложенного к вершине В этого треугольника и
совпадающего с его высотой BD по базису , . Найти разложение вектора,
приложенного к вершине В этого треугольника и
совпадающего с его высотой BD по базису , . | |
| 808 | Векторы и образуют угол ; зная, что , , вычислить угол между векторами и . | |
| 809 | Вычислить тупой угол, образованный медианами, проведенными из вершин острых углов равноберденного прямоугольного треугольника. | |
| 810 | Определить геометрическое место концов переменного вектора , если его начало находится в данной точке А и вектор удовлетворяет условию , где — данный вектор и — данное число. | |
| 811 | Определить
геометрическое место концов переменного вектора
, если его начало находится в данной
точке А и вектор удовлетворяет условиям , , где и — данные
неколлинеарные векторы и , — данные числа.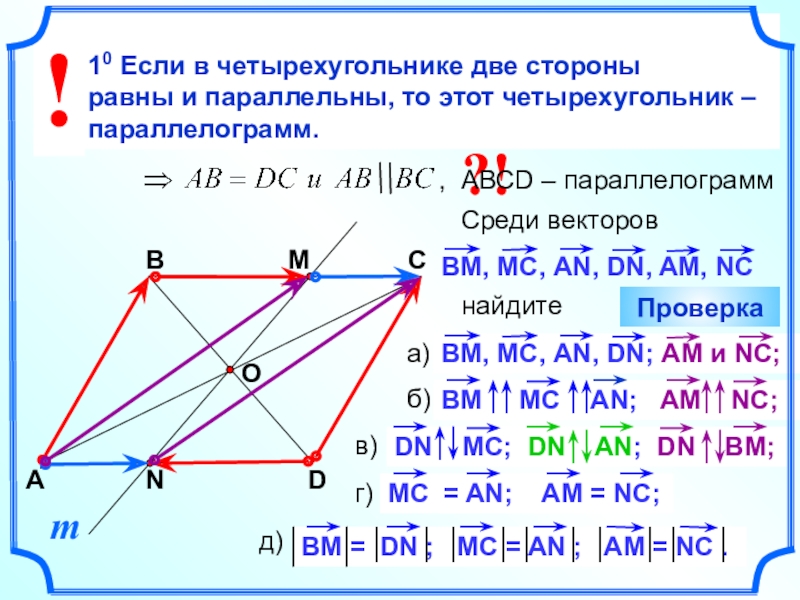 | |
| 812 | Даны векторы ={4; -2; -4}, ={6; -3; 2}. Вычислить: | |
| 812.1 | ; | |
| 812.2 | ; | |
| 812.3 | ; | |
| 812.4 | ; | |
| 812.5 | ; | |
| 812.6 | .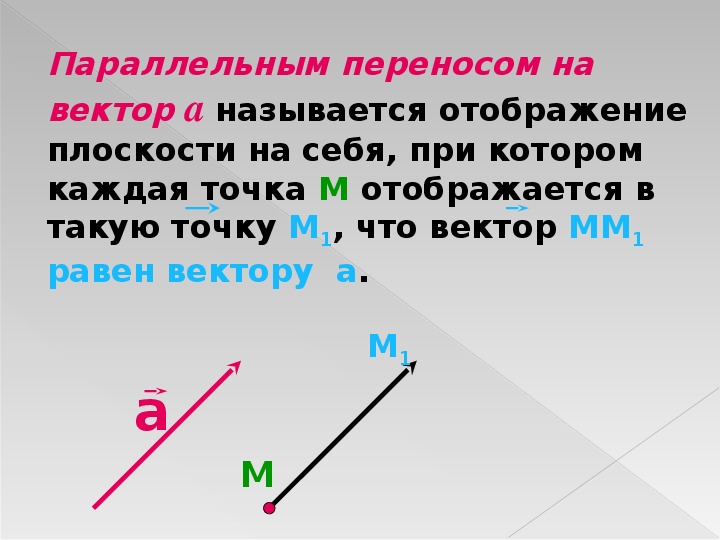 | |
| 813 | Вычислить, какую работу произведет сила f={3; -5; 2}, когда ее точка приложения перемещается из начала в конец вектора ={2; -5; -7}. | |
| 814 | Даны точки A(-1; 3; -7), B(2; -1; 5), C(0; 1; -5). Вычислить: | |
| 814.1 | ; | |
| 814.2 | ; | |
| 814.3 | ; | |
814. 5 5 | Найти координаты векторов и . | |
| 815 | Вычислить, какую работу производит сила f={3; -2; -5}, когда ее точка приложения, двигаясь прямолинейно, перемещается из положения A(2; -3; 5} в положение B(3; -2; -1). | |
| 816 | Даны силы ={3; -4; 2}, ={2; 3; -5}, ={-3; -2; 4}, приложенные к одной точке. Вычислить, какую работу производит равнодействующая этих сил, когда ее точка приложения, двигаясь прямолинейно, перемещается из положения M1(5; 3; -7) в положение M2(4; -1; -4). | |
| 817 | Даны вершины
четырехугольника A(1; -2; 2), B(1; 4; 0), C(-4; 1; 1), D(-5; -5; 3). Доказать, что его диагонали AC и BD взаимно
перпендикулярны. Доказать, что его диагонали AC и BD взаимно
перпендикулярны. | |
| 818 | Определить, при каком значении векторы и взаимно перпендикулярны. | |
| 819 | Вычислить косинус угла, образованного векторами ={2; -4; 4} и ={-3; 2; -6}. | |
| 820 | Даны вершины треугольника A(-1; -2; 4), B(-4; -2; 0), C(3; -2; 1). Определить его внутренний угол при вершине В. | |
| 821 | Даны вершины
треугольника A(3; 2; -3), B(5; 1; -1), C(1; -2; 1). Определить
его внешний угол при вершине А. | |
| 822 | Вычислив внутренние углы треугольника с вершинами A(1; 2; 1), B(3; -1; 7), C(7; 4; -2), убедиться, что этот треугольник равнобедренный. | |
| 823 | Вектор , коллинеарный вектору ={6; -8; -7,5}, образует острый угол с осью Oz. Зная, что =50, найти его координаты. | |
| 824 | Найти вектор , коллинеарный вектору ={2; 1; -1} и удовлетворяющий условию . | |
| 825 | Вектор , перпендикулярный
к векторам и ,
образует с осью Oy тупой угол.
Найти его координаты, зная, что . | |
| 826 | Найти вектор , зная, что он перпендикулярен к ={2; 3; -1}, ={1; -2; 3} и удовлетворяет условию . | |
| 827 | Даны векторы ={3; -1; 5}, ={1; 2; -3}. Найти вектор при условии, что он перпендикулярен к оси Oz и удовлетворяет условиям , . | |
| 828 | Даны векторы , и . Найти вектор , удовлетворяющий условиям , , . | |
| 829 | Найти проекцию вектора ={4; -3; 2} на ось, составляющую с координатными осями равные острые углы. | |
| 830 | Найти проекцию
вектора ={; -3; -5} на ось, составляющую с координатными
осями Ox, Oz углы ,
, а
с осью Oy – острый угол . | |
| 831 | Даны точки A(3; -4; -2), B(2; 5; -2). Найти проекцию вектора на ось, составляющую с координатными осями Ox, Oy углы , , а с осью Oz – тупой угол . | |
| 832 | Вычислить проекцию вектора ={5; 2; 5} на ось вектора ={2; -1; 2}. | |
| 833 | Даны векторы , , . Вычислить . | |
| 834 | Даны векторы ={1; -3; 4}, ={3; -4; 2} и ={-1; 1; 4}. Вычислить . | |
| 835 | Даны векторы , , . Вычислить . Вычислить . | |
| 836 | Сила, определяемая вектором ={1; -8; -7}, разложена по трем направлениям, одно из которых задано вектором . Найти составляющую силы в направлении вектора . | |
| 837 | Даны точки M(-5; 7; -6), N(7; -9; 9). Вычислить проекцию вектора ={1; -3; 1} на ось вектора . | |
| 838 | Даны точки A(-2; 3; -4), B(3; 2; 5), C(1; -1; 2), D(3; 2; -4). Вычислить . |
Урок 6. повторительно-обобщающий урок по теме «векторы» — Геометрия — 9 класс
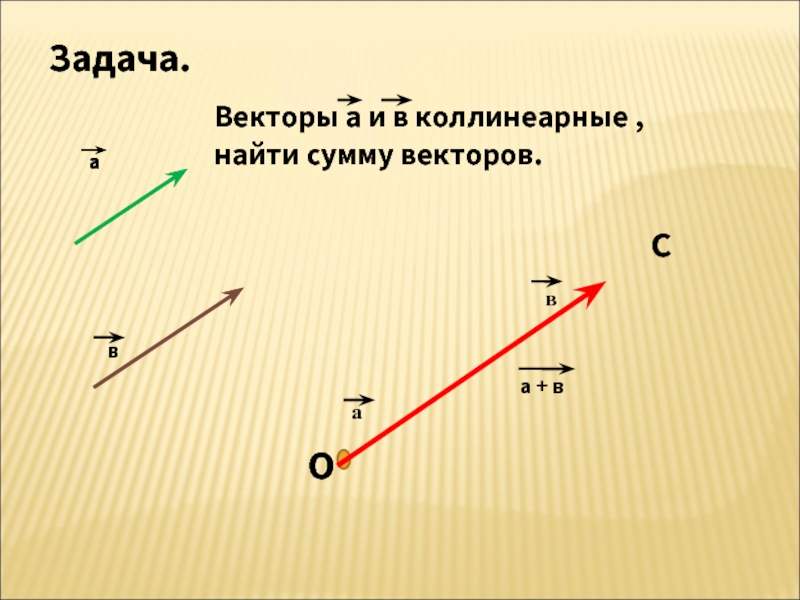
Коллинеарные векторы
Коллинеарные векторы – векторы, лежащие на одной прямой или на параллельных прямых.
 Нулевой вектор считается коллинеарным любому вектору.
Нулевой вектор считается коллинеарным любому вектору.| Виды коллинеарных векторов | |
| Сонаправленные a ⃗ ↑↑ b ⃗ | Противоположно направленные a ⃗ ↑↓ b ⃗ |
| Равные a ⃗ = b ⃗ ↔ a ⃗ ↑↑ b ⃗, |a ⃗| = |b ⃗| | Противоположные a ⃗= — b ⃗↔ a ⃗ ↑↓ b ⃗, |a ⃗| = |b ⃗| |
Сложение векторов.
Для любых трех точек A, B и C справедливо равенство AC ⃗ = AB ⃗ + BC ⃗
Свойства сложения векторов:
Для любых векторов a ⃗, b ⃗ и c ⃗
1) a ⃗+ b ⃗ = b ⃗+ a ⃗ (переместительный закон)
2) (a ⃗+ b ⃗) + c ⃗ = a ⃗+ (b ⃗ + c ⃗) (сочетательный закон)
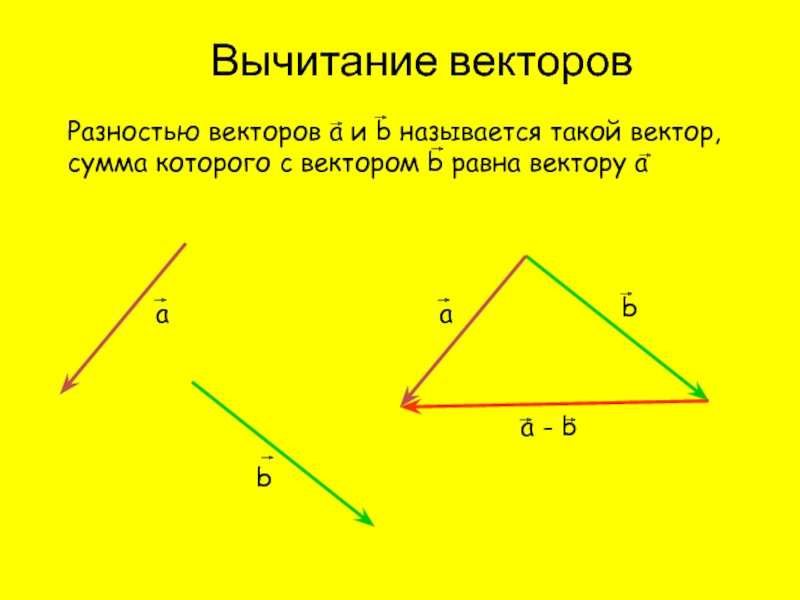
Вычитание векторов.
Разностью векторов a ⃗ и b ⃗ называется такой вектор c ⃗, сумма которого с вектором b ⃗ равна вектору a ⃗.
Для любых векторов a ⃗и b ⃗ справедливо равенство
a ⃗- b ⃗ = a ⃗+ (- b ⃗)
Умножение вектора на число.
Произведение ненулевого вектора a ⃗ на число k – это вектор b ⃗, сонаправленный с вектором a ⃗, если k>0, и противоположно направленный с вектором a ⃗, если k<0, причём |b ⃗| = |k||a ⃗|.
Свойства умножения вектора на число
Для любых векторов a ⃗, b ⃗ и чисел k, l выполняются равенства:
1) (kl)a ⃗ = k(la ⃗) (сочетательный закон)
2) (k + l)a ⃗ = ka ⃗ + la ⃗ (первый распределительный закон)
3) k(a ⃗ + b ⃗) = ka ⃗ + kb ⃗ (второй распределительный закон)
Понятие вектора.
 Равенство векторов — презентация онлайн
Равенство векторов — презентация онлайн2. 1.1. Понятие вектора. Равенство векторов
Нам известны два вида величин . Например, длина, площадь,объем, масса и т.д. полностью определяются заданием своих
численных величин. Такие величины называются скалярными
величинами или просто скалярами.
А многие физические величины, например, сила, перемещение
материальной точки, скорость и т.д. характеризуются не только
своим числовым значением, но и направлением в пространстве.
Такие физические величины называются векторными величинами
или просто векторами. Например, если на какое-либо тело
воздействовать определенной силой, то эта сила изображается
«направленным отрезком». Здесь длина отрезка соответствует
численной величине силы, а
стрелка указывает на направление воздействия этой силы.
F
3. Геометрические векторы рассматриваются просто как «направленные отрезки».Так, например, всякий отрезок имеет два конца. Назовем
один из этих концов начальной точкой, илиначалом, а другой концом и будем считать, что отрезок
направлен от начала к концу
А
В
А
В
А
В
Любой направленный отрезок называется вектором.

Так же существует понятие Нулевой вектор.
Нулевым вектором называется вектор, у которого начальная и
конечная точка совпадают.
Нулевой вектор обычно обозначается как 0.
Длина нулевого вектора равна нулю.
Нулевой вектор определяет тождественное движение пространства,
при котором каждая точка пространства переходит в себя.
4. 1.2. Равенство векторов Если 2 вектора лежат на одной прямой или на параллельных прямых, то такие векторы называются
коллинеарными. Коллинеарностьвекторов а и b запишут так a||b.
Если векторы а и b лежат на перпендикулярных прямых, то их
называют перпендикулярными (ортогональными) векторами и
записывают a_|_b.
5. Если коллинеарные векторы имеют одинаковые направления, то их называют сонаправленными векторами. Сонаправленность векторов а и
b записывают так: a b. Если векторы с и d коллинеарны и имеютразные направления, то их называют противоположно
направленными и записывают так: c d.

Векторы называются равными, если они сонаправлены и их модули
равны. Иными словами, если a
b и |a|=|b|, то векторы a и b
называются равными, т.е. а=b.
2.Сложение и вычитание векторов
2.1. Сложение векторов
B
A
C
7. 2.2. Свойства сложения векторов Сложение векторных величин производится по правилу параллелограмма: Cумма двух векторов a и b,
приведенных к общему началу, естьтретий вектор c , длина которого равна длине параллелограмма,
построенного на векторах a и b , а направлен он от точки A к точке В.
а+ b =c
Для нахождения суммы нескольких векторов называется
правилом многоугольника или правилом
последовательгого складывания векторов.
Разностью векторов а и b называется вектор, который в сумме с вектором
b равен вектору а. Разность векторов а и b обозначается так: а – b.
От некоторой точки О откладываем векторы ОА=а, ОВ=b. Тогда вектор
ВА равен разности a – b. Так как ОА=ОВ+ВА, то ВА=ОА-ОВ= а – b.
Произведением вектора а≠0 на число К называется вектор, модуль
которого равен числу |K| · |a| и сонаправлен с вектором а при К >0,
противоположно направлен с вектором а при К
К на вектор а записывают так: К · а.
Если К=0, то 0 · а = 0.
(a , b)
Скалярным произведением двух векторов называется число, равное
произведению модулей этих векторов на косинус угла угла между ними,
т.е. скалярное произведение векторов равно числу |a|·|b| · cos(a , b).
Скалярное произведение равных векторов называется скалярным
квадратом этого вектора и обозначается через а². По формуле 1
имеем а² = а · а = |a| · |a| · cos0° = | а²|, т.е. Выполняется равенство
а² = |a|²
Теорема. Если ненулевые векторы а и b не коллинеарны, то для любого вектора с
найдутся числа х и у такие, что выполняется равенство
с = ха + уb,
Если на плоскости выбраны два неколинеарных вектора, то они
называются базисными векторами плоскости. Любые два
неколлинеарных вектора можно принять в качестве базисных
векторов и любой вектор этой плоскости однозначно разлагается по
этим базисным векторам .
 В доказанной теореме а и b – базисные
В доказанной теореме а и b – базисныевекторы. А действительные числа х и у называются координатами
вектора с в базисе а,b.
2. При сложении векторов складываются их
соответствующие
координаты: если а=(х;у), b=(u;v), то а+b=(x+u; y+v).
a+b=(xi+yj)+(ui+vj)=(x+u)i + (y + v)j.
3. При умножении вектора на число его координаты
умножаются на это же число, если а=(х; у) и λ- число,
то λ · а =(λ · х; λ · у).
Следствие. Координаты разности векторов равны
разности соответствующих координат этих векторов :
если а= (х; у), b= (u; v), то a – b = (x-u; y-v).
6.2. Координатный вид коллинеарности и перпенди-кулярности
векторов. Определение угла между векторами
Если векторы а=(х1;у1) и b=(х2;у2) взаимно перпендикулярны, то (a , b) = 90°.
Поэтому их скалярное произведение равно нулю, т.е. a · b=|a| · |b| · cos90° = 0.
Тогда имеем: х1х2+у1у2=0.
Это и есть условие перпендикулярности ненулевых векторов.
Соответственно что соответствующие координаты коллинеарных векторов
пропорциональны.

7.1. Уравнение прямой. Направляющий вектор и
вектор нормали прямой
Уравнение прямой можно задать различными способами. Например, в
8
классе мы определили прямую как серединный перпендикуляр
некоторого отрезка. Теперь определим уравнение прямой с помощью
векторов.
Пусть дана точка Мₒ (хₒ ;уₒ ) и вектор р = (α;β). Тогда
через точку Мₒ параллельно вектору р проходит одна и только одна
прямая l. Точка Мₒ называется начальной точкой прямой l, а вектор рнаправляющим вектором этой прямой. Если М (х;у) является
произвольной точкой прямой l, то МₒМ || р. Здесь направляющий
вектор р = (α;β)не параллелен осям координат, т.е. α≠0, β≠0. Используя
условие коллинеарности векторов, р и МₒМ = (х-хₒ ;у- уₒ ), получим
уравнение:
х-хₒ
α
у-уₒ
β
2.4 Произведения векторов | University Physics Volume 1
Вектор можно умножить на другой вектор, но нельзя разделить на другой вектор. Есть два вида произведений векторов, широко используемых в физике и технике.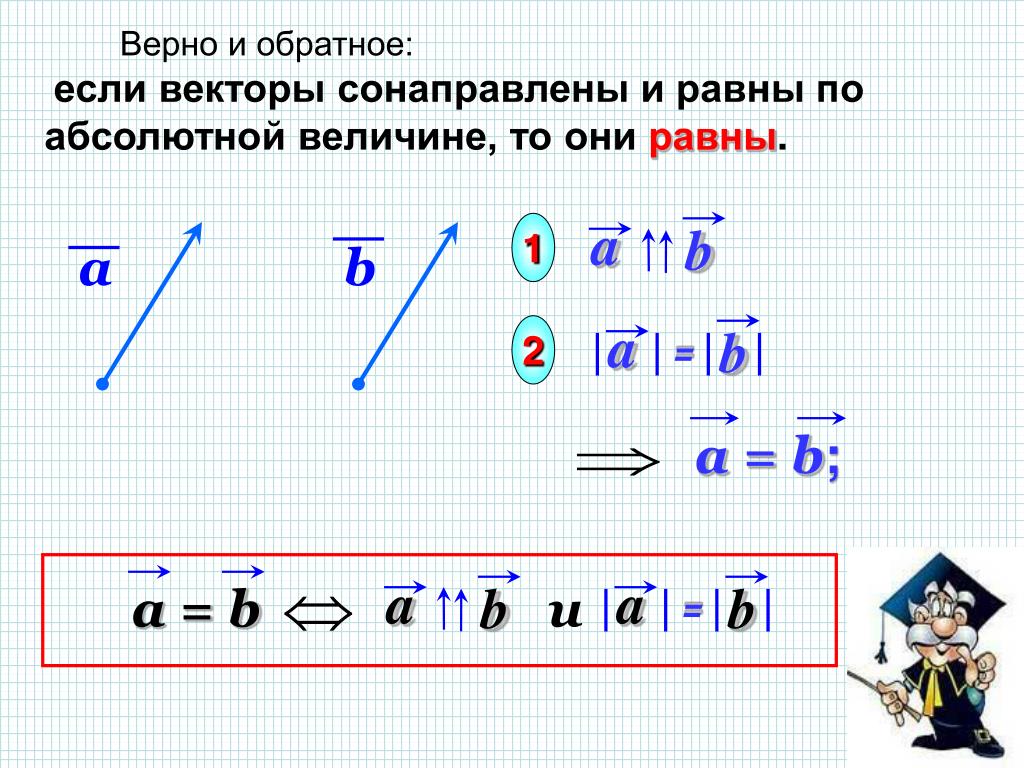 Один из видов умножения — это скалярное умножение двух векторов . В результате скалярного произведения двух векторов получается число (скаляр), как указывает его название. Скалярные произведения используются для определения отношений между работой и энергией. Например, работа, которую сила (вектор) выполняет с объектом, вызывая его смещение (вектор), определяется как скалярное произведение вектора силы на вектор смещения.Совершенно другой вид умножения — это векторное умножение векторов . Получение векторного произведения двух векторов возвращает в результате вектор, как следует из его названия. Векторные произведения используются для определения других производных векторных величин. Например, при описании вращений векторная величина, называемая крутящим моментом , определяется как векторное произведение приложенной силы (вектора) и ее расстояния от точки поворота до силы (вектор). Важно различать эти два вида векторных умножений, потому что скалярное произведение — это скалярная величина, а векторное произведение — это векторная величина.
Один из видов умножения — это скалярное умножение двух векторов . В результате скалярного произведения двух векторов получается число (скаляр), как указывает его название. Скалярные произведения используются для определения отношений между работой и энергией. Например, работа, которую сила (вектор) выполняет с объектом, вызывая его смещение (вектор), определяется как скалярное произведение вектора силы на вектор смещения.Совершенно другой вид умножения — это векторное умножение векторов . Получение векторного произведения двух векторов возвращает в результате вектор, как следует из его названия. Векторные произведения используются для определения других производных векторных величин. Например, при описании вращений векторная величина, называемая крутящим моментом , определяется как векторное произведение приложенной силы (вектора) и ее расстояния от точки поворота до силы (вектор). Важно различать эти два вида векторных умножений, потому что скалярное произведение — это скалярная величина, а векторное произведение — это векторная величина.
Скалярное произведение двух векторов (скалярное произведение)
Скалярное умножение двух векторов дает скалярное произведение.
Скалярное произведение (скалярное произведение)
Скалярное произведение [латекс] \ overset {\ to} {A} · \ overset {\ to} {B} [/ latex] двух векторов [латекс] \ overset {\ to} {A} [/ latex ] и [латекс] \ overset {\ to} {B} [/ latex] — это число, определяемое уравнением
[латекс] \ overset {\ to} {A} · \ overset {\ to} {B} = AB \, \ text {cos} \, \ phi, [/ latex]
где [latex] \ phi [/ latex] — угол между векторами (показан на (Рисунок)).Скалярное произведение также называется скалярным произведением из-за точечной записи, которая его указывает.
В определении скалярного произведения направление угла [латекс] \ phi [/ latex] не имеет значения, и [латекс] \ phi [/ latex] может быть измерен от одного из двух векторов к другому, потому что [ latex] \ text {cos} \, \ phi = \ text {cos} \, (\ text {-} \ phi) = \ text {cos} \, (2 \ pi — \ phi) [/ latex].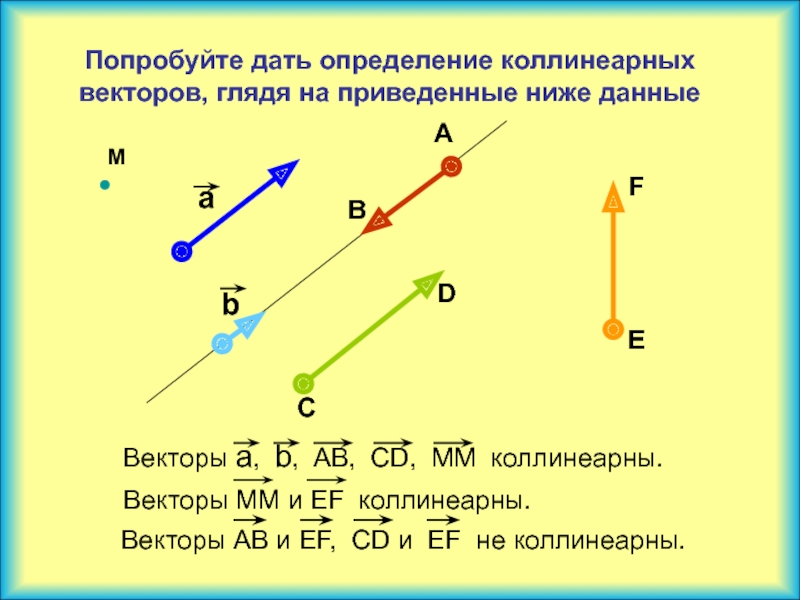 {2}.[/ латекс]
{2}.[/ латекс]
Рисунок 2.27 Скалярное произведение двух векторов. (а) Угол между двумя векторами. (b) Ортогональная проекция [латекс] {A} _ {\ perp} [/ latex] вектора [латекс] \ overset {\ to} {A} [/ latex] на направление вектора [латекс] \ overset { \ to} {B} [/ латекс]. (c) Ортогональная проекция [латекс] {B} _ {\ perp} [/ latex] вектора [латекс] \ overset {\ to} {B} [/ latex] на направление вектора [латекс] \ overset { \ to} {A} [/ латекс].
Пример
Скалярное произведение
Для векторов, показанных на (Рисунок), найдите скалярное произведение [latex] \ overset {\ to} {A} · \ overset {\ to} {F} [/ latex].
Стратегия
Из (Рисунок), величины векторов [latex] \ overset {\ to} {A} [/ latex] и [latex] \ overset {\ to} {F} [/ latex] равны A = 10,0 и F = 20,0. Угол [латекс] \ theta [/ latex] между ними является разницей: [latex] \ theta = \ phi — \ alpha = 110 \ text {°} -35 \ text {°} = 75 \ text {°} [/латекс]. Подстановка этих значений в (рисунок) дает скалярное произведение.
Подстановка этих значений в (рисунок) дает скалярное произведение.
Решение
Покажи ответ Простой расчет дает нам[латекс] \ overset {\ to} {A} · \ overset {\ to} {F} = AF \, \ text {cos} \, \ theta = (10.0) (20,0) \, \ text {cos} \, 75 \ text {°} = 51,76. [/ латекс]
Проверьте свое понимание
Для векторов, указанных на (Рисунок), найдите скалярные произведения [latex] \ overset {\ to} {A} · \ overset {\ to} {B} [/ latex] и [latex] \ overset {\ to} {F} · \ overset {\ to} {C} [/ latex].
Показать решение[латекс] \ overset {\ to} {A} · \ overset {\ to} {B} = — 57,3 [/ латекс], [латекс] \ overset {\ to} {F} · \ overset {\ to} {C} = 27,8 [/ латекс]
В декартовой системе координат скалярные произведения единичного вектора оси на другие единичные векторы осей всегда обращаются в нуль, потому что эти единичные векторы ортогональны:
[латекс] \ begin {array} {c} \ hat {i} · \ hat {j} = | \ hat {i} || \ hat {j} | \, \ text {cos} \, 90 \ text {°} = (1) (1) (0) = 0, \ hfill \\ \ hat {i} · \ hat {k} = | \ hat {i} || \ hat {k} | \, \ text {cos} \, 90 \ text {°} = (1) (1) (0) = 0, \ hfill \\ \ hat {k} · \ hat {j} = | \ hat {k} || \ hat {j} | \, \ text {cos} \, 90 \ text {°} = (1) (1) (0) = 0. {2} = 1. [/ латекс]
{2} = 1. [/ латекс]
Скалярное произведение [латекс] \ overset {\ to} {A} · \ overset {\ to} {B} [/ latex] также можно интерпретировать как произведение B с ортогональной проекцией [латекс] { A} _ {\ perp} [/ latex] вектора [latex] \ overset {\ to} {A} [/ latex] на направление вектора [latex] \ overset {\ to} {B} [/ latex] ((Рисунок) (b)) или произведение A с ортогональной проекцией [латекс] {B} _ {\ perp} [/ latex] вектора [латекс] \ overset {\ to} {B} [/ латекс] в направлении вектора [латекс] \ overset {\ to} {A} [/ latex] ((Рисунок) (c)):
[латекс] \ begin {array} {ll} \ hfill \ overset {\ to} {A} · \ overset {\ to} {B} & = AB \, \ text {cos} \, \ phi \ hfill \ \ & = B (A \, \ text {cos} \, \ phi) = B {A} _ {\ perp} \ hfill \\ & = A (B \, \ text {cos} \, \ phi) = A {B} _ {\ perp}.\ hfill \ end {array} [/ latex]
Например, в прямоугольной системе координат на плоскости скалярная компонента вектора размером x является его скалярным произведением на единичный вектор [latex] \ hat {i} [/ latex] и скаляр y -компонент вектора — это его скалярное произведение с единичным вектором [latex] \ hat {j} [/ latex]:
[латекс] \ {\ begin {array} {l} \ overset {\ to} {A} · \ hat {i} = | \ overset {\ to} {A} || \ hat {i} | \, \ text {cos} \, {\ theta} _ {A} = A \, \ text {cos} \, {\ theta} _ {A} = {A} _ {x} \\ \ overset {\ to} {A} · \ hat {j} = | \ overset {\ to} {A} || \ hat {j} | \, \ text {cos} \, (90 \ text {°} — {\ theta} _ {A}) = A \, \ text {sin} \, {\ theta} _ {A} = {A} _ {y} \ end {array}. [/ латекс]
[/ латекс]
Скалярное умножение векторов коммутативно,
[латекс] \ overset {\ to} {A} · \ overset {\ to} {B} = \ overset {\ to} {B} · \ overset {\ to} {A}, [/ latex]
и подчиняется закону о распределении доходов:
[латекс] \ overset {\ to} {A} · (\ overset {\ to} {B} + \ overset {\ to} {C}) = \ overset {\ to} {A} · \ overset {\ to} {B} + \ overset {\ to} {A} · \ overset {\ to} {C}. [/ латекс]
Мы можем использовать законы коммутативности и распределения для вывода различных соотношений для векторов, таких как выражение скалярного произведения двух векторов через их скалярные компоненты.
Проверьте свое понимание
Для вектора [латекс] \ overset {\ to} {A} = {A} _ {x} \ hat {i} + {A} _ {y} \ hat {j} + {A} _ {z} \ hat {k} [/ latex] в прямоугольной системе координат, используйте (Рисунок) — (Рисунок), чтобы показать, что [latex] \ overset {\ to} {A} · \ hat {i} = {A} _ {x } [/ латекс] [латекс] \ overset {\ to} {A} · \ hat {j} = {A} _ {y} [/ latex] и [латекс] \ overset {\ to} {A} · \ шляпа {k} = {A} _ {z} [/ latex].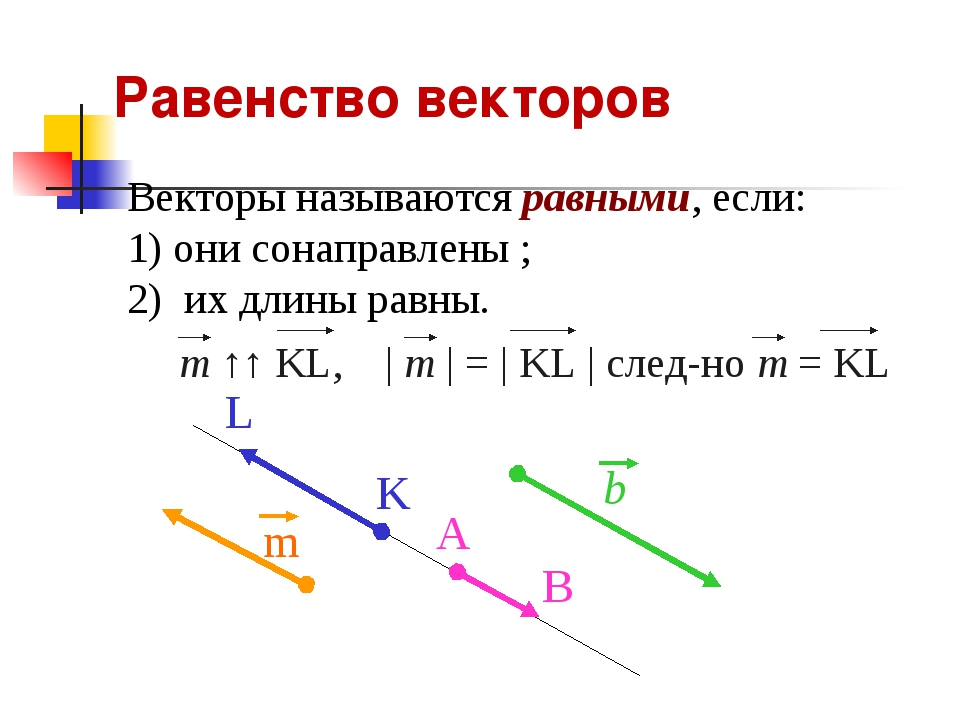
Когда векторы на (Рисунок) даны в форме их векторных компонентов,
[латекс] \ overset {\ to} {A} = {A} _ {x} \ hat {i} + {A} _ {y} \ hat {j} + {A} _ {z} \ hat { k} \, \ text {и} \, \ overset {\ to} {B} = {B} _ {x} \ hat {i} + {B} _ {y} \ hat {j} + {B} _ {z} \ hat {k}, [/ latex]
, мы можем вычислить их скалярное произведение следующим образом:
[латекс] \ begin {array} {lll} \ hfill \ overset {\ to} {A} · \ overset {\ to} {B} & = \ hfill & ({A} _ {x} \ hat {i } + {A} _ {y} \ hat {j} + {A} _ {z} \ hat {k}) · ({B} _ {x} \ hat {i} + {B} _ {y} \ hat {j} + {B} _ {z} \ hat {k}) \ hfill \\ & = \ hfill & \ enspace {A} _ {x} {B} _ {x} \ hat {i} · \ hat {i} + {A} _ {x} {B} _ {y} \ hat {i} · \ hat {j} + {A} _ {x} {B} _ {z} \ hat {i } · \ Hat {k} \ hfill \\ & & + {A} _ {y} {B} _ {x} \ hat {j} · \ hat {i} + {A} _ {y} {B} _ {y} \ hat {j} · \ hat {j} + {A} _ {y} {B} _ {z} \ hat {j} · \ hat {k} \ hfill \\ & & + {A } _ {z} {B} _ {x} \, \ hat {k} · \ hat {i} + {A} _ {z} {B} _ {y} \ hat {k} · \ hat {j } + {A} _ {z} {B} _ {z} \, \ hat {k} · \ hat {k}. \ hfill \ end {array} [/ latex]
\ hfill \ end {array} [/ latex]
Поскольку скалярные произведения двух различных единичных векторов осей дают ноль, а скалярные произведения единичных векторов сами на себя дают единицу (см. (Рисунок) и (рисунок)), в этом выражении есть только три ненулевых члена. Таким образом, скалярное произведение упрощается до
.[латекс] \ overset {\ to} {A} · \ overset {\ to} {B} = {A} _ {x} {B} _ {x} + {A} _ {y} {B} _ {y} + {A} _ {z} {B} _ {z}. [/ латекс]
Мы можем использовать (рисунок) для скалярного произведения в терминах скалярных компонентов векторов, чтобы найти угол между двумя векторами .Когда мы разделим (рисунок) на AB , мы получим уравнение для [латекса] \ text {cos} \, \ phi [/ latex], в которое подставим (рисунок):
[латекс] \ text {cos} \, \ phi = \ frac {\ overset {\ to} {A} · \ overset {\ to} {B}} {AB} = \ frac {{A} _ {x } {B} _ {x} + {A} _ {y} {B} _ {y} + {A} _ {z} {B} _ {z}} {AB}. [/ латекс]
Угол [латекс] \ phi [/ latex] между векторами [latex] \ overset {\ to} {A} [/ latex] и [latex] \ overset {\ to} {B} [/ latex] получается путем взятия обратный косинус выражения на (рисунок).
Пример
Угол между двумя силами
Три собаки тянут палку в разные стороны, как показано на (Рисунок). Первая собака тянет с силой [латекс] {\ overset {\ to} {F}} _ {1} = (10.0 \ hat {i} -20.4 \ hat {j} +2.0 \ hat {k}) \ text { N} [/ latex], вторая собака тянет с силой [latex] {\ overset {\ to} {F}} _ {2} = (- 15.0 \ hat {i} -6.2 \ hat {k}) \ text {N} [/ latex], а третья собака тянет с силой [латекс] {\ overset {\ to} {F}} _ {3} = (5.0 \ hat {i} +12.5 \ hat {j}) \ текст {N} [/ latex]. Каков угол между силами [латекс] {\ overset {\ to} {F}} _ {1} [/ latex] и [латекс] {\ overset {\ to} {F}} _ {2} [/ latex ]?
Рисунок 2.28 Три собаки играют палкой.
Стратегия
Компоненты вектора силы [латекс] {\ overset {\ to} {F}} _ {1} [/ latex] равны [латекс] {F} _ {1x} = 10.0 \, \ text {N} [/ латекс], [латекс] {F} _ {1y} = — 20,4 \, \ text {N} [/ latex] и [латекс] {F} _ {1z} = 2,0 \, \ text {N} [/ латекс], а вектор силы [латекс] {\ overset {\ to} {F}} _ {2} [/ latex] — [латекс] {F} _ {2x} = — 15. 0 \, \ text {N } [/ latex], [latex] {F} _ {2y} = 0.0 \, \ text {N} [/ latex] и [latex] {F} _ {2z} = — 6.2 \, \ text {N } [/ латекс].{-1} (- 0,439) = 116,0 \ text {°}. [/ латекс]
0 \, \ text {N } [/ latex], [latex] {F} _ {2y} = 0.0 \, \ text {N} [/ latex] и [latex] {F} _ {2z} = — 6.2 \, \ text {N } [/ латекс].{-1} (- 0,439) = 116,0 \ text {°}. [/ латекс]
Значение
Обратите внимание, что когда векторы задаются в терминах единичных векторов осей, мы можем найти угол между ними, не зная специфики географических направлений, которые представляют единичные векторы. Здесь, например, направление + x может быть на восток, а направление + y — на север. Но угол между силами в задаче будет таким же, если + x — направление на запад, а + y — направление на юг.
Проверьте свое понимание
Найдите угол между силами [латекс] {\ overset {\ to} {F}} _ {1} [/ latex] и [латекс] {\ overset {\ to} {F}} _ {3} [/ latex ] в (Рисунок).
Показать решение[латекс] 131.9 \ text {°} [/ латекс]
Пример
Работа силы
Когда сила [латекс] \ overset {\ to} {F} [/ latex] тянет объект и вызывает его смещение [латекс] \ overset {\ to} {D} [/ latex], мы говорим, что сила выполняет работу. Количество работы, совершаемой силой, — это скалярное произведение [латекс] \ overset {\ to} {F} · \ overset {\ to} {D} [/ latex].Если палка на (рис.) На мгновение сдвинется и смещается вектором [латекс] \ overset {\ to} {D} = (- 7.9 \ hat {j} -4.2 \ hat {k}) \, \ text {cm} [/ latex], сколько работы проделывает третья собака на (Рисунок)?
Количество работы, совершаемой силой, — это скалярное произведение [латекс] \ overset {\ to} {F} · \ overset {\ to} {D} [/ latex].Если палка на (рис.) На мгновение сдвинется и смещается вектором [латекс] \ overset {\ to} {D} = (- 7.9 \ hat {j} -4.2 \ hat {k}) \, \ text {cm} [/ latex], сколько работы проделывает третья собака на (Рисунок)?
Стратегия
Мы вычисляем скалярное произведение вектора смещения [latex] \ overset {\ to} {D} [/ latex] на вектор силы [latex] {\ overset {\ to} {F}} _ {3} = (5.0 \ hat {i} +12.5 \ hat {j}) \ text {N} [/ latex], который является натяжением третьей собаки. Давайте использовать [latex] {W} _ {3} [/ latex] для обозначения работы, выполняемой силой [latex] {\ overset {\ to} {F}} _ {3} [/ latex] при перемещении [латекс] \ overset {\ to} {D} [/ латекс].
Решение
Покажи ответ Расчет работы — это простое применение скалярного произведения: [латекс] \ begin {array} {cc} \ hfill {W} _ {3} & = {\ overset {\ to} {F}} _ {3} · \ overset {\ to} {D} = { F} _ {3x} {D} _ {x} + {F} _ {3y} {D} _ {y} + {F} _ {3z} {D} _ {z} \ hfill \\ & = ( 5.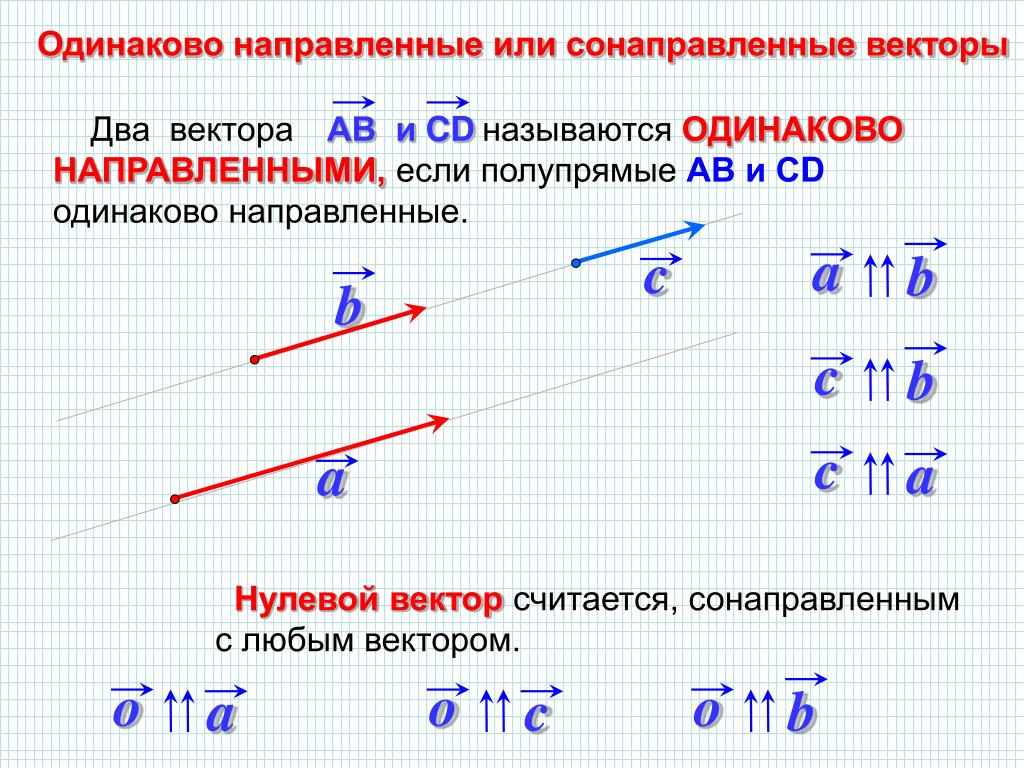 0 \, \ text {N}) (0.0 \, \ text {cm}) + (12.5 \, \ text {N}) (- 7.9 \, \ text {cm}) + (0.0 \, \ text {N }) (- 4.2 \, \ text {cm}) \ hfill \\ & = -98.7 \, \ text {N} · \ text {cm}. \ Hfill \ end {array} [/ latex]
0 \, \ text {N}) (0.0 \, \ text {cm}) + (12.5 \, \ text {N}) (- 7.9 \, \ text {cm}) + (0.0 \, \ text {N }) (- 4.2 \, \ text {cm}) \ hfill \\ & = -98.7 \, \ text {N} · \ text {cm}. \ Hfill \ end {array} [/ latex]
Значение
Единица работы в системе СИ называется джоуль [латекс] (\ text {J}) [/ latex], где 1 Дж = 1 [латекс] \ text {N} · \ text {m} [/ latex].{-2} \ text {J} [/ latex], поэтому ответ можно выразить как [latex] {W} _ {3} = — 0,9875 \, \ text {J} \ приблизительно -1,0 \, \ text { J} [/ латекс].
Проверьте свое понимание
Сколько работы выполняет первая собака и вторая собака на (Рис.) Над смещением на (Рис.)?
Показать решение[латекс] {W} _ {1} = 1,5 \, \ text {J} [/ latex], [латекс] {W} _ {2} = 0,3 \, \ text {J} [/ latex]
Векторное произведение двух векторов (перекрестное произведение)
Векторное умножение двух векторов дает векторное произведение.
Векторное произведение (перекрестное произведение)
Векторное произведение двух векторов [латекс] \ overset {\ to} {A} [/ latex] и [latex] \ overset {\ to} {B} [/ latex] обозначается [латекс] \ overset {\ to} {A} \, × \, \ overset {\ to} {B} [/ latex] и часто упоминается как перекрестное произведение . Векторное произведение — это вектор, направление которого перпендикулярно обоим векторам [latex] \ overset {\ to} {A} [/ latex] и [latex] \ overset {\ to} {B} [/ latex]. Другими словами, вектор [латекс] \ overset {\ to} {A} \, × \, \ overset {\ to} {B} [/ latex] перпендикулярен плоскости, содержащей векторы [латекс] \ overset {\ to} {A} [/ latex] и [latex] \ overset {\ to} {B} [/ latex], как показано на (Рисунок).Величина векторного произведения определяется как
Векторное произведение — это вектор, направление которого перпендикулярно обоим векторам [latex] \ overset {\ to} {A} [/ latex] и [latex] \ overset {\ to} {B} [/ latex]. Другими словами, вектор [латекс] \ overset {\ to} {A} \, × \, \ overset {\ to} {B} [/ latex] перпендикулярен плоскости, содержащей векторы [латекс] \ overset {\ to} {A} [/ latex] и [latex] \ overset {\ to} {B} [/ latex], как показано на (Рисунок).Величина векторного произведения определяется как
[латекс] | \ overset {\ to} {A} \, × \, \ overset {\ to} {B} | = \, AB \, \ text {sin} \, \ phi, [/ latex]
где угол [латекс] \ phi [/ latex] между двумя векторами измеряется от вектора [latex] \ overset {\ to} {A} [/ latex] (первый вектор в продукте) до вектора [латекс] \ overset {\ to} {B} [/ latex] (второй вектор в продукте), как показано на (Рисунок), и находится между [latex] 0 \ text {°} [/ latex] и [latex] 180 \ текст {°} [/ латекс].
Согласно (Рисунок), векторное произведение исчезает для пар векторов, которые либо параллельны [латекс] (\ phi = 0 \ text {°}) [/ latex], либо антипараллельны [латекс] (\ phi = 180 \ text { °}) [/ latex], потому что [латекс] \ text {sin} \, 0 \ text {°} = \ text {sin} \, 180 \ text {°} = 0 [/ latex].
Рисунок 2.29 Векторное произведение двух векторов нарисовано в трехмерном пространстве. (a) Векторное произведение [латекс] \ overset {\ to} {A} \, × \, \ overset {\ to} {B} [/ latex] — это вектор, перпендикулярный плоскости, который содержит векторы [латекс] \ overset {\ to} {A} [/ latex] и [latex] \ overset {\ to} {B} [/ latex]. Маленькие квадраты, нарисованные в перспективе, обозначают прямые углы между [латексом] \ overset {\ to} {A} [/ latex] и [latex] \ overset {\ to} {C} [/ latex], а также между [latex] \ overset {\ to} {B} [/ latex] и [latex] \ overset {\ to} {C} [/ latex], так что если [latex] \ overset {\ to} {A} [/ latex] и [latex ] \ overset {\ to} {B} [/ latex] лежать на полу, вектор [latex] \ overset {\ to} {C} [/ latex] направлен вертикально вверх к потолку.(b) Векторное произведение [латекс] \ overset {\ to} {B} \, × \, \ overset {\ to} {A} [/ latex] является вектором, антипараллельным вектору [латекс] \ overset {\ to } {A} \, × \, \ overset {\ to} {B} [/ latex].
На линии, перпендикулярной плоскости, которая содержит векторы [латекс] \ overset {\ to} {A} [/ latex] и [latex] \ overset {\ to} {B} [/ latex], есть два альтернативных направления — либо вверх, либо вниз, как показано на (Рисунок) — и направление векторного произведения может быть одним из них. В стандартной правой ориентации, когда угол между векторами измеряется против часовой стрелки от первого вектора, vector [latex] \ overset {\ to} {A} \, × \, \ overset {\ to} {B} [/ латекс] указывает на вверх на , как показано на (Рисунок) (а).Если мы изменим порядок умножения на обратный, так что теперь [latex] \ overset {\ to} {B} [/ latex] идет первым в продукте, затем vector [latex] \ overset {\ to} {B} \, × \, \ overset {\ to} {A} [/ latex] должен указывать на вниз на , как показано на (Рисунок) (b). Это означает, что векторы [латекс] \ overset {\ to} {A} \, × \, \ overset {\ to} {B} [/ latex] и [latex] \ overset {\ to} {B} \, × \, \ overset {\ to} {A} [/ latex] антипараллельны друг другу, а умножение векторов не коммутативно , а антикоммутативно . Антикоммутативное свойство означает, что векторное произведение меняет знак при обратном порядке умножения:
Антикоммутативное свойство означает, что векторное произведение меняет знак при обратном порядке умножения:
[латекс] \ overset {\ to} {A} \, × \, \ overset {\ to} {B} = \ text {-} \ overset {\ to} {B} \, × \, \ overset { \ to} {A}. [/ латекс]
Штопор , правый , Правило — это обычная мнемоника, используемая для определения направления векторного произведения. Как показано на (Рисунок), штопор помещается в направлении, перпендикулярном плоскости, которая содержит векторы [латекс] \ overset {\ to} {A} [/ latex] и [латекс] \ overset {\ to} {B} [/ latex], а его ручка повернута в направлении от первого вектора ко второму в изделии.Направление поперечного произведения задается движением штопора.
Рис. 2.30 Правило правой руки штопора можно использовать для определения направления перекрестного произведения [латекс] \ overset {\ to} {A} \, × \, \ overset {\ to} {B} [/ латекс]. Поместите штопор в направлении, перпендикулярном плоскости, содержащей векторы [латекс] \ overset {\ to} {A} [/ latex] и [latex] \ overset {\ to} {B} [/ latex], и поверните его в направлении от первого вектора ко второму в произведении. Направление поперечного произведения задается движением штопора. (а) Движение вверх означает, что вектор перекрестного произведения направлен вверх. (b) Движение вниз означает, что вектор перекрестного произведения направлен вниз.
Направление поперечного произведения задается движением штопора. (а) Движение вверх означает, что вектор перекрестного произведения направлен вверх. (b) Движение вниз означает, что вектор перекрестного произведения направлен вниз.
Пример
Крутящий момент силы Механическое преимущество, которое дает знакомый инструмент под названием гаечный ключ ((Рисунок)), зависит от величины F приложенной силы, ее направления по отношению к рукоятке гаечного ключа и от того, насколько далеко от гайки это усилие. применяемый.Расстояние R от гайки до точки, где приложен вектор силы [latex] \ overset {\ to} {F} [/ latex], и представлено радиальным вектором [latex] \ overset {\ to} {R } [/ латекс]. Физическая векторная величина, которая заставляет гайку поворачиваться, называется крутящий момент (обозначается [latex] \ overset {\ to} {\ tau}) [/ latex], и это векторное произведение расстояния между стержнем и силой с силой: [латекс] \ overset {\ to} {\ tau} = \ overset {\ to} {R} \, × \, \ overset {\ to} {F} [/ latex].
Чтобы ослабить ржавую гайку, к рукоятке гаечного ключа прикладывают усилие 20,00 Н под углом [латекс] \ phi = 40 \ text {°} [/ latex] и на расстоянии 0,25 м от гайки, как показано на (Рисунок) (а). Найдите величину и направление крутящего момента, прилагаемого к гайке. Какой была бы величина и направление крутящего момента, если бы сила была приложена под углом [латекс] \ phi = 45 \ text {°} [/ latex], как показано на (Рисунок) (b)? Для какого значения угла [латекс] \ фи [/ латекс] крутящий момент имеет наибольшую величину?
Рисунок 2.31 Гаечный ключ обеспечивает сцепление и механическое преимущество при приложении крутящего момента для поворота гайки. (a) Поверните против часовой стрелки, чтобы ослабить гайку. (b) Поверните по часовой стрелке, чтобы затянуть гайку.
Стратегия
Мы принимаем систему отсчета, показанную на (Рисунок), где векторы [латекс] \ overset {\ to} {R} [/ latex] и [latex] \ overset {\ to} {F} [/ latex] лежат в плоскость xy , а начало координат находится в положении гайки. Радиальное направление вдоль вектора [латекс] \ overset {\ to} {R} [/ latex] (указывающее от начала координат) является опорным направлением для измерения угла [латекс] \ phi [/ latex], потому что [латекс] \ overset {\ to} {R} [/ latex] — это первый вектор в векторном произведении [latex] \ overset {\ to} {\ tau} = \ overset {\ to} {R} \, × \, \ overset {\ to} {F} [/ латекс].Вектор [latex] \ overset {\ to} {\ tau} [/ latex] должен лежать вдоль оси z , потому что это ось, перпендикулярная плоскости xy , где оба [latex] \ overset {\ to} {R} [/ latex] и [latex] \ overset {\ to} {F} [/ latex] лгут. Чтобы вычислить величину [латекс] \ тау [/ латекс], мы используем (рисунок). Чтобы найти направление [latex] \ overset {\ to} {\ tau} [/ latex], мы используем правило правой руки со штопором ((Рисунок)).
Радиальное направление вдоль вектора [латекс] \ overset {\ to} {R} [/ latex] (указывающее от начала координат) является опорным направлением для измерения угла [латекс] \ phi [/ latex], потому что [латекс] \ overset {\ to} {R} [/ latex] — это первый вектор в векторном произведении [latex] \ overset {\ to} {\ tau} = \ overset {\ to} {R} \, × \, \ overset {\ to} {F} [/ латекс].Вектор [latex] \ overset {\ to} {\ tau} [/ latex] должен лежать вдоль оси z , потому что это ось, перпендикулярная плоскости xy , где оба [latex] \ overset {\ to} {R} [/ latex] и [latex] \ overset {\ to} {F} [/ latex] лгут. Чтобы вычислить величину [латекс] \ тау [/ латекс], мы используем (рисунок). Чтобы найти направление [latex] \ overset {\ to} {\ tau} [/ latex], мы используем правило правой руки со штопором ((Рисунок)).
Решение
Покажи ответ Для ситуации в (а) правило штопора дает направление [латекс] \ overset {\ to} {R} \, × \, \ overset {\ to} {F} [/ latex] в положительном направлении ось z. Физически это означает, что вектор крутящего момента [latex] \ overset {\ to} {\ tau} [/ latex] направлен за пределы страницы перпендикулярно рукоятке гаечного ключа. Мы определяем F = 20,00 N и R = 0,25 м и вычисляем величину, используя (Рисунок):
Физически это означает, что вектор крутящего момента [latex] \ overset {\ to} {\ tau} [/ latex] направлен за пределы страницы перпендикулярно рукоятке гаечного ключа. Мы определяем F = 20,00 N и R = 0,25 м и вычисляем величину, используя (Рисунок):[латекс] \ tau \, = | \ overset {\ to} {R} \, × \, \ overset {\ to} {F} | = \, RF \, \ text {sin} \, \ phi = (0,25 \, \ text {m}) (20,00 \, \ text {N}) \, \ text {sin} \, 40 \ text {°} = 3,21 \, \ text {N} · \ text {m} . [/ latex] Для ситуации в (b) правило штопора дает направление [latex] \ overset {\ to} {R} \, × \, \ overset {\ to} {F} [/ latex] в отрицательное направление оси z.Физически это означает, что вектор [латекс] \ overset {\ to} {\ tau} [/ latex] указывает на страницу перпендикулярно рукоятке гаечного ключа. Величина этого крутящего момента
[латекс] \ tau \, = | \ overset {\ to} {R} \, × \, \ overset {\ to} {F} | = \, RF \, \ text {sin} \, \ phi = (0,25 \, \ text {m}) (20,00 \, \ text {N}) \, \ text {sin} \, 45 \ text {°} = 3,53 \, \ text {N} · \ text {m} .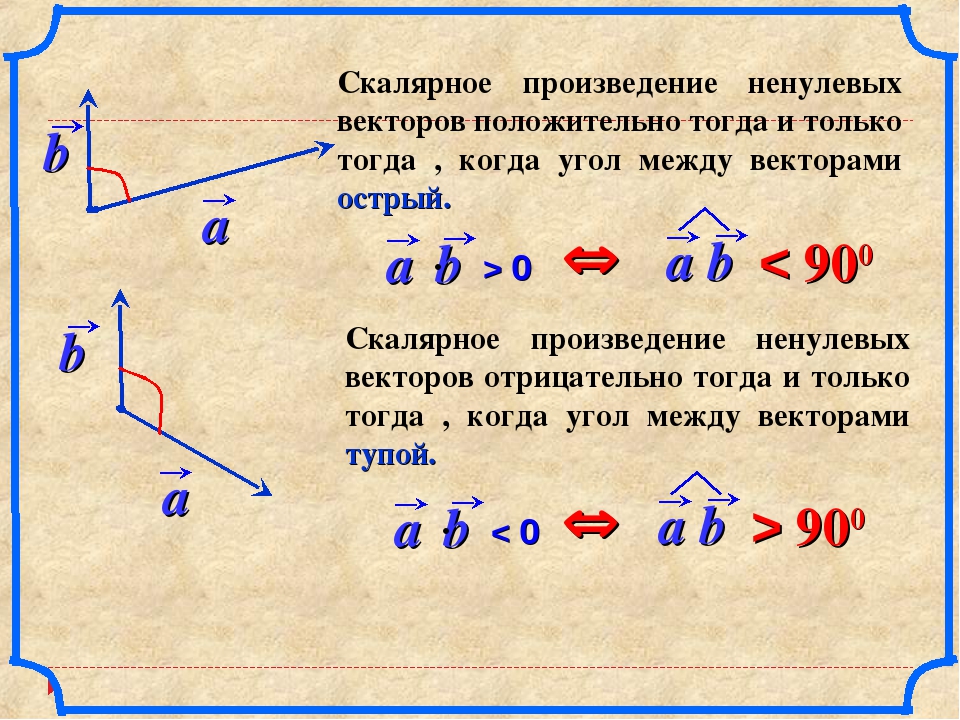 [/ latex] Крутящий момент имеет наибольшее значение, когда [latex] \ text {sin} \, \ phi = 1 [/ latex], что происходит, когда [latex] \ phi = 90 \ text {°} [/ latex]. Физически это означает, что гаечный ключ наиболее эффективен — что дает нам лучшее механическое преимущество — когда мы прикладываем силу перпендикулярно рукоятке гаечного ключа.Для ситуации в этом примере это значение наилучшего крутящего момента [latex] {\ tau} _ {\ text {best}} = RF = (0.25 \, \ text {m}) (20.00 \, \ text {N} ) = 5,00 \, \ text {N} · \ text {m} [/ latex].
[/ latex] Крутящий момент имеет наибольшее значение, когда [latex] \ text {sin} \, \ phi = 1 [/ latex], что происходит, когда [latex] \ phi = 90 \ text {°} [/ latex]. Физически это означает, что гаечный ключ наиболее эффективен — что дает нам лучшее механическое преимущество — когда мы прикладываем силу перпендикулярно рукоятке гаечного ключа.Для ситуации в этом примере это значение наилучшего крутящего момента [latex] {\ tau} _ {\ text {best}} = RF = (0.25 \, \ text {m}) (20.00 \, \ text {N} ) = 5,00 \, \ text {N} · \ text {m} [/ latex].
Значение
При решении задач механики нам часто вообще не нужно использовать правило штопора, как мы сейчас увидим в следующем эквивалентном решении. Обратите внимание: как только мы определили, что вектор [латекс] \ overset {\ to} {R} \, × \, \ overset {\ to} {F} [/ latex] лежит вдоль оси z , мы можем написать этот вектор в терминах единичного вектора [latex] \ hat {k} [/ latex] оси z :
[латекс] \ overset {\ to} {R} \, × \, \ overset {\ to} {F} = RF \, \ text {sin} \, \ phi \ hat {k}. [/ латекс]
[/ латекс]
В этом уравнении число, умножающее [latex] \ hat {k} [/ latex], является скалярной z -компонентой вектора [latex] \ overset {\ to} {R} \, × \, \ overset {\ to} {F} [/ latex]. При вычислении этого компонента необходимо позаботиться о том, чтобы угол [латекс] \ phi [/ latex] измерялся против часовой стрелки от [latex] \ overset {\ to} {R} [/ latex] (первый вектор) до [латекс] \ overset {\ to} {F} [/ latex] (второй вектор). Следуя этому принципу для углов, мы получаем [latex] RF \, \ text {sin} \, (+ 40 \ text {°}) = + 3.2 \, \ text {N} · \ text {m} [/ latex] для ситуации в (a), и мы получаем [latex] RF \, \ text {sin} \, (- 45 \ text {°} ) = — 3.5 \, \ text {N} · \ text {m} [/ latex] для ситуации в (b). В последнем случае угол отрицательный, потому что график на (Рисунок) показывает, что угол измеряется по часовой стрелке; но тот же результат получается, когда этот угол измеряется против часовой стрелки, потому что [латекс] + (360 \ text {°} -45 \ text {°}) = + 315 \ text {°} [/ latex] и [latex] \ текст {грех} \, (+ 315 \ текст {°}) = \ текст {грех} \, (- 45 \ текст {°}) [/ латекс]. Таким образом, мы получаем решение без привязки к правилу штопора. Для ситуации в (a) решением является [latex] \ overset {\ to} {R} \, × \, \ overset {\ to} {F} = + 3.2 \, \ text {N} · \ text {м} \ шляпа {к} [/ латекс]; для ситуации в (b) решением является [latex] \ overset {\ to} {R} \, × \, \ overset {\ to} {F} = — 3.5 \, \ text {N} · \ text {m} \ hat {k} [/ латекс].
Таким образом, мы получаем решение без привязки к правилу штопора. Для ситуации в (a) решением является [latex] \ overset {\ to} {R} \, × \, \ overset {\ to} {F} = + 3.2 \, \ text {N} · \ text {м} \ шляпа {к} [/ латекс]; для ситуации в (b) решением является [latex] \ overset {\ to} {R} \, × \, \ overset {\ to} {F} = — 3.5 \, \ text {N} · \ text {m} \ hat {k} [/ латекс].
Проверьте свое понимание
Для векторов, указанных на (Рисунок), найдите векторные произведения [latex] \ overset {\ to} {A} \, × \, \ overset {\ to} {B} [/ latex] и [latex] \ overset {\ to} {C} \, × \, \ overset {\ to} {F} [/ latex].
Показать решение [латекс] \ overset {\ to} {A} \, × \, \ overset {\ to} {B} = — 40.1 \ hat {k} [/ latex] или, что то же самое, [латекс] | \ overset { \ to} {A} \, × \, \ overset {\ to} {B} | = 40,1 [/ latex], и направление — внутрь страницы; [латекс] \ overset {\ to} {C} \, × \, \ overset {\ to} {F} = + 157.6 \ hat {k} [/ latex] или, что то же самое, [латекс] | \ overset {\ to} {C} \, × \, \ overset {\ to} {F} | = 157,6 [/ latex], и направление — вне страницы.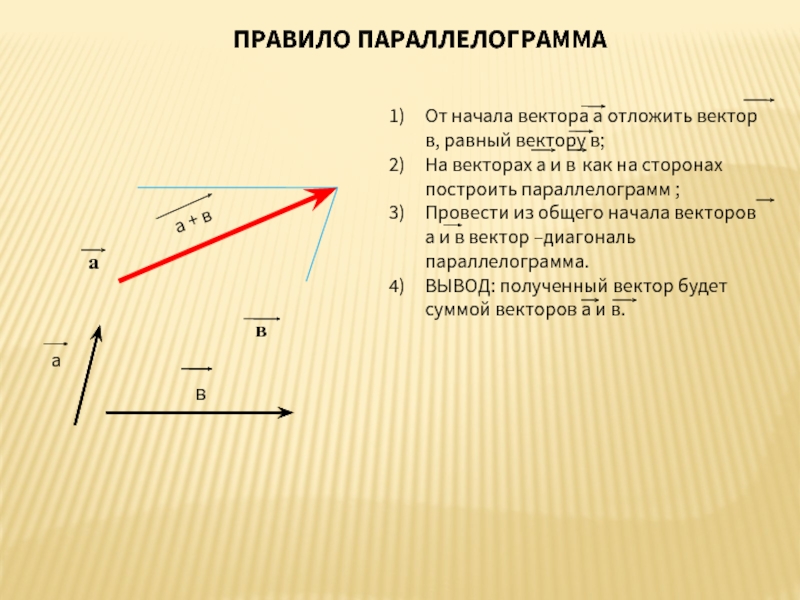
Подобно скалярному произведению ((Рисунок)), перекрестное произведение имеет следующее свойство распределения:
[латекс] \ overset {\ to} {A} \, × \, (\ overset {\ to} {B} + \ overset {\ to} {C}) = \ overset {\ to} {A} \ , × \, \ overset {\ to} {B} + \ overset {\ to} {A} \, × \, \ overset {\ to} {C}.[/ латекс]
Свойство распределения часто применяется, когда векторы выражаются в их составных формах в терминах единичных векторов декартовых осей.
Когда мы применяем определение перекрестного произведения (рисунок) к единичным векторам [latex] \ hat {i} [/ latex], [latex] \ hat {j} [/ latex] и [latex] \ hat {k} [/ latex], которые определяют положительные x -, y — и z — направления в пространстве, мы находим, что
[латекс] \ hat {i} \, × \, \ hat {i} = \ hat {j} \, × \, \ hat {j} = \ hat {k} \, × \, \ hat {k } = 0.[/ латекс]
Все другие перекрестные произведения этих трех единичных векторов должны быть векторами единичной величины, потому что [latex] \ hat {i} [/ latex], [latex] \ hat {j} [/ latex] и [latex] \ hat { k} [/ latex] ортогональны. Например, для пары [латекс] \ hat {i} [/ latex] и [latex] \ hat {j} [/ latex] величина будет [latex] | \ hat {i} \, × \, \ шляпа {j} | = ij \, \ text {sin} \, 90 \ text {°} = (1) (1) (1) = 1 [/ latex]. Направление векторного произведения [латекс] \ hat {i} \, × \, \ hat {j} [/ latex] должно быть ортогонально плоскости xy , что означает, что оно должно быть вдоль z — ось.Единственные единичные векторы вдоль оси z — это [latex] \ text {-} \ hat {k} [/ latex] или [latex] + \ hat {k} [/ latex]. По правилу штопора направление вектора [латекс] \ hat {i} \, × \, \ hat {j} [/ latex] должно быть параллельно положительной оси z . Следовательно, результат умножения [latex] \ hat {i} \, × \, \ hat {j} [/ latex] идентичен [latex] + \ hat {k} [/ latex]. Мы можем повторить аналогичные рассуждения для остальных пар единичных векторов. Результатом умножения будет
Например, для пары [латекс] \ hat {i} [/ latex] и [latex] \ hat {j} [/ latex] величина будет [latex] | \ hat {i} \, × \, \ шляпа {j} | = ij \, \ text {sin} \, 90 \ text {°} = (1) (1) (1) = 1 [/ latex]. Направление векторного произведения [латекс] \ hat {i} \, × \, \ hat {j} [/ latex] должно быть ортогонально плоскости xy , что означает, что оно должно быть вдоль z — ось.Единственные единичные векторы вдоль оси z — это [latex] \ text {-} \ hat {k} [/ latex] или [latex] + \ hat {k} [/ latex]. По правилу штопора направление вектора [латекс] \ hat {i} \, × \, \ hat {j} [/ latex] должно быть параллельно положительной оси z . Следовательно, результат умножения [latex] \ hat {i} \, × \, \ hat {j} [/ latex] идентичен [latex] + \ hat {k} [/ latex]. Мы можем повторить аналогичные рассуждения для остальных пар единичных векторов. Результатом умножения будет
[латекс] \ {\ begin {array} {l} \ hat {i} \, × \, \ hat {j} = + \ hat {k}, \\ \ hat {j} \, × \, \ hat {k} = + \ hat {i}, \\ \ hat {k} \, × \, \ hat {i} = + \ hat {j}. \ end {array} [/ latex]
\ end {array} [/ latex]
Обратите внимание, что на (Рисунок) три единичных вектора [latex] \ hat {i} [/ latex], [latex] \ hat {j} [/ latex] и [latex] \ hat {k} [/ latex ] появляются в циклическом порядке , показанном на диаграмме (Рисунок) (a). Циклический порядок означает, что в формуле продукта [latex] \ hat {i} [/ latex] следует за [latex] \ hat {k} [/ latex] и предшествует [latex] \ hat {j} [/ latex] , или [latex] \ hat {k} [/ latex] следует за [latex] \ hat {j} [/ latex] и предшествует [latex] \ hat {i} [/ latex], или [latex] \ hat { j} [/ latex] следует за [latex] \ hat {i} [/ latex] и предшествует [latex] \ hat {k} [/ latex].Перекрестное произведение двух разных единичных векторов всегда является третьим единичным вектором. Когда два единичных вектора в перекрестном произведении появляются в циклическом порядке, результатом такого умножения является оставшийся единичный вектор, как показано на (Рисунок) (b). Когда единичные векторы в перекрестном произведении появляются в другом порядке, результатом является единичный вектор, антипараллельный оставшемуся единичному вектору (т. Е. Результат со знаком минус, как показано в примерах на (Рисунок) (c). и (Рисунок) (d). На практике, когда задача состоит в том, чтобы найти перекрестные произведения векторов, которые даны в форме компонентов вектора, это правило перекрестного умножения единичных векторов очень полезно.
Е. Результат со знаком минус, как показано в примерах на (Рисунок) (c). и (Рисунок) (d). На практике, когда задача состоит в том, чтобы найти перекрестные произведения векторов, которые даны в форме компонентов вектора, это правило перекрестного умножения единичных векторов очень полезно.
Рисунок 2.32 (а) Диаграмма циклического порядка единичных векторов осей. (b) Единственные перекрестные произведения, в которых единичные векторы появляются в циклическом порядке. Эти продукты имеют положительный знак. (c, d) Два примера перекрестных произведений, где единичные векторы не появляются в циклическом порядке. Эти продукты имеют отрицательный знак.
Предположим, мы хотим найти перекрестное произведение [латекс] \ overset {\ to} {A} \, × \, \ overset {\ to} {B} [/ latex] для векторов [latex] \ overset {\ to} {A} = {A} _ {x} \ hat {i} + {A} _ {y} \ hat {j} + {A} _ {z} \ hat {k} [/ латекс] и [латекс] \ overset {\ to} {B} = {B} _ {x} \ hat {i} + {B} _ {y} \ hat {j} + {B} _ {z} \ hat {k} [/ латекс].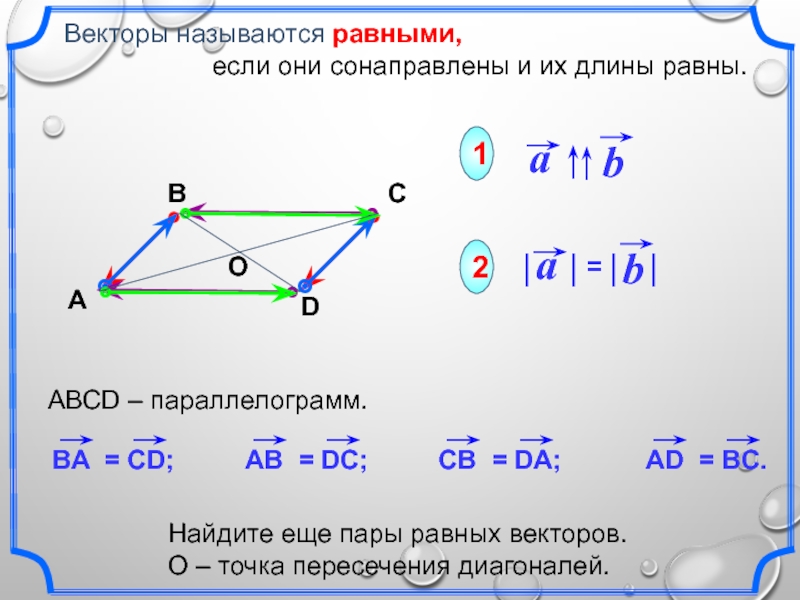 Мы можем использовать свойство распределенности ((Рисунок)), антикоммутативное свойство ((Рисунок)) и результаты (Рисунок) и (Рисунок) для единичных векторов, чтобы выполнить следующую алгебру:
Мы можем использовать свойство распределенности ((Рисунок)), антикоммутативное свойство ((Рисунок)) и результаты (Рисунок) и (Рисунок) для единичных векторов, чтобы выполнить следующую алгебру:
[латекс] \ begin {array} {ccc} \ hfill \ overset {\ to} {A} \, × \, \ overset {\ to} {B} & = \ hfill & ({A} _ {x} \ hat {i} + {A} _ {y} \ hat {j} + {A} _ {z} \ hat {k}) \, × \, ({B} _ {x} \ hat {i} + {B} _ {y} \ hat {j} + {B} _ {z} \ hat {k}) \ hfill \\ & = \ hfill & {A} _ {x} \ hat {i} \, × \, ({B} _ {x} \ hat {i} + {B} _ {y} \ hat {j} + {B} _ {z} \ hat {k}) + {A} _ {y } \ hat {j} \, × \, ({B} _ {x} \ hat {i} + {B} _ {y} \ hat {j} + {B} _ {z} \ hat {k} ) + {A} _ {z} \ hat {k} \, × \, ({B} _ {x} \ hat {i} + {B} _ {y} \ hat {j} + {B} _ {z} \ hat {k}) \ hfill \\ & = \ hfill & \ enspace {A} _ {x} {B} _ {x} \ hat {i} \, × \, \ hat {i} + {A} _ {x} {B} _ {y} \ hat {i} \, × \, \ hat {j} + {A} _ {x} {B} _ {z} \ hat {i} \ , × \, \ hat {k} \ hfill \\ & & + {A} _ {y} {B} _ {x} \ hat {j} \, × \, \ hat {i} + {A} _ {y} {B} _ {y} \ hat {j} \, × \, \ hat {j} + {A} _ {y} {B} _ {z} \ hat {j} \, × \, \ hat {k} \ hfill \\ & & + {A} _ {z} {B} _ {x} \ hat {k} \, × \, \ hat {i} + {A} _ {z} { B} _ {y} \ hat {k} \, × \, \ hat {j} + {A} _ {z} {B} _ {z} \ hat {k} \, × \, \ hat {k } \ hfill \\ & = \ hfill & \ enspace {A} _ {x} {B} _ {x} (0) + {A} _ {x} {B} _ {y} (+ \ hat {k }) + {A} _ {x} {B} _ {z} (\ text {-} \ hat {j}) \ hfill \\ & & + {A} _ {y} {B} _ {x} (\ text {-} \ hat {k}) + {A} _ {y} {B} _ {y} (0) + {A} _ {y} {B} _ {z} (+ \ hat { i}) \ hfill \\ & & + {A} _ {z} {B} _ {x} (+ \ hat {j} ) + {A} _ {z} {B} _ {y} (\ text {-} \ hat {i}) + {A} _ {z} {B} _ {z} (0). \ hfill \ end {array} [/ latex]
\ hfill \ end {array} [/ latex]
При выполнении алгебраических операций с перекрестным произведением будьте очень осторожны с соблюдением правильного порядка умножения, потому что перекрестное произведение антикоммутативно. Последние два шага, которые нам еще предстоит сделать для выполнения нашей задачи, — это, во-первых, группировка терминов, содержащих общий единичный вектор, и, во-вторых, разложение на множители. Таким образом, мы получаем следующее очень полезное выражение для вычисления перекрестного произведения:
[латекс] \ overset {\ to} {C} = \ overset {\ to} {A} \, × \, \ overset {\ to} {B} = ({A} _ {y} {B} _ {z} — {A} _ {z} {B} _ {y}) \ hat {i} + ({A} _ {z} {B} _ {x} — {A} _ {x} {B } _ {z}) \ hat {j} + ({A} _ {x} {B} _ {y} — {A} _ {y} {B} _ {x}) \ hat {k}.[/ латекс]
В этом выражении скалярные компоненты вектора перекрестного произведения равны
[латекс] \ {\ begin {array} {c} {C} _ {x} = {A} _ {y} {B} _ {z} — {A} _ {z} {B} _ {y }, \\ {C} _ {y} = {A} _ {z} {B} _ {x} — {A} _ {x} {B} _ {z}, \\ {C} _ {z } = {A} _ {x} {B} _ {y} — {A} _ {y} {B} _ {x}.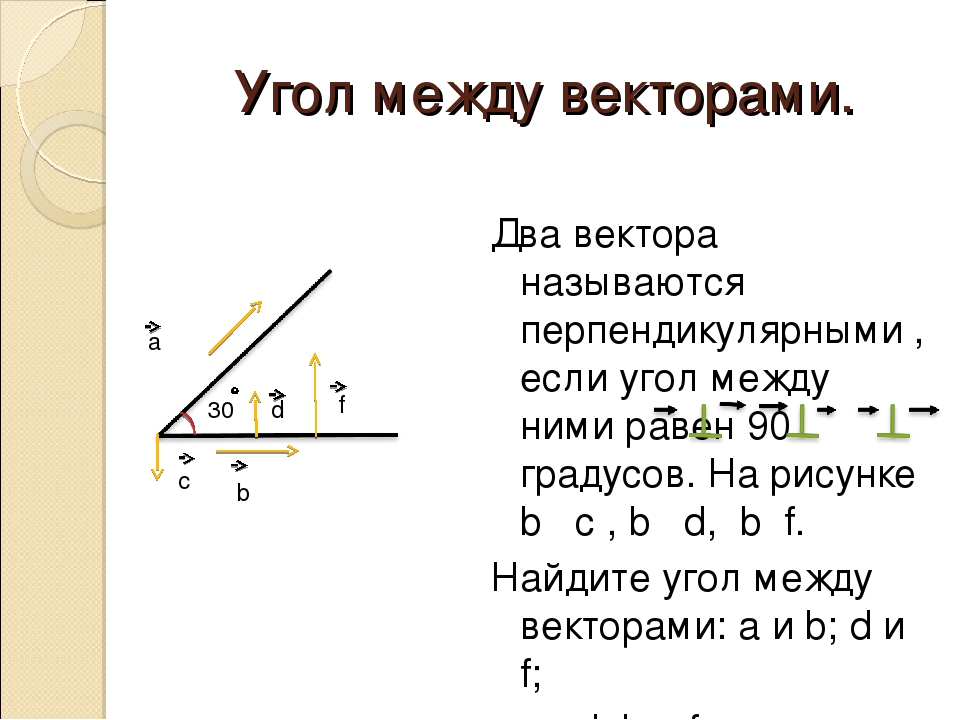 \ End {array} [/ latex]
\ End {array} [/ latex]
На практике при нахождении перекрестного произведения мы можем использовать либо (рисунок), либо (рисунок), в зависимости от того, какое из них кажется менее сложным в вычислительном отношении. Оба они приводят к одному и тому же конечному результату. Один из способов убедиться, что окончательный результат верен, — использовать их оба.
Пример
Частица в магнитном поле
При движении в магнитном поле некоторые частицы могут испытывать магнитную силу. Не вдаваясь в подробности — подробное изучение магнитных явлений будет в следующих главах — давайте признаем, что магнитное поле [латекс] \ overset {\ to} {B} [/ latex] является вектором, магнитная сила [латекс] \ overset {\ to} {F} [/ latex] — это вектор, а скорость [latex] \ overset {\ to} {u} [/ latex] частицы — это вектор. Вектор магнитной силы пропорционален векторному произведению вектора скорости на вектор магнитного поля, которое мы выражаем как [latex] \ overset {\ to} {F} = \ zeta \ overset {\ to} {u} \, × \, \ overset {\ to} {B} [/ латекс]. В этом уравнении константа [latex] \ zeta [/ latex] заботится о согласованности физических единиц, поэтому мы можем опустить физические единицы на векторах [latex] \ overset {\ to} {u} [/ latex] и [ латекс] \ overset {\ to} {B} [/ латекс]. В этом примере предположим, что константа [latex] \ zeta [/ latex] положительна.
В этом уравнении константа [latex] \ zeta [/ latex] заботится о согласованности физических единиц, поэтому мы можем опустить физические единицы на векторах [latex] \ overset {\ to} {u} [/ latex] и [ латекс] \ overset {\ to} {B} [/ латекс]. В этом примере предположим, что константа [latex] \ zeta [/ latex] положительна.
Частица, движущаяся в пространстве с вектором скорости [latex] \ overset {\ to} {u} = — 5.0 \ hat {i} -2.0 \ hat {j} +3.5 \ hat {k} [/ latex], входит в область с магнитным полем и испытывает магнитную силу.Найдите магнитную силу [латекс] \ overset {\ to} {F} [/ latex] на этой частице в точке входа в область, где вектор магнитного поля равен (a) [latex] \ overset {\ to} {B } = 7.2 \ hat {i} — \ hat {j} -2.4 \ hat {k} [/ latex] и (b) [latex] \ overset {\ to} {B} = 4.5 \ hat {k} [/ латекс]. В каждом случае найдите величину F магнитной силы и угол [latex] \ theta [/ latex], который вектор силы [latex] \ overset {\ to} {F} [/ latex] создает с заданным вектором магнитного поля. [латекс] \ overset {\ to} {B} [/ латекс].{2}} [/ latex], или вычислением величины [latex] | \ overset {\ to} {u} \, × \, \ overset {\ to} {B} | [/ latex] напрямую с помощью (рисунок). В последнем подходе нам нужно будет найти угол между векторами [latex] \ overset {\ to} {u} [/ latex] и [latex] \ overset {\ to} {B} [/ latex]. Когда у нас есть [latex] \ overset {\ to} {F} [/ latex], общий метод определения угла направления [latex] \ theta [/ latex] включает вычисление скалярного произведения [latex] \ overset { \ to} {F} · \ overset {\ to} {B} [/ latex] и подставляем в (рисунок).Для вычисления векторного произведения мы можем либо использовать (рисунок), либо вычислить произведение напрямую, в зависимости от того, что будет проще.
[латекс] \ overset {\ to} {B} [/ латекс].{2}} [/ latex], или вычислением величины [latex] | \ overset {\ to} {u} \, × \, \ overset {\ to} {B} | [/ latex] напрямую с помощью (рисунок). В последнем подходе нам нужно будет найти угол между векторами [latex] \ overset {\ to} {u} [/ latex] и [latex] \ overset {\ to} {B} [/ latex]. Когда у нас есть [latex] \ overset {\ to} {F} [/ latex], общий метод определения угла направления [latex] \ theta [/ latex] включает вычисление скалярного произведения [latex] \ overset { \ to} {F} · \ overset {\ to} {B} [/ latex] и подставляем в (рисунок).Для вычисления векторного произведения мы можем либо использовать (рисунок), либо вычислить произведение напрямую, в зависимости от того, что будет проще.
Решение
Покажи ответ Компоненты вектора скорости: [латекс] {u} _ {x} = — 5.0 [/ latex], [latex] {u} _ {y} = — 2.0 [/ latex] и [latex] {u} _ {z} = 3,5 [/ латекс]. (a) Компонентами вектора магнитного поля являются [латекс] {B} _ {x} = 7,2 [/ латекс], [латекс] {B} _ {y} = — 1,0 [/ латекс] и [латекс ] {B} _ {z} = — 2,4 [/ латекс]. Подстановка их в (рисунок) дает скалярные компоненты вектора [latex] \ overset {\ to} {F} = \ zeta \ overset {\ to} {u} \, × \, \ overset {\ to} {B} [/ latex]:
Подстановка их в (рисунок) дает скалярные компоненты вектора [latex] \ overset {\ to} {F} = \ zeta \ overset {\ to} {u} \, × \, \ overset {\ to} {B} [/ latex]:
[латекс] \ {\ begin {array} {l} {F} _ {x} = \ zeta ({u} _ {y} {B} _ {z} — {u} _ {z} {B} _ {y}) = \ zeta [(-2.{2}} = 7,6, [/ latex] и скалярное произведение [latex] \ overset {\ to} {F} · \ overset {\ to} {B} [/ latex]:
[латекс] \ overset {\ to} {F} · \ overset {\ to} {B} = {F} _ {x} {B} _ {x} + {F} _ {y} {B} _ {y} + {F} _ {z} {B} _ {z} = (8.3 \ zeta) (7.2) + (13.2 \ zeta) (- 1.0) + (19.4 \ zeta) (- 2.4) = 0. [/ latex] Теперь замена в (Рисунок) дает угол [латекс] \ theta [/ latex]:
[латекс] \ text {cos} \, \ theta = \ frac {\ overset {\ to} {F} · \ overset {\ to} {B}} {FB} = \ frac {0} {(18.2 \ zeta) (7.6)} = 0 \, ⇒ \ enspace \ theta = 90 \ text {°}. [/ латекс]
Следовательно, вектор магнитной силы перпендикулярен вектору магнитного поля.(Мы могли бы сэкономить время, если бы вычислили скалярное произведение раньше. )
)
(b) Поскольку вектор [latex] \ overset {\ to} {B} = 4.5 \ hat {k} [/ latex] имеет только один компонент, мы можем быстро выполнить алгебру и найти векторное произведение напрямую:
[латекс] \ begin {array} {ll} \ hfill \ overset {\ to} {F} & = \ zeta \ overset {\ to} {u} \, × \, \ overset {\ to} {B} = \ zeta (-5.0 \ hat {i} -2.0 \ hat {j} +3.5 \ hat {k}) \, × \, (4.5 \ hat {k}) \ hfill \\ & = \ zeta [(- 5.0) (4.5) \ hat {i} \, × \, \ hat {k} + (- 2.0) (4.5) \ hat {j} \, × \, \ hat {k} + (3.{2}} = 24,2 \ дзета. [/ latex] Поскольку скалярное произведение равно
[латекс] \ overset {\ to} {F} · \ overset {\ to} {B} = {F} _ {x} {B} _ {x} + {F} _ {y} {B} _ {y} + {F} _ {z} {B} _ {z} = (- 9.0 \ zeta) (0) + (22.5 \ zeta) (0) + (0) (4.5) = 0, [/ латекс ] вектор магнитной силы [латекс] \ overset {\ to} {F} [/ latex] перпендикулярен вектору магнитного поля [latex] \ overset {\ to} {B} [/ latex].
Значение
Даже не вычисляя фактически скалярное произведение, мы можем предсказать, что вектор магнитной силы всегда должен быть перпендикулярен вектору магнитного поля из-за способа построения этого вектора. А именно, вектор магнитной силы — это векторное произведение [латекс] \ overset {\ to} {F} = \ zeta \ overset {\ to} {u} \, × \, \ overset {\ to} {B} [/ латекс] и, по определению векторного произведения (см. (рисунок)), вектор [латекс] \ overset {\ to} {F} [/ latex] должен быть перпендикулярен обоим векторам [латекс] \ overset {\ to} {u} [/ latex] и [latex] \ overset {\ to} {B} [/ latex].
А именно, вектор магнитной силы — это векторное произведение [латекс] \ overset {\ to} {F} = \ zeta \ overset {\ to} {u} \, × \, \ overset {\ to} {B} [/ латекс] и, по определению векторного произведения (см. (рисунок)), вектор [латекс] \ overset {\ to} {F} [/ latex] должен быть перпендикулярен обоим векторам [латекс] \ overset {\ to} {u} [/ latex] и [latex] \ overset {\ to} {B} [/ latex].
Проверьте свое понимание
Даны два вектора [латекс] \ overset {\ to} {A} = \ text {-} \ hat {i} + \ hat {j} [/ latex] и [latex] \ overset {\ to} {B} = 3 \ hat {i} — \ hat {j} [/ latex], найдите (a) [latex] \ overset {\ to} {A} \, × \, \ overset {\ to} {B} [/ латекс], (b) [латекс] | \ overset {\ to} {A} \, × \, \ overset {\ to} {B} | [/ latex], (c) угол между [латексом] \ overset {\ to} {A} [/ latex] и [latex] \ overset {\ to} {B} [/ latex], и (d) угол между [латексом] \ overset {\ to} {A} \, × \, \ overset {\ to} {B} [/ latex] и вектором [латексом] \ overset {\ to} {C} = \ hat { i} + \ hat {k} [/ латекс].
а. [латекс] -2 \ шляпа {k} [/ латекс], б. 2, в. [латекс] 153.4 \ text {°} [/ латекс], d. [латекс] 135 \ text {°} [/ латекс]
В заключение этого раздела мы хотим подчеркнуть, что «скалярное произведение» и «перекрестное произведение» — это совершенно разные математические объекты, которые имеют разное значение. Скалярное произведение — это скаляр; перекрестное произведение — это вектор. В последующих главах термины скалярное произведение и скалярное произведение используются как взаимозаменяемые. Точно так же термины cross product и vector product используются взаимозаменяемо.
Умножение векторов— гипертекст по физике
Обсуждение
скалярно-векторное умножение
Умножение вектора на скаляр изменяет величину вектора, но оставляет его направление неизменным. Скаляр изменяет размер вектора. Скаляр «масштабирует» вектор. Например, вектор полярной формы…
r = r r̂ + θ θ̂
, умноженное на скаляр , равно…
a r = ar r̂ + θ θ̂
Умножение вектора на скаляр является дистрибутивным.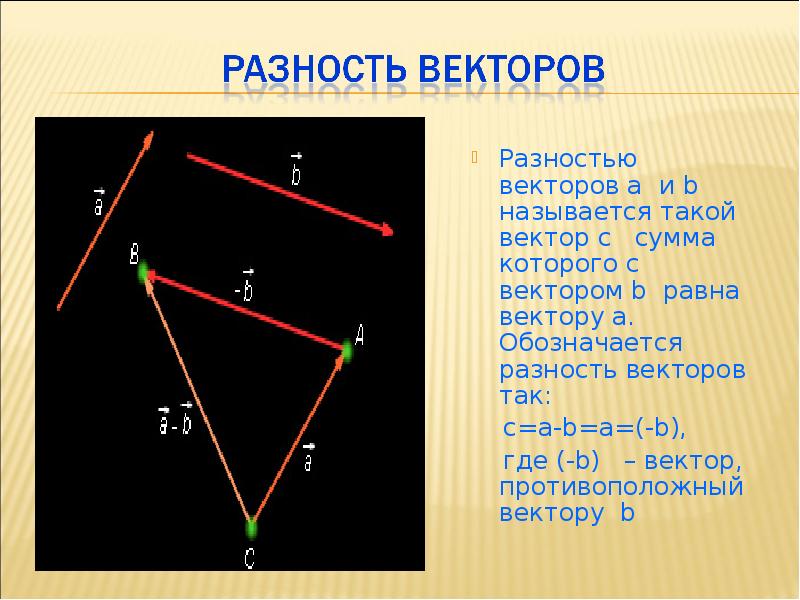
a ( A + B ) = a A + a B
Следовательно, вектор прямоугольной формы…
r = x î + y ĵ
, умноженное на скаляр , равно…
a r = ax î + ay ĵ
точечный продукт
Геометрически скалярное произведение двух векторов является величиной, умноженной на проекцию второго на первый.
Символ, используемый для представления этой операции, представляет собой небольшую точку на средней высоте (·), отсюда и произошло название «скалярный продукт». Поскольку это произведение имеет только величину, оно также известно как скалярное произведение .
A · B = AB cos θ
Скалярное произведение распределительное…
A · ( B + C ) = A · B + A · C
и коммутативный…
A · B = B · A
Поскольку проекция вектора на сам себя оставляет его величину неизменной, скалярное произведение любого вектора на себя является квадратом величины этого вектора.
A · A = AA cos 0 ° = A 2
Применение этого следствия к единичным векторам означает, что скалярное произведение любого единичного вектора с самим собой равно единице. Кроме того, поскольку вектор не имеет проекции, перпендикулярной самому себе, скалярное произведение любого единичного вектора на любой другой равно нулю.
î · î = ĵ · ĵ = k · k̂ = (1) (1) (cos 0 °) = 1
î · = ĵ · k̂ = k̂ · î = (1) (1) (cos 90 °) = 0
Используя эти знания, мы можем вывести формулу для скалярного произведения любых двух векторов в прямоугольной форме.Полученный продукт выглядит ужасно беспорядочно, но состоит в основном из нулевых членов.
| A · B = | ( A x î + A y ĵ + A z k̂ ) · ( B x 4 905 905 905 ĵ + B z k̂ ) | |||||||||||
| A · B = | A x или | · | B x или | + | A x или | · | B y ĵ | + | A x или | · | B z k̂ | |
| + | A y ĵ | · | B x или | + | A y ĵ | · | B y ĵ | + | A y ĵ | · | B z k̂ | |
| + | A z k̂ | · | B x или | + | A z k̂ | · | B y ĵ | + | A z k̂ | · | B z k̂ | |
| A · B = | A x B x + A y B y + A z B z | |||||||||||
Точечное произведение двух векторов, таким образом, является суммой произведений их параллельных компонентов. Отсюда мы можем вывести теорему Пифагора в трех измерениях.
Отсюда мы можем вывести теорему Пифагора в трех измерениях.
A · A = AA cos 0 ° = A x A x + A y A y + A z 097 A 20 9 A 2 = A x 2 + A y 2 + A z 2 Геометрически перекрестное произведение двух векторов — это площадь параллелограмма между ними. Символ, используемый для представления этой операции, представляет собой большой диагональный крест (×), отсюда и произошло название «перекрестное произведение». Поскольку это произведение имеет величину и направление, оно также известно как векторное произведение . A × B = AB sin θ n̂ Вектор n̂ (n шляпа) — это единичный вектор, перпендикулярный плоскости, образованной двумя векторами. Перекрестное произведение распределительное… A × ( B + C ) = ( A × B ) + ( A × C ) , а не , а не , коммутативный… A × B = — B × A Изменение порядка перекрестного умножения меняет направление произведения на противоположное. Так как два идентичных вектора образуют вырожденный параллелограмм без площади, перекрестное произведение любого вектора на себя равно нулю… A × A = 0 Применение этого следствия к единичным векторам означает, что произведение любого единичного вектора на себя равно нулю. î × î = ĵ × ĵ = k̂ × k̂ = (1) (1) (sin 0 °) = 0 Следует отметить, что произведение любого единичного вектора на любой другой будет иметь величину, равную единице. Правая система координат , которая является обычной системой координат, используемой в физике и математике, — это система, в которой любое циклическое произведение трех осей координат положительно, а любое антициклическое произведение отрицательно.Представьте себе часы с тремя буквами x-y-z вместо обычных двенадцати цифр. Используя эти знания, мы можем вывести формулу для векторного произведения любых двух векторов в прямоугольной форме. Полученный продукт выглядит так, как будто это будет ужасный беспорядок, и это так! A × B = ( A x î + A y ĵ + A z ” k̂ ) × ( крестообразное произведение
 Направление n̂ определяется правилом правой руки, которое мы вскоре обсудим.
Направление n̂ определяется правилом правой руки, которое мы вскоре обсудим. (В конце концов, синус 90 ° равен единице.) Однако направление не является интуитивно очевидным. Правило правой руки для перекрестного умножения связывает направление двух векторов с направлением их произведения. Поскольку перекрестное умножение , а не коммутативно, порядок операций важен.
(В конце концов, синус 90 ° равен единице.) Однако направление не является интуитивно очевидным. Правило правой руки для перекрестного умножения связывает направление двух векторов с направлением их произведения. Поскольку перекрестное умножение , а не коммутативно, порядок операций важен. Любое произведение этих трех букв, которое работает круглосуточно в том же направлении, что и последовательность x-y-z, равно циклическим и положительным. Любой продукт, который движется в обратном направлении, — это антициклический и отрицательный.
Любое произведение этих трех букв, которое работает круглосуточно в том же направлении, что и последовательность x-y-z, равно циклическим и положительным. Любой продукт, который движется в обратном направлении, — это антициклический и отрицательный. Перекрестное произведение циклической пары единичных векторов
равно положительным . Перекрестное произведение антициклической пары
единичных векторов равно отрицательным .
Произведение двух трехчленов состоит из девяти членов.
| A × B | = | A x или | × | B x или | + | A x или | × | B y ĵ | + | A x или | × | B z k̂ |
| + | A y ĵ | × | B x или | + | A y ĵ | × | B y ĵ | + | A y ĵ | × | B z k̂ | |
| + | A z k̂ | × | B x или | + | A z k̂ | × | B y ĵ | + | A z k̂ | × | B z k̂ |
Три из них равны нулю.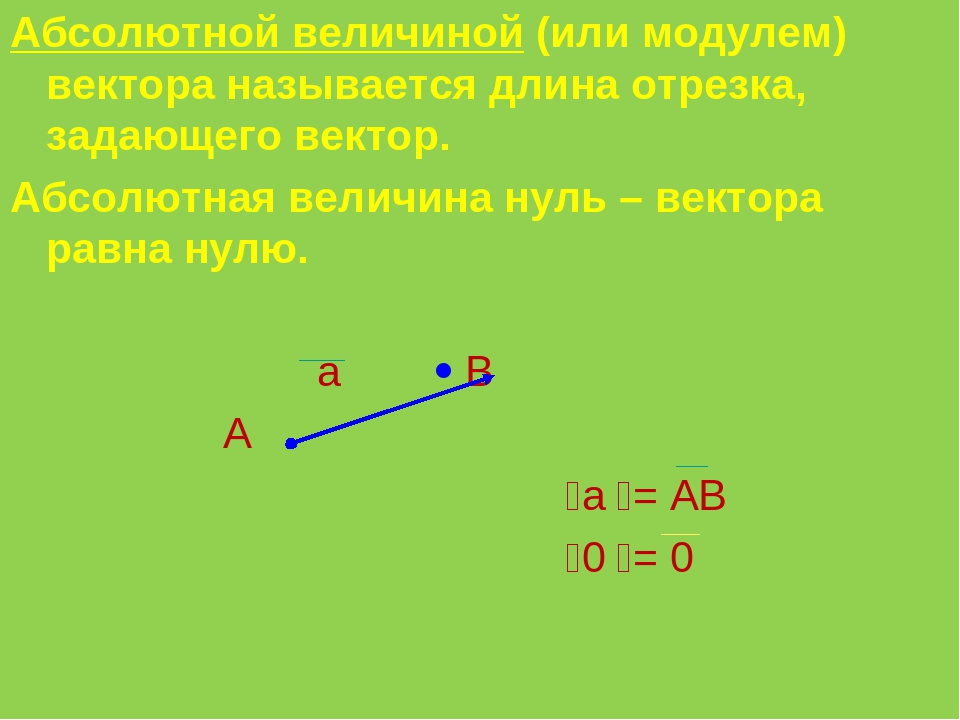 Устраните их.
Устраните их.
| A × B | = | A x B y k̂ | – | A x B z ĵ |
| – | A y B x k̂ | + | A y B z до | |
| + | A z B x ĵ | – | A z B y î |
Сгруппируйте термины по единичному вектору и коэффициенту.
A × B = ( A y B z — A z B y ) î Есть более простой способ написать это. Для тех из вас, кто знаком с матрицами, перекрестное произведение двух векторов является определителем матрицы, первая строка которой является единичными векторами, вторая строка — первым вектором, а третья строка — вторым вектором.Условно… Расширение определителя 3 × 3 его первой строкой является первым шагом.Это дает нам три определителя 2 × 2. Эти детерминанты 2 × 2 можно найти быстро.Они также дают нам решение, предварительно отсортированное по единичному вектору, поэтому нет необходимости сортировать термины и множители. A × B = ( A y B z — A z B y ) î % PDF-1.3
%
9 0 объект
>
эндобдж
xref
9 914
0000000016 00000 н.
0000018627 00000 п.
0000019679 00000 п.
0000019893 00000 п.
0000031109 00000 п.
0000031158 00000 п.
0000031207 00000 п.
0000031256 00000 п.
0000031305 00000 п.
0000031354 00000 п.
0000031403 00000 п.
0000031452 00000 п.
0000031501 00000 п.
0000031550 00000 п.
0000031599 00000 н.
0000031648 00000 н.
0000031697 00000 п.
0000031746 00000 п.
0000031795 00000 п.
0000031844 00000 п.
0000031893 00000 п.
0000031942 00000 п.
0000031991 00000 п.
0000032040 00000 п.
0000032089 00000 п.
0000032138 00000 п.
0000032187 00000 п.
0000032236 00000 п.
0000032285 00000 п.
0000032334 00000 п.
0000032383 00000 п.
0000032432 00000 п.
0000032481 00000 п.
0000032530 00000 п.
0000032579 00000 п.
0000032628 00000 н.
0000032677 00000 п.
0000032726 00000 п.
0000032775 00000 п.
0000032824 00000 н.
0000032873 00000 п.
0000032922 00000 н.
0000032971 00000 п.
0000033020 00000 п.
0000033069 00000 п.
0000033118 00000 п.
0000033167 00000 п.
0000033216 00000 п.
0000033265 00000 п.
0000033314 00000 п.
0000033363 00000 п.
0000033596 00000 п.
0000033809 00000 п.
0000034110 00000 п.
0000034264 00000 п.
0000034304 00000 п.
0000034353 00000 п.
0000034402 00000 п.
0000034451 00000 п.
0000034500 00000 н.
0000034549 00000 п.
0000034910 00000 п.
0000035456 00000 п.
0000035685 00000 п.
0000035914 00000 п.
0000036137 00000 п.
0000036475 00000 п.
0000036868 00000 н.
0000037022 00000 п.
0000037242 00000 п.
0000037574 00000 п.
0000037809 00000 п.
0000038244 00000 п.
0000038293 00000 п.
0000038342 00000 п.
0000038391 00000 п.
0000038440 00000 п.
0000038489 00000 п.
0000038538 00000 п.
0000038587 00000 п.
0000038636 00000 п.
0000038685 00000 п.
0000038734 00000 п.
0000038783 00000 п.
0000038832 00000 п.
0000038881 00000 п.
0000038930 00000 н.
0000038979 00000 п.
0000039028 00000 н.
0000039077 00000 п.
0000039126 00000 п.
0000039175 00000 п.
0000039225 00000 п.
0000039275 00000 п.
0000039325 00000 п.
0000039375 00000 п.
0000039425 00000 п.
0000039475 00000 п.
0000039524 00000 п.
0000039574 00000 п.
0000039623 00000 п.
0000039673 00000 п.
0000039723 00000 п.
0000039772 00000 п.
0000039822 00000 н.
0000039872 00000 н.
0000039922 00000 н.
0000039971 00000 н.
0000040021 00000 п.
0000040070 00000 п.
0000040119 00000 п.
0000040169 00000 п.
0000040219 00000 п.
0000040268 00000 п.
0000040318 00000 п.
0000040368 00000 п.
0000040418 00000 п.
0000040468 00000 п.
0000040518 00000 п.
0000040568 00000 п.
0000040618 00000 п.
0000040667 00000 п.
0000040717 00000 п.
0000040767 00000 п.
0000040817 00000 п.
0000040867 00000 п.
0000040917 00000 п.
0000040967 00000 п.
0000041017 00000 п.
0000041066 00000 п.
0000041115 00000 п.
0000041165 00000 п.
0000041215 00000 п.
0000041265 00000 п.
0000041315 00000 п.
0000041364 00000 п.
0000041414 00000 п.
0000041464 00000 п.
0000041514 00000 п.
0000041564 00000 п.
0000041614 00000 п.
0000041664 00000 н.
0000041714 00000 п.
0000041764 00000 п.
0000041787 00000 п.
0000044405 00000 п.
0000044428 00000 п.
0000047178 00000 п.
0000047201 00000 п.
0000049858 00000 п.
0000049881 00000 п.
0000052053 00000 п.
0000052076 00000 п.
0000053790 00000 п.
0000053813 00000 п.
0000055442 00000 п.
0000055465 00000 п.
0000056976 00000 п.
0000056999 00000 н.
0000058687 00000 п.
0000058795 00000 п.
0000058885 00000 п.
0000068293 00000 п.
0000068407 00000 п.
0000068488 00000 н.
0000068593 00000 п.
0000068698 00000 п.
0000068785 00000 п.
0000068890 00000 н.
0000068998 00000 п.
0000069103 00000 п.
0000069330 00000 п.
0000072008 00000 п.
0000072113 00000 п.
0000072212 00000 п.
0000072323 00000 п.
0000072404 00000 п.
0000072512 00000 п.
0000072591 00000 п.
0000072705 00000 п.
0000086491 00000 п.
0000086599 00000 п.
0000086686 00000 п.
0000086776 00000 п.
0000086878 00000 п.
0000097258 00000 п.
0000131918 00000 н.
0000132029 00000 н.
0000148878 00000 н.
0000149774 00000 н.
0000149864 00000 н.
0000149945 00000 н.
0000150230 00000 н.
0000150326 00000 н.
0000150413 00000 н.
0000150503 00000 н.
0000150590 00000 н.
0000150683 00000 н.
0000150767 00000 н.
0000150863 00000 н.
0000158545 00000 н.
0000158626 00000 н.
0000158716 00000 н.
0000158803 00000 н.
0000158908 00000 н.
0000158986 00000 н.
0000159192 00000 н.
0000159276 00000 н.
0000159375 00000 п.
0000159459 00000 н.
0000159558 00000 н.
0000159651 00000 н.
0000159741 00000 н.
0000159825 00000 н.
0000160032 00000 н.
0000167288 00000 н.
0000167372 00000 н.
0000167465 00000 н.
0000167582 00000 н.
0000167755 00000 н.
0000167875 00000 н.
0000167989 00000 н.
0000168106 00000 н.
0000168226 00000 н.
0000168328 00000 н.
0000168457 00000 н.
0000168627 00000 н.
0000168756 00000 н.
0000168926 00000 н.
0000169049 00000 н.
0000169169 00000 н.
0000169265 00000 н.
0000169358 00000 н.
0000169528 00000 н.
0000169639 00000 н.
0000169816 00000 н.
0000169939 00000 н.
0000170059 00000 н.
0000170161 00000 п.
0000170269 00000 н.
0000170380 00000 н.
0000170488 00000 н.
0000170587 00000 н.
0000170686 00000 н.
0000170788 00000 н.
0000170884 00000 н.
0000170983 00000 п.
0000171085 00000 н.
0000171190 00000 н.
0000171295 00000 н.
0000171400 00000 н.
0000171517 00000 н.
0000171622 00000 н.
0000171727 00000 н.
0000171841 00000 н.
0000171949 00000 н.
0000172057 00000 н.
0000172159 00000 н.
0000172264 00000 н.
0000172351 00000 н.
0000172465 00000 н.
0000172549 00000 н.
0000172663 00000 н.
0000172753 00000 н.
0000172876 00000 н.
0000172996 00000 н.
0000173089 00000 н.
0000173191 00000 н.
0000173299 00000 н.
0000173410 00000 н.
0000173518 00000 н.
0000173629 00000 н.
0000173737 00000 н.
0000173848 00000 н.
0000173953 00000 н.
0000174055 00000 н.
0000174169 00000 н.
0000174283 00000 н.
0000174391 00000 н.
0000174490 00000 н.
0000174595 00000 н.
0000174703 00000 н.
0000174805 00000 н.
0000174907 00000 н.
0000175009 00000 н.
0000175108 00000 н.
0000175204 00000 н.
0000175297 00000 н.
0000175405 00000 н.
0000175495 00000 н.
0000175606 00000 н.
0000175717 00000 н.
0000175822 00000 н.
0000175924 00000 н.
0000176032 00000 н.
0000176125 00000 н.
0000176313 00000 н.
0000176497 00000 н.
0000176682 00000 н.
0000176867 00000 н.
0000177052 00000 н.
0000177242 00000 н.
0000177437 00000 н.
0000177630 00000 н.
0000177827 00000 н.
0000178022 00000 н.
0000178220 00000 н.
0000178418 00000 н.
0000178615 00000 н.
0000178817 00000 н.
0000179011 00000 н.
0000179210 00000 п.
0000179405 00000 н.
0000179600 00000 н.
0000179795 00000 н.
0000179989 00000 н.
0000180184 00000 н.
0000180379 00000 н.
0000180574 00000 н.
0000180796 00000 н.
0000181018 00000 н.
0000181240 00000 н.
0000181458 00000 н.
0000181676 00000 н.
0000181897 00000 н.
0000182115 00000 н.
0000182344 00000 н.
0000182580 00000 н.
0000182812 00000 н.
0000183043 00000 н.
0000183275 00000 н.
0000183495 00000 н.
0000183718 00000 н.
0000183936 00000 н.
0000184159 00000 н.
0000184361 00000 н.
0000184557 00000 н.
0000184755 00000 н.
0000184952 00000 н.
0000185149 00000 н.
0000185328 00000 н.
0000185537 00000 н.
0000185716 00000 н.
0000185926 00000 н.
0000186105 00000 н.
0000186313 00000 н.
0000186492 00000 н.
0000186705 00000 н.
0000186884 00000 н.
0000187093 00000 н.
0000187272 00000 н.
0000187483 00000 н.
0000187662 00000 н.
0000187872 00000 н.
0000188068 00000 н.
0000188265 00000 н.
0000188460 00000 н.
0000188656 00000 н.
0000188852 00000 н.
0000189053 00000 н.
0000189256 00000 н.
0000189459 00000 н.
0000189664 00000 н.
0000189870 00000 н.
00001 00000 н.
00001 00000 н.
00001 00000 н.
00001 00000 н.
00001 00000 н.
00001 00000 н.
00002 00000 н.
00002 00000 н.
00002 00000 н.
00002 00000 н.
00002 00000 н.
00002 00000 н.
00002 A × B = – ĵ k A x A y A z B x B y B z A × B = A y A z до — A x A z ĵ + A x A y k B y B z B x B z B x B y 00000 н.
00001 00000 н.
00001 00000 н.
0000192910 00000 н.
0000193117 00000 н.
0000193349 00000 н.
0000193548 00000 н.
0000193772 00000 н.
0000193971 00000 н.
0000194203 00000 н.
0000194395 00000 н.
0000194625 00000 н.
0000194820 00000 н.
0000195048 00000 н.
0000195240 00000 н.
0000195439 00000 н.
0000195631 00000 н.
0000195828 00000 н.
0000196024 00000 н.
0000196227 00000 н.
0000196437 00000 н.
0000196633 00000 н.
0000196841 00000 н.
0000197037 00000 н.
0000197244 00000 н.
0000197440 00000 н.
0000197645 00000 н.
0000197841 00000 н.
0000198045 00000 н.
0000198248 00000 н.
0000198451 00000 п.
0000198652 00000 н.
0000198848 00000 н.
0000199047 00000 н.
0000199243 00000 н.
0000199443 00000 н.
0000199643 00000 н.
0000199839 00000 н.
0000200038 00000 н.
0000200234 00000 н.
0000200439 00000 п.
0000200641 00000 п.
0000200837 00000 н.
0000201037 00000 н.
0000201238 00000 н.
0000201438 00000 н.
0000201646 00000 н.
0000201842 00000 н.
0000202057 00000 н.
0000202274 00000 н.
0000202495 00000 н.
0000202690 00000 н.
0000202899 00000 н.
0000203091 00000 н.
0000203303 00000 н.
0000203499 00000 н.
0000203709 00000 н.
0000203901 00000 н.
0000204110 00000 н.
0000204302 00000 н.
0000204519 00000 н.
0000204711 00000 н.
0000204921 00000 н.
0000205131 00000 н.
0000205321 00000 н.
0000205528 00000 н.
0000205718 00000 н.
0000205925 00000 н.
0000206111 00000 н.
0000206315 00000 н.
0000206496 00000 н.
0000206682 00000 н.
0000206885 00000 н.
0000207066 00000 н.
0000207252 00000 н.
0000207455 00000 н.
0000207636 00000 н.
0000207822 00000 н.
0000208024 00000 н.
0000208205 00000 н.
0000208391 00000 н.
0000208594 00000 н.
0000208775 00000 н.
0000208962 00000 н.
0000209161 00000 н.
0000209343 00000 н.
0000209530 00000 н.
0000209731 00000 н.
0000209911 00000 н.
0000210090 00000 н.
0000210292 00000 п.
0000210479 00000 н.
0000210677 00000 н.
0000210856 00000 н.
0000211053 00000 н.
0000211251 00000 н.
0000211448 00000 н.
0000211642 00000 п.
0000211821 00000 н.
0000212015 00000 н.
0000212215 00000 н.
0000212394 00000 н.
0000212588 00000 н.
0000212784 00000 н.
0000212963 00000 н.
0000213154 00000 н.
0000213348 00000 п.
0000213527 00000 н.
0000213707 00000 н.
0000213912 00000 н.
0000214093 00000 н.
0000214274 00000 н.
0000214455 00000 н.
0000214637 00000 п.
0000214840 00000 н.
0000215018 00000 н.
0000215197 00000 н.
0000215401 00000 п.
0000215582 00000 н.
0000215763 00000 н.
0000215966 00000 н.
0000216145 00000 н.
0000216346 00000 н.
0000216527 00000 н.
0000216707 00000 н.
0000216907 00000 н.
0000217088 00000 н.
0000217294 00000 н.
0000217475 00000 н.
0000217680 00000 н.
0000217861 00000 н.
0000218063 00000 н.
0000218244 00000 н.
0000218441 00000 н.
0000218623 00000 н.
0000218818 00000 н.
0000219000 00000 н.
0000219205 00000 н.
0000219386 00000 н.
0000219590 00000 н.
0000219771 00000 п.
0000219972 00000 н.
0000220154 00000 н.
0000220349 00000 н.
0000220543 00000 н.
0000220736 00000 н.
0000220915 00000 н.
0000221107 00000 н.
0000221288 00000 н.
0000221480 00000 н.
0000221671 00000 н.
0000221870 00000 н.
0000222060 00000 н.
0000222259 00000 н.
0000222448 00000 н.
0000222626 00000 н.
0000222815 00000 н.
0000223009 00000 н.
0000223206 00000 н.
0000223394 00000 н.
0000223591 00000 н.
0000223779 00000 п.
0000223981 00000 н.
0000224169 00000 н.
0000224350 00000 н.
0000224538 00000 н.
0000224740 00000 н.
0000224921 00000 н.
0000225106 00000 п.
0000225291 00000 н.
0000225491 00000 п.
0000225672 00000 н.
0000225857 00000 н.
0000226038 00000 н.
0000226235 00000 н.
0000226419 00000 н.
0000226604 00000 н.
0000226785 00000 н.
0000226985 00000 н.
0000227172 00000 н.
0000227357 00000 н.
0000227542 00000 н.
0000227742 00000 н.
0000227930 00000 н.
0000228111 00000 п.
0000228293 00000 н.
0000228493 00000 н.
0000228682 00000 н.
0000228863 00000 н.
0000229048 00000 н.
0000229247 00000 н.
0000229436 00000 н.
0000229614 00000 н.
0000229799 00000 н.
0000229999 00000 н.
0000230192 00000 н.
0000230370 00000 н.
0000230567 00000 н.
0000230760 00000 н.
0000230956 00000 н.
0000231152 00000 п.
0000231330 00000 н.
0000231550 00000 н.
0000231746 00000 н.
0000231973 00000 н.
0000232172 00000 н.
0000232392 00000 н.
0000232598 00000 н.
0000232817 00000 н.
0000232998 00000 н.
0000233203 00000 н.
0000233384 00000 п.
0000233588 00000 н.
0000233767 00000 н.
0000233972 00000 н.
0000234151 00000 п.
0000234356 00000 п.
0000234537 00000 п.
0000234732 00000 н.
0000234913 00000 н.
0000235114 00000 п.
0000235305 00000 п.
0000235506 00000 н.
0000235707 00000 н.
0000235906 00000 н.
0000236084 00000 н.
0000236274 00000 н.
0000236465 00000 н.
0000236655 00000 н.
0000236845 00000 н.
0000237026 00000 н.
0000237215 00000 н.
0000237396 00000 н.
0000237589 00000 н.
0000237767 00000 н.
0000237948 00000 н.
0000238137 00000 н.
0000238326 00000 н.
0000238505 00000 н.
0000238683 00000 н.
0000238864 00000 н.
0000239057 00000 н.
0000239260 00000 н.
0000239449 00000 н.
0000239630 00000 н.
0000239816 00000 н.
0000240005 00000 н.
0000240191 00000 п.
0000240379 00000 н.
0000240565 00000 н.
0000240753 00000 п.
0000240934 00000 п.
0000241120 00000 н.
0000241301 00000 н.
0000241482 00000 н.
0000241667 00000 н.
0000241857 00000 н.
0000242042 00000 н.
0000242223 00000 н.
0000242417 00000 н.
0000242598 00000 н.
0000242779 00000 н.
0000242960 00000 н.
0000243141 00000 н.
0000243322 00000 н.
0000243507 00000 н.
0000243693 00000 н.
0000243879 00000 п.
0000244061 00000 н.
0000244246 00000 н.
0000244427 00000 н.
0000244606 00000 н.
0000244809 00000 н.
0000244996 00000 н.
0000245177 00000 н.
0000245358 00000 н.
0000245540 00000 н.
0000245747 00000 н.
0000245928 00000 н.
0000246109 00000 н.
0000246318 00000 н.
0000246523 00000 н.
0000246704 00000 н.
0000246885 00000 н.
0000247066 00000 н.
0000247271 00000 н.
0000247452 00000 н.
0000247637 00000 н.
0000247842 00000 н.
0000248023 00000 н.
0000248208 00000 н.
0000248419 00000 н.
0000248600 00000 н.
0000248788 00000 н.
0000249010 00000 н.
0000249191 00000 н.
0000249381 00000 п.
0000249590 00000 н.
0000249771 00000 н.
0000249952 00000 н.
0000250149 00000 н.
0000250330 00000 н.
0000250525 00000 н.
0000250725 00000 н.
0000250924 00000 н.
0000251105 00000 н.
0000251307 00000 н.
0000251523 00000 н.
0000251704 00000 н.
0000251921 00000 н.
0000252134 00000 н.
0000252315 00000 н.
0000252501 00000 н.
0000252687 00000 н.
0000252873 00000 н.
0000253073 00000 н.
0000253254 00000 н.
0000253435 00000 н.
0000253630 00000 н.
0000253811 00000 н.
0000254006 00000 н.
0000254187 00000 н.
0000254382 00000 н.
0000254563 00000 н.
0000254763 00000 н.
0000254945 00000 н.
0000255140 00000 н.
0000255322 00000 н.
0000255517 00000 н.
0000255715 00000 н.
0000255910 00000 н.
0000256089 00000 н.
0000256268 00000 н.
0000256467 00000 н.
0000256662 00000 н.
0000256857 00000 н.
0000257036 00000 н.
0000257235 00000 н.
0000257430 00000 н.
0000257624 00000 н.
0000257803 00000 н.
0000257989 00000 н.
0000258179 00000 н.
0000258369 00000 н.
0000258555 00000 н.
0000258736 00000 н.
0000258929 00000 н.
0000259119 00000 н.
0000259300 00000 н.
0000259493 00000 н.
0000259698 00000 н.
0000259895 00000 н.
0000260094 00000 н.
0000260275 00000 н.
0000260456 00000 н.
0000260658 00000 н.
0000260860 00000 н.
0000261064 00000 н.
0000261275 00000 н.
0000261456 00000 н.
0000261667 00000 н.
0000261852 00000 н.
0000262066 00000 н.
0000262275 00000 н.
0000262482 00000 н.
0000262688 00000 п.
0000262883 00000 н.
0000263078 00000 н.
0000263273 00000 н.
0000263468 00000 н.
0000263662 00000 н.
0000263856 00000 н.
0000264050 00000 н.
0000264235 00000 н.
0000264420 00000 н.
0000264602 00000 н.
0000264781 00000 н.
0000264963 00000 н.
0000265148 00000 н.
0000265333 00000 п.
0000265522 00000 н.
0000265703 00000 п.
0000265884 00000 н.
0000266069 00000 н.
0000266254 00000 н.
0000266439 00000 н.
0000266620 00000 н.
0000266801 00000 п.
0000266982 00000 н.
0000267163 00000 н.
0000267344 00000 н.
0000267525 00000 н.
0000267706 00000 н.
0000267891 00000 н.
0000268072 00000 н.
0000268253 00000 н.
0000268432 00000 н.
0000268613 00000 н.
0000268799 00000 н.
0000268980 00000 н.
0000269160 00000 н.
0000269341 00000 п.
0000269527 00000 н.
0000269708 00000 н.
0000269888 00000 н.
0000270069 00000 н.
0000270249 00000 н.
0000270430 00000 н.
0000270611 00000 п.
0000270797 00000 н.
0000270979 00000 п.
0000271159 00000 н.
0000271340 00000 н.
0000271520 00000 н.
0000271706 00000 н.
0000271887 00000 н.
0000272068 00000 н.
0000272248 00000 н.
0000272428 00000 н.
0000272609 00000 н.
0000272795 00000 н.
0000272976 00000 н.
0000273156 00000 н.
0000273336 00000 н.
0000273517 00000 н.
0000273698 00000 н.
0000273878 00000 н.
0000274058 00000 н.
0000274239 00000 н.
0000274419 00000 н.
0000274600 00000 н.
0000274780 00000 н.
0000274961 00000 н.
0000275141 00000 п.
0000275322 00000 н.
0000275503 00000 н.
0000275683 00000 н.
0000275864 00000 н.
0000276050 00000 н.
0000276230 00000 н.
0000276410 00000 н.
0000276591 00000 н.
0000276772 00000 н.
0000276952 00000 н.
0000277133 00000 н.
0000277313 00000 н.
0000277494 00000 н.
0000277673 00000 н.
0000277854 00000 н.
0000278034 00000 н.
0000278215 00000 н.
0000278394 00000 н.
0000278574 00000 н.
0000278755 00000 н.
0000278941 00000 н.
0000279122 00000 н.
0000279301 00000 н.
0000279482 00000 н.
0000279668 00000 н.
0000279847 00000 н.
0000280027 00000 н.
0000280209 00000 н.
0000280388 00000 н.
0000280569 00000 н.
0000280748 00000 н.
0000280929 00000 н.
0000281114 00000 н.
0000281295 00000 н.
0000281476 00000 н.
0000281657 00000 н.
0000281838 00000 н.
0000282019 00000 н.
0000282200 00000 н.
0000282381 00000 п.
0000282562 00000 н.
0000282743 00000 н.
0000282928 00000 н.
0000283117 00000 н.
0000283298 00000 н.
0000283483 00000 н.
0000283664 00000 н.
0000283849 00000 н.
0000284030 00000 н.
0000284215 00000 н.
0000284396 00000 н.
0000284581 00000 п.
0000284762 00000 н.
0000284943 00000 н.
0000285124 00000 н.
0000285309 00000 н.
0000285494 00000 н.
0000285674 00000 н.
0000285855 00000 н.
0000286036 00000 н.
0000286217 00000 н.
0000286397 00000 н.
0000286582 00000 н.
0000286767 00000 н.
0000286947 00000 н.
0000287128 00000 н.
0000287307 00000 н.
0000287488 00000 н.
0000287667 00000 н.
0000287848 00000 н.
0000288029 00000 н.
0000288209 00000 н.
0000288390 00000 н.
0000288570 00000 н.
0000288750 00000 н.
0000288932 00000 н.
0000289112 00000 н.
0000289293 00000 н.
0000289474 00000 н.
0000289654 00000 н.
0000289833 00000 н.
00002 00000 н.
00002 00000 н.
00002 00000 н.
00002 00000 н.
00002 00000 н.
00002
00000 н.
00002 00000 п.
00002
00000 н.
00002
Определить, являются ли два вектора параллельными или перпендикулярными
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее то информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
вектор | Определение, физика и факты
Вектор , в физике величина, которая имеет как величину, так и направление. Обычно он представлен стрелкой, направление которой совпадает с направлением количества, а длина пропорциональна величине величины.Хотя вектор имеет величину и направление, у него нет позиции. То есть, пока его длина не изменяется, вектор не изменяется, если он смещается параллельно самому себе.
В отличие от векторов, обычные величины, которые имеют величину, но не направление, называются скалярами. Например, смещение, скорость и ускорение — векторные величины, а скорость (величина скорости), время и масса — скаляры.
Чтобы считаться вектором, величина, имеющая величину и направление, также должна подчиняться определенным правилам комбинирования.Одним из них является сложение векторов, символически записываемое как A + B = C (векторы обычно обозначаются жирным шрифтом). С геометрической точки зрения векторную сумму можно визуализировать, поместив хвост вектора B в начало вектора A и нарисовав вектор C, начиная с хвоста A и заканчивая в голове B, так, чтобы он завершал треугольник. Если A, B и C являются векторами, должна быть возможность выполнить ту же операцию и получить тот же результат (C) в обратном порядке, B + A = C. Величины, такие как смещение и скорость, обладают этим свойством (закон коммутативности). , но есть количества (например,g., конечные вращения в пространстве), которые не являются векторами и поэтому не являются векторами.
Векторный параллелограмм для сложения и вычитанияОдин из методов сложения и вычитания векторов состоит в том, чтобы соединить их хвосты вместе, а затем подвести еще две стороны, чтобы сформировать параллелограмм. Вектор от их хвостов к противоположному углу параллелограмма равен сумме исходных векторов. Вектор между их головами (начиная с вычитаемого вектора) равен их разности.
Encyclopædia Britannica, Inc.Другими правилами обработки векторов являются вычитание, умножение на скаляр, скалярное умножение (также известное как скалярное произведение или внутреннее произведение), умножение векторов (также известное как перекрестное произведение) и дифференцирование. Нет операции, соответствующей делению на вектор. Описание всех этих правил см. В векторном анализе .
Правило правой руки для векторного векторного произведенияОбычное, или точечное, произведение двух векторов — это просто одномерное число или скаляр.Напротив, перекрестное произведение двух векторов приводит к другому вектору, направление которого ортогонально обоим исходным векторам, как показано правилом правой руки. Величина или длина вектора векторного произведения определяется выражением v w sin θ , где θ — это угол между исходными векторами v и w .
Encyclopædia Britannica, Inc. Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.Подпишитесь сейчасХотя векторы математически просты и чрезвычайно полезны при обсуждении физики, они не были разработаны в их современной форме до конца XIX века, когда Джозайя Уиллард Гиббс и Оливер Хевисайд (из США и Англии соответственно) применили векторный анализ в своих исследованиях. чтобы помочь выразить новые законы электромагнетизма, предложенные Джеймсом Клерком Максвеллом.
Добавление компонентов (т. Е. Аналитический метод сложения векторов)
Ранее в этом уроке мы узнали, что векторы, ориентированные под прямым углом друг к другу, можно сложить вместе с помощью теоремы Пифагора.Например, два вектора смещения с величиной и направлением 11 км, север и 11 км, восток, могут быть сложены вместе, чтобы получить результирующий вектор, направленный как на север, так и на восток. Когда два вектора складываются вместе, как показано ниже, в результате получается гипотенуза прямоугольного треугольника. Стороны прямоугольного треугольника имеют длину 11 км и 11 км. Результирующий можно определить с помощью теоремы Пифагора; его величина составляет 15,6 км. Решение показано под диаграммой.Этот подход Пифагора является полезным подходом для добавления любых двух векторов, направленных под прямым углом друг к другу. Прямоугольный треугольник имеет две стороны плюс гипотенузу; так что теорема Пифагора идеально подходит для сложения двух векторов под прямым углом. Но есть пределы полезности теоремы Пифагора при решении задач сложения векторов. Например, сложение трех или четырех векторов не приводит к образованию прямоугольного треугольника с двумя сторонами и гипотенузой.Поэтому на первый взгляд может показаться, что невозможно использовать теорему Пифагора для определения результата сложения трех или четырех векторов. Кроме того, теорема Пифагора работает, когда два добавленных вектора находятся под прямым углом друг к другу — например, для добавления вектора севера и вектора востока. Но что делать, если два складываемых вектора не расположены под прямым углом друг к другу? Есть ли способ использования математики для надежного определения результирующей для таких ситуаций сложения векторов? Или студенту-физику остается определять такие результирующие с помощью масштабированной векторной диаграммы? Здесь, на этой странице, мы узнаем, как подходить к более сложным ситуациям сложения векторов, комбинируя концепцию векторных компонентов (обсуждавшихся ранее) и принципов векторного разрешения (обсужденных ранее) с использованием теоремы Пифагора (обсуждавшейся ранее).
Добавление трех или более прямоугольных векторов
В качестве первого примера рассмотрим следующую задачу сложения векторов:Пример 1:
Студент едет на своей машине 6,0 км на север, затем делает поворот направо и едет на 6,0 км на восток. Наконец, ученик поворачивает налево и едет еще 2,0 км на север. Какова величина общего перемещения студента?
Как и любая проблема в физике, успешное решение начинается с выработки мысленной картины ситуации.Построение диаграммы, подобной приведенной ниже, часто оказывается полезным в процессе визуализации. Когда эти три вектора складываются вместе по принципу «голова к хвосту», результатом является вектор, который простирается от хвоста первого вектора (6,0 км, север, показан красным) до стрелки третьего вектора (2,0 км, Север, показан зеленым цветом). Схема сложения векторов «голова к хвосту» показана ниже. Как видно на диаграмме, результирующий вектор (нарисованный черным цветом) не является гипотенузой какого-либо прямоугольного треугольника — по крайней мере, не любого сразу очевидного прямоугольного треугольника.Но можно ли заставить этот результирующий вектор быть гипотенузой прямоугольного треугольника? Ответ — да! Для этого необходимо изменить порядок добавления трех векторов. Вышеуказанные векторы были нарисованы в том порядке, в котором они были запущены. Студент поехал на север, затем на восток, а затем снова на север. Но если сложить три вектора в порядке 6.0 км, N + 2.0 км, N + 6.0 км, E, то диаграмма будет выглядеть так: После изменения порядка добавления трех векторов результирующий вектор теперь является гипотенузой прямоугольного треугольника.Длина перпендикулярных сторон прямоугольного треугольника составляет 8,0 м, север (6,0 км + 2,0 км) и 6,0 км, восток. Величину результирующего вектора (R) можно определить с помощью теоремы Пифагора.
R 2 = (8,0 км) 2 + (6,0 км) 2
R 2 = 64,0 км 2 + 36,0 км 2
R 2 = 100,0 км 2
R = SQRT (100,0 км2)
R = 10,0 км
(SQRT означает квадратный корень)
На первой диаграмме сложения векторов выше три вектора были добавлены в том порядке, в котором они управляются.На второй диаграмме сложения векторов (непосредственно выше) порядок, в котором были добавлены векторы, был изменен. Это изменение порядка не повлияло на размер полученного результата. Это иллюстрирует важный момент о добавлении векторов: результат не зависит от порядка, в котором они добавляются. Сложение векторов A + B + C дает тот же результат, что и добавление векторов B + A + C или даже C + B + A . Пока все три вектора включены с указанными величиной и направлением, результат будет таким же.Это свойство векторов является ключом к стратегии, используемой при определении ответа на приведенный выше пример проблемы. Чтобы проиллюстрировать эту стратегию, давайте рассмотрим ситуацию сложения векторов, описанную в Примере 2 ниже.
Пример 2:
Mac и Тош делают Vector Walk Lab . Начиная с дверей своего класса физики, они проходят 2 метра на юг. Они делают поворот направо и идут 16.0 метров, запад. Они снова поворачивают направо и проходят 24,0 метра на север. Затем они поворачивают налево и проходят 36 метров на запад. Какова величина их общего смещения?
Графическое представление данной проблемы поможет визуализировать происходящее. На схеме ниже показано такое представление.
Когда эти четыре вектора складываются вместе по принципу « голова к хвосту », в результате получается вектор, идущий от хвоста первого вектора (2.0 м, юг, показан красным) до стрелки четвертого вектора (36,0 м, запад, показан зеленым). Схема сложения векторов «голова к хвосту» показана ниже. Результирующий вектор (нарисованный черным цветом и обозначенный R ) на приведенной выше диаграмме сложения векторов не является гипотенузой какого-либо сразу очевидного правого треугольника. Но, изменив порядок сложения этих четырех векторов, можно заставить этот результирующий вектор быть гипотенузой прямоугольного треугольника. Например, добавляя векторы в порядке 2.0 м, S + 24,0 м, N + 16,0 м, W + 36,0 м. W, результирующая становится гипотенузой прямоугольного треугольника. Это показано на диаграмме сложения векторов ниже. После перестановки векторов результирующая теперь гипотенуза прямоугольного треугольника, имеющего две перпендикулярные стороны длиной 22,0 м, север и 52,0 м, запад. 22,0 м, северная сторона, получается из 2,0 м, юга и 24,0 м, сложенных вместе. 52,0 м, западная сторона — результат 16,0 м, запад и 36,0 м, сложенные вместе.Величину результирующего вектора (R) можно определить с помощью теоремы Пифагора.
R 2 = (22,0 м) 2 + (52,0 м) 2
R 2 = 484,0 м 2 + 2704,0 м 2
R 2 = 3188,0 м 2
R = SQRT (3188,0 м2 2 )
R = 56,5 м
(SQRT означает квадратный корень)
Как видно из этих двух примеров, результат сложения трех или более векторов под прямым углом может быть легко определен с помощью теоремы Пифагора.Это включает добавление векторов в другом порядке.
SOH CAH TOA и направление векторов
Вышеупомянутое обсуждение объясняет метод определения величины результирующего для трех или более перпендикулярных векторов. Тема направления в обсуждении проигнорирована. Теперь обратимся к способу определения направления результирующего вектора. В качестве беглого обзора напомним, что ранее в этом уроке было введено соглашение для выражения направления вектора.Эта конвенция известна как «против часовой стрелки» от восточного соглашения, часто сокращенно CCW . Используя это соглашение, направление вектора часто выражается как угол поворота вектора против часовой стрелки вокруг его хвоста с востока.Чтобы начать обсуждение, вернемся к , Пример 1 выше, где мы попытались добавить три вектора: 6.0 км, N + 6.0 км, E + 2.0 км, N. В решении порядок сложения трех векторов был переставлен так, чтобы образовался прямоугольный треугольник, в результате чего получилась гипотенуза треугольника.Треугольник перерисовывается справа. Обратите внимание, что угол в нижнем левом углу треугольника обозначен как тета (Θ). Тета (Θ) представляет угол, который вектор образует с северной осью. Тета (Θ) можно вычислить с помощью одной из трех тригонометрических функций, представленных ранее в этом уроке — синуса, косинуса или тангенса. Мнемоника SOH CAH TOA — полезный способ запомнить, какую функцию использовать. В этой задаче мы хотим определить угловую меру тэты (), и нам известна длина стороны, противоположной тэте () — 6.0 км — и длина стороны, прилегающей к углу тета (Θ) — 8,0 км. TOA SOH CAH TOA указывает на то, что тангенс любого угла — это отношение длин стороны, противоположной стороне, к стороне, прилегающей к этому углу. Таким образом, тангенциальная функция будет использоваться для вычисления угловой меры теты (Θ). Работа представлена ниже.
Касательная (Θ) = напротив / рядом
Касательная (Θ) = 6,0 / 8,0
Касательная (Θ) = 0,75
Θ = загар -1 (0,75)
Θ = 36.869… °
Θ = 37 °
Проблема не исчезнет после того, как будет вычислено значение тета (Θ). Теперь эту угловую меру необходимо использовать для определения направления. Один из способов сделать это — просто указать, что направление полученного результата — 37 ° к востоку от севера. В качестве альтернативы можно использовать условное обозначение против часовой стрелки. Поскольку угол, который получается в результате с востоком, является дополнением к углу, который получается с севером, мы могли бы выразить направление как 53 ° против часовой стрелки.
Теперь мы рассмотрим Пример 2 как второй пример того, как использовать SOH CAH TOA для определения направления результирующего.В Примере 2 мы пытались определить величину 2,0 м. S + 16,0 м, W + 24,0 м, N + 36,0 м, W. Решение заключалось в изменении порядка сложения так, чтобы в результате получилась гипотенуза прямоугольного треугольника с известными сторонами. Правый треугольник показан ниже. Результат отображается черным цветом. Еще раз обратите внимание, что угол в правом нижнем углу треугольника обозначен как тета (Θ). Тета (Θ) представляет угол, который вектор образует с северной осью.
Theta (Θ) можно вычислить с помощью касательной функции.В этой задаче мы хотим определить угловую меру тета (), и нам известна длина стороны, противоположной тета (Θ) — 52,0 м — и длина стороны, примыкающей к углу тета (Θ) — 22,0 м. TOA SOH CAH TOA указывает на то, что тангенс любого угла — это отношение длин стороны, противоположной стороне, к стороне, прилегающей к этому углу. Таким образом, тангенциальная функция будет использоваться для вычисления угловой меры теты (Θ). Работа представлена ниже.
Касательная (Θ) = напротив / рядом
Касательная (Θ) = 52.0 / 22,0
Касательная (Θ) = 2,3636…
Θ = загар -1 (2,3636…)
Θ = 67,067… °
Θ = 67,1 °
Проблема не исчезнет после того, как будет вычислено значение тета (Θ). Теперь эту угловую меру необходимо использовать для определения направления. Один из способов сделать это — просто указать, что направление полученного результата составляет 67,1 ° к западу от севера. В качестве альтернативы можно использовать условное обозначение против часовой стрелки. Ось севера повернута на 90 ° против часовой стрелки от востока, и этот вектор равен дополнительным 67.1 ° против часовой стрелки после севера. Таким образом, направление CCW составляет 157,1 ° CCW.
Таким образом, направление вектора может быть определено так же, как и всегда — путем определения угла поворота против часовой стрелки с востока. Поскольку результат — гипотенуза прямоугольного треугольника, этого можно достичь, сначала найдя угол, который получается с одной из ближайших осей треугольника. После этого нужно немного подумать, чтобы связать угол с направлением.
Добавление неперпендикулярных векторов
Теперь мы рассмотрим ситуации, в которых два (или более) добавляемых вектора не расположены под прямым углом друг к другу. Теорема Пифагора неприменима к таким ситуациям, поскольку применима только к прямоугольным треугольникам. Два неперпендикулярных вектора не образуют прямоугольный треугольник. Тем не менее, можно заставить два (или более) неперпендикулярных вектора преобразовываться в другие векторы, которые образуют прямоугольный треугольник.Уловка включает в себя концепцию векторного компонента и процесс векторного разрешения.Компонент вектора описывает влияние вектора в заданном направлении. Любой вектор под углом имеет две компоненты; один направлен горизонтально, а другой — вертикально. Например, северо-западный вектор имеет северную составляющую и западную составляющую. Вместе эффект этих двух компонентов равен общему эффекту вектора под углом . В качестве примера рассмотрим самолет, который летит на северо-запад из аэропорта Чикаго О’Хара в сторону границы с Канадой.Вектор северо-западного смещения плоскости имеет две составляющие — северную и западную. При сложении эти две составляющие равны общему северо-западному смещению. Это показано на схеме ниже.
Вектор северо-запад имеет северную и западную составляющие, которые представлены как A x и A y . Можно сказать что
A = A x + A y
Поэтому всякий раз, когда мы думаем о векторе северо-запад, мы можем думать вместо двух векторов — вектора севера и вектора запада.Два компонента A x + A y могут быть заменены на один вектор A в задаче.Теперь предположим, что ваша задача заключается в сложении двух неперпендикулярных векторов. Мы будем называть векторы A и B . Вектор A — это вектор под неприятным углом, который не является ни горизонтальным, ни вертикальным. А вектор B — красивый, вежливый вектор, направленный горизонтально. Ситуация показана ниже.
Конечно, неприятный вектор A, имеет два компонента — A x и A y . Эти два компонента вместе равны вектору A . То есть A = A x + A y .
Чтобы увидеть, как этот процесс работает с реальной проблемой сложения векторов, рассмотрим пример 3, показанный ниже.
Пример 3:
Макс играет среднего полузащитника футбольной команды Юга.Во время одной игры в матче в прошлую пятницу вечером против Академии Нью-Грир, он сделал следующие движения после того, как мяч был захвачен на третьем падении. Сначала он дал задний ход в южном направлении на 2,6 метра. Затем он переместился влево (на запад) на расстояние 2,2 метра. Наконец, он сделал пол-оборота и пробежал вниз по полю на расстояние 4,8 метра в направлении 240 ° против часовой стрелки с востока (30 ° з.д.), прежде чем окончательно выбить ветер из широкого приемника New Greer. Определите величину и направление общего смещения Макса.
Как обычно, решение начинается с диаграммы добавляемых векторов.
Для облегчения обсуждения три вектора были помечены как векторы A , B и C . Результат — векторная сумма этих трех векторов; диаграмма сложения векторов «голова к хвосту» показывает, что результат направлен на юго-запад. Из трех добавляемых векторов вектор C явно является отвратительным вектором .Его направление не строго на юг и не на запад. Решение состоит в том, чтобы разложить этот вектор на его составляющие.
Процесс векторного разрешения обсуждался ранее в этом уроке. Этот процесс включает использование модуля и функций синуса и косинуса для определения x- и y-компонентов вектора. Вектор C составляет угол 30 ° с южным направлением. Изобразив прямоугольный треугольник с горизонтальным и вертикальным катетами и C в качестве гипотенузы, становится возможным определить компоненты вектора C.Это показано на схеме ниже. Сторона, примыкающая к этому углу в 30 ° в треугольнике, является вертикальной стороной; вертикальная сторона представляет собой вертикальную (южную) составляющую C — C y . Итак, чтобы определить C y , используется функция косинуса. Сторона, противоположная углу 30 °, является горизонтальной стороной; горизонтальная сторона представляет собой горизонтальную (западную) составляющую C — C x . Значения C x и C y можно определить с помощью SOH CAH TOA. Функция косинуса используется для определения компонента, направленного на юг, поскольку компонент, направленный на юг, примыкает к углу 30 °.Синусоидальная функция используется для определения западной составляющей, поскольку западная составляющая является стороной, противоположной углу 30 °. Работа представлена ниже.
Теперь наша задача сложения векторов была преобразована из добавления двух хороших векторов и одного неприятного вектора в добавление четырех хороших векторов.
Поскольку все векторы ориентированы вдоль обычных осей север-юг и восток-запад, они могут быть добавлены в любом порядке, чтобы получить прямоугольный треугольник, гипотенуза которого является результирующей.Такая диаграмма представлена ниже.
Перпендикулярные стороны треугольника имеют длину 4,6 метра и 6,756 метра. Длина горизонтальной стороны (4,6 м) была определена путем сложения значений B (2,2 м) и C x (2,4 м). Длина вертикальной стороны (6,756… м) определялась сложением значений A (2,6 м) и C y (4,156… м). Результирующая величина (R) теперь может быть определена с помощью теоремы Пифагора.
R 2 = (6.756… м) 2 + (4,6 м) 2
R 2 = 45,655… м 2 + 21,16 м 2
R 2 = 66,815… м 2
R = SQRT (66,815… м 2 )
R = 8,174… м
R = ~ 8,2 м
Направление результирующей можно определить, найдя угол, который она составляет с вектором север-юг или восток-запад. На диаграмме справа показан угол тета (Θ), отмеченный внутри треугольника сложения векторов.Этот угол тета — это угол, который получается в результате с западом. Его значение можно определить с помощью функции касательной. Функция касательной (как в TOA) связывает значение угла с отношением длин противоположной стороны к соседней стороне. Это,
касательная (Θ) = (6,756… м) / (4,6 м) = 1,46889…
Используя функцию обратной тангенсации, можно определить угол тета (Θ). На большинстве калькуляторов для этого используются кнопки 2-го касания.
Θ = загар -1 (1.46889…) = 55,7536… °
Θ = ~ 56 °
Пример 4 представляет собой последний пример того, как объединить разрешение вектора со сложением векторов, чтобы добавить три или более неперпендикулярных вектора.Поскольку этот пример включает в себя три особенно неприятных вектора , таблица будет использоваться для организации информации о величине и направлении компонентов. Использование таблицы — разумная идея, когда проблемы усложняются.
Пример 4:
Кэмерон Пер (его друзья зовут его Кэмом) и Бакстер Натур отправляются в поход. Начиная с домашней базы, они совершают следующие движения.A: 2,65 км, 140 ° против часовой стрелки
Определите величину и направление их общего смещения.
А: 4.77 км, 252 ° против часовой стрелки
C: 3,18 км, 332 ° против часовой стрелки
Наглядное представление ситуации показано ниже.
Чтобы определить результат, три отдельных вектора разделяются на горизонтальные и вертикальные компоненты. Информация об угле каждого вектора используется для формирования прямоугольного треугольника, в котором вектор является гипотенузой, а его перпендикулярные стороны ориентированы по осям восток-запад и север-юг.Это показано на схеме ниже.
Затем тригонометрические функции — синус, косинус и тангенс — используются для определения величины горизонтальной и вертикальной составляющих каждого вектора. Работа показана и организована в таблице ниже.
Вектор | Компонент Восток-Запад | Компонент Север-Юг |
| A 2.65 км 140 ° против часовой стрелки | (2,65 км) • cos (40 °) = 2,030… км, запад | (2,65 км) • sin (40 °) = 1,703… км, север |
| B 4.77 км 252 ° против часовой стрелки | (4,77 км) • sin (18 °) = 1,474… км, запад | (4,77 км) • cos (18 °) = 4,536… км, юг |
| С 3.18 км 332 ° против часовой стрелки | (3.18 км) • cos (28 °) = 2,808… км, восток | (3,18 км) • sin (28 °) = 1,493… км, юг |
| Сумма А + В + С | 0.696 км, Запад | 4.326 км, юг |
Последняя строка вышеприведенной таблицы представляет собой сумму всех компонентов Восток-Запад и сумму всех компонентов Север-Юг. Результирующий состоит из этих двух компонентов.Результирующая определяется путем сложения этих двух компонентов, чтобы сформировать прямоугольный треугольник, гипотенуза которого равна результирующей. Обычно это включает добавление всех горизонтальных компонентов для определения общей длины горизонтальной стороны прямоугольного треугольника… и добавление всех вертикальных компонентов для определения общей длины вертикальной стороны прямоугольного треугольника. Это делается в таблице выше, просто добавляя еще одну строку в таблицу для векторной суммы всех компонентов.При сложении компонентов восток-запад всех отдельных векторов необходимо учитывать, что компонент, направленный на восток, и компонент, направленный на запад, суммируются как положительный и отрицательный . Некоторые студенты предпочитают думать об этом как о вычитании, а не как о сложении. На самом деле это действительно сложение — сложение векторов с противоположным направлением. Точно так же северная и южная составляющие также суммируются как положительный и отрицательный .Как только нижняя строка определена точно, величина результирующего может быть определена с помощью теоремы Пифагора.
R 2 = (0,696 км) 2 + (4,326 км) 2
R 2 = 0,484 км 2 + 18,714 км 2
R 2 = 19,199 км 2
R = SQRT (19,199 км 2 )
R = ~ 4,38 км
Направление результирующего смещения можно определить, построив последний треугольник из составляющих результирующего.Компоненты результирующего — это просто сумма компонентов восток-запад и север-юг. После этого SOH CAH TOA используется для определения угла, который получается в результате с ближайшей осью. Схема показана справа. Угол, обозначенный как тета (Θ), представляет собой угол между результирующим вектором и западной осью. Этот угол можно рассчитать следующим образом:
Касательная (Θ) = напротив / рядом
Касательная (Θ) = (4,326 км) / (0,696 км)
Касательная (Θ) = 6,216
Θ = загар -1 (6.216)
Θ = 80,9 °
Эта угловая мера представляет собой угол поворота вектора к югу от западного направления. Его можно было бы записать как 80,9 ° к югу от запада. Поскольку запад равен 180 ° против часовой стрелки от востока, направление также может быть выражено против часовой стрелки (CCW) от восточного соглашения как 260,9 °.
Итак, результатом нашего анализа является то, что общее смещение составляет 4,38 км при направлении 260,9 ° (против часовой стрелки).
На этой странице были рассмотрены следующие вопросы:
- Как можно сложить три или более перпендикулярных вектора, чтобы определить результат?
- Как можно сложить два или более неперпендикулярных вектора, чтобы определить результат?
Поэкспериментируйте с виджетом ниже, а затем попробуйте выполнить задачи в разделе «Проверьте свое понимание», чтобы проверить свои навыки добавления векторов с помощью компонентов.
Практика! Виджет ниже вычисляет сумму трех векторов, если известны x- и y-компоненты.Используйте виджет, чтобы попрактиковаться и проверить проблему. Проверьте свое понимание Рассмотрим схему ниже. В сетке представлены девять уникальных помеченных мест. Каждый квадрат в сетке представляет собой площадь 20 х 20 метров. Справа по сетке — в восточном направлении, а вверх по сетке — в северном направлении. Используйте сетку, чтобы ответить на несколько следующих вопросов.1.Предположим, что человек начинает с позиции A и идет в позицию E, а затем в позицию G. Заполните таблицу ниже, указав компоненты восток-запад и север-юг отдельных этапов прогулки и компоненты результирующего смещения. . Делайте измерения вне сетки. Наконец, используйте теорему Пифагора и SOH CAH TOA, чтобы определить величину и направление результирующего смещения.
Вектор | Компонент Восток-Запад | Компонент Север-Юг |
| от A до E | ||
| от E до G | ||
| Результат От A до G |
Величина результата: _________________________
Направление результата: _________________________
2.Используя ту же сетку, повторите измерения для прогулки от точки C до точки B и до точки F. Выполните измерения вне сетки и используйте теорему Пифагора и SOH CAH TOA, чтобы определить величину и направление результирующего смещения.
Вектор | Компонент Восток-Запад | Компонент Север-Юг |
| C до B | ||
| От B до F | ||
| Результат C по F |
Величина результата: _________________________
Направление результата: _________________________
3.Наконец, используйте ту же сетку, чтобы повторить измерения для прогулки от точки I до точки B, от точки G до точки H. Сделайте измерения вне сетки и используйте теорему Пифагора и SOH CAH TOA, чтобы определить величину и направление движения. результирующее смещение.
Вектор | Компонент Восток-Запад | Компонент Север-Юг |
| I к B | ||
| от B до G | ||
| от G до H | ||
| Результат I к H |
Величина результата: _________________________
Направление результата: _________________________
4.Во время своего недавнего похода в продуктовый магазин Клэр де Иль прошла 28 м до конца прохода. Затем она повернула направо и прошла 12 м до конца прохода. Наконец, она сделала еще один поворот направо и прошла 12 м в направлении, противоположном ее первоначальному направлению. Определите величину результирующего смещения Клэр. (Фактическое направление — восток, запад, север, юг — не в фокусе.)
5. В заключительной игре прошлогоднего регулярного сезона Саут играл в Академии Нью-Грира за Чемпионат Конференции.В последней игре игры звездный квотербек Эйвери отвлекся от схватки и ускользнул назад (на север) на 8,0 ярдов. Затем он пробежал боком (на запад) из кармана на 12,0 ярдов, прежде чем, наконец, бросил пас на 34,0 ярда прямо вниз (на юг) Кендаллу для выигрышного тачдауна. Определите величину и направление смещения мяча.
6. Миа Андер выходит через парадную дверь своего дома и идет по дорожке, показанной на схеме справа (не в масштабе).Прогулка состоит из четырех этапов и имеет следующие величины:
A = 46 м
B = 142 м
C = 78 м
D = 89 м
Определите величину и направление результирующего смещения Миа. Рассмотрите возможность использования таблицы для организации своих расчетов.
MathScene — Векторы — Урок 3
MathScene — Векторы — Урок 32008 Расмус Эхф и Джанн Сак |
Урок 3
Векторы в системе координат
Пример 1
В точка A имеет координаты (2, 2), а точка B — координаты (6, 5) (см. диаграмму).Координаты вектора
Мы
можно использовать формулу для расстояния между двумя точками, чтобы найти расстояние
между A и B, то есть длина вектора
(см. Правило Пифагора в уроке 2). Формула выглядит следующим образом:
Подставляя заданные координаты в формулу, получаем:
Мы видим, что числа под квадратным корнем — это просто координаты вектор.Это, конечно, потому, что длина вектора — это просто гипотенуза в прямоугольном треугольнике с более короткими сторонами 3 и 4.
Формула длины вектора, начинающегося в точке
A = (x 1 , y 1 ) и заканчивается на B = (x 2 ,
y 2 ) равен:
Если координаты вектора равны то у нас есть следующее правило:
Пример 2
Найдите вектор что параллельно и который имеет длину 2 единицы (видеть диаграмму).
Два треугольника на диаграмме похожи, поэтому соответствующие
стороны находятся в одинаковом соотношении.
||
= t ∙ ||. Число t — это соотношение между соответствующими сторонами. Соотношение есть.
Мы можем найти координаты как
следует:
Если векторы а также находятся параллельно, то существует такое число t, что:
= т ∙ |
Пример 3
Какие из следующих векторов параллельны а также .
Если векторов а также находятся параллельно, то существует такое число t, что = т ∙. Если векторы а также находятся параллельно существует такое число r, что знак равно г ∙.
Мы можно найти числа t и r, используя координаты x, а затем проверить, чтобы увидеть будут ли найдены те же значения, когда мы используем координаты y.
= т ∙
3 = t ∙ 13 дает t = 3/13 = 2/9
4 = t ∙ 18 также дает t = 4/18 = 2/9
В векторов и соток параллель .
= г ∙
3 = r ∙ 6 дает r =
4 = r ∙ 9 дает r = 4/9
В векторов и соток не параллельно (Это значит, что а также находятся тоже не параллельно).
Вектор на схеме имеет координаты . В вектор начинается в точке (0, 0) и заканчивается в (3, 2), поэтому координаты конечная точка совпадает с координатами самого вектора.Это верно для все векторы, которые начинаются в начале системы координат, то есть в точка (0, 0).
Вектор, начинающийся в точке (0, 0), имеет те же координаты, что и его конечная точка. Этот вектор называется вектором положения для A. |
Каждая точка в системе координат может быть представлена своим вектором положения. Координаты точки и ее вектор положения совпадают.Это может быть очень полезно при просмотре переводов в системе координат.
Пример 4
Треугольник, изображенный на схеме, должен быть переведен на вектор .
Мы используем векторы положения вершин точек (−3, 0),
(2, −2) и (3, 1) и складываем вектор
каждому из них.
Это дает нам новый вектор положения каждой вершины.Схема ниже показывает перевод.
Пример 5
Теперь мы будем использовать векторы положения, чтобы найти середину отрезка AB, если A = (1, 2) и B = (4, 3).
Как обычно, точка O является началом системы координат. Если M середина AB тогда:
знак равно + ∙
Вектор является вектор положения точки M и, следовательно, имеет те же координаты, что и точка M, которую мы хотим вычислить.Вектор вектор положения A. Чтобы достичь средней точки M, нам нужно добавить половину вектор. Нарисуйте диаграмму, чтобы увидеть это.
Сначала нам нужно найти вектор .
Теперь мы можем найти .
знак равно + ∙
Координаты M такие же, как у вектора положения. или (2, 2) .
Легко найти формулу, по которой мы сможем найти координаты середина отрезка AB.
2 = + ∙ + — ∙
Мы видим, что вектор положения середины отрезка линии является своего рода
среднее из векторов положения конечных точек. Таким образом, мы можем найти
координаты средней точки путем нахождения среднего значения координат x и y
координаты соответственно.
Это приводит нас к правилу, которое мы называем правилом средней точки.
Середина M отрезка AB задается правилом: .Правило использования координат: . |
Пример 6
Вершины треугольника ABC равны A = (1, 2), B = (4, 3) и C = (3, 0).
Найдите длину линии от A до середины стороны BC (медиана треугольник ABC).
Начнем с поиска середины BC, используя указанное выше правило.
Назовем среднюю точку M и найдем ее вектор положения (видеть диаграмму).
Следовательно, M, середина BC имеет координаты
.
М = (3, 1).
Далее находим координаты вектора .
Наконец, мы можем найти длину вектора как обязательный.
≈ 2,55
= + ∙
= + ∙ — ∙
= — ∙ — ∙
Когда мы складываем их вместе, выходит и получаем:
3 = + +
Чтобы найти координаты T, мы берем среднее значение x и y координаты вершин соответственно. |
Таким образом, мы находим точку пересечения T медиан треугольник, найдя своего рода среднее из векторов положения вершины. Таким образом, это правило является расширением правила средней точки.
Пример 7
Найдите точку пересечения T медиан треугольника ABC ( центр) при условии, что A = (1, 2), B = (4, 3) и C = (3, 0) (см. |

