Конденсаторы: меняем толщину диэлектрика

В этой статье предложены задачи, которые помогут отработать формулы пересчета последовательного и параллельного соединения конденсаторов в эквивалентную емкость, причем одновременно будем менять либо диэлектрическую проницаемость, либо толщину слоя диэлектрика.

Задача 1. Плоский воздушный конденсатор, расстояние между пластинами которого м, до половины погрузили в масло. На какое расстояние следует раздвинуть пластины, чтобы емкость конденсатора не изменилась?

Сначала емкость конденсатора была равна

   

Затем, когда половину площади пластин погрузили в масло, мы получили словно два конденсатора, соединенных параллельно: один с масляным диэлектриком, второй – без. Площади их пластин одинаковы и равны . Тогда емкость такой системы будет равна

   

– это то новое расстояние, на которое мы раздвинем пластины, чтобы емкость не изменилась. Приравняем обе емкости:

   

   

   

   

Расстояние изменили на

   

Ответ: нужно раздвинуть пластины на 6 мм.

 

Задача 2. Конденсатор какой емкости следует подключить последовательно к конденсатору емкостью пФ, чтобы емкость батареи  была С = 160 пФ?

При последовательном соединении двух конденсаторов их эквивалентная емкость будет равна

   

(Она получается из формулы приведением к общему знаменателю.)

Тогда:

   

   

   

   

Ответ: 200 пФ

Задача 3. Два последовательно соединенных конденсатора емкостями мкФ и мкФ присоединены к источнику постоянного напряжения В. Определить напряжение на каждом конденсаторе.

Так как конденсаторы соединены последовательно, их заряды одинаковы. Тогда

   

Сумма напряжений на последовательно соединенных элементах равна напряжению на источнике:

   

Тогда можно записать:

   

   

   

Тогда В.

Ответ: В, В.

Задача 4.  Два одинаковых воздушных конденсатора соединены последовательно и подключены к батарее с постоянной ЭДС. Один из них заполняют диэлектриком с диэлектрической проницаемостью . Во сколько раз изменится напряженность электрического поля в  этом конденсаторе?

Так как напряженность непосредственно связана с напряжением на конденсаторе, то определим, как изменится напряжение на каждом из конденсаторов.

Сначала на конденсаторах одинаковое напряжение, так как они соединены последовательно, и емкости у них одинаковые – . Затем емкость второго конденсатора меняется в раз, и заряды  по-прежнему остаются одинаковыми на обоих конденсаторах, а напряжения – нет:

   

   

Решаем систему:

   

   

   

Найдем отношение  напряженностей:

   

Ответ: напряженность изменится в 0,4 раза.
Задача 5. Пространство между обкладками плоского конденсатора заполнено двумя слоями диэлектриков толщиной и , которые параллельны обкладкам конденсатора. Диэлектрические проницаемости диэлектриков  и соответственно. Площадь пластин . Найти емкость конденсатора С.

Такое расположение слоев диэлектриков приводит к тому, что емкость такого конденсатора равна (эквивалентна) двум последовательно соединенным конденсаторам с емкостями и .

Эквивалентная емкость двух последовательно соединенных конденсаторов:

   

Задача 6. У плоского конденсатора, заполненного твердым диэлектриком с диэлектрической проницаемостью одну  пластину отодвигают от диэлектрика на расстояние, равное  половине толщины диэлектрического слоя. При каком значении  емкость конденсатора изменится в  2 раза?

Полученный конденсатор эквивалентен двум последовательно включенным: один с диэлектриком, второй воздушный.

Первоначальная емкость:

   

После изменения:

   

Где :

   

   

   

Так как по условию

   

(емкость уменьшается, ведь мы увеличиваем расстояние между пластинами),то

   

   

   

Ответ:

 

Задача 7. У плоского воздушного конденсатора, заполненного слюдой, удаляют треть толщины диэлектрического слоя. Как и во сколько раз меняется при этом емкость конденсатора?

Первоначальная емкость:

   

После изменения:

   

Где – емкость конденсатора с утонченным слоем диэлектрика, а – емкость воздушного конденсатора:

   

   

   

   

Найдем отношение:

   

Ответ: емкость уменьшится, в 2,66 раза.

Чертов (Задачи 6-10)

Электрическая емкость плоского конденсатора

 

17.6. Определить электроемкость С плоского слюдяного конденсатора, площадь S пластин которого равна 100 , а расстояние между ними равно 0,1 мм.

 

Дано:                                                 Решение:

S=100 =10^{-2 м2}

d=0,1 мм=10^-4м

 

С-?

Ответ: 6,3×10

-9 Ф

 

 17.7. Между платинами плоского конденсатора, заряженного до разности потенциалов U=600 В, находится два слоя диэлектриков: стекла толщиной =7 мм и эбонита толщиной =3 мм. Площадь S каждой пластины конденсатора равна 200 . Найти: 1) электроемкость С конденсатора; 2) смещение D, напряженность Е поля и падение потенциала  в каждом слое.

 

Дано:                                                                         Решение:

U=600 В

=7 мм=7×10^{-4 м}

=3 мм=3×10^{-4 м}

S=200 =2×10^{-2 м2}

 

С-?   D-? Е-?  -?

 

 

 

 

 

 

Ответ: 88,5×10^-12 Ф ; 2,66 мкКл/м² ; 100 кВ/м ; 300 В ; 300 В

 

17.8. Расстояние d между пластинами плоского конденсатора равно 1,33 м, площадь S пластин равна 20 . В пространстве между пластинами конденсатора находятся два слоя диэлектриков: слюды толщиной

=0,7 мм и эбонита толщиной =0,3 мм. Определить электроемкость С конденсатора.

 

Дано:                                                                         Решение:

d=1,33 м

S=20 =0,2×10^{-2 м2}

=0,7 мм=0,7×10^{-4 м}

=0,3 мм=0,3×10^{-4 м}

 

С-?

 

Ответ: 35,4×10^-12 Ф

 

17.9. На пластинах плоского конденсатора равномерно распределен заряд с поверхностной плотностью =0,2

. Расстояние d между пластинами равно 1 мм. На сколько изменится разность потенциалов на его обкладках при увеличении расстояния d между пластинами до 3 мм?

 

Дано:                                                                         Решение:

=

d=1 мм=1×10^{-4 м}

 

 

 

 

 

 

Ответ: 45,2 В

 

17.10. В плоский конденсатор вдвинули плитку парафина толщиной d=1 см, которая вплотную прилегает к его пластинам. Насколько нужно увеличить расстояние между пластинами, чтобы получить прежнюю емкость?

 

Дано:                                                             Решение:

d=0,01 м

 

 

 

 

 

 

Ответ: 0,5 см

 

Решение задач В 📝 плоском конденсаторе находятся два слоя диэлектрика с

1. Сколько стоит помощь?

Цена, как известно, зависит от объёма, сложности и срочности. Особенностью «Всё сдал!» является то, что все заказчики работают со экспертами напрямую (без посредников). Поэтому цены в 2-3 раза ниже.

2. Каковы сроки?

Специалистам под силу выполнить как срочный заказ, так и сложный, требующий существенных временных затрат. Для каждой работы определяются оптимальные сроки. Например, помощь с курсовой работой – 5-7 дней. Сообщите нам ваши сроки, и мы выполним работу не позднее указанной даты. P.S.: наши эксперты всегда стараются выполнить работу раньше срока.

3. Выполняете ли вы срочные заказы?

Да, у нас большой опыт выполнения срочных заказов.

4. Если потребуется доработка или дополнительная консультация, это бесплатно?

Да, доработки и консультации в рамках заказа бесплатны, и выполняются в максимально короткие сроки.

5. Я разместил заказ. Могу ли я не платить, если меня не устроит стоимость?

Да, конечно — оценка стоимости бесплатна и ни к чему вас не обязывает.

6. Каким способом можно произвести оплату?

Работу можно оплатить множеством способом: картой Visa / MasterCard, с баланса мобильного, в терминале, в салонах Евросеть / Связной, через Сбербанк и т.д.

7. Предоставляете ли вы гарантии на услуги?

На все виды услуг мы даем гарантию. Если эксперт не справится — мы вернём 100% суммы.

8. Какой у вас режим работы?

Мы принимаем заявки 7 дней в неделю, 24 часа в сутки.

Задачи по элдектростатике повышенной сложности

Физика на 100 Электродинамика Гойхман ГС

Задача 1 (Олимпиада «Физтех-2015). Две проводящие пластины с зарядами Q>О и -4Q расположены параллельно и напротив друг друга (см. рис.). Площадь каждой пластины S, размеры пластин велики по сравнению с расстоянием d между ними, и можно считать, что заряды распределены по каждой поверхности пластин равномерно.

1) Найти разность потенциалов левой и правой пластин.

2) Найти заряд на левой стороне левой пластины.

3) Найти силу притяжения пластин.

Решение. Изобразим на рисунке линии напряженности электрического поля каждой пластины. Напряжённость электрического поля между пластинами равна геометрической сумме напряжённостей составляющих полей. Видно, что направление векторов напряженностей «синих» и «красных» полей совпадает. А потому 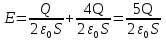. А разность потенциалов между пластинами равна 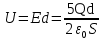. Силу притяжения пластин определим по формуле 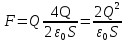. Это справедливо, учитывая, что левая пластина находится в поле правой пластины.

Для определения заряда на левой стороне левой пластины учтём, что поля внутри металического проводника нет. Под действием поля правой пластины произойдёт перераспределение зарядов на левой и правой сторонах левой пластины (электростатическая индукция). Пусть на левой стороне левой пластины индуцируется заряд q, тогда на правой стороне заряд будет равен Q-q. Таким образом, внутри левой пластины создаётся, как бы, поле трех пластин: левой и правой сторон левой пластины и целиком правой пластины. Их векторная сумма равна нулю: .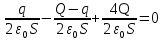

Отсюда 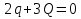и .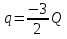

Ответ: , ,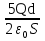

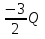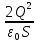
Задача 2 (Олимпиада «Физтех-2015). Три небольших по размерам положительно заряженных шарика связаны попарно тремя легкими непроводящими нитями и находятся неподвижно в вершинах равнобедренного треугольника со сторонами a, 2а, 2а. Каждый из шариков, связанных короткой нитью, имеет массу m и заряд q. Третий шарик имеет массу 3m и заряд 2q. Короткую нить пережигают, и шарики начинают двигаться. В момент, когда шарики оказались на одной прямой, скорость шарика массой 3m оказалась v.

1) Найдите в этот момент скорость двух других шариков.

2) Найдите q, считая известными m, v, а.

Решение. После пережигания короткой нити в результате взаимодействия только друг с другом заряженные шарики приходят в движение. Нить при этом остаётся натянутой, так как шарики все заряжены одноименным зарядом.

3m

2q

m

q

m

q

Рис. 1

m

m

3m

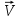
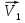
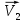
Рис. 2

По закону сохранения импульса 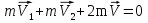. С учётом направления векторов скорости 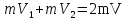и из соображений симметрии .

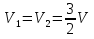Для нахождения заряда q воспользуемся законом сохранения энергии. Связанная в соответствии с рис. 1 система шаров обладает потенциальной энергией; в ней все шары взаимодействуют друг с другом попарно. Та же система шаров на рис.2 кроме попарного взаимодействия еще и движется; следовательно имеется и энергия кинетическая. Поэтому

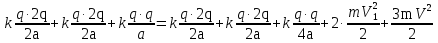
После упрощений и с учётом 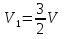получим

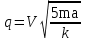
Здесь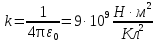

Ответ: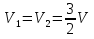

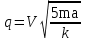
Задача 3 (Олимпиада «Физтех-2014). Плоский воздушный конденсатор ёмкостью С₀ и расстоянием между обкладками d заряжен до напряжения U₀ и отсоединён от источника.

1. Найдите силу притяжения обкладок.

2. Какую минимальную работу надо совершить, чтобы увеличить расстояние между обкладками на ?

Решение. Если полагать, что расстояние d между пластинами значительно меньше размеров самих пластин, то поле внутри однородно и имеет напряженность, равную 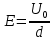. Каждая из пластин находится в поле другой пластины с напряженностью, равной 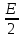. Поэтому сила притяжения равна

.

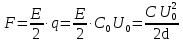Ёмкость плоского воздушного конденсатора определяется формулой 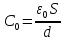. Увеличение расстояния между пластинами на 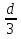сделает ёмкость конденсатора, равной 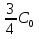.Заряд при этом не изменится и останется равным q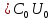. Вначале энергия электрического поля конденсатора была равна 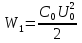, а затем — 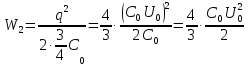. Работа, совершённая при раздвигании обкладок, увеличила энергию конденсатора. При этом

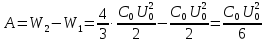
Ответ: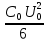

Задача 4 (Олимпиада «Физтех-2011). Плоский конденсатор заряжен и отключён от источника постоянного напряжения. В конденсатор вставляют пластину из диэлектрика (см. рис.) так, что диэлектрик заполняет половину объёма конденсатора, из-за чего разность потенциалов между пластинами уменьшается в два раза.

1. Во сколько раз и как изменилась напряжённость электрического поля внутри конденсатора в области без диэлектрика?

2. Найдите диэлектрическую проницаемость ε материала диэлектрической пластины.

Решение. Если конденсатор без диэлектрика равна C, то накопленный на нём заряд равен 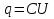. Заполненный наполовину диэлектриком конденсатор можно представить в виде двух параллельно включённых конденсаторов: один с ёмкостью 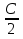, а второй — ёмкостью 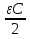. По условию напряжение снизилось вдвое. При этом заряд первого равен 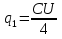, а заряд второго — 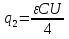. При этом 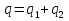. Отсюда 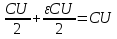. Поэтому ε=3.

Первоначально напряжённость поля равна 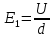, где d — расстояние между пластинами. После ввода диэлектрика 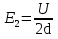. Таким образом, .

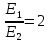Ответ: 1) уменьшилась вдвое; 2) ε=3

Задача 5 (Олимпиада «Физтех-2011). Плоский конденсатор подключён к источнику постоянного напряжения. Не отключая источника, в конденсатор вставляют пластину из диэлектрика (см. рис.), толщина которой равна 2/3 от расстояния между пластинами конденсатора (диэлектрик заполняет 2/3 объёма конденсатора), из-за чего заряд на пластинах конденсатора увеличивается в два раза.

1. Во сколько раз и как изменилась напряжённость электрического поля внутри конденсатора в области без диэлектрика?

2. Найдите диэлектрическую проницаемость материала диэлектрической пластины.

Решение. В отсутствии пластины из диэлектрика заряд на конденсаторе равен 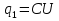. После ввода пластины этот конденсатор можно представить как два последовательно включённых конденсатора, один из которых заполнен диэлектриком. По условию ёмкость верхнего конденсатора равна 3C, а нижнего — 1,5εC. Тогда общая ёмкость равна 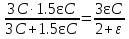. Тогда заряд на пластинах этого конденсатора равен 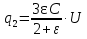. Так как по условию 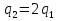, то 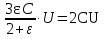. Отсюда 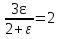. И, наконец, ε=4.

Так как заряд вырос в два раза, то напряженность поля в воздушном промежутке также выросла в два раза.

Ответ: 1) увеличится в два раза; 2) ε=4.

Задача 6 (Олимпиада «Физтех-2013). Проводящий шарик радиусом R с зарядом Q имеет потенциал φ₁=200 В. Каким станет потенциал φ₂ шарика, если он окажется внутри полого проводящего шара с радиусами сферических поверхностей 2R и 3R и зарядом 2Q? Центры заряженного шарика и полого шара совпадают.

R

2R

3R

Q

q₁

q₂

Решение. На внутренней и внешней поверхностях полого шара индуцируются заряды q₁ и q₂, причём q₁+q₂=2Q. Для начала определим эти индуцированные заряды. Следует напомнить, что потенциал на поверхности одиночной сферы и вне её обратно пропорционален расстоянию от центра сферы, а внутри одиночной сферы равен потенциалу на поверхности. Тогда по принципу суперпозиции полей потенциал на внешней поверхности сферического слоя

,

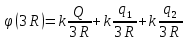а на внутренней поверхности того же сферического слоя —

.

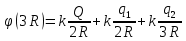Но внутри проводника потенциал одинаковый, поэтому

.

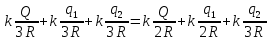Отсюда, учитывая q₁+q₂=2Q, получим q₁=-Q и q₂=3Q. Тогда искомый потенциал

.

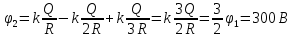Ответ: 300 В

ε₁

ε₂

_+Q

-Q

Задача 7 (Олимпиада «Физтех-2006). Две одинаковые половинки плоского конденсатора заполнены разными диэлектриками с диэлектрическими проницаемостями ε₁ и ε₂ (см. рис.). Заряд на обкладках конденсатора равен Q. Определить величину и знак связанного (поляризационного) заряда верхнего диэлектрика у левой обкладки конденсатора.

Решение. Напряжённость электрического поля между обкладками конденсатора складывается из напряжённостей полей зарядов на обкладках и поляризационного заряда диэлектрика. Для верхней половины конденсатора по принципу суперпозиции полей 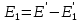. Здесь 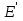— напряжённость в отсутствие диэлектрика при тех же зарядах Q, а 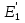— напряжённость поля поляризационного заряда. Учтено, что индуцированный заряд слева на диэлектрике отрицательный. Аналогично в нижней половине конденсатора 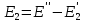. 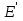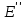Значения и различны, так как при поляризации различных диэлектриков произошло перераспределение зарядов на обкладках конденсатора.

Учитывая, что 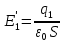, 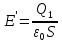и 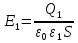. Здесь 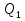— заряд верхней половины пластин, 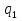— индуцированный заряд верхнего диэлектрика, а S — площадь половинки обкладки. Отсюда

,

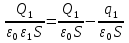далее

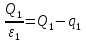и

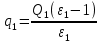
Аналогично

.

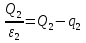Кроме того, 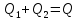и, учитывая 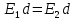(разность потенциалов) или 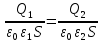, получим, опуская алгебраические подробности,

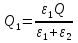
и

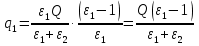
Ответ: 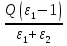, отрицательный.

Задачи для самостоятельного решения.

1. (Олимпиада «Физтех-2015). Две проводящие пластины с положительными зарядами Q и 5Q расположены параллельна и напротив друг друга (см. рис.). Площадь каждой пластины S, размеры пластин велики по сравнению с расстоянием d между ними, и можно считать, что заряды распределены по каждой поверхности пластин равномерно.

1. Найти разность потенциалов правой и левой пластин.

2. Найти заряд на правой стороне левой пластины.

3. Найти силу отталкивания пластин.

2. (Олимпиада «Физтех-2015). Две проводящие пластины с зарядами Q>О и -3Q расположены параллельно и напротив друг друга (см. рис.). Площадь каждой пластины S, размеры пластин велики но сравнению с расстоянием d между ними, и можно считать, что заряды распределены но каждой поверхности пластин равномерно.

1. Найти разность потенциалов левой и правой пластин.

2. Найти заряд на правой стороне правой пластины.

3. Найти силу притяжения пластин.

3. (Олимпиада «Физтех-2011). Плоский конденсатор заряжен и отключён от источника постоянного напряжения. В конденсатор вставляют пластину из диэлектрика (см. рис.) так, что диэлектрик заполняет половину объёма конденсатора, из-за чего разность потенциалов между пластинами уменьшается в три раза.

1. Во сколько раз и как изменилась напряжённость электрического поля внутри конденсатора в области без диэлектрика?

2. Найдите диэлектрическую проницаемость ε материала диэлектрической пластины.

3. Ответ: 1) уменьшилась втрое; 2) ε=5

4. (Олимпиада «Физтех-2011). Плоский конденсатор заряжен и отключён от источника постоянного напряжения. В конденсатор вставляют пластину из диэлектрика (см. рис.) так, что диэлектрик заполняет треть объёма конденсатора, из-за чего разность потенциалов между пластинами уменьшается в два раза.

1. Во сколько раз и как изменилась напряжённость электрического поля внутри конденсатора в области без диэлектрика?

2. Найдите диэлектрическую проницаемость ε материала диэлектрической пластины.

Ответ: 1) уменьшилась в два раза; 2) ε=4

5. (Олимпиада «Физтех-2011). Плоский конденсатор заряжен и отключён от источника постоянного напряжения. В конденсатор вставляют пластину из диэлектрика (см. рис.) так, что диэлектрик заполняет треть объёма конденсатора, из-за чего разность потенциалов между пластинами уменьшается в три раза.

1. Во сколько раз и как изменилась напряжённость электрического поля внутри конденсатора в области без диэлектрика?

2. Найдите диэлектрическую проницаемость ε материала диэлектрической пластины.

Ответ: 1) уменьшилась в три раза; 2) ε=7

6. (Олимпиада «Физтех-2011). Плоский конденсатор подключён к источнику постоянного напряжения. Не отключая источника, в конденсатор вставляют пластину из диэлектрика (см. рис.), толщина которой равна 5/6 от расстояния между пластинами конденсатора (диэлектрик заполняет 5/6 объёма конденсатора), из-за чего заряд на пластинах конденсатора увеличивается в три раза.

1. Во сколько раз и как изменилась напряжённость электрического поля внутри конденсатора в области без диэлектрика?

2. Найдите диэлектрическую проницаемость материала диэлектрической пластины.

Ответ: 1) увеличится в 3 раза; 2) ε=5.

7. (Олимпиада «Физтех-2013). Потенциал электростатического поля в точке А на расстоянии R от точечного заряда Q равен φ₁=300 В. Каким станет потенциал φ₂ в точке А, если заряд Q окажется в центре полого проводящего шара радиусами поверхностей 3R и 4R и зарядом 3Q?

Ответ: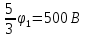

8. (Олимпиада «Физтех-2013). Проводящий шарик радиусом R с зарядом Q имеет потенциал φ₁=400 В. Каким станет потенциал φ₂ шарика, если он окажется внутри полого проводящего шара с радиусами сферических поверхностей 4R и 5R и зарядом 4Q? Центры заряженного шарика и полого шара совпадают.

Ответ: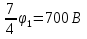

9. (Олимпиада «Физтех-2013). Потенциал электростатического поля в точке А на расстоянии R от точечного заряда Q равен φ₁=500 В. Каким станет потенциал φ₂ в точке А, если заряд Q окажется в центре полого проводящего шара радиусами поверхностей 5R и 7R и зарядом 6Q?

Ответ: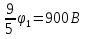

(Олимпиада «Физтех-2006). ε₁

ε₂

d₁

d₂

E

Плоский конденсатор с площадью пластин S полностью заполнен двумя слоями диэлектрика с толщинами d₁ и d₂ и диэлектрическими проницаемостями ε₁ и ε₂ (см. рис.). Между обкладками конденсатора поддерживается разность потенциалов E. Определить величину и знак связанного (поляризационного) заряда диэлектрика у нижней обкладки конденсатора.

Ответ: