Последовательное и параллельное соединение проводников в электрических цепях, отличия
Что такое проводник
В каждой электрической цепи в качестве проводников рассматривается материал или вещество, наделенные свойством проведения электрического тока и обладающие определенным уровнем сопротивления. Этот коэффициент вычисляется по формуле:
- p — обозначен уровень удельного сопротивления, Oм*м,
- R — указывает на эффективное сопротивление проводника, Ом,
- S — это площадь поперечного сечения, м2,
- I — значение длины проводника, м.
Из вышесказанного следует, что любой проводник может рассматриваться, как резистор, имеющий собственное сопротивление.
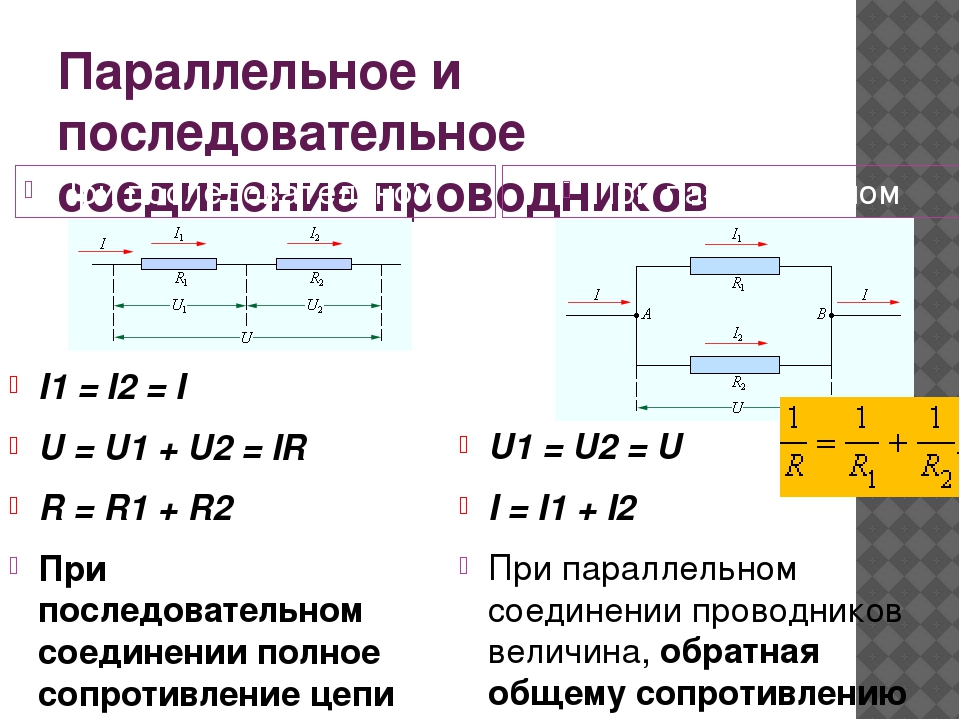
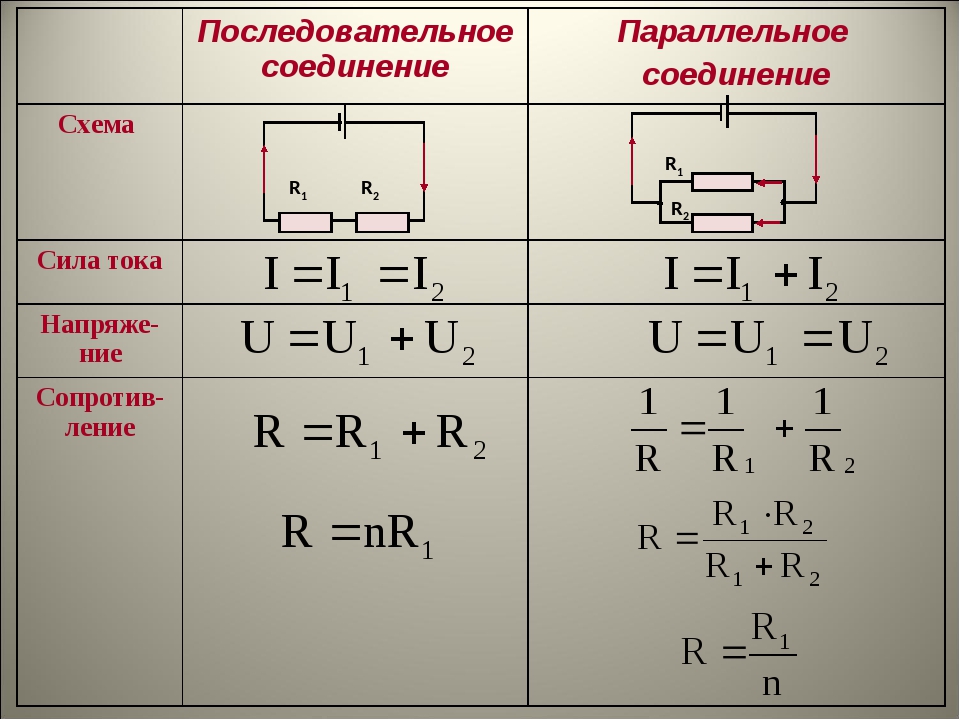
В случае, если проводники соединены с использованием последовательной схемы, коэффициент силы тока для каждого из них является одинаковым. А величина общего напряжения в созданной электроцепи представляет собой совокупность напряжений на концах каждого отдельно взятого проводника.
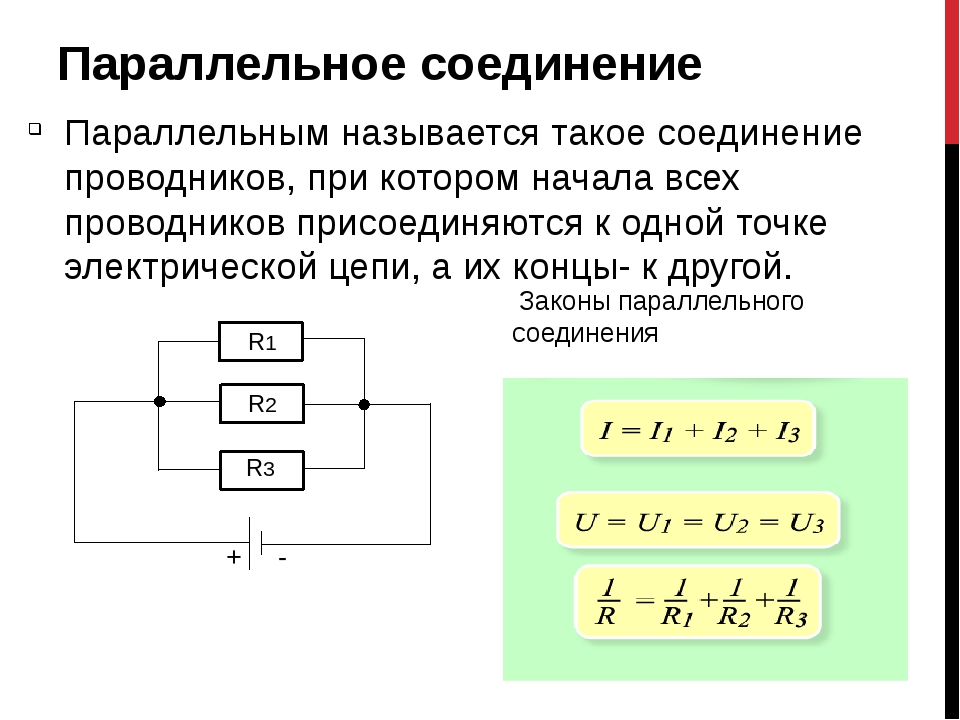
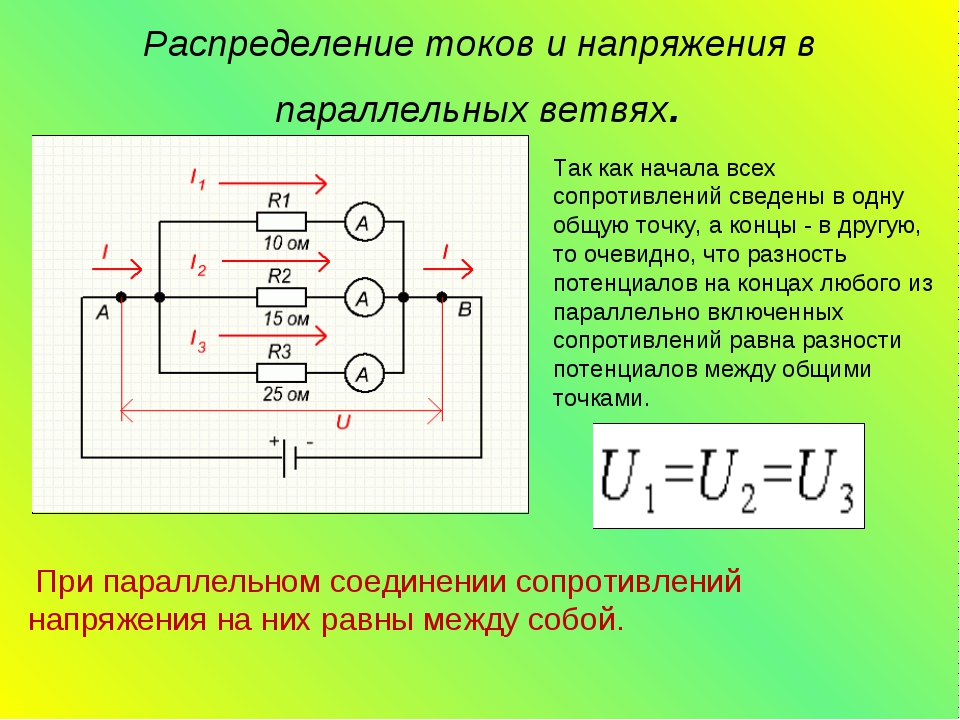
Если используется параллельная схема подсоединения
Особенности последовательного соединения
Специфика использования данного способа предполагает подсоединение проводников, используя последовательную схему подключения. Это означает, что концы одного проводящего элемента соединяются с концами двух других входящих в схему проводников. Главная особенность такого типа соединения – отсутствие каких-либо разветвлений в цепи, проводники имеют принадлежность к одному и тому же кабелю. Другими словами, через каждый новоприсоединенный проводник может протекать электрический ток с одинаковым значением. В сумме же напряжение в токопроводящих элементах равно значениям, имеющимся на концах каждого из них.
К примеру, если последовательно соединить несколько резисторов в одну цепь, не оставив ни одного разветвления, величина заряда из одного какого-либо проводника будет равной величинам заряда в других. Во всех проводящих элементах цепи сила тока будет иметь одно и то же значение.
В то же время, при этом типе соединения допускается замена всех используемых резисторов на один эквивалентный. Величина тока на нем, как правило, совпадает с общим током, движущимся по остальным резисторам. А значение общего напряжения складывается из напряжений в каждом отдельно взятом резисторе. Это позволяет объяснить разность потенциалов на примере единого эквивалентного резистора.
С учетом этих правил и закона Ома, которые применимы для всех резисторов, очень легко доказывается равность между значением сопротивления на эквивалентном резисторе и суммой всех сопротивлений.
Где применяется этот способ соединения
Этот способ соединения применяется в устройствах с целенаправленным включением и выключением. К примеру, звон электрического звонка раздастся лишь при условии, если он последовательно был соединен с источником питания и кнопкой нажатия. Исходя из вышеперечисленных правил, если электрический ток будет отсутствовать на одном из проводников, его не будет и на остальных проводниках. А если электричество будет хотя бы на одном из проводящих элементов, он будет выявлен и на остальных.
К примеру, звон электрического звонка раздастся лишь при условии, если он последовательно был соединен с источником питания и кнопкой нажатия. Исходя из вышеперечисленных правил, если электрический ток будет отсутствовать на одном из проводников, его не будет и на остальных проводниках. А если электричество будет хотя бы на одном из проводящих элементов, он будет выявлен и на остальных.
По этому же принципу функционируют обычные карманные фонарики. В их конструкции предусмотрены три важных элемента. Цепь формируется из маленькой лампочки, батареи и кнопки. Чтобы одно такое устройство засветило, необходимо последовательно подключить обозначенные элементы при помощи простого нажатия кнопки.
В то же время, в доме или городской квартире, где установлено большое количество устройств и приборов освещения разного типа, их не обязательно соединять по последовательной схеме. Ведь зачастую включать и выключать свет в каждом помещении не нужно. Подключение лампочек и люстр в данном случае выполняется с использованием параллельной схемы.
Особенности параллельного соединения
Эта схема предполагает подсоединение заданного количества проводящих устройств параллельно по отношению к друг другу. Так, в одну точку сперва объединяются все начала проводников, в другую точку – их концы. На примере нескольких резисторов рассмотрим схему параллельного подсоединения.
Это разветвленное соединение, где в каждой указанной в схеме ветви есть по одному резистору. После того, как ток достигает точки разветвления, происходит условное разделение электричества к каждому существующему резистору. В результате составляется суммарное значение электрических токов, действительных для всех сопротивлений, которые подключены в данный момент к электроцепи. В то же время, элементы с параллельными соединениями имеют одинаковые значения для всех напряжений. В данном способе также допускается замена всех включенных резисторов на один эквивалентный.
При составлении схем параллельных соединений учитываются следующие закономерности:
- Общее значение сопротивления в электроцепи находится путем складывания обратных величин сопротивлений в цепи проводников.

- Значение тока в электроцепи равно сумме токов в каждом из используемых для формирования цепи проводников.
- На выходах из электроцепи напряжение является равным значению, присутствующему на любом из проводников этой цепи.
Где может применяться параллельная схема соединений
Для бытовых условий подойдет пример с устройствами освещения. В такой схеме приборы освещения соединяются, как правило, параллельно. Если использовать последовательный способ, получится, что при включении одной люстры или лампы загорятся остальные в доме. Параллельное соединение же позволяет добавлять в каждую из используемых ветвей соответствующего выключателя и включать осветительные устройства, где и когда это нужно.
Важно отметить, что для соединения всех электроприборов в быту используется параллельная схема и сеть 220B. Таким же образом все элементы сети подключаются к распределительному щиту, независимо друг от друга.
Для проведения электроизмерительных работ обращайтесь в электролабораторию компании ТМ Электро.
Сила тока. Закон Ома для участка цепи. Сопротивление. Последовательное и параллельное соединение проводников
Похожие презентации:
Последовательное и параллельное соединение проводников
Реостаты. Последовательное соединение проводников. Параллельное соединение проводников
Применение закона Ома для участка цепи при решении задач
Изучение последовательного и параллельного соединения проводников
Сила тока. Закон Ома
Постоянный ток. Закон Ома для однородного участка цепи
Последовательное соединение проводников
Параллельное и последовательное соединение
Параллельное соединение проводников
1. Сила тока. Закон Ома для участка цепи. Сопротивление. Последовательное и параллельное соединение проводников
10 класс2. Сила тока
——
—
I
• Электрический ток возникает при упорядоченном перемещении
свободных электронов или ионов.
• За направление принимают направление движения
положительно заряженных частиц. Если ток образован
движением отрицательно заряженных частиц, то направление
тока считают противоположным движению частиц.
3. Сила тока
В• Количественной мерой
электрического тока служит сила
тока I – скалярная физическая
величина, равная отношению
заряда Δq, переносимого через
поперечное сечение проводника
за интервал времени Δt, к
этому интервалу времени:
А
q
I
t
4. Сила тока
• Если сила тока и его направление неизменяются со временем, то такой ток
называется постоянным
5. Сила тока в связи со скоростью электронов
q q0 nS lI
t
l
I q0 n S
6. Единицы силы тока
Ампер – сила тока, который припрохождении по двум
параллельным прямолинейным
проводникам бесконечной
длины и ничтожно малого
кругового сечения,
расположенным на расстоянии
1 м один от другого в вакууме,
вызвал бы между этими
проводниками силу магнитного
взаимодействия, равную 2∙10–7
Н на каждый метр длины.
7. Условия существования тока
Наличиесвободных
заряженных частиц
Электрический ток
Наличие
электрического
поля
8. Закон Ома для участка цепи
1827 г. –установлена связь
между силой тока,
напряжением и
сопротивлением
9. Зависимость силы тока от напряжения
I ~U10. Зависимость силы тока от сопротивления
1I ~
R
11. Закон Ома для участка цепи
UI
R
Сила тока на участке цепи прямо
пропорциональна приложенному к нему
напряжению и обратно пропорциональна
сопротивлению этого участка
12. Сопротивление
Сопротивление – основная характеристикапроводника, представляющая собой меру
противодействия проводника
направленному движению электрических
зарядов
13. Сопротивление
lR
S
• — удельное сопротивление проводника
(зависит от рода вещества) – [Ом мм2/м];
• l – длина проводника – [м];
• S – площадь сечения проводника – [мм2]
14.
 СопротивлениеПроводник имеет сопротивление 1 Ом, если
СопротивлениеПроводник имеет сопротивление 1 Ом, еслипри разности потенциалов 1 В в нем
возникает сила тока в 1 А
Виды соединений
проводников
Последовательное
Параллельное
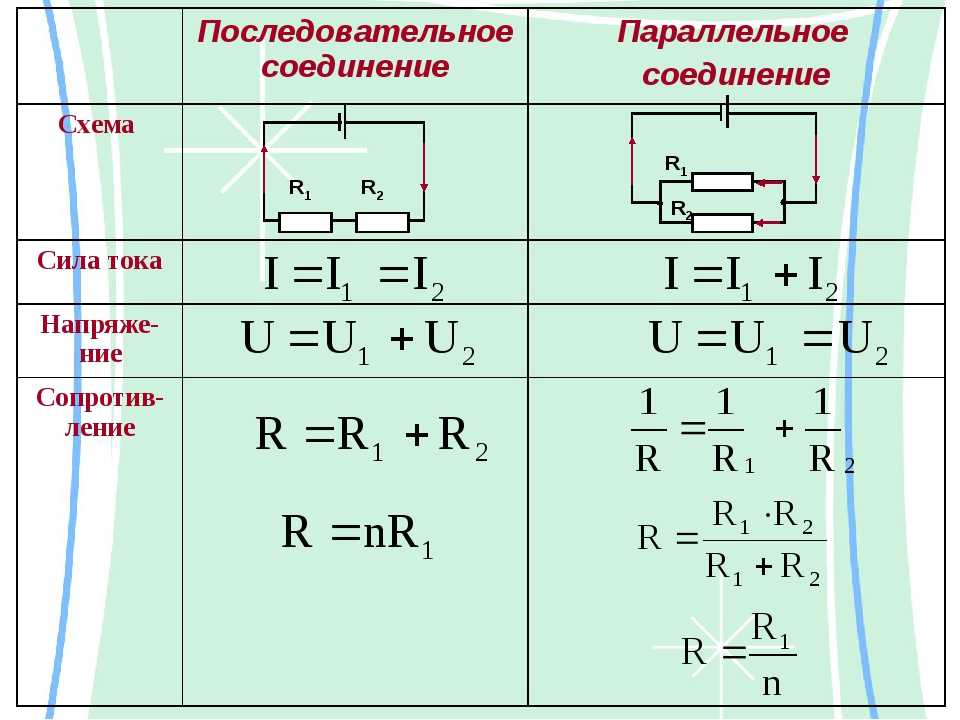
16. Последовательное соединение проводников
I=I1=I2U= U1+U2
R=R1+R2
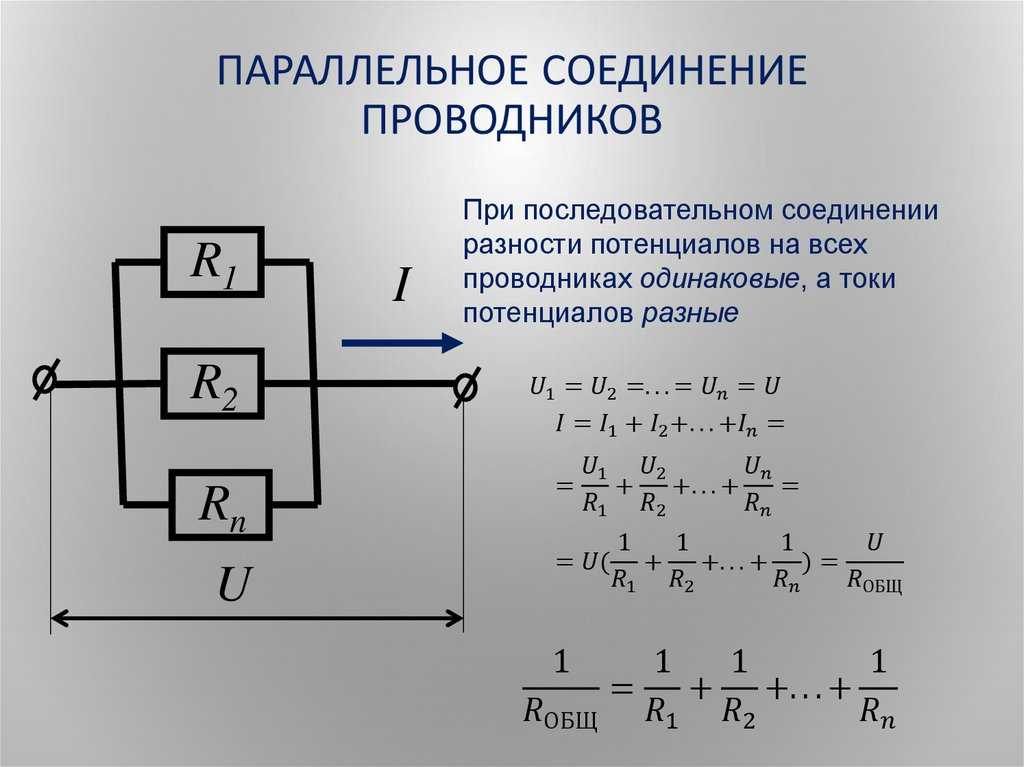
17. Параллельное соединение
I=I1+I2U= U1=U2
1/R=1/R1+1/R2
English Русский Правила
5.3: Простые параллельные схемы — Workforce LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 714
- Tony R. Kuphaldt
- Schweitzer Engineering Laboratories via All About Circuits
Начнем с параллельной цепи, состоящей из трех резисторов и одной батареи:
Принцип параллельных цепей
Первый принцип, который нужно понять о параллельных цепях, заключается в том, что напряжение одинаково для всех компонентов в цепи.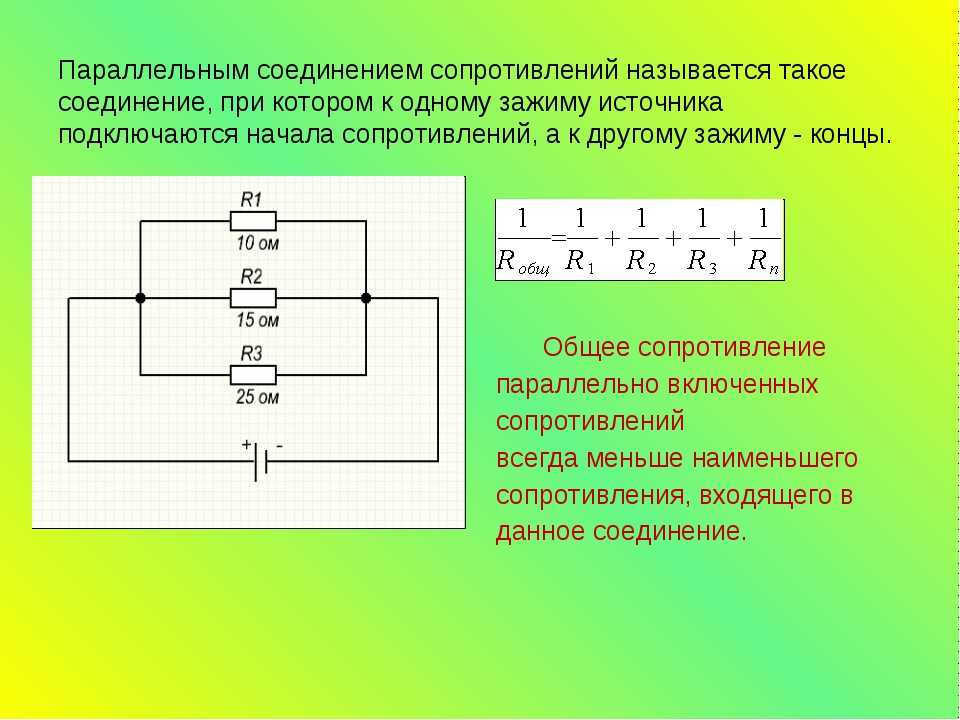 Это связано с тем, что в параллельной цепи есть только два набора электрически общих точек, и напряжение, измеренное между наборами общих точек, всегда должно быть одинаковым в любой момент времени. Следовательно, в приведенной выше схеме напряжение на R 1 равно напряжению на R 2 , которое равно напряжению на R 3 , которое равно напряжению на батарее. Это равенство напряжений может быть представлено в другой таблице для наших начальных значений:
Это связано с тем, что в параллельной цепи есть только два набора электрически общих точек, и напряжение, измеренное между наборами общих точек, всегда должно быть одинаковым в любой момент времени. Следовательно, в приведенной выше схеме напряжение на R 1 равно напряжению на R 2 , которое равно напряжению на R 3 , которое равно напряжению на батарее. Это равенство напряжений может быть представлено в другой таблице для наших начальных значений:
Применение закона Ома для простых параллельных цепей
Так же, как и в случае последовательных цепей, применяется то же предостережение для закона Ома: значения для напряжения, тока , и сопротивление должны быть в одном контексте, чтобы расчеты работали правильно. Однако в приведенной выше схеме мы можем немедленно применить закон Ома к каждому резистору, чтобы найти его ток, потому что мы знаем напряжение на каждом резисторе (9вольт) и сопротивление каждого резистора:
На данный момент мы все еще не знаем, каков общий ток или полное сопротивление для этой параллельной цепи, поэтому мы не можем применить закон Ома к крайнему правому элементу (« Итого»).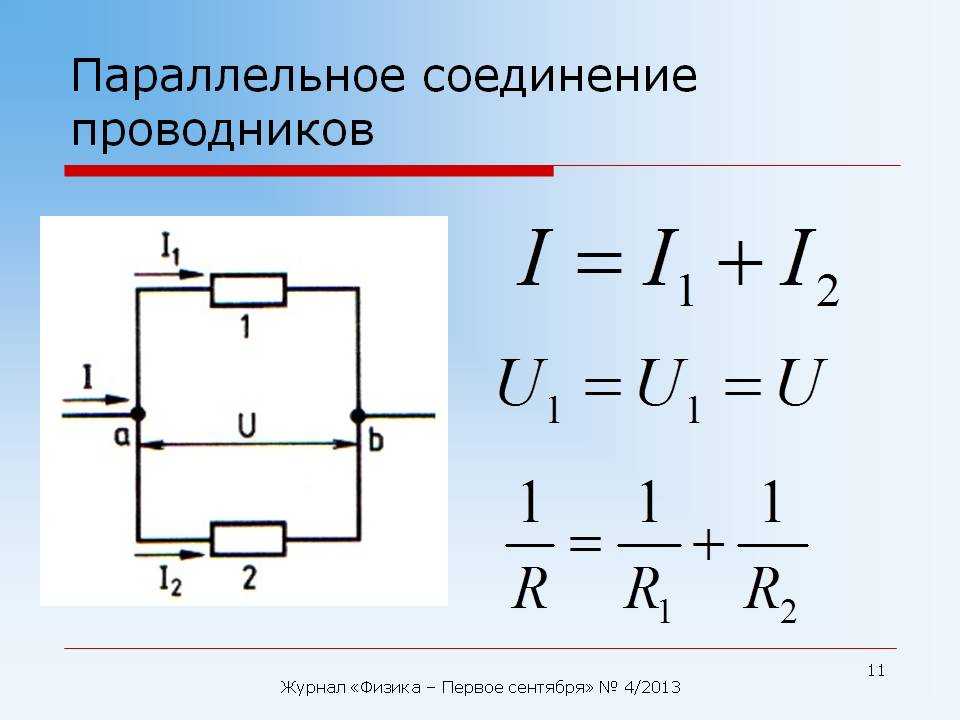 Однако, если мы хорошенько подумаем о том, что происходит, должно стать очевидным, что общий ток должен равняться сумме токов всех отдельных резисторов («ветвей»):
Однако, если мы хорошенько подумаем о том, что происходит, должно стать очевидным, что общий ток должен равняться сумме токов всех отдельных резисторов («ветвей»):
точка 8 и проходит по контуру, часть потока разделяется в точке 7 и проходит вверх через R 1 , еще несколько отщепляются в точке 6 и идут вверх через R 2 , а остальные идут вверх через R 3 . Подобно реке, разветвляющейся на несколько более мелких ручьев, суммарный расход всех ручьев должен равняться расходу всей реки. То же самое происходит, когда токи через R 1 , R 2 и R 3 объединяются, чтобы течь обратно к положительной клемме батареи (+) к точке 1: поток электронов от точки 2 к точке 1. точка 1 должна равняться сумме токов (ветви) через R 1 , R 2 и R 3 .
Это второй принцип параллельных цепей: общий ток цепи равен сумме токов отдельных ветвей. Используя этот принцип, мы можем заполнить место I T в нашей таблице суммой I R1 , I R2 и I R3 :
Наконец, применив закон Ома к крайнему правому числу ( «Всего»), мы можем вычислить общее сопротивление цепи:
Уравнение для параллельных цепей
Обратите внимание на очень важную вещь.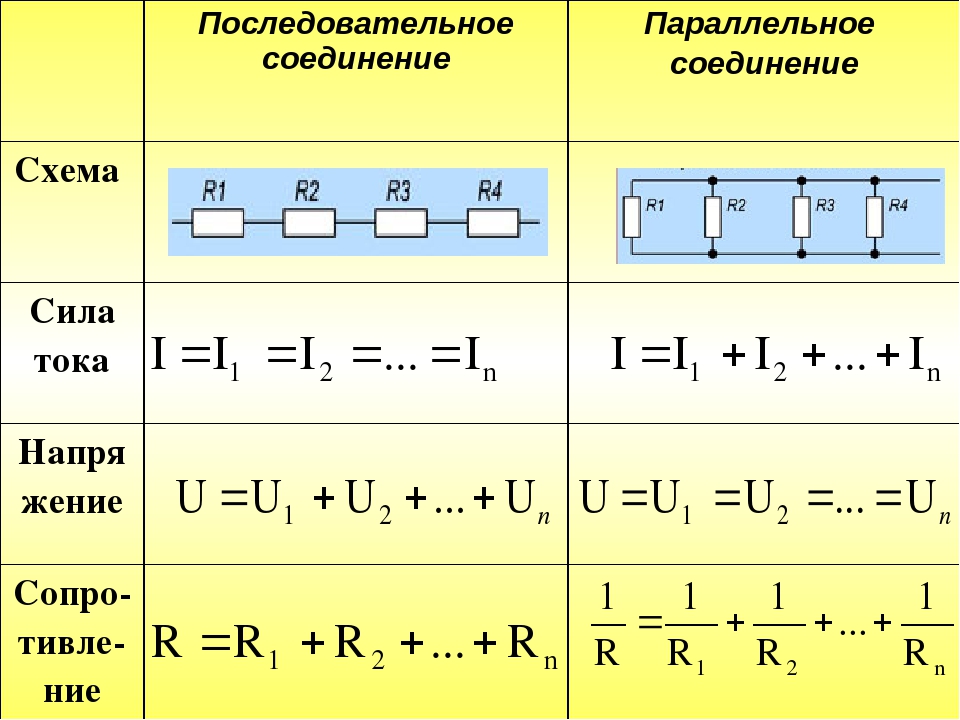 Общее сопротивление цепи составляет всего 625 Ом: на меньше, чем на , чем у любого из отдельных резисторов. В последовательной цепи, где общее сопротивление было суммой отдельных сопротивлений, общее значение должно было быть на больше, чем на , чем у любого из резисторов по отдельности. Однако здесь, в параллельной цепи, верно обратное: мы говорим, что отдельные сопротивления уменьшаются в 9 раз.0099 вместо добавьте , чтобы получить общее количество. Этот принцип завершает нашу триаду «правил» для параллельных цепей, точно так же, как было обнаружено, что для последовательных цепей действуют три правила для напряжения, тока и сопротивления. Математически взаимосвязь между общим сопротивлением и отдельными сопротивлениями в параллельной цепи выглядит следующим образом: знаменатель дроби, необходимый для размещения всех параллельных резисторов в цепи.
Общее сопротивление цепи составляет всего 625 Ом: на меньше, чем на , чем у любого из отдельных резисторов. В последовательной цепи, где общее сопротивление было суммой отдельных сопротивлений, общее значение должно было быть на больше, чем на , чем у любого из резисторов по отдельности. Однако здесь, в параллельной цепи, верно обратное: мы говорим, что отдельные сопротивления уменьшаются в 9 раз.0099 вместо добавьте , чтобы получить общее количество. Этот принцип завершает нашу триаду «правил» для параллельных цепей, точно так же, как было обнаружено, что для последовательных цепей действуют три правила для напряжения, тока и сопротивления. Математически взаимосвязь между общим сопротивлением и отдельными сопротивлениями в параллельной цепи выглядит следующим образом: знаменатель дроби, необходимый для размещения всех параллельных резисторов в цепи.
Как и в случае с последовательной схемой, мы можем использовать компьютерный анализ для перепроверки наших расчетов.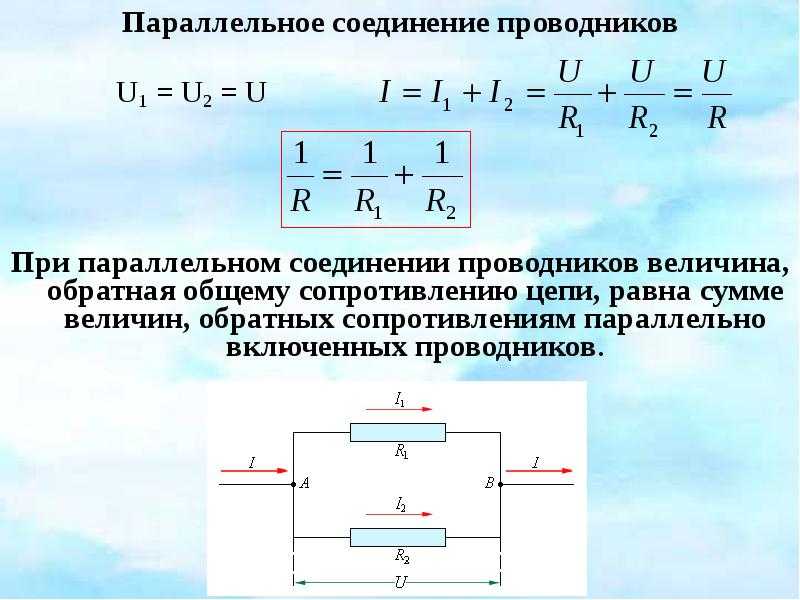 Во-первых, конечно, мы должны описать наш пример схемы компьютеру в терминах, которые он может понять. Я начну с перерисовки схемы:
Во-первых, конечно, мы должны описать наш пример схемы компьютеру в терминах, которые он может понять. Я начну с перерисовки схемы:
Как изменить схемы нумерации параллельных цепей для SPICE
И снова мы обнаруживаем, что исходная схема нумерации, используемая для обозначения точек в схеме, должна быть изменена в пользу специй. В SPICE все электрически общие точки должны иметь одинаковые номера узлов. Вот как SPICE знает, что с чем связано и как. В простой параллельной цепи все точки электрически общие в одном из двух наборов точек. Для схемы нашего примера провод, соединяющий верхние части всех компонентов, будет иметь один номер узла, а провод, соединяющий нижние части компонентов, будет иметь другой. Оставаясь верным соглашению о включении нуля в качестве номера узла, я выбираю числа 0 и 1:9.0032
Подобный пример делает обоснование номеров узлов в SPICE довольно понятным для понимания. Поскольку все компоненты имеют общие наборы чисел, компьютер «знает», что все они соединены параллельно друг с другом.
Чтобы отобразить токи ветвей в SPICE, нам нужно вставить источники нулевого напряжения в линию (последовательно) с каждым резистором, а затем сопоставить наши измерения тока с этими источниками. По какой-то причине создатели программы SPICE сделали так, что ток можно было рассчитать только 9от 0098 до источник напряжения. Это несколько раздражающее требование программы моделирования SPICE. При добавлении каждого из этих «фиктивных» источников напряжения необходимо создать несколько новых номеров узлов, чтобы соединить их с соответствующими ветвевыми резисторами:
Как проверить результаты компьютерного анализа
Все фиктивные источники напряжения настроены на 0 вольт, поэтому чтобы не влиять на работу цепи. Файл описания схемы, или netlist , выглядит так:
Запустив компьютерный анализ, мы получили следующие результаты (я снабдил распечатку описательными метками):
Эти значения действительно соответствуют рассчитанным ранее по закону Ома: 0,9 мА для I R1 , 4,5 мА для I R2 и 9 мА для I R3 .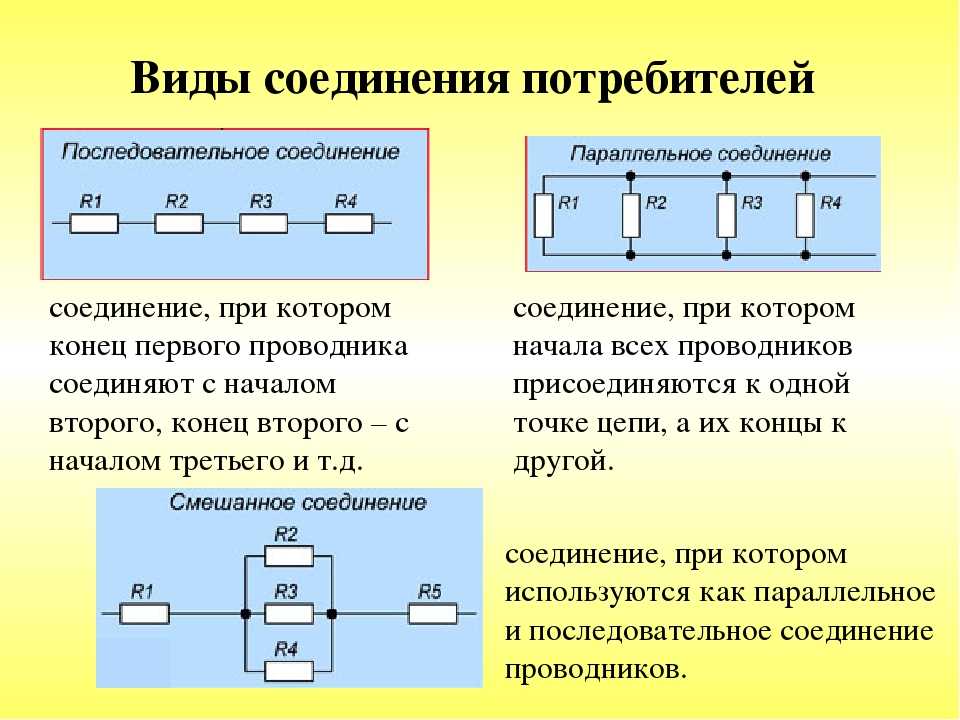 Разумеется, при параллельном соединении все резисторы имеют одинаковое падение напряжения (9 вольт, как и батарея).
Разумеется, при параллельном соединении все резисторы имеют одинаковое падение напряжения (9 вольт, как и батарея).
Три правила параллельных цепей
Таким образом, параллельная цепь определяется как цепь, в которой все компоненты соединены между одним и тем же набором электрически общих точек. Другими словами, все компоненты подключены через терминалы друг друга. Из этого определения следуют три правила параллельных цепей: все компоненты имеют одинаковое напряжение; сопротивления уменьшаются, чтобы равняться меньшему общему сопротивлению; а токи ветвей складываются, чтобы равняться большему общему току. Как и в случае с последовательными цепями, все эти правила уходят корнями в определение параллельной цепи. Если вы полностью понимаете это определение, то правила — не что иное, как сноски к определению.
Обзор
- Компоненты в параллельной цепи имеют одинаковое напряжение: E Итого = E 1 = E 2 = . . . Е п
- Общее сопротивление в параллельной цепи на меньше , чем любое из сопротивлений в отдельности: R Всего = 1 / (1/R 1 + 1/R 2 + .

- Суммарный ток в параллельной цепи равен сумме токов отдельных ответвлений: I Итого = I 1 + I 2 + . . . я п .
Эта страница под названием 5.3: Простые параллельные схемы распространяется в соответствии с лицензией GNU Free Documentation License 1.3. Автором, ремиксом и/или куратором выступил Тони Р. Купхалдт (Все о цепях) через исходный контент, отредактированный в соответствии со стилем и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Тони Р.
 Купхалдт
Купхалдт
- Лицензия
- ГНУ ФДЛ
- Версия лицензии
- 1,3
- Показать оглавление
- нет
- Теги
- источник@https://www.allaboutcircuits.com/textbook/alternating-current
- источник@https://www.allaboutcircuits.com/textbook/direct-current
Видео с вопросами: Определение соотношения токов, протекающих через различные резисторы в параллельной цепи
Стенограмма видео
Какой из следующих графиков
представляет отношение тока, протекающего через резисторы A, B и C в данном
фигура? График (A), график (B), график (C) или
график (D).
Для расчета коэффициента токи, проходящие через каждый резистор, нам нужно вспомнить, как ток разделяется по каждому параллельному пути. Полный ток в цепи с параллельные компоненты задаются по правилу 𝐼 сумма равна 𝐼 один плюс 𝐼 два плюс 𝐼 три и так далее. То есть общий ток разделяется по всем параллельным ветвям. В этом вопросе у нас три разные ветви A, B и C, так что это правило становится 𝐼 total равно 𝐼 A плюс 𝐼 B плюс 𝐼 С.
Мы также можем вспомнить, что
разность потенциалов на каждой ветви параллельной цепи одинакова, поэтому 𝑉 A
равно 𝑉 B равно 𝑉 C. То есть разность потенциалов
на каждом из этих трех резисторов одинакова. Поскольку три потенциала
различия одинаковы, мы будем говорить, что разность потенциалов на каждом
ветвь равна 𝑉. Итак, мы знаем о текущем и
разность потенциалов для каждой параллельной ветви.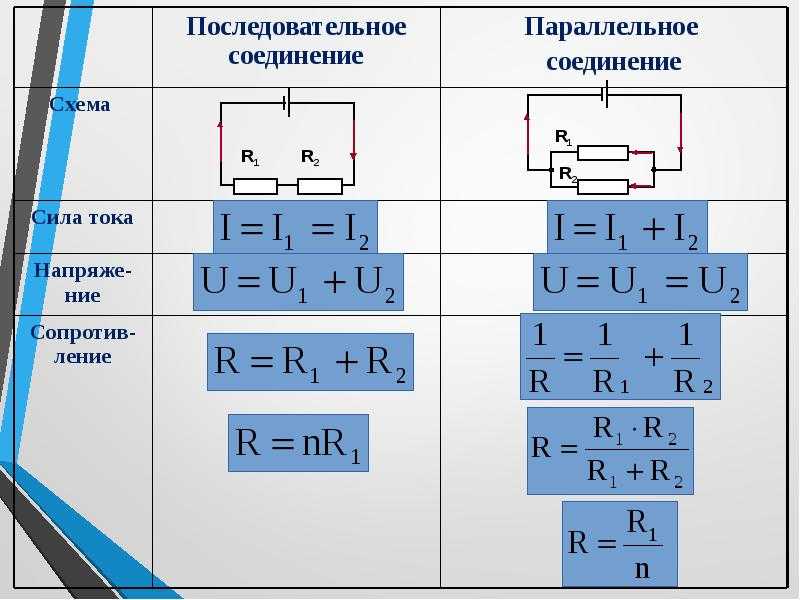 Нам также даны сопротивления
для каждого резистора. Резистор А имеет сопротивление два 𝑅,
резистор B имеет сопротивление три 𝑅, а резистор C имеет сопротивление 𝑅.
Нам также даны сопротивления
для каждого резистора. Резистор А имеет сопротивление два 𝑅,
резистор B имеет сопротивление три 𝑅, а резистор C имеет сопротивление 𝑅.
Теперь мы можем использовать закон Ома для каждого путь, чтобы определить токи в каждом пути, а затем сравнить токи, чтобы увидеть какой из графиков правильно отображает отношение тока, проходящего через резисторы. Закон Ома можно записать как 𝑉 равно 𝐼, умноженному на 𝑅, где 𝑉 — разность потенциалов, 𝐼 — ток, а 𝑅 является сопротивление.
Нам нужно найти
ток, так что давайте изменим уравнение, чтобы ток, 𝐼, стал субъектом. Мы можем сделать это, разделив оба
стороны уравнения сопротивлением 𝑅. Сопротивления справа
стороны компенсируют друг друга, и мы остаемся с уравнением, которое говорит текущий 𝐼
равна разности потенциалов 𝑉, деленной на сопротивление 𝑅.
Для пути A имеем 𝐼 A равно 𝑉 разделить на два 𝑅. Для пути B имеем 𝐼 B равно 𝑉 разделить на три 𝑅. Для пути C имеем 𝐼 C равно 𝑉 разделить на 𝑅. Мы можем переписать эти первые два уравнения, вынося числовые значения на множители. Тогда из этих трех уравнений для токов 𝐼 A, 𝐼 B и 𝐼 C мы видим, что ток через резистор C — наибольший, ток через резистор B — наименьший, а ток через резистор А находится между этими двумя значениями.
Мы можем выразить это как
неравенство 𝐼 C больше, чем 𝐼 A, которое, в свою очередь, больше, чем 𝐼 B. Глядя на каждый из графиков, мы
можно увидеть, что график в варианте (А) соответствует соотношению токов, которое мы только что
вычислено. Следовательно, правильный ответ
вариант (А).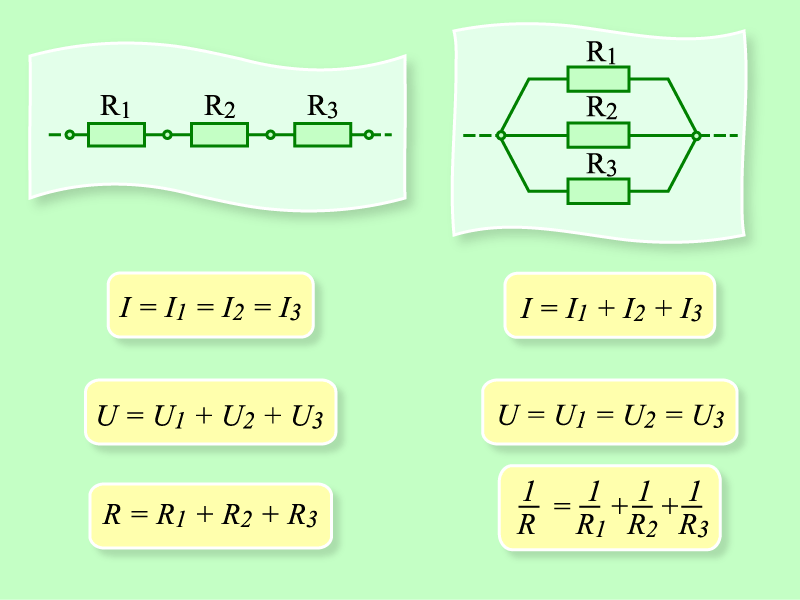


 Купхалдт
Купхалдт