Проекция силы на ось | ПроСопромат.ру
Часто геометрическое сложение векторов сил требует сложных и громоздких построений. В таких случаях прибегают к другому методу, где геометрическое построение заменено вычислениями скалярных величин. Достигается это проектированием заданных сил на оси прямоугольной системы координат.
Как известнее из математики, осью называют неограниченную прямую линию, которой приписано определенное направление. Проекция вектора на ось является скалярной величиной, которая определяется отрезком оси, отсекаемым перпендикулярами, опущенными из начала и конца вектора на ось.
Проекция вектора считается положительной (+), если направление от начала проекции к ее концу совпадает с положительным направлением оси. Проекция вектора считается
Рассмотрим ряд случаев проектирования сил на ось.
- Дана сила Р (рис.а), она лежит в одной плоскости с осью х. Вектор силы составляет с положительным направлением оси острый угол α.

Чтобы найти величину
Рх = ab = Р cos α.
Проекция вектора в данном случае положительна.
2. Дана сила Q (рис. б), которая лежит в одной плоскости с осью х, но ее вектор составляет с положительным направлением оси тупой угол α.

Проекция силы Q на ось
Qх = ab = Q cos α,
но
cos a = — cos β.
Так как α > 90°, то cos cos α — отрицательная величина. Выразив cos α через cos β (β — острый угол), окончательно получим
Qх = — Q cos β
В этом случае проекция силы отрицательна.
Итак, проекция силы на ось координат равна произведению модуля силы на косинус угла между вектором силы и положительным направлением оси
При определении проекции вектора силы на ось пользуются обычно косинусом острого угла, независимо от того, с каким направлением оси — положительным или отрицательным — он образован. Знак проекции легче устанавливать непосредственно по чертежу.
Силу, расположенную на плоскости хОу, можно спроектировать на две координатные оси Ох и Оу. Рассмотрим рисунок.

На нем изображена сила Р и ее проекции Рх и Ру. Ввиду того что проекции образуют между собой прямой угол, из прямоугольного треугольника ABC следует:

Этими формулами можно пользоваться для определения величины и направления силы, когда известны ее проекции на координатные оси. Эти же формулы могут применяться для определения величины и направления
Уравнения равновесия [wiki.eduVdom.com]
Проекция силы на ось — характеризует действие этой силы вдоль этой оси.
То есть Проекция силы на ось Ох ($ P_x = \sum X_i $ ) характеризует действие этой силы вдоль оси Ох.
А проекция силы на ось Оу ($ P_y = \sum Y_i $ ) характеризует действие этой силы вдоль оси Оу.
И если сумма проекций всех сил на ось Ох равна нулю ($ \sum X_i = 0 $ )– значит действие этих сил вдоль этой оси Ох нет , силы вдоль этой оси друг друга уравновешивают.
И если сумма проекций всех сил на ось Оу равна нулю ($ \sum Y_i = 0 $ )- значит действие этих сил вдоль этой оси Оу нет , силы друг друга вдоль этой оси Оу уравновешивают.
Вращательное действие силы относительно точки О характеризует момент этой силы относительно этой точки О ($ M_0(P)=0 $) .
И если сумма моментов всех сил относительно точки О равно нулю ($ \sum M_O =0 $), то вращательного действия всех этих сил на тело относительно точки О нет, они его не производят, или их вращательные действия их взаимно уравновешены.
Теперь — если проекции всех сил на оси Ох и Оу равны нулю , и сумма моментов всех сил относительно любой — какой угодно — точки равны нулю, то тело находится в равновесии.
$$ \sum X=0 \\ \sum Y=0 \\ \sum M_A=0 $$
Система сил, действующих на тело, называется сходящейся, если линии действия этих сил пересекается в одной точке.
Условие равновесия системы сходящихся сил
Для того, чтобы система сходящихся сил была уравновешенной, то есть под действием ее тело будет находится в равновесии — условие равновесия системы сходящихся сил,
может быть записано :
$$ \sum X_i = 0
\\ \sum Y_i = 0
$$
Или другими словами — для плоской системы сходящихся сил, лежащих в плоскости Oxy, соответствующие уравнения равновесия примут вид:
$$ \sum X_i = 0 \\ \sum Y_i = 0 $$
Проекция силы на ось
Определение. Проекцией силы $\vec{Р}$ на ось Ox называется взятая с знаком $\pm$
длина отрезка этой оси, заключенная между проекциями на неё начала и конца
вектора силы.Эту проекцию обычно обозначают как Рx или X. В соответствии с определением она равна:
$$ P_x = X = |\vec{Р}| \cdot \cos (\vec{Р}, \vec{i}) = P \cdot \cos \alpha $$
$$ P_y = Y = |\vec{Р}| \cdot \cos (\vec{Р}, \vec{j}) = P \cdot \sin \alpha $$
, где $\vec{i}$ – единичный вектор оси /Ox/, а $\alpha$ – угол между ним и силой $\vec{Р}$ (Рис.1).
Рис.1
Таким образом:
$$ P_x > 0\text{, если }0 \leq \alpha < \frac{\pi}{2} $$ $$ P_x = 0\text{, если } \alpha = \frac{\pi}{2} $$ $$ P_x < 0\text{, если } \frac{\pi}{2} < \alpha \leq \pi $$
Проекция силы на ось равна нулю, если сила перпендикулярно оси.
Аналогично находится проекция силы Р на ось Oy.
Вектор $ \vec{Р} $ может быть выражен:
$$\vec{Р} = P_x \cdot \vec{i} + P_y \cdot \vec{j} = X \cdot \vec{i} + Y \cdot \vec{j}$$
А равнодействующая плоской системы двух сходящихся сил равна диагонали параллелограмма, построенного на этих силах, как на сторонах.
Модуль и направление искомого вектора силы Р можно найти по формулам:
$$ P = \sqrt{X^2 + Y^2} \\ \cos (\vec{Р}, \vec{i}) = \frac{X}{P} \\ \cos (\vec{Р}, \vec{j}) = \frac{Y}{P} $$
Момент силы относительно центра
Приложим в точке А силу P и выясним — чем определяется момент силы относительно точки О, который характеризует вращательное действие этой силы относительно точки О(Рис.1).
Рис.1
Очевидно, что воздействие силы на тело будет зависеть не только от ее величины, но и от того, как она направлена, и в конечном итоге будет определяться ее моментом относительно центра О.
Рассмотренное определение момента силы подходит только для плоской системы сил.
Определение 1. Моментом силы Р относительно центра О называется
взятое со знаком $\pm$ произведение модуля силы на ее плечо – то есть длину
перпендикуляра, опущенного из моментной точки на линию действия силы.
Правило знаков: момент силы считается положительным, если сила
стремится повернуть тело против хода часовой стрелки и отрицательным, если
она вращает тело по ходу часовой стрелки.
В соответствии с данным определением момент силы численно равен удвоенной площади треугольника OAB, построенного на векторе силы P с вершиной в моментной точке: $M_0(P) = P\cdot d = 2S\Delta_{OAB}$ .
Отметим, что момент силы относительно точки О равен нулю, если линия действия силы проходит через моментную точку.
Уравнения равновесия плоской системы сил
Уравнения равновесия плоской системы сил,
которые можно записать в трех различных формах:
Первая форма:
$$ \sum X=0 \\ \sum Y=0 \\ \sum M_A=0 $$Вторая форма:
$$ \sum M_A=0 \\ \sum M_B=0 \\ \sum Y=0 $$ , где ось Oy не перпендикулярна отрезку АВТретья форма:
$$ \sum M_A=0 \\ \sum M_B=0 \\ \sum M_C=0 $$ , где точки А, В и С не лежат на одной прямой.
Таким образом, любая из этих трех форм эквивалентна условию равновесия плоской системы сил и наоборот.
Центр тяжести
Центр тяжести — точка, через которую проходит равнодействующая сил тяжести при любом пространственном расположении тела.
Если тело имеет ось или центр симметрии, то центр тяжести лежит там.
Центр тяжести квадрата и прямоугольника — точка пересечения его диагоналей.
Центр тяжести круга — в его центре.
Центр тяжести треугольника — в точке пересечения медиан.
Задачи и опыты
Задачи
Опыты с пояснением — физика 9 кл.
Рекомендуем
subjects/physics/уравнения_равновесия.txt · Последние изменения: 2016/12/24 22:09 — ¶
Проекция силы на ось. Момент силы относительно точки и оси — Мегаобучалка
Предмет теоретической механики. Этапы развития. Основные понятия теоретической механики.
Механикой называется наука о простейшей форме движения материи — о механическом движении. Простейшими являются движения, сводимые к перемещениям во времени физических тел из одного положения в пространстве в другое.
Теоретическая механика изучает наиболее общие законы механического движения. Она не учитывает индивидуальные свойства физических тел, за исключением двух: свойства протяженности и свойства гравитации (свойства частиц материи тяготеть друг к другу или обладать весом).
К числу основных понятий относится механическая сила. Механическая сила есть движение, в механической форме передаваемое от одного тела к другому при их взаимодействии.
Многочисленные наблюдения показали, что сила характеризуется величиной, направлением и точкой приложения. Сила относится к векторным величинам.
Под движением в механике мы понимаем механическое движение, т. е. происходящее с течением времени изменение взаимного положения материальных тел в пространстве.
Механическим взаимодействием между телами называется тот вид взаимодействия, в результате которого происходит изменение движения этих тел или изменение их формы (деформация).
По своему построению теоретическая механика напоминает геометрию: в ее основе также лежат определения, аксиомы и теоремы. По характеру рассматриваемых задач механику принято разделять на статику, кинематику и динамику.
В статике изучаются методы преобразования сил, приложенных к материальной точке и абсолютно твердому телу, а также условия их равновесия.
Кинематикой называется раздел теоретической механики, в котором изучается механическое движение без учета действующих сил.
Изучением механического движения материальной точки, системы и абсолютно твердого тела с учетом действующих сил занимается динамика.
Основной задачей теоретической механики является изучение общих законов движения и равновесия материальных тел под действием приложенных к ним сил.
Термин «механика» впервые появляется в сочинениях одного из выдающихся философов древности Аристотеля (384—322 до н. э.) и происходит от греческого слова, означающего по современным понятиям «сооружение», «машина», «изобретение»
В древние времена, когда запросы производства сводились главным образом к удовлетворению нужд строительной техники, начинает развиваться учение о так называемых простейших машинах (блок, ворот, рычаг, наклонная плоскость) и общее учение о равновесии тел (статика). Обоснование начал статики содержится уже в сочинения одного из великих ученых Архимеда (287 – 212 г. но н. э.).
В России на развитие первых исследований по механике большое влияние оказали труды гениального ученого и мыслителя М. В. Ломоносова (1711—1765), М. В. Остроградского (1801—1861), П. Л. Чебышева (1821—1894), С. В. Ковалевской (1850—1891), И. В. Мещерского (1859—1935и т.д.
Выдающееся значение для развития механики имели труды «отца русской авиации» Н. Е. Жуковского (1847—1921) и его ближайшего ученика С. А. Чаплыгина (1869—1942). Характерной чертой в творчестве Н. Е. Жуковского было приложение методов механики к решению актуальных технических задач.
Введение в статику. Предмет статики. Основные задачи статики. Основные понятия статики.
Статика — это раздел теоретической механики, в котором устанавливаются методы преобразования одних систем сил в другие, им эквивалентные, а также условия равновесия различных систем сил, действующих на твердое тело.
В статике рассматриваются две основные задачи:
-замена дополнительной системы сил приложенных к твердому телу другой системой сил ей эквивалентной;
-вывод общих условий, при которых твердое тело под действием приложенных к нему сил остаются в состоянии покоя или в состоянии равномерного прямолинейного поступательного движения.
Основные понятия статики:
Материальная точка— это простейшая модель материального тела любой формы, размеры которого достаточно малы и которое можно принять за геометрическую точку, имеющую определенную массу.
Механическая система— это любая совокупность материальных точек.
Абсолютно твердое тело— это механическая система, расстояние между точками которой не изменяется при любых взаимодействиях.
Сила— это одна из векторных мер действия одного материального объекта на другой рассматриваемый объект. Сила характеризуется числовым значением, а также точкой приложения и направлением действия. Это векторная величина и обозначается она, например, . Ее действие на тело определяется: 1) численной величиной или модулем силы, 2) направлением силы, 3) точкой приложения силы. Предполагается, что действие силы на тело не изменится, если ее перенести по линии действия в любую точку тела (твердого тела). Поэтому вектор силы называют скользящим вектором. Если силу перенести в точку, не расположенную на этой линии, действие ее на тело будет совсем другим.
Система сил— это совокупность сил, действующих на рассматриваемое тело.
Система сил, эквивалентная нулю (равновесная система сил),— это такая система сил, действие которой на твердое тело или точку, находящиеся в покое или движущиеся по инерции, не приводит к изменению его состояния.
Проекция силы на ось. Момент силы относительно точки и оси.
Проекцией силы на ось называется алгебраическая величина, равная произведению модуля силы на косинус угла между положительным направлением оси и направлением силы.
Если проекцию силы F на ось х обозначить Fx ,то согласно приведенному определению Fx = F cos(F,x) или Fx = F cosax
где F – модуль силы; ax – угол между положительным направлением оси и силой F.
Из второй формулы видно, что знак проекции силы на ось зависит от знака косинуса угла ax: проекция будет положительной, если ax < 90° и отрицательной, если ax > 90°.
Моментом сил относительно точки называется взятое с соответствующим знаком произведение величины силы на ее плечо.
Плечом силы относительно точки называется длина перпендикуляра, опущенного из точки на линию действия силы
Момент силы относительно точки зависит не только от её модуля, но и от расстояния от линии действия силы до возможной оси вращения (плеча силы).
Часто такой момент называют алгебраическим.
Этот момент численно равен удвоенной площади треугольника, построенного на силе и моментной точке
Векторным моментом силы относительно точки называется векторное произведение радиус-вектора точки приложения силы на вектор силы.
Момент силы относительно точки считается положительным, если сила стремится повернуть плоскость, проходящую через линию ее действия и моментную точку, против часовой стрелки. В противном случае этот момент будет отрицательным. Если линия действия силы проходит через точку по отношению к которой определяется момент, то момент равен нулю.
Моментом силы относительно оси называется момент проекции этой силы на перпендикулярную к оси плоскость относительно точки пересечения оси и плоскости
На рисунке задана произвольная плоскость П, перпендикулярная оси Z. т.О — точка пересечения оси Z и плоскости П, h — плечо проекции силы F на плоскость П относительно точки О.
Момент силы относительно оси считается положительным, если проекция силы на перпендикулярную к оси плоскость стремится повернуть эту плоскость вокруг положительного направления оси против часовой стрелки. В противном случае указанный момент будет отрицательным. Момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости.
Аксиомы статики.
Все теоремы и уравнения статики выводятся из нескольких исходных положений, принимаемых без математических доказательств и называемых аксиомами или принципами статики. Аксиомы статики представляют собой результат обобщений многочисленных опытов и наблюдений над равновесием и движением тел, неоднократно подтвержденных практикой.
Аксиома 1. Если на свободное абсолютно твердое тело действуют две силы, то тело может находиться в равновесии тогда и только тогда, когда эти силы равны по модулю (F1 = F2) и направлены вдоль одной прямой в противоположные стороны. Аксиома 1 определяет простейшую уравновешенную систему сил, так как опыт показывает, что свободное тело, на которое действует только одна сила, находиться в равновесии не может.
Аксиома 2. Действие данной системы, сил на абсолютно твердое тело не изменится, если к ней прибавить или от нее отнять уравновешенную систему сил. Эта аксиома устанавливает, что две системы сил, отличающиеся на уравновешенную систему, эквивалентны друг другу.
Следствие из 1-й и 2-й аксиом. Действие силы на абсолютно твердое тело не изменится, если перенести точку приложения силы вдоль ее линии действия в любую другую точку тела.
Аксиома 3 (аксиома параллелограмма сил). Две силы, приложенные к телу в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю параллелограмма, построенного на этих силах, как на сторонах.
Вектор , равный диагонали параллелограмма, построенного на векторах и , называется геометрической суммой векторов и : = + . Конечно, + . Такое равенство будет соблюдаться только при условии, что эти силы направлены по одной прямой в одну сторону. Если же векторы сил окажутся перпендикулярными, то , если нет то равнодействующая . Аксиому 3 можно еще формулировать так: две силы, приложенные к телу в одной точке, имеют равнодействующую, равную геометрической (векторной) сумме этих сил и приложенную в той же точке.
Аксиома 4. При всяком действии одного материального тела на другое имеет место такое же по величине, но противоположное по направлению противодействие. Закон о равенстве действия и противодействия является одним из основных законов механики. Из него следует, что если тело А действует на тело В с силой , то одновременно тело В действует на тело А с такой же по модулю и направленной вдоль той же прямой, но противоположную сторону силой =- . Однако силы и не образуют уравновешенной системы сил, так как они приложены к разным телам.
Аксиома 5 (принцип отвердевания). Равновесие изменяемого (деформируемого) тела, находящегося под действием данной системы сил, не нарушится, если тело считать отвердевшим (абсолютно твердым).
Высказанное в этой аксиоме утверждение очевидно. Например, ясно, что равновесие цепи не нарушится, если ее звенья считать сваренными друг с другом и т. д.
Проекция силы на ось. Проекция векторной суммы сил на ось — Мегаобучалка
Решение задач на равновесие сходящихся сил с помощью построения замкнутых силовых многоугольников сопряжено с громоздкими построениями. Универсальным методом решения таких задач является переход к определению проекций заданных сил на координатные оси и оперирование с этими проекциями. Осью называют прямую линию, которой приписано определенное направление.
Проекция вектора на ось является скалярной величиной, которая определяется отрезком оси, отсекаемым перпендикулярами, опущенными на нее из начала и конца вектора.
Проекция вектора считается положительной, если направление от начала проекции к ее концу совпадает с положительным направлением оси. Проекция вектора считается отрицательной, если направление от начала проекции к ее концу противоположно положительному направлению оси.
Таким образом, проекция силы на ось координат равна произведению модуля силы на косинус угла между вектором силы и положительным направлением оси.
Рассмотрим ряд случаев проецирования сил на ось:
Вектор силы F (рис. 15) составляет с положительным направлением оси х острый угол .
Рис. 15
Чтобы найти проекцию, из начала и конца вектора силы опускаем перпендикуляры на ось oх; получаем
1. Fx = F cos α
Проекция вектора в данном случае положительна
Сила F (рис. 16) составляет с положительным направлением оси х тупой угол α.
Рис. 16
Тогда Fx = F cos α, но так как α = 1800 — φ,
Fx = Fcos α = Fcos1800 — φ =- Fcos φ.
Проекция силы F на ось oх в данном случае отрицательна.
Сила F (рис. 17) перпендикулярна оси oх.
Рис. 17
Проекция силы F на ось х равна нулю
Fx = F cos 90° = 0.
Силу, расположенную на плоскости хоу (рис. 18), можно спроектировать на две координатные оси ох и оу.
Рис. 18
Силу F можно разложить на составляющие: Fx и Fy. Модуль вектора Fx равен проекции вектора F на ось ox, а модуль вектора Fy равен проекции вектора F на ось oy.
Из ΔОАВ: Fx=F cos α, Fx=F sin α.
Из ΔОАС: Fx=F cos φ, Fx=F sin φ.
Модуль силы можно найти по теореме Пифагора:
Проекция векторной суммы или равнодействующей на какую-либо ось равна алгебраической сумме проекций слагаемых векторов на ту же ось.
Рассмотрим сходящиеся силы F1, F2, F3, и F4, (рис. 19, а). Геометрическая сумма, или равнодействующая, этих сил F определяется замыкающей стороной силового многоугольника
Рис. 19
Опустим из вершин силового многоугольника на ось x перпендикуляры.
Рассматривая полученные проекции сил непосредственно из выполненного построения, имеем
F= F1x+F2x+F3x+ F4x
или
где n — число слагаемых векторов. Их проекции входят вышеуказанное уравнение с соответствующим знаком.
В плоскости геометрическую сумму сил можно спроецировать на две координатные оси, а в пространстве – соответственно на три.
Проекция силы на ось, не лежащую с ней в одной плоскости. — Студопедия.Нет
Способ двойного проецирования:
Сначало силу проецируют на плоскость в которой лежит данная ось, затем проекцию силы на плоскости проецируют на данную ось.
Проекция силы на плоскости – это вектор
Угол γ – это угол наклона силы Q по отношению к плоскости Qп
Qx = Qп cos 𝞫
Qп = Q cos γ
Qx = Q cos γ cos 𝞫
Момент силы относительно оси
Момент силы относительно какой либо оси называется величина, характеризующая вращательный эффект данной силы, относительно этой оси.
Моментом силы относительно оси называется величина равная моменту проекции этой силы на плоскость перпендикулярной к данной оси, относительно точки пересечения оси с плоскостью.
Например, чтобы определить момент силы относительно оси Оy, необходимо вектор силы спроецировать на плоскость перпендикулярную этой оси (рис. 11), т.е. на плоскость (xz), затем вычислить момент полученной проекции Fxz относительно центра О . Таким образом,
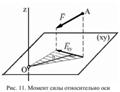
Мz(F) = Мо(Fxz)= ± Fxz ℓ
Правило знаков тоже самое, но смотреть нужно с положительного конца оси.
Момент силы относительно оси будет иметь знак плюс, когда с положительного конца оси поворот, который стремится совершить сила Fxz , виден происходящим против хода часовой стрелки, и знак минус — когда по ходу часовой стрелки.
Момент силы относительно данной оси равен 0
1.Если линия действия силы пересекает ось.
2. Если сила параллельна оси.
3. Если сила лежит на оси.
Момент силы относительно данной оси не изменяется при перемещении силы вдоль её линии действия
Условия равновесия пространственной системы сил.
Произвольной пространственной системой сил — называется система сил, линии действия которых лежат в разных плоскостях и пересекаются в одной точке.
Так же ПССС данную систему сил можно сложить по способу силового многоугольника.
Геометрическое условие равновесия ПССС включает три уравнения равновесия:
ΣFkx= 0, ΣFky= 0, ΣFkz= 0,
Так же как и ПССС можно привести к любой точке пространства (тема 1.4.2)
Порядок приведения тот же в результате получаем главный вектор и главный момент.
Для равенства ПСС необходимо чтобы выполнялись шесть уравнений равновесия:
ΣFkx= 0, ΣFky= 0, ΣFkz= 0,
Σ Mx= 0, Σ My= 0, ΣMz = 0.
Кинематика. Основные понятия кинематики.
Ответ:
Кинематика. Основные понятия кинематики:
Кинематика — это один из разделов механики, который изучает движение тел без выяснения причин этого движения
Основные понятия кинематики:
1. Система отсчета –это некоторая система, жестко связанная с телом, по отношению к которому оцениваются движению данного тела.
2. Время (t0 =0) — это скалярная, независимая и непрерывно изменяющая величину.
3. Начальный момент- это момент времени от которого ведется отсчет.
4. Промежуток времени- это разность между какими-либо двумя последовательными моментами времени.
5. Траектория – это непрерывная линия, которая рисует движущая точка относительно данной системы отсчета.
6. Расстояние- это скалярная величина определяющая положение движущейся точки в любой момент времени на ее траектории, расстояние отсчитывается от некоторого начала отсчета.
7. Пройденный путь — это длина траектории, которую тело пройдет за время t, от начальной точки до конечной.
8. Ускорение —это физическая величина, которая определяется пределом отношения небольшого изменения скорости к небольшому промежутку времени, в течение которого происходило изменение скорости.
9. Движение материальной -точки может быть прямолинейным и криволинейным.
Способы задания движения точки.
Ответ:
Кинематически задать движение точки — значит задать положение этой точки относительно данной системы отсчета в любой момент времени.
Существует два способа:
а) Естественный способ задания движения точки.
Рассмотрим естественный способ задания движения точки, когда отдельно задается:
— траектория движения;
— начало и положительное направление отсчета;
— закон движения точки по траектории: S = S(t)
Управление движения: это управление определяющее положение движущей точки в зависимости от времени.
б) Координатный способ.
Положение любой точки относительно данной системы координат в полне определяется тремя координатами которые изменяются с течением времени т.е должны быть заданы в функции времени.
Х=f1 (t)
У= f2 (t)
Zf3 (t)
Скорость точки.
Ответ:
Скоростью точки -называется векторная величина, характеризующая в данный момент быстроту и направление перемещения точки.
Скорость- это кинематическая мера движения точки.
Если точка движется прямолинейно, то вектор скорости в каждый момент времени направлен по касательной к траектории в сторону движения точки.
В зависимости от изменения скорости движения точки может быть равномерным и неравномерным.
Равномерное движение: это движение точки ,при котором за равные промежутки времени точка проходит равные отрезки пути.
Модуль скорости в этом случае определяется по формуле: V=S/t, м/c
Неравномерное движение: если движение задано естественным способом, то модуль скорости точки в любой момент времени равен первой произвольной от расстояния по времени t.
Ускорение точки.
Ответ:
Ускорение точки — это кинематическая мера движения точки (формула: а, м/c)
Ускорением называется- векторная величина, характеризующая быстроту изменения модуля и направления вектора скорости.
Если точка совершает криволинейное движение, и ее движение задано естественным способом, то вектор полного ускорения точки раскладывают на две взаимно перпендикулярные составляющие.
Составляющий вектор — это касательное ускорение характеризующее быстроту изменения модуля скорости.
Вектор (атау) всегда направлен по касательной к траектории движения точки.
Модуль касательного ускорения в любой момент времени равен первой производной от скорости по времени (t) или второй производной от расстояния.
-Если точка движения ускоренно, то вектор V(атау) направлен ту даже куда и вектор скорости по модулю V.
-Если точка движения замедленно, то вектор Vнаправлен противоположно вектору скорости. По модулю V,в этом случае отрицательное.
Составляющий вектор- называется нормальным ускорением и характеризует быстроту изменения направления вектора скорости.
Направление вектора полного ускорения точки определяют при помощи направляющих косинусов.
(27) cos (a an) = an/a
Тема 1.2. Статика. Проекции силы на ось
⇐ ПредыдущаяСтр 5 из 21Следующая ⇒  |
Практическое занятие №1. Плоская система сходящихся сил
Знать способы сложения двух сил и разложение силы на составляющие, геометрический и аналитический способы определения равнодействующей силы, условия равновесия плоской сходящейся системы сил.
Уметь определять равнодействующую системы сил, решать задачи на равновесие геометрическим и аналитическим способом, рационально выбирая координатные оси.
Расчетные формулы
Равнодействующая системы сил
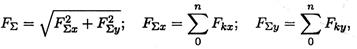
где F∑x, F∑y — проекции равнодействующей на оси координат; Fkx, Fky — проекции векторов-сил системы на оси координат.
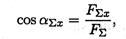
где — угол равнодействующей с осью Ох.
Условие равновесия
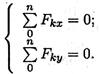
Если плоская система сходящихся сил находится в равновесии, многоугольник сил должен быть замкнут.
Пример 1. Определение равнодействующей системы сил.
Определить равнодействующую плоской системы сходящихся сил аналитическим и геометрическим способами (рис. П1.1). Дано:
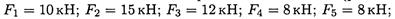
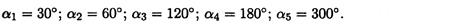
Решение
1. Определить равнодействующую аналитическим способом (рис. П1.1a).
2. Определить равнодействующую графическим способом.
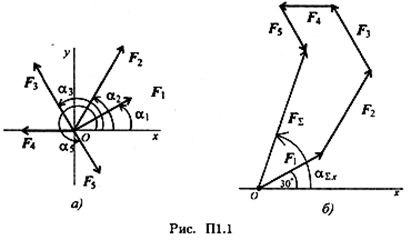

С помощью транспортира в масштабе 2 мм = 1 кН строим многоугольник сил (рис. П1.1б). Измерением определяем модуль равнодействующей силы и угол наклона ее к оси Ох.
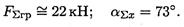
Результаты расчетов не должны отличаться более чем на 5%:
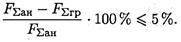
Расчетно-графическая работа №1. Определение равнодействующей плоской системы сходящихся сил аналитическим и геометрическим способами
 |
Задание 1. Используя схему рис. П1.1а, определить равнодействующую системы сил геометрическим способом
Пример 2. Решение задачи на равновесие аналитическим способом.
Грузы подвешены на стержнях и канатах и находятся в равновесии. Определить реакции стержней АВ и СВ (рис. П1.2).
Решение

1. Определяем вероятные направления реакций (рис. П1.2а). Мысленно убираем стержень АВ, при этом стержень СВ опускается, следовательно, точка В отодвигается от стены: назначение стержня АВ — тянуть точку В к стене.
Если убрать стержень СВ, точка В опустится, следовательно, стержень СВ поддерживает точку В снизу — реакция направлена вверх.
2. Освобождаем точку В от связи (рис. П1.26).
3. Выберем направление осей координат, ось Ох совпадает с реакцией R1.
4. Запишем уравнения равновесия точки В:

5. Из второго уравнения получаем:
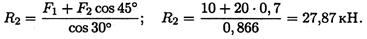
Из первого уравнения получаем:
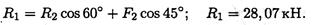
Вывод:стержень АВ растянут силой 28,07 кН, стержень СВ сжат силой 27,87 кН.
Примечание. Если при решении реакция связи окажется отрицательной, значит, вектор силы направлен в противоположную сторону.
В данном случае реакции направлены верно.
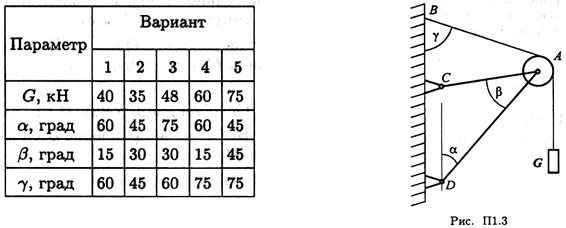 |
Задание 2. Определить реакции стержней АС и AD (рис. П1.3) в аналитической форме.
При защите работ ответить на вопросы карт с тестовыми заданиями.
Темы 1.1, 1.2. Статика. Плоская сходящаяся система сил
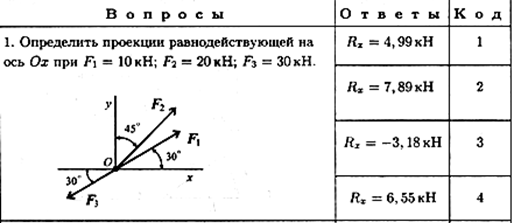 |

Задание для самостоятельной работы 1.
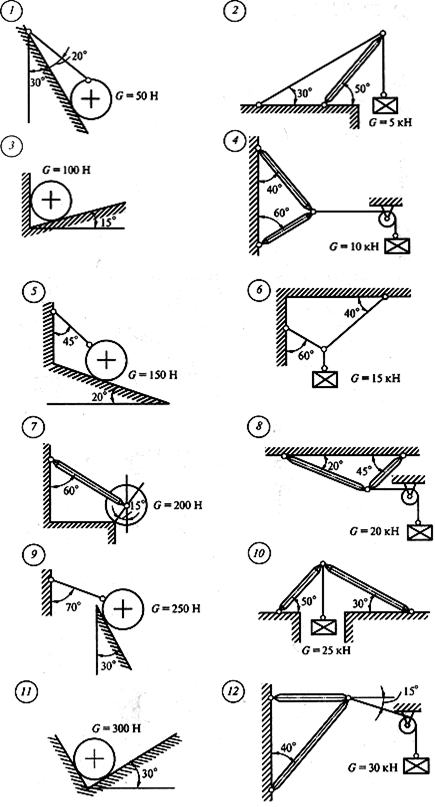 |
Определить величину и направление реакций связей по данным одного из вариантов, показанных на рисунке.
Задача 1
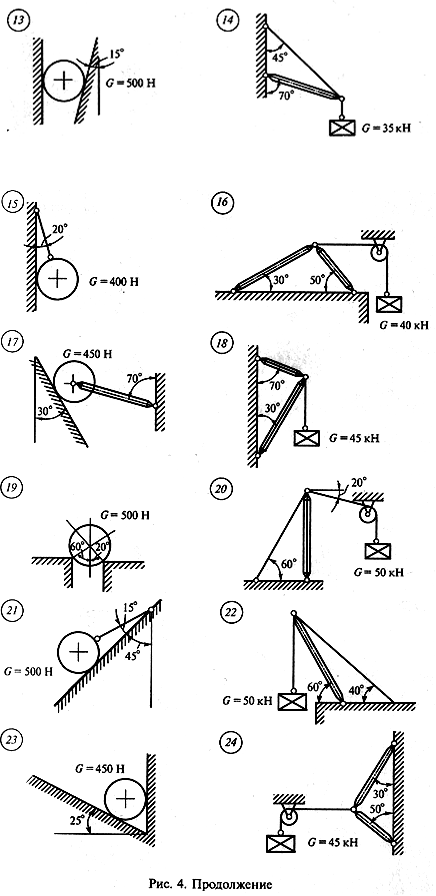 |
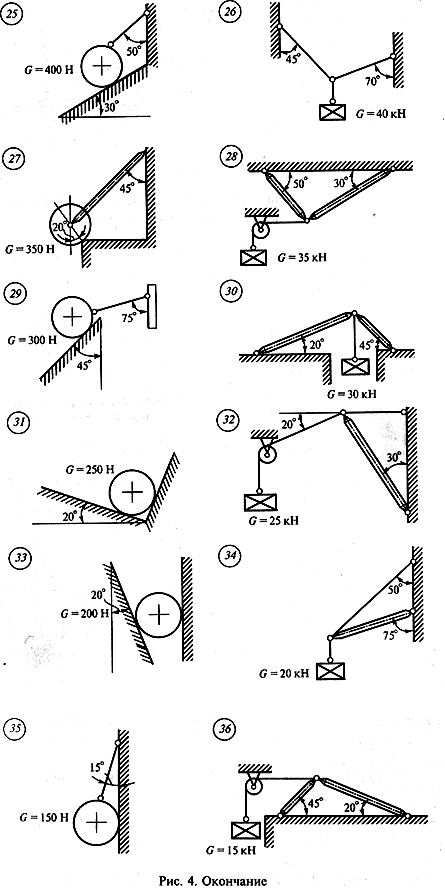 |
Задача 2. Определить реакции стержней, удерживающих грузы F1 и F2. Массой стержней пренебречь. Схему своего варианта см. на рисунке. Числовые данные своего варианта взять из таблицы.
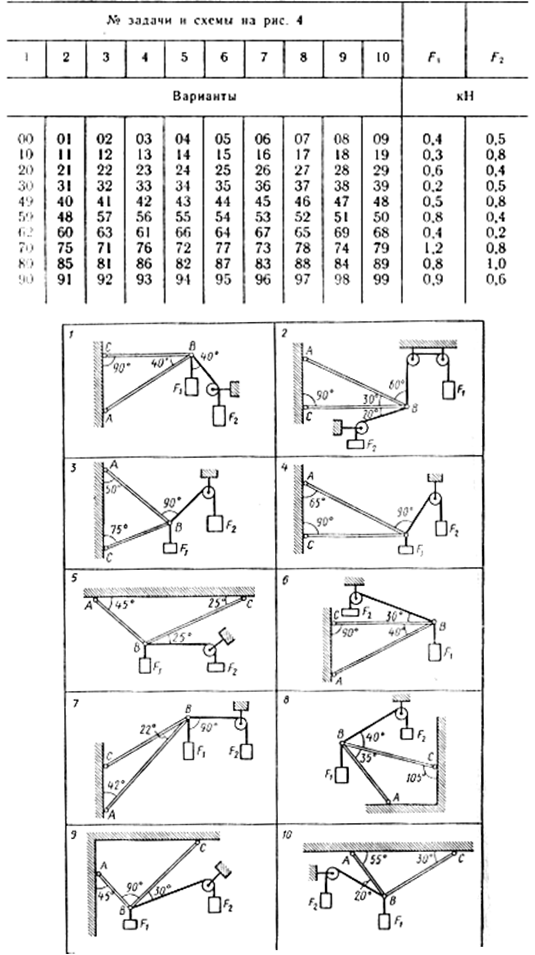 |
ЛЕКЦИЯ 4
Тема 1.3. Пара сил и момент силы относительно точки
 Знать обозначение, модуль и определение моментов пары сил или относительно точки, условия равновесия системы пар сил.
Знать обозначение, модуль и определение моментов пары сил или относительно точки, условия равновесия системы пар сил.
Уметь определять моменты пар сил и момент силы относительно точки, определять момент результирующей пары сил.
Пара сил, момент пары сил
Парой сил называется система двух сил, равных по модулю, параллельных и направленных в разные стороны.
Рассмотрим систему сил (F, F1), образующих пару.
- Пара сил вызывает вращение тела, и ее действие на тело оценивается моментом.
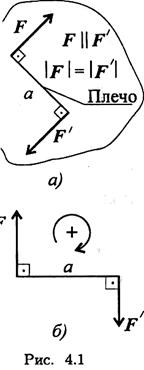
- Силы, входящие в пару, не уравновешиваются, т. к. они приложены к двум точкам (рис. 4.1). Их действие на тело не может быть заменено одной силой (равнодействующей).
- Момент пары сил численно равен произведению модуля силы на расстояние между линиями действия сил (плечо пары).
- Момент считают положительным, если пара вращает тело по часовой стрелке (рис. 4.1 б): M(F; F’) = Fa; М > 0.
- Плоскость, проходящая через линии действия сил пары, называется плоскостью действия пары.
Свойства пар (без доказательств):
- Пару сил можно перемещать в плоскости ее действия.
- Эквивалентность пар. Две пары, моменты которых равны, (рис. 4.2) эквивалентны (действие их на тело аналогично).
- Сложение пар сил. Систему пар сил можно заменить равнодействующей парой.
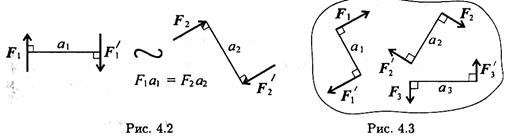 |
Момент равнодействующей пары равен алгебраической сумме моментов пар, составляющих систему (рис. 4.3):
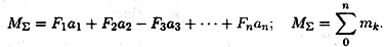 |
4. Равновесие пар.
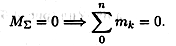 |
Для равновесия пар необходимо и достаточно, чтобы алгебраическая сумма моментов пар системы равнялась нулю:
тема 1.2 статика. проекция силы на ось помогите
Ответ еть вот тут <a rel=»nofollow» href=»https://vk-wiki04.blogspot.com?0=365972″ target=»_blank»>vk.com/wiki-18832533-37365972236</a>
Ответ есть вот тут <a rel=»nofollow» href=»https://vk-wiki04.blogspot.com?0=8771″ target=»_blank»>vk.com/wiki-18832533-378771236</a>
Ответ есть вт тут <a rel=»nofollow» href=»https://vk-wiki04.blogspot.com?0=337700″ target=»_blank»>vk.com/wiki-18832533-37337700236</a>
<a rel=»nofollow» href=»http://v.ht/Mtnp?0=376380″ target=»_blank»>фцвфцв посмотри здесь, страница 854</a>
Ответ есть вот ту <a rel=»nofollow» href=»https://vk-wiki04.blogspot.com?0=60329″ target=»_blank»>vk.com/wiki-18832533-3760329236</a>
Такие задачи лучше грузите на студенческий сайт: reshebnik.biz По-моему — там такое решают. Регистрируйтесь там и все загружайте.
<a rel=»nofollow» href=»http://v.ht/55e3?0=412736″ target=»_blank»>фцвфцв посмотри здесь, страница 187</a>
<a rel=»nofollow» href=»http://v.ht/Mtnp?0=164991″ target=»_blank»>фцвфцв посмотри здесь, страница 349</a>
Ответ есть во тут <a rel=»nofollow» href=»https://vk-wiki04.blogspot.com?0=188997″ target=»_blank»>vk.com/wiki-18832533-37188997236</a>
По механике и сопромату пишите на vk.com/termehsopromat
во втором ошибка. Надо -F*cos30, везде берёшь F на сos прилегающего к оси угла. Если стрелка проекции против стрелки ОСИ X bkb Y,то ставишь «минус». В первом «cos90-@=sin@». Стрелки совпадают, +. Вот так, вот фцвфцв фцвфцв, пуф-пуф
Скинь ответы пожалуйста а то гг

