Определение момента инерции диска и сил трения в подшипниках, страница 2
Опыт №3:
m | h1 | h2 | t | M | I |
Опыт №1:
h2ср=
tср=
Момент сил трения:
M=
Момент инерции:
I=
Опыт №2:
h2ср=
tср=
Момент сил трения:
M=
Момент инерции:
I=
Опыт №3:
h2ср=
tср=
Момент сил трения:
M=
Момент инерции:
I=
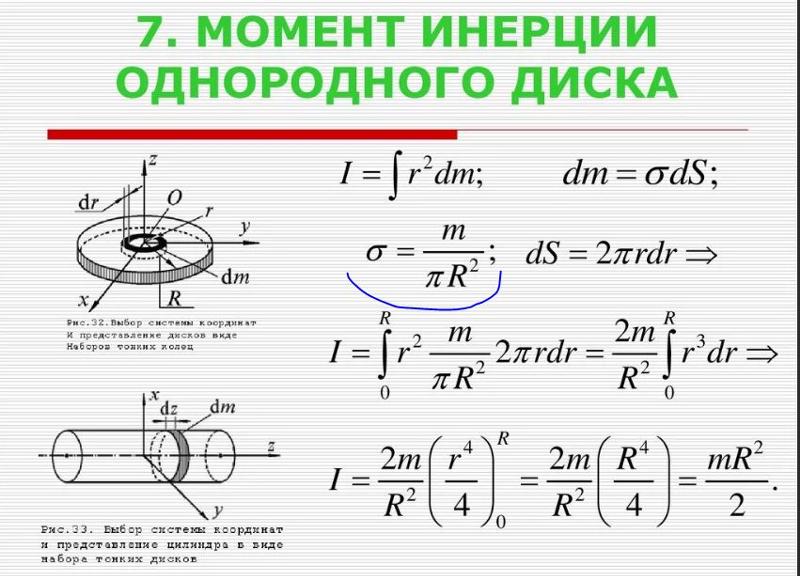
Найдем момент инерции диска теоретически:
I=
Rвнутр=
I=
Получилось расхождение значений, измерения при опыте были

Контрольные вопросы:
1)Что называется моментом инерции материальной точки? От чего зависит момент инерции тела?
Величина I равна сумме произведений масс mi всех материальных точек, образующих механическую систему, на квадрат их расстояний pi от данной оси, называется моментом инерции системы.
2)Что называется моментом силы относительно точки, неподвижной оси? Как определить его направление, и в каких единицах измеряется.
Моментом силы относительно точки называется величина равная векторному произведению радиус-вектора точки, проведенного из этой точки на силу.M=[rk],[Н*м].
3)Определение угловой скорости и углового ускорения. Как направлен вектор угловой скорости?
Угловая скорость – кинематическая величина, характеризующая направление ее быстроту вращения тела. Угловая скорость направлена по оси вращения и связана с направлением вращения по правилу правого винта.
Угловое ускорение – это вектор, характеризующий
быстроту изменения угловой скорости тела.
4)Связь между угловыми и векторными величинами.
V=R*W; ar=E*R; an=R*W2=W*V
5)Вывести уравнение основного закона динамики вращательного движения.
, где l – момент импульса вращающегося тела относительно оси вращения.
6)Какая сила сообщает вращательный момент маятнику.
Это сила тяжести, так как при подъеме тела на высоту h под действием силы тяжести тело возвращается в исходное положение и тем самым заставляет маятник вращаться.
Что такое Момент инерции? Определение, Уравнение, Формула, Единицы, Масса, Полярный MI
Что такое момент инерции? Самый популярный вопрос. Когда полый цилиндр, сплошной цилиндр и сфера одинаковой массы свободно катятся по склону, какой из них опустится первым и почему?
Давайте сначала пройдемся по основам!
Что такое Момент инерции? Определение
Прежде чем понять момент инерции, вам необходимо понять понятия момента, инерции, центра тяжести, центроида и изгибающего момента.
Основы момента инерции
Мы изучим основы момента инерции. Сначала позвольте мне задать вам один простой вопрос: крутящий момент и момент одинаковы?
В физике это одно и то же, но в механике они имеют существенно разные значения.
У них одна и та же единица измерения – ньютон-метр (Нм).
Крутящий момент и момент – Основы момента инерцииДавайте посмотрим на разницу между крутящим моментом и моментом!
| Крутящий момент | Момент |
| Крутящий момент — это сила, которая может заставить объект вращаться вокруг оси. | Момент силы — это мера ее способности заставить тело вращаться вокруг заданной точки или оси. |
| Используется при вращении. | Используется там, где не требуется вращение. |
| Применение Турбины, динамо-машины, валы. | Области применения Гибка, мосты, несущие конструкции. |
 Разница крутящего момента и момента
Разница крутящего момента и моментаЦентр тяжести
- Центр тяжести — это область тела, на которую действует весь вес тела. Для всех ориентаций тело имеет только один центр тяжести.
- Обозначается как C.G или просто G.
Центроид
- Центроид — это точка, в которой предполагается сконцентрировать всю площадь плоской фигуры. В данном контексте плоской фигурой является прямоугольник, треугольник, квадрат, четырехугольник, круг и так далее. Центроид обозначается символом G.
- Центроид и центр тяжести — это одни и те же точки на теле. Если предмет находится в равновесии в любой точке вдоль вертикальной линии, проходящей через его центр тяжести, он останется в покое.
Момент инерции Определение
Определяется как величина, указываемая телом, сопротивляющимся угловому ускорению, которая является суммой произведения массы каждой частицы на ее квадрат расстояния от оси вращения [Момент инерции I = Σ м i r i 2 ]
- Обозначается I
Момент инерции I элемента массы m, расположенного на расстоянии r от центра вращения, равен
I=mr 2
Проще говоря, это величина крутящего момента, необходимая для определенного углового ускорения на вращающейся оси.
- Это означает просто отношение углового момента к угловой скорости.
- Момент инерции может быть записан как I = L/ ω ,
где,
- I = момент инерции
- L = угловой момент
- ω 9097 = угловая скорость
. Это не то же самое!
Ознакомьтесь с нашим «Обучающим приложением MechStudies» в iOS и Android
Разница между инерцией и моментом инерции даже при движении с постоянной скоростью по прямой.
| Инерция | Момент инерции |
| Инерция определяется как свойство или склонность объекта сопротивляться изменениям в его состоянии движения. | Момент инерции — это измерение сопротивления объекта изменению вращения. Он указывается по отношению к определенной оси вращения. |
| Когда к объекту, которому он сопротивляется, прикладывается сила, это инерция. | При приложении крутящего момента он сопротивляется изгибу, это момент инерции |
| Есть 3 типа, инерция направления, покоя и движения | Есть 3 типа моментов – ИМ площади, МИ массы, и Полярный МИ. |
Уравнение или формула для момента инерции и единиц измерения
Что такое сила, момент силы?
Пожалуйста, включите JavaScript
Что такое сила, момент силы?
Уравнение или формула для момента инерции
Рассмотрим очень маленький шарик незначительной массы, прикрепленный к стержню на конце и вращающийся вокруг неподвижной оси.
Формула определения момента инерции- m = масса (пренебрежимо мала)
- l = длина стержня
- a = ускорение
- F = сила, действующая на шарик
Основано на втором законе линейного движения Ньютона,
- Сила = масса x ускорение
- F = ma
Теперь, исходя из определения крутящего момента, мы можем написать:
- Крутящий момент = сила x радиус
- as F = ma]
- 𝜏 = mar
Из угловых величин мы также можем написать,
- L = I ω
- L = I a/r [as ω = a/r]
У нас есть два уравнения,
- 𝜏 = марта
- L = I a/r
Приравнивая эти вышеприведенные уравнения,
- I a/r = mar
- I = mr 2
Это простое уравнение или формула для момента инерции2, I=mr 2
- Таким образом, когда объект находится в угловом движении, компоненты массы в теле часто находятся на различных расстояниях от центра вращения.

- Общий ИМ представляет собой сумму ИМ массовых частей тела.
- По сравнению с массой, которая постоянна для любого данного тела, на момент инерции влияет расположение центра вращения.
- ИМ часто определяют с помощью интегрального исчисления.
- Момент инерции (I) рассчитывается путем умножения массы каждой частицы вещества в конкретном теле на квадрат ее расстояния от оси. При вычислении углового момента твердого тела ИМ аналогичен массе в линейном движении. Линейный импульс p равен массе m, умноженной на скорость v, а угловой момент L равен моменту инерции I, умноженному на угловую скорость ω.
- MI также называют вторым моментом площади.
Предположим, есть объект, в котором два стальных шарика приварены к стержню, а стержень прикреплен к стержню. Если пренебречь массой стержня, к которому приварены шары, и принять массу шаров за «m», сосредоточенную на расстоянии «r» от центра.
Формула уравнения инерции моментаМомент инерции установки будет определяться как:
I = 2mr 2
- Это не скаляр и не вектор, но считается тензором.
 (обобщение понятийного вектора)
(обобщение понятийного вектора)
Единицы момента инерции – единицы СИ
Давайте посмотрим, что является единицей МИ?
Мы уже выучили формулу уравнения МИ, I=mr 2
Следовательно,
Единица момента инерции в единице СИ
- Единица МИ = Единица массы x ( единица радиуса) 2
- Единица МИ = кг x м 2 [в качестве единицы массы = кг, единица радиуса = м, в единицах СИ]
- Единица МИ = кг.м 2
Следовательно, единицей площади в МИ являются кг.м 2 в системе СИ
Момент инерции Единицы
Единица момента инерции в единице FPS
- Единица МИ = Единица массы x (единица радиуса) 2
- Единица МИ = фунт-сила x фут 2 [как единица массы = фунт-сила, единица измерения радиуса = фут, единица FPS]
- Единица MI = lbf.ft 2
Следовательно, единицей площади MI является lbf.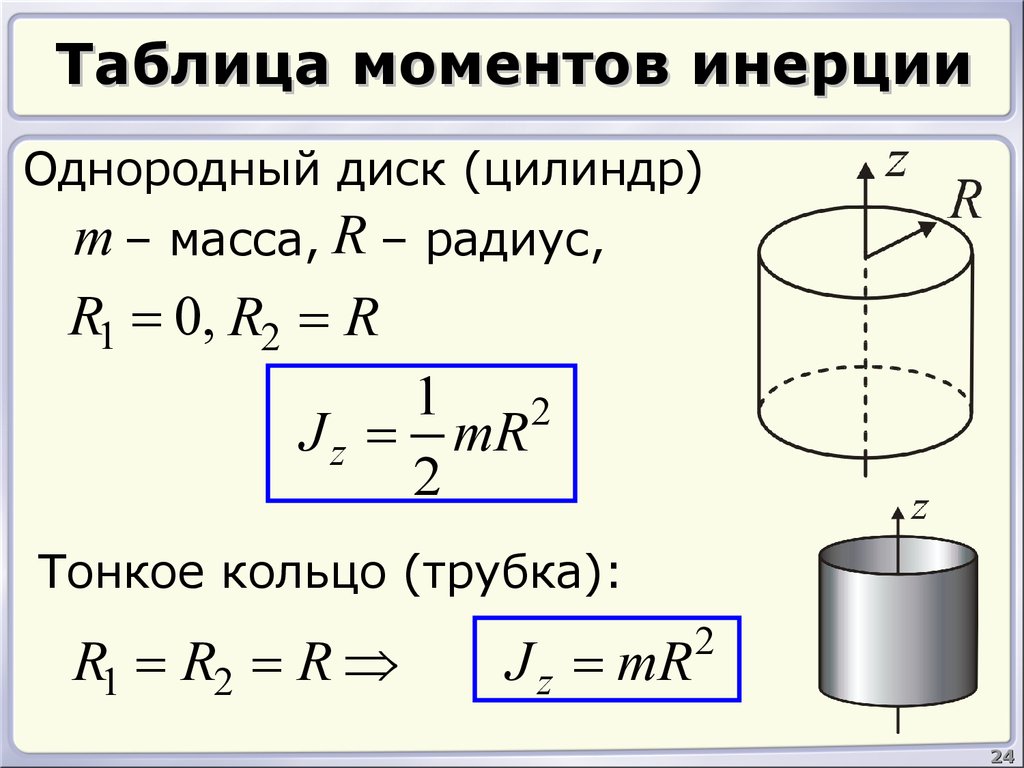 ft 2 в FPS.
ft 2 в FPS.
Размерность момента инерции
Размерность MI составляет M.L 2
Момент инерции Примеры
Существует так много примеров момента инерции, некоторые из них показаны ниже,
Практический пример – Колесо
- Если MI очень большой, очень трудно ускориться в угловом направлении.
- Если индекс MI мал, его относительно легко повернуть под углом.
- Следовательно, колесо с меньшим ИМ разгоняется быстрее.
- Если масса (m) увеличивается, MI увеличивается, поэтому они прямо пропорциональны друг другу. Так что гораздо сложнее вращать объект с большей массой с тем же радиусом.
- Если радиус (r) увеличивается, MI также увеличивается. Так что гораздо сложнее вращать объект с той же массой и большим радиусом.
Практический пример – удочка
- Удочку легко крутить, удерживая ее за центр.
МИ = (ML 2 )/12
- Однако, если цилиндр держать за один конец, масса рассеивается довольно далеко от оси вращения, что затрудняет вращение.

МИ = (ML 2 )/3
- Момент инерции спиннинга относительно оси, проходящей через конец стержня, больше, чем МИ спиннинга относительно оси, проходящей через середину стержня.
- Таким образом, мы можем заключить, что МИ зависит от массы, радиуса и оси объекта.
- Масса полого цилиндра распределена дальше от центра. Даже если и сплошной, и полый цилиндры имеют одинаковую массу, полый будет сложнее разогнать или затормозить. Он имеет сравнительно больший момент инерции.
Примечания к моменту инерции
- ИМ является мерой сопротивления объекта изменениям вращения.
- Также описывается как способность сечения выдерживать изгиб.
- MI должен быть указан по отношению к определенной оси вращения.
- Обычно измеряется в м 4 или в кгм 2 .
Применение момента инерции
- Многие сечения в форме двутаврового сечения или сечения C, круглого стержня или углового сечения образуют структурную часть любых конструкций.
 Для проверки напряжений и моментов на них нужен момент инерции.
Для проверки напряжений и моментов на них нужен момент инерции. - Вантовые подвески в вантовых или вантовых мостах.
- Крепления в многоэтажных зданиях, производственных зданиях, наливных резервуарах.
- Анкер и провисающие стержни в ферме крыши.
- Растяжки и хомут в стальном дымоходе/трубе.
- Мобильные опоры, электрические опоры, железнодорожные пути.
- Строительство плотин.
Момент инерции массы
Масса MI, широко известная как инерция вращения, представляет собой число, используемое для расчета сопротивления тела изменению направления вращения или углового момента.
По сути, это описывает ускорение, испытываемое объектом или телом при приложении крутящего момента.
Символ I G обычно используется для обозначения момента инерции массы.
- I G обозначает «момент инерции массы» тела относительно оси, проходящей через его центр масс G.
- I G определяется как: IG= ∫r 2 дм Единицы: кг-м 2 или slug-ft 2
- I G применяется к различным ситуациям вращения твердого тела, включая:
(a) F=ma расчетное уравнение момента (ΣM G = I G α).
(b) Кинетическая энергия вращения (T = ½I G ω2)
(c) Угловой момент (H G = I G ω)
- I G угловое сопротивление тел . То есть, для данного результирующего момента или крутящего момента тела, чем больше I G тела, тем меньше будет его угловое ускорение α.
- I G также влияет на угловой момент тела и на то, как тело накапливает кинетическую энергию при вращении.
- I G для тела зависит от массы тела и расположения массы. Чем больше расстояние массы от оси вращения, тем больше будет I G . Например, маховики имеют здоровенный внешний фланец, который отводит как можно больше массы от ступицы.
Практический пример – мы используем кольцеобразные колеса вместо дисковых.
Теорема о перпендикулярной оси для момента инерции
Эта теорема применима только к плоским телам. Тела, которые плоские и имеют очень небольшую толщину или не имеют ее вовсе.
Теорема утверждает, что момент инерции плоского тела при оси, перпендикулярной его плоскости, равен сумме его моментов инерции по двум перпендикулярным осям, совпадающим с перпендикулярной осью и лежащим в плоскости тела.
Это означает момент инерции I z = I x +I y
Теорема о параллельности оси для момента инерции
Теорема о параллельности оси применима к телам любой формы и формы.
Согласно теореме о параллельных осях, момент инерции тела относительно оси, параллельной оси, проходящей через центр масс, равен сумме моментов инерции тела относительно оси, проходящей через центр масс масса, произведение массы и квадрат расстояния между двумя осями.
По существу, теорему можно математически сформулировать так: I XX = I G + Ad 2
- A — площадь поперечного сечения.
- Перпендикулярное расстояние между центральной и параллельной осями равно d.

Радиус вращения k
GЧто такое Радиус вращения?
Радиус вращения иногда используется для выражения момента инерции тела относительно оси. Что именно вы подразумеваете под «радиусом вращения»?
Радиус инерции можно определить как воображаемое расстояние от центра тяжести, на котором считается, что площадь поперечного сечения сосредоточена в точке для достижения того же момента инерции.
Радиус уравнения и примеров уравнения и примеров.
Другими словами, радиус вращения определяет распределение общей площади поперечного сечения вокруг его центральной оси. Чем больше площадь удалена от оси, тем больше сопротивление продольному изгибу.
Чем больше площадь удалена от оси, тем больше сопротивление продольному изгибу.
Круглая труба является наиболее эффективной секцией колонны с точки зрения сопротивления продольному изгибу, поскольку ее площадь разбросана настолько далеко от центра тяжести, насколько это возможно.
- Ix = k x 2 A
- Iy = k y 2 A
- k = I/A
Где используется радиус вращения?
Радиус вращения используется для сравнения поведения различных структурных геометрий при сжатии вдоль оси. Он применим при прогнозировании потери устойчивости в сжатой балке или элементе.
Полярный момент инерции
- Полярный момент инерции объекта является мерой его способности противодействовать или сопротивляться скручиванию, когда к нему прикладывается определенный крутящий момент вдоль определенной оси.
- Скручивание, с другой стороны, представляет собой скручивание объекта, вызванное приложенным крутящим моментом.
 Полярный момент инерции объясняет сопротивление цилиндрического объекта (включая его сегменты) деформации кручения при приложении крутящего момента в плоскости, параллельной площади поперечного сечения или перпендикулярной центральной оси объекта.
Полярный момент инерции объясняет сопротивление цилиндрического объекта (включая его сегменты) деформации кручения при приложении крутящего момента в плоскости, параллельной площади поперечного сечения или перпендикулярной центральной оси объекта. - В ситуациях, требующих кручения цилиндрических валов и вращения пластин, полярный момент инерции является существенной величиной.
- Сопротивление вала или балки деформации при кручении в зависимости от формы. Жесткость исходит из площади поперечного сечения объекта и не зависит от его материала.
- Символ J используется для обозначения полярного MI
J = Ix + Iy
Подводя итог, можно сказать, что полярный момент инерции — это сопротивление, оказываемое балкой или валом при изгибе при кручении. Это сопротивление часто обусловлено площадью поперечного сечения, и следует подчеркнуть, что оно не связано с составом материала.
Чем больше полярный момент инерции, тем больше будет сопротивление тела кручению. Для поворота вала под углом потребуется больший крутящий момент.
Для поворота вала под углом потребуется больший крутящий момент.
Область момента инерции по сравнению с массовым моментом инерции
давайте посмотрим на разницу между МИ и массой MAS MI, следующим образом:
| Площадь MI | MASS MI | . мера способности сечения сопротивляться изгибу вокруг базовой оси. | Масса MI является мерой способности твердого тела сопротивляться вращению (т. е. угловому ускорению) вокруг базовой оси. |
| Больше момент инерции · Меньше будет напряжение изгиба · Больше будет жесткость балки · Меньше будет прогиб балки | Меньше масса MI и, следовательно, меньше сопротивление ее вращению. |
| Это свойство двумерных сечений или областей плоскостей. | Это свойство трехмерных твердых тел. |
| Применение Проектирование балок и конструкций | Применение Проектирование зубчатых колес, зубчатых передач и коробок передач. (вращающиеся элементы) Также используется в гироскопической паре и ее влиянии на автомобиль, корабль, самолет. (вращающиеся элементы) Также используется в гироскопической паре и ее влиянии на автомобиль, корабль, самолет. |
Заключение
Момент инерции – это вычисление величины силы, необходимой для вращения объекта. Значение можно изменить для увеличения или уменьшения инерции. Спортсмены, занимающиеся фигурным катанием, прыжками в воду и гимнастикой, постоянно изменяют структуру своего тела. МИ увеличивается по мере увеличения радиуса от оси вращения, замедляя вращение.
Если спортсмен хочет улучшить скорость вращения, он должен уменьшить радиус, переместив сегменты тела ближе к оси вращения, тем самым уменьшив радиус и ИМ.
Момент инерции используется в механике, физике, а также в реальных ситуациях для достижения желаемой скорости вращения.
Наши приложения и викторина
Проверьте наши «Mechstudies — The Learning App» в IOS и Android
Наш YouTube
Проверьте наши оживленные видео
Диаграмма свободного тела
Основы напряжения и деформации
Коэффициент Пуассона
Круг
Кривая напряжения деформации
Момент определения инерции, формула, единицы и уравнения
Определения: МОМ тело — это величина, которая определяет количество крутящего момента, необходимого для желаемого углового ускорения вокруг оси вращения.
MOI объекта относительно оси вращения является мерой сопротивления объекта изменению углового ускорения объекта из-за действия пары или крутящего момента.
МВД твердого тела можно получить путем визуализации тела, разделенного на несколько частиц. Затем массу каждой частицы умножают на квадрат расстояния от оси, а затем суммируют эти произведения для всех частиц в теле.
Момент инерционных единиц:
Момент инерции SI Блок- кг.м 2
МОМЕНТ Инерции- мм 4 ИЛИ В 4
или в 4 9007.0024 кг.м 2 или ft.lb. s 2Dimensional Formula- M 1 L 2 T 0
Factors affecting MOI: It is scalar quantity because its value about a given axis of rotation remains unchanged by меняет направление вращения вокруг этой оси.
Чем больше момент инерции тела, тем больше пара (крутящий момент), необходимая для создания заданного углового ускорения.
MOI зависит от того, как масса объекта распределена относительно его оси вращения.
У тела нет единого Момента Инерции, но потенциально бесконечное количество Моментов Инерции, по одному на каждую ось вращения.
Если MOI мал, относительно легко повернуть под углом. Следовательно, при меньшем моменте инерции ускоряться быстрее.
Гораздо сложнее вращать объект большей массы с тем же радиусом. Точно так же гораздо сложнее вращать объект с той же массой и большим радиусом.
Момент инерции Формула:В случае трансляционного движения значение инерции зависит только от массы тела. Кинетическая энергия при таком движении зависит от массы и линейной скорости тела.
При вращении тела вокруг оси вращения кинетическая энергия вращения определяется не только его массой и угловой скоростью, но также зависит от положения оси, вокруг которой оно вращается, и распределения массы вокруг этой оси вращения.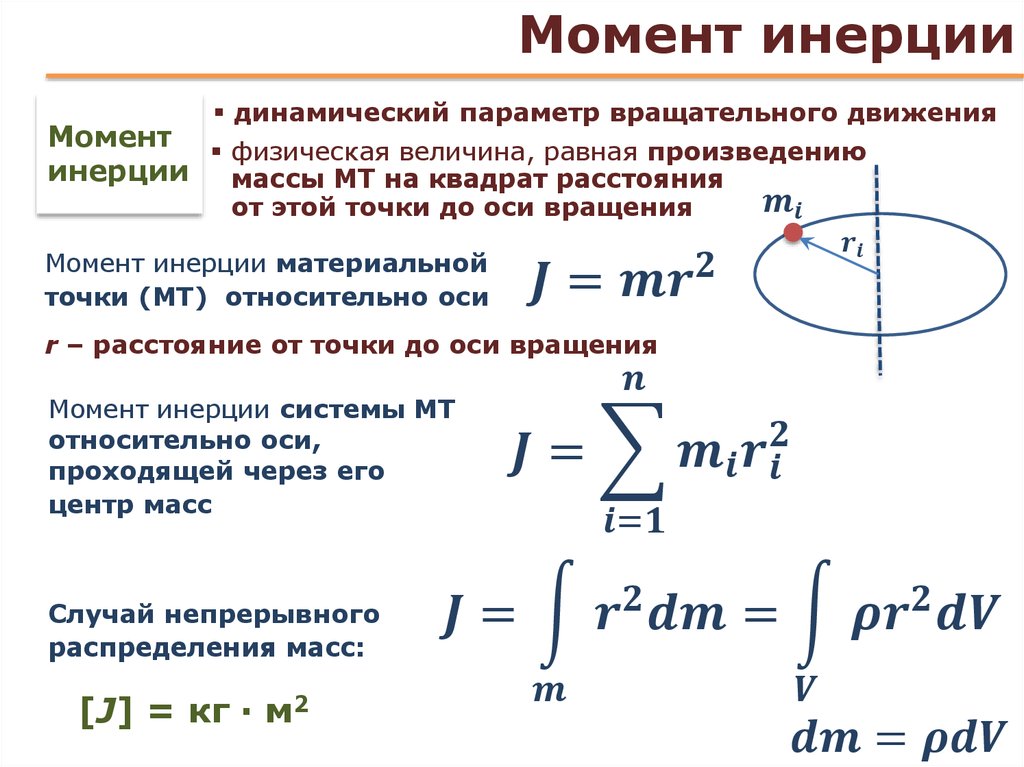


 (обобщение понятийного вектора)
(обобщение понятийного вектора)
 Для проверки напряжений и моментов на них нужен момент инерции.
Для проверки напряжений и моментов на них нужен момент инерции.
 Полярный момент инерции объясняет сопротивление цилиндрического объекта (включая его сегменты) деформации кручения при приложении крутящего момента в плоскости, параллельной площади поперечного сечения или перпендикулярной центральной оси объекта.
Полярный момент инерции объясняет сопротивление цилиндрического объекта (включая его сегменты) деформации кручения при приложении крутящего момента в плоскости, параллельной площади поперечного сечения или перпендикулярной центральной оси объекта.