| Частота какая буква в физике. В чем измеряется частота? Период и частота |
– физическая величина, являющаяся основной характеристикой периодических процессов или процессов, происходящих по определенным закономерностям. Показывает количество полных колебаний (циклов) за единицу времени. Колебания – физические процессы, точно или приблизительно повторяющиеся через одинаковые интервалы времени. Колебания, в зависимости от физической природы, бывают двух основных типов: механические, электромагнитные. Иногда выделяют еще смешанный тип, который является комбинацией основных типов. Типы колебанийМеханические колебания — такие движения тел, при которых через равные интервалы времени координаты движущегося тела, его скорость и ускорение принимают исходные значения. Электромагнитные — взаимосвязанные колебания магнитного и электрического полей. По характеру взаимодействия с окружающей средой колебания подразделяютСвободные — колебания, происходящие в механической системе под действием внутренних сил системы после кратковременного воздействия внешней силы. Такие колебания называют затухающими. Вынужденные – колебания, возникающие под действием внешних сил, изменяющихся со временем по величине и направлению. Такие колебания называют незатухающими. Автоколебания — система изначально имеет запас потенциальной энергии, который и идет на совершение колебаний. Величины, характеризующие колебанияПонятие «колебания» тесно связано с волнами. Но при колебательном движение, в отличие от волнового, отсутствует процесс переноса энергии из одной точки пространства в другую. Основными характеристиками колебательного движения, как и волнового, являются период (Т), амплитуда (А) и частота(v иногда f ). Причем период и частота величины взаимообратные – чем больше частота, тем меньше период: Т=1/v . Период – это промежуток времени, за который совершается одно полное колебание (цикл), измеряется в секундах. Также единицей измерения частоты в международной метрической системе единиц Си с 1933 года является герц. Единица измерения названа в честь немецкого профессора физики Генриха Рудольфа Герца (1858-1894), который опытным путем, исследуя дифракцию, интерференцию, поляризацию и отражение, подтвердил существование электромагнитных волн. Доказал, что свет является разновидностью электромагнитных волн, чем обосновал существующую электромагнитную теорию света Максвелла. Также Герц занимался изучением электрических полей, возникающих вокруг движущихся тел. На основе наблюдений создал теорию, но опытного подтверждения она не получила. Исследования же внешнего фотоэффекта, проведенные Герцем, легли в основу дальнейших научных изысканий. Также для описания колебательных и волновых процессов используют циклическую частоту, фазу. Циклическая частота показывает количество полных колебаний за единицу времени, равную 2П (где П=3,14), а фаза – это величина смещения в любой, отдельно взятый, момент времени. Нужно также отметить, что если колебания возможно описать по закону синуса или косинуса, то они являются гармоническими. Соответственно, в уравнении для математического описания обязательно присутствует функция sin или cos. Итак, прежде чем определить, в чем измеряется частота, важно понять, что же это такое? Мы не будем углубляться в сложные физические термины, но некоторые понятия из этой дисциплины нам все-таки понадобятся. Во-первых, понятие «частота» — может относиться только к какому либо периодическому процессу. То есть, это действие, которое постоянно повторяется во времени. Вращение Земли вокруг Солнца, сокращение сердца, смена дня и ночи – всё это происходит с определенной частотой. Во-вторых, свою частоту, или периодичность колебаний имеют явления, или предметы, которые нам, людям, могут казаться вполне статичными и неподвижными. Хороший пример этого – обыкновенный дневной свет. Мы не замечаем, какого либо его изменения, или мерцания, но он, всё-же, имеет свою частоту колебаний, поскольку представляет собой высокочастотные электромагнитные волны. Единицы измеренияВ чем измеряется частота, в каких единицах? Для низкочастотных процессов существуют свои, отдельные единицы. Например, в космических масштабах – галактический год (обращение Солнца вокруг центра Галактики), земной год, сутки и т.д. Понятно, что для измерения меньших величин, пользоваться такими единицами неудобно, поэтому в физике используется более универсальная величина «секунда в минус первой степени» (с -1). Возможно, вы никогда не слышали о подобной мере, и это не удивительно – она обычно применяется лишь в научной, или технической литературе. К счастью для нас, в 1960-ом году, меру частоты колебаний назвали на честь немецкого физика Генриха Герца. Эта величина (герц, сокр. Гц) и используется нами сегодня. Обозначает она количество колебаний (импульсов, действий) совершаемых объектом в 1 секунду. По-сути, 1 Гц = 1 с -1 . Человеческое сердце, например, имеет частоту колебаний приблизительно 1 Гц, т.е. сокращается один раз в секунду. Частота процессора вашего компьютера, может быть, скажем, 1 гигагерц (1 млрд. Как измерить частоту?Вообще, основных способов измерения частоты есть два: непосредственный подсчет импульсов в секунду, и сравнительный метод. Первый способ реализован в частотомерах (цифровых и аналоговых). Второй – в компараторах частот. Метод измерения с частотомером – проще, в то время как измерение компаратором – точнее. Одной из разновидностей сравнительного метода, является измерение частоты с помощью осциллографа (знаком нам по кабинетам физики еще со школы) и т. Время, в течение которого совершается одно полное изменение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания переменного тока (рисунок 1). Рисунок 1. Период и амплитуда синусоидального колебания. Период — время одного колебания; Аплитуда — его наибольшее мгновенное значение. Период выражают в секундах и обозначают буквой Т . Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды. 1 мс =0,001сек =10 -3 сек. 1 мкс=0,001 мс = 0,000001сек =10 -6 сек. 1000 мкс = 1 мс. Число полных изменений ЭДС или число оборотов радиуса-вектора, то есть иначе говоря, число полных циклов колебаний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока . Частота обозначается буквой f и выражается в периодах в секунду или в герцах. Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц. 1000 Гц = 10 3 Гц = 1 кГц; 1000 000 Гц = 10 6 Гц = 1000 кГц = 1 МГц; 1000 000 000 Гц = 10 9 Гц = 1000 000 кГц = 1000 МГц = 1 ГГц; Чем быстрее происходит изменение ЭДС, то есть чем быстрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая. Математическая связь между периодом и частотой переменного тока и напряжения выражается формулами Например, если частота тока равна 50 Гц, то период будет равен: Т = 1/f = 1/50 = 0,02 сек. И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек. f = 1/T=1/0,02 = 100/2 = 50 Гц Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц. Частоты от 20 до 20 000 Гц называются звуковыми частотами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие высокие частоты называются радиочастотами или колебаниями высокой частоты. Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше. Амплитуда переменного токаНаибольшее значение, которого достигает ЭДС или сила тока за один период, называется амплитудой ЭДС или силы переменного тока . Легко заметить, что амплитуда в масштабе равна длине радиуса-вектора. Амплитуды тока, ЭДС и напряжения обозначаются соответственно буквами Im, Em и Um (рисунок 1). Угловая (циклическая) частота переменного тока. Скорость вращения радиуса-вектора, т. е. изменение величины угла поворота в течение одной секунды, называется угловой (циклической) частотой переменного тока и обозначается греческой буквой ? (омега). Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах. Радианом называется угловая величина дуги окружности, длина которой равна радиусу этой окружности (рисунок 2). Вся окружность, составляющая 360°, равна 6,28 радиан, то есть 2. Рисунок 2. 1рад = 360°/2 Следовательно, конец радиуса-вектора в течение одного периода пробегают путь, равный 6,28 радиан (2). Так как в течение одной секунды радиус-вектор совершает число оборотов, равное частоте переменного тока f , то за одну секунду его конец пробегает путь, равный 6,28 * f радиан. Это выражение, характеризующее скорость вращения радиуса-вектора, и будет угловой частотой переменного тока — ?
. ? = 6,28*f = 2f Угол поворота радиуса-вектора в любое данное мгновение относительно его начального положения называется фазой переменного тока . Фаза характеризует величину ЭДС (или тока) в данное мгновение или, как говорят, мгновенное значение ЭДС, ее направление в цепи и направление ее изменения; фаза показывает, убывает ли ЭДС или возрастает. Рисунок 3. Полный оборот радиуса-вектора равен 360°. С началом нового оборота радиуса-вектора изменение ЭДС происходит в том же порядке, что и в течение первого оборота. Следовательно, все фазы ЭДС будут повторяться в прежнем порядке. Например, фаза ЭДС при повороте радиуса-вектора на угол в 370° будет такой же, как и при повороте на 10°. В обоих этих случаях радиус-вектор занимает одинаковое положение, и, следовательно, мгновенные значения ЭДС будут в обоих этих случаях одинаковыми по фазе. (лат. amplitude — величина) — это наибольшее отклонение колеблющегося тела от положения равновесия. Для маятника это максимальное расстояние, на которое удаляется ша-рик от своего положения равновесия (рисунок ниже). Для колебаний с малыми амплитудами за такое расстояние можно принимать как длину дуги 01 или 02, так и длины этих отрезков. Амплитуда колебаний измеряется в единицах длины — метрах , санти-метрах и т. д. На графике колебаний амплитуда определяется как макси-мальная (по модулю) ордината синусоидальной кривой, (см. рис. ниже). Период колебаний.Период колебаний — это наименьший промежуток времени, через который система, соверша-ющая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент времени, выбранный произвольно. Другими словами, период колебаний (Т ) — это время, за которое совершается одно полное ко-лебание. Например, на рисунке ниже это время, за которое грузик маятника перемещается из крайней правой точки через точку равновесия О в крайнюю левую точку и обратно через точку О снова в крайнюю правую. За полный период колебаний, таким образом, тело проходит путь, равный четы-рем амплитудам. Период колебаний измеряется в единицах времени — секундах , минутах и т. д. Период колебаний может быть определен по известному графику колебаний, (см. рис. ниже). Понятие «период колебаний», строго говоря, справедливо, лишь когда значения колеблющей-ся величины точно повторяются через определенный промежуток времени, т. е. для гармоничес-ких колебаний. Однако это понятие применяется также и для случаев приблизительно повторяю-щихся величин, например, для затухающих колебаний . Частота колебаний.Частота колебаний — это число колебаний, совершаемых за единицу времени, например, за 1 с . Единица частоты в СИ названа герцем (Гц ) в честь немецкого физика Г. Герца (1857-1894). Если частота колебаний (v ) равна 1 Гц , то это значит, что за каждую секунду совершается одно колебание. Частота и период колебаний связаны соотношениями: В теории колебаний пользуются также понятием циклической , или круговой частоты ω . . Циклическая частота — это число колебаний, совершаемых за 2π секунд. >>Физика: Период и частота обращения Равномерное движение по окружности характеризуют периодом и частотой обращения. Период обращения — это время, за которое совершается один оборот. Если, например, за время t = 4 с тело, двигаясь по окружности, совершило n = 2 оборота, то легко сообразить, что один оборот длился 2 с. Это и есть период обращения. Обозначается он буквой Т и определяется по формуле: Итак, чтобы найти период обращения, надо время, за которое совершено п оборотов, разделить на число оборотов . Другой характеристикой равномерного движения по окружности является частота обращения. Частота обращения — это число оборотов, совершаемых за 1 с. Если, например, за время t = 2 с тело совершило n = 10 оборотов, то легко сообразить, что за 1 с оно успевало совершить 5 оборотов. Итак, чтобы найти частоту обращения, надо число оборотов разделить на время, в течение которого они произошли. За единицу частоты обращения в СИ принимают частоту обращения, при которой за каждую секунду тело совершает один оборот. Эта единица обозначается так: 1/с или с -1 (читается: секунда в минус первой степени). Раньше эту единицу называли «оборот в секунду», но теперь это название считается устаревшим. Сравнивая формулы (6.1) и (6.2), можно заметить, что период и частота — величины взаимно обратные. Поэтому Формулы (6.1) и (6.3) позволяют найти период обращения Т, если известны число n и время оборотов t или частота обращения V . Однако его можно найти и в том случае, когда ни одна из этих величин неизвестна. Вместо них достаточно знать скорость тела V и радиус окружности r, по которой оно движется. Для вывода новой формулы вспомним, что период обращения — это время, за которое тело совершает один оборот, т. е. проходит путь, равный длине окружности (l окр = 2 П r, где П ≈3,14- число «пи», известное из курса математики). Но мы знаем, что при равномерном движении время находится делением пройденного пути на скорость движения. Таким образом, Итак, чтобы найти период обращения тела, надо длину окружности, по которой оно движется, разделить на скорость его движения. ??? 1. Что такое период обращения? 2. Как можно найти период обращения, зная время и число оборотов? 3. Что такое частота обращения ? 4. Как обозначается единица частоты? 5. Как можно найти частоту обращения, зная время и число оборотов? 6. Как связаны между собой период и частота обращения? 7. Как можно найти период обращения, зная радиус окружности и скорость движения тела? Отослано читателями из интернет-сайтов Сборник конспектов уроков по физике, рефераты на тему из школьной программы. |
Частота периодического процесса | это.
 .. Что такое Частота периодического процесса?
.. Что такое Частота периодического процесса?ТолкованиеПеревод
- Частота периодического процесса
Частота́ — физическая величина, характеристика периодического процесса, равная числу полных циклов, совершённых за единицу времени. Стандартные обозначения в формулах — , или . Единицей частоты в Международной системе единиц (СИ) в общем случае является герц (Гц, Hz). Величина, обратная частоте, называется периодом.
Содержание
- 1 Мгновенная частота и частоты спектральных составляющих
- 2 Циклическая частота
- 3 Частота дискретных событий
- 4 Частота вращения
- 5 Другие величины, связанные с частотой
- 6 Метрологические аспекты
- 6.1 Измерения
- 6.2 Эталоны
- 7 Литература
- 8 Ссылки
- 9 См.
 также
также
Мгновенная частота и частоты спектральных составляющих
Периодический сигнал характеризуется мгновенной частотой, являющейся скоростью изменения фазы, но тот же сигнал можно представить в виде суммы гармонических спектральных составляющих, имеющих свои частоты. Свойства мгновенной частоты и частоты спектральной составляющей различны, подробнее об этом можно прочитать, например, в книге Финка.
Циклическая частота
Основная статья: Угловая частота
В теории электромагнетизма, теоретической физике, а также в некоторых прикладных электрорадиотехнических расчётах удобно использовать дополнительную величину — циклическую (круговую, радиальную, угловую) частоту (обозначается ). Циклическая частота связана с частотой колебаний соотношением . В математическом смысле циклическая частота — это первая производная полной фазы колебаний по времени. Единица циклической частоты — радиан в секунду (рад/с, rad/s) .

В механике при рассмотрении вращательного движения аналогом циклической частоты служит угловая скорость.
Частота дискретных событий
Частота дискретных событий (частота импульсов) — физическая величина, равная числу дискретных событий, происходящих за единицу времени. Единица частоты дискретных событий секунда в минус первой степени (с−1, s−1), однако на практике для выражения частоты импульсов обычно используют герц.
Частота вращения
Частота вращения — физическая величина, равная числу полных оборотов за единицу времени. Единица частоты вращения — секунда в минус первой степени (с−1, s−1), оборот в секунду. Часто используются такие единицы, как оборот в минуту, оборот в час и т. д.
Другие величины, связанные с частотой
- Ширина полосы частот —
- Частотный интервал —
- Девиация частоты —
- Период —
- Длина волны —
- Угловая скорость (скорость вращения) —
Метрологические аспекты
Измерения
- Для измерения частоты применяются частотомеры разных видов, в том числе: для измерения частоты импульсов — электронно-счётные и конденсаторные, для определения частот спектральных составляющих — резонансные и гетеродинные частотомеры, а также анализаторы спектра.

- Для воспроизведения частоты с заданной точностью используют различные меры — стандарты частоты (высокая точность), синтезаторы частот, генераторы сигналов и др.
- Сравнивают частоты компаратором частоты или с помощью осциллографа по фигурам Лиссажу.
Эталоны
- Государственный первичный эталон единиц времени, частоты и национальной шкалы времени ГЭТ 1-98 — находится во ВНИИФТРИ
- Вторичный эталон единицы времени и частоты ВЭТ 1-10-82 — находится в СНИИМ (Новосибирск)
Литература
- Сигналы, помехи, ошибки… Финк Л. М. — М.: Радио и связь, 1984
- Единицы физических величин. Бурдун Г. Д., Базакуца В. А. — Харьков: Вища школа, 1984
- Справочник по физике. Яворский Б. М., Детлаф А. А. — М.: Наука, 1981
Ссылки
- Радио Технические цепи и Сигналы
- Очерк А.Б.Сергиенко «Аналоговая модуляция»
- Сигналы и линейные системы
- ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАДИОТЕХНИКИ
См.
 также
также- Частоты
- Физическая величина
- Период
- Спектр
- Диапазон частот
- Частотомер
- Герц (единица измерения)
- Девиация частоты
Wikimedia Foundation. 2010.
Поможем написать курсовую
- Частота события
- Частота системной шины
Полезное
единиц СИ – время | НИСТ
Секунда (с) определяется путем принятия фиксированного числового значения частоты цезия ∆ν Cs , частоты невозмущенного сверхтонкого перехода атома цезия-133 в основном состоянии, равной 9 192 631 770 при выражении в единицах Гц, что равно s −1 .
Число периодов или циклов в секунду называется частотой. Единицей частоты в системе СИ является герц (Гц). Один герц равен одному циклу в секунду. Стандартные частоты и точное время транслируют радиостанции WWV и WWVB в Колорадо и WWVH на Гавайях. NIST доставляет цифровые сигналы синхронизации по телефону и через Интернет.
NIST доставляет цифровые сигналы синхронизации по телефону и через Интернет.
Официальное время правительства США предоставляется NIST и USNO. NIST также предлагает Интернет-службу времени (ITS) и Автоматизированную компьютерную службу времени (ACTS), которые позволяют устанавливать компьютерные и другие часы через Интернет или по стандартным коммерческим телефонным линиям. Там можно скачать бесплатное программное обеспечение для использования этих сервисов на нескольких типах популярных компьютеров. Информацию об этих услугах можно найти на веб-сайте Time and Frequency Division.
Ресурсы для студентов и преподавателей- Второе: Введение. Время, вероятно, является самой измеряемой величиной на Земле. В науке мы используем время, чтобы измерить и лучше понять множество вещей в нашем мире. (НИСТ)
- Как мы измеряем время? (серия NIST HDYMI) – Временные интервалы, продолжительность между двумя событиями, наиболее точно измеряются с помощью атомных часов.

- Что такое время? (НИСТ, видео)
- Измерение времени и частоты. Узнайте больше об истории NIST, включая краткую историю атомных часов и другие ответы на часто задаваемые вопросы (FAQ). (НИСТ)
- Совершите прогулку во времени. Пройдите историческое путешествие по эволюции измерения времени. Щелкните ссылку, чтобы загрузить прикрепленный файл PDF . (НИСТ)
- Связь времени и места. Если вы хотите знать, где вы находитесь, вам нужны надежные часы. Погрузитесь в эти ресурсы Смитсоновского института, чтобы узнать больше о связи между временем и местом. (Смитсоновский институт)
- Самое время – осмотреть этот экспонат. Узнайте интересные вещи о точности часов, включая историческую временную шкалу (каламбур)! (Университет Висконсина)
Какое сейчас всемирное координированное время?
NIST и Военно-морская обсерватория США совместно управляют веб-сайтом, который предоставляет официальное время США. Показания часов этих двух агентств вносят вклад в мировое время, называемое всеобщим скоординированным временем (UTC).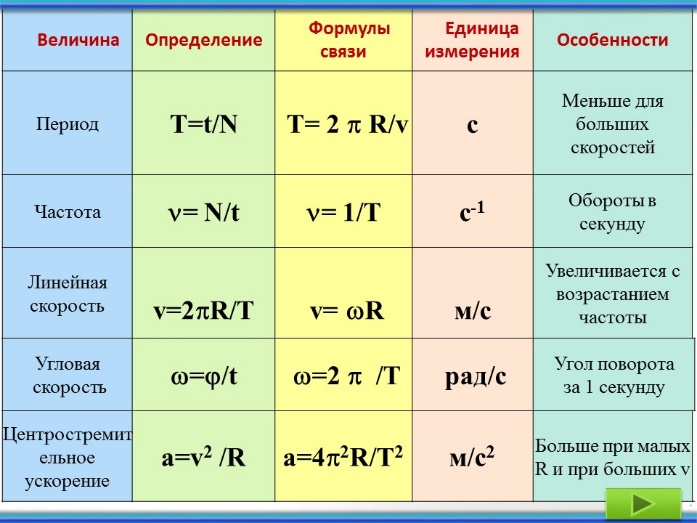 Узнать больше… Как узнать время с помощью телефона, компьютера или радиосигналов? Что такое дополнительная секунда? Каковы правила перехода на летнее время? Посетите раздел часто задаваемых вопросов по времени и частоте для получения дополнительной информации.
Узнать больше… Как узнать время с помощью телефона, компьютера или радиосигналов? Что такое дополнительная секунда? Каковы правила перехода на летнее время? Посетите раздел часто задаваемых вопросов по времени и частоте для получения дополнительной информации.
Ресурсы
Кредит: Дж. Ван и Б. Хейс/NIST
League of SI Superheroes – Professor Second
Этот анимационный видеосериал в стиле комиксов был разработан, чтобы помочь учащимся средней школы узнать о 7 базовых единицах измерения SI. Считывая колебания своих атомов цезия, охлаждаемых лазером, профессор Второй может синхронизировать любую частоту и корректировать любые часы. Секунда — это время, за которое возбужденный атом цезия совершает 9 колебаний.192 631 770 раз.
Перейти к дополнительной информации о базовых единицах СИ:- Единицы СИ
- Длина – метр (м)
- Количество вещества – моль (моль)
- Электрический ток – ампер (А)
- Температура – Кельвин (К)
- Сила света – кандела (кд)
- Масса – килограмм (кг)
Ресурсы
- Знакомство с SI
- Ежедневная оценка
- Вопросы и ответы по метрике
- Префиксы
- SI Образование и обучение
- Публикации СИ
- Понимание метрики
- Запись в единицах СИ (метрических)
- Национальная метрическая неделя
NEST-R (Реестр STEM)
Образовательные ресурсы NIST
Метрология и метрология времени и частоты
Что такое единица измерения частоты?(a).
 Герц (б). Джоуль (с). Ом (д). Килокалория
Герц (б). Джоуль (с). Ом (д). КилокалорияОтвет
Проверено
249,6 тыс.+ просмотров
— Подсказка: единица измерения Герц (Гц) используется для измерения количества циклов, происходящих в секунду при периодическом движении или событии. Так как по определению частоты ее единица измерения должна иметь размерность , то эту задачу можно решить, найдя в заданном варианте единицу той же размерности
Полное пошаговое решение —
Частота периодического движения или события — это число циклов, которое движение совершает за одну секунду.
Герц (Гц) является единицей измерения частоты в системе СИ и имеет размерность, обратную секунде (с-1).
Таким образом, правильный ответ — вариант А) Герц.
Единица названа Герц в честь немецкого физика Генриха Герца.
$1Hz=\dfrac{\text{1 Cycle}}{1\text{ Second}}$
Дополнительная информация:
герц чаще всего используется в единицах измерения частоты всех волн. В зависимости от частоты электромагнитным волнам даются различные названия, такие как инфракрасные, ультрафиолетовые и т. д.
В зависимости от частоты электромагнитным волнам даются различные названия, такие как инфракрасные, ультрафиолетовые и т. д.
Таким образом, звук также является волной, и его частота измеряется в герцах.
Диапазон человеческого слуха составляет от звуковых волн от 20 Гц до 20 000 Гц. Однако некоторые другие животные, такие как собаки, могут слышать даже ниже 20 Гц (так называемый инфразвук), а некоторые другие, такие как летучие мыши, могут слышать выше 20000 Гц (так называемый ультразвук).
В музыкальных инструментах частота определяет высоту звука. Чем выше частота, тем выше высота звука. Например, звук с низкой частотой имеет низкий тон и называется плоским или басовым. С другой стороны, звук с высокой частотой имеет высокий тон и называется пронзительным звуком. Средняя нота C на клавиатуре имеет частоту 262 Гц.
Примечание: учащиеся не должны смущаться, когда в некоторых вопросах они видят слово «тон» вместо «частоты», так как по сути оба они относятся к одному и тому же, то есть к циклам в секунду.



 Причем амплитуда (величина максимального отклонения от точки равновесия) не зависит от начальных условий, а определяется свойствами системы. Пример: колебательное движение маятника часов под действием тяжести гири или пружины, колебания листьев, веток деревьев под действием постоянного потока воздуха.Также определяют параметрические колебания (возникают при изменении одного из параметров системы) и случайные.
Причем амплитуда (величина максимального отклонения от точки равновесия) не зависит от начальных условий, а определяется свойствами системы. Пример: колебательное движение маятника часов под действием тяжести гири или пружины, колебания листьев, веток деревьев под действием постоянного потока воздуха.Также определяют параметрические колебания (возникают при изменении одного из параметров системы) и случайные. Соответственно частота измеряется в (
Соответственно частота измеряется в (

 герц) – это значит, что в нем происходит 1 миллиард каких-то действий в секунду.
герц) – это значит, что в нем происходит 1 миллиард каких-то действий в секунду.

 ), то частота будет равна:
), то частота будет равна:


 Она связана с обычной частотой v и периодом колебаний Т соотношениями:
Она связана с обычной частотой v и периодом колебаний Т соотношениями: Это число и выражает частоту обращения. Обозначается она греческой буквой V (читается: ню) и определяется по формуле:
Это число и выражает частоту обращения. Обозначается она греческой буквой V (читается: ню) и определяется по формуле:
 Календарно тематическое планирование. физика 8 класс онлайн, книги и учебники по физике. Школьнику подготовиться к уроку.
Календарно тематическое планирование. физика 8 класс онлайн, книги и учебники по физике. Школьнику подготовиться к уроку. также
также

 также
также