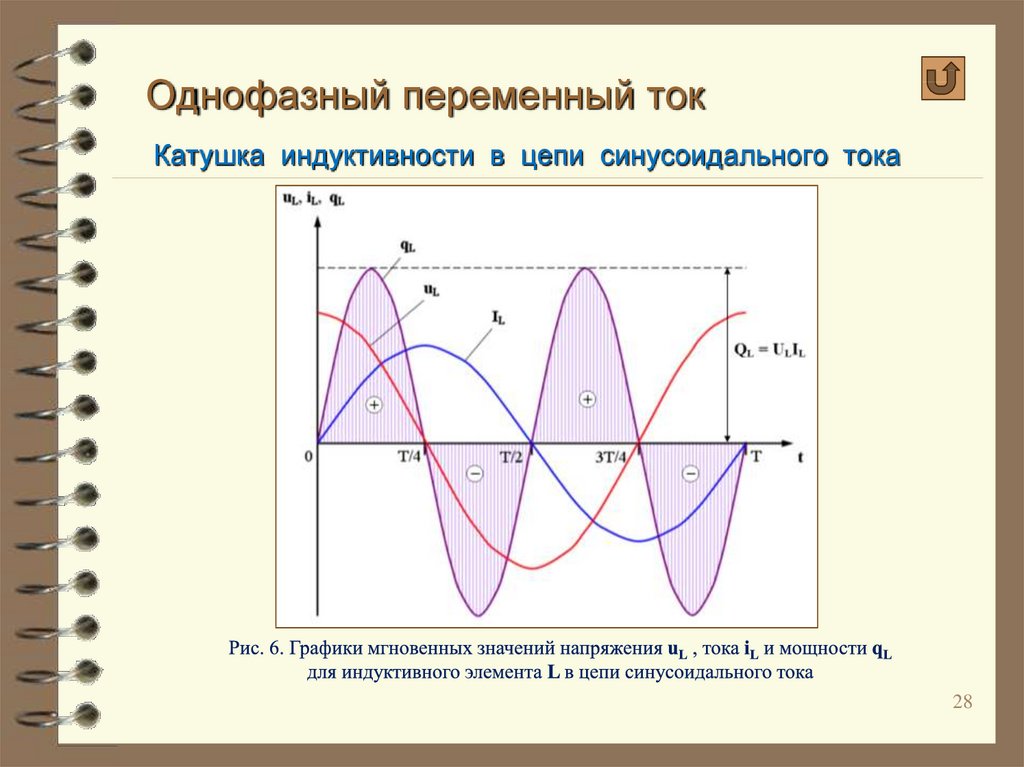
5.5 Индуктивная катушка в цепи синусоидального тока

     Сначала рассмотрим идеальную индуктивную катушку, активное сопротивление которой равно нулю. Пусть по идеальной катушке с индуктивностью L протекает синусоидальный ток . Этот ток создает в индуктивной катушке переменное магнитное поле, изменение которого вызывает в катушке ЭДС самоиндукции

(5.9)

     Эта ЭДС уравновешивается напряжением, подключенным к катушке: u = e_L = 0.

(5.10)

     Таким образом, ток в индуктивности отстает по фазе от напряжения на 90^o из-за явления самоиндукции.      Уравнение вида (6.10) для реальной катушки, имеющей активное сопротивление R, имеет следующий вид:

(5.11)

     Анализ выражения (6.11) показывает, что ЭДС самоиндукции оказывает препятствие (сопротивление) протеканию переменного тока, из-за чего ток в реальной индуктивной катушке отстает по фазе от напряжения на некоторый угол φ (0^o< φ < 90^o), величина которого зависит от соотношения R и L.

     Выражение (6.11) в комплексной форме записи имеет вид:

(5.12)

      где Z_L — полное комплексное сопротивление индуктивной катушки ;             Z_L — модуль комплексного сопротивления;            — начальная фаза комплексного сопротивления;- индуктивное сопротивление (фиктивная величина, характеризующая реакцию электрической цепи на переменное магнитное поле).       Полное сопротивление индуктивной катушки или модуль комплексного сопротивления

.

       Комплексному уравнению (6.12) соответствует векторная диаграмма (рис.5.5).

Рис. 6.5

       Из анализа диаграммы видно, что вектор напряжения на индуктивности опережает вектор тока на 90

o.     В цепи  переменного тока напряжения на  участках цепи складываются не арифметически, а геометрически.        Если мы поделим стороны треугольника напряжений на величину тока I_m, то перейдем к подобному треугольнику сопротивлений (рис. 5.6).

 Из треугольника сопротивлений получим несколько формул:                      ;;     Рис. 5.6

;

;           .

5.6 Емкость в цепи синусоидального тока

     Если к конденсатору емкостью C подключить синусоидальное напряжение, то в цепи протекает синусоидальный ток

;

.    (5.13)

      Из анализа выражений 5.13 следует, что ток опережает напряжение по фазе на 90^o.

      Выражение (5.13) в комплексной форме записи имеет вид:

,    (5.14)

       где — емкостное сопротивление, фиктивная расчетная величина, имеющая размерность сопротивления.

        Если комплексное сопротивление индуктивности положительно        , то комплексное сопротивление емкости отрицательно.

       На рис. 6.7 изображена векторная диаграмма цепи с емкостью.        Вектор тока опережает вектор напряжения на 90

o.

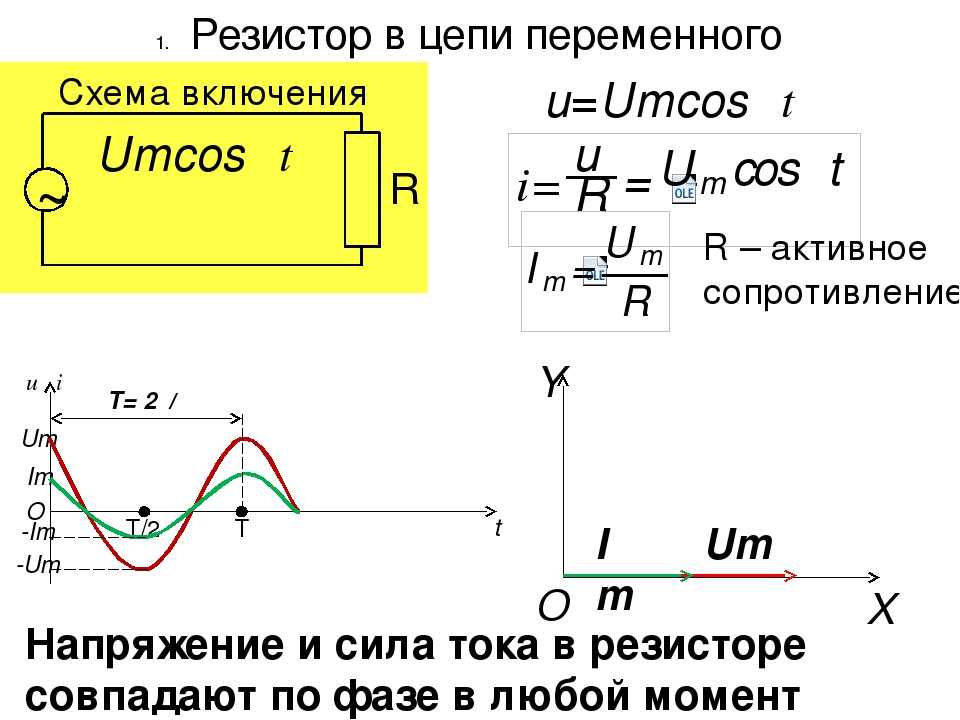Рис. 5.7

5.7. Последовательно соединенные реальная индуктивная катушка и конденсатор в цепи синусоидального тока

       Катушка с активным сопротивлением   R  и индуктивностью   L  и конденсатор емкостью  С  включены последовательно (рис.5.8). В схеме протекает синусоидальный ток

.

 Определим напряжение на входе схемы.        В соответствии со вторым законом Кирхгофа,

           (5.15)

       Подставим эти формулы в уравнение (5.15). Получим:

       (5.16)

     Из выражения (5.16) видно: напряжение в активном сопротивлении совпадает по фазе с током, напряжение на индуктивности опережает по фазе ток на 90^o, напряжение по емкости отстает по фазе от тока на 90^o.      Запишем уравнение 5.16) в комплексной форме:

(5.17)

           Рис. 5.8

       Поделим левую и правую части уравнения (6.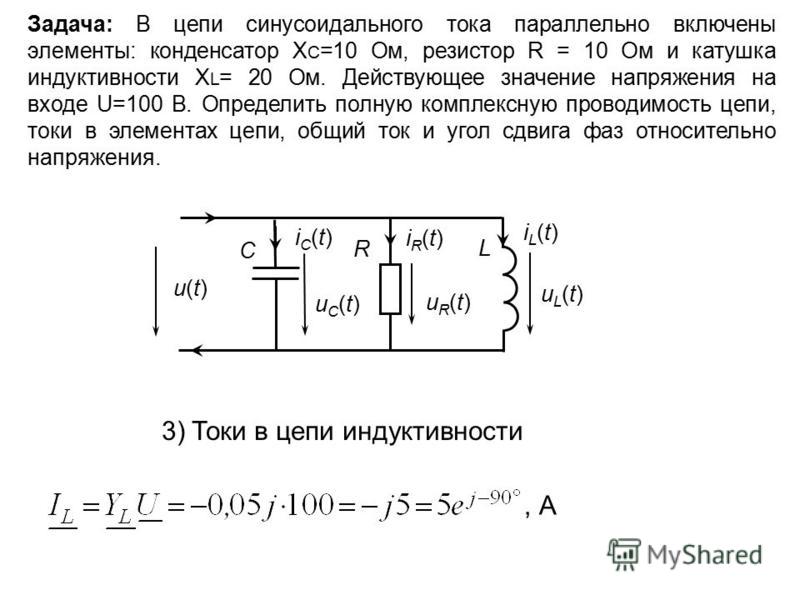 17) на √2.        Получим уравнение для комплексов действующих значений токов и напряжений

       ,     (5.18)

       где — комплексное сопротивление цепи;- модуль комплексного сопротивления, или полное сопротивление цепи;- начальная фаза комплексного сопротивления.

       При построении векторных диаграмм цепи рассмотрим три случая.

1. X_L > X_C, цепь носит индуктивный характер. Векторы напряжений на индуктивности и емкости направлены в противоположные стороны, частично компенсируют друг друга. Вектор напряжения на входе схемы опережает вектор тока (рис5.9).

2. Индуктивное сопротивление меньше емкостного. Вектор напряжения на входе схемы отстает от вектора тока. Цепь носит емкостный характер (рис.5.10).

3. Индуктивное и емкостное сопротивления одинаковы. Напряжения на индуктивности и емкости полностью компенсируют друг друга. Ток в цепи совпадает по фазе с входным напряжением.

   В электрической цепи наступает режим резонансного напряжения (рис.5.11).

       Ток в резонансном режиме достигает максимума, так как полное сопротивление (z) цепи имеет минимальное значение.

         Условие возникновения резонанса: , отсюда резонансная частота равна

      .

         Из формулы следует, что режима резонанса можно добиться следующими способами:

1. изменением частоты;

2. изменением индуктивности;

3. изменением емкости.

      В резонансном режиме входное напряжение равно падению напряжения в активном сопротивлении. На индуктивности и емкости схемы могут возникнуть напряжения, во много раз превышающие напряжение на входе цепи. Это объясняется тем, что каждое напряжение равно произведению тока I₀ (а он наибольший), на соответствующее индуктивное или емкостное сопротивление (а они могут быть большими).

.

Рис. 5.9                            Рис. 5.10                              Рис. 5.11

Индуктивная катушка в цепи синусоидального тока

КАТЕГОРИИ: Главная Случайная страница Познавательное Новые статьи Контакты Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)

⇐ Предыдущая12 Индуктивная катушка как элемент схемы замещения реальной цепи синусои­дального тока дает возможность учитывать при расчете явление самоиндук­ции и явление накопления энергии в ее магнитном поле. Пусть в цепь перемен­ного тока (рис 2.7 а) включена катушка с бесконечно малым сопро­тивлением провода = 0. Непрерывное во времени изменение тока вызывает появ­ление в витках катушки ЭДС самоиндукции. В соответствии с правилом Ленца эта ЭДС противодействует изменению тока. Допустим, ток через катушку изменяется по закону . В этом случае ЭДС самоиндукции . Поэтому напряжение на катушке . Сравнивая формулы (2.13) и (2.15), можно сделать вывод о том, что напряже­ние на катушке опережает ток на угол или ток отстает от напряжения по фазе на угол (рис 2.7 б). Угол сдвига фаз в этом случае положительный (рис. 2.7 в) . Параметр цепи– индуктивное сопротивление, имеющее размерность Ом. Оно зависит от частоты и представляет собой величину, с помо­щью которой учитывается явление самоиндукции. Из анализа (2.14) видно, что амплитуды напряжения и тока связаны законом Ома: . Аналогично для действующих значений . Мгновенная мощность цепи с катушкой . (2.16) Из графика (рис 2.7 г), построенного по уравнению (2.16), видно, что за пер­вую четверть периода, когда > 0 и > 0, площадь, ограниченная кривой и осью абсцисс, пропорциональна энергии, потребляемой катушкой на создание магнитного поля. Во вторую четверть периода (ток убывает от максимума до нуля) энергия магнитного поля катушки передается источнику питания. При этом мгновен­ная мощность отрицательна, а процесс повторяется. Таким образом, происходит колебание энергии между источником и катушкой, причем активная мощность, поступающая в катушку, равна нулю. Амплитуду колебания мгновенной мощ­ности в цепи с катушкой называют реактивной (индуктивной) мощностью . Реактивную мощность в отличие от активной мощности измеряют в вар (вольт-ампер реактивный).     ⇐ Предыдущая12 Поделиться с друзьями: Дата добавления: 2014-01-03; Просмотров: 3568; Нарушение авторских прав?; Мы поможем в написании вашей работы! Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

реакция катушки индуктивности на синусоидальное напряжение

Для последовательной конфигурации на рис. 1 напряжение $v_{элемент}$ замкнутый элемент противостоит источнику e и тем самым уменьшает величину тока i. Величина напряжения на элементе определяется противодействием элемента потоку заряд, или ток i. Для резистивного элемента мы нашли, что противодействие является его сопротивлением, а $v_{элемент}$ и i определяются $v_{элемент} = iR$.

Рис. 1: Определение противопоставления элемента поток заряда через элемент.

В предыдущей главе о индукторе мы обнаружили, что напряжение на индукторе напрямую связано со скоростью изменения тока через катушку. Следовательно, чем выше частота, тем больше будет скорость изменения тока через катушку и тем больше величина напряжения. Кроме того, в той же главе мы обнаружили, что индуктивность катушки будет определять скорость изменения потока, соединяющего катушку, при конкретном изменении тока через катушку. Чем выше индуктивность, тем больше скорость изменения потокосцепления и тем больше результирующее напряжение на катушке. Следовательно, индуктивное напряжение напрямую связано с частотой (или, точнее, угловая скорость синусоидального переменного тока через катушку) и индуктивность катушки. Для увеличения значений f и L на рис. 2, величина vL будет увеличиваться, как описано выше.

Рис. 2: Определение параметров, определяющих противодействие индуктивного элемента потоку заряда.

Используя сходство между рис. 1 и 2, мы находим, что увеличение уровней vL напрямую связано с увеличением уровней оппозиции на рис. 1. Поскольку vL будет увеличиваться как с $w (= 2\pi f )$, так и с L, противопоставление индуктивного элемента показано на рис. 2. Теперь мы проверим некоторые из предыдущих выводов, используя более математический подход, а затем определить несколько важных величин, которые используемые в следующих разделах и главах.

Рис. 3: Исследование синусоидальной характеристики индуктивный элемент.

Рис. 4: Для чистого индуктора напряжение на катушке опережает ток через катушка на 90.

Для индуктора рис. 3 $$ v_L = L{di_L \over dt}$$ и, применяя дифференцирование $$ v_L = L{di_L \over dt}\\ = L {d(I_m \sin wt) \over dt}\\ = w L I_m \cos wt\\ =V_m \sin(вес + 90)\\ $$ Где $$\bbox[10px,border:1px сплошной серый]{V_m = wLI_m = 2 \pi fLI_m} \tag{1}$$ Обратите внимание, что пиковое значение vL напрямую связано с $w (= 2\pi f )$ и L как и предсказывалось в обсуждении выше.

График vL и iL на рис. 4 показывает, что

для индуктора, vL опережает iL на 90 градусов или iL отстает от vL на 90 градусов.

Если фазовый угол включен в синусоидальное выражение для iL, такое как $$ i_L = I_m \sin(wt + \theta)$$ затем $$ v_L = V_m \sin(wt + \theta + 90)$$ Противодействие, создаваемое катушкой индуктивности в синусоидальной сети переменного тока теперь можно найти по: $$следствие = {причина \препятствие}$$ что для наших целей можно записать $$оппозиция = {причина \над следствием}$$ Подставляя значения, имеем $$opposition = {V_m \over I_m} = {wLI_m \over I_m} = wL$$ показывая, что противодействие, создаваемое индуктором в асинусоидальной сети, напрямую связано с произведением угловой скорости ($w = 2\pi f$ ) и индуктивность, что подтверждает наши предыдущие выводы. Величина $wL$, называемая реактивным сопротивлением (от слова реакция) индуктор, символически обозначается $X_L$ и измеряется в омах; то есть, $$\bbox[10px,border:1px сплошной серый]{X_L = wL } (Ом) \tag{2}$$ В формате закона Ома его величина может быть определена из $$\bbox[10px,border:1px сплошной серый]{X_L = {V_m \over I_m} } (Ом) \tag{3}$$

Индуктивное сопротивление – это сопротивление протеканию тока, которое происходит постоянный обмен энергией между источником и магнитное поле индуктора. Другими словами, индуктивное сопротивление, в отличие от сопротивления (которое рассеивает энергию в виде тепла), не рассеивать электрическую энергию (без учета влияния внутреннего сопротивления индуктора).

Индуктивность в цепях переменного тока — Цепи переменного тока

Цепи переменного тока

Индуктивность была определена как свойство цепи противостоять изменению в текущем. Это противодействие приводит к индуцированной ЭДС. Индуцированная ЭДС равна пропорциональна скорости изменения тока, а также величина индуктивности. Эта связь может быть представлена ​​уравнением

Если в индуктивности, показанной на рисунке ниже, протекает синусоидальный ток, индуцированное напряжение на индуктивности можно изобразить в зависимости от времени.

Чистая индуктивная цепь.

График тока на рисунке ниже увеличивается от времени t ₀ до т ₁ . Ток растет с убывающей скоростью, и в момент времени t ₁ мгновенная скорость изменения тока равна нуль. Следовательно, v _L равно нулю в момент времени t ₁ . От времени t ₁ до t ₂ ток уменьшение; скорость изменения тока отрицательна и v _L отрицательный. В момент т ₂ курс изменения тока максимально, и, таким образом, v _L максимально в негативное направление. В момент времени t ₃ скорость изменения ток равен нулю, и, таким образом, v _L снова равно нулю. От t ₃ до t ₄ , ток увеличивается, скорость изменения положительна, а v _L положительна, достигая максимум в t ₄ , где скорость изменения максимальна.

Соотношение напряжение-ток в чисто индуктивной цепи.

Максимальное положительное значение напряжения возникает на 90° впереди максимального положительное значение тока. Говорят, что ток отстает от напряжения на 90 градусов. Это фазовое соотношение можно вывести математически, применив исчисление.

Из предыдущего уравнения, которое

где

дифференцированием найдено d i /d t .

но

Поэтому

По общему виду периодической функции (т. е. В _м sin ( ωt + θ)),

и

Поскольку отношение вольта к амперу определяется как противодействие току в омах, величина ωL измеряется в омах. Количество ωL называется индуктивным сопротивлением и обозначается как X _L

Если В _м = 1,414 В и I _м = 1,414 I подставляем в уравнение ωL = В _м / I _м , видно что отношение действующих значений напряжения и тока также равно индуктивное сопротивление

Обратная величина индуктивного сопротивления называется индуктивная проводимость и имеет обозначение B _L . Единица индуктивности восприимчивость — это mho (или сименс S), когда частота в герцах и индуктивность в генри.

Пример 1: Переменный ток с частотой 2 кГц и максимальным значением 0,15 А протекает в катушке с индуктивностью 175 мГн. (1) Найдите максимум напряжение, развивающееся на индуктивности. (2) Найдите эффективное значение напряжение на индуктивности. (3) Запишите периодические функции, представляющие напряжение и ток.

Решение:

1.

2.

Действующее значение напряжения также можно найти, вычислив сначала эффективное значение тока

Затем

3. Если в качестве эталона берется ток,

Напряжение опережает ток в индуктивной цепи

Пример 2: Напряжение на индуктивности составляет 40 В, когда ток 120 мА. Частота тока и напряжения 400 Гц. Найдите индуктивность.

Решение: Величину индуктивного сопротивления можно найти

Теперь можно рассчитать индуктивность.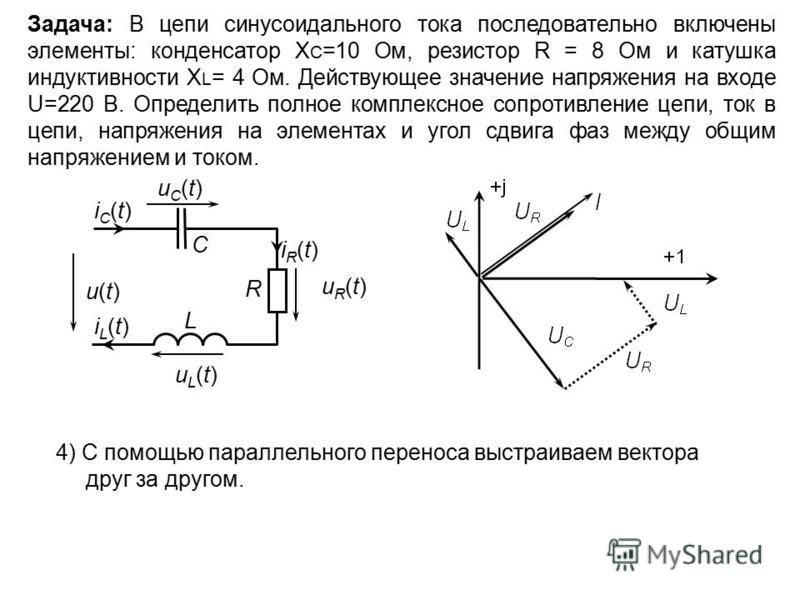

Соотношение мощностей в индуктивной цепи можно проанализировать, написав уравнение для мощности с мгновенными значениями

Применяя это уравнение к рисунку выше, мы видим, что мгновенная мощность равна положительный от t ₀ до t ₁ , отрицательный от t ₁ до t ₂ , положительный от t ₂ до t ₃ , и минус от т ₃ до т ₄ . Мгновенная мощность изображен на рисунке ниже. Положительная мощность указывает, что энергия берется из источника, и отрицательная сила , что энергия возвращается в источник. Так как за один полный цикл, от t ₀ до t ₄ , возвращается столько энергии, сколько забирается из источник, чистая энергия, полученная от источника, равна нулю. Власть над поэтому полный цикл равен нулю. Это поддерживает определение, что Индуктивность – это свойство цепи запасать энергию в виде магнитное поле.