Постоянная Больцмана — Википедия

Материал из Википедии — свободной энциклопедии

Значения постоянной Больцмана в разных единицах

Численное значение	Единица
1,380 649⋅10−23	Дж·К−1[1]
1,380 649⋅10−16	эрг·К−1
8,617 333 262… ⋅10−5	эВ·К−1[2]

Постоя́нная Бо́льцмана (k{\displaystyle k} или kB{\displaystyle k_{\rm {B}}}) — физическая постоянная, определяющая связь между температурой и энергией. Названа в честь австрийского физика Людвига Больцмана, сделавшего большой вклад в статистическую физику, в которой эта постоянная играет ключевую роль. Её значение в Международной системе единиц СИ согласно изменениям определений основных единиц СИ точно равно

k=1,380649×10−23{\displaystyle k=1{,}380\,649\times 10^{-23}} Дж/К.

В системе единиц Планка постоянная Больцмана выбрана в качестве одной из основных единиц системы^[3].

Универсальная газовая постоянная определяется как произведение постоянной Больцмана на число Авогадро, R=kNA{\displaystyle R=kN_{\mathrm {A} }}. Газовая постоянная более удобна, когда число частиц задано в молях.

В однородном идеальном газе, находящемся при абсолютной температуре T{\displaystyle T}, энергия, приходящаяся на каждую поступательную степень свободы, равна, как следует из распределения Максвелла, kT/2{\displaystyle kT/2}. При комнатной температуре (300 К) эта энергия составляет 2,07×10−21{\displaystyle 2{,}07\times 10^{-21}} Дж, или 0,025851 эВ. В одноатомном идеальном газе каждый атом обладает тремя степенями свободы, соответствующими трём пространственным осям, что означает, что на каждый атом приходится энергия в 32kT{\displaystyle {\frac {3}{2}}kT}.

Зная тепловую энергию, можно вычислить среднеквадратичную скорость атомов, которая обратно пропорциональна квадратному корню атомной массы. Среднеквадратичная скорость при комнатной температуре изменяется от 1370 м/с для гелия до 240 м/с для ксенона. В случае молекулярного газа ситуация усложняется, например, двухатомный газ имеет 5 степеней свободы — 3 поступательных и 2 вращательных (при низких температурах, когда не возбуждены колебания атомов в молекуле и не добавляются дополнительные степени свободы).

Энтропия термодинамической системы определяется как величина, пропорциональная натуральному логарифму от числа различных микросостояний Z{\displaystyle Z}, соответствующих данному макроскопическому состоянию (например, состоянию с заданной полной энергией).

S=kln⁡Z.{\displaystyle S=k\ln Z.}

Коэффициент пропорциональности k{\displaystyle k} и есть постоянная Больцмана. Это выражение, определяющее связь между микроскопическими (Z{\displaystyle Z}) и макроскопическими состояниями (S{\displaystyle S}), выражает центральную идею статистической механики.

XXIV Генеральная конференция по мерам и весам, состоявшаяся 17—21 октября 2011 года, приняла резолюцию^[4], в которой, в частности, было предложено будущую ревизию Международной системы единиц произвести так, чтобы зафиксировать значение постоянной Больцмана, после чего она будет считаться определённой точно. В результате должно было выполняться точное равенство

k = 1,380 6X⋅10⁻²³ Дж/К, где Х заменяет одну или более значащих цифр, которые должны были быть определены в дальнейшем на основании наиболее точных рекомендаций CODATA. Такая фиксация была связана со стремлением переопределить единицу термодинамической температуры кельвин, связав его величину со значением постоянной Больцмана.

Жёсткость — Википедия

Удлинение δ цилиндрической пружины, вызванное приложенной осевой силой F

Механическая жесткость (также жесткость) — способность твердого тела, конструкции или её элементов сопротивляться деформации

[1]^[2][3] (изменение формы и / или размеров) от приложенного усилия вдоль выбранного направления в заданной системе координат. Обратная к характеристике называется механической податливостью. Для случая упругих деформаций в записи закона Гука рассматривается как физико-геометрическая характеристика сечения элемента конструкции и равна произведению модуля упругости материала и соответствующей геометрической характеристики сечения.

Механическая жесткость является одним из важных факторов, определяющих работоспособность конструкции и имеет такое же, а иногда и большее значение для обеспечения её надежности, как и прочность. Конструкция может быть прочной, но не жесткой, поскольку значительные деформации могут привести к появлению опасных с точки зрения прочности напряжений.

Недостаточная жесткость и связанные с ней повышенные деформации могут вызвать потерю работоспособности конструкции по различным причинам. Повышенные деформации могут нарушить равномерность распределения нагрузки и вызвать их концентрацию на отдельных участках, создавая высокие местные напряжения, что может привести к разрушению. Недостаточная жесткость корпусных деталей нарушает взаимодействие размещенных в них механизмов, вызывая повышенное трение и износ в кинематических парах, появление вибраций. Недостаточная жесткость валов и опор зубчатых передач изменяет нормальное зацепление колес, что приводит к быстрому усталостному выкрашиванию и износу их рабочих поверхностей. Кроме того, увеличиваются углы перекосов подшипников, уменьшается их долговечность, а в отдельных случаях даже недостаточная жёсткость приводит к быстрому разрушению. В технологических машин, выполняющих точные операции, недостаточная жесткость системы «станок   — инструмент — устройство — деталь» не позволяет получить размеры с заданной точностью.

Параметры для определения жесткости балки на двух опорах

Оценивать жесткость принято коэффициентом жесткости (k)   — отношением усилия (силы), прилагаемого к конструкции, к максимальной деформации, вызванные этой силой.

Коэффициент жесткости k тела является мерой сопротивления упругого тела деформации. Для упругого тела при нагрузке (например, растяжение или сжатие стержня вызванные приложенной силой), жесткость определяется, как

k=Fδ,{\displaystyle k={\frac {F}{\delta }},}

где F   — сила, приложенная к телу; δ   — деформация, вызванная силой F вдоль направления действия силы (например, изменение длины растянутой пружины или прогиб балки).

В системе СИ коэффициент механической жесткости измеряется в ньютонах на метр (Н/м).

Для упругого тела можно рассматривать и механическую жесткость при кручении, тогда коэффициент жесткости k:

k=Mθ,{\displaystyle k={\frac {M}{\theta }},}

где M — приложенный к телу крутящий момент, θ — угол закручивания тела в направлении приложения крутящего момента.

В системе СИ коэффициент жесткости при кручении обычно измеряется в ньютон-метрах на радиан (Н·м/рад).

Механическая жесткость и упругие свойства материала[править | править код]

Между модулем упругости материала и жесткостью детали, изготовленной из этого материала есть существенная разница. Модуль упругости — это свойство материала; механическая жесткость — это свойство конструкции или её компонента, а следовательно, она зависит не только от материала, из которого он изготовлен, но и от геометрических размеров, которые описывают этот компонент. То есть модуль упругости — это интенсивная величина (не зависит от размеров объекта), характеризующий материал; с другой стороны, механическая жесткость — это экстенсивная характеристика (зависимая от размеров) твердого тела, которая зависит как от материала, так и от его характерных геометрических размеров, формы и граничных условий.

Например, для элемента в виде бруса, испытывающего растяжения или сжатия, коэффициент осевой жесткости равен

k=FEL{\displaystyle k={\frac {FE}{L}}},

где F   — площадь поперечного сечения, перпендикулярной линии приложения усилия,E   — модуль Юнга (модуль упругости первого рода), L   — длина элемента.

Для деформации сдвига коэффициент жесткости:

k=GFl{\displaystyle k={\frac {GF}{l}}},

где F   — площадь поперечного сечения в плоскости сдвига, G   — модуль сдвига (модуль упругости второго рода) для данного материала, l   — высота элемента смещения перпендикулярно направлению сдвига.

Для коэффициента жесткости при кручении цилиндрического стержня можно записать

k=GJ0L{\displaystyle k={\frac {GJ_{0}}{L}}},

где J0{\displaystyle J_{0}}   — полярный момент инерции, G   — модуль сдвига (модуль упругости второго рода) для данного материала, L   — длина элемента.

По аналогии коэффициент жесткости для условий чистого изгиба

k=GJxL,{\displaystyle k={\frac {GJ_{x}}{L}},},

где G — модуль сдвига (модуль упругости второго рода) для данного материала, Jx{\displaystyle J_{x}} — осевой момент инерции, L — длина элемента.

Расчет на жесткость предусматривает ограничение упругих перемещений допустимыми величинами. Значения допустимых перемещений ограничены условиями работы сопряженных деталей (зацепление зубчатых колес, работа подшипников в условиях изгиба валов) или технологическими требованиями (точность обработки на металлорежущих станках).

Различают собственную жесткость деталей, обусловленную деформациями всего материала деталей рассматриваются как балки, пластины, оболочки с идеализированными опорами, и контактную жесткость,

которая связана с деформациями поверхностных слоев материала в зоне контактного взаимодействия деталей. Если площадь контакта мала, то возникают существенные контактные деформации, и их расчет производится по формулам Герца. Преимущественно при значительных нагрузках основную роль играет собственная жесткость, однако, в прецизионных машинах или устройствах при относительно малых нагрузках контактные деформации играют значительную роль и могут даже превышать собственные.

При большой контактной площади деформации, обусловленные смятием микронеровностей, определяются по эмпирическим формулам с использованием экспериментально установленных коэффициентов контактной податливости.

Условия обеспечения жесткости записываются в виде:

• Δl ≤ [Δl]   — для деформации растяжения-сжатия;
• θ ≤ [θ]   — для деформации кручения;
• f ≤ [f]   — для стрелы прогиба детали в виде балки на опорах.

Мероприятия по обеспечению механической жесткости[править | править код]

Главным практическим средством повышения жесткости является маневрирование геометрическими параметрами детали с целью обеспечения достаточной жесткости формы. Главными конструктивными средствами повышения жесткости деталей и конструкций являются:

• по возможности устранения деформации изгиба, как невыгодной с точки зрения обеспечения жесткости и прочности, замена её деформацией растяжения (сжатия)
• для деталей, работающих на изгиб, выбор рациональных типов опор и их размещения, исключение по возможности консолей и уменьшения их длины, стремясь к равномерному распределению нагрузки по длине;
• рациональное, но без роста массы, увеличение моментов инерции сечений путем удаления материала от нейтральной оси, усиление закладных участков и участков перехода от одного сечения к другому;
• для коробчатых деталей — использование криволинейных выпуклых стенок;
• блокировки деформаций путем установления раскосов (для рам), обечаек и перемычек (для полых тонкостенных цилиндров), оребрения тонких стенок, рифление плоских поверхностей крышек и тому подобное.

Наряду с собственной жесткостью в соединениях деталей значительную роль играет контактная жесткость, которая может определять точность движения контактирующих деталей, вызвать дополнительные динамические нагрузки, влиять на износостойкость поверхностей и их долговечность, на рассеяние энергии колебаний.

Важнейшими конструктивными мерами по повышению контактной жесткости являются:

• Сопротивление материалов. Учебник / Г.   С.   Писаренко, А.   Л.   Цветок, Е.   С.   Уманский. Под ред. Г.   С.   Писаренко   — М .: Высшая школа, 1993.   — 655 с.   — ISBN 5-11-004083-4
• Детали машин: учебник / Миняйло А. В., Тищенко Л. М., Мазоренко Д. И. и др.   — М .: Агроосвита 2013.   — 448 c.   — ISBN 978-966-2007-28-2
• Решетов Д. Н. Детали машин. Учебник для студентов машиностроительных и механических специальностей вузов. 4-ое издание, переработанное и дополненное.   — М .: Машиностроение, 1989.   — 496 с.   — ISBN 5-217-00335-9

Джоуль — Википедия

Материал из Википедии — свободной энциклопедии

Джо́уль (англ. Joule; русское обозначение: Дж; международное: J) — единица измерения работы, энергии и количества теплоты в Международной системе единиц (СИ). Джоуль равен работе, совершаемой при перемещении точки приложения силы, равной одному ньютону, на расстояние одного метра в направлении действия силы^[1]. Таким образом, 1 Дж = 1 Н·м=1 кг·м²/с². В электричестве джоуль означает работу, которую совершают силы электрического поля за 1 секунду при напряжении в 1 вольт для поддержания силы тока в 1 ампер^[2].

В соответствии с правилами СИ, касающимися производных единиц, названных по имени учёных, наименование единицы джоуль пишется со строчной буквы, а её обозначение — с заглавной. Такое написание обозначения сохраняется и в обозначениях других производных единиц, образованных с использованием джоуля. Например, обозначение единицы молярной внутренней энергии «джоуль на моль» записывается как Дж/моль.

Джоуль был введён в абсолютные практические электрические единицы в качестве единицы работы и энергии электрического тока на Втором международном конгрессе электриков, проходившем в год смерти Джеймса Джоуля (1889). Международная конференция по электрическим единицам и эталонам (Лондон, 1908) установила «международные» электрические единицы, в том числе «международный джоуль». После возвращения с 1 января 1948 к абсолютным электрическим единицам было принято соотношение: 1 международный джоуль = 1,00020 абсолютного джоуля^[3]. В Международную систему единиц (СИ) джоуль введён решением XI Генеральной конференцией по мерам и весам в 1960 году одновременно с принятием системы СИ в целом^[4].

• 1 Дж = 1 кг·м²/с² = 1 Н·м = 1 Вт·с = 1 Кл·В.
• 1 Дж = 10⁷эрг.
• 1 Дж ≈ 6,24151⋅10¹⁸эВ.
• 1 МДж = 0,277(7) кВт·ч.
• 1 кВт·ч = 3,6 МДж.
• 1 Дж ≈ 0,238846 калориям.
• 1 калория_м (международная) = 4,1868 Дж^[5].
• 1 термохимическая калория = 4,1840 Дж^[5].
• 1 килотонна ТНТ (=Ткал_т) ≈ 4,1840 ТДж (4,184⋅10¹² Дж).
• 1 килограмм-сила-метр (кгс·м) = 9,80665 Дж (точно).
• 1 Дж ≈ 0,101972 кгс·м.

В соответствии с полным официальным описанием СИ, содержащемся в действующей редакции Брошюры СИ (фр. Brochure SI), опубликованной Международным бюро мер и весов (МБМВ), десятичные кратные и дольные единицы джоуля образуются с помощью стандартных приставок СИ^[6]. «Положение о единицах величин, допускаемых к применению в Российской Федерации», принятое Правительством Российской Федерации, предусматривает использование в РФ тех же приставок^[7].

Кратные				Дольные
величина	название	обозначение		величина	название	обозначение
101 Дж	декаджоуль	даДж	daJ	10−1 Дж	дециджоуль	дДж	dJ
102 Дж	гектоджоуль	гДж	hJ	10−2 Дж	сантиджоуль	сДж	cJ
103 Дж	килоджоуль	кДж	kJ	10−3 Дж	миллиджоуль	мДж	mJ
106 Дж	мегаджоуль	МДж	MJ	10−6 Дж	микроджоуль	мкДж	µJ
109 Дж	гигаджоуль	ГДж	GJ	10−9 Дж	наноджоуль	нДж	nJ
1012 Дж	тераджоуль	ТДж	TJ	10−12 Дж	пикоджоуль	пДж	pJ
1015 Дж	петаджоуль	ПДж	PJ	10−15 Дж	фемтоджоуль	фДж	fJ
1018 Дж	эксаджоуль	ЭДж	EJ	10−18 Дж	аттоджоуль	аДж	aJ
1021 Дж	зеттаджоуль	ЗДж	ZJ	10−21 Дж	зептоджоуль	зДж	zJ
1024 Дж	иоттаджоуль	ИДж	YJ	10−24 Дж	иоктоджоуль	иДж	yJ
применять не рекомендуется

• Средняя энергия теплового движения, приходящаяся на одну степень свободы молекул при температуре 1 К: 0,690⋅10⁻²³ Дж.
• Энергия фотона красного видимого света: 2,61⋅10⁻¹⁹ Дж.
• Энергия Ферми металлического золота при нормальных условиях: 8,8⋅10⁻¹⁹ Дж^[8].
• Атомная единица энергии (энергия Хартри), Eh=mec2α2{\displaystyle E_{h}=m_{\mathrm {e} }c^{2}\alpha ^{2}}: 4,360⋅10⁻¹⁸ Дж.
• Дульная энергия пули при выстреле из АКМ: 2030 Дж^[9].
• Энергия, необходимая для нагрева 1 литра воды от 20 до 100 °C: 3,35⋅10⁵ Дж.
• Энергия, выделяемая при взрыве 1 тонны тринитротолуола (тротиловый эквивалент): 4,184⋅10⁹ Дж.
• Энергия, выделенная при атомной бомбардировке Хиросимы: около 6⋅10¹³ Дж.
• Энергия, выделившаяся при столкновении астероида с Землёй, в результате которого образовался кратер Маникуаган: 10²³ Дж.

Скорость — Википедия

Скорость
v→=dr→dt{\displaystyle {\vec {v}}={\frac {\mathrm {d} {\vec {r}}}{\mathrm {d} t}}}
Размерность	LT−1
СИ	м/с
СГС	см/с
вектор

Ско́рость (часто обозначается v→{\displaystyle {\vec {v}}}, от англ. velocity или фр. vitesse, исходно от лат. vēlōcitās) — векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки относительно выбранной системы отсчёта; по определению, равна производной радиус-вектора точки по времени^[1]. Этим же словом называют и скалярную величину — либо модуль вектора скорости, либо алгебраическую скорость точки, то есть проекцию этого вектора на касательную к траектории точки^[2].

Термин «скорость» используют в науке и в широком смысле, понимая под ним быстроту изменения какой-либо величины (не обязательно радиус-вектора) в зависимости от другой (чаще подразумеваются изменения во времени, но также в пространстве или любой другой). Так, например, говорят об угловой скорости, скорости изменения температуры, скорости химической реакции, групповой скорости, скорости соединения и т. д. Математически «быстрота изменения» характеризуется производной рассматриваемой величины.

Расширениями понятия скорости являются четырёхмерная скорость, или скорость в релятивистской механике, и обобщённая скорость, или скорость в обобщённых координатах.

Скорость точки в классической механике[править | править код]

Вектор скорости материальной точки в каждый момент времени определяется как производная по времени радиус-вектора r→{\displaystyle {\vec {r}}} текущего положения этой точки, так что^[3]:

v→=dr→dt≡vττ→,{\displaystyle {\vec {v}}={\mathrm {d} {\vec {r}} \over \mathrm {d} t}\equiv v_{\tau }{\vec {\tau }},}

где τ→≡dr→/ds{\displaystyle {\vec {\tau }}\equiv \mathrm {d} {\vec {r}}/\mathrm {d} s} — единичный вектор касательной, проходящей через текущую точку траектории (он направлен в сторону возрастания дуговой координаты s{\displaystyle s} движущейся точки), а vτ≡s˙{\displaystyle v_{\tau }\equiv {\dot {s}}} — проекция вектора скорости на направление упомянутого единичного вектора, равная производной дуговой координаты по времени и именуемая алгебраической скоростью точки. В соответствии с приведёнными формулами, вектор скорости точки всегда направлен вдоль касательной, а алгебраическая скорость точки может отличаться от модуля v{\displaystyle v} этого вектора лишь знаком^[4]. При этом:

• если дуговая координата возрастает, то векторы v→{\displaystyle {\vec {v}}} и τ→{\displaystyle {\vec {\tau }}} сонаправлены, а алгебраическая скорость положительна;
• если дуговая координата убывает, то векторы v→{\displaystyle {\vec {v}}} и τ→{\displaystyle {\vec {\tau }}} противонаправлены, а алгебраическая скорость отрицательна.

Не следует смешивать дуговую координату и пройденный точкой путь. Путь s~{\displaystyle {\tilde {s}}}, пройденный точкой за промежуток времени от t0{\displaystyle t_{0}} до t{\displaystyle t}, может быть найден так:

s~=∫t0t|s˙|dt;{\displaystyle {\tilde {s}}=\int _{t_{0}}^{t}|{\dot {s}}|\,\mathrm {d} t\;;}

лишь в случае, когда алгебраическая скорость точки всё время неотрицательна, связь пути и дуговой координаты достаточно проста: путь совпадает с приращением дуговой координаты за время от t0{\displaystyle t_{0}} до t{\displaystyle t} (если же при этом начало отсчёта дуговой координаты совпадает с начальным положением движущейся точки, то s~{\displaystyle {\tilde {s}}} будет совпадать с s{\displaystyle s}).

Если алгебраическая скорость точки не меняется с течением времени (или, что то же самое, модуль скорости постоянен), то движение точки называется^[5]равномерным (алгебраическое касательное ускорение s¨{\displaystyle {\ddot {s}}} при этом тождественно равно нулю).

Предположим, что s¨⩾0{\displaystyle {\ddot {s}}\geqslant {0}}. Тогда при равномерном движении скорость точки (алгебраическая) будет равна отношению пройденного пути s~{\displaystyle {\tilde {s}}} к промежутку времени t−t0{\displaystyle t-t_{0}}, за который этот путь был пройден:

s˙cp=s~t−t0.{\displaystyle {\dot {s}}^{\,\mathrm {cp} }={{\tilde {s}} \over t-t_{0}}\;.}

В общем же случае аналогичные отношения

v→cp=r→−r→0t−t0≡Δr→Δt{\displaystyle {\vec {v}}^{\,\,\mathrm {cp} }={{\vec {r}}-{\vec {r}}_{0} \over t-t_{0}}\equiv {\Delta {\vec {r}} \over \Delta {t}}}     и     s˙cp=s−s0t−t0≡ΔsΔt{\displaystyle {\dot {s}}^{\,\mathrm {cp} }={s-s_{0} \over t-t_{0}}\equiv {\Delta {s} \over \Delta {t}}}

определяют соответственно среднюю скорость точки^[6] и её среднюю алгебраическую скорость; если термином «средняя скорость» пользуются, то о величинах v→{\displaystyle {\vec {v}}} и s˙{\displaystyle {\dot {s}}} говорят (чтобы избежать путаницы) как о мгновенных скоростях.

Иллюстрация средней и мгновенной скорости

Не следует смешивать два введённых выше понятия средней скорости. Во-первых, v→cp{\displaystyle {\vec {v}}^{\,\,\mathrm {cp} }} — вектор, а s˙cp{\displaystyle {\dot {s}}^{\,\mathrm {cp} }} — скаляр. Во-вторых, эти величины могут не совпадать по модулю. Так, пусть точка движется движется по винтовой линии и за время своего движения проходит один виток; тогда модуль средней скорости этой точки будет равен отношению шага винтовой линии (то есть расстояния между её витками) ко времени движения, а модуль средней алгебраической скорости — отношению длины витка ко времени движения.

Для тела протяжённых размеров понятие «скорости» (тела как такового, а не одной из его точек) не может быть определено; исключение составляет случай мгновенно-поступательного движения. Говорят, что абсолютно твёрдое тело совершает мгновенно-поступательное движение, если в данный момент времени скорости всех составляющих его точек равны^[7]; тогда можно, разумеется, положить скорость тела равной скорости любой из его точек. Так, например, равны скорости всех точек кабинки колеса обозрения (если, конечно, пренебречь колебаниями кабинки).

В общем же случае скорости точек, образующих твёрдое тело, не равны между собой. Так, например, для катящегося без проскальзывания колеса модули скоростей точек на ободе относительно дороги принимают значения от нуля (в точке касания с дорогой) до удвоенного значения скорости центра колеса (в точке, диаметрально противоположной точке касания). Распределение скоростей точек абсолютно твёрдого тела описывается кинематической формулой Эйлера.

В декартовых координатах[править | править код]

В прямоугольной декартовой системе координат^[8]:

v=vxi+vyj+vzk.{\displaystyle \mathbf {v} =v_{x}\mathbf {i} +v_{y}\mathbf {j} +v_{z}\mathbf {k} .}

В то же время r=xi+yj+zk,{\displaystyle \mathbf {r} =x\mathbf {i} +y\mathbf {j} +z\mathbf {k} ,} поэтому

v=d(xi+yj+zk)dt=dxdti+dydtj+dzdtk.{\displaystyle \mathbf {v} ={\frac {\mathrm {d} (x\mathbf {i} +y\mathbf {j} +z\mathbf {k} )}{\mathrm {d} t}}={\frac {\mathrm {d} x}{\mathrm {d} t}}\mathbf {i} +{\frac {\mathrm {d} y}{\mathrm {d} t}}\mathbf {j} +{\frac {\mathrm {d} z}{\mathrm {d} t}}\mathbf {k} .}

Таким образом, координаты вектора скорости — это скорости изменения соответствующей координаты материальной точки^[8]:

vx=dxdt;vy=dydt;vz=dzdt.{\displaystyle v_{x}={\frac {\mathrm {d} x}{\mathrm {d} t}};v_{y}={\frac {\mathrm {d} y}{\mathrm {d} t}};v_{z}={\frac {\mathrm {d} z}{\mathrm {d} t}}.}

В цилиндрических координатах[править | править код]

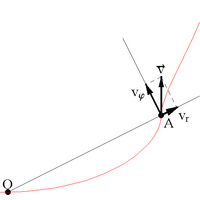Скорость в полярных координатах

В цилиндрических координатах R,φ,z{\displaystyle R,\varphi ,z}^[8]:

vR=dRdt;vφ=Rdφdt;vz=dzdt.{\displaystyle v_{R}={\frac {\mathrm {d} R}{\mathrm {d} t}};v_{\varphi }=R{\frac {\mathrm {d} \varphi }{\mathrm {d} t}};v_{z}={\frac {\mathrm {d} z}{\mathrm {d} t}}.}

vφ{\displaystyle v_{\varphi }} носит название поперечной скорости, vR{\displaystyle v_{R}} — радиальной.

В сферических координатах[править | править код]

В сферических координатах R,φ,θ{\displaystyle R,\varphi ,\theta }^[8]:

vR=dRdt;vφ=Rsin⁡θdφdt;vθ=Rdθdt.{\displaystyle v_{R}={\frac {\mathrm {d} R}{\mathrm {d} t}};v_{\varphi }=R\sin \theta {\frac {\mathrm {d} \varphi }{\mathrm {d} t}};v_{\theta }=R{\frac {\mathrm {d} \theta }{\mathrm {d} t}}.}

Обобщениями понятия скорости является четырёхмерная скорость, или скорость в релятивистской механике, и обобщённая скорость, или скорость в обобщённых координатах^[8].

Четырёхмерная скорость[править | править код]

В специальной теории относительности каждому событию ставится в соответствие точка пространства Минковского, три координаты которого представляют собой декартовы координаты трёхмерного евклидова пространства, а четвёртая ― временну́ю коодинату ct{\displaystyle ct}, где c{\displaystyle c} ― скорость света, t{\displaystyle t} ― время события. Компоненты четырёхмерного вектора скорости связаны с проекциями трёхмерного вектора скорости следующим образом^[8]:

v0=c1−v2c2;v1=vx1−v2c2;v2=vy1−v2c2;v3=vz1−v2c2.{\displaystyle v_{0}={\frac {c}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}};v_{1}={\frac {v_{x}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}};v_{2}={\frac {v_{y}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}};v_{3}={\frac {v_{z}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}.}

Четырёхмерный вектор скорости является времениподобным вектором, то есть лежит внутри светового конуса^[8].

В обобщённых координатах[править | править код]

Следует различать координатную и физическую скорости. При введении криволинейных или обобщённых координат положение тел описывается их зависимостью от времени. Производные от координат тела по времени при этом называются координатными скоростями.

В классической механике Ньютона скорости преобразуются при переходе из одной инерциальной системы отсчёта в другую согласно преобразованиям Галилея. Если скорость тела в системе отсчёта S{\displaystyle S} была равна v→{\displaystyle {\vec {v}}}, а скорость системы отсчёта S′{\displaystyle S’} относительно системы отсчёта S{\displaystyle S} равна u→{\displaystyle {\vec {u}}}, то скорость тела при переходе в систему отсчёта S′{\displaystyle S’} будет равна^[8]

v→′=v→−u→.{\displaystyle {\vec {v}}’={\vec {v}}-{\vec {u}}.}

Для скоростей, близких к скорости света преобразования Галилея становятся несправедливы. При переходе из системы S{\displaystyle S} в систему S′{\displaystyle S’} необходимо использовать преобразования Лоренца для скоростей^[8]:

vx′=vx−u1−(vxu)/c2,vy′=vy1−u2c21−(vxu)/c2,vz′=vz1−u2c21−(vxu)/c2,{\displaystyle v_{x}’={\frac {v_{x}-u}{1-(v_{x}u)/c^{2}}},v_{y}’={\frac {v_{y}{\sqrt {1-{\frac {u^{2}}{c^{2}}}}}}{1-(v_{x}u)/c^{2}}},v_{z}’={\frac {v_{z}{\sqrt {1-{\frac {u^{2}}{c^{2}}}}}}{1-(v_{x}u)/c^{2}}},}

в предположении, что скорость u→{\displaystyle {\vec {u}}} направлена вдоль оси x{\displaystyle x} системы S{\displaystyle S}. Легко убедиться, что в пределе нерелятивистских скоростей преобразования Лоренца сводятся к преобразованиям Галилея.

Ряд понятий классической механики выражаются через скорость.

Импульс, или количество движения, — это мера механического движения точки, которая определяется как произведение массы точки на его скорость p→=mv→{\displaystyle {\vec {p}}=m{\vec {v}}}. Импульс является векторной величиной, его направление совпадает с направлением скорости. Для замкнутой системы выполняется закон сохранения импульса. Обобщением импульса в релятивистских системах является четырёхимпульс, временная компонента которого равна E/c{\displaystyle E/c}. Для обобщённого импульса также выполняется равенство^[9]:

pμ=mUμ,{\displaystyle p^{\mu }=m\,U^{\mu }\!,}

где Uμ{\displaystyle U^{\mu }} — обобщённая четырёхмерная скорость.

От скорости также зависит кинетическая энергия механической системы. Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения^[10][11]:

T=mv22+Iω→22,{\displaystyle T={\frac {mv^{2}}{2}}+{\frac {{\mathcal {I}}{\vec {\omega }}^{2}}{2}},}

где  m{\displaystyle \ m} — масса тела,  v{\displaystyle \ v} — скорость центра масс тела, I{\displaystyle {\mathcal {I}}} — момент инерции тела, ω→{\displaystyle {\vec {\omega }}} — угловая скорость тела.

Изменение скорости по времени характеризуется ускорением. Ускорение отражает изменение скорости как по величине (тангенциальное ускорение), так и по направлению (центростремительное ускорение)^[12]:

a→=dv→dt=a→τ+a→n=d|v→|dte→τ+v2re→n,{\displaystyle {\vec {a}}={\frac {\mathrm {d} {\vec {v}}}{\mathrm {d} t}}={\vec {a}}_{\tau }+{\vec {a}}_{n}={\frac {\mathrm {d} |{\vec {v}}|}{\mathrm {d} t}}{\vec {e}}_{\tau }+{v^{2} \over r}{\vec {e}}_{n},}

где  r{\displaystyle \ r} — радиус кривизны траектории точки.

В релятивистской механике угол между касательной к мировой линии частицы и осью времени в базовой системе отсчёта носит название быстроты (обозначается θ{\displaystyle \theta }). Быстрота выражается формулой:

θ=cArthvc=c2ln⁡1+vc1−vc,{\displaystyle \theta =c\,\mathrm {Arth} \,{\frac {v}{c}}={\frac {c}{2}}\ln {\frac {1+{\dfrac {v}{c}}}{1-{\dfrac {v}{c}}}},}

где Arthx{\displaystyle \mathrm {Arth} \,x} — ареатангенс, или гиперболический арктангенс. Быстрота стремится к бесконечности когда скорость

Измерение — Википедия

Измерение — совокупность действий для определения отношения одной (измеряемой) величины к другой однородной величине, принятой всеми участниками за единицу, хранящуюся в техническом средстве (средстве измерений).

Получившееся значение называется числовым значением измеряемой величины, числовое значение совместно с обозначением используемой единицы называется значением физической величины. Измерение физической величины опытным путём проводится с помощью различных средств измерений — мер, измерительных приборов, измерительных преобразователей, систем, установок и т. д. Измерение физической величины включает в себя несколько этапов: 1) сравнение измеряемой величины с единицей; 2) преобразование в форму, удобную для использования (различные способы индикации).

• Принцип измерений — физическое явление или эффект, положенный в основу измерений.
• Метод измерений — приём или совокупность приёмов сравнения измеряемой физической величины с её единицей в соответствии с реализованным принципом измерений. Метод измерений обычно обусловлен устройством средств измерений.

Характеристикой точности измерения является его погрешность или неопределённость. Примеры измерений:

1. В простейшем случае, прикладывая линейку с делениями к какой-либо детали, по сути сравнивают её размер с единицей, хранимой линейкой, и, произведя отсчёт, получают значение величины (длины, высоты, толщины и других параметров детали).
2. С помощью измерительного прибора сравнивают размер величины, преобразованной в перемещение указателя, с единицей, хранимой шкалой этого прибора, и проводят отсчёт.

В тех случаях, когда невозможно выполнить измерение (не выделена величина как физическая, или не определена единица измерений этой величины) практикуется оценивание таких величин по условным шкалам, например, Шкала Рихтера интенсивности землетрясений, Шкала Мооса — шкала твёрдости минералов.

Частным случаем измерения является сравнение без указания количественных характеристик.

Наука, предметом изучения которой являются все аспекты измерений, называется метрологией.

По видам измерений[править | править код]

Согласно РМГ 29-99 «Метрология. Основные термины и определения» выделяют следующие виды измерений:

• Прямое измерение — измерение, при котором искомое значение физической величины получают непосредственно.
• Косвенное измерение — определение искомого значения физической величины на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной.
• Совместные измерения — проводимые одновременно измерения двух или нескольких не одноимённых величин для определения зависимости между ними.
• Совокупные измерения — проводимые одновременно измерения нескольких одноимённых величин, при которых искомые значения величин определяют путём решения системы уравнений, получаемых при измерениях этих величин в различных сочетаниях.
• Равноточные измерения — ряд измерений какой-либо величины, выполненных одинаковыми по точности средствами измерений в одних и тех же условиях с одинаковой тщательностью.
• Неравноточные измерения — ряд измерений какой-либо величины, выполненных различающимися по точности средствами измерений и (или) в разных условиях.
• Однократное измерение — измерение, выполненное один раз.
• Многократное измерение — измерение физической величины одного и того же размера, результат которого получен из нескольких следующих друг за другом измерений, то есть состоящее из ряда однократных измерений
• Статическое измерение — измерение физической величины, принимаемой в соответствии с конкретной измерительной задачей за неизменную на протяжении времени измерения.
• Динамическое измерение — измерение изменяющейся по размеру физической величины.
• Абсолютное измерение — измерение, основанное на прямых измерениях одной или нескольких основных величин и (или) использовании значений физических констант.
• Относительное измерение — измерение отношения величины к одноимённой величине, играющей роль единицы, или измерение изменения величины по отношению к одноимённой величине, принимаемой за исходную (см. ниже нулевой метод).

Также стоит отметить, что в различных источниках дополнительно выделяют такие виды измерений: метрологические и технические, необходимые и избыточные и др.

По методам измерений[править | править код]

• Метод непосредственной оценки — метод измерений, при котором значение величины определяют непосредственно по показывающему средству измерений.
• Метод сравнения с мерой — метод измерений, в котором измеряемую величину сравнивают с величиной, воспроизводимой мерой.
  • Нулевой (компенсационный) метод измерений — метод сравнения с мерой, в котором результирующий эффект воздействия измеряемой величины и меры на прибор сравнения доводят до нуля.
  • Метод измерений замещением — метод сравнения с мерой, в котором измеряемую величину замещают мерой с известным значением величины.
  • Метод измерений дополнением — метод сравнения с мерой, в котором значение измеряемой величины дополняется мерой этой же величины с таким расчётом, чтобы на прибор сравнения воздействовала их сумма, равная заранее заданному значению.
  • Дифференциальный метод измерений — метод измерений, при котором измеряемая величина сравнивается с однородной величиной, имеющей известное значение, незначительно отличающееся от значения измеряемой величины, и при котором измеряется разность между этими двумя величинами.

По условиям, определяющим точность результата[править | править код]

• Метрологические измерения
  • Измерения максимально возможной точности, достижимой при существующем уровне техники. В этот класс включены все высокоточные измерения и в первую очередь эталонные измерения, связанные с максимально возможной точностью воспроизведения установленных единиц физических величин. Сюда относятся также измерения физических констант, прежде всего универсальных, например измерение абсолютного значения ускорения свободного падения^[1].
  • Контрольно-поверочные измерения, погрешность которых с определённой вероятностью не должна превышать некоторого заданного значения. В этот класс включены измерения, выполняемые лабораториями государственного контроля (надзора) за соблюдением требований технических регламентов, а также состоянием измерительной техники и заводскими измерительными лабораториями. Эти измерения гарантируют погрешность результата с определённой вероятностью, не превышающей некоторого, заранее заданного значения^[1].
• Технические измерения, в которых погрешность результата определяется характеристиками средств измерений. Примерами технических измерений являются измерения, выполняемые в процессе производства на промышленных предприятиях, в сфере услуг и др.^[1]

По отношению к изменению измеряемой величины[править | править код]

Динамическое и статическое.

По результатам измерений[править | править код]

• Абсолютное измерение — измерение, основанное на прямых измерениях одной или нескольких основных величин и (или) использовании значений физических констант.
• Относительное измерение — измерение отношения величины к одноимённой величине, играющей роль единицы, или измерение изменения величины по отношению к одноимённой величине, принимаемой за исходную.

По точности[править | править код]

• Равноточные измерения — однотипные результаты, получаемые при измерениях одним и тем же инструментом или им подобным по точности прибором, одним и тем же (или аналогичным) методом и в тех же условиях.
• Неравноточные измерения — измерения, произведённые в случае, когда нарушаются эти условия.

По числу измерений[править | править код]

• Однократное измерение — измерение, выполненное один раз.
• Многократное измерение — измерение физической величины одного и того же размера, результат которого получен из нескольких следующих друг за другом измерений, т. е. состоящее из ряда однократных измерений.

По точности[править | править код]

• Детерминированные и случайные.

По результатам измерений[править | править код]

• Равнорассеянные и неравнорассеянные.

Стандартизация измерений[править | править код]

В начале 1840 г. во Франции была введена метрическая система мер.

В 1867 г. Д. И. Менделеев выступил с призывом содействовать подготовке метрической реформы в России. По его инициативе Петербургская академия наук предложила учредить международную организацию, которая обеспечивала бы единообразие средств измерений в международном масштабе. В 1875 г. была принята Метрическая конвенция. Принятие Конвенции ознаменовало начало международной стандартизации.

В физике и технике единицы измерения (единицы физических величин, единицы величин^[2]) используются для стандартизованного представления результатов измерений. Использование термина единица измерения противоречит нормативным документам^[3] и рекомендациям метрологических изданий^[4], однако он широко употребляется в научной литературе^[5]. Численное значение физической величины представляется как отношение измеренного значения к некоторому стандартному значению, которое и является единицей измерения. Число с указанием единицы измерения называется именованным. Различают основные и производные единицы. Основные единицы в данной системе единиц устанавливаются для тех физических величин, которые выбраны в качестве основных в соответствующей системе физических величин. Так, Международная система единиц (СИ) основана на Международной системе величин (англ. International System of Quantities, ISQ), в которой основными являются семь величин: длина, масса, время, электрический ток, термодинамическая температура, количество вещества и сила света. Соответственно, в СИ основными единицами являются единицы указанных величин. Размеры основных единиц устанавливаются по соглашению в рамках соответствующей системы единиц и фиксируются либо с помощью эталонов (прототипов), либо путём фиксации численных значений фундаментальных физических постоянных.

Международная система единиц[править | править код]

Основная статья: СИ Семь базовых величин в СИ. Стрелки указывают зависимости между величинами.

Система единиц физических величин, современный вариант метрической системы. СИ является наиболее широко используемой системой единиц в мире, как в повседневной жизни, так и в науке и технике. В настоящее время СИ принята в качестве основной системы единиц большинством стран мира и почти всегда используется в области техники, даже в тех странах, в которых в повседневной жизни используются традиционные единицы. В этих немногих странах (например, в США) определения традиционных единиц были изменены таким образом, чтобы связать их фиксированными коэффициентами с соответствующими единицами СИ. Официальным международным документом по системе СИ является Брошюра СИ (фр. Brochure SI, англ. SI Brochure), издающаяся с 1970 года. С 1985 года выходит на французском и английском языках, переведена также на ряд других языков. В 2006 году вышло 8-е издание.

Метрическая система мер[править | править код]

Общее название международной десятичной системы единиц, основанной на использовании метра и килограмма. На протяжении двух последних веков существовали различные варианты метрической системы, различающиеся выбором основных единиц. В настоящее время международно признанной является система СИ. Основное отличие метрической системы от применявшихся ранее традиционных систем заключается в использовании упорядоченного набора единиц измерения. Для любой физической величины существует лишь одна главная единица и набор дольных и кратных единиц, образуемых стандартным образом с помощью десятичных приставок. Тем самым устраняется неудобство от использования большого количества разных единиц (таких, например, как дюймы, футы, фадены, мили и т. д.) со сложными правилами преобразования между ними. В метрической системе преобразование сводится к умножению или делению на степень числа 10, то есть к простой перестановке запятой в десятичной дроби.

Система СГС[править | править код]

Основная статья: СГС

Система единиц измерения, которая широко использовалась до принятия Международной системы единиц (СИ). Другое название — абсолютная^[7] физическая система единиц. В рамках СГС существуют три независимые размерности (длина, масса и время), все остальные сводятся к ним путём умножения, деления и возведения в степень (возможно, дробную). Кроме трёх основных единиц измерения — сантиметра, грамма и секунды, в СГС существует ряд дополнительных единиц измерения, которые являются производными от основных. Некоторые физические константы получаются безразмерными. Есть несколько вариантов СГС, отличающихся выбором электрических и магнитных единиц измерения и величиной констант в различных законах электромагнетизма (СГСЭ, СГСМ, Гауссова система единиц). СГС отличается от СИ не только выбором конкретных единиц измерения. Из-за того, что в СИ были дополнительно введены основные единицы для электромагнитных физических величин, которых не было в СГС, некоторые единицы имеют другие размерности. Из-за этого некоторые физические законы в этих системах записываются по-разному (например, закон Кулона). Отличие заключается в коэффициентах, большинство из которых — размерные. Поэтому, если в формулы, записанные в СГС, просто подставить единицы измерения СИ, то будут получены неправильные результаты. Это же относится и к разным разновидностям СГС — в СГСЭ, СГСМ и Гауссовой системе единиц одни и те же формулы могут записываться по-разному.

Английская система мер[править | править код]

Используется в Великобритании, США и других странах. Отдельные из этих мер в ряде стран несколько различаются по своему размеру, поэтому ниже приводятся в основном округлённые метрические эквиваленты английских мер, удобные для практических расчётов.

Техническое средство, предназначенное для измерений, имеющее нормированные метрологические характеристики, воспроизводящее и (или) хранящее единицу физической величины, размер которой принимают неизменным (в пределах установленной погрешности) в течение известного интервала времени. Законом РФ «Об обеспечении единства измерений» средство измерений определено как техническое средство, предназначенное для измерений. Формальное решение об отнесении технического средства к средствам измерений принимает Федеральное агентство по техническому регулированию и метрологии. Классификация:

• по техническому назначению
• по степени автоматизации
• по стандартизации средств измерений
• по положению в поверочной схеме
• по значимости измеряемой физической величины
• по измерительным физико-химическим параметрам

1. Точность средства измерений — степень совпадения показаний измерительного прибора с истинным значением измеряемой величины. Чем меньше разница, тем больше точность прибора. Точность эталона или меры характеризуется погрешностью или степенью воспроизводимости. Точность измерительного прибора, откалиброванного по эталону, всегда хуже или равна точности эталона.
2. Точность результата измерений — одна из характеристик качества измерения, отражающая близость к нулю погрешности результата измерения. Следует отметить, что о повышении качества измерений всегда говорят термином «увеличить точность» — притом, что величина, характеризующая точность, при этом должна уменьшиться.

Погрешность измерения[править | править код]

Оценка отклонения измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения. Поскольку выяснить с абсолютной точностью истинное значение любой величины невозможно, то невозможно и указать величину отклонения измеренного значения от истинного. (Это отклонение принято называть ошибкой измерения. В ряде источников, например, в Большой советской энциклопедии, термины ошибка измерения и погрешность измерения используются как синонимы, но согласно РМГ 29-99^[8] термин ошибка измерения не рекомендуется применять как менее удачный). Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов. На практике вместо истинного значения используют действительное значение величины х_д, то есть значение физической величины, полученное экспериментальным путём и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него^[8]. Такое значение, обычно, вычисляется как среднестатистическое значение, полученное при статистической обработке результатов серии измерений. Это полученное значение не является точным, а лишь наиболее вероятным. Поэтому в измерениях необходимо указывать, какова их точность. Для этого вместе с полученным результатом указывается погрешность измерений. Например, запись T=2,8±0,1 c. означает, что истинное значение величины T лежит в интервале от 2,7 с. до 2,9 с. с некоторой оговорённой вероятностью (см. доверительный интервал, доверительная вероятность, стандартная ошибка).

1. ↑ ^{1 2 3} Метрология и технические измерения. Колчков В. И. Ресурс «ТОЧНОСТЬ-КАЧЕСТВО»]
2. ↑ Официальное название по ГОСТ 8.417-2002 Государственная система обеспечения единства измерений. Единицы величин.
3. ↑ Постановление Правительства РФ от 31 октября 2009 г. N 879 Об утверждении положения о единицах величин, допускаемых к применению в Российской Федерации (неопр.) (недоступная ссылка). Дата обращения 1 июня 2013. Архивировано 2 ноября 2013 года.
4. ↑ «Не допускается применять термин единица измерения физической величины или единица измерения вместо стандартизированного термина единица физической величины или единица, поскольку понятие измерение определяют через понятие единица. Надо писать: ампер — единица силы тока, квадратный метр — единица площади и нельзя писать: ампер — единица измерения силы тока, квадратный метр — единица измерения площади» (Словарь-справочник автора / Сост. Л.А.Гильберг и Л.И.Фрид. — М.: Книга, 1979. — С. 98–99. — 304 с.).
5. ↑ Аналогичная вариативность имеется и в иностранной терминологии. Так, в английском языке наряду с термином unit используется unit of measure(ment): Are, a metric unit of measurement, equal to 100 square metres (Concise Oxford English Dictionary, 11th edition, 2004).
6. ↑ По историческим причинам, название «килограмм» уже содержит десятичную приставку «кило», поэтому кратные и дольные единицы образуют, присоединяя стандартные приставки СИ к названию или обозначению единицы измерения «грамм» (которая в системе СИ сама является дольной: 1 г = 10⁻³ кг).
7. ↑ Абсолютными называются системы, в которых в качестве основных единиц для механических величин приняты единицы длины, массы и времени.
8. ↑ ^{1 2} РМГ 29-99 Рекомендации по межгосударственной сертификации. Основные термины и определения.

Литература[править | править код]

• Кушнир Ф. В. Радиотехнические измерения: Учебник для техникумов связи. — М.: Связь, 1980
• Нефедов В. И., Хахин В. И., Битюков В. К. Метрология и радиоизмерения: Учебник для вузов. — 2006
• Пронкин Н. С. Основы метрологии: Практикум по метрологии и измерениям. — М.: Логос, 2007
• Воронцов Ю. И. Теория и методы макроскопических измерений. — М.: Наука, 1989. — 280 с. — ISBN 5-02-013852-5
• Пытьев Ю. П. Математические методы интерпретации эксперимента. — М.: Высшая школа, 1989. — 351 с. — ISBN 5-06-001155-0

Нормативно-техническая документация[править | править код]