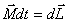Момент силы — Википедия
Момент силы, приложенный к гаечному ключу. Направлен от зрителя
Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению вектора силы и радиус-вектора, проведённого от оси вращения к точке приложения этой силы. Характеризует вращательное действие силы на твёрдое тело.
Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).
Общие сведения
В физике момент силы можно понимать как «вращающая сила». В Международной системе единиц (СИ) единицей измерения момента силы является ньютон-метр. Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метра от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров от оси вращения. Более точно момент силы частицы определяется как векторное произведение:
- M→=[r→×F→],{\displaystyle {\vec {M}}=\left[{\vec {r}}\times {\vec {F}}\right],}
где F→{\displaystyle {\vec {F}}} — сила, действующая на частицу, а r→{\displaystyle {\vec {r}}} — радиус-вектор частицы.
Предыстория
Для того чтобы понять, откуда появилось обозначение момента сил и как к нему пришли, стоит рассмотреть действие силы на рычаг, поворачивающийся относительно неподвижной оси. Работа, совершаемая при действии силы F→{\displaystyle {\vec {F}}} на рычаг r→{\displaystyle {\vec {r}}}, совершающий вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок dl{\displaystyle dl}, которому соответствует бесконечно малый угол dφ{\displaystyle d\varphi }. Обозначим через d→l{\displaystyle {\vec {d}}l} вектор, который направлен вдоль бесконечно малого отрезка dl{\displaystyle dl} и равен ему по модулю. Угол между вектором силы F→{\displaystyle {\vec {F}}} и вектором d→l{\displaystyle {\vec {d}}l} равен β{\displaystyle \beta }, а угол между векторами r→{\displaystyle {\vec {r}}} и F→{\displaystyle {\vec {F}}} — α{\displaystyle \alpha }.
Следовательно, бесконечно малая работа dA{\displaystyle dA}, совершаемая силой F→{\displaystyle {\vec {F}}} на бесконечно малом участке dl{\displaystyle dl}, равна скалярному произведению вектора d→l{\displaystyle {\vec {d}}l} и вектора силы, то есть dA=F→⋅d→l{\displaystyle dA={\vec {F}}\cdot {\vec {d}}l}.
Теперь попытаемся выразить модуль вектора d→l{\displaystyle {\vec {d}}l} через радиус-вектор r→{\displaystyle {\vec {r}}}, а проекцию вектора силы F→{\displaystyle {\vec {F}}} на вектор d→l{\displaystyle {\vec {d}}l} — через угол α{\displaystyle \alpha }.
Так как для бесконечно малого перемещения рычага dl{\displaystyle dl} можно считать, что траектория перемещения перпендикулярна рычагу r→{\displaystyle {\vec {r}}}, используя соотношения для прямоугольного треугольника, можно записать следующее равенство: dl=rtgdφ{\displaystyle dl=r\mathrm {tg} \,d\varphi }, где в случае малого угла справедливо tgdφ=dφ{\displaystyle \mathrm {tg} \,d\varphi =d\varphi } и, следовательно, |dl→|=|r→|dφ{\displaystyle \left|{\vec {dl}}\right|=\left|{\vec {r}}\right|d\varphi }.
Для проекции вектора силы F→{\displaystyle {\vec {F}}} на вектор d→l{\displaystyle {\vec {d}}l} видно, что угол β=α−π2{\displaystyle \beta =\alpha -{\frac {\pi }{2}}}, а так как cos(α−π2)=sinα{\displaystyle \cos {\left(\alpha -{\frac {\pi }{2}}\right)}=\sin \alpha }, получаем, что |F→|cosβ=|F→|sinα{\displaystyle \left|{\vec {F}}\right|\cos \beta =\left|{\vec {F}}\right|\sin \alpha }.
Теперь запишем бесконечно малую работу через новые равенства: dA=|r→|dφ|F→|sinα{\displaystyle dA=\left|{\vec {r}}\right|d\varphi \left|{\vec {F}}\right|\sin \alpha }, или dA=|r→||F→|sin(α)dφ{\displaystyle dA=\left|{\vec {r}}\right|\left|{\vec {F}}\right|\sin(\alpha )d\varphi }.
Теперь видно, что произведение |r→||F→|sinα{\displaystyle \left|{\vec {r}}\right|\left|{\vec {F}}\right|\sin \alpha } есть не что иное, как модуль векторного произведения векторов r→{\displaystyle {\vec {r}}} и F→{\displaystyle {\vec {F}}}, то есть |r→×F→|{\displaystyle \left|{\vec {r}}\times {\vec {F}}\right|}, которое и было принято обозначить за момент силы M{\displaystyle M}, или модуль вектора момента силы |M→|{\displaystyle \left|{\vec {M}}\right|}.
Теперь полная работа записывается просто: A=∫0φ|r→×F→|dφ{\displaystyle A=\int \limits _{0}^{\varphi }\left|{\vec {r}}\times {\vec {F}}\right|d\varphi }, или A=∫0φ|M→|dφ{\displaystyle A=\int \limits _{0}^{\varphi }\left|{\vec {M}}\right|d\varphi }.
Единицы
Момент силы имеет размерность «сила на расстояние» и единицу измерения ньютон-метр в системе СИ. Энергия и механическая работа также имеют размерность «сила на расстояние» и измеряются в системе СИ в джоулях. Следует заметить, что энергия — это скалярная величина, тогда как момент силы — величина (псевдо) векторная. Совпадение размерностей этих величин не случайность: момент силы 1 Н·м, приложенный через целый оборот, совершает механическую работу и сообщает энергию 2π{\displaystyle 2\pi } джоулей. Математически:
- E=Mθ,{\displaystyle E=M\theta ,}
где E{\displaystyle E} — энергия, M{\displaystyle M} — вращающий момент, θ{\displaystyle \theta } — угол в радианах.
Специальные случаи
Формула момента рычага
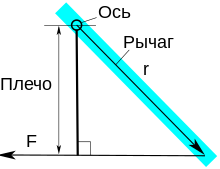 Момент, действующий на рычаг
Момент, действующий на рычагОчень интересен особый случай, представляемый как определение момента силы в поле:
- |M→|=|M→1||F→|,{\displaystyle \left|{\vec {M}}\right|=\left|{\vec {M}}_{1}\right|\left|{\vec {F}}\right|,}
где: |M→1|{\displaystyle \left|{\vec {M}}_{1}\right|} — момент рычага, |F→|{\displaystyle \left|{\vec {F}}\right|} — величина действующей силы.
Недостаток такого представления в том, что оно не дает направления момента силы, а только его величину. Если сила перпендикулярна вектору r→{\displaystyle {\vec {r}}}, момент рычага будет равен расстоянию от центра до точки приложения силы и момент силы будет максимален:
- |T→|=|r→||F→|.{\displaystyle \left|{\vec {T}}\right|=\left|{\vec {r}}\right|\left|{\vec {F}}\right|.}
Сила под углом
Если сила F→{\displaystyle {\vec {F}}} направлена под углом θ{\displaystyle \theta } к рычагу r, то M=rFsinθ{\displaystyle M=rF\sin \theta }.
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для двумерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0,ΣV=0{\displaystyle \Sigma H=0,\,\Sigma V=0} и момент силы в третьем измерении ΣM=0{\displaystyle \Sigma M=0}.
Момент силы как функция от времени
Момент силы — производная по времени от момента импульса,
Видеоурок: вращающий момент- M→=dL→dt,{\displaystyle {\vec {M}}={\frac {d{\vec {L}}}{dt}},}
где L→{\displaystyle {\vec {L}}} — момент импульса.
Возьмём твердое тело. Движение твёрдого тела можно представить как движение конкретной точки и вращения вокруг неё.
Момент импульса относительно точки O твёрдого тела может быть описан через произведение момента инерции и угловой скорости относительно центра масс и линейного движения центра масс.
- Lo→=Icω→+[M(ro→−rc→),vc→].{\displaystyle {\vec {L_{o}}}=I_{c}\,{\vec {\omega }}+[M({\vec {r_{o}}}-{\vec {r_{c}}}),{\vec {v_{c}}}].}
Будем рассматривать вращающиеся движения в системе координат Кёнига, так как описывать движение твёрдого тела в мировой системе координат гораздо сложнее.
Продифференцируем это выражение по времени. И если I{\displaystyle I} — постоянная величина во времени, то
- M→=Idω→dt=Iα→,{\displaystyle {\vec {M}}=I{\frac {d{\vec {\omega }}}{dt}}=I{\vec {\alpha }},}
где α→{\displaystyle {\vec {\alpha }}} — угловое ускорение, измеряемое в радианах в секунду за секунду (рад/с2). Пример: вращается однородный диск.
Если тензор инерции меняется со временем, то движение относительно центра масс описывается с помощью динамического уравнения Эйлера:
- Mc→=Icdω→dt+[w→,Icw→].{\displaystyle {\vec {M_{c}}}=I_{c}{\frac {d{\vec {\omega }}}{dt}}+[{\vec {w}},I_{c}{\vec {w}}].}
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Так же и момент силы, если совершает действие через угловое расстояние, он совершает работу.
- P=M→⋅ω→.{\displaystyle P={\vec {M}}\cdot {\vec {\omega }}.}
В системе СИ мощность P{\displaystyle P} измеряется в Ваттах, момент силы — в ньютон-метрах, а угловая скорость — в радианах в секунду.
Отношение между моментом силы и работой
- A=∫θ1θ2|M→|dθ.{\displaystyle A=\int _{\theta _{1}}^{\theta _{2}}\left|{\vec {M}}\right|\mathrm {d} \theta .}
В случае постоянного момента получаем:
- A=|M→|θ.{\displaystyle A=\left|{\vec {M}}\right|\theta .}
В системе СИ работа A{\displaystyle A} измеряется в джоулях, момент силы — в ньютон·метр, а угол — в радианах.
Обычно известна угловая скорость ω{\displaystyle \omega } в радианах в секунду и время действия момента t{\displaystyle t}.
Тогда совершённая моментом силы работа рассчитывается как:
- A=|M→|ωt.{\displaystyle A=\left|{\vec {M}}\right|\omega t.}
Момент силы относительно точки
Если имеется материальная точка OF{\displaystyle O_{F}}, к которой приложена сила F→{\displaystyle {\vec {F}}}, то момент силы относительно точки O{\displaystyle O} равен векторному произведению радиус-вектора r→{\displaystyle {\vec {r}}}, соединяющего точки O{\displaystyle O} и OF{\displaystyle O_{F}}, на вектор силы F→{\displaystyle {\vec {F}}}:
- MO→=[r→×F→].{\displaystyle {\vec {M_{O}}}=\left[{\vec {r}}\times {\vec {F}}\right].}
Момент силы относительно оси
Момент силы относительно оси равен алгебраическому моменту проекции этой силы на плоскость, перпендикулярную этой оси относительно точки пересечения оси с плоскостью, то есть
- Mz(F)=Mo(F′)=F′h′.{\displaystyle M_{z}(F)=M_{o}(F’)=F’h’.}
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н·м — это момент, который производит сила 1 Н на рычаг длиной 1 м, приложенная к концу рычага и направленная перпендикулярно ему.
Измерение момента силы
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки.
См. также
Момент сил — это… Что такое Момент сил?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
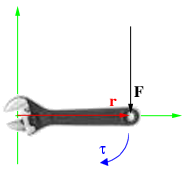
Момент силы приложенный к гаечному ключу
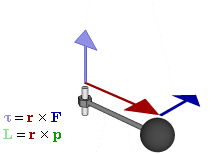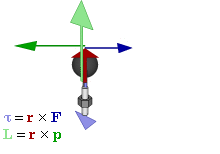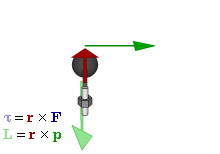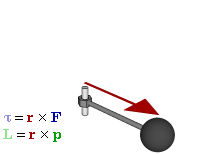
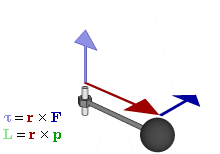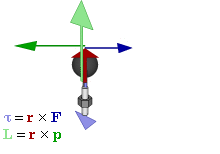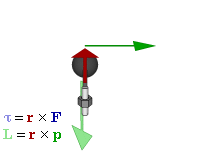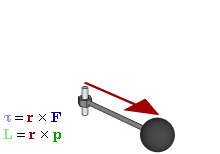
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
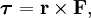
где 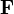 — сила, действующая на частицу, а
— сила, действующая на частицу, а 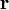 — радиус-вектор частицы!
— радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы 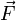 на рычаг
на рычаг 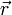 , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
, совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок 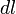 , которому соответствует бесконечно малый угол
, которому соответствует бесконечно малый угол 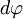 . Обозначим через
. Обозначим через 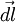 вектор, который направлен вдоль бесконечно малого отрезка
вектор, который направлен вдоль бесконечно малого отрезка 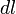 и равен ему по модулю. Угол между вектором силы
и равен ему по модулю. Угол между вектором силы 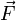 и вектором
и вектором 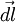 равен
равен 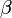 , а угол
, а угол 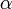
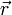 и вектором силы
и вектором силы 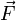 .
.
Следовательно, бесконечно малая работа 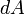 , совершаемая силой
, совершаемая силой 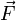 на бесконечно малом участке
на бесконечно малом участке 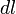 равна скалярному произведению вектора
равна скалярному произведению вектора 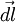 и вектора силы, то есть
и вектора силы, то есть 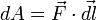 .
.
Теперь попытаемся выразить модуль вектора 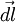 через радиус вектор
через радиус вектор 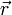 , а проекцию вектора силы
, а проекцию вектора силы 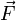
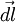 , через угол
, через угол 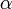 .
.В первом случае, используя теорему Пифагора, можно записать следующее равенство 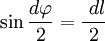 , где в случае малого угла справедливо
, где в случае малого угла справедливо 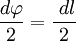
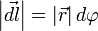
Для проекции вектора силы 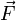 на вектор
на вектор 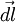 , видно, что угол
, видно, что угол 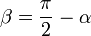 , так как для бесконечно малого перемещения рычага
, так как для бесконечно малого перемещения рычага 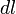
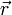 , а так как
, а так как 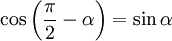 , получаем, что
, получаем, что 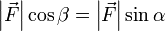 .
.Теперь запишем бесконечно малую работу через новые равенства 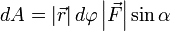
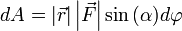 .
.Теперь видно, что произведение 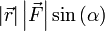 есть ни что иное как модуль векторного произведения векторов
есть ни что иное как модуль векторного произведения векторов 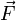 и
и 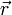 , то есть
, то есть 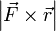
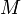 или модуля вектора момента силы
или модуля вектора момента силы 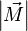 .
.И теперь полная работа записывается очень просто 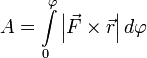 или
или 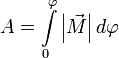 .
.
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
 ,
,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
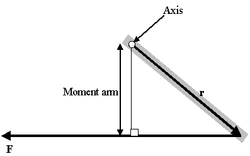
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
 = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
= РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
 ,
,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
 ,
,
То есть если I постоянная, то
 ,
,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
 = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
= МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность 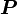 измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
 = МОМЕНТ СИЛЫ * УГОЛ
= МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа  измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость 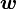 в радианах в секунду и время действия МОМЕНТА
в радианах в секунду и время действия МОМЕНТА 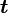 .
.
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
 = МОМЕНТ СИЛЫ *
= МОМЕНТ СИЛЫ *  *
* 
Момент силы относительно точки
Если имеется материальная точка 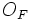 , к которой приложена сила
, к которой приложена сила 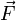 , то момент силы относительно точки
, то момент силы относительно точки 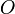 равен векторному произведению радиус-вектора
равен векторному произведению радиус-вектора 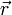 , соединяющий точки O и OF, на вектор силы
, соединяющий точки O и OF, на вектор силы 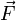 :
:
![\vec M_O = \left[ \vec r \times \vec F \right]](/800/600/https/dal.academic.ru/pictures/wiki/files/48/060f481774ea2ae7875fb856dd7d28d8.png) .
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
Wikimedia Foundation. 2010.
Момент сили — Вікіпедія
Матеріал з Вікіпедії — вільної енциклопедії.
 Момент М0 від сили F
Момент М0 від сили FМоме́нт си́ли — векторна фізична величина, що дорівнює векторному добутку радіус-вектора, проведеного від заданої точки (відносно якої він розраховується) до точки прикладення сили, на вектор цієї сили. Момент сили є мірою зусилля, напрямленого на обертання тіла.
Момент сили зазвичай позначають латинською літерою M{\displaystyle \mathbf {M} } і вимірюють в СІ в Н ⋅{\displaystyle \cdot } м, що збігається із розмірністю енергії.

Момент сили F{\displaystyle \mathbf {F} }, яка діє на матеріальну точку із радіус-вектором r{\displaystyle \mathbf {r} } визначається як
- M0=r×F{\displaystyle \mathbf {M_{0}} =\mathbf {r} \times \mathbf {F} }.
тобто є векторним добутком радіус-вектора r{\displaystyle \mathbf {r} } на силу F{\displaystyle \mathbf {F} }.
Момент сили — це вектор перпендикулярний як до радіус-вектора точки, так і до сили, яка на цю точку діє. За абсолютною величиною момент сили дорівнює добутку сили на плече або
- M0=Frsinα{\displaystyle M_{0}=Fr\sin \alpha \,},
де α — кут між напрямком сили й радіус-вектором точки.
Момент сили адитивна величина, тобто момент сил, що діють на систему матеріальних точок, дорівнює сумі моментів сил, які діють на окремі точки системи.
- M=∑iri×Fi{\displaystyle \mathbf {M} =\sum _{i}\mathbf {r} _{i}\times \mathbf {F} _{i}}
Характерною властивістю момента сили є те, що в останню формулу входять лише зовнішні сили, а взаємодію матеріальних точок між собою можна не враховувати, оскільки згідно із третім законом Ньютона сили, які діють на пару точок рівні за величиною й обернені за напрямком. Враховуючи цей факт, легко показати, що плече таких сил дорівнює нулю.
При обертанні тіла навколо якоїсь осі, природною узагальненою координатою є кут повороту φ{\displaystyle \varphi }.
У цьому випадку момент сили відіграє роль узагальненої сили
- M=∂L∂φ{\displaystyle M={\frac {\partial {\mathcal {L}}}{\partial \varphi }}},
де L{\displaystyle {\mathcal {L}}} — функція Лагранжа.
3. Что называют моментом силы, моментом импульса, моментом инерции? в каких единицах они измеряются?
Момент силы(синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, т.к в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).
Момент силы 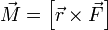
Размерность — L2MT−2
Единицы измерения:
СИ — Ньютон-метр
Моме́нт и́мпульса(кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.
Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, не лежащей на линии движения, оно также обладает моментом импульса. Наибольшую, пожалуй, роль момент импульса играет при описании собственно вращательного движения. Однако крайне важен и для гораздо более широкого класса задач (особенно — если в задаче есть центральная или осевая симметрия, но не только в этих случаях).
Момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — псевдоскаляр.
Момент импульса замкнутой системы сохраняется.
Момент импульса 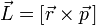
Размерность — L2MT−1
Единицы измерения:
СИ — м2·кг·с−1
СГС — см2·г·с−1
Момент инерции— скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.
Момент инерции 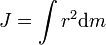
Размерность — L2M
Единицы измерения:
СИ — кг·м²
СГС — г·cм²
4. Вывести основное уравнение динамики вращательного движения
Согласно
уравнению (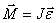 )второй закон Ньютона для вращательного
движения
)второй закон Ньютона для вращательного
движения
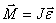
По
определению угловое ускорение  и
тогда это уравнение можно
и
тогда это уравнение можно
переписать следующим образом

с учетом (5.9)

или
| (5.10) |
Это
выражение носит название основного
уравнения динамики вращательного
движения и формулируется следующим
образом: изменение момента количества
движения твердого тела 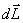 ,
равно импульсу момента
,
равно импульсу момента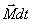 всех
внешних сил, действующих на это тело.
всех
внешних сил, действующих на это тело.
5. Сформулируйте теорему Гюйгенса-Штейнера.
Теоре́ма Гю́йгенса — Ште́йнера, или простотеорема Штейнера(названа по имени швейцарского математика Якоба Штейнера и голландского математика, физика и астронома Христиана Гюйгенса): момент инерции телаIотносительно произвольной оси равен сумме момента инерции этого телаIcотносительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы телаmна квадрат расстоянияdмежду осями:
Inew=Ic+md2,
где m— масса тела,d— расстояние между осями.
Например, Момент инерции стержня относительно оси, проходящей через его центр и перпендикулярной стержню, (назовём её осью C) равен
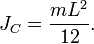
Тогда согласно теореме Штейнера его момент относительно произвольной параллельной оси будет равен
J=JC+md2,
где d— расстояние между искомой осью и осьюC. В частности, момент инерции стержня относительно оси, проходящей через его конец и перпендикулярной стержню, можно найти положив в последней формулеd=L/ 2:
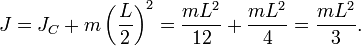
Теорема
Гюйнеса — Штейнера допускает обобщение
на тензор момента инерции, что позволяет
получать тензор  относительно
произвольной точки из тензора
относительно
произвольной точки из тензора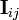 относительно
центра масс. Пусть
относительно
центра масс. Пусть —
смещение от центра масс, тогда
—
смещение от центра масс, тогда
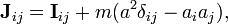
где
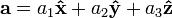 —
вектор смещения от центра масс, а δij—
символ Кронекера.
—
вектор смещения от центра масс, а δij—
символ Кронекера.
Как видно, для диагональных элементов тензора (при i=j) формула имеет вид теоремы Гюйгенса — Штейнера для момента относительно новой оси.
Иллюстрация теоремы для момента площади. 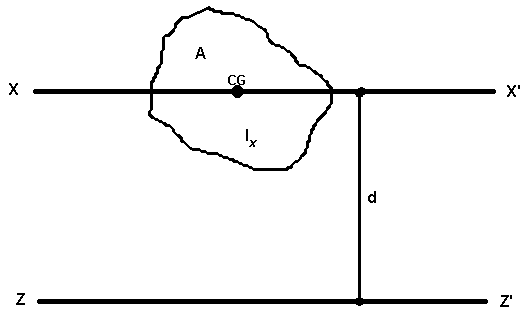
Момент инерции — Википедия
Моме́нт ине́рции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения в Международной системе единиц (СИ): кг·м².
Обозначение: I или J.
Различают несколько моментов инерции — в зависимости от типа базового множества до которого отсчитываются расстояния от элементарных масс.
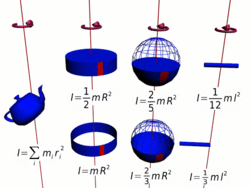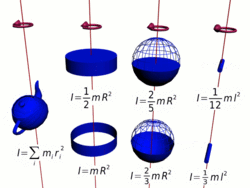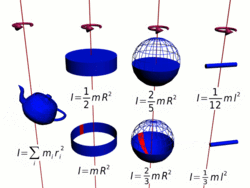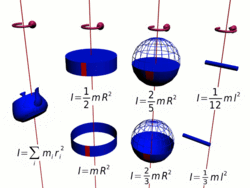 Осевые моменты инерции некоторых тел
Осевые моменты инерции некоторых телМоментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси[1]:
- Ja=∑i=1nmiri2,{\displaystyle J_{a}=\sum _{i=1}^{n}m_{i}r_{i}^{2},}
где:
- mi — масса i-й точки,
- ri — расстояние от i-й точки до оси.
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
- Ja=∫(m)r2dm=∫(V)ρr2dV,{\displaystyle J_{a}=\int \limits _{(m)}r^{2}dm=\int \limits _{(V)}\rho r^{2}dV,}
где:
- dm = ρ dV — масса малого элемента объёма тела dV,
- ρ — плотность,
- r — расстояние от элемента dV до оси a.
Если тело однородно, то есть его плотность всюду одинакова, то
- Ja=ρ∫(V)r2dV.{\displaystyle J_{a}=\rho \int \limits _{(V)}r^{2}dV.}
Теорема Гюйгенса — Штейнера[править | править код]
Момент инерции твёрдого тела относительно какой-либо оси зависит от массы, формы и размеров тела, а также и от положения тела по отношению к этой оси. Согласно теореме Гюйгенса — Штейнера, момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями[1]:
- J=Jc+md2,{\displaystyle J=J_{c}+md^{2},}
где m — полная масса тела.
Например, момент инерции стержня относительно оси, проходящей через его конец, равен:
- J=Jc+md2=112ml2+m(l2)2=13ml2.{\displaystyle J=J_{c}+md^{2}={\frac {1}{12}}ml^{2}+m\left({\frac {l}{2}}\right)^{2}={\frac {1}{3}}ml^{2}.}
Осевые моменты инерции некоторых тел[править | править код]
Вывод формул[править | править код]
Тонкостенный цилиндр (кольцо, обруч)
Вывод формулы
Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобьём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJi. Тогда
- J=∑dJi=∑Ri2dm.(1).{\displaystyle J=\sum dJ_{i}=\sum R_{i}^{2}dm.\qquad (1).}
Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду
- J=∑R2dm=R2∑dm=mR2.{\displaystyle J=\sum R^{2}dm=R^{2}\sum dm=mR^{2}.}
Толстостенный цилиндр (кольцо, обруч)
Вывод формулы
Однородный диск (сплошной цилиндр)
Вывод формулы
Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R1 = 0), получим формулу для момента инерции цилиндра (диска):
- J=12mR2.{\displaystyle J={\frac {1}{2}}mR^{2}.}
Сплошной конус
Вывод формулы
Разобьём конус на тонкие диски толщиной dh, перпендикулярные оси конуса. Радиус такого диска равен
- r=RhH,{\displaystyle r={\frac {Rh}{H}},}
где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска. Масса и момент инерции такого диска составят
- dm=ρdV=ρ⋅πr2dh;{\displaystyle dm=\rho dV=\rho \cdot \pi r^{2}dh;}
- dJ=12r2dm=12πρr4dh=12πρ(RhH)4dh;{\displaystyle dJ={\frac {1}{2}}r^{2}dm={\frac {1}{2}}\pi \rho r^{4}dh={\frac {1}{2}}\pi \rho \left({\frac {Rh}{H}}\right)^{4}dh;}
Интегрируя, получим
- J=∫0HdJ=12πρ(RH)4∫0Hh5dh=12πρ(RH)4h55|0H==110πρR4H=(ρ⋅13πR2H)310R2=310mR2.{\displaystyle {\begin{aligned}J=\int _{0}^{H}dJ={\frac {1}{2}}\pi \rho \left({\frac {R}{H}}\right)^{4}\int _{0}^{H}h^{4}dh={\frac {1}{2}}\pi \rho \left({\frac {R}{H}}\right)^{4}\left.{\frac {h^{5}}{5}}\right|_{0}^{H}=={\frac {1}{10}}\pi \rho R^{4}H=\left(\rho \cdot {\frac {1}{3}}\pi R^{2}H\right){\frac {3}{10}}R^{2}={\frac {3}{10}}mR^{2}.\end{aligned}}}
Сплошной однородный шар
Вывод формулы
Разобьём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле
- r=R2−h3.{\displaystyle r={\sqrt {R^{2}-h^{2}}}.}
Масса и момент инерции такого диска составят
- dm=ρdV=ρ⋅πr2dh;{\displaystyle dm=\rho dV=\rho \cdot \pi r^{2}dh;}
- dJ=12r2dm=12πρr4dh=12πρ(R2−h3)2dh=12πρ(R4−2R2h3+h5)dh.{\displaystyle dJ={\frac {1}{2}}r^{2}dm={\frac {1}{2}}\pi \rho r^{4}dh={\frac {1}{2}}\pi \rho \left(R^{2}-h^{2}\right)^{2}dh={\frac {1}{2}}\pi \rho \left(R^{4}-2R^{2}h^{2}+h^{4}\right)dh.}
Момент инерции шара найдём интегрированием:
- J=∫−RRdJ=2∫0RdJ=πρ∫0R(R4−2R2h3+h5)dh==πρ(R4h−23R2h4+15h5)|0R=πρ(R5−23R5+15R5)=815πρR5==(43πR3ρ)⋅25R2=25mR2.{\displaystyle {\begin{aligned}J&=\int _{-R}^{R}dJ=2\int _{0}^{R}dJ=\pi \rho \int _{0}^{R}\left(R^{4}-2R^{2}h^{2}+h^{4}\right)dh=\\&=\pi \rho \left.\left(R^{4}h-{\frac {2}{3}}R^{2}h^{3}+{\frac {1}{5}}h^{5}\right)\right|_{0}^{R}=\pi \rho \left(R^{5}-{\frac {2}{3}}R^{5}+{\frac {1}{5}}R^{5}\right)={\frac {8}{15}}\pi \rho R^{5}=\\&=\left({\frac {4}{3}}\pi R^{3}\rho \right)\cdot {\frac {2}{5}}R^{2}={\frac {2}{5}}mR^{2}.\end{aligned}}}
Тонкостенная сфера
Вывод формулы
Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:
- J0=25MR2=815πρR5.{\displaystyle J_{0}={\frac {2}{5}}MR^{2}={\frac {8}{15}}\pi \rho R^{5}.}
Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.
- J=dJ0dRdR=ddR(815πρR5)dR==83πρR4dR=(ρ⋅4πR2dR)23R2=23mR2.{\displaystyle {\begin{aligned}J&={\frac {dJ_{0}}{dR}}dR={\frac {d}{dR}}\left({\frac {8}{15}}\pi \rho R^{5}\right)dR=\\&={\frac {8}{3}}\pi \rho R^{4}dR=\left(\rho \cdot 4\pi R^{2}dR\right){\frac {2}{3}}R^{2}={\frac {2}{3}}mR^{2}.\end{aligned}}}
Тонкий стержень (ось проходит через центр)
Вывод формулы
Разобьём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна
- dm=mdrl;dJ=r2dm=mr2drl.{\displaystyle dm={\frac {mdr}{l}};\qquad dJ=r^{2}dm={\frac {mr^{2}dr}{l}}.}
Интегрируя, получим
- J=∫−l/2l/2dJ=2∫0l/2dJ=2ml∫0l/2r2dr=2mlr33|0l/2=2mll324=112ml2.{\displaystyle J=\int _{-l/2}^{l/2}dJ=2\int _{0}^{l/2}dJ={\frac {2m}{l}}\int _{0}^{l/2}r^{2}dr={\frac {2m}{l}}\left.{\frac {r^{3}}{3}}\right|_{0}^{l/2}={\frac {2m}{l}}{\frac {l^{3}}{24}}={\frac {1}{12}}ml^{2}.}
Тонкий стержень (ось проходит через конец)
Вывод формулы
При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l⁄2. По теореме Штейнера новый момент инерции будет равен
- J=J0+mr2=J0+m(l2)2=112ml2+14ml2=13ml2.{\displaystyle J=J_{0}+mr^{2}=J_{0}+m\left({\frac {l}{2}}\right)^{2}={\frac {1}{12}}ml^{2}+{\frac {1}{4}}ml^{2}={\frac {1}{3}}ml^{2}.}
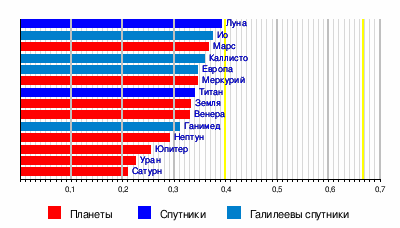
Безразмерные моменты инерции планет и спутников[править | править код]
Большое значение для исследований внутренней структуры планет и их спутников имеют их безразмерные моменты инерции. Безразмерный момент инерции тела радиуса r и массы m равен отношению его момента инерции относительно оси вращения к моменту инерции материальной точки той же массы относительно неподвижной оси вращения, расположенной на расстоянии r (равному mr2). Эта величина отражает распределение массы по глубине. Одним из методов её измерения у планет и спутников является определение доплеровского смещения радиосигнала, передаваемого АМС, пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара — 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра[5][6].
Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины[1][7]:
- Jxy=∫(m)xydm=∫(V)xyρdV,{\displaystyle J_{xy}=\int \limits _{(m)}xydm=\int \limits _{(V)}xy\rho dV,}
- Jxz=∫(m)xzdm=∫
формула, направление, единицы измерения и физический смыл :: SYL.ru
При изучении динамики в физике большое внимание уделяют рассмотрению законов Ньютона применительно к прямолинейному перемещению тел. Тем не менее вращательное движения также играет важную роль в технике и природе. В данной статье ответим на вопрос, связанный с динамикой вращательного движения, разберемся, что такое момент сил.
О какой величине пойдет речь?
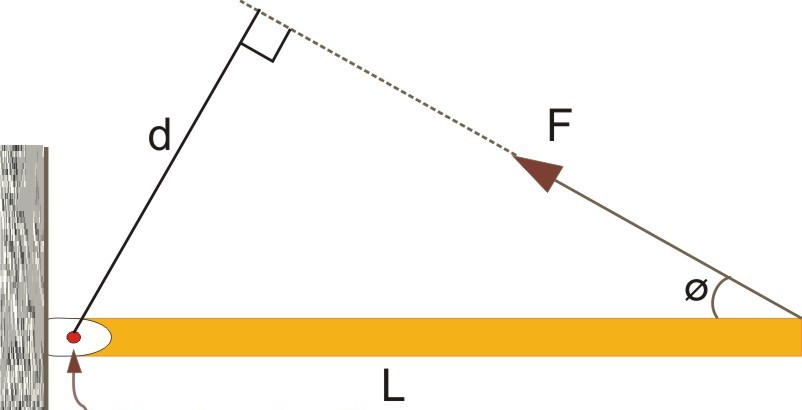
Начнем статью с определения, что такое момент силы. Под ним понимают физическую величину, которая получается, если умножить радиус-вектор на вектор силы. В данном случае речь идет о векторном умножении. Математически момент M¯ записывается так:
M¯ = [r¯*F¯].
Поясним значение каждого множителя в правой части равенства. Радиус-вектор r¯ — это вектор, который направлен от оси вращения к точке приложения внешней силы F¯. Последняя, собственно, действуя на систему, имеющую ось вращения, заставляет ее совершать вращательные движения.
В соответствии с определением векторного произведения, абсолютное значение момента силы может быть вычислено по такой формуле:
M = r*F*sin(φ).
Здесь φ — это угол между векторами r¯ и F¯. Если рассмотреть с точки зрения геометрии эту ситуацию, то можно записать формулу выше в виде:
M = d*F*, где d = r*sin(φ).
Величина d называется плечом момента или плечом силы. Она равна дистанции между осью вращения и вектором силы F¯. От значения плеча зависит возможность силы создать вращательный момент.
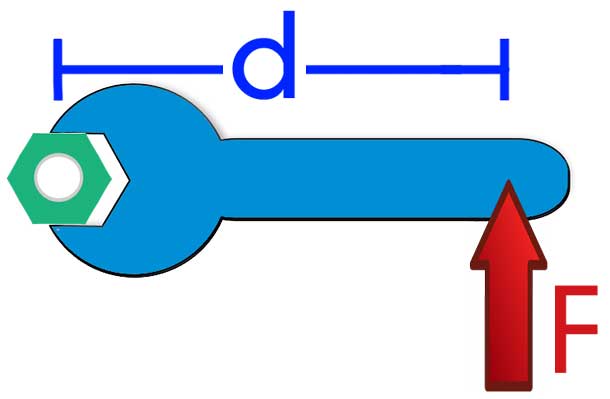
Направление величины M¯
Разобравшись, что такое момент силы в физике, необходимо пояснить, куда он направлен. Как известно, результатом векторного произведения является направленный отрезок, перпендикулярный плоскости, в которой лежат исходные вектора. Например, если речь идет о горизонтальном вращающемся диске на вертикальной оси, то M¯ будет направлен вдоль этой оси. Вверх или вниз — это уже зависит от направления действующей силы. Определить это можно по правилу правой руки: направляя четыре пальца правой руки по ходу вектора r¯ к вектору F¯, оттопыренный большой палец покажет, куда действует момент силы.
Существует еще один способ определения направления величины M¯. Для этого следует представить, что если смотреть с конца вектора M¯ на приложенную силу, то система должна поворачиваться против часовой стрелки. Если же она поворачивается по часовой стрелки, значит, момент направлен в противоположную сторону.
Во время решения задач полагают, что если сила создает вращение против часовой стрелки, то такой момент считается положительным, и наоборот.
Единицы измерения
Раскрывая вопрос о том, что такое момент силы, следует несколько слов сказать о его единицах измерения. Если исходить из формулы, то можно сказать, что рассматриваемая величина измеряется в ньютонах на метр и записывается сокращенно Н*м. Однако, это единица измерения совпадает с работой в физике, которая выражается в джоулях (Дж). Для описания момента сил используют именно Н*м, поскольку джоуль по своему смыслу является энергетической величиной, а не силовой характеристикой.
Если момент силы, действуя на систему, приводит к ее повороту на некоторый угол θ, то произведение этого угла в радианах на M в Н*м даст величину работы в джоулях.
Физический смысл

Выше мы дали математическое определение, что такое момент силы, но практически ничего не сказали о том, какой смысл он несет. Изучаемая величина определяет возможность совершения поворота в системе. Чтобы понять лучше, о какой возможности идет речь, рассмотрим следующий пример: известно, что дверь все открывают за ручку. Сделать это может даже ребенок, поскольку плечо силы d велико, а значит, большим будет и создаваемый крутящий момент. Предлагается читателю попытаться открыть дверь, надавливая на нее близко от петель. В этом случае выполнить задачу гораздо труднее, поскольку для создания того же крутящего момента, необходимо приложить большую силу, компенсирующую маленькое плечо.
Другими примерами момента силы в действии является использование гаечных ключей или удержание человеком веса на вытянутой или на прижатой к телу руке.
Момент силы — Циклопедия
Момент силы — векторная физическая величина, равная векторному произведению радиус-вектора, проведенного от оси вращения до точки приложения силы, на вектор этой силы. Момент силы является мерой усилия, направленного на вращение тела.
Момент силы обычно обозначается латинской буквой [math] \mathbf{M}[/math] и измеряется в СИ в Н·м, что совпадает с размерностью энергии.
Момент силы [math] \mathbf{F} [/math], действующий на материальную точку с радиус-вектором [math] \mathbf{r} [/math] определяется как
- [math] \mathbf{M_0} = \mathbf{r} \times \mathbf{F} [/math].
то есть векторным произведением радиус-вектора [math] \mathbf{r} [/math] на силу [math] \mathbf{F} [/math].
Момент силы — это вектор, перпендикулярный как к радиус-вектору точки, так и к силе, которая на эту точку действует. По абсолютной величине момент силы равен произведению силы на плечо или
- [math] M_0 = Fr \sin\alpha \,[/math],
где α — угол между направлением силы и радиус-вектором точки.
Момент силы — аддитивная величина, то есть момент сил, действующих на систему материальных точек, равен сумме моментов сил, действующих на отдельные точки системы.
- [math] \mathbf{M} = \sum_i \mathbf{r}_i \times \mathbf{F}_i [/math]
Характерным свойством момента силы является то, что в последнюю формулу входят только внешние силы, а взаимодействие материальных точек между собой можно не учитывать, так как по третьему закону Ньютона силы, действующие на пару точек равны по величине и обратны по направлению. Учитывая этот факт, легко показать, что плечо таких сил равно нулю.
[править] Механика Лагранжа
При вращении тела вокруг какой-то оси, естественной обобщенной координатой является угол поворота [math] \varphi [/math].
В этом случае момент силы играет роль обобщенной силы
- [math] M = \frac{\partial \mathcal{L}}{\partial \varphi} [/math],
где [math] \mathcal{L} [/math] — функция Лагранжа.


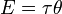 ,
,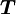 = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
= РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ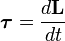 ,
,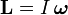 ,
,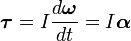 ,
,