формула, чему равна, в каких единицах измеряется

Содержание:

• Что такое энергия заряженного конденсатора
  • Где сосредоточена, в каких единицах измеряется
• Чему равна энергия заряженного конденсатора
  • По какой формуле можно найти
• Применение конденсаторов

Содержание

• Что такое энергия заряженного конденсатора
  • Где сосредоточена, в каких единицах измеряется
• Чему равна энергия заряженного конденсатора
  • По какой формуле можно найти
• Применение конденсаторов

Что такое энергия заряженного конденсатора

Конденсатор состоит из двух проводников, разделенных слоем диэлектрика.

Простейший конденсатор — две металлические пластины-обкладки, расположенные параллельно, с тонкой прослойкой воздуха между ними. Когда заряды пластин противоположны по знаку, электрическое поле оказывается сосредоточено внутри конденсатора и почти не взаимодействует с внешним миром, что позволяет накапливать на пластинах заряд. Для описания работы, которую нужно затратить, чтобы разделить положительные и отрицательные заряды и полностью зарядить конденсатор, вводится понятие энергии.

Энергия заряженного конденсатора равна работе внешних сил, затраченной, чтобы зарядить его.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Где сосредоточена, в каких единицах измеряется

Вся энергия конденсатора сосредоточена в электрическом поле его пластин. Единица измерения СИ — джоуль.

Чему равна энергия заряженного конденсатора

Согласно закону сохранения энергии, энергия заряженного конденсатора равна работе, которую совершит электрическое поле при сближении пластин вплотную.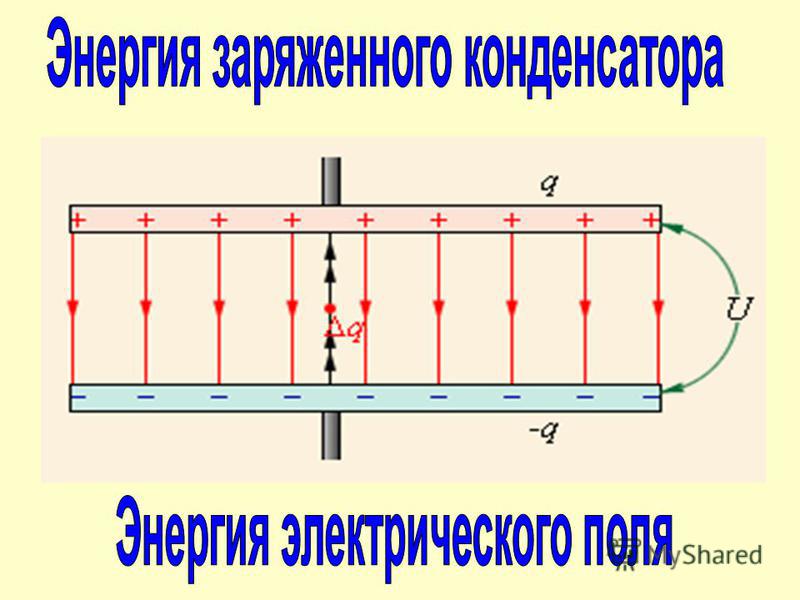

По какой формуле можно найти

Основная характеристика поля, напряженность, создаваемая одной из пластин, равна половине напряженности поля во всем конденсаторе. Заряд q, распределенный по поверхности одной пластины, находится в однородном электрическом поле другой. Потенциальную энергию заряда можно найти по формуле:

\(W_п\;=\;q\frac E2d\)

где Е — напряженность поля во всем конденсаторе, а d — расстояние между пластинами.

В этой формуле могут использоваться другие известные величины, например, разность потенциалов между пластинами, обозначаемая буквой U. Чтобы вычислить ее, нужно умножить напряженность поля Е на расстояние между пластинами d. Тогда формула для вычисления энергии будет иметь вид:

\(W_п\;=\;\frac{qU}2\)

Электроемкость изолированного проводника С равна отношению изменения заряда q к изменению потенциала проводника \(\varphi\). Ее можно найти по формуле:

\(С\;=\;\frac qU\)

Таким образом, для решения задач можно использовать три выражения:

\(W_п\;=\;\frac{qU}2\;=\;\frac{q^2}{2C}\;=\;\frac{CU^2}2\)

Эти формулы справедливы для любого конденсатора, не только для плоского. 2}{2C}\).

 

Применение конденсаторов

Емкость конденсатора не слишком велика, но энергия при разрядке отдается почти мгновенно. Свойство конденсаторов быстро выдавать импульс большой мощности находит применение в лампах-вспышках для фотографирования, электромагнитных ускорителях, импульсных лазерах.Примером может служить генератор Ван де Граафа, позволяющий создавать в лабораторных условиях напряжение в миллионы вольт, чтобы моделировать разряды молний. Также конденсаторы используют в радиотехнике.

Существует тип компьютерных клавиатур, целиком состоящий из конденсаторов под каждой клавишей, при нажатии которой его пластины сближаются. Электронная схема, к которой они подсоединены, распознает, какую клавишу нажали, и передает эту информацию дальше.

Насколько полезной была для вас статья?

Рейтинг: 5.00 (Голосов: 1)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

Энергия конденсатора

Details

01 February 2017

Господа, всем приветище! Сегодня речь пойдет про энергию конденсаторов. Внимание, сейчас будет спойлер: конденсатор может накапливать в себе энергию. Причем иногда очень большую. Что? Это не спойлер, это и так было всем очевидно? Здорово если так! Тогда поехали в этом более подробно разбираться!

В прошлой статье мы пришли к выводу, что заряженный конденсатор, отсоединенный от источника напряжения, может сам в течении некоторого времени (пока не разрядится) давать некоторый ток. Например, через какой-то резистор. По закону Джоуля-Ленца если через резистор течет ток, то на нем выделяется тепло. Тепло – значит, энергия. И берется эта самая энергия из конденсатора – больше, собственно, неоткуда. Значит, в конденсаторе может хранится некоторая энергия. Итак, физика процессов более-менее понятна, поэтому теперь давайте поговорим, как это все описать математически. Потому что одно дело все описать на словах – это круто, замечательно, это должно быть, но в жизни часто надо что-то рассчитать и тут уже обычных слов не достаточно.

Для начала давайте вспомним определение работы из механики. Работа A силы F это произведение этой самой силы F на вектор перемещения s.

Полагаю, что механику вы изучали когда-то и это знаете . Страшные значки векторов нужны только в случае, если направление силы не совпадает с перемещением: вроде случая, когда сила тянет строго прямо, а перемещение идет под каким-то углом к силе. Такое бывает, например, когда груз перемещается по наклонной плоскости. Если же направление силы и перемещения совпадают, то можно смело отбросить вектора и просто перемножать силу на длину пути, получая таким образом работу:

Вспомним теперь статью про закон Кулона. Мы там получили замечательную формулу, которую сейчас самое время вспомнить:

То есть, если у нас есть электрическое поле с напряженностью Е и мы в него помещаем некоторый заряд q, то на этот заряд будет действовать сила F, которую можно рассчитать по этой формуле.

Нам никто не мешает подставить эту формулу в чуть выше написанную формулу для работы. И таким образом найти работу, которую совершает поле при перемещении в нем заряда q на расстояние s. Будем полагать, что мы перемещаем наш заряд q точно по направлению силовых линий поля.  Это позволяет использовать формулу работы без векторов:

Теперь, господа, внимание. Напоминаю одну важную штуку из той же механики. Есть такой особый класс сил, которые называются потенциальные. Если говорить упрощенным языком, то для них верно утверждение, что если эта сила на каком-то отрезке пути совершила работу А, то это значит, что в начале этого пути у тела, над которым совершалась работа, энергия была на это самое А больше, чем в конце. То есть на сколько поработали, на столько и изменилась потенциальная энергия. Работа потенциальных сил не зависит от траектрии и определяется только начальной и конечной точкой. А на замнкнутом пути она вообще равна нулю. Как раз-таки сила электрического поля относится к этому классу сил.

Вот мы помещаем наш зарядик q в поле. Он под действием этого поля перемещается на некоторое расстояние от точки С до точки D. Пусть для определенности в точке D энергия заряда будет равна 0. При этом перемещении поле совершает работу А. Из этого следует, что в начале пути (в точке C) наш зарядик обладал некоторой энергией W=A. То есть, мы можем записать

Теперь самое время рисовать картинки. Взглянем на рисунок 1. Это немного упрощенная иллюстрация физики процессов плоского конденсатора. Более полное мы рассматривали это в прошлый раз.

Рисунок 1 – Плоский конденсатор

Давайте теперь чуть-чуть искривим свое сознание и глянем на наш конденсатор по-другому, чем раньше. Давайте предположим, что у нас за основу взята, например, синяя пластина. Она создает некоторое поле с некоторой напряженностью. Безусловно, и красная пластина тоже создает поле, но в данный момент это не интересно.

Давайте смотреть на красную пластину, как на некоторый заряд +q, расположенный в поле синей пластины. И сейчас мы попробуем применить все вышеописанное к красной пластине как будто это и не пластина вовсе, а просто некоторый заряд +q. Вот так вот хитро. Почему, собственно, нет? Возможно, вы скажите – как же так, раньше мы везде исходили из того, что заряды у нас точечные, а тут – целая большая пластина. Она как-то на точку не совсем тянет. Спокойствие, господа. Никто нам не мешает разбить красную пластину на огромную кучу маленьких частичек, каждую из которых можно считать точечным зарядом Δq. Тогда уже можно без проблем применять все вышеописанное. И если мы выполним все расчеты сил, напряженностей, энергий и прочего для вот таких вот отдельных Δq и потом сложим результаты между собой, то получится, что мы зря так переусердствовали – результат будет ровно таким же, как если бы мы просто при расчетах брали заряд +q. Кто хочет – может проверить, я только за . Однако мы будем сразу работать по упрощенной схеме. Хотелось бы только отметить, что это верно для случая, когда поле у нас однородно и заряды по всем пластинам распределены равномерно.

В действительности это не всегда так, однако такое упрощение позволяет существенно облегчить все расчеты и избежать всяких градиентов и интегралов без существенного вреда для практики.

Итак, вернемся к рисунку 1. На нем показано, что между обкладками конденсатора существует поле с некоторой напряженностью Е. Но мы договорились сейчас разделить роли обкладок – синяя у нас источник поля, а красная – заряд в поле. Какое же поле создает одна синяя обкладка отдельно от красной? Какова его напряженность? Очевидно, что она в два раза меньше общей напряженности. Почема это так? Да потому, что если забыть про нашу абстракцию (типа красная пластина – и не пластина вовсе, а просто заряд), то в результирующую напряженность Е вносят одинаковый вклад обе обкладки – и красная, и синяя: каждая по Е/2. В результате суммы этих Е/2 как раз и получается та самая Е, которая у нас на картинке. Таким образом (отбрасывая вектора), можно записать

Теперь посчитаем, если можно так выразиться, потенциальную энергию красной обкладки в поле синей обкладки. Заряд мы знаем, напряженность мы знаем, расстояние между обкладками тоже знаем. Поэтому смело записываем

Идем дальше. На деле же никто не мешает поменять местами красную и синюю обкладки. Давайте рассуждать наоборот. Будем рассматривать теперь красную обкладку как источник поля, а синюю – как некоторый заряд –q в этом поле. Думаю, даже без проведения расчета будет очевидно, что результат будет точно такой же. То есть энергия красной пластины в поле синей пластины равна энергии синей пластины в поле красной пластины. И, как вы возможно уже догадались, это и есть энергия конденсатора. Да, вот по этой самой формуле можно произвести расчет энергии заряженного конденсатора:

Слышу, как мне уже кричат: стоп, стоп, опять ты втираешь мне какую-то дичь! Ну ладно, расстояние между пластинами я еще как-то смогу измерить. Но меня почему-то опять заставляют считать заряд, что не понятно как сделать, да еще и напряженность надо знать, а чем я ее померяю?! Мультиметр вроде как не умеет это делать! Все верно, господа, сейчас мы займемся преобразованиями, которые позволят вам измерить энергию конденсатора всего лишь с применением обыкновенного мультиметра.

Давайте сперва избавимся от напряженности. Для этого вспомним замечательную формулу, которая связывает напряженность с напряжение:

Да, напряжение между двумя точками в поле равно произведению напряженности этого поля на расстояние между этими двумя точками. Итак, подставляя это полезнейшее выражение в формулу для энергии, получаем

Уже легче, напряженность ушла. Но остался еще заряд, который не понятно как мерить. Что бы от него избавиться, давайте вспомним формулу емкости конденсатора из предыдущей статьи:

Да, для тех, кто забыл, напоминаю, что емкость определяется как отношение этого злополучного заряда, накопленного конденсатором, к напряжению на конденсаторе. Давайте из этой формулы выразим заряд q и подставим его в формулу энергии конденсатора. Получаем

Вот это уже дельная формула, для энергии заряженного конденсатора! Если нам нужно узнать, какая энергия запасена в конденсаторе с емкостью С, заряженного до напряжения U, мы вполне можем это сделать по вот этой вот формуле.

Емкость С обычно пишется на самом конденсаторе или на его упаковке, а напряжение всегда можно измерить мультиметром. Из формулы видно, что энергии в конденсаторе тем больше, чем больше емкость самого конденсатора и напряжение на нем. Причем энергия растет прямо пропорционально квадрату напряжения. Это важно помнить. Увеличение напряжения гораздо быстрее приведет к росту энергии, запасенной в конденсаторе, чем увеличение его емкости.

Для особых любителей зарядов можно из формулы определения емкости выразить не заряд, а напряжение и подставить его в формулу для энергии конденсатора. Таким образом, получаем еще одну формулу энергии

Используется эта формула довольно редко, а на практике вообще не припомню, что б по ней что-то считал, но раз она есть, то путь тут тоже будет для полноты картины. Самая ходовая формула – это средняя.

Давайте для интереса произведем некоторые расчеты. Пусть у нас есть вот такой вот конденсатор

Рисунок 2 – Конденсатор

И давайте мы его зарядим до напряжения, скажем, 8000 В. Какая энергия будет запасена в таком конденсаторе? Как мы видим из фотографии, емкость данного конденсатора составляет 130 мкФ. Теперь легко выполнить расчет энергии:

Много это или мало? Безусловно, не мало! Даже очень не мало! Скажем так, разрешенная энергия электрошокеров составляет какие-то там смешные единицы джоулей, а тут их тысячи! Принимая во внимание высокое напряжение (8кВ) можно смело утверждать, что для человека контакт с таким заряженным конденсатором скорее всего закончится очень и очень печально. Следует соблюдать особую осторожность при больших напряжениях и энергиях! У нас был случай, когда произошло короткое замыкание нескольких таких вот конденсаторов, соединенных параллельно и заряженных до нескольких киловольт. Господа, это было зрелище не для слабонервных! Бабахнуло так, что у меня потом в ушах пол дня звенело! А на стенах лаборатории осела медь от расплавленных проводов! Спешу успокоить, никто не пострадал, но это стало хорошим поводом дополнительно подумать над способами отвода такой гигантской энергии в случае нештатных ситуаций.

Кроме того, господа, важно всегда помнить, что конденсаторы блоков питания приборов тоже не могут мгновенно разрядиться после отключения прибора от сети, хотя там, безусловно, должно быть какие-то цепи, предназначенные для их разряда. Но должны быть, это не значит, что они там точно есть . Поэтому в любом случае после отключения любого прибора от сети, прежде чем лезть к нему внутрь, лучше подождать пару минут для разряда всех кондеров. И потом, после снятия крышки, прежде чем лапками хвататься за все подряд, следует сначала померить напряжение на силовых накопительных конденсаторах и при необходимости выполнить их принудительный разряд каким-нибудь резистором. Можно, конечно, просто отверткой замкнуть их выводы, если емкости не слишком большие, но такое делать крайне не рекомендуется!

Итак, господа, сегодня мы познакомились с различными методами расчета энергии, запасенной в конденсаторе, а также обсудили, как эти расчеты можно выполнять на практике. На этом потихоньку закругляемся. Всем вам удачи, и до новых встреч!

Вступайте в нашу группу Вконтакте

Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.

Social button for Joomla

электростатика — Как рассчитать (или преобразовать) $\rm Втч$ конденсатора, энергия которого выражена в фарадах?

$\begingroup$

При попытке сравнить энергию батареи с энергией конденсатора единицы измерения не совпадают. Как можно сравнить батарею, емкость которой равна 10 Ач, а напряжение равно 3 (всего 30 Втч), с конденсатором, у которого фарады равны X, а напряжение равно Y?

• энергия
• электростатика
• емкость
• единица преобразования
• батареи

$\endgroup$

$\begingroup$

Для начала давайте называть вещи своими именами (без обид). В фарадах измеряется емкость $C$. В $Ач$ измеряется заряд, который может храниться в батарее или конденсаторе.

Из определения емкости заряд на стенках конденсатора емкостью $C$ и разностью потенциалов $V$ равен $$ q = CV $$ так вы получите интересующее вас значение. Однако, если $C$ в фарадах, а $V$ в вольтах, $q$ будет измеряться в кулонах. $$ \text{Ампер} = \frac{\text{Кулон}}{\text{Секунда}} $$ так 92/2 = QV/2$, потому что его напряжение начинается с 0, когда оно не заряжено (в отличие от батареи, где напряжение более или менее постоянно). См. примечание 8 в документе Максвелла, на который вы ссылались, в котором используется эта формула, а затем преобразуется из джоулей в ватт-часы таким же образом, как правильно описано в ответе Бзазза.

$\endgroup$

$\begingroup$

В=J/C

30Втч x 60мин x 60сек = 10800Вс(или Дж)/3В = 3600C

$\endgroup$

2

$\begingroup$

В моем реальном примере мне пришлось оценить то же самое для Maxwell Nesscap UltraCapacitors 2.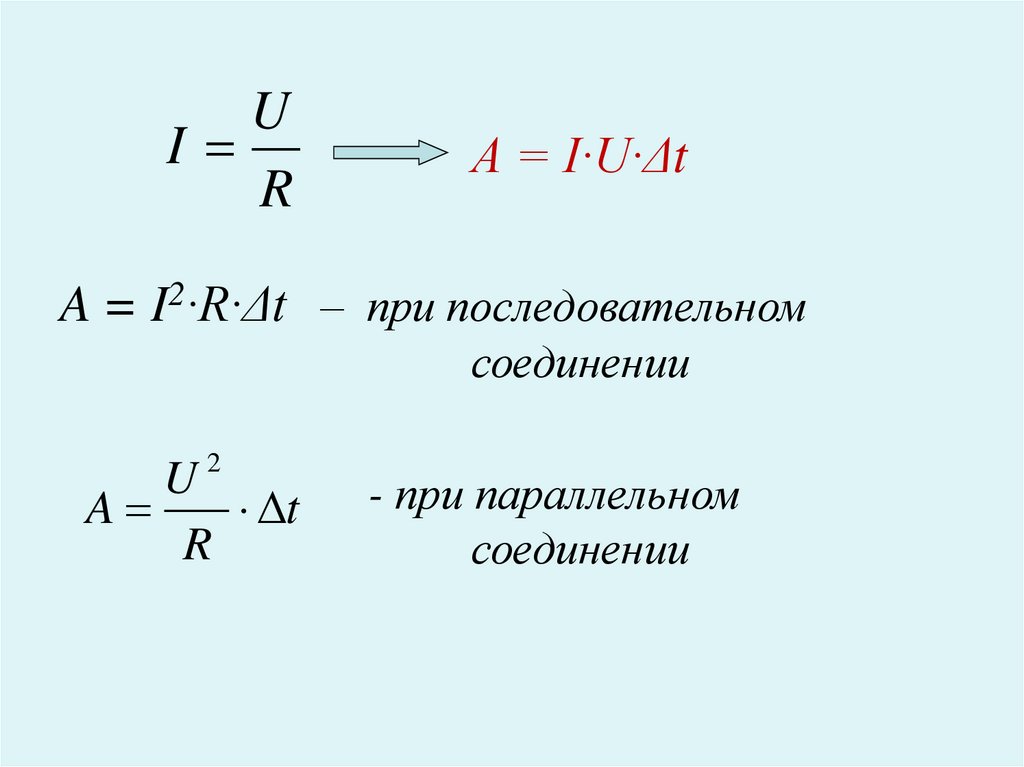 2/2 ** 92 x 3000F/2 = 7,29 x 1500 = 10935 Вт-секунд / 3600 секунд в час = 3,0375 Втч x 18 для всего пакета = 54,675 Втч

Конечно, мне понадобится сильноточный повышающий DC-DC преобразователь, чтобы получить доступ к большей части накопленной энергии и подавать ее выход на контроллер, который заряжает свинцово-кислотные аккумуляторы. В противном случае конденсаторы не разряжались бы почти до 0 В и улавливали остаточный заряд как непригодный для использования.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Физика электричества

Физика электричества

Физика электричества

Заряд (q) ^__ возникает из-за избытка протонов (+) или электронов (-). Единицы — кулоны, которые измеряют сколько превышение + или — заряд есть. Таким образом, кулон является мерой количества заряда в системе. Заряд одного электрона равен 1,602 х 10 ^-19 кулонов.
Ток (I, A) ^__ движение заряда в среде под действием градиента потенциала. В твердых телах (например, в медной проволоке) ток обычно является результатом движения электронов, но в растворах обычно движутся катионы и/или анионы. Так, физиологи будут говорить о «натриевом токе», «калиевом токе», «холидном токе» и т. д. Единицы — ампер (1 ампер = кулон сек ^-1 ). В биологических системах токи обычно измеряются в пикоамперах (1 пА = 10 ^-12 ампер)
Сопротивление (R) ^__ мера того, насколько трудно зарядам (электронам или ионам) двигаться через средний; единицы — Омы. Согласно закону Ома, сопротивление в один Ом создает разность потенциалов в один вольт между двумя точками, если через резистивную среду, соединяющую две точки, проходит ток в один ампер. Сопротивление per se редко используется физиологами, которые обычно предпочитают использовать проводимость .
Проводимость (g) ^__ обратная или обратная величина сопротивления (т. е. g = 1/R = R ^-1 ), проводимость представляет собой меру легкости переноса зарядов (электронов или ионов) двигаться через среду. Единицы измерения — mhos (= инверсия омов. Понятно? Ха, ха, ха! Только это не шутка.) или, что чаще встречается в биологии, Сименс. В биологических системах токи обычно измеряются в пикосименсах (1 пСм = 10 ^-12 Симен)
Потенциал (V, y, E, e) ^__ форма энергии, которая способна вызывать движение зарядов. В биологических системах возникает в результате разделения + и зарядов, обычно по разные стороны барьера, такого как плазматическая мембрана. Определяется по закону Ома:
E = IR
Единицами измерения являются вольты (1 вольт = энергия, необходимая для того, чтобы ток силой 1 ампер прошел через среду, сопротивление которой равно 1 Ом)
Емкость ( C ) ^__ возможность хранить заряд, в частности + и заряды хранятся отдельно друг от друга. Единицы — фарады (1 фарад = 1 кулон-вольт ^-1 ). В биологических системах емкость обычно измеряют в единицах микрофарад (1 мф = 10 ^-6 фарад), а емкость плазматических мембран обычно находится в пределах от 0,8 до 3 мф. Что-то со способностью накапливать заряд называется конденсатором . Когда конденсатор полностью заряжен , выполняется следующее соотношение:
В = q/C
, где V — разность потенциалов между двумя пластинами конденсатора, q — общий заряд, накопленный конденсатором, а C — его емкость. Обратите внимание, что из-за знака равенства изменение параметров на любой стороне изменит значение параметров на другой стороне. Таким образом, изменение значения q изменит значение V, а изменение значения V изменит значение q (C обычно считается постоянным). Это последнее предложение — очень важная концепция, которую следует иметь в виду, когда вы пытаетесь понять мембранные потенциалы.
Мощность (Вт) ^__ мощность , с которой выполняется работа или «используется» энергия. Стандартной единицей измерения является ватт (Вт), который определяется как 1 Дж с ^-1 . В электричестве мы можем выразить 1 ватт как энергию (тепло), выделяющуюся при протекании тока в 1 ампер «через» разность потенциалов в 1 вольт, что позволяет нам рассчитать мощность (в ваттах) из соотношения: ватт = вольт. * текущий
или
W = V*I = V ² /R

R-C Circuit ^__ электрическая цепь, состоящая из конденсатора, соединенного с батареей или другой электродвижущей силой через сопротивление. Электрическое и временное «поведение» RC-цепи определяется емкостью (мкФ) и сопротивлением (Ом) ее компонентов.