{-6}Гц.$ Биения здорового человеческого сердца в спокойном состоянии происходят с частотой 1Гц.

Иногда частоту периодических колебаний обозначают буквой $f$.

Часто в расчётах используют циклическую частоту (угловую частоту, радиальную частоту, круговая частота) ($\omega $), которая равна:

\[\omega =2\pi {\mathbf \nu }\left(2\right).\]

Угловая частота измеряется в радианах, деленных на секунду:

\[\left[\omega \right]=\frac{рад}{с}.\]

В системах СИ и СГС единицы измерения круговой частоты одинаковы.

Секунда в минус первой степени — единица измерения частоты дискретных событий

Частота дискретных колебаний ($n$) — это физическая величина, которая равна количеству действий (событий) в единицу времени. Если время, которое занимает одно событие обозначить как $\tau $, то частота дискретных событий равна:

\[n=\frac{1}{\tau }\left(3\right).\]

Из определения (3) следует, что обратная секунда (секунда в минус первой степени) — единица измерения частоты дискретных событий:

\[\left[n\right]=\frac{1}{с}. \]

Секунда в минус первой степени равна частоте дискретных событий, если за время, равное одной секунде происходит одно событие.

Секунда в минус первой степени — единица измерения частоты вращения

Частота вращения ($n$) — это величина, равная количеству полных оборотов в единицу времени. Если $\tau $ — время, затрачиваемое на один полный оборот, то:

\[n=\frac{1}{\tau }\left(4\right).\]

Секунда в минус первой степени — единица измерения частоты вращения:

\[\left[n\right]=\frac{1}{с}.\]

Обратная секунда (оборот в секунду) — это частота вращения, при которой за время в одну секунду происходит один оборот (цикл вращения). Кроме обратной секунды для обозначения единиц частоты вращения применяют: оборот в минуту или час.

Примеры задач с решением

Пример 1

Задание. Какова частота колебаний пружинного маятника (рис.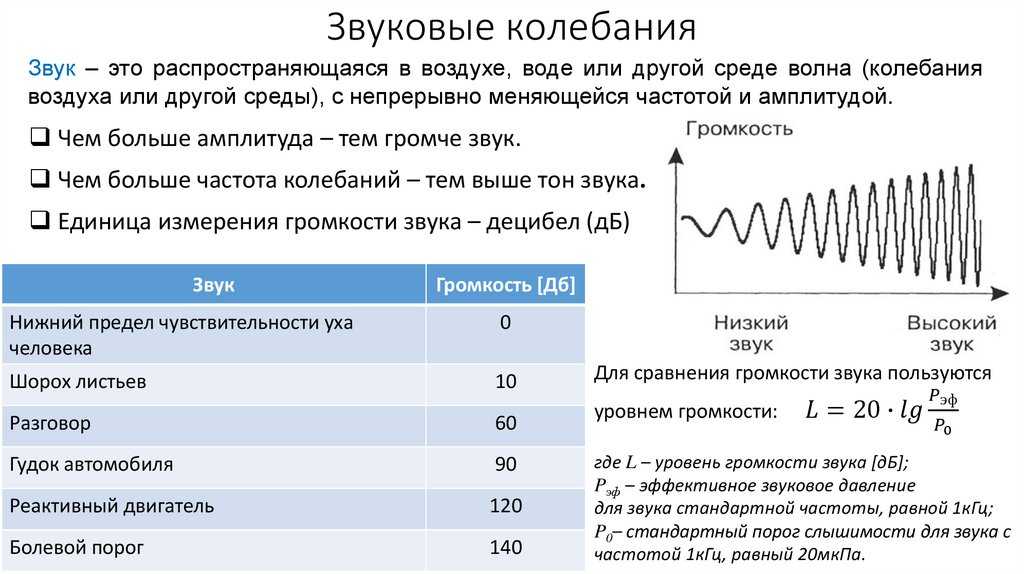 6Гц=4МГц.\]

Ответ. $\nu =4\ МГц$

Читать дальше: единица измерения электрической мощности.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Обозначение герц в физике. Частота, период сигнала, изменения напряжения, силы тока. Периодический. Единицы измерения. Герц, Гц, Hz. Hertz. Доли. килогерц, кгц, мегагерц, мгц. Скорость звука в км в час и метры в секунду

Языке для ее обозначения принято сокращение «Гц», в англоязычной для этих целей применяется обозначение Hz. При этом, по правилам системы СИ, в случае, если употребляется сокращенное название этой единицы, ее следует с , а если в тексте используется полное наименование — то со строчной.

Происхождение термина

Единица измерения частоты, принятая в современной системе СИ, получила свое название в 1930 году, когда соответствующее решение приняла Международная электротехническая комиссия. Оно было связано со стремлением увековечить память знаменитого немецкого ученого- Генриха Герца, который внес большой вклад в развитие этой науки, в частности, в области исследований электродинамики.

Значение термина

Герц применяется для измерения частоты колебаний любого рода, поэтому сфера его использования является весьма широкой. Так, например, в количестве герц принято измерять звуковые частоты, биение человеческого сердца, колебания электромагнитного поля и другие движения, повторяющиеся с определенной периодичностью. Так, например, частота биения сердца человека в спокойном состоянии составляет около 1 Гц.

Содержательно единица в данном измерении интерпретируется как количество колебаний, совершаемых анализируемым объектом в течение одной секунды. В этом случае специалисты говорят, что частота колебаний составляет 1 герц. Соответственно, большее количество колебаний в секунду соответствует большему количеству этих единиц. Таким образом, с формальной точки зрения величина, обозначаемая как герц, является обратной по отношению к секунде.

Значительные величины частот принято называть высокими, незначительные — низкими. Примерами высоких и низких частот могут служить звуковые колебания различной интенсивности. Так, например, частоты, находящиеся в диапазоне от 16 до 70 Гц, образуют так называемые басовые, то есть очень низкие звуки, а частоты диапазона от 0 до 16 Гц и вовсе неразличимы для человеческого уха. Самые высокие звуки, которые способен слышать человек, лежат в диапазоне от 10 до 20 тысяч герц, а звуки с более высокой частотой относятся к категории ультразвуков, то есть тех, которые человек не способен слышать.

Для обозначения больших величин частот к обозначению «герц» добавляют специальные приставки, призванные сделать употребление этой единицы более удобным. При этом такие приставки являются стандартными для системы СИ, то есть используются и с другими физическими величинами. Так, тысяча герц носит название «килогерц», миллион герц — «мегагерц», миллиард герц — «гигагерц».

Резонансный метод измерения частот.

Метод сравнения частот;

Метод дискретного счета основывается на подсчете импульсов необходимой частоты за конкретный промежуток времени. Его наиболее часто используют цифровые частотомеры, и именно благодаря этому простому методу можно получить довольно точные данные.

Более подробно о частоте переменного тока Вы можете узнать из видео:

Метод перезаряда конденсатора тоже не несет в себе сложных вычислений. В этом случае среднее значение силы тока перезаряда пропорционально соотносится с частотой, и измеряется при помощи магнитоэлектрического амперметра. Шкала прибора, в таком случае, градуируется в Герцах.

Погрешность подобных частотомеров находится в пределах 2%, и поэтому такие измерения вполне пригодны для бытового использования.

Способ измерения базируется на электрическом резонансе, возникающем в контуре с подстраиваемыми элементами. Частота, которую необходимо измерить, определяется по специальной шкале самого механизма подстройки.

Такой метод дает очень низкую погрешность, однако применяется только для частот больше 50 кГц.

Метод сравнения частот применяется в осциллографах, и основан на смешении эталонной частоты с измеряемой. При этом возникают биения определенной частоты. Когда же этих биений достигает нуля, то измеряемая становится равной эталонной. Далее, по полученной на экране фигуре с применением формул можно рассчитать искомую частоту электрического тока.

Ещё одно интересное видео о частоте переменного тока:

М ир един и целостен, и каждая его часть является фрагментарным отображением всего общего в малом.

Частота 432 Гц является альтернативной настройкой, которая находится в соответствии с гармониками Мироздания.

Музыка на основе 432 Гц обладает благотворной целительной энергией, потому что это чистый тон математической основы природы.

Архаичные египетские инструменты, которые были обнаружены до сих пор, в основном, были настроены на 432 Гц.

В Древней Греции музыкальные инструменты были преимущественно настроены на 432 Гц. В архаических греческих мистериях Орфей являлся богом музыки, смерти и возрождения, а также хранителем Амброзии и музыки трансформации (его инструменты были настроены на 432 Hz). И это не случайно, древние знали о единстве Мироздания больше, нежели современники.

Текущая настройка музыки на основе 440 Гц не гармонирует ни на одном уровне и не соответствует космическому движению, ритму или естественной вибрации.

Когда же произошло замещение частоты 432 Гц на 440 Гц?

Впервые попытка массово изменить волны произошла в 1884, но усилиями Дж.Верди сохранили прежний строй, после чего и стали настройку “Ля”=432 Гц именовать «Вердиевским строем».

Позднее Дж. К.Диген, служащий в ВМС США, ученик физика Германа Хелмхольца, в 1910 году убедил Американскую Федерацию Музыкантов в её ежегодном собрании принять A=440 Гц, как стандартный универсальный строй для оркестров и музыкальных групп. Он был профессионалом в области астрономии, геологии, химии, изучал многие разделы физики, особенно теории света и звука. Его мнение являлось основополагающим при изучении музыкальной акустики. Дж.К.Диген спроектировал военный перезвон на 440 Гц, который использовался для пропагандистских новостей во время Второй мировой войны.

Так же, незадолго до Второй мировой войны, в 1936 году, министр нацистского движения и тайный лидер в управлении массами П. Й. Геббельс пересмотрел стандарт на 440 Гц — частоту, которая сильнее всего воздействует на мозг человека и может быть использована для управления большим количеством людей и пропаганды нацизма. Это объяснялось тем, что, если лишить человеческий организм естественной настройки, и поднять натуральный тон немного выше, то мозг будет регулярно получать раздражение. Кроме того, люди перестанут развиваться, появится множество психических отклонений, человек начнет закрываться в себе, и им станет гораздо легче руководить. Это явилось основной причиной, по которой нацисты приняли новую частоту ноты «Ля».

Около 1940г. власти США ввели настрой в 440 Гц во всём мире, и, наконец, в 1953 году он стал ISO 16-стандартом. Замена частоты 432 Гц на 440 Гц объясняется : войной Фонда Рокфеллера по контролю сознания путем замены и наложения частоты 440 Гц вместо стандартной настройки.

440 Гц являются неестественным стандартом настройки, и музыка в частоте 440 Гц конфликтует с . Музыкальная индустрия использует введение этой частоты для влияния на население, чтобы добиться большей агрессии, психо-социальной ажитации и эмоционального дистресса, приводящего людей к физическим болезням. Такая музыка также может генерировать нездоровые эффекты или антиобщественное поведение, разлад в сознании человека.

Наука киматика (изучающая визуализацию звука и вибрации) доказывает, что частота и вибрация являются мастер-ключами и организационной основой для создания всей материи и жизни на этой планете. Когда звуковые волны движутся на физическом носителе (песок, воздух, вода и т.д.), частота волн имеет непосредственное отношение к формированию структур, которые создаются звуковыми волнами, когда они проходят через определённую среду, такую как, например, человеческое тело, которое состоит на более чем 70% из воды!

Сравнение частот можно видеть на картинке.

Спецоперация по смене классической частоты музыки 432 на 440

Что мы знаем о ноте “Ля” 432 Гц? Думаю, не так много, ведь с тех пор, как “Международная Организация по Стандартизации (ISO)” приняла строй “Ля” 440 Гцгерц, как основной — концертный, прошло уже 58 лет.

Строй в 432 Гц уже никто не играет.

Музыканты, исполняющие произведения эпохи барокко, предпочитают “Ля” — 415 Гц, которая чаще всего использовалась до эпохи классицизма. Современные музыканты чаще используют 440-442 Гц, а иногда и выше, как наиболее привычный и удобный строй. Но долгий период в музыкальной истории использовалась именно нота “Ля” частотой — 432 Гц.

Даже после принятия стандарта, в 1953 году, 23 тысячи музыкантов из Франции провели референдум в поддержку «Вердиевского» строя 432 Герца, но были вежливо проигнорированы. Откуда появилась “Ля” 440 Гц, и почему именно она заменила столь долго просуществовавшую аналогичную ноту 432 Гц?

Строй 432 существовал еще в Древней Греции, начиная от Платона, Гиппократа, Аристотеля, Пифагора и др. великих мыслителей и философов античности, которые, как известно, обладали бесценными знаниями о целебном воздействии музыки на человека и вылечивали многих людей именно силой музыки!

С какой ноты начинается классический звукоряд? С ноты “До”, не так ли!? Так вот, нота “До” в данном строю будет равна 512 Гц, на октаву ниже 256 Гц, ещё ниже — 128-64-32-16-8-4-2-1. Т.е. самая низкая нота будет равна одной вибрации в секунду, соответственно, это и есть первая нота звукоряда!

Величайший скрипичный мастер всех времен — Антонио Страдивари (секрет мастерства создания инструментов которого не раскрыт до сих пор), создавал свои шедевры именно в настройке 432 Гц! Звучание 432 гораздо спокойнее, теплее и ближе. Его чувствуешь всем сердцем.

Запрещенная частота 432 Гц

Несмотря на контроль, установленный иллюминатами со времен Гельмгольца и нациста Геббельса в том, что касается замены частоты 432 на 440, музыканты продолжают играть в независимой обстановке на частоте 432. Потому что идет уменьшение растяжения по струнам, барабанщик таким образом ослабляет немного кожу барабана, клавишнику легче настроиться на контроль.

Геббельс знал, что частота 432 имеет совершенный гармонический баланс. Это единственная частота, которая вызывает пифагорейскую музыкальную спираль, содержащую в себе знаменитый и неразгаданный КОД ПЛАТОНА.

Правда, недавно американский математик и историк науки Джей Кеннеди, который работает в Манчестерском университете в Великобритании, объявил, что взломал тайный код, скрытый в произведениях древнегреческого философа Платона. Как утверждает Кеннеди, Платон разделял пифагорейские представления о музыке сфер — неслышной музыкальной гармонии мироздания — и свои произведения строил по законам музыкальной гармонии.

«Один из самых знаменитых платоновских диалогов, “Государство”, разделён на двенадцать частей, по числу звуков в хроматической музыкальной гамме, представления о которой были у древних греков. Причём на каждый стык приходятся фразы, так или иначе относящиеся к музыке или звукам », — заявил исследователь.

Что собой представляют древние частоты сольфеджио? Это оригинальные звуковые частоты, используемые в древних григорианских песнопениях, например, таких как великий гимн Св. Иоанна Крестителя. Многие из них, как утверждают церковные власти, были потеряны много веков назад.

Эти мощные частоты были обнаружены доктором Джозефом Пулео. Это описано в книге «Целительные коды для биологического апокалипсиса» доктора Леонарда Горовица.

• До — 396 Гц — Освобождение от чувства вины и страха
• Ре — 417 Гц — Нейтрализация ситуаций и содействие изменениям
• Ми — 528 Гц — Трансформация и чудеса (восстановление ДНК)
• Фа — 639 Гц — Подключение и отношения
• Соль — 741 Гц — Пробуждение Интуиции
• Ля — 852 Гц — Возвращение к духовному порядку.

Частота 432 получается интересным образом 700: PHI = 432.624 Или вот 24 часа x 60 минут x 60 секунд = 864 | 000 864 / 2 = 432

Окружающая нас музыка не только отвлекает наше сознание, но и в обход него загружается напрямую в подсознание, трансформируя скрытую в нём информацию таким образом, чтобы людьми можно было управлять.

Параметры, значения которых выражены в герцах, можно встретить в технических характеристиках различных устройств: компонентов компьютера, радиоприемников, измерительного оборудования – везде, где протекают переменные электрические сигналы. Тем не менее не задумываясь ответить на вопрос, что измеряется в герцах, может не каждый.

Герц (Гц) – производная единица СИ, служащая для выражения частоты периодических, то есть повторяющихся через определенный промежуток времени, процессов. Численное значение этой величины означает количество реализаций указанного процесса за секунду, что математически можно записать как 1 Гц=1/с=с -1 . В герцах можно количественно оценить частоту явлений любой физической природы, будь то изменение от времени тока в бытовой электросети, сокращения сердечной мышцы, колебания качелей, возникновение импульсов или распространение звуковых волн.

Наиболее просто понять смысл единицы измерения, о которой идет речь, на примере синусоидальных зависимостей сигналов от времени. На картинке представлены графики звуковых колебаний различной частоты. На первом рисунке за промежуток, равный секунде, возникает одно максимальное значение волны, а на втором – десять. То есть появление одних и тех же состояний параметров процесса в последнем случае происходит в десять раз чаще ­– с частотой 10 Гц.

Передача данных в системах связи, распространение звуковых волн и многие другие процессы могут характеризоваться частотами на несколько порядков больше, чем 1 Гц. Поэтому с данной единицей измерения применяются стандартные приставки СИ, обозначающие кратные величины (1 кГц=10 3 Гц, 1 МГц=10 6 Гц и другие).

Помимо герца существует еще одна единица измерения, которая соответствует 1/с или с -1 – беккерель. В отличие от первой, служащей для описания периодических сигналов, эта величина характеризует активность источников радиоактивного распада, который представляет собой случайный процесс.

Приведем несколько занимательных фактов по теме статьи.

• Примерный диапазон частот звуков, слышимых человеком, составляет от 20 Гц до 20 кГц. Причем с возрастом верхняя граница смещается в сторону уменьшения – большинство людей постепенно теряют способность восприятия высоких звуков.
• В России и странах Европы частота переменного тока в электросетях равна 50 Гц, в США, Канаде – 60 Гц, а в Японии, в зависимости от региона, данный параметр сети может быть равен и 50, и 60 Гц.
• Сердце здорового человека, не испытывающего значительных физических нагрузок, бьется с частотой, равной примерно 1 Гц.
• FM-диапазон радиовещания составляет от 87,5 до 108 МГц, частота электромагнитных волн, генерируемых для приготовления и разогрева пищи в СВЧ-печи, – 2450 МГц.

Когда, как и зачем физики визуализировали звук / Хабр

Всю школу и универ я прошла с установкой «точные науки — не моё». Сейчас мне интересно «доучиться», закрыть пробелы в математике, химии, физике.

Школьная физика для меня — это задачи, где надо выписать дано, привести единицы измерения, записать решение и ответ. О физике с точки зрения «когда и как люди до этого дошли», я не задумывалась, пока не наткнулась на лекцию физика-теоретика Игоря Иванова «Звучащий мир: голос, ультразвук, терагерцы». Я сделала конспект его лекции.

Игорь Иванов — физик-теоретик, кандидат физико-математических наук, старший научный сотрудник Лаборатории ядерных проблем Объединенного института ядерных исследований (Дубна).

В этот раз конспект подробный, минут на 20 чтения.

Базовые понятия звука

Звуковые колебания — это колебания той среды, в которой распространяется звук. Это по сути волны сгущения и разрежения, которые движутся вперёд, как вы видите на анимации:

У среды, скажем, у воздуха, есть средняя плотность, среднее давление. Когда в среде распространяется звуковая волна, то ее плотность и давление колеблются относительно среднего значения. Можно нарисовать график плотности, это будет периодическая кривая.

Волна заключается в том, что это кривая не просто стоит, а движется вперед во времени.

Звук, звуковые колебания — это периодический процесс, причем периодичность у него есть как и во времени, так и в пространстве. Это важная характеристика волны, а не просто колебания.

Периодичность во времени описывается с помощью периода Т, то есть через сколько времени колебания повторяются. Но удобнее периодичность описывать с помощью частоты, это обратная характеристика ко времени.

Если период составляет одну миллисекунду, то есть одну тысячную секунды, то обратная величина, частота, составляет 1000 герц или 1 килогерц, кГц, МГц и т.д. — это высокие частоты звуковых колебаний.

Периодичность в пространстве описывается длиной волны, то есть через какую дистанцию в пространстве волна повторяет сама себя. На рисунке это расстояние между двумя одинаковыми впадинами волны или одинаковыми буграми волны.

Звуковая волна в веществе может идти в разные стороны, необязательно вдоль какого-то удобного направления.

Квадрат из точек в правом углу рисунка — двухмерный кристалл, в котором есть волны сгущения и разрежения и даже изгибные волны. Всё это дело вместе по диагонали бежит вперёд.

Точки гуще — фронты сгущения, там где реже — фронты разряжения. Волна бежит перпендикулярно этим фронтам. Длина волны — это расстояние между двумя одинаковыми фазами колебания, между линиями сгущения и линиями разряжения.

Две периодичности, в пространстве и во времени, связаны друг с другом. Длина волны связана с периодом через скорость звука. Скорость волны, в данном случае, — скорость звука. Вместо периода можно поставить частоту и тогда связь получается вот такая:

λ = с T = с / f

Скорость звуковой волны практически не меняется. Она почти не зависит от частоты или длины волны, зато она зависит от среды, в которой распространяется волна.

В нормальных условиях, при обычной температуре и обычном давлении, скорость звука в воздухе составляет примерно 340 м/с.

В воде скорость примерно в 5 раз больше, ≈1,5 км/с. В твёрдых телах скорость может быть несколько километров в секунду.

У волн есть поляризация. Бывают продольные волны, бывают поперечные.

Продольные волны — это волны, в которых сами частички колеблются в том направлении, вдоль которого бежит волна.

Поперечные волны — это, когда частички колеблются поперек направления, вдоль которого бежит волна.

Обычный звук в воздухе или в воде — это продольный звук. А в твёрдом теле, поскольку у него есть упругость на изгиб, может распространяться звук и в виде поперечной волны, как нарисовано справа. 13 Гц. Это много, примерно 10 терагерц. Так что есть смысл обсуждать звук в твёрдом теле с частотами вплоть до нескольких ТГц.

В воздухе ситуация другая. Там молекулы не «держатся» друг за друга, они свободно летают и иногда сталкиваются. В качестве минимальной длины волны нужно брать не расстояние между молекулами, а среднюю длину пробега для молекул в воздухе. При нормальных условиях она около сотни нанометров.

Подставив в ту же формулу это расстояние, мы получаем максимальную частоту звука в воздухе несколько ГГц — на три порядка ниже, чем в твёрдом теле.

В сплошных телах или в жидкости у нас бывает намного более частотный, высокочастотный звук, чем в воздухе.

Даже 1 ГГц в воздухе толком не распространяется, а тут же затухает превращаясь тепловые колебания. Когда мы говорим про очень высокие частоты, про звук в воздухе говорить не очень осмысленно.

Наконец, у звука есть ещё одна очень важная вещь. Это его профиль по времени.

Звук — это более-менее периодическое колебание, оно повторяется, точно или не точно — не важно. Главное, что повторяется. Но внутри каждого периода есть профиль колебания, он может быть очень сложным.

В таком профиле закодировано всё богатство звучания голоса человека или инструментов.
Как именно наше ухо и наш мозг восстанавливает это звучание — это отдельный разговор.

Сложный профиль можно разложить на сумму простых колебания разных частот. У периодического колебания всегда есть основная частота, на основную частоту накладываются кратные частоты — двукратные, трёхкратный и так далее. И вместе они суммируясь, дают сложный профиль.

Для примера. Здесь я поигрался с программой для изучения звуков Praat:

Я записал два звука собственного голоса на одинаковой основной частоте. Это звуки «А» и «И». Частоты здесь примерно одинаковые — 150 герц. То есть в 26 миллисекунд попадает примерно 4 периода. И вы видите насколько профили отличаются.

В этом звучании закодирован как-то звук «А» и звук «И», которые мы чувствуем по-разному, воспринимаем по-разному. В этих же мелких колебаниях зашифрован тембр голоса.

Можно подумать, что основная частота очень важна для восприятия речи. На самом деле нет. Вы можете полностью вырезать основную частоту, и всё равно будете хорошо воспринимать речь человека. Так происходит, когда мы говорим шёпотом. Звуки определяются высокочастотными колебаниями внутри этого профиля.

Ранняя история акустики

В XVIII-XIX века люди научились визуализировать звук.

Изобретение фотографии было шокирующим для публики открытием, люди не думали, что можно захватить свет и зафиксировать его надолго. Зафиксировать звук кажется ещё более сложной задачей, потому что звук мы не видим.

Исследователи понимали, что звук это колебания. Похоже, человек начал исследовать звук ещё в эпоху античности.

Пифагор и его ученики интересовались звучанием музыкальных инструментов, потому что для Древней Греции музыка была важным элементом. Они выяснили, что струны, которые имеют кратные длины, производят гармоничные звуки.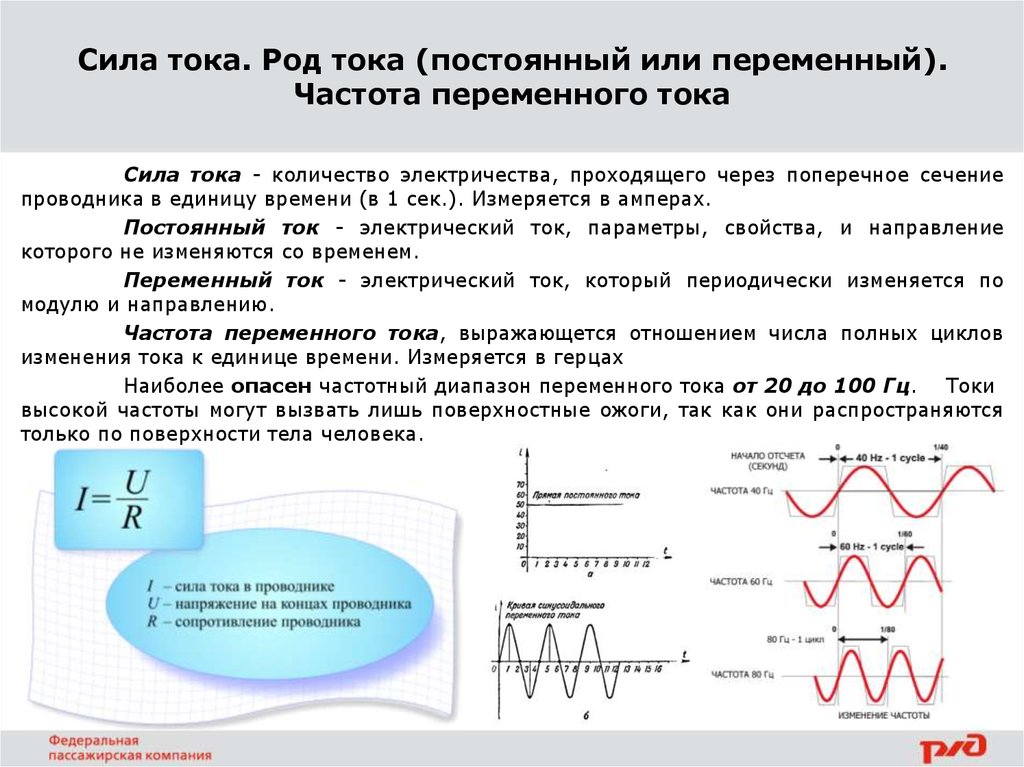 Это для Пифагора стало важным подтверждением, что всё в нашем мире можно свести к целым числам.

Аристотель тоже исследовал звук. Он впервые указал, что звук может распространяться не только в воздухе, но и в воде. В это время люди понимали, что есть связь между колебаниями и звуком.

Это не очевидно, когда мы слышим звук, мы не слышим пульсаций. Обычный звук — это просто звук какой-то частоты, который как-то меняется во времени, но мы не слышим сами колебания.
Леонардо да Винчи исследовал звук и убедился, что звук в воде распространяется намного дальше, чем воздухе. В 1490 году он описал опыт, что если в спокойной воде остановиться и опустить трубочку, то можно услышать звук корабля, который находится так далеко, что мы его не видим и не слышим через воздух, но можем услышать через воду.

Исследования звуковых колебаний начались в XVII веке: Френсис Бэкон, Галилео Галилей.
Первый, кто с помощью формул связал высоту звукового колебания с частотой, был Марен Мерсенн. В 1636 году он построил теорию звуковых колебаний, вывел формулу колебаний струны в зависимости от её длины и высоты. Он впервые измерил скорость звука в воздухе, она правда у него получилось чуть больше — 450 м/с.

В начале XVIII века результаты Мерсенна перепроверил и уточнил исследователь Жозеф Совёр, который ввёл термин «акустика».

Совёр говорил, что до этого люди изучали звучания музыкальных инструментов. Их интересовали звуки с точки зрения благозвучия. Жозеф Совёр считал, что есть смысл исследовать звуки сами по себе, как природное явление.

Он измерил скорость звука своим способом. Совёр достаточно точно смог сопоставить высоту ноты, которую мы слышим, с частотой колебаний. Сделал он это с помощью явления, которое называется «биение».

Когда у нас звучит какая-то нота на определенной частоте, то мы слышим «сплошное» звучание, условный писк на какой-то частоте. Если у нас есть два источника звука на двух близких частотах, то они накладываются друг на друга, их одновременное звучание порождает интересный эффект.

Появляется не просто какая-то средняя нота, появляется звук, который становится то громче, то тише. Это и есть «биение». Нота как будто пульсирует, эти пульсации происходят медленнее, чем сами колебания и мы можем их посчитать. Так люди начали измерять частоты, которые напрямую не смогли бы измерить.

С помощью биения и разных инструментов, которые его используют, например, камертона, люди научились измерять частоты колебаний: струн, голоса.

Исследования Совёра привели к созданию серии из настроенных камертонов, которые назывались тонометры. По ним бы можно было настраивать музыкальные инструменты.

В конце XVII века было понятно, что звук — это колебания, там есть частоты, эти частоты соответствуют воспринимаемый высоте звука. Не было понятно, как именно внутри каждого периода колеблется звук, непонятно до каких частот человек может слышать.

Возникла задача не измерить частоту звучания, которую производит музыкальный инструмент, а наоборот, получить звук при заданной частоте.

В 1830 году французский физик Феликс Савар построил зубчатую машину, которая как раз решала эту задачу.

В ней было несколько колёс, рукоятка и ременная передача. У колеса были зубчики, когда человек вращал одну рукоятку, то зубчики могли с очень высокой частотой задевать пластинку, когда они задевали пластинку, к примеру, тысячу раз в секунду, они порождали звук на этой частоте. Зная скорость вращения и количество зубчиков, Феликс Савар мог исследовать, какой частоты звук человек слышит.

После несколько экспериментов, он убедился, что начиная примерно с 24 кГц, человек перестает слышать звук. Фактически, он впервые получил ультразвук руками.

24 кГц, как верхний предел доступного для слуха диапазона — это очень близко к современному пониманию, около 20 кГц.

В течении всего XIX века исследователи акустики независимо пытались измерить верхнюю частоту доступного слуху диапазона, и получали сильно разные оценки.

В конце XIX века Гельмгольц, один из отцов современной акустики, получил значения почти в 40 килогерц. Он ошибался.

Кёниг зафиксировал значение около 20 килогерц и убедился, что верхний порог снижается с возрастом: у детей он выше, но по мере взросления снижается.

Сейчас есть музыканты, которые используют современные вариации колеса Савара как музыкальный инструмент.

Стало понятно соотношение между высотой звука и частотой, но всё равно не было понятно, что происходит внутри каждого колебания, что представляет из себя звуковой профиль, чем отличаются разные звуки друг от друга.

Звуковой профиль надо было визуализировать. Но звук не видно. И звук — это очень быстро, нужно что-то показывать с частотой в тысячи, десятки тысяч раз в секунду. Как это все сделать?

Интересное устройство придумал Жуль Антуан Лиссажу в 1855 году. Он взял два одинаковых камертона и установил у них зеркала. Колебания камертонов настроены перпендикулярно, частоты у них одинаковые, в результате лучик света в отражении двух зеркал выписывает фигуры. Такие загогулины называются с тех пор «фигуры Лиссажу».

Джон Тиндалл чуть позже усовершенствовал технологию. Он вместо одного из камертонов поставил равномерно поворачивающееся зеркало.

Колебания простых инструментов, типа камертона, научились видеть. Но остался сложный звук, например, звук музыкальных инструментов или звук голоса.

Эту задачу смог впервые решить Рудольф Кёниг, которого называют «Фарадеем звука». Он родился в Кёнигсберге, но в молодости переехал в Париж, поступил на службу ассистентом в фирме, которая изготовляла скрипки. После он сам переключился на изготовление акустических инструментов, не только музыкальных, но и научных.

В течение 40 лет он изготавливал приборы, которыми пользовались все акустики того времени. Это были приборы непревзойденного качества и многие из них работают до сих пор. Огромный тонометр, который он построил из нескольких сотен настроенных камертонов, рабочий, по нему можно настраивать инструменты и сейчас.

Кёниг сотрудничал с Гельмгольцем и, впервые, они начали проводить в конце XIX века эксперименты с электрическим синтезатором голоса.

Как Кёниг смог визуализировать звуковое колебание.

Он взял газовую горелку, где камера, через которую шел газ, была разделена на две части эластичной каучуковой мембраной. В нормальном состоянии газ входит через канал А, потом передается в трубочку В и горит равномерно.

Если со стороны D во вторую половину камеры, попадает звук, то резиновая мембрана начинает колебаться, и когда она колеблется, то выдавливает или втягивает газ. Поступление газа меняется, пламя становится то ярче, то тусклее.

Плюс нужно взять вращающееся зеркало, чтобы видеть быстрые колебания в реальном времени. К примеру, параллелепипед как на рисунке, который со всех сторон покрыт зеркалами, нужно вращать с большой скоростью. В отражении языков пламени вы увидите закодированный звуковой профиль.

Кёниг был товарищ систематический и эксперимент повторял много раз. Он садился перед горелкой, в трубочку D напевал звук на определённой высоте, стараясь держать высоту. В процессе напевания, он смотрел на отражение, на форму пламени и зарисовывал. При этом у него был ассистент, который независимо от него тоже зарисовывал. Если рисунки сходились, то считалось, что оба зарисовали правильно. Если нет, то Кёниг повторял эксперимент. Он изучил 5 гласных звуков на 15 разных нотах.

С возрастом он уже не смог продолжать работу, собрал все зарисовки звука и опубликовал в конце 1880-х.

Все эти красивые и хитроумные приспособления почти сразу же стали достоянием истории, как только появился способ механически записывать звук на долгую память.

Томас Эдисон предложил способ, как зафиксировать профиль звукового колебания на твердом носителе с помощью фонографа.

Фонограф люди подхватили и буквально за несколько лет усовершенствовали до граммофона, патефона и т.д… Дальше пошла вся индустрия звукозаписи, которая сохранялась почти до 1980-х. Она была доминирующей, пока люди не перешли на звуковые кассеты.

Появился способ записать звук. Если он записан, то его можно дальше исследовать, эксперименты с зарисовками стали не сильно важны.

Вот если вам хочется изучать звуковые колебания в реальном времени, то фонограф не очень подходящая вещь. Здесь прогресс шел долго. Он начался с изобретение телефона, как комбинация микрофона и динамика, в 70-х годах 19 века. Для нормальной записи и воспроизведения звука эти устройства совершенствовали еще несколько десятилетий.

Такого типа картинки на экране осциллографа, люди научились получать только в 1920-е. С этого момента все можно считать, что мы можем исследовать звук во всех его сложных колебаниях в реальном времени.

Краткая история ультразвука и гидроакустики

Частоты ниже примерно 20 Гц человеческое ухо уже не воспринимает, это называется инфразвук. Рабочий диапазон человеческого уха ≈ 20 Гц — 20 кГц. Это наш акустический диапазон. При этом основная частота голоса занимает очень узкий интервал ≈100-200 Гц.

Начиная с 20 кГц, начинается ультразвук. Все, что выше 20 кГц, можно называть ультразвуком, но в районе 100 МГЦ используется часто иной термин — «гиперзвук».

Уточнение, гиперзвук — это ультразвук, с частотой 100 МГЦ, а есть еще «гиперзвуковая скорость» — это скорость летательных аппаратов, выше скорости звука в 5 раз и больше. Это разные термины, случайно получилось, что в них одинаковое слово используется.

Чтобы совсем запутать людей, в начале XX века вместо слова ультразвук или «ultrasonic», использовали термин «supersonic», то есть то, что сейчас мы называем «сверхзвук». Сейчас это не используется, потому что под словом «сверхзвук» связан с летательными аппаратами, которые движутся со скоростью больше скорости звук. Но если вы будете читать какую-то литературу по ультразвуку 100-летней давности, то будьте готовы увидеть там вместо ультразвука – сверхзвук.

Звук отличается не только длиной волны, но и поглощением. Это вот очень важная вещь, которая реально влияет на приложение.

Чем больше частота звука, то есть чем меньше длина волны звука, тем сильнее он поглощается в среде. При этом темп поглощения, то есть насколько далеко звук может распространяться, зависит не только от самой среды, но и от конкретных условий в ней.

Если взять обычный звук на частоте 1 кГц, то он в воздухе затухает на расстоянии 1 километра. На расстоянии в несколько километров вы высокие частоты вообще не услышите, они затухнут.

Если взять ультразвук на частоте 100 кГц, это довольно высокий ультразвук уже, то он затухает на считанных метрах. Если взять 1 МГц, то он буквально на десятках сантиметров затухнет. Поэтому в воздухе ультразвук выше 1МГц не используется, он просто далеко не улетает.

В воде, на той же частоте 1 КГц, звук может распространяться сотни километров, 1 МГЦ может распространяться на десятки метров. 1 ГГц распространяется на несколько миллиметров.
По мере уменьшения длины волны, то есть по мере роста частоты, у нас резко уменьшается дальность ультразвука. Он резко поглощается, поэтому 1 ГГц уже поглощается на долях миллиметра, ТГц буквально на несколько межатомных расстояний.

В воде 1 МГц, звук может распространяться на десятки метров, а в организме, если говорить про медицинское применение ультразвука, ультразвук распространяется еще меньше, потому что он не просто поглощается, но и рассеивается.

Если взять тот же 1 МГц и запустить его в человека, то в жировой ткани, во внутренних органах, он пройдет несколько десятков сантиметров. В мышцах пройдет всего 5 сантиметров, а в кости вообще несколько миллиметров.

Звук слишком высокой частоты вообще в организме использовать бессмысленно, т.к. он быстро поглотится.

У ультразвука есть 2 главных характеристики, которые делают его очень удобным:

• маленькая длина волны
• способность отражаться от границы раздела сред

Если мы переходим из жировой ткани в мышцы или в кость, то у нас на границе раздела происходит отражение звука.

Если у нас длина волны сильно меньше, чем размеры излучателя, то из звука можно создать узкий сфокусированный звуковой луч и не тратить попусту звуковой энергию.

Если длина волны много меньше размеров препятствий, тогда этот звук будет хорошо отражаться от этих препятствий. От сравнительно маленьких препятствий он как бы не отражается, он их огибает. Если препятствие крупное, размером с длину волны или больше, тогда звук хорошо отражается.

С одной стороны, поглощение звука — вроде бы плохо. Крикнули, а звук никуда не долетел.
Но с другой стороны, это способ внедрять энергию в вещество.

Вы можете без разрезания тела, заставить маленькую опухоль внутри тела нагреваться, просто сфокусировав там ультразвук. Это используется и медицине и в материаловедении.

Приложение ультразвука так велико, что существуют десятки научных журналов, в которых публикуются статьи только по приложениям ультразвука.

Впервые человек столкнулся с ультразвуком, не осознавая того, что речь идёт про ультразвук.

В XVIII веке итальянский исследователь Ладзаро Спалланцани заинтересовался тем фактом, что летучие мыши свободно и безошибочно ориентируется в полной темноте.

Спалланцани провел ряд экспериментов на летучих мышах, из чего сделал вывод, что даже не имея зрения, летучие мыши способны уклоняться от препятствий, избегать натянутых проволочек и спокойно летать. Потом выяснилось, что за эту навигацию отвечают уши, а не глаза.

То есть Спалланцани и его последователи его, они проводили другие эксперименты, фактически, заливая воском ушки мышкам. Тогда летучие мышки не могли избегать препятствий и натыкались на них.

Спалланцани никакого вывода из своего исследования не сделал, просто опубликовал работу, где сообщил о том, что он открыл новый орган чувств у летучих мышей. Он не догадался, что это не слышимый нами ультразвук.

Это было бы революционным заявлением для той эпохи, потому что тогда исследователи считали, что если что-то есть, мы обязательно должны это или видеть или слышать.

Только в 1920-х и 30-х годах, исследователи, вооружившись современными технологиями, вернулись к летучим мышам и, доказали, что, они испускают ультразвук и с помощью отражения ультразвука ориентируются в окружающем пространстве.

«Занимательная биоакустика» рассказывает очень подробно про эту историю.

Как летучей мыши используют ультразвук для ориентации и охоты

У летучих мышей есть орган, который испускает высокий писк, от 30 до 100 КГц. В воздухе длина волны отвечающая этим частотам, всего несколько миллиметров.

Мышка летит в полной темноте, испускает десятки раз в секунду короткие ультразвуковые импульсы. Ультразвуковой импульс, если есть какое-то препятствие, отражается и возвращается обратно к летучей мыши. По времени задержки между испусканием импульса и приходом эха, мышка определяет размеры предмета и расстояние до него.

Как только мышь поняла, что есть какая-то мишень, она начинает на нее охотится, испускает звуковые волны чаще. За доли секунды перед поимкой, мышь переключается на другой режим, сотни раз в секунду испускает сигнал. В момент поимки мышь с точностью до миллиметра знает расстояние до цели. Это все происходит в полной темноте, только с помощью эхолокации.

Примерно то же самое человек тоже научился делать в XX веке.

Ультразвук в воздухе распространяется плохо, поэтому дальнейшие успехи ультразвука будут относиться к распространению в сплошных средах, например, в воде или в теле, поэтому сразу поговорим про гидроаккустику.

Люди пытались заниматься гидроакустикой еще в XVII-XVIII веках, но еще не понимали с какой скоростью звук распространяется.

Это значение в 1826 году измерил Жан-Даниэль Колладон. Он с ассистентом провел на Женевском озере серию экспериментов и измерил скорость звука. Она оказалась примерно 1,5 км/с.

Поскольку мы знаем скорость звука, теоретически появляется возможность дистанционно под водой измерять расстояние до каких-нибудь препятствий, если мы запустим туда сигнал какой-то и потом послушаем эхо.

С 1830-х годов, как только Колладон измерил скорость звука в воде, десятилетиями люди проводили бесчисленное количество экспериментов. Они пытались измерить глубину океана, услышав эхо от его дна. Безуспешно.

Только 1890-е люди научились с помощью звука связываться между кораблями.

В 1914 году с помощью новых инструментов, электрических, мощных генераторов звука, впервые люди научились детектировать айсберги на расстоянии и прослушивать дно. Но для «Титаника» это было поздновато.

Похоже, «Титаник» стал вызовом для инженеров того времени.

В первые недели после катастрофы, Льюис Ричардсон, британский математик получил два патента на такую акустическую дистанционную эхолокацию, сначала в воздухе, а потом под водой.

Он понял, что нужно сформировать из звука узкий звуковой луч, направить его на нужную мишень и послушать эхо от этого луча.

Микрофон, который будет под водой слушать эхо, должен находиться в фокусе акустического зеркала, то есть надо максимально усилить приходящий слабый звук.

Ричардсон впервые подчеркнул, что если уже мы хотим реально излучать узконаправленные лучи звука, нам нужно, чтоб наш излучатель был размерами намного больше, чем длина волны звука. Для звука обычной частоты, около 1 кГц, длина волны составляет метры, получается излучатель должен быть размером в десятки метров. Это слишком затратно. Если мы хотим создать узконаправленный луч, надо использовать ультразвук, то есть звук маленькой длинной волны. В этом польза ультразвука.

Не всегда предложения изобретателей реализуются. По поводу гибели «Титаника», было внесено еще одно интересное предложение про дистанционное детектирование айсбергов, которое внес оружейник Хайрам Максим.

Это оружейник американского происхождения, который потом переехал в Европу, в течении XIX века он изобретал разные варианты оружия, в том числе пулемет Максим, который был очень популярен в России.

Хайрам Максим предложил детектировать айсберги, как это делают летучие мыши, то есть с помощью инфразвука. В тот момент люди еще не знали на самом деле, чем пользоваться летучие мыши. Многие думали, что летучие мыши используют инфразвук, звук низких частот от собственных крыльев. Поэтому он предложил поставить на корабль излучатели инфразвука и потом детектировать отражение инфразвука.

Как мы сейчас понимаем, это не очень полезная технология, потому что звук сильно рассеивается и плохо отражается, если он длинноволновый. Так что его идея не прижилась.

Когда началась первая мировая война, она резко потребовала от британцев, американцев, французов найти способ детектировать подводные лодки Германии.

У Германии был отличный подводный флот, который топил корабли и гражданские суда. Сначала было вообще не понятно, что с ними делать.

Константин Шиловский — электротехник, изобретатель из России. Первая мировая война застала его в Швейцарии. Еще до начала войны он уехал в Швейцарию лечиться.

Шиловский, узнав про проблемы с подводным флотом, предложил французскому правительству схему, которая представляла из себя улучшенную версию идеи Ричардсона, то есть ультразвуковую эхолокацию.

Правительство рассмотрело, одобрило и подключило к этому исследованию физика Поля Ланжевена.

Вместе с Шиловским, они за год создали первый прибор, вот который одновременно работал как излучатель и микрофон, назвали «трансдьюсер».

В 1916 году с помощью него уже начали передавать сигналы между кораблями и впервые стали регистрировать отражение от металлического листа на расстоянии 100 метров.

Два года спустя Ланжевен с помощью пьезоэлектрического эффекта, создал улучшенный трансдьюсер, который от одного кристалла кварца выдавал киловатт энергии.

Технология ультразвуковой гидрологации была создана, готова, ее можно было бы использовать на войне, но война к тому времени уже закончилась.

В последующие годы было бурное развитие тех же самых технологий для мирных целей: исследования глубины океана, детектирования подводных препятствий.

Ко второй мировой войне воюющие державы подошли во всеоружии, не просто эхолокация была, а торпеды, которые самонаводились по звуку.

В послевоенное время опять начались исследований океана, морских жителей с помощью ультразвука.

Сегодня сонары — приборы, которые сканируют с помощью гидроэхолокации предметы под водой, доступны в магазинах. Если вы занимаетесь рыбалкой, то возможно видели их в профмагазинах.

Типичные частоты, на которых работают современные сонары это килогерцы, в т.ч. десятки и даже сотни килогерц, вплоть до мегагерца.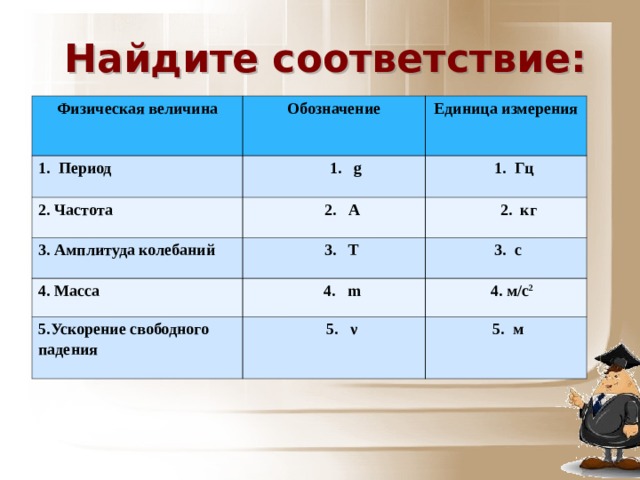 Частота зависит от того, что вы хотите.

На картинке — затонувший корабль на глубине несколько десятков метров. Изображение получили с помощью сонар бокового действия с частотой 325 кГц.

Ультразвук в медицине

Вот типичная картинка, которую часто видят беременные.

Когда хотят посмотреть в каком виде плод, как он развивается, все ли в порядке, делают ультразвуковое исследование.

Как двумерные картинки получаются. По сути, та же самая эхолокация, но только уже в организме человека.

Прибор для УЗИ — это тоже трансдьюсер, то есть одновременно и датчик и излучатель. Он излучает направленный луч ультразвука на частоте нескольких мегагерц.

Например, его направляют сверху вниз. Ультразвук распространяется сквозь ткани. Если есть какая-то граница раздела, скажем жировая ткань и органы или там плод начинается, то тогда от границы происходит отражение звука и звук возвращается обратно к датчику. По времени возвращения эха можно определить, на какой глубине находится эта граница.

Сканирование с помощью одного луча занимает очень немного времени. При типичной скорости звука, 200 микросекунд вполне достаточно для того, чтобы измерить такой профиль в одну сторону. 200 микросекунд означает, что такие измерения вы можете делать 5 000 раз в секунду, то есть 5 000 раз в секунду вы можете получать такие одномерные картинки.

Двумерная картинка строится очень просто. Внутри головки датчика есть вращающийся источник звука. Он, поворачиваясь туда-сюда, каждый раз посылает одномерный луч 5 000 раз в секунду. Это означает, что он может колебнуться туда-сюда 30 раз в секунду, и за каждое колебание он около 100 раз может просканировать одномерное направление.

В результате этого за 1/30-ую секунды вы сможете получить такую двумерную картинку, как совокупность одномерных картинок в разных направлениях.

Все это занимает всего лишь 1/30-ую секунды, вы можете 30 раз в секунду обновлять эту картинку, т.е. у вас получается настоящее видео в реальном времени, что происходит внутри. Так происходит ультразвуковая диагностика тел. Есть еще более тонкие технологии, в которых не просто изучается, что там внутри, а еще измеряется скорость кровотока.

Диагностика с помощью ультразвука использует ультразвук низкой интенсивности. Такой ультразвук вообще никакого вредного воздействия не оказывает, это просто звуковое колебание, которые так есть, но просто в другом частотном диапазоне.

Однако, еще в 1920-х выяснили, если интенсивность ультразвука повышать, то он поглощается, выделяет энергию в виде теплоты и локально нагревает предметы. Раз нагревает, значит приводит к механическим воздействиям.

Когда Ланжевен вместе с Шиловским делали первый трансдьюсер и получили киловатные мощности ультразвука, они обнаружили, что если на аквариум с рыбами направить интенсивный ультразвук, то рыбы умирают.

В 20-х годах проводили разного типа исследования.

Был любопытный эксперимент Роберта Вуда и Альфреда Лумиса. Роберт Вуд был известным в то время профессором физики. Альфред Лумис был адвокат по образованию, из обеспеченной семьи, интересовался и наукой и техникой, инвестировал свои деньги разные исследования и поддерживал науку.

Лумис скооперировался с Вудом, выкупил несколько зданий, где они построили лаборатории и проводили исследования, как воздействует ультразвук высокой интенсивности на всё подряд.

В огромном исследовании 1927 года они перечислили кучу экспериментов, которые они проводили: нагрев жидкости, вскипание жидкости, превращение жидкости в эмульсии, воспламенение дерева, воспламенение тканей, прижатие предмета друг к другу, эффект сверления и так далее. В т.ч. они изучали и биологические воздействия на мелкие организмы, к примеру, они измеряли на каком пороге интенсивности происходит смерть рыбок.

Потом началась Вторая мировая война, от этих исследований временно отказались. После войны, уже с новой техникой, люди вернулись к вопросу, как действует ультразвук высокой интенсивности на живые организмы.

В 50-х годах в США в университете Иллинойса, два брата-исследователя Фрай создали специальную лабораторию для изучения нейрохирургии с помощью ультразвукового скальпеля.

Хирургия внутри головы обычным способом — дело опасное, приходится разрезать череп и залезать внутрь. А ультразвуковой луч позволяет без вскрытия организма наносить внутренние точечные воздействия на ткани с точностью в миллиметры.

Фрай сначала теорию разработали, потом на разных материалах опробовали действие ульразвукового луча, потом проводили эксперименты на животных и уже в 1955 году начали лечить опухоли мозга.

С тех пор эта технология сильно развилась сейчас широко используется. Единственное ограничение этого метода в том, что вы не сможете обрабатывать большие участки ткани, требуется фокусировать ультразвук с точностью до миллиметров. Если вам нужно, скажем, прижечь орган, чтобы остановить внутреннее кровотечение, для этого вполне достаточно ультразвука.

Терагерцы

Зачем нам вообще нужен ультразвук такой высокой частоты? Что с помощью такого ультразвука можно изучить?

Поскольку длина поглощения терагерца составляет десятки расстояний между атомами, то нет смысла как-то воздействовать на макроскопические предметы.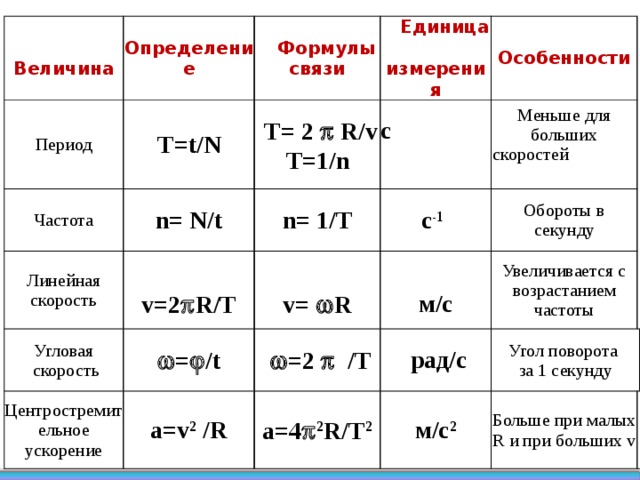 (-12) секунды. Вот один пример:

Вода в твердом состоянии, в виде льда, образует кристаллическую решетку с помощью водородных связей. Это такие связи, которые как бы через протоны связывают друг с другом разные молекулы. Эти связи во льду прочные, они держатся.

А что происходит в воде? В воде тоже толпа молекул, она даже более плотная, чем лёд, поэтому там тоже образуется водородные связи. Но поскольку в воде молекулы толкутся туда-сюда, эти связи устанавливаются на небольшое время, потом разрушаются.

На масштабе порядка долей пикосекунды в воде появляется дополнительная упругость, потому что эти связи еще держатся, но если вы посмотрите на время порядка наносекунд, то эти связи разрушаются и жидкость течет.

Возникает желание найти какой-то способ проверить долговременность этих водородных связей внутри воды и то, как они влияют на структурные свойства, на упругость воды на временах порядка пикасекунды. Это можно делать с помощью ультразвука огромной частоты, порядка терагерц.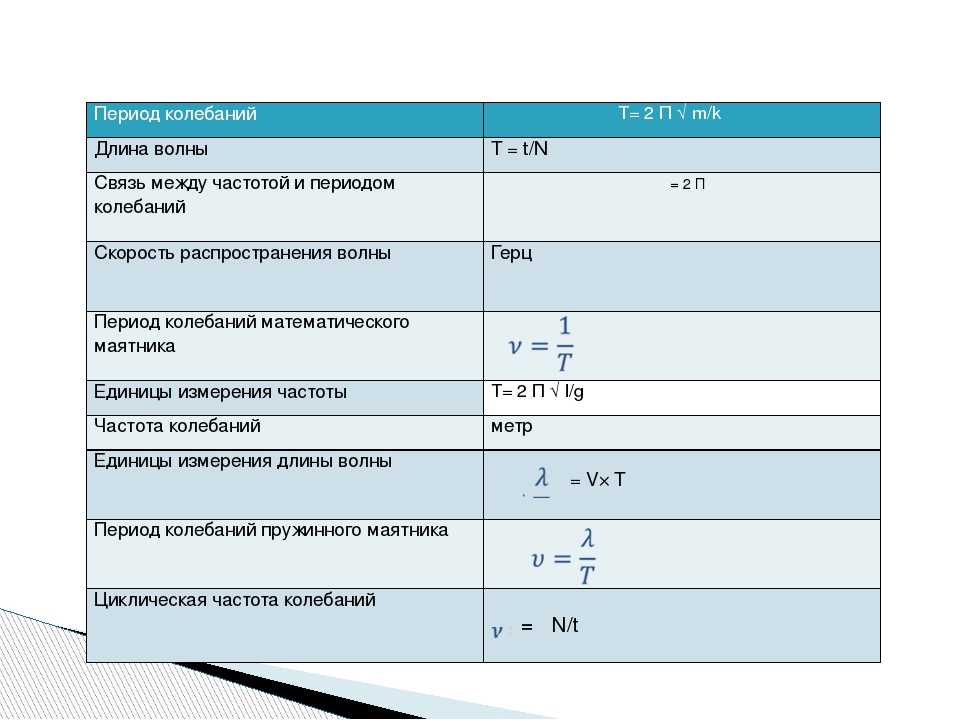

С середины XX века, когда появились первые компьютеры, люди стали исследовать, как разные молекулы внутри вещества движутся относительно друг друга и как складывается из движения отдельных молекул свойства сплошных веществ.

В 1974 году провели эксперимент и применили метод молекулярной динамики на 216 молекул воды. Кроме обычного звукового колебания, исследователи нашли еще какую-то новую форму колебаний, они назвали это «быстрым звуком».

Вот это то, что мы при обычных частотах не видим, мы можем в воде измерить звук и мы видим, что вот он составляет 1500 метров в секунду примерно и он один, а в моделировании люди обнаружили, что есть какой-то 2-й быстрый звук, который имеет скорость примерно вдвое быстрее.

В 1985 году эти расчеты были экспериментально подтверждены, исследователи фиксировали быстрый звук в воде, но что это за звук, было непонятно. В 1990-х годах с помощью серии экспериментов и теоретических расчетов, люди разобрались в этой картине.

Оказывается быстрый звук — это обычный звук, продольный звук, он такой как и всегда. Но из-за того, что при ультразвуковых частотах вода приобретает дополнительную упругость, звук распространяется быстрее, как будто во льду, со скоростью примерно 3 км/с.

А то, что люди сначала восприняли как обычный звук на скорости ≈1,5-1,8 км/с, был новый поперечный звук в воде. Это очень необычная вещь.

В кристаллах такой звук вполне может быть, потому что в кристаллах есть упругость. Вы можете в кристалле сдвинуть относительно друг друга плоскости, и они будут пытаться восстановиться. В воде, казалось бы, никакой упругости нет, она текучая, но оказывается, что текучесть изменяется на времени порядка пикосекунд. На частоте порядка терагерц, из-за водородных связей, которые не успевают еще разрушится, вода начинает себя вести не просто как обычная жидкость, а как вискоэластик. Вискоэластик — некая среда, у которой есть одновременно есть и текучесть и упругости. Поэтому в воде при очень высоких частотах возможны и поперечный и продольный звуки.

Сам факт, что некоторые жидкости допускают существование поперечного звука — не тривиальный. Неизвестно заранее, та или иная жидкость способна это делать или нет, и при каких температурах и давлениях. В последние годы люди начали исследовать, когда этот звук может появляться, во всех ли жидкостях, при всех ли температурах и так далее.

В серии работ, выполненных в институте высокого давления в Троицке, Вадим Брашкин и его коллеги смогли доказать, что есть области на фазовой диаграмме, то есть давления температуры, например, аргоном, в которой у нас может существовать быстрый звук, а в другой области не существует. Эти две области разделены фазовым переходом. Этот фазовый переход они предложили назвать «линии Френкеля», в честь знаменитого российского советского физика Якова Френки. Этот фазовый переход был обнаружен экспериментально буквально несколько лет назад. Так что это видите звук на терагерцах и необычный взгляд на вещество — это самая современная физика звука.

PhysBook:Электронный учебник физики — PhysBook

Содержание

• 1 Учебники
• 2 Механика
  • 2. 1 Кинематика
  • 2.2 Динамика
  • 2.3 Законы сохранения
  • 2.4 Статика
  • 2.5 Механические колебания и волны
• 3 Термодинамика и МКТ
  • 3.1 МКТ
  • 3.2 Термодинамика
• 4 Электродинамика
  • 4.1 Электростатика
  • 4.2 Электрический ток
  • 4. 3 Магнетизм
  • 4.4 Электромагнитные колебания и волны
• 5 Оптика. СТО
  • 5.1 Геометрическая оптика
  • 5.2 Волновая оптика
  • 5.3 Фотометрия
  • 5.4 Квантовая оптика
  • 5.5 Излучение и спектры
  • 5.6 СТО
• 6 Атомная и ядерная
  • 6.1 Атомная физика. Квантовая теория
  • 6.2 Ядерная физика
• 7 Общие темы
• 8 Новые страницы

Здесь размещена информация по школьной физике:

1. материалы из учебников, лекций, рефератов, журналов;
2. разработки уроков, тем;
3. flash-анимации, фотографии, рисунки различных физических процессов;
4. ссылки на другие сайты

и многое другое.

Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.

Учебники

Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –

Механика

Кинематика

Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве

Динамика

Законы Ньютона – Силы в механике – Движение под действием нескольких сил

Законы сохранения

Закон сохранения импульса – Закон сохранения энергии

Статика

Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика

Механические колебания и волны

Механические колебания – Механические волны

---

Термодинамика и МКТ

МКТ

Основы МКТ – Газовые законы – МКТ идеального газа

Термодинамика

Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение

---

Электродинамика

Электростатика

Электрическое поле и его параметры – Электроемкость

Электрический ток

Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках

Магнетизм

Магнитное поле – Электромагнитная индукция

Электромагнитные колебания и волны

Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны

---

Оптика.

СТО

Геометрическая оптика

Прямолинейное распространение света. Отражение света – Преломление света – Линзы

Волновая оптика

Свет как электромагнитная волна – Интерференция света – Дифракция света

Фотометрия

Фотометрия

Квантовая оптика

Квантовая оптика

Излучение и спектры

Излучение и спектры

СТО

СТО

---

Атомная и ядерная

Атомная физика. Квантовая теория

Строение атома – Квантовая теория – Излучение атома

Ядерная физика

Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы

---

Общие темы

Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике

Новые страницы

Запрос не дал результатов.

Какой буквой обозначают частоту — Строй Обзор

Содержание

1. частота обозначение
2. Как написать хороший ответ?
3. Формула частоты колебаний
4. Формулы для вычисления частоты дискретных событий, частота вращения
5. Примеры задач с решением

частота обозначение

Автор Ёветлана Тула задал вопрос в разделе Домашние задания

какой буквой обозначается частота? и получил лучший ответ

Ответ от Lmn[гуру]
Стандартные обозначения в формулах —

F. Единицей частоты в Международной системе единиц (СИ) в общем случае является Герц (Гц, Hz)

30 МГц = 10 метров
Около 2,9 метра

Длина волны измеряется в метрах, и каждому
подробнее.

F. Единицей частоты в Международной системе единиц (СИ) в общем случае является Герц (Гц, Hz). Величина, обратная частоте, называется периодом.

Вопрос по физике:

Какой буквой обозначается частота в физике?

Ответы и объяснения 2

оно обозначается в и измеряется в герцах

Единицей измерения частоты в Международной системе единиц (СИ) является герц (русское обозначение: Гц; международное: Hz), названный в честь немецкого физика Генриха Герца.

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Физика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Физика — область естествознания: естественная наука о простейших и вместе с тем наиболее общих законах природы, о материи, её структуре и движении.

Частота — это физический параметр, которые используют для характеристики периодических процессов. Частота равна количеству повторений или свершения событий в единицу времени.

Чаще всего в физике частоту обозначают буквой $
u ,$ иногда встречаются другие обозначения частоты, например $f$ или $F$.

Частота (наряду со временем) является самой точно измеряемой величиной.

Формула частоты колебаний

При помощи частоты характеризуют колебания. В этом случае частота является физической величиной обратной периоду колебаний $(T).$

Частота, в этом случае — это число полных колебаний ($N$), совершающихся за единицу времени:

где $Delta t$ — время за которое происходят $N$ колебаний.

Единицей измерения частоты в Международной системе единиц (СИ) служат в герцы или обратные секунды:

Герц — это единица измерения частоты периодического процесса, при которой за время равное одной секунде происходит один цикл процесса. Единица измерения частоты периодического процесса получила свое наименование в честь немецкого ученого Г. Герца.

Частота биений, которые возникают при сложении двух колебаний, происходящих по одной прямой с разными, но близкими по величине частотами ($<
u >_1 и <
u >_2$) равна:

Еще одно величиной характеризующей колебательный процесс является циклическая частота ($<omega >_0$), связанная с частотой как:

Циклическая частота измеряется в радианах, деленных на секунду:

Частота колебаний тела, имеющего массу$ m,$ подвешенного на пружине с коэффициентом упругости $k$ равна:

Формула (4) верна для упругих, малых колебаний. Кроме того масса пружины должна быть малой по сравнению с массой тела, прикрепленного к этой пружине.

Для математического маятника частоту колебаний вычисляют как: длина нити:

где $g$ — ускорение свободного падения; $ l$ — длина нити (длина подвеса) маятника.

Физический маятник совершает колебания с частотой:

где $J$ — момент инерции тела, совершающего колебания относительно оси; $d$ — расстояние от центра масс маятника до оси колебаний.

Формулы (4) — (6) приближенные. Чем меньше амплитуда колебаний, тем точнее значение частоты колебаний, вычисляемых с их помощью.

Формулы для вычисления частоты дискретных событий, частота вращения

дискретных колебаний ($n$) — называют физическую величину, равную числу действий (событий) в единицу времени. Если время, которое занимает одно событие обозначить как $ au $, то частота дискретных событий равна:

Единицей измерения частоты дискретных событий является обратная секунда:

Секунда в минус первой степени равна частоте дискретных событий, если за время, равное одной секунде происходит одно событие.

Частотой вращения ($n$) — называют величину, равную количеству полных оборотов, которое совершает тело в единицу времени. Если $ au $ — время, затрачиваемое на один полный оборот, то:

Примеры задач с решением

Задание. Колебательная система совершила за время равное одной минуте ($Delta t=1 мин$) 600 колебаний. Какова частота этих колебаний?

Решение. Для решения задачи воспользуемся определением частоты колебаний: Частота, в этом случае — это число полных колебаний, совершающихся за единицу времени.

Прежде чем переходить к вычислениям, переведем время в единицы системы СИ: $Delta t=1 мин=60 с$. Вычислим частоту:

Ответ. $
u =10Гц$

Задание. На рис.1 изображен график колебаний некоторого параметра $xi (t)$, Какова амплитуда и частота колебаний этой величины?

Решение. Из рис.1 видно, что амплитуда величины $xi left(t
ight)=<xi >_=5 (м)$. Из графика получаем, что одно полное колебание происходит за время, равное 2 с, следовательно, период колебаний равен:

Частота — величина обратная периоду колебаний, значит:

Ответ. 1) $<xi >_=5 (м)$. 2) $
u =0,5$ Гц

Механические колебания — материалы для подготовки к ЕГЭ по Физике

 

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ : гармонические колебания; амплитуда, период, частота, фаза колебаний; свободные колебания, вынужденные колебания, резонанс.

Колебания — это повторяющиеся во времени изменения состояния системы. Понятие колебаний охватывает очень широкий круг явлений.

Колебания механических систем, или механические колебания — это механическое движение тела или системы тел, которое обладает повторяемостью во времени и происходит в окрестности положения равновесия. Положением равновесия называется такое состояние системы, в котором она может оставаться сколь угодно долго, не испытывая внешних воздействий.

Например, если маятник отклонить и отпустить, то начнутся колебания. Положение равновесия — это положение маятника при отсутствии отклонения. В этом положении маятник, если его не трогать, может пребывать сколь угодно долго. При колебаниях маятник много раз проходит положение равновесия.

Сразу после того, как отклонённый маятник отпустили, он начал двигаться, прошёл положение равновесия, достиг противоположного крайнего положения, на мгновение остановился в нём, двинулся в обратном направлении, снова прошёл положение равновесия и вернулся назад. Совершилось одно полное колебание. Дальше этот процесс будет периодически повторяться.

Амплитуда колебаний тела — это величина его наибольшего отклонения от положения равновесия.

Период колебаний — это время одного полного колебания. Можно сказать, что за период тело проходит путь в четыре амплитуды.

Частота колебаний — это величина, обратная периоду: . Частота измеряется в герцах (Гц) и показывает, сколько полных колебаний совершается за одну секунду.

Гармонические колебания.

 

Будем считать, что положение колеблющегося тела определяется одной-единственной координатой . Положению равновесия отвечает значение . Основная задача механики в данном случае состоит в нахождении функции , дающей координату тела в любой момент времени.

Для математического описания колебаний естественно использовать периодические функции. Таких функций много, но две из них — синус и косинус — являются самыми важными. У них много хороших свойств, и они тесно связаны с широким кругом физических явлений.

Поскольку функции синус и косинус получаются друг из друга сдвигом аргумента на , можно ограничиться только одной из них. Мы для определённости будем использовать косинус.

Гармонические колебания — это колебания, при которых координата зависит от времени по гармоническому закону:

(1)

Выясним смысл входящих в эту формулу величин.

Положительная величина является наибольшим по модулю значением координаты (так как максимальное значение модуля косинуса равно единице), т. е. наибольшим отклонением от положения равновесия. Поэтому — амплитуда колебаний.

Аргумент косинуса называется фазой колебаний. Величина , равная значению фазы при , называется начальной фазой. Начальная фаза отвечает начальной координате тела: .

Величина называется циклической частотой. Найдём её связь с периодом колебаний и частотой . Одному полному колебанию отвечает приращение фазы, равное радиан: , откуда

(2)

(3)

Измеряется циклическая частота в рад/с (радиан в секунду).

В соответствии с выражениями (2) и (3) получаем ещё две формы записи гармонического закона (1):

.

График функции (1), выражающей зависимость координаты от времени при гармонических колебаниях, приведён на рис. 1.

Рис. 1. График гармонических колебаний

 

Гармонический закон вида (1) носит самый общий характер. Он отвечает, например, ситуации, когда с маятником совершили одновременно два начальных действия: отклонили на величину и придали ему некоторую начальную скорость. Имеются два важных частных случая, когда одно из этих действий не совершалось.

Пусть маятник отклонили, но начальной скорости не сообщали (отпустили без начальной скорости). Ясно, что в этом случае , поэтому можно положить . Мы получаем закон косинуса:

.

График гармонических колебаний в этом случае представлен на рис. 2.

Рис. 2. Закон косинуса

 

Допустим теперь, что маятник не отклоняли, но ударом сообщили ему начальную скорость из положения равновесия. В этом случае , так что можно положить . Получаем закон синуса:

.

График колебаний представлен на рис. 3.

Рис. 3. Закон синуса

 

Уравнение гармонических колебаний.

 

Вернёмся к общему гармоническому закону (1). Дифференцируем это равенство:

. (4)

Теперь дифференцируем полученное равенство (4):

. (5)

Давайте сопоставим выражение (1) для координаты и выражение (5) для проекции ускорения. Мы видим, что проекция ускорения отличается от координаты лишь множителем :

. (6)

Это соотношение называется уравнением гармонических колебаний. Его можно переписать и в таком виде:

. (7)

C математической точки зрения уравнение (7) является дифференциальным уравнением. Решениями дифференциальных уравнений служат функции (а не числа, как в обычной алгебре).
Так вот, можно доказать, что:

-решением уравнения (7) является всякая функция вида (1) с произвольными ;

-никакая другая функция решением данного уравнения не является.

Иными словами, соотношения (6), (7) описывают гармонические колебания с циклической частотой и только их. Две константы определяются из начальных условий — по начальным значениям координаты и скорости.

Пружинный маятник.

 

Пружинный маятник — это закреплённый на пружине груз, способный совершать колебания в горизонтальном или вертикальном направлении.

Найдём период малых горизонтальных колебаний пружинного маятника (рис. 4). Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими.

Трением пренебрегаем. Груз имеет массу , жёсткость пружины равна .

Координате отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза.

Рис. 4. Пружинный маятник

 

В горизонтальном направлении на груз действует только сила упругости со стороны пружины. Второй закон Ньютона для груза в проекции на ось имеет вид:

. (8)

Если (груз смещён вправо, как на рисунке), то сила упругости направлена в противоположную сторону, и . Наоборот, если , то . Знаки и всё время противоположны, поэтому закон Гука можно записать так:

Тогда соотношение (8) принимает вид:

или

.

Мы получили уравнение гармонических колебаний вида (6), в котором

.

Циклическая частота колебаний пружинного маятника, таким образом, равна:

. (9)

Отсюда и из соотношения находим период горизонтальных колебаний пружинного маятника:

. (10)

Если подвесить груз на пружине, то получится пружинный маятник, совершающий колебания в вертикальном направлении. Можно показать, что и в этом случае для периода колебаний справедлива формула (10).

Математический маятник.

 

Математический маятник — это небольшое тело, подвешенное на невесомой нерастяжимой нити (рис. 5). Математический маятник может совершать колебания в вертикальной плоскости в поле силы тяжести.

Рис. 5. Математический маятник

 

Найдём период малых колебаний математического маятника. Длина нити равна . Сопротивлением воздуха пренебрегаем.

Запишем для маятника второй закон Ньютона:

,

и спроектируем его на ось :

.

Если маятник занимает положение как на рисунке (т. е. ), то:

.

Если же маятник находится по другую сторону от положения равновесия (т. е. ), то:

.

Итак, при любом положении маятника имеем:

. (11)

Когда маятник покоится в положении равновесия, выполнено равенство . При малых колебаниях, когда отклонения маятника от положения равновесия малы (по сравнению с длиной нити), выполнено приближённое равенство . Воспользуемся им в формуле (11):

,

или

.

Это — уравнение гармонических колебаний вида (6), в котором

.

Следовательно, циклическая частота колебаний математического маятника равна:

. (12)

Отсюда период колебаний математического маятника:

. (13)

Обратите внимание, что в формулу (13) не входит масса груза. В отличие от пружинного маятника, период колебаний математического маятника не зависит от его массы.

Свободные и вынужденные колебания.

 

Говорят, что система совершает свободные колебания, если она однократно выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких периодических внешних
воздействий система при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания, в системе нет.

Рассмотренные выше колебания пружинного и математического маятников являются примерами свободных колебаний.

Частота, с которой совершаются свободные колебания, называется собственной частотой колебательной системы. Так, формулы (9) и (12) дают собственные (циклические) частоты колебаний пружинного и математического маятников.

В идеализированной ситуации при отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует трение, поэтому свободные колебания постепенно затухают (рис. 6).

Рис. 6. Затухающие колебания

 

Вынужденные колебания — это колебания, совершаемые системой под воздействием внешней силы , периодически изменяющейся во времени (так называемой вынуждающей силы).

Предположим, что собственная частота колебаний системы равна , а вынуждающая сила зависит от времени по гармоническому закону:

.

В течение некоторого времени происходит установление вынужденных колебаний: система совершает сложное движение, которое является наложением выужденных и свободных колебаний. Свободные колебания постепенно затухают, и в установившемся режиме система совершает вынужденные колебания, которые также оказываются гармоническими. Частота установившихся вынужденных колебаний совпадает с частотой
вынуждающей силы (внешняя сила как бы навязывает системе свою частоту).

Амплитуда установившихся вынужденных колебаний зависит от частоты вынуждающей силы. График этой зависимости показан на рис. 7.

Рис. 7. Резонанс

 

Мы видим, что вблизи частоты наступает резонанс — явление возрастания амплитуды вынужденных колебаний. Резонансная частота приближённо равна собственной частоте колебаний системы: , и это равенство выполняется тем точнее, чем меньше трение в системе. При отсутствии трения резонансная частота совпадает с собственной частотой колебаний, , а амплитуда колебаний возрастает до бесконечности при .

 

Формула частоты и измерение | Как рассчитать частоту — видео и стенограмма урока

Научные курсы / MEGA Physics: практическое и учебное пособие Курс / Волны и интерференция Глава

Карен Петерсон, Дэмиен Ховард

• Автор Карен Петерсон

  За последние 30 лет Карен преподавала множество различных курсов естественных наук в средней школе. Она имеет степень бакалавра биологии и химии Линфилд-колледжа и прошла дополнительные курсы для получения лицензии на профессиональное преподавание биологии, химии и физики.

  Посмотреть биографию
• Инструктор Дэмиен Ховард

  Дэмиен имеет степень магистра физики и преподавал физическую лабораторию студентам колледжа.

  Посмотреть биографию

Узнайте о различных формулах частоты и поймите, когда использовать каждую формулу частоты. Поймите, как найти частоту различных волн и событий. Обновлено: 02.02.2022

Содержание

• Что такое частота?
• Формула частоты
• Как найти частоту, используя период времени?
• Как рассчитать частоту волны, используя длину волны?
• Как определить частоту волны в вакууме?
• Как измерить частоту с помощью угловой скорости?
• Как рассчитать частоту события?
• Как найти таблицу частот?
• Краткое содержание урока

Показать

Что такое частота?

Частота — количество раз, когда событие происходит. Обычно присутствует временной компонент, такой как количество циклов в единицу времени или количество повторений результата в течение определенного промежутка времени. Примером частоты, с которой сталкивается каждый, является частота сердечных сокращений. Сердце бьется определенное количество раз в минуту, это может быть 60 ударов в минуту или, может быть, 80 ударов в минуту. Другим примером является маятник, который совершает определенное количество колебаний в минуту, как маятник, показанный на напольных часах.

Маятник на напольных часах.

Что такое частота?

Когда вы думаете о частоте, что первое приходит вам на ум? Для многих людей это, вероятно, имеет какое-то отношение к волнам. Когда вы звоните на радиостанцию, вы выбираете частоту излучаемых ею радиоволн. Однако знаете ли вы, что частота — это не понятие, ограниченное только волнами?

Частота ( f ) можно определить как количество раз, когда событие происходит за заданный промежуток времени. Математически мы можем записать это понятие так:

По существу, все, что повторяется, имеет связанную с ним частоту. Это включает в себя все, от того, сколько длин волн радиоволн повторяется каждую секунду, до того, сколько раз вы моете руки в день.

При использовании единиц СИ частота измеряется в единицах герц , что мы сокращенно обозначаем как Гц. Герц — это мера количества циклов события за одну секунду. Таким образом, частота 1 Гц будет означать, что один цикл события произошел за одну секунду.

Произошла ошибка при загрузке этого видео.

Попробуйте обновить страницу или обратитесь в службу поддержки.

Вы студент или преподаватель?

Присоединяйся сейчас

Больше 84 000 уроков по математике, английскому языку, естественным наукам, истории и многому другому в одном месте!

Более 30 000
Видеоуроки

Практика
Вопросы

Присоединяйся сейчас

Больше 30 000 видеоуроков и учебные ресурсы, все в одном месте!

Более 84 000
Уроки

Викторины и
Рабочие листы

Классная комната
Интеграция

Планы уроков

Далее: Поперечные и продольные волны: определение и примеры

пройти викторину Смотреть Следующий урок

 Повторить

Просто отмечаюсь.

Вы все еще смотрите? Да! Продолжай играть.

Ваш следующий урок будет играть в 10 секунд

• 0:04 Что такое частота?
• 1:01 Частота и период
• 1:35 Частотные задачи
• 4:55 Итоги урока

Сохранять Сохранять Сохранять

Хронология

Автовоспроизведение

Автовоспроизведение

Скорость

Скорость

Формула частоты

Существуют различные уравнения, которые можно использовать для расчета частоты. Если известно время, необходимое для одного колебания, то по нему можно определить частоту. Это время называется период и представлен буквой T . Уравнение: {eq}\mathrm{f=\frac{1}{T}} {/eq}. Если период указан в секундах, то частота имеет единицы {eq}\mathrm{\frac{1}{s}} {/eq}, что совпадает с герцем, сокращенно Гц.

Если известны длина волны и скорость волны, их можно использовать для определения частоты волны с помощью уравнения {eq}\mathrm{f=\frac{v}{\lambda }} {/eq}, где {eq}\lambda {/eq} — длина волны в метрах, а v — скорость волны в м/с. Это также дает частоту волны в герцах.

Если угловая скорость известна, то частоту можно рассчитать с помощью уравнения {eq}\mathrm{f=\frac{\omega }{2\pi }} {/eq}, где {eq}\omega {/eq} — угловая скорость. Единицами для частоты, рассчитанной по этому уравнению, будут радианы в секунду.

Использование различных частотных уравнений

Эти различные уравнения используются в определенных обстоятельствах. {-9{8}\mathrm{\:\frac{m}{s}} {/eq}.

Чтобы найти частоту раскачивания девочки на качелях, когда каждое движение вперед и назад занимает 5 секунд, уравнение

{eq}\mathrm{f=\frac{1}{T}} {/eq} будет использовал. Каждое движение вперед и назад занимает 5 секунд, так что это будет период, представленный T в этом уравнении.

Угловая частота измеряет количество оборотов в единицу времени. Единицами, используемыми для угловой частоты, являются обороты в секунду. Это уравнение можно использовать для решения такой задачи, как нахождение угловой частоты колеса обозрения, имеющего угловую скорость {eq}\pi/12\:\mathrm{rad/s} {/eq}. Имея угловую скорость, уравнение для нахождения угловой частоты будет {eq}\mathrm{f=\frac{\omega}{2\pi}} {/eq}.

Колесо обозрения

Как найти частоту, используя период времени?

Первым шагом в решении задач по физике является определение того, какая информация известна, что ищется, и, используя это, определение используемого уравнения. Для следующей задачи известна информация о периоде, и вопрос заключается в том, чтобы рассчитать частоту. Это будет уравнение {eq}\mathrm{f=\frac{1}{T}} {/eq}.

Маятник имеет период 0,4 секунды. Какова его частота?

Уравнение: {eq}\mathrm{f=\frac{1}{T}} {/eq}.

Следующий шаг — подставить полученные значения в уравнение:

{экв}\mathrm{f=\frac{1}{0,4 сек}} {/экв}.

Последним шагом является вычисление:

{eq}\mathrm{f=\frac{1}{0.4 sec}=2.5\:Hz} {/eq}

Как рассчитать частоту волны используя длину волны?

В следующем примере известны длина волны и скорость волны:

Фортепианный провод излучает звуковую волну с длиной волны 0,68 м. Скорость звука 340 м/с, какая частота волны?

Чтобы найти частоту по длине волны и скорости, используйте уравнение:

{eq}\mathrm{f=\frac{v}{\lambda }} {/eq}.

Следующим шагом является подстановка значений в уравнение:

{экв}\mathrm{f=\frac{340\:м/с}{0,68\:м}} {/экв}.

Затем выполните вычисление:

{экв}\mathrm{f=\frac{340\:м/с}{0,68\:м}=500\:Гц} {/экв} 9{14}\:Hz} {/eq}

Как измерить частоту с помощью угловой скорости?

Если угловая скорость равна {eq}60\pi \mathrm{\frac{rad}{s}} {/eq}, какова частота?

Уравнение для решения этой задачи: {eq}\mathrm{f=\frac{\omega }{2\pi }} {/eq}.

Затем подставьте числа в уравнение:

{eq}\mathrm{f=\frac{60\pi рад/с} }{2\pi }} {/eq}.

Наконец, вычислите ответ: {eq}\frac{60\pi \mathrm{\frac{rad}{s}}}{2\pi }=30 \: \mathrm{rotations/second} {/eq}

Как рассчитать частоту события?

Частота события — это количество раз, когда событие происходит. Например, если учащийся берет мяч из корзины, в которой есть красные, синие, желтые и зеленые шары, число раз, когда учащийся выбирает красный шар, будет частотой. Если учащийся сколько раз выбирал каждый цвет, можно также определить относительную частоту. Относительная частота — это отношение числа случаев возникновения события к общему числу событий. Если учащийся выбрал мяч 40 раз, и 15 из них он был красным, то относительная частота красного мяча будет равна {экв}15/40 = 0,375{/экв}. Если известно, сколько раз выбирался каждый из других цветов, то можно было бы рассчитать относительную частоту для всех из них.

Как найти таблицу частот?

Один из способов просмотреть данные, подобные описанным в предыдущем разделе, — создать таблицу частот . Здесь перечислены частоты различных событий. Частотная таблица часто состоит из трех столбцов. Первый столбец представляет собой список результатов, второй столбец предназначен для подсчета баллов для отслеживания количества каждого результата, а третий столбец — для частоты, которая определяется путем подсчета подсчета баллов для каждого из результатов.

Например, ученик бросил шестигранный кубик и получил следующие результаты: 2, 4, 1, 6, 5, 3, 3, 5, 1, 2, 6, 4, 5, 2, 4, 3 , 5, 1, 6, 2, 3, 5, 6.

Чтобы определить частоту каждого числа, ученик может составить таблицу частот.

Номер	Подсчет	Частота
1	111	3
2	1111	4
3	1111	4
4	111	3
5	11111	5
6	1111	4

Эта таблица позволяет легко увидеть частоту каждого из возможных бросков кости. Эти таблицы можно использовать для отображения количества результатов для всего, что имеет несколько результатов.

Резюме урока

Частота может быть описана как количество раз, когда событие происходит за заданный промежуток времени. В физике это обычно описывается как количество циклов в единицу времени, например, количество ударов сердца в минуту. Существуют различные уравнения, которые можно использовать для расчета частоты в зависимости от предоставленной информации. Некоторыми из них являются {eq}\mathrm{f=\frac{1}{T}} {/eq}, которые используются, если известно время одного цикла ( период ), {eq}\mathrm{f =\frac{v}{\lambda }} {/eq}, если известны длина волны и скорость волны, и {eq}\mathrm{f=\frac{\omega }{2\pi }} {/eq } если угловая скорость известна. Эти уравнения можно использовать для расчета частоты во многих различных ситуациях. Один из них — найти частоту 9{8}\mathrm{\frac{m}{s}} {/eq}, поэтому, если известна длина волны, можно рассчитать частоту.

Также можно определить частоты для различных событий. Одним из примеров является определение того, сколько раз синий мяч вытаскивают из ведра с разноцветными мячами. Чтобы показать данные для этого типа проблемы, часто создается таблица частот .

Частота и период

Хотя формулу из предыдущего раздела, безусловно, можно использовать для расчета частоты, чаще используется формула, связывающая частоту с чем-то, называемым периодом. Период ( T ) — количество времени, которое требуется для одного цикла повторяющегося события. На нашей диаграмме повторения волн периодом будет время, за которое одна длина волны полностью пройдет мимо наблюдателя. Частота и период на самом деле обратны друг другу. Это означает, что они связаны следующим образом:

Если вы знаете период, вы можете найти частоту и наоборот.

Проблемы с частотами

Частота и период могут применяться во многих ситуациях. Давайте рассмотрим несколько примеров, решая некоторые практические задачи.

Во время тренировки вы делаете 9 отжиманий за 30 секунд. Мы можем использовать эту информацию, чтобы найти вашу частоту отжиманий в герцах. Для этого воспользуемся первой найденной формулой частоты: f = отжимания/секунды. Отжимания — это наше повторяющееся событие, и время, которое вам потребовалось, чтобы отжаться, измеряется в секундах.

Вам может показаться странным, что вы отжимаетесь с частотой 0,3 Гц. Обычно мы не измеряем что-то вроде отжиманий в герцах. Однако не заблуждайтесь, герц — это всего лишь мера циклов в секунду. Выполнение отжиманий с частотой 0,3 Гц означает, что вы делаете 0,3 отжимания в секунду. Все, что имеет частоту, можно измерить в герцах, даже если это не принято.

Теперь давайте попробуем решить задачу, в которой используется вторая найденная нами формула частоты. Вы смотрите гонку по телевизору, и ваш любимый гонщик набирает в среднем 42 секунды за круг. Один круг — это один цикл в повторении многих кругов. Таким образом, период гонщика будет равен 42 секундам, необходимым для прохождения одного круга. Поскольку мы знаем период гонщика, мы можем найти его частоту круга.

Наш гонщик проезжает 0,02 круга каждую секунду. Это небольшое число имеет смысл, поскольку гонщику требуется 42 секунды, чтобы проехать всего один круг.

Мы решили две задачи, показывающие два разных способа нахождения частоты. 7 Гц в научных обозначениях. Теперь давайте попробуем найти период этой радиостанции.

Это уравнение показывает, что частота обратно пропорциональна периоду. Однако ранее мы говорили, что частота и период являются противоположностями друг друга. Это означает, что мы можем использовать тот факт, что период обратно пропорционален частоте, чтобы решить проблему.

Для нашей последней задачи мы соберем все вместе и найдем частоту и период вращения лопасти вертолета. Допустим, у нас есть лопасть вертолета с числом оборотов в минуту (оборотов в минуту) 480. Используя нашу первую формулу, мы видим, что число оборотов в минуту представляет собой частоту. Здесь полные обороты лопасти вертолета — это наши повторяющиеся события, а минута — это время, за которое они происходят.

Однако мы хотим, чтобы наша частота была в единицах СИ. Это означает, что нам нужно время в секундах, а не в минутах. Если мы преобразуем 1 минуту в 60 секунд, мы можем получить ответ для частоты в герцах.

Теперь, когда у нас есть частота вращения лопасти вертолета в герцах, мы можем найти ее период, используя ту же формулу из нашей последней задачи.

Резюме урока

Количество раз, когда событие происходит за заданный промежуток времени, называется частотой ( f ) . Если бы мы записали это определение в виде уравнения, оно выглядело бы так.

Всякий раз, когда какое-либо событие повторяется, оно имеет связанную с ним частоту. Для единиц СИ мы записываем наши частоты в единицах герц или сокращенно Гц. Герц — это измерение, которое мы используем для описания того, сколько раз повторяющееся событие повторяется за одну секунду.

Один из наиболее распространенных способов расчета частоты — сравнение ее с периодом. Период ( T ) — количество времени, которое требуется для одного цикла повторяющегося события. Получается, что частота и период обратны друг другу. Это означает, что мы можем связать их с помощью следующих формул.

Чтобы разблокировать этот урок, вы должны быть участником Study.com.
Создайте свою учетную запись

Что такое частота?

Когда вы думаете о частоте, что первое приходит вам на ум? Для многих людей это, вероятно, имеет какое-то отношение к волнам. Когда вы звоните на радиостанцию, вы выбираете частоту излучаемых ею радиоволн. Однако знаете ли вы, что частота — это не понятие, ограниченное только волнами?

Частота ( f ) можно определить как количество раз, когда событие происходит за заданный промежуток времени. Математически мы можем записать это понятие так:

По существу, все, что повторяется, имеет связанную с ним частоту. Это включает в себя все, от того, сколько длин волн радиоволн повторяется каждую секунду, до того, сколько раз вы моете руки в день.

При использовании единиц СИ частота измеряется в единицах герц , что мы сокращенно обозначаем как Гц. Герц — это мера количества циклов события за одну секунду. Таким образом, частота 1 Гц будет означать, что один цикл события произошел за одну секунду.

Частота и период

Хотя формулу из предыдущего раздела, безусловно, можно использовать для расчета частоты, чаще используется формула, связывающая частоту с чем-то, называемым периодом. Период ( T ) — количество времени, которое требуется для одного цикла повторяющегося события. На нашей диаграмме повторения волн периодом будет время, за которое одна длина волны полностью пройдет мимо наблюдателя. Частота и период на самом деле обратны друг другу. Это означает, что они связаны следующим образом:

Если вы знаете период, вы можете найти частоту и наоборот.

Проблемы с частотами

Частота и период могут применяться во многих ситуациях. Давайте рассмотрим несколько примеров, решая некоторые практические задачи.

Во время тренировки вы делаете 9 отжиманий за 30 секунд. Мы можем использовать эту информацию, чтобы найти вашу частоту отжиманий в герцах. Для этого воспользуемся первой найденной формулой частоты: f = отжимания/секунды. Отжимания — это наше повторяющееся событие, и время, которое вам потребовалось, чтобы отжаться, измеряется в секундах.

Вам может показаться странным, что вы отжимаетесь с частотой 0,3 Гц. Обычно мы не измеряем что-то вроде отжиманий в герцах. Однако не заблуждайтесь, герц — это всего лишь мера циклов в секунду. Выполнение отжиманий с частотой 0,3 Гц означает, что вы делаете 0,3 отжимания в секунду. Все, что имеет частоту, можно измерить в герцах, даже если это не принято.

Теперь давайте попробуем решить задачу, в которой используется вторая найденная нами формула частоты. Вы смотрите гонку по телевизору, и ваш любимый гонщик набирает в среднем 42 секунды за круг. Один круг — это один цикл в повторении многих кругов. Таким образом, период гонщика будет равен 42 секундам, необходимым для прохождения одного круга. Поскольку мы знаем период гонщика, мы можем найти его частоту круга.

Наш гонщик проезжает 0,02 круга каждую секунду. Это небольшое число имеет смысл, поскольку гонщику требуется 42 секунды, чтобы проехать всего один круг. 97 Гц в экспоненциальном представлении. Теперь давайте попробуем найти период этой радиостанции.

Это уравнение показывает, что частота обратно пропорциональна периоду. Однако ранее мы говорили, что частота и период являются противоположностями друг друга. Это означает, что мы можем использовать тот факт, что период обратно пропорционален частоте, чтобы решить проблему.

Для нашей последней задачи мы соберем все вместе и найдем частоту и период вращения лопасти вертолета. Допустим, у нас есть лопасть вертолета с числом оборотов в минуту (оборотов в минуту) 480. Используя нашу первую формулу, мы видим, что число оборотов в минуту представляет собой частоту. Здесь полные обороты лопасти вертолета — это наши повторяющиеся события, а минута — это время, за которое они происходят.

Однако мы хотим, чтобы наша частота была в единицах СИ. Это означает, что нам нужно время в секундах, а не в минутах. Если мы преобразуем 1 минуту в 60 секунд, мы можем получить ответ для частоты в герцах.

Теперь, когда у нас есть частота вращения лопасти вертолета в герцах, мы можем найти ее период, используя ту же формулу из нашей последней задачи.

Резюме урока

Количество раз, когда событие происходит за заданный промежуток времени, называется частотой ( f ) . Если бы мы записали это определение в виде уравнения, оно выглядело бы так.

Всякий раз, когда какое-либо событие повторяется, оно имеет связанную с ним частоту. Для единиц СИ мы записываем наши частоты в единицах герц или сокращенно Гц. Герц — это измерение, которое мы используем для описания того, сколько раз повторяющееся событие повторяется за одну секунду.

Один из наиболее распространенных способов расчета частоты — сравнение ее с периодом. Период ( T ) — количество времени, которое требуется для одного цикла повторяющегося события. Получается, что частота и период обратны друг другу. Это означает, что мы можем связать их с помощью следующих формул.

Чтобы разблокировать этот урок, вы должны быть участником Study.com.
Создайте свою учетную запись

По какой формуле найти частоту?

В общих чертах частота определяется путем деления количества событий на время, затраченное на события. Итак, если волна проходит мимо определенной точки 4 раза за одну секунду, то частота равна 4 раза за 1 секунду или 4 Гц.

Чему равна частота?

Частота равна количеству событий за определенный промежуток времени. Это может быть количество раз, которое колебание совершает взад-вперед в течение минуты, или количество раз, когда волна проходит определенную точку в секунду.

По какой формуле можно найти частоту, зная длину волны?

Если задана длина волны, формула для определения частоты представляет собой деление скорости волны на длину волны. Если скорость волны 6 м/с, а длина волны 2 м, то частота 6/2 = 3 Гц.

Зарегистрируйтесь для просмотра этого урока

Вы студент или преподаватель?

Разблокируйте свое образование

Убедитесь сами, почему 30 миллионов человек используют Study.com

Станьте участником Study.com и начните учиться прямо сейчас.

Стать участником

Уже зарегистрирован? Войти

Назад

Ресурсы, созданные учителями для учителей

Более 30 000 видеоуроков и учебные ресурсы‐все в одном месте.

Видеоуроки

Тесты и рабочие листы

Интеграция в классе

Планы уроков

Я определенно рекомендую Study.com своим коллегам. это как Учитель взмахнул волшебной палочкой и сделал работу за меня. Я чувствую, что это спасательный круг.

Дженнифер Б.

Учитель

Попробуй это сейчас

Спинка

единиц частоты и длины волны Рона Куртуса

SfC Home > Physics > Wave Motion >

Рон Куртус

Форма волны характеризуется амплитудой, длиной волны, частотой и скоростью. Амплитуда – это высота волны или ее интенсивность. Длина волны – это расстояние между максимумами амплитуды. Частота — это то, как часто максимумы или гребни перемещаются за заданную точку. И, наконец, скорость — или скорость движения волны — это произведение частоты, умноженной на длину волны ( v = fλ ).

единицы измерения частоты выражены в герцах (Гц) или кратных им единицах. единиц длины волны выражены в метрах, кратных или долях метра. По мере увеличения частоты длина волны уменьшается при условии, что скорость остается постоянной. Например, волны чрезвычайно высоких частот имеют очень короткие длины волн.

Экспоненциальные степени 10 используются, когда частоты или длины волн становятся очень большими. Очень короткие длины волн обозначаются как отрицательные экспоненты.

У вас могут возникнуть следующие вопросы:

• Что такое экспоненциальное представление числа 10?
• Что такое частотные термины?
• Что такое длина волны?

Этот урок ответит на эти вопросы. Полезный инструмент: Преобразование единиц

---

---

Степени 10

Удобным способом выражения больших и малых чисел является использование показателей или степеней 10 , которые кратны 10 .

Большие числа

Большое число, такое как 1 000 000 , можно обозначить как показатель степени или степень 10 , подсчитав количество нулей и записав число как 10 ⁶ 704042 6 или 1* 9 .

Если число было 300 000 000 , вы должны написать его как 3*10 ⁸ .

Если число было 2 524 200 , вы должны округлить его и использовать экспоненциальное представление числа меньше 10 с двумя десятичными знаками, например приблизительное значение 98 и 3E8 .

Маленькие числа

Следуя тому же методу для маленького числа 1/100,000 = 1/10 ⁵ , так как 100,000 имеет 5 нулей. Это можно записать как 10 ⁻⁵ . Обратите внимание, что десятичная версия 1/100 000 равна 0,00001 , который имеет только 4 нуля после запятой. Это то, о чем нужно знать. Некоторые другие примеры:

3/10 000 000 = 0,0000003 = 3*10 ⁻⁷

0,00252 = 2,52*10 ⁻⁴

0,000000004026 округляется до 4,03*10 ⁻⁹

Частоты

Частоты измеряются в герцах (Гц), что означает количество циклов или гребней волны в секунду. Вы можете записать частоту с версиями символа, как большое число или как показатель степени.

Символ	Номер	Экспонента
1 Гц (герц)	1 Гц	1 Гц
1 кГц (килогерц)	1000 Гц	1*10 3 Гц
1 МГц (мегагерц)	1 000 000 Гц	1*10 6 Гц
1 ГГц (гигагерц)	1 000 000 000 Гц	1*10 9 Гц

Частота некоторых волновых форм, таких как водная волна цунами, может меняться очень медленно. В таком случае частота может быть указана в циклах в минуту или час. 1/3600 Гц — это 1 цикл в час.

Длины волн

Длины волн обычно выражаются в метрической системе или системе СИ, поскольку более удобно иметь число, кратное 10. Длины волн могут варьироваться от многих километров до чрезвычайно коротких длин или долей метра.

Имя	метров	Экспонента
1 км (километр)	1000 м (метров)	1*10 3 м
1 м	1 м	1 м
1 см (сантиметр)	0,01 м	1*10 −2 м
1 мм (миллиметр)	0,001 м	1*10 −3 м
1 мкм (микрометр или микрон)	0,000001 м	1*10 −6 м
1 нм (нанометр)	0,000000001 м	1*10 −9 м
1 Å (ангстрем)	0,1 нм	1*10 −10 м

Резюме

Связь между частотой и длиной волны заключается в том, что при заданной скорости с увеличением частоты длина волны уменьшается. На очень высоких частотах у вас могут быть очень короткие волны.

Поскольку числа частот становятся очень большими, они обозначаются такими фразами, как «мега» и «гига» или степенью 10. Очень короткая длина волны обозначается как отрицательная экспонента.

---

Всегда делайте все возможное

---

Ресурсы и ссылки

Рон Куртус. Условия

Веб -сайты

Wave Motion Resources. покупки)

Книги с самым высоким рейтингом по Wave Motion

---

Поделитесь этой страницей

Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:

---

Студенты и исследователи

Веб-адрес этой страницы:
www.school-for-champions.com/science/
waves_units.htm

Разместите его в качестве ссылки на своем веб-сайте или в качестве ссылки в своем отчете, документе или диссертации.

Copyright © Ограничения

---

Где ты сейчас?

Школа чемпионов

Темы по физике

Единицы измерения частоты и длины волны

---

Калькулятор частоты | Period to Frequency and More

Создано Rita Rain

Отзыв от Dominik Czernia, кандидата наук, и Jack Bowater

Последнее обновление: 26 сентября 2022 г.

Содержание:

• Определение частоты и формула частоты
• Уравнение частоты по длине волны
• Как пользоваться калькулятором частоты?
• Пример: Как рассчитать частоту по периоду?
• Пример: Как найти частоту волны?
• Реальное применение
• Часто задаваемые вопросы

Калькулятор частоты позволит вам найти частоту волны по заданной длине волны и ее скорости или периоду в кратчайшие сроки. Вы можете выбрать скорость волны из предустановленного списка, так что вам не нужно запоминать.

В тексте вы также найдете определение частоты , две формулы частоты (отношение периода к частоте и длины волны к частоте) и несколько примеров, показывающих, как вычислять частоту.

Если вы хотите узнать больше о волнах, воспользуйтесь калькулятором длины волны, а если вы хотите узнать частоту музыкальных нот, воспользуйтесь калькулятором частоты нот.

Определение частоты и формула частоты

Посмотрите на следующую модель волны; это поможет вам понять термины, используемые в приведенном ниже определении частоты.

Источник: Британская энциклопедия

Частота — это количество полных волновых циклов в секунду . Другими словами, частота говорит нам, сколько гребней волны проходит данную точку за секунду.

Это определение частоты приводит нас к простейшей частотной формуле :

f=1Tf=\frac{1}{T}f=T1​

fff обозначает частоту, а TTT обозначает время, необходимое для завершения одного волновой цикл измеряется в секундах.

Единицей измерения частоты SI является Герц (Гц) , что равно 1/с (один цикл в секунду). Другие единицы частоты включают миллигерц (мГц), килогерц (кГц), мегагерц (МГц), гигагерц (ГГц) и терагерц (ТГц).

Частотное уравнение от длины волны

Посмотрите на другую картинку, которая позволит нам увидеть связь между частотой и длиной волны. Длина волны — это расстояние между двумя соседними гребнями (или впадинами). Другими словами — это длина одного волнового цикла. Чем длиннее длина волны, тем ниже частота :

Источник: Британская энциклопедия

Еще один факт, который нам нужен — скорость распространения волн (скорость волн) определяет, сколько из них пройдет заданную точку в секунду. Это означает , что чем выше скорость волны, тем выше частота .

Эти два соотношения между частотой и длиной волны (λ\lambdaλ) и между частотой и скоростью (vvv) приводят нас к следующему частотному уравнению :

f=vλf=\frac{v}{\lambda}f=λv​

Как пользоваться частотным калькулятором?

Наш калькулятор частоты включает вышеупомянутые формулы частоты. Таким образом, вы можете использовать его в качестве калькулятора периода для частоты или калькулятора длины волны для частоты.

Как использовать его в качестве калькулятора преобразования периода в частоту? (Как найти частоту, если известен период?)

1. Введите время, в течение которого происходит один цикл волны ( период ). Калькулятор определит частоту.

2. Вы можете использовать этот калькулятор для определения периода, если знаете его частоту.

Как использовать его в качестве калькулятора преобразования длины волны в частоту? (Как рассчитать частоту по длине волны?)

1. Введите скорость волны во второе поле или выберите тип волны и ее среду из списка в первом поле. По умолчанию у нас установлено значение свет в вакууме .

2. Введите длину волны, появится значение частоты.

Так что, в принципе, можно ввести любые две переменные, и сразу появится третья 😀

Пример: Как рассчитать частоту по периоду?

Чтобы развеять сомнения, как рассчитать частоту по периоду, разберем несколько простых примеров. Во-первых, вспомним частотное уравнение:

f=1Tf=\frac{1}{T}f=T1​

Пример 1:

Как найти частоту волны, в которой один цикл завершается за 0,25 s:

f=1T=10,25 s=4×1s\begin{align*} f&=\frac{1}{T}\\[1.2em] &=\frac{1}{0,25\ \text{s}}\\[1,2em] &= 4\times\frac{1}{\text{s}} \end{align*}f​=T1​=0,25 s1​=4×s1​​

Не забудьте преобразовать 1s\frac{1}{\text{s}}s1​ в единицу измерения частоты:

f=4 Hzf = 4\ \text{Hz}f=4 Hz

Пример 2:

Как найти частоту волны, в которой за 1 минуту происходит 360 циклов:

f=3601 m=36060 s=6s=6 Hz\begin{align*} f&=\frac{360}{1\ \text{m}}\\[1.2em] &=\frac{360}{60\ \text{s}}\\[1.2em] &= \frac{6}{\text{s}}\\[1.2em] &= 6\ \text{Гц} \end{align*}f​=1 m360​=60 s360​=s6​=6 Hz​

Пример: Как найти частоту волны?

На этот раз мы хотим узнать, как найти частоту волны, если известны скорость и длина волны. Вам необходимо использовать следующую формулу частоты:

f=vλf=\frac{v}{\lambda}f=λv​

Пример 1:

Скорость волны равна 320 м/с, а длина волны равна 8 м. Найдя его частоту, имеем:

f=vλ=320 мс8 m=40с≈40 Гц\begin{align*} f&=\frac{v}{\lambda}\\[1.2em] &=\frac{320\\tfrac{\text{m}}{\text{s}}}{8\ \text{m}}\\[1.2em] &= \frac{40}{\text{s}}\\[1.2em] &\около 40\ \text{Гц} \end{align*}f​=λv​=8 м320 см​=s40​≈40 Гц​

Пример 2:

Найдите частоту света, если длина волны равна 3000 км. Скорость волны равна 90 127 скорости света в вакууме 90 128, приблизительно равной 300 000 км300,\hspace{-0,05 см}000\ \tfrac{\text{км}}{\text{s}}300 000 скм​. Используя формулу частоты, получаем:

f=vλ=300 000 км3 000 км=100 с≈100 Гц\begin{align*} f&=\frac{v}{\lambda}\\[1.2em] &=\frac{300,\hspace{-0,05см}000\ \tfrac{\text{км}}{\text{s}}}{3,\hspace{-0,05cm}000\ \text{км} }\\[1.2em] &= \frac{100}{\text{s}}\\[1.2em] &\примерно 100\\текст{Гц} \end{align*}f​=λv​=3000 км300 000 skm​=s100​≈100 Гц​

Реальное приложение

В беспроводной связи у нас есть объем эллипсоида между антенной передатчика и антенной приемника . Эта область определяется расстоянием между антеннами и частотой беспроводной волны. Она называется Зона Френеля и выглядит так:

Из основной формулы зоны Френеля мы делаем вывод, что чем выше частота, тем меньший объем эллипсоида должен быть свободен для правильной беспроводной связи. Наоборот, для низкой частоты мы получаем большую зону Френеля, которую здания или деревья могут легко блокировать и, таким образом, создавать нестабильную беспроводную связь.

💡 Вы можете узнать больше о зоне Френеля, посмотрев наш Калькулятор зоны Френеля.

Волны с разной частотой вызывают биения и задаются вопросом, как рассчитать частоту биений, а объем камеры сильно влияет на частоту резонанса Гельмгольца.

Часто задаваемые вопросы

Как рассчитать частоту?

Вам необходимо знать либо длину волны и скорость, либо период волны (время, необходимое для завершения одного цикла волны). Если вы знаете период:

1. Преобразуйте в секунды, если нужно, и разделите 1 на период .
2. Результатом будет частота , выраженная в Герцах .

Если вы хотите рассчитать частоту по длине волны и скорости волны:

1. Убедитесь, что имеют одинаковые единицы измерения длины.
2. Разделите скорость волны на длину волны .
3. Преобразовать результат в герцы. 1/с равняется 1 Герцу.

Как найти длину волны по частоте?

1. Определить скорость волны.
2. Определить частоту.
3. Преобразовать Герц в 1/с.
4. Убедитесь, что скорость волны и частота имеют одну и ту же единицу времени.
5. Разделите скорость волны на частоту.

Какая связь между частотой и длиной волны?

Частота равна скорости волны, деленной на длину волны. Следовательно, чем длиннее длина волны, тем ниже частота, а чем короче длина волны, тем выше частота. Другими словами, 9Частота 0127 обратно пропорциональна длине волны .

В чем измеряется частота?

Частота волны измеряется в Герцах . 1 герц равен 1/с — один цикл в секунду. Связанные единицы включают миллигерц (одна тысячная герца), килогерц (тысяча герц), мегагерц (миллион герц) и гигагерц (миллиард герц). Единица названа в честь Генриха Рудольфа Герца, физика, доказавшего существование электромагнитных волн.

Как найти частоту волны?

1. Определить скорость волны.
2. Определить длину волны.
3. Убедитесь, что скорость волны и длина волны имеют одну и ту же единицу длины, например, если скорость выражается в метрах в секунду, длина волны должна быть выражена в метрах.
4. Разделите скорость волны на длину волны.
5. Преобразовать результат в герцы. Один герц равен 1/с — один цикл в секунду.

Какая частота у 5G?

5G, который является технологическим стандартом пятого поколения для сотовых сетей, работает в различных диапазонах частот, которые попадают в два частотных диапазона. Диапазон частот 1 — от 450 МГц до 6 ГГц , а диапазон частот 2 — от 24,25 ГГц до 52,6 ГГц .

Какой цвет имеет самую высокую частоту?

Фиолетовый — это цвет с самой высокой частотой , которая колеблется от 670 до 750 терагерц. На другой стороне спектра находится красный цвет с частотой от 430 до 480 терагерц.

Какая связь между частотой и энергией?

Энергия прямо пропорциональна частоте . Другими словами, чем выше частота, тем больше энергия. Связь между частотой и энергией описывается следующей формулой для энергии фотона:

E = h × f

«E» — символ энергии, «h» — постоянная Планка, а «f» обозначает частоту.

Какая волна имеет самую высокую частоту?

Гамма-лучи — это электромагнитные волны с наивысшей частотой , то есть более 10 ¹⁹ Гц. У них самая высокая энергия и самая короткая длина волны среди всех электромагнитных волн. Их высокая энергия позволяет им отрывать электроны от атомов и повреждать живые клетки. Источниками гамма-излучения являются нейтронные звезды, сверхновые звезды, ядерные взрывы и молнии.

Как получить период из частоты?

1. Формула для периода: T = 1 / f , где «T» — период — время, необходимое для завершения одного цикла, а «f» — частота.
2. Чтобы получить период из частоты, сначала преобразуйте частоту из герц в 1/с .
3. Теперь делим 1 на частоту . Результатом будет время (период), выраженное в секундах.

Rita Rain

Скорость волны

Скорость волны (v)

Длина волны (λ)

Период (T)

Частота (f)

Посмотреть 22 похожих калькулятора волн 🔊

Акустический импедансАльфвеновская скоростьБитовая частота… Еще 19

Единица частоты — символ, формула Методы измерения и примеры

Согласно физике, частота обычно определяется как количество волн, проходящих через фиксированную точку в единицу времени. Частоту также можно определить как количество циклов или колебаний тела, совершаемых в одну единицу времени при периодическом движении. Периодическое движение тела может быть в виде одного цикла или одной вибрации, которая проходит через ряд событий или положений и возвращается в исходное состояние. Что похоже на угловую скорость или простое гармоническое движение.

В этой статье объясняется, что такое частота, формула частоты, единица измерения частоты, методы измерения частоты, виды частоты с примерами приведены здесь.

(Изображение будет загружено в ближайшее время)

Как рассчитать частоту?

Частоту волны можно рассчитать, учитывая время, необходимое волне для совершения одного цикла или одного колебания. Если волне требуется ½ секунды, чтобы завершить один цикл или вибрацию, то частота волны равна 2 секундам. Если волне требуется около 1/100 часа для завершения цикла или вибрации, то частота волны равна 100 в час.

Обычно частота волны обратно пропорциональна периоду времени или интервалу времени.

Это означает, что Частота (f) = 1/время или 1/временной интервал.

В среднем Луне требуется немногим более 12 циклов в год, чтобы совершить оборот вокруг Земли. Точно так же частота струны в скрипке составляет около 440 колебаний или циклов в секунду.

Символы частоты

Частота волны обычно обозначается словом (f). Иногда частота волны может быть представлена ​​греческой буквой ню (𝛎) и омега (ω). Как правило, греческое слово ню (𝛎) может использоваться для определения частоты электромагнитных волн, рентгеновских, ультрафиолетовых и гамма-лучей. Букву Омега (ω) можно использовать для описания угловой частоты объекта или частицы. Угловая частота показывает направление вращения объекта или оборот объекта в радианах в единицу времени.

Немецкий физик Генрих Рудольф Герц нашел выражение для обозначения частоты в Международной электротехнической комиссии в 1930 году. Единицей частоты в системе СИ является герц (Гц). Итак, единица измерения частоты обычно обозначается как Герц.

Один герц равен одному циклу в секунду. 1000 Гц соответствует одному килогерцу (кГц), а 1 000 000 Гц соответствует одному мегагерцу (МГц). В спектроскопии частота волны также может быть представлена ​​другими словами, такими как волновые числа, количество волн на единицу расстояния и т. д. Здесь циклы волн обычно исчисляются секундами. И традиционной единицей для расчета вращающихся механических устройств является число оборотов в минуту (об/мин). Один герц (Гц) равен 60 об/мин.

(Изображение будет загружено в ближайшее время)

Типы частоты

Угловая частота

Скорость изменения углового смещения или скорость изменения аргумента синусоидальной волны или скорость изменения фазы синусоидальной формы волны определяется как угловая частота. Угловая частота обычно выражается в виде омеги (ω).

y(t) = sin(θ(t)) = sin (ωt) = sin (2πft)

dθ/dt= ω = 2πf

Угловая частота обычно измеряется в радианах в секунду (рад/ с). Для дискретного сигнала угловая частота может быть выражена в радианах на интервал дискретизации. Потому что сигнал дискретного времени является безразмерной величиной. Обычно угловая частота больше частоты боеприпасов в 2π раза.

Пространственная частота

Пространственная частота аналогична временной частоте. Но временная ось во временной частоте заменяется одной или несколькими пространственными осями.

y(t) = sin(θ(t, x)) = sin (ωt + kx)

dθ/dx= k

Здесь длина волны k представляет собой пространственную частоту и измеряется в радианах на метр. Если волна имеет более одного пространственного измерения, то волновые числа являются векторными величинами.

Если периодические волны находятся в средах без дисперсии, то частота будет находиться в обратной зависимости от длины волны λ. В диспергирующих средах частота f синусоидальной волны прямо пропорциональна фазовой скорости v и обратно пропорциональна длине волны λ.

Можно представить как

f = v/ λ

Для электромагнитных волн, движущихся в вакууме, скорость заменяется скоростью света. Итак, v = с. Тогда частоту можно вычислить по формуле f = c /  λ

. Если монохроматический свет распространяется из одной среды в другую, то длина волны и скорость волны изменятся, а частота останется прежней.

Что такое совокупная частота?

Сумма общего количества частот, лежащих ниже или выше эталонного значения, называется кумулятивной частотой.

Что такое распределение частот?

Распределение частот представляет собой графическое или табличное представление частоты, наблюдаемой наблюдателями в определенное время. Частотное распределение бывает трех типов: негруппированное частотное распределение, групповое или кумулятивное частотное распределение и относительное частотное распределение.

Что такое полигон частот?

Графическое представление частотного распределения известно как полигон частот. Этот метод помогает анализировать формы распределения.

Что такое частотная модуляция?

Частотная модуляция является одним из наиболее часто используемых методов модуляции в системе связи. Если частота несущих волн модулируется в соответствии с частотой волны сообщения, то метод модуляции известен как частотная модуляция. Обычно они предпочитают такие методы, так как частота волны сообщения не может передаваться на большие расстояния без потерь.

(Изображение скоро будет загружено)

Приборы для измерения частоты 

• В старину люди использовали стробоскопы для измерения частоты вращения или вибрации объектов.

• Люди использовали электрическое устройство, называемое частотомером, для расчета высокочастотных волн. Частотомер показывает результат в герцах.

• Частоту волн, лежащую выше уровня частотомера, можно измерить гетеродинным методом.

В этой статье подробно описаны формула частоты, символы частоты, типы частоты, многоугольник частоты, частотная модуляция, инструменты, которые используются для измерения частоты волн.

Физика Highworth — Измерение волн Карточки

Похожие карточки

Пожалуйста, войдите, чтобы добавить в папки.

Войти

Вы создали 2 папки. Пожалуйста, обновитесь до Cram Premium, чтобы создавать сотни папок!

Обновление

• Перемешать

  Включить

  Выключить

• В алфавитном порядке

  Включить

  Выключить

• Передний Первый

  Включить

  Выключить

• Обе стороны

  Включить

  Выключить

• Читать

  Включить

  Выключить

Чтение. ..

Фронт

Диапазон карт для изучения

через

Кнопка воспроизведения

Кнопка воспроизведения

Прогресс

1/17

Нажмите, чтобы перевернуть

Используйте клавиши со стрелками ВЛЕВО и ВПРАВО для перемещения между карточками;

Используйте клавиши со стрелками ВВЕРХ и ВНИЗ, чтобы перевернуть карту;

H показать подсказку;

A читает текст в речь;

• Делиться
• Распечатать
• Экспорт
• Клон

17 карт в этом наборе

• Передняя часть
• Спина

	Назовите три свойства, которые мы используем для описания волн.	Волны можно описать по их амплитуде, длине волны и частоте.
	Как рассчитать скорость волны?	Скорость волны можно рассчитать по ее частоте и длине волны.
	Объясните амплитуду.	Амплитуда волны – это ее максимальное отклонение от невозмущенного положения. Амплитуда — это не расстояние между вершиной и основанием волны.
	Объясните длину волны.	Длина волны — это расстояние между точкой одной волны и той же точкой следующей волны. Часто проще всего измерить это расстояние от гребня одной волны до гребня следующей волны, но не имеет значения, где именно, если это одна и та же точка в каждой волне.
	Объясните частоту.	Частота волны – это количество волн, создаваемых источником каждую секунду. Это также количество волн, которые каждую секунду проходят через определенную точку.
	Какова единица измерения частоты?	Единицей частоты является герц (Гц). Килогерцы (кГц), мегагерцы (МГц) и гигагерцы (ГГц) обычно используются, когда волны имеют очень высокие частоты.
	Что такое разрежение? Что такое сжатие?	Разрежение – это рассредоточение частиц. Сжатие — это сжатие частиц. Продольные волны показывают области сжатия и разрежения.
	Как рассчитать скорость волны?	Скорость волны связана с ее частотой и длиной волны согласно следующему уравнению: v = f × λ v — скорость волны в метрах в секунду, м/с f — частота в герцах, Гц λ (лямбда) – длина волны в метрах, м.
	Десять волн проходят точку на веревке за 4 с. Какова их частота?	10 волн ÷ 4 с = 2,5 Гц.¸
	Пять волн имеют длину 25 см и проходят точку за 1 с. Что такое: (а) длина волны? (б) частота?	(a) 25 см ÷ 5 волн = 5 см (b) 5 волн ÷ 1 с = 5 Гц (или 25 см/с ¸ 5 см = 5 Гц)
	Волны в пружине имеют частоту 8 Гц и распространяются со скоростью 4 м/с. Какова их длина волны?	4 м/с ÷ 8 Гц = 0,5 м
	Световые волны имеют длину волны 0,0000005 м и частоту 600 000 000 000 000 Гц. Какова скорость света?	0,000 000 5 м × 600 000 000 000 000 Гц = 300 000 000 м/с.
	Водяные волны с длиной волны 1,5 см проходят через резервуар со скоростью 0,021 м/с. Какова их частота?	1,5 см = 0,015 м, 0,021 м/с ÷ 0,015 м = 1,4 Гц
	Если частоту волн увеличить вдвое, что произойдет с: (а) скоростью волн? (б) длина волны?	(а) Скорость волны остается прежней. (б) Длина волны уменьшается вдвое.
	Продольные волны распространяются по стали со скоростью 6000 м/с. Если частота 2000 Гц, каково расстояние между центром сжатия и центром разрежения?	Длина волны = 6000 м/с ÷ 2000 Гц = 3 м, Расстояние = ½ длины волны = 1,5 м
	Нарисуйте схему поперечной волны и с ее помощью объясните, что подразумевается под длиной волны, амплитудой, частотой и скоростью волны, а также в каких единицах измеряется каждая из этих величин.	Скорость волны — это скорость, с которой волна распространяется в среде; скорость волны измеряется в м/с Длина волны – это расстояние для одной целой волны или от гребня до гребня; длина волны измеряется в метрах Частота – это число волн/циклов в секунду и измеряется в герцах.
	Какие ключевые моменты следует помнить?	Частота волны — это количество циклов в секунду. Частота измеряется в герцах (Гц). Длина волны — это длина одной полной волны. Амплитуда – это максимальное смещение. ν = f × λ скорость волны = частота × длина волны. Скорость волны зависит от среды.

Подсчет ряби в световой волне

25 мая 2000 г. • Физ. Rev. Focus 5, 24

Новая схема позволяет измерять оптические частоты так же точно, как и в лучших лабораториях мира, используя только один лазер.

Bell Labs, Lucent Technologies

Радужное волокно. Недавно разработанное оптическое волокно может превращать монохроматический свет в белый свет, охватывающий весь видимый спектр. (На этом изображении преобладают разные цвета в разных местах вдоль волокна.) Волокно является важной частью новой схемы измерения оптических частот настолько точно, насколько это возможно в лучших лабораториях с использованием только одного лазера. Радужное волокно. Недавно разработанное оптическое волокно может превращать монохроматический свет в белый свет, охватывающий весь видимый спектр. (На этом изображении преобладают разные цвета в разных местах вдоль волокна.) Волокно является важной частью … Подробнее

Bell Labs, Lucent Technologies

Радужное волокно. Недавно разработанное оптическое волокно может превращать монохроматический свет в белый свет, охватывающий весь видимый спектр. (На этом изображении преобладают разные цвета в разных местах вдоль волокна.) Волокно является важной частью новой схемы измерения оптических частот настолько точно, насколько это возможно в лучших лабораториях с использованием только одного лазера.

×

Измерить частоту сердцебиения довольно просто — просто посчитайте удары за определенный период времени. Даже радиочастотный сигнал на частоте 100 МГц может быть измерен электронным счетчиком почти таким же образом. Но световая волна 600 ТГц (6×1014 Гц) колеблется слишком быстро, чтобы ее можно было сосчитать, поэтому для прецизионных измерений оптических частот традиционно использовались огромные и громоздкие установки, доступные только нескольким лабораториям по всему миру. В 29Май PRL группа физиков сообщает, что они радикально упростили процесс до такой степени, что почти любая физическая лаборатория может измерять оптические частоты почти так же точно, как это делают институты стандартов. Новая методика приведет к новым проверкам множества фундаментальных физических принципов.

Измерение с точностью до 12 знаков после запятой — это не просто скучная работа с деталями, считает Джон Холл из Национального института стандартов и технологий (NIST) и Университета Колорадо в Боулдере. Поскольку за последнее столетие измерения света, связанного с атомными переходами, стали более точными, исследователи узнали больше о квантовом мире и физике атомов. «Это как одна из тех русских кукол — вы никогда не подходите к последней», — говорит Холл.

В 1983 году Холл и его коллеги опубликовали самое точное на тот момент измерение оптической частоты, но для этого потребовалось восемь физиков и, возможно, 20 лазеров. Начиная с сигнала 9 ГГц цезиевых атомных часов, который определяет единицу частоты (Герц), им нужно было удвоить и утроить частоты различных осцилляторов в «цепочке», чтобы напрямую соединиться с измеряемой частотой света. . Тщательное сравнение каждой частоты в цепочке со следующей позволяет эквивалентно подсчету количества циклов световой волны каждую секунду.

Холл, Тед Хенш из Института Макса Планка в Гархинге, Германия, и их коллеги преодолели этот пробел за один шаг. В системе используется лазер, генерирующий сверхкороткие световые импульсы — 12 фс или 1,2 × 10–14 с в ширину — с частотой около 100 МГц, которые синхронизируются с атомными часами. Спектр (преобразование Фурье) этого света представляет собой «гребенку» ультраузких линий, разнесенных по частоте через каждые 100 МГц, в ограниченном диапазоне световых частот. Команда посылает этот свет через оптическое волокно нового типа, которое распределяет красноватые импульсы по большей части видимого диапазона, создавая гребенку с миллионами линий, расстояние между которыми точно определяется цезиевыми часами. По сравнению, скажем, с утроением частоты лазера для получения третьей гармоники — насколько это было возможно в прошлом — гребенка позволяет получить доступ к четырехмиллионной гармонике. «Это четыре миллиона стабильных лазеров», — говорит Холл.

В идеале частоту любого лазерного луча можно было бы определить, используя стандартные методы определения частотного расстояния между линией лазера и одной из линий гребенки. Единственная проблема заключается в том, что, хотя шаг гребенки точно известен (около 100 МГц), ее абсолютное положение не определено. Поэтому команда использовала основные линии и линии второй гармоники неодимового: YAG-лазера (частоты различаются ровно в два раза), чтобы получить дополнительную информацию, необходимую для определения любой оптической частоты. В процессе они сделали самое точное измерение частоты YAG на уровне 10-11. Они также измерили две стандартные лазерные линии с одинаковой точностью, чтобы доказать, что система дает результаты, равные или лучшие, чем у международных агентств по стандартизации. Более поздние уточнения, недавно опубликованные в журнале Science, позволили команде исключить YAG-лазер из установки.

Холл предполагает, что через пять лет на рынке появится коммерческий прибор, который позволит любому физику измерять оптическую частоту вплоть до уровня кГц так же легко, как сейчас он измеряет радиочастоты. Технология уже породила эксперименты, которые расширяют теории фундаментальной атомной физики до новых пределов. Лео Холлберг, также из Национального института стандартов и технологий, но не участвовавший в работе напрямую, говорит, что новая методика — это «революция в измерении частоты», которая, скорее всего, приведет к созданию новых сверхточных часов, основанных на оптических частотах, а не на микроволнах современных атомных часов. . Холл ожидает много непредсказуемых применений для устройства, которое обеспечивает четыре миллиона стабильных лазерных линий одновременно.

Дополнительная информация

• История Nobel Focus 2005 года посвящена этой статье.

---

Области субъекта

Оптика

Связанные статьи

Оптика

Shining Light на электронном микроскопии

СЕНТЯБРЯ 26, 2022

A NEW MATER, который использует LOSER LIREN LIREN LISTEN LISTEN LISTEN LISTEN LISTEN LISER LISTEN LISER. разрешение электронной микроскопии. Подробнее »

Физика конденсированного состояния

Твердое наблюдение сильной керровской нелинейности

19 сентября 2022 г.

Исследователи продемонстрировали, что твердое тело может проявлять усиленное нелинейное оптическое явление, обычно наблюдаемое только в холодных атомарных газах.