Список физических величин | это… Что такое Список физических величин?
Размерности физических величин зависят от выбранной системы единиц либо от выбранной системы физических величин. В приведенной таблице показаны размерности физических величин, принятые в СИ.
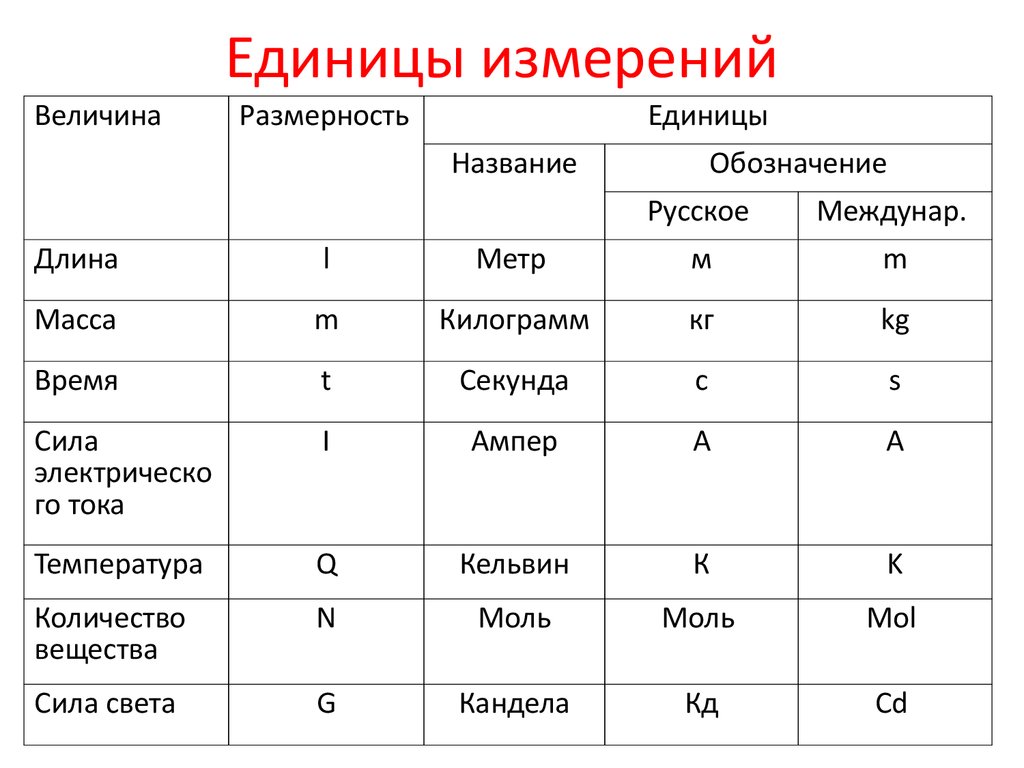
| Основные величины | Символ | Описание | Единица измерения в СИ | Примечания |
|---|---|---|---|---|
| Длина | l | Протяжённость объекта в одном измерении. | метр (м) | |
| Масса | m | Величина, определяющая инерционные и гравитационные свойства тел. | килограмм (кг) | Экстенсивная величина |
| Время | t | Продолжительность события. | секунда (с) | |
| Сила тока | I | Протекающий в единицу времени заряд. | ампер (А) | |
| Температура | T | Средняя кинетическая энергия частиц объекта. | кельвин (К) | Интенсивная величина |
| Количество вещества | ν | Количество частиц, отнесенное к количеству атомов в 0,012 кг 12C. | моль (моль) | Экстенсивная величина |
| Сила света | J | Количество световой энергии, излучаемой в заданном направлении в единицу времени. | кандела (кд) | Световая, экстенсивная величина |
| Производные величины | Символ | Описание | Единица СИ | Примечания |
|---|---|---|---|---|
| Площадь | S | Протяженность объекта в двух измерениях. | м2 | |
| Объём | V | Протяжённость объекта в трёх измерениях. | м3 | экстенсивная величина |
| Скорость | v | Быстрота изменения координат тела. | м/с | вектор |
| Ускорение | a | Быстрота изменения скорости объекта. | м/с² | вектор |
| Импульс | p | Произведение массы и скорости тела. | кг·м/с | экстенсивная, сохраняющаяся величина |
| Сила | F | Действующая на объект внешняя причина ускорения. | кг·м/с2 (ньютон, Н) | вектор |
| Механическая работа | A | Скалярное произведение силы и перемещения. | кг·м2/с2 (джоуль, Дж) | скаляр |
| Энергия | E | Способность тела или системы совершать работу. | кг·м2/с2 (джоуль, Дж) | экстенсивная, сохраняющаяся величина, скаляр |
| Мощность | P | Скорость изменения энергии. | кг·м2/с3 (ватт, Вт) | |
| Давление | p | Сила, приходящаяся на единицу площади. | кг/(м·с2) (паскаль, Па) | интенсивная величина |
| Плотность | ρ | Масса на единицу объёма. | кг/м3 | интенсивная величина |
| Поверхностная плотность | ρA | Масса на единицу площади. | кг/м2 | |
| Линейная плотность | ρl | Масса на единицу длины. | кг/м | |
| Количество теплоты | Q | Энергия, передаваемая от одного тела к другому немеханическим путём | кг·м2/с2 (джоуль, Дж) | скаляр |
| Электрический заряд | q | А·с (кулон, Кл) | экстенсивная, сохраняющаяся величина | |
| Напряжение | U | Изменение потенциальной энергии, приходящееся на единицу заряда. | м2·кг/(с3·А) (вольт, В) | скаляр |
| Электрическое сопротивление | R | сопротивление объекта прохождению электрического тока | м2·кг/(с3·А2) (ом, Ом) | скаляр |
| Магнитный поток | Величина, учитывающая интенсивность магнитного поля и занимаемую им область. | кг/(с2·А) (вебер, Вб) | ||
| Частота | ν | Число повторений события за единицу времени. | с−1 (герц, Гц) | |
| Угол | α | Величина изменения направления. | радиан (рад) | |
| Угловая скорость | ω | Скорость изменения угла. | с−1 (радиан в секунду) | |
| Угловое ускорение | ε | Быстрота изменения угловой скорости | с−2 (радиан на секунду в квадрате) | |
| Момент инерции | I | Мера инертности объекта при вращении. | кг·м2 | тензорная величина |
| Момент импульса | L | Мера вращения объекта. | кг·м2/c | сохраняющаяся величина |
| Момент силы | M | Произведение силы на длину перпендикуляра, опущенного из точки на линию действия силы. | кг·м2/с2 | вектор |
| Телесный угол | Ω | стерадиан (ср) |
Обозначения в физике — единицы измерения физических величин
Каждое измерение — это сравнение измеряемой величины с другой, однородной с ней величиной, которую считают единичной. Теоретически единицы для всех величин в физике можно выбрать независимыми друг от друга. Но это крайне неудобно, так как для каждой величины следовало бы ввести свой эталон. Кроме этого во всех физических уравнениях, которые отображают связь между разными величинами, возникли бы числовые коэффициенты.
Основная особенность используемых в настоящее время систем единиц состоит в том, что между единицами разных величин имеются определенные соотношения. Эти соотношения установлены теми физическими законами (определениями), которыми связываются между собой измеряемые величины. Так, единица скорости выбрана таким образом, что она выражается через единицы расстояния и времени. При выборе единиц скорости используется определение скорости. Единицу силы, например, устанавливают при помощи второго закона Ньютона.
При выборе единиц скорости используется определение скорости. Единицу силы, например, устанавливают при помощи второго закона Ньютона.
При построении определенной системы единиц, выбирают несколько физических величин, единицы которых устанавливают независимо друг от друга. Единицы таких величин называют основными. Единицы остальных величин выражают через основные, их называют производными.
Содержание
- Таблица единиц измерения «Пространство и время»
- Таблица единиц измерения «Механика»
- Таблица единиц измерения «Периодические явления, колебания и волны»
- Таблица единиц измерения «Тепловые явления»
- Таблица единиц измерения «Молекулярная физика»
- Таблица единиц измерения «Электричество и магнетизм»
- Таблица единиц измерения «Оптика, электромагнитное излучение»
- Таблица единиц измерения «Акустика»
- Таблица единиц измерения «Атомная и ядерная физика. Радиоактивность»
- Обозначения в физике с несколькими буквами
- Специальные символы
- Скобки
- Диакритические знаки
Таблица единиц измерения «Пространство и время»
Физическая величина | Символ | Единица измерения физической величины | Ед. | Описание | Примечания |
Длина | l, s, d | метр | м | Протяжённость объекта в одном измерении. | |
Площадь | S | квадратный метр | м2 | Протяженность объекта в двух измерениях. | |
Объем, вместимость | V | кубический метр | м3 | Протяжённость объекта в трёх измерениях. | экстенсивная величина |
Время | t | секунда | с | Продолжительность события. | |
Плоский угол | α, φ | радиан | рад | Величина изменения направления. | |
Телесный угол | α, β, γ | стерадиан | ср | Часть пространства | |
Линейная скорость | v | метр в секунду | м/с | Быстрота изменения координат тела. | вектор |
Линейное ускорение | a, w | метр в секунду в квадрате | м/с2 | Быстрота изменения скорости объекта. | вектор |
Угловая скорость | ω | радиан в секунду | рад/с = (с−1) | Скорость изменения угла. | |
Угловое ускорение | ε | радиан на секунду в квадрате | рад/с2 = (с−2) | Быстрота изменения угловой скорости |
Таблица единиц измерения «Механика»
Физическая величина | Символ | Единица измерения физической величины | Ед. изм. физ. вел. | Описание | Примечания |
Масса | m | килограмм | кг | Величина, определяющая инерционные и гравитационные свойства тел. | экстенсивная величина |
Плотность | ρ | килограмм на кубический метр | кг/м3 | Масса на единицу объёма. | интенсивная величина |
Поверхностная плотность | ρA | Масса на единицу площади. | кг/м2 | Отношение массы тела к площади его поверхности | |
Линейная плотность | ρl | Масса на единицу длины. | кг/м | Отношение массы тела к его линейному параметру | |
Удельный объем | v | кубический метр на килограмм | м3/кг | Объём, занимаемый единицей массы вещества | |
Массовый расход | Qm | килограмм в секунду | кг/с | Масса вещества, которая проходит через заданную площадь поперечного сечения потока за единицу времени | |
Объемный расход | Qv | кубический метр в секунду | м3/с | Объёмный расход жидкости или газа | |
Импульс | P | килограмм-метр в секунду | кг•м/с | Произведение массы и скорости тела. | экстенсивная, сохраняющаяся величина |
Момент импульса | L | килограмм-метр в квадрате в секунду | кг•м2/с | Мера вращения объекта. | сохраняющаяся величина |
Момент инерции | J | килограмм-метр в квадрате | кг•м2 | Мера инертности объекта при вращении. | тензорная величина |
Сила, вес | F, Q | ньютон | Н | Действующая на объект внешняя причина ускорения. | вектор |
Момент силы | M | ньютон-метр | Н•м = (кг·м2/с2) | Произведение силы на длину перпендикуляра, опущенного из точки на линию действия силы. | вектор |
Импульс силы | I | ньютон-секунда | Н•с | Произведение силы на время её действия | вектор |
Давление, механическое напряжение | p, σ | паскаль | Па = (кг/(м·с2)) | Сила, приходящаяся на единицу площади. | интенсивная величина |
Работа | A | джоуль | Дж = (кг·м2/с2) | Скалярное произведение силы и перемещения. | скаляр |
Энергия | E, U | джоуль | Дж = (кг·м2/с2) | Способность тела или системы совершать работу. | экстенсивная, сохраняющаяся величина, скаляр |
Мощность | N | ватт | Вт = (кг·м2/с3) | Скорость изменения энергии. |
Таблица единиц измерения «Периодические явления, колебания и волны»
Физическая величина | Символ | Единица измерения физической величины | Ед. изм. физ. вел. | Описание | Примечания |
Период | T | секунда | с | Промежуток времени, за который система совершает одно полное колебание | |
Частота периодического процесса | v, f | герц | Гц = (с−1) | Число повторений события за единицу времени. | |
Циклическая (круговая) частота | ω | радиан в секунду | рад/с | Циклическая частота электромагнитных колебаний в колебательном контуре. | |
Частота вращения | n | секунда в минус первой степени | с-1 | Периодический процесс, равный числу полных циклов, совершённых за единицу времени. | |
Длина волны | λ | метр | м | Расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе. | |
Волновое число | k | метр в минус первой степени | м-1 | Пространственная частота волны |
Таблица единиц измерения «
Тепловые явления»Физическая величина | Символ | Единица измерения физической величины | Ед. | Описание | Примечания |
Температура | T | кельвин | К | Средняя кинетическая энергия частиц объекта. | Интенсивная величина |
Температурный коэффициент | α | кельвин в минус первой степени | К-1 | Зависимость электрического сопротивления от температуры | |
Температурный градиент | gradT | кельвин на метр | К/м | Изменение температуры на единицу длины в направлении распространения теплоты. | |
Теплота (количество теплоты) | Q | джоуль | Дж = (кг·м2/с2) | Энергия, передаваемая от одного тела к другому немеханическим путём | |
Удельная теплота | q | джоуль на килограмм | Дж/кг | Кол-во теплоты, которое необходимо подвести к веществу, взятому при температуре плавления, чтобы расплавить его. | |
Теплоемкость | C | джоуль на кельвин | Дж/К | Кол-во теплоты, поглощаемой (выделяемой) телом в процессе нагревания. | |
Удельная теплоемкость | c | джоуль на килограмм-кельвин | Дж/(кг•К) | Теплоёмкость единичной массы вещества. | |
Энтропия | S | джоуль на килограмм | Дж/кг | Мера необратимого рассеивания энергии или бесполезности энергии. |
Таблица единиц измерения «
Молекулярная физика»Физическая величина | Символ | Единица измерения физической величины | Ед. | Описание | Примечания |
Количество вещества | v, n | моль | моль | Количество однотипных структурных единиц, из которых состоит вещество. | Экстенсивная величина |
Молярная масса | M, μ | килограмм на моль | кг/моль | Отношение массы вещества к количеству молей этого вещества. | |
Молярная энергия | Hмол | джоуль на моль | Дж/моль | Энергия термодинамической системы. | |
Молярная теплоемкость | смол | джоуль на моль-кельвин | Дж/(моль•К) | Теплоёмкость одного моля вещества. | |
Концентрация молекул | c, n | метр в минус третьей степени | м-3 | Число молекул, содержащихся в единице объема. | |
Массовая концентрация | ρ | килограмм на кубический метр | кг/м3 | Отношение массы компонента, содержащегося в смеси, к объёму смеси. | |
Молярная концентрация | смол | моль на кубический метр | моль/м3 | Содержание компонента относительно всей смеси. | |
Подвижность ионов | В, μ | квадратный метр на вольт-секунду | м2/(В•с) | Коэффициент пропорциональности между дрейфовой скоростью носителей и приложенным внешним электрическим полем. |
Таблица единиц измерения «
Электричество и магнетизм»Физическая величина | Символ | Единица измерения физической величины | Ед. изм. физ. вел. | Описание | Примечания |
Сила тока | I | ампер | А | Протекающий в единицу времени заряд. | |
Плотность тока | j | ампер на квадратный метр | А/м2 | Сила электрического тока, протекающего через элемент поверхности единичной площади. | Векторная величина |
Электрический заряд | Q, q | кулон | Кл = (А·с) | Способность тел быть источником электромагнитных полей и принимать участие в электромагнитном взаимодействии. | экстенсивная, сохраняющаяся величина |
Электрический дипольный момент | p | кулон-метр | Кл•м | Электрические свойства системы заряженных частиц в смысле создаваемого ею поля и действия на неё внешних полей. | |
Поляризованность | P | кулон на квадратный метр | Кл/м2 | Процессы и состояния, связанные с разделением каких-либо объектов, преимущественно в пространстве. | |
Напряжение | U | вольт | В | Изменение потенциальной энергии, приходящееся на единицу заряда. | скаляр |
Потенциал, ЭДС | φ, σ | вольт | В | Работа сторонних сил (некулоновских) по перемещению заряда. | |
Напряженность электрического поля | E | вольт на метр | В/м | Отношение силы F, действующей на неподвижный точечный заряд, помещённый в данную точку поля, к величине этого заряда q | |
Электрическая емкость | C | фарад | Ф | Мера способности проводника накапливать электрический заряд | |
Электрическое сопротивление | R, r | ом | Ом = (м2·кг/(с3·А2)) | сопротивление объекта прохождению электрического тока | |
Удельное электрическое сопротивление | ρ | ом-метр | Ом•м | Способность материала препятствовать прохождению электрического тока | |
Электрическая проводимость | G | сименс | См | Способность тела (среды) проводить электрический ток | |
Магнитная индукция | B | тесла | Тл | Векторная величина, являющаяся силовой характеристикой магнитного поля | Векторная величина |
Магнитный поток | Ф | вебер | Вб = (кг/(с2·А)) | Величина, учитывающая интенсивность магнитного поля и занимаемую им область. | |
Напряженность магнитного поля | H | ампер на метр | А/м | Разность вектора магнитной индукции B и вектора намагниченности M | Векторная величина |
Магнитный момент | pm | ампер-квадратный метр | А•м2 | Величина, характеризующая магнитные свойства вещества | |
Намагниченность | J | ампер на метр | А/м | Величина, характеризующая магнитное состояние макроскопического физического тела. | векторная величина |
Индуктивность | L | генри | Гн | Коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и полным магнитным потоком | |
Электромагнитная энергия | N | джоуль | Дж = (кг·м2/с2) | Энергия, заключенная в электромагнитном поле | |
Объемная плотность энергии | w | джоуль на кубический метр | Дж/м3 | Энергия электрического поля конденсатора | |
Активная мощность | P | ватт | Вт | Мощность в цепи переменного тока | |
Реактивная мощность | Q | вар | вар | Величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи переменного тока | |
Полная мощность | S | ватт-ампер | Вт•А | Суммарная мощность с учетом активной и реактивной ее составляющих, а также отклонения формы тока и напряжения от гармонической |
Таблица единиц измерения «Оптика, электромагнитное излучение»
Физическая величина | Символ | Единица измерения физической величины | Ед. | Описание | Примечания |
Сила света | J, I | кандела | кд | Количество световой энергии, излучаемой в заданном направлении в единицу времени. | Световая, экстенсивная величина |
Световой поток | Ф | люмен | лм | Физическая величина, характеризующая количество «световой» мощности в соответствующем потоке излучения | |
Световая энергия | Q | люмен-секунда | лм•с | Физическая величина, характеризует способность энергии, переносимой светом, вызывать у человека зрительные ощущения | |
Освещенность | E | люкс | лк | Отношение светового потока, падающего на малый участок поверхности, к его площади. | |
Светимость | M | люмен на квадратный метр | лм/м2 | Световая величина, представляющая собой световой поток | |
Яркость | L, B | кандела на квадратный метр | кд/м2 | Сила света, излучаемая единицей площади поверхности в определенном направлении | |
Энергия излучения | E, W | джоуль | Дж = (кг·м2/с2) | Энергия, переносимая оптическим излучением |
Таблица единиц измерения «Акустика»
Физическая величина | Символ | Единица измерения физической величины | Ед. | Описание | Примечания |
Звуковое давление | p | паскаль | Па | Переменное избыточное давление, возникающее в упругой среде при прохождении через неё звуковой волны | |
Объемная скорость | c, V | кубический метр в секунду | м3/с | Отношение объема сырья, подаваемого в реактор в час к объему катализатора | |
Скорость звука | v, u | метр в секунду | м/с | Скорость распространения упругих волн в среде | |
Интенсивность звука | l | ватт на квадратный метр | Вт/м2 | Величина, характеризующая мощность, переносимую звуковой волной в направлении распространения | скалярная физическая величина |
Акустическое сопротивление | Za, Ra | паскаль-секунда на кубический метр | Па•с/м3 | Отношение амплитуды звукового давления в среде к колебательной скорости её частиц при прохождении через среду звуковой волны | |
Механическое сопротивление | Rm | ньютон-секунда на метр | Н•с/м | Указывает силу, необходимую для движения тела при каждой частоте |
Таблица единиц измерения «
Атомная и ядерная физика. Радиоактивность»
Радиоактивность»Физическая величина | Символ | Единица измерения физической величины | Ед. изм. физ. вел. | Описание | Примечания |
Масса (масса покоя) | m | килограмм | кг | Масса объекта, находящегося в состоянии покоя. | |
Дефект массы | Δ | килограмм | кг | Величина, выражающая влияние внутренних взаимодействий на массу составной частицы | |
Элементарный электрический заряд | e | кулон | Кл | Минимальная порция (квант) электрического заряда, наблюдающегося в природе у свободных долгоживущих частиц | |
Энергия связи | Eсв | джоуль | Дж = (кг·м2/с2) | Разность между энергией состояния, в котором составляющие части системы бесконечно удалены | |
Период полураспада, среднее время жизни | T, τ | секунда | с | Время, в течение которого система распадается в примерном отношении 1/2 | |
Эффективное сечение | σ | квадратный метр | м2 | Величина, характеризующая вероятность взаимодействия элементарной частицы с атомным ядром или другой частицей | |
Активность нуклида | A | беккерель | Бк | Величина, равная отношению общего числа распадов радиоактивных ядер нуклида в источнике ко времени распада | |
Энергия ионизирующего излучения | E,W | джоуль | Дж = (кг·м2/с2) | Вид энергии, высвобождаемой атомами в форме электромагнитных волн (гамма- или рентгеновское излучение) или частиц | |
Поглощенная доза ионизирующего излучения | Д | грей | Гр | Доза, при которой массе 1 кг передаётся энергия ионизирующего излучения в 1 джоул | |
Эквивалентная доза ионизирующего излучения | H, Дэк | зиверт | Зв | Поглощенная доза любого ионизирующего излучения, равная 100 эрг на 1 грамм облученного вещества | |
Экспозиционная доза рентгеновского и гамма-излучения | Х | кулон на килограмм | Кл/кг | отношение суммарного электрического заряда ионов одного знака от внешнего гамма-излучения |
Обозначения в физике с несколькими буквами
Для обозначения некоторых величин иногда используют несколько букв или и отдельные слова или аббревиатуры. Так, постоянная величина в формуле обозначается часто как
Так, постоянная величина в формуле обозначается часто как
. Дифференциал обозначается малой буквой перед названием величины, например .
Специальные символы
Для удобства написания и чтения в среде ученых физиков принято использовать специальные символы, характеризующие те или иные явления и свойства.
Скобки
В физике принято использовать не только формулы, которые применяют в математике, но и специализированные скобки.
Диакритические знаки
Диакритические знаки добавляются к символу физической величины для обозначения определённых различий. Ниже диакритические знаки добавлены для примера к букве x.
Предыдущая
ФизикаМолекулярная физика — основные положения, формулы и законы
Следующая
ФизикаУдельная теплота плавления — определение, формула и обозначение
Все формулы по физике за 7 класс с пояснениями — таблица и шпаргалки
Шпаргалки по физике за 7 класс
В рамках одной статьи сложно охватить весь курс по физике, но мы осветили основные темы за 7 класс и этого достаточно, чтобы освежить знания в памяти. Скачайте и распечатайте обе шпаргалки — одна из них (подробная) пригодится для вдумчивой подготовки к ОГЭ и ЕГЭ, а вторая (краткая) послужит для решения задач.
Скачайте и распечатайте обе шпаргалки — одна из них (подробная) пригодится для вдумчивой подготовки к ОГЭ и ЕГЭ, а вторая (краткая) послужит для решения задач.
Скачать шпаргалку со всеми формулами и определениями по физике за 7 класс (мелко на одной странице).
Для тех, кто находится на домашнем обучении или вынужден самостоятельно изучать материал ввиду пропусков по болезни, рекомендуем также учебник по физике А. В. Перышкина с формулами за 7 класс и легкими, доступными пояснениями по всем темам. Он был написан несколько десятилетий назад, но до сих пор очень популярен и востребован.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Измерение физических величин
Измерением называют определение с помощью инструментов и технических средств числового значения физической величины. Результат измерения сравнивают с неким эталоном, принятым за единицу. В итоге значением физической величины считается полученное число с указанием единиц измерения. |
В курсе по физике за 7 класс изучают правила измерений с использованием приборов со шкалой. Если цена деления шкалы неизвестна, узнать ее можно с помощью следующей формулы:
ЦД = (max − min) / n, где ЦД — цена деления, max — максимальное значение шкалы, min — минимальное значение шкалы, n — количество делений между ними.
Вместо максимального и минимального можно взять любые другие значения шкалы, числовое выражение которых нам известно.
Выделяют прямое и косвенное измерение:
при прямом измерении результат можно увидеть непосредственно на шкале инструмента;
при косвенном измерении значение величины вычисляется через другую величину (например, среднюю скорость определяют на основе нескольких замеров скорости).

Для удобства и стандартизации измерений в 1963 году была принята Международная система единиц СИ. Она регламентирует, какие единицы измерения считать основными и использовать для формул. Обозначения этих единиц также учат в программе по физике за 7 класс.
Механическое движение: формулы за 7 класс
Механическое движение — перемещение тела в пространстве, в результате которого оно меняет свое положение относительно других тел. Закономерности такого движения изучают в рамках механики и конкретно ее раздела — кинематики. |
Для того, чтобы описать движение, требуется тело отсчета, система координат, а также инструмент для измерения времени. Это составляющие системы отсчета.
Изучение механического движения в курсе по физике за 7 класс включает следующие термины:
Перемещение тела — минимальное расстояние, которое соединяет две выбранные точки траектории движения.

Траектория движения — мысленная линия, вдоль которой перемещается тело.
Путь — длина траектории тела от начальной до конечной точки.
Скорость — быстрота перемещения тела или отношение пройденного им пути ко времени прохождения.
Ускорение — быстрота изменения скорости, с которой движется тело.
Равномерное движение — механическое движение, при котором тело за любые равные промежутки времени проходит одно и то же расстояние. |
Формула скорости равномерного прямолинейного движения:
V = S / t, где S — путь тела, t — время, за которое этот путь пройден.
Формула скорости равномерного криволинейного движения:
где S1 и S2 — отрезки пути, а t1 и t2 — время, за которое был пройден каждый из них.
Единица измерения скорости в СИ: метр в секунду (м/с).
Формула скорости равноускоренного движения:
V = V0 + at, где V0— начальная скорость, а — ускорение.
Единица измерения ускорения в СИ: м/с2.
Учёба без слёз (бесплатный гайд для родителей)
Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.
Сила тяжести, вес, масса, плотность
Формулы, понятия и определения, описывающие эти физические характеристики, изучают в 7 классе в рамках такого раздела физики, как динамика.
Вес тела или вещества — это физическая величина, которая характеризует, с какой силой оно действует на горизонтальную поверхность или вертикальный подвес. |
Обратите внимание: вес тела измеряется в ньютонах, масса тела — в граммах и килограммах.
Формула веса:
P = mg, где m — масса тела, g — ускорение свободного падения.
Ускорение свободного падения возникает под действием силы тяжести, которой подвержены все находящиеся на нашей планете тела.
g = 9,806 65 м/с2 или 9,8 Н/кг
Если тело находится в покое или в прямолинейном равномерном движении, его вес равен силе тяжести.
Fтяж = mg
Но эти понятия нельзя отождествлять: сила тяжести действует на тело ввиду наличия гравитации, в то время как вес — это сила, с которой само тело действует на поверхность.
Плотность тела или вещества — величина, указывающая на то, какую массу имеет данное вещество, занимая единицу объема. Плотность прямо пропорциональна массе и обратно пропорциональна объему. |
Формула плотности:
ρ = m / V, где m — масса тела или вещества, V — занимаемый объем.
Единица измерения плотности в СИ: кг/м3.
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
Механический рычаг, момент силы
О механическом рычаге говорил еще Архимед, когда обещал перевернуть Землю, если только найдется подходящая точка опоры. Это простой механизм, который помогает поднимать грузы, закрепленные на одном его конце, прилагая силу к другому концу. При этом вес груза намного превосходит прилагаемое усилие. В 7 классе физические формулы, описывающие этот процесс, изучаются в том же разделе динамики.
Это простой механизм, который помогает поднимать грузы, закрепленные на одном его конце, прилагая силу к другому концу. При этом вес груза намного превосходит прилагаемое усилие. В 7 классе физические формулы, описывающие этот процесс, изучаются в том же разделе динамики.
Рычаг — это некое твердое тело, способное вращаться вокруг неподвижной точки опоры, на один конец которого действует сила, а на другом находится груз. Перпендикуляр, проведенный от точки опоры до линии действия силы, называется плечом силы. |
Рычаг находится в равновесии, если произведение силы на плечо с одной его стороны равно произведению силы на плечо с другой стороны.
Уравнение равновесия рычага:
F1 × l1 = F2 × l2
Из этого следует, что рычаг уравновешен, когда модули приложенных к его концам сил обратно пропорциональны плечам этих сил.
Момент силы — это физическая величина, равная произведению модуля силы F на ее плечо l. |
Формула момента силы:
M = F × l, где F — модуль силы, l — длина плеча.
Единица измерения момента силы в СИ: ньютон-метр (Н·м).
Эта формула верна, если сила приложена перпендикулярно оси рычага. Если же она прилагается под углом, такой случай выходит за рамки курса физики за 7 класс и подробно изучается в 9 классе.
Правило моментов: рычаг уравновешен, если сумма всех моментов сил, которые поворачивают его по часовой стрелке, равна сумме всех моментов сил, которые поворачивают его в обратном направлении. |
Можно сказать иначе: рычаг в равновесии, если сумма моментов всех приложенных к нему сил относительно любой оси равна нулю.
М1 + М2 + Мn + … = 0
Давление, сила давления
Прилагая одну и ту же силу к предмету, можно получить разный результат в зависимости от того, на какую площадь эта сила распределена. Объясняют этот феномен в программе 7 класса физические термины «давление» и «сила давления».
Объясняют этот феномен в программе 7 класса физические термины «давление» и «сила давления».
Давление — это величина, равная отношению силы, действующей на поверхность, к площади этой поверхности. Сила давления направлена перпендикулярно поверхности. |
Формула давления:
p = F / S, где F — модуль силы, S — площадь поверхности.
Единица измерения давления в СИ: паскаль (Па).
1 Па = 1 Н/м2
Понятно, что при одной и той же силе воздействия более высокое давление испытает та поверхность, площадь которой меньше.
Формулу для расчета силы давления вывести несложно:
F = p × S
В задачах по физике за 7 класс сила давления, как правило, равна весу тела.
Давление газов и жидкостей
Жидкости и газы, заполняющие сосуд, давят во всех направлениях: на стенки и дно сосуда. Это давление зависит от высоты столба данного вещества и от его плотности.
Формула гидростатического давления:
р = ρ × g × h, где ρ — плотность вещества, g — ускорение свободного падения, h — высота столба.
g = 9,8 м/с2
Единица измерения давления жидкости или газа в СИ: паскаль (Па).
Однородная жидкость или газ давит на стенки сосуда равномерно, поскольку это давление создают хаотично движущиеся молекулы. И внешнее давление, оказываемое на вещество, тоже равномерно распределяется по всему его объему.
Закон Паскаля: давление, производимое на поверхность жидкого или газообразного вещества, одинаково передается в любую его точку независимо от направления. |
Внешнее давление, оказываемое на жидкость или газ, рассчитывается по формуле:
p = F / S, где F — модуль силы, S — площадь поверхности.
Сообщающиеся сосуды
Сообщающимися называются сосуды, которые имеют общее дно либо соединены трубкой. |
Если ρ1 = ρ2, то h1 = h2 и ρ1gh1 = ρ2gh2, где:
p — плотность жидкости,
h — высота столба жидкости,
g = 9,8 м/с2.
Если жидкость в сообщающихся сосудах неоднородна, т. е. имеет разную плотность, высота столба в сосуде с более плотной жидкостью будет пропорционально меньше.
Высоты столбов жидкостей с разной плотностью обратно пропорциональны плотностям.
Гидравлический пресс — это механизм, созданный на основе сообщающихся сосудов разных сечений, заполненных однородной жидкостью. Такое устройство позволяет получить выигрыш в силе для оказания статического давления на детали (сжатия, зажимания и т. д.). |
Если под поршнем 1 образуется давление p1 = f1/s1, а под поршнем 2 будет давление p2 = f2/s2, то, согласно закону Паскаля, p1 = p2
Следовательно,
Силы, действующие на поршни гидравлического пресса F1 и F2, прямо пропорциональны площадям этих поршней S1 и S2.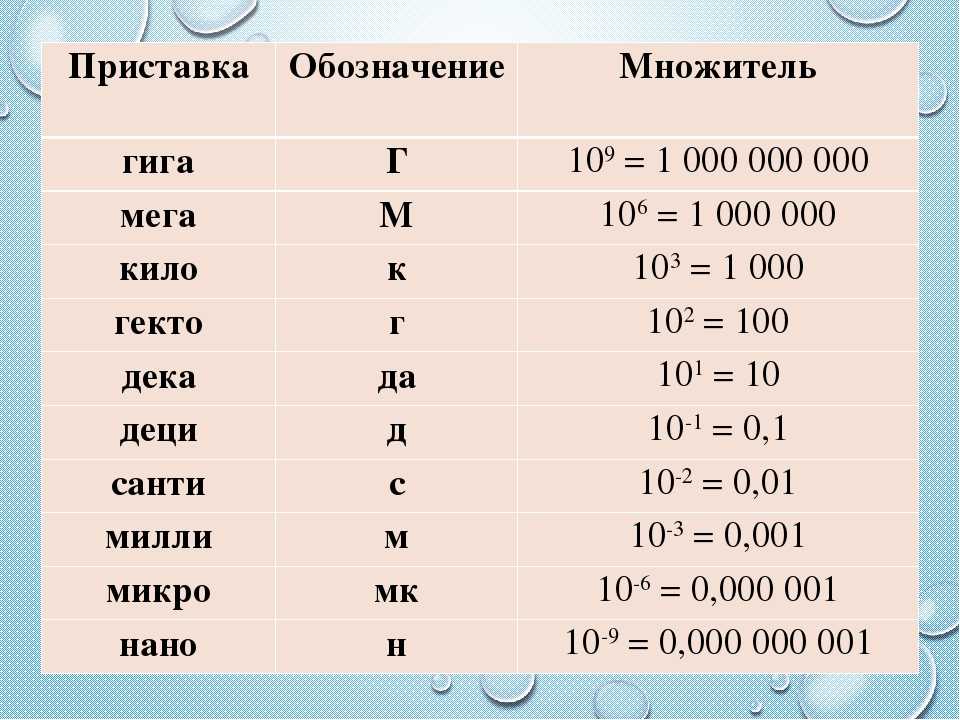
Другими словами, сила поршня 1 больше силы поршня 2 во столько раз, во сколько его площадь больше площади поршня 2. Это позволяет уравновесить в гидравлической машине с помощью малой силы многократно бóльшую силу.
Закон Архимеда
На тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу объема жидкости или газа, вытесненного частью тела, погруженной в жидкость или газ. |
Формула архимедовой силы:
Fa = ρ × g × V, где ρ — плотность жидкости, V — объем погруженной части тела, g — ускорение 9,8 м/с2.
Закон Архимеда помогает рассчитать, как поведет себя тело при погружении в среды разной плотности. Верны следующие утверждения:
если плотность тела выше плотности среды, оно уйдет на дно;
если плотность тела ниже, оно всплывет на поверхность.
Другими словами, тело поднимется на поверхность, если архимедова сила больше силы тяжести.
Работа, энергия, мощность
Механическая работа — это физическая величина, которая равна произведению перемещения тела на модуль силы, под действием которой было выполнено перемещение. |
Формула работы в курсе физики за 7 класс:
A = F × S, где F — действующая сила, S — пройденный телом путь.
Единица измерения работы в СИ: джоуль (Дж).
Такое понятие, как мощность, описывает скорость выполнения механической работы. Оно говорит о том, какая работа была совершена в единицу времени.
Мощность — это физическая величина, равная отношению работы к временному промежутку, потребовавшемуся для ее выполнения. |
Формула мощности:
N = A / t, где A — работа, t — время ее совершения.
Также мощность можно вычислить, зная силу, воздействующую на тело, и среднюю скорость перемещения этого тела.
N = F × v, где F — сила, v — средняя скорость тела.
Единица измерения мощности в СИ: ватт (Вт).
Тело может совершить какую-либо работу, если оно обладает энергией — кинетической и/или потенциальной.
Кинетической называют энергию движения тела. Она говорит о том, какую работу нужно совершить, чтобы придать телу определенную скорость.
Потенциальной называется энергия взаимодействия тела с другими телами или взаимодействия между частями одного целого. Потенциальная энергия тела, поднятого над Землей, характеризует, какую работу должна совершить сила тяжести, чтобы опустить это тело снова на нулевой уровень.
Таблица с формулами по физике за 7 класс для вычисления кинетической и потенциальной энергии:
Кинетическая энергия | Пропорциональна массе тела и квадрату его скорости. | Ek = mv2/2 |
Потенциальная энергия | Равна произведению массы тела, поднятого над Землей, на ускорение свободного падения и высоту поднимания. | Ep= mgh |
Полная механическая энергия | Складывается из кинетической и потенциальной энергии. | E = Ek+Ep |
Сохранение и превращение энергии | Если механическая энергия не переходит в другие формы, то сумма потенциальной энергии и кинетической представляет собой константу. | Ek+ Ep= const |
Для того, чтобы понять, какая часть совершенной работы была полезной, вычисляют коэффициент полезного действия или КПД. С его помощью определяется эффективность различных механизмов, инструментов и т. д.
Коэффициент полезного действия (КПД) отражает полезную часть выполненной работы. Также его можно выразить через отношение полезно использованной энергии к общему количеству полученной энергии. |
Формула для расчета КПД:
где Ап— полезная работа, Аз— затраченная работа.
КПД выражается в процентах и составляет всегда меньше 100%, поскольку часть энергии затрачивается на трение, повышение температуры воздуха и окружающих тел, преодоление силы тяжести и т. д.
Удачи на экзаменах!
Измерение физических величин | Физика
Теперь мы знаем, что такое физическая величина и как ее записать. Для того чтобы узнать ее значение в каждом конкретном случае, проводят измерения.
Нахождение значения физической величины опытным путем с помощью специальных технических средств называют измерением физической величины.
Только проводя измерения с помощью соответствующих приборов, физики экспериментально устанавливают количественные соотношения между физическими величинами. Великий русский ученый Дмитрий Иванович Менделеев писал: «Наука начинается с тех пор, как начинают измерять; точная наука немыслима без меры».
Без проведения измерений физических величин невозможно описать свойства объектов и обнаружить количественные закономерности в природе.
В самом простом случае, чтобы измерить какую-либо величину, необходимо сравнить ее с единицей этой величины, т. е. определить, во сколько раз измеряемая величина отличается от ее единицы. К примеру, при измерении длины ручки можно использовать линейку. Линейка является простейшим физическим прибором, предназначенным для измерений длин. Как и на других приборах, например на часах, термометрах, на линейке нанесена шкала — ряд делений.
Прежде чем проводить измерения с помощью прибора, имеющего шкалу, необходимо определить цену деления его шкалы (рис. 1). То есть нужно узнать, сколько единиц измеряемой величины приходится на одно деление — расстояние между двумя соседними отметками шкалы (штрихами). Обычно одно деление линейки соответствует 1 мм. Определять цену деления других измерительных приборов вы научитесь, выполняя лабораторные работы.
Цена деления шкалы — разность значений измеряемой величины, соответствующим двум соседним отметкам (штрихам) шкалы.
После нахождения цены деления шкалы можно проводить измерение длины. Измерим с помощью линейки длину карандаша (рис. 2). Для этого совместим один из концов карандаша с началом шкалы. Затем найдем штрих на шкале, ближайший ко втором у концу карандаша (на рисунке он отмечен пунктирной линией). Подсчитаем число делений шкалы между началом и найденным штрихом. После этого цену деления умножим на найденное число делений. Полученный результат можно выразить в различных единицах (например, в миллиметрах, сантиметрах или метрах).
Но линейкой нельзя измерить точно длину предмета, по крайней мере, по двум причинам. Первая заключается в том, что невозможно точно нанести штрихи на шкалу. Вторая причина: измеряемый предмет может оказаться чуть длиннее или короче, чем длина целого числа делений шкалы. Имеется и целый ряд других причин. Так, человеческий глаз улавливает различия в длине только до определенного значения, штрихи имеют конечную толщину, торец карандаша не идеально ровный и т. п. Обычно линейки изготавливают так, чтобы ошибка (погрешность) при измерении не превышала половины цены деления в любом месте шкалы. Поэтому, как правило, не имеет смысла пытаться измерить длину предмета с точностью, превышающей половину цены деления линейки. В данной ситуации можно лишь утверждать, что измеренная длина карандаша больше 92, но меньше 93 мм.
п. Обычно линейки изготавливают так, чтобы ошибка (погрешность) при измерении не превышала половины цены деления в любом месте шкалы. Поэтому, как правило, не имеет смысла пытаться измерить длину предмета с точностью, превышающей половину цены деления линейки. В данной ситуации можно лишь утверждать, что измеренная длина карандаша больше 92, но меньше 93 мм.
Как правило, для линеек цена деления шкалы составляет 1 мм. Поэтому не имеет смысла пытаться измерить длину предмета с помощью линейки с точностью, превышающей половину цены деления шкалы линейки, — 0,5 мм.
К сожалению, за очень редким исключением, любое измерение не в состоянии дать результат без погрешности. Поэтому почти все измеренные физические величины известны нам приблизительно. Следовательно, обычно мы можем говорить лишь об измерении с некоторой точностью, которая зависит от измерительного прибора и метода измерения.
Развитие физики связано с появлением все более точных приборов и методов измерений, дающих все меньшую погрешность. Очень наглядно это проявилось при измерении такой физической величины, как время. В древнейшие времена единицами времени были сутки и год. Наблюдения за движением Солнца по небу позволили создать солнечные часы. С их помощью в Древнем Вавилоне научились измерять более короткие отрезки времени, разделив и день, и ночь на 12 часов, а час — на 60 минут. Люди поняли, что час нужно задавать как постоянный промежуток времени. Его длительность можно определить через регулярно повторяющийся природный процесс, например суточное вращение небесной сферы.
Очень наглядно это проявилось при измерении такой физической величины, как время. В древнейшие времена единицами времени были сутки и год. Наблюдения за движением Солнца по небу позволили создать солнечные часы. С их помощью в Древнем Вавилоне научились измерять более короткие отрезки времени, разделив и день, и ночь на 12 часов, а час — на 60 минут. Люди поняли, что час нужно задавать как постоянный промежуток времени. Его длительность можно определить через регулярно повторяющийся природный процесс, например суточное вращение небесной сферы.
В Древнем Вавилоне использовалась не десятичная система счисления, а двенадцатеричная (и основанная на ней шестидесятиричная). Напоминанием об этих древних временах служит деление суток на 24 часа, часа — на 60 минут, а минуты — на 60 секунд.
Изобретение стекла дало возможность создать песочные часы (1). К сожалению, такие часы не позволяли измерять интервалы времени, меньшие нескольких секунд. Галилео Галилей в начале XVII в. в экспериментах по изучению движения тел измерял временные промежутки, считая удары собственного пульса (примерно один удар в секунду), пока не открыл периодичность колебаний маятника. Используя это открытие, другой физик, Христиан Гюйгенс, изобрел маятниковые часы (2).
в экспериментах по изучению движения тел измерял временные промежутки, считая удары собственного пульса (примерно один удар в секунду), пока не открыл периодичность колебаний маятника. Используя это открытие, другой физик, Христиан Гюйгенс, изобрел маятниковые часы (2).
Открытие и исследования электрических явлений привели к созданию многих электронных приборов, в том числе и электронных часов (3). А открытие тайн микромира позволило изготовить сверхточные атомные часы (4).
Интересно, что усовершенствование измерительных приборов подталкивает развитие всех наук. Например, изобретение хронометра — точных механических часов (5) — дало возможность морякам определять свое положение в море и привело к множеству географических открытий; развитие угломерных инструментов позволило получить более точную информацию о небесных телах и Земле и т. п. Поэтому в физике уделяется большое внимание усовершенствованию методов измерений и созданию новых приборов.
Итоги
Измерение физической величины — нахождение ее значения опытным путем с помощью специальных технических средств.
Чтобы измерить какую-либо величину, необходимо сравнить ее с единицей этой величины, т. е. определить, какое число раз в измеряемой величине содержится эта единица.
Перед проведением измерения с помощью измерительного прибора, имеющего шкалу, определяют цену деления шкалы.
Все измерения производятся с погрешностью. Для простых приборов со шкалой погрешность обычно принимают равной половине цены деления шкалы.
Вопросы
- Что такое измерение физической величины? Для чего необходимо измерять физические величины?
- Как провести измерение физической величины? С чем сравнивают физическую величину при ее измерении?
- Что такое цена деления шкалы? Как ее определяют?
- Почему с помощью линейки нельзя точно измерить длину любого тела?
- Как погрешность измерения связана с ценой деления шкалы измерительного прибора?
Физические величины. Давайте познакомимся.
Репетиторы
❯
Физика
❯
Физические величины. Давайте познакомимся.
Давайте познакомимся.
Автор: Андрей П., онлайн репетитор по физике и математике.
●
26.12.2011
●
Раздел: Физика
Как известно, физика – наука о природе. Все явления, которые объясняет этот предмет, описываются с помощью физических формул, состоящих из физических величин и математических действий над ними. Эти формулы универсальны и понятны физикам всех стран, независимо от государственного языка общения. Физические величины имеют индивидуальные буквенные обозначения (чаще всего это буквы латинского алфавита), состоят из числового значения и единиц измерения в СИ (международной системе измерения единиц). Физическую величину можно либо измерить прибором, либо рассчитать по формуле.
Физическую величину можно либо измерить прибором, либо рассчитать по формуле.
Например:
- физическая величина масса обозначается m (М), в СИ измеряется в кг (килограммах) с помощью весов или рассчитывается по формуле: m = ρ · V, где ρ – плотность тела, V – объём тела,
- физическая величина время обозначается t, в СИ измеряется в c (секундах) с помощью часов,
- физическая величина путь обозначается s, в СИ измеряется в м (метрах) с помощью линейки или рассчитывается по формуле s = ϑ · t, где ϑ – скорость тела, t – время движения, и т.д.
Надо помнить, что все физические величины делятся на скалярные и векторные.
Скалярные величины – это величины, не имеющие направления. К скалярным величинам отнесём массу тела, объём тела, плотностьвысоту, пройдённый путь, температуру тела, силу тока, давление и т д.
К скалярным величинам отнесём массу тела, объём тела, плотностьвысоту, пройдённый путь, температуру тела, силу тока, давление и т д.
Векторные величины – это величины, имеющие не только числовое значение (говорят: «модуль величины»), но и направление. Про векторную величину всегда можно сказать, куда она направлена. К векторным величинам относим силу, ускорение, скорость, импульс тела, импульс силы.
При выполнении математических действий над физическими величинами, необходимо помнить некоторые правила.
- Складывать или вычитать можно только одноимённые величины! И в ответе получаем ту же по наименованию величину!
Например: 3 кг + 5 кг = 8 кг, 6 Н – 2 Н = 4 Н. - Сокращать можно только одноименные величины.
- При умножении или делении величины на число, получается таже величина.
Например: 8 м/с · 2 = 16 м/с., 4 А · 5 = 20 А и т. д.
д. - При умножении одной физической величины на другую, получается новая физическая величина.
Например: 4 кг · 2 м/с 2 = 8 кг м/с 2 = 8 Н, 10 B / 5 A = 2 Ом.
Если работаем с векторными величинами, то к правилам, написанным выше, добавим ещё следующие правила:
- При сложении или вычитании векторных одноименных величин получаем векторную величину. Но помним, что выполняем геометрическое сложение векторов (по правилу треугольника или параллелограмма находим направление результирующего вектора, а по теореме косинусов (CC = AА + BВ – 2ABсоs a) находим длину результирующего вектора).
- При умножении векторной величины на число, получаем векторную величину.
- Если векторную величину умножаем на положительное число, то направление вектора не меняется, если умножаем на отрицательное число, то направление вектора меняется на противоположное.
Запомнив эти несложные правила, можно задачи по физике решать с лёгкостью. Удачи!
Удачи!
Остались вопросы? Не знаете, что такое физические величины?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
Задать вопрос
Физика
Курсы физики для студентов нефизических специальностей
Физика
Курсы по физике 10 класс
Информатика и ИКТ
Курс ЕГЭ по информатике
Математика
Курсы по математике 10 класс
Математика
Курсы по алгебре 7 класс
Английский язык
Курсы по бизнес английскому
Высшая математика
Высшая математика для студентов технических специальностей
Физические величины и их измерение
Конспект по физике для 7 класса «Физические величины и их измерение»: единицы физических величин, кратные и дольные физические величины, действия над физическими величинами.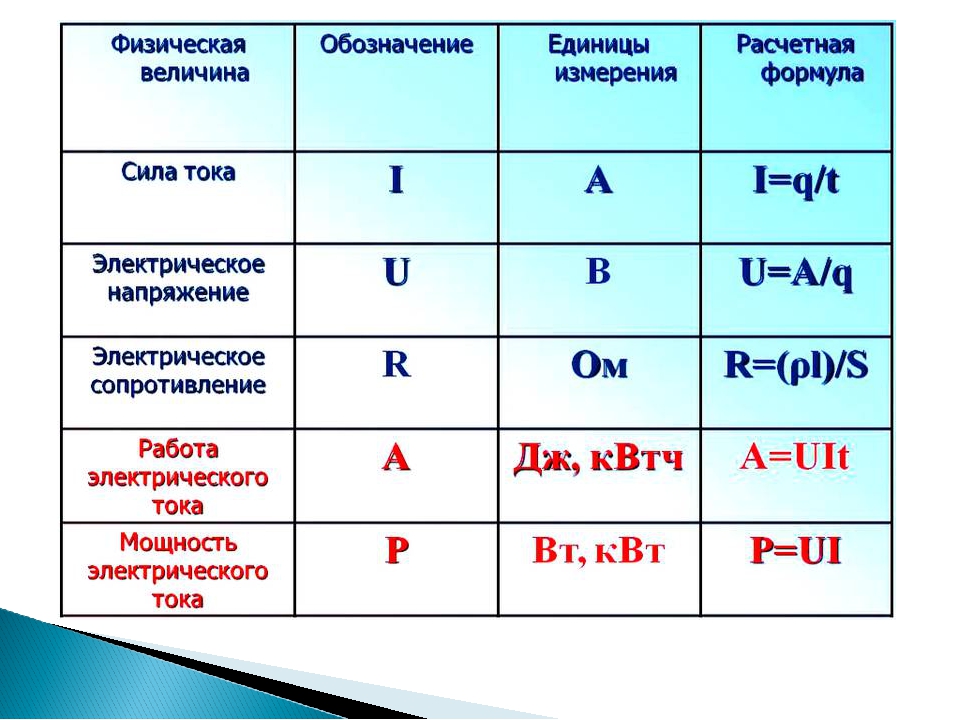
Конспекты по физике Учебник физики Тесты по физике
Все физические тела обладают набором определенных свойств. Все физические явления протекают во времени. Задача физики — понять причины тех или иных физических явлений и описать их.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
Для описания какого-либо свойства физического тела и явления служит физическая величина.
Одна и та же физическая величина используется для характеристики одного и того же свойства различных физических явлений и тел.
Например, мы можем говорить о длине шага, длине стола, длине доски. При этом значения вышеперечисленных длин будут разными.
Для того чтобы количественно описать физическую величину, необходимо знать её числовое значение и единицу физической величины. Говоря о том, что урок в школе длится 45 минут, мы описываем физическую величину время. Сочетание «45 минут» — это время, показывающее длительность урока, состоящее из числового значения 45 и единиц времени минут.
ЕДИНИЦЫ ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ
Говоря о значении физической величины, мы всегда должны учитывать, в каких единицах она выражена. Для каждой физической величины существуют свои единицы. Например, единицами длины могут быть сантиметр, метр, километр. Что же в этом случае означает измерить физическую величину?
Измерение физической величины – это сравнение её с эталоном. Уже более двух веков все страны мира стремятся использовать одинаковые эталоны для измерения основных физических величин. Для этот и была создана Международная система единиц СИ (система интернациональная).
| Единицы СИ | |
| Единица длины | Метр (1 м) |
| Единица времени | Секунда (1 с) |
| Единица массы | Килограмм (1 кг) |
Если сравнивать длину какого-либо тела с эталоном метра, мы получим длину, выраженную в метрах.
КРАТНЫЕ И ДОЛЬНЫЕ ЕДИНИЦЫ
Итак, эталоном длины служит метр.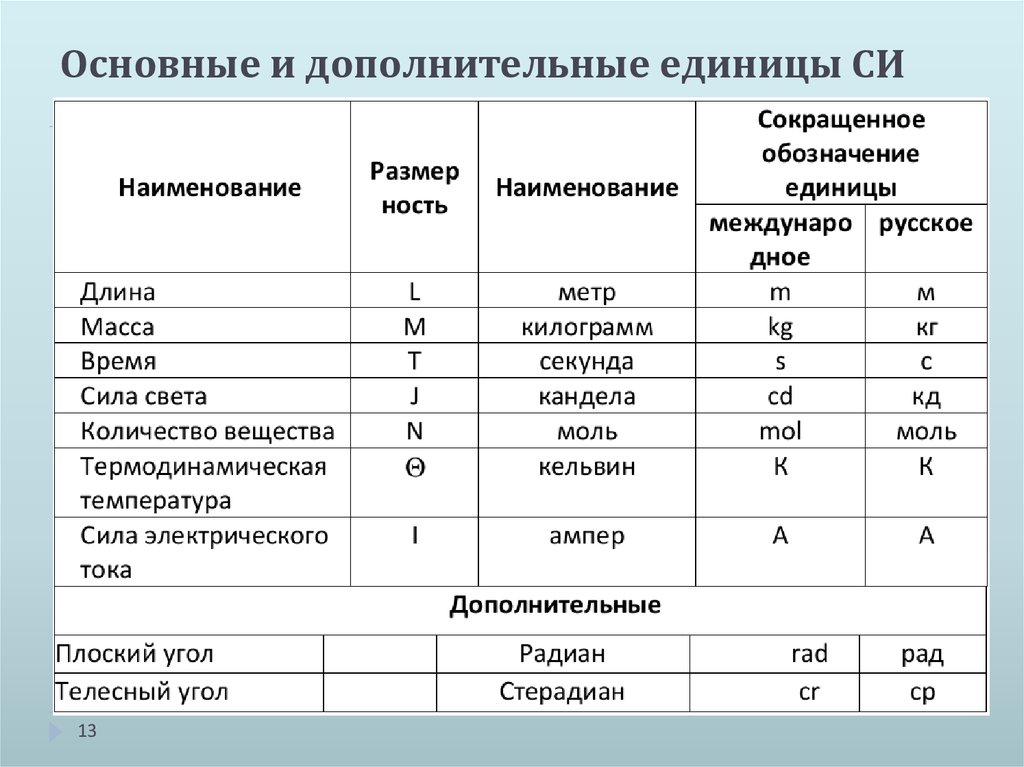 Но ведь существуют тела, обладающие совсем маленькими или очень большими размерами. Так, длина инфузории-туфельки, которая составляет примерно 0,0002 м, очень мала, а длина экватора Земли, составляющая 40 075 696 м, велика.
Но ведь существуют тела, обладающие совсем маленькими или очень большими размерами. Так, длина инфузории-туфельки, которая составляет примерно 0,0002 м, очень мала, а длина экватора Земли, составляющая 40 075 696 м, велика.
Эти величины часто неудобно выражать в метрах, поэтому для таких целей используют единицы, которые могут быть меньше метра в 10, 100 и т. д. раз (их называют дольными), или больше метра в 10, 100 и т. д. раз (их называют кратными).
| Название приставки | Название единицы, кратной или дольной метру | Множитель |
| милли (м) | миллиметр (мм) | 0,001 |
| санти (с) | сантиметр (см) | 0,01 |
| деци (д) | дециметр (дм) | 0,1 |
| кило (к) | километр (км) | 1000 |
Например, километр является кратной единицей для метра и равен 10(H) метрам. При этом в названии «километр» появилась приставка «кило», которая и определяет, насколько одна величина больше другой.
Для того чтобы величину, выраженную в метрах, перевести в сантиметры, необходимо её значение умножить на 100. В этом случае число 100 называют множителем.
В качестве примеров дольных единиц можно рассмотреть: единица в тысячу раз меньше метра называется миллиметр, в миллион раз меньше метра — микрометр или кратко — микрон, в миллиард раз меньше метра — нанометр.
ДЕЙСТВИЯ НАД ФИЗИЧЕСКИМИ ВЕЛИЧИНАМИ
Нельзя напрямую сравнивать две физические величины, выраженные в разных единицах.
Например, расстояние между школой и домом одного ученика равно 1 километру, а расстояние от школы до дома другого ученика — 1100 метров. Как понять, кто живёт дальше от школы?
Чтобы сравнение было правильным, нужно сначала выразить значения величин в одинаковых единицах:
1 км = 1000 м;
1000 м < 1100 м.
При этом всегда надо помнить, что нельзя сравнивать неоднородные величины, например такие, как масса и расстояние, или расстояние и время.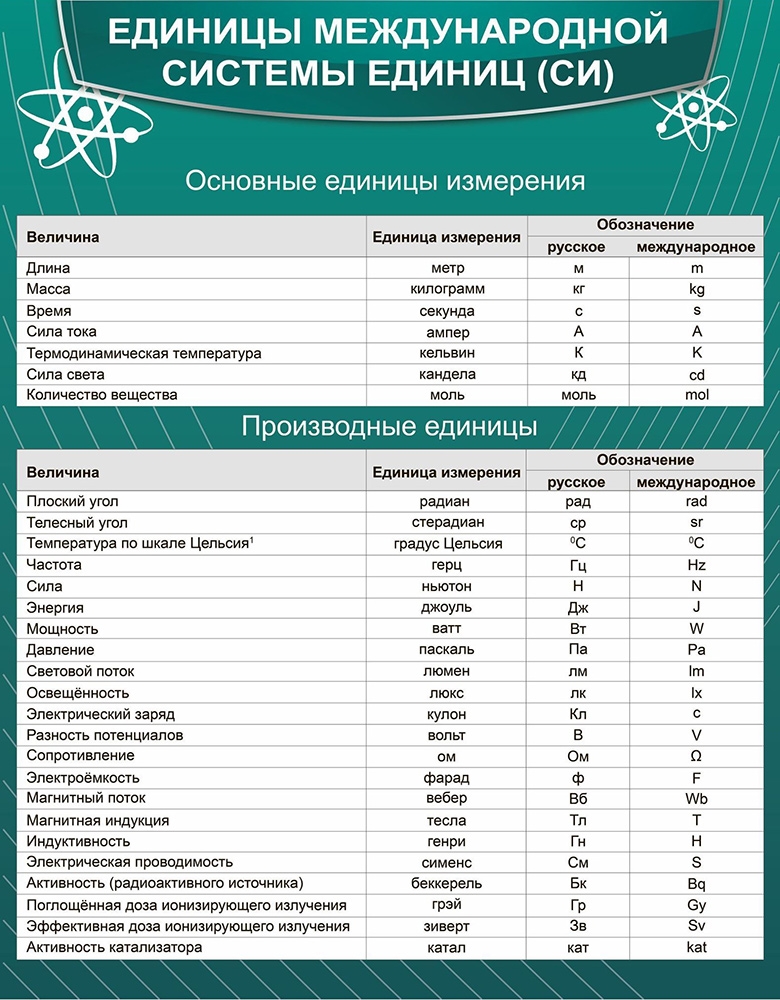 Такое сравнение не имеет никакого смысла.
Такое сравнение не имеет никакого смысла.
Старинные меры
С давних времен человеку приходилось проводить измерения. В русской системе мер, которая традиционно применялась на Руси, мерой длины, например, мог быть сам человек. Так, косая сажень — это расстояние от носка левой ноги до конца среднего пальца поднятой вверх правой руки. Пядь или четверть — расстояние между концами расставленных большого и указательного пальцев руки.
В 1899 году наряду с русской системой мер к использованию была разрешена метрическая система.
Сегодня в России применяется Международная система единиц, а старинные меры сохранились лишь в пословицах и поговорках.
Вы смотрели конспект по физике для 7 класса «Физические величины и их измерение»: единицы физических величин, кратные и дольные физические величины, действия над физическими величинами.
Вернуться к Списку конспектов по физике (оглавление).
Пройти онлайн-тест «Наблюдения. Опыты. Физические величины»
специальная теория относительности — система отсчета $c$
Еще один способ мышления, который может быть вам полезен, заключается в том, чтобы принять во внимание, что $c$ не является в первую очередь скоростью света. косвенно означает скорость, наблюдаемую любым наблюдателем любой безмассовой частицы , а поскольку, насколько нам известно, свет не имеет массы, это косвенно означает скорость света. Но в своей наиболее фундаментальной форме $c$ — это всего лишь параметр, имеющий размерность скорости. В первую очередь это не относится к скорости: вот как мы ее определяем.
Подумайте об интуитивном галилеевском сложении скоростей. Комбинационный закон линейный. Итак, предполагая закон линейной комбинации, есть некоторые основные симметрии и характеристики этого повседневного закона, о которых вам, возможно, захочется подумать. Следующее может сначала показаться немного пугающим, но на самом деле оно интуитивно понятно, и мы не говорим сначала о чем-то, что противоречит повседневной теории относительности Галилея, поэтому я призываю вас подумать о применении этих идей к простой задаче, где у нас есть три кадры: $F_1$, улица, $F_2$ автобус, едущий по улице, и $F_3$ человек, идущий по проходу движущегося автобуса. В дальнейшем переход от одной системы отсчета к другой, равномерно относительно движущейся системе отсчета будем называть boost :
Следующее может сначала показаться немного пугающим, но на самом деле оно интуитивно понятно, и мы не говорим сначала о чем-то, что противоречит повседневной теории относительности Галилея, поэтому я призываю вас подумать о применении этих идей к простой задаче, где у нас есть три кадры: $F_1$, улица, $F_2$ автобус, едущий по улице, и $F_3$ человек, идущий по проходу движущегося автобуса. В дальнейшем переход от одной системы отсчета к другой, равномерно относительно движущейся системе отсчета будем называть boost :
- ( Линейность ) Если я перейду из кадра $F_1$ в кадр $F_2$, движущийся с постоянной скоростью $v_{1,2}$ в каком-то направлении, то мои координаты расстояния и времени $(x, t)$ преобразуются некоторой матрицей $2\times2$ $T(v_{1,2})$, т.е. $X=\left(\begin{array}{c}x\\t\ конец {массив}\справа)\mapsto T(v_{1,2}) X$;
- ( Транзитивность и Ассоциативность ): Если я , то преобразуются в третий кадр $F_3$, который движется со скоростью $v_{2,3}$ в то же (исходное) направление относительно преобразованного кадра $F_2$ (при использовании матрицы $T(v_{2,3})$ это должно быть эквивалентно одному преобразованию $T(v_{1,3}) $ с первого кадра на третий с некоторой относительной скоростью $v_{1,3}$ Или, с помощью нашего слова «ускорение»: ускорение, объединенное с другим ускорением в том же направлении, все равно равносильно ускорению с некоторой относительной скоростью.
 скорость: преобразования в одном и том же направлении не меняют своего характера от того, что они составлены из ускорений или даже от того, как (нашим из бесконечного числа способов) они могут состоять из ускорений.Если я иду с некоторой скоростью вдоль самого движущегося автобуса по дороге, то мое движение должно быть описано как движение по дороге с некоторой относительной скоростью, забыв об автобусе;
скорость: преобразования в одном и том же направлении не меняют своего характера от того, что они составлены из ускорений или даже от того, как (нашим из бесконечного числа способов) они могут состоять из ускорений.Если я иду с некоторой скоростью вдоль самого движущегося автобуса по дороге, то мое движение должно быть описано как движение по дороге с некоторой относительной скоростью, забыв об автобусе; - ( Симметрия описания ) В частности, если система $F_3$ движется относительно системы $F_2$ со скоростью $-v$, то системы $F_1$ и $F_3$ должны быть одинаковыми и $T(v ) T(-v) = I$ (здесь $I$ = преобразование тождества — мой бег от вас со скоростью $v$ должен казаться таким же, как ваш бег от меня с той же скоростью в противоположном направлении). Эта симметрия возникает из базовой «однородности» (пространство и время в каком-то смысле везде «одинаковы») и коперниканского представления об отсутствии специальной системы отсчета. Внимательно подумайте об этом, и вы увидите, что преобразование Галилея удовлетворяет всем этим интуитивным симметриям.

Теперь главный вопрос:
Определяют ли условия с 1 по 3 полностью преобразование Галилея? Или, более приземленно, Какова наиболее общая форма матрицы $T(v)$, удовлетворяющая условиям с 1 по 3?
Оказывается, не только закон Галилея $v_{1,2}+v_{2,3} = v_{1,3}$ удовлетворяет всем приведенным выше аксиомам, но и существует целое семейство возможных преобразований , каждое из которых параметризуется параметром $c$, причем закон Галилея является законом преобразования, который мы получаем как $c\to\infty$. Такими законами являются преобразования Лоренца. См. Раздел «Из групповых постулатов» на странице Википедии «Выводы преобразований Лоренца». Обратите внимание, как у одного есть НЕ предполагалось, что $v_{1,2}+v_{2,3} = v_{1,3}$, за исключением особого случая, когда $v_{1,2} = -v_{2,3 }$. Кажется вероятным, что Игнатовский (см. страницу Википедии) был одним из первых, кто понял, что можно вывести относительность только из этих предположений в 1911 году, хотя Эйнштейн фактически упоминает групповую структуру преобразований Лоренца в своей знаменитой статье 1905 года «Об электродинамике электродинамики». Движущиеся тела».
Движущиеся тела».
Итак, представьте, что мы внимательно изучили теорию относительности Галилея, как описано выше, но ничего не знаем о специальной теории относительности. Возможно, именно так развивалась бы наука в конце девятнадцатого века, если бы не эксперимент Майкельсона-Морли. Теперь мы поняли бы, что наши повседневные галилеевские законы могли бы на самом деле возникать из вселенной, в которой у нас есть этот странный параметр $c$, который не бесконечен, а просто очень велик: это все равно будет согласовываться с нашим повседневным добавлением законов скорости с достаточно большим $с$. На данный момент мы знали бы только форму преобразования Лоренца и то, что существует параметр $c$ (возможно, бесконечный) с измерениями скорости, поэтому мы хотели бы придумать какой-нибудь эксперимент, чтобы измерить, имеет ли наша Вселенная конечное значение $c$. Не сразу было бы очевидно, что этот параметр скорости является скоростью чего-либо в частности, и действительно ли он даже может быть скоростью чего угодно.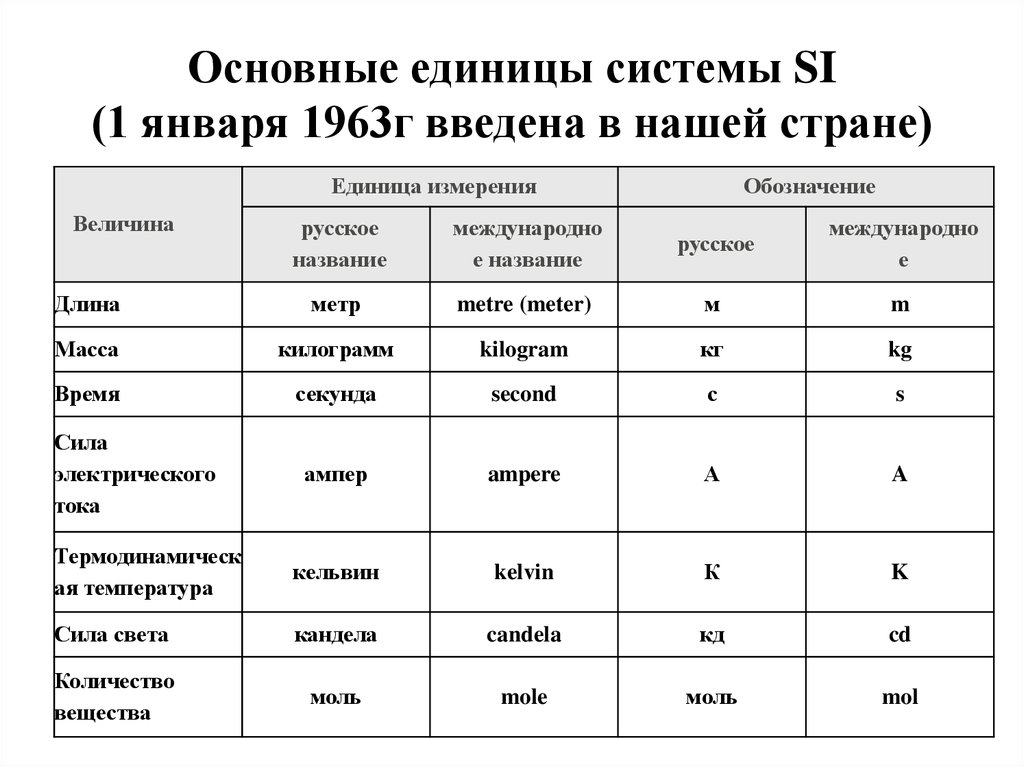 Но теперь мы говорим себе: что, если бы что-то двигалось с такой скоростью относительно нас? Простое изучение преобразования Лоренца показало бы нам, что:
Но теперь мы говорим себе: что, если бы что-то двигалось с такой скоростью относительно нас? Простое изучение преобразования Лоренца показало бы нам, что:
- Измеренная скорость этого тела $c$ будет одинаковой во всех инерциальных системах отсчета . Более того, чтобы обеспечить эту инвариантность $c$, должно быть своеобразное правило сложения для скоростей, не совсем такое же, как правило параллелограмма;
- Никакой материальный объект не может двигаться быстрее, чем $c$, и действительно что-то может двигаться со скоростью $c$, только если его масса покоя равна нулю.
Итак, теперь эксперимент Майкельсона Морли можно рассматривать не столько как подтверждение теории относительности, сколько как демонстрацию того, что свет, если он состоит из частиц, должен состоять из безмассовых частиц. В эксперименте Майкельсона-Морели было обнаружено что-то, скорость которого изменяется точно так, как предсказывает общее преобразование Лоренца с конечным $c$, так что это было бы сильной догадкой (а не доказательством) того, что наша Вселенная действительно имеет конечное $c$ и что свет это то, что движется с этой скоростью. В этом контексте положительный результат эксперимента Майкельсона-Морли ( т. е. тот, который показывает зависимость скорости света от кадра) можно рассматривать как (i) обнаружение эфира (среда для света), но в равной степени (ii) можно считать, что эфира нет но что легкая частица имеет небольшую массу. Ни один из результатов не противоречит нашим недавно открытым законам относительности.
В этом контексте положительный результат эксперимента Майкельсона-Морли ( т. е. тот, который показывает зависимость скорости света от кадра) можно рассматривать как (i) обнаружение эфира (среда для света), но в равной степени (ii) можно считать, что эфира нет но что легкая частица имеет небольшую массу. Ни один из результатов не противоречит нашим недавно открытым законам относительности.
Конечно, многие другие эксперименты с тех пор подтвердили все, что предсказала теория относительности, основанная на конечном $c$, где $c$ установлена на скорость света, поэтому вполне разумно говорить о $c$ как о скорости света. в относительности. Но я надеюсь, что показал, что это не основное его значение.
Примечание: К сожалению, эти идеи не работают более чем в одном измерении. В одном измерении два ускорения действительно составляют усиление, но последовательность ускорений в разных направлениях обычно составляет одно усиление вместе с вращением. Это вращение называется прецессией Томпсона. Итак, мы говорим о группе Лоренца как о наименьшей группе всех преобразований, которые можно получить из последовательности вращений и повышений, но нет многомерной группы повышений, а есть только одномерная группа повышений с «одним параметром». 92$, $c$ — скорость света. Однако скорость света не является уникальным числом. Например, это может быть выражено в километрах в секунду или милях в секунду, что дает разные числа. Я понимаю, что это отношение пройденного расстояния ко времени, однако оба они, безусловно, являются значениями, созданными человеком, так как же уравнение может иметь реальную ценность? Если нет, то уравнение бессмысленно? Кроме того, $c$ обозначает скорость видимого света в вакууме. Почему универсальное преобразование массы в энергию и наоборот должно зависеть только от скорости видимого света, а не, скажем, ультрафиолетового или рентгеновского?
Это вращение называется прецессией Томпсона. Итак, мы говорим о группе Лоренца как о наименьшей группе всех преобразований, которые можно получить из последовательности вращений и повышений, но нет многомерной группы повышений, а есть только одномерная группа повышений с «одним параметром». 92$, $c$ — скорость света. Однако скорость света не является уникальным числом. Например, это может быть выражено в километрах в секунду или милях в секунду, что дает разные числа. Я понимаю, что это отношение пройденного расстояния ко времени, однако оба они, безусловно, являются значениями, созданными человеком, так как же уравнение может иметь реальную ценность? Если нет, то уравнение бессмысленно? Кроме того, $c$ обозначает скорость видимого света в вакууме. Почему универсальное преобразование массы в энергию и наоборот должно зависеть только от скорости видимого света, а не, скажем, ультрафиолетового или рентгеновского?
- специальная теория относительности
- электромагнитное излучение
- единицы
- масса-энергия
- физические константы
$\endgroup$
1
$\begingroup$
Во-первых, вы совершенно неправы, говоря, что видимый свет отличается от ультрафиолетового или рентгеновского. 2}= J$, который также называют джоулем.
2}= J$, который также называют джоулем.
Итак, в основном все фундаментальные уравнения в физике работают таким образом. Вы можете вводить любые единицы измерения, которые вам нравятся, при условии, что вы следите за этими единицами (т. е. вы не отменяете термины, такие как км/мили или что-то в этом роде). в которых говорится, что вы должны вводить данные в определенных единицах измерения.Однако обычно это нефундаментальные уравнения, где (для упрощения/сокращения вещей) например, избавились от постоянных предфакторов, которые также имели бы единицу измерения.
На второй вопрос. $c$ в этом уравнении — это скорость света (электромагнитной волны) в вакууме, которая не зависит от частоты света и представляет собой число, фиксированное на определенном значении: $c=299 792 458 м/с$ точно ( не измеренное значение).
$\endgroup$
$\begingroup$
Уравнение справедливо в любой системе единиц, которую вы выберете. Если вы используете $\rm mi/s$ вместо $\rm m/s$, тогда $E$ и/или $m$ будут иметь соответственно разные единицы измерения.
Если вы используете $\rm mi/s$ вместо $\rm m/s$, тогда $E$ и/или $m$ будут иметь соответственно разные единицы измерения.
$c$ представляет собой скорость всего света, а не только видимого света. Рентгеновские лучи, ультрафиолетовые лучи и видимый свет имеют одинаковую скорость.
$\endgroup$
0
$\begingroup$
Все электромагнитные волны распространяются в вакууме с одинаковой скоростью. Свет в узком смысле — это в основном только видимый свет, но радиоволны, микроволны, рентгеновские лучи и гамма-лучи — это одно и то же: связанные колеблющиеся электрические и магнитные поля. Их скорость распространения является фундаментальной константой, которая зависит от диэлектрической и магнитной проницаемости свободного пространства (тоже две константы). 92}$ (СИ), масса равна $kg$ и $c$, очевидно, $\frac{m}{s}$. Как видите, они соответствуют друг другу. Вы можете перейти к другой системе единиц, которая изменяет задействованные числа, но их отношение остается прежним.
Вы можете перейти к другой системе единиц, которая изменяет задействованные числа, но их отношение остается прежним.
По сути, $c$ — это больше, чем просто скорость света, это очень фундаментальная константа, которая связывает электрические и магнитные поля, а также проявляется в специальной теории относительности.
$\endgroup$
Скорость и скорость – Гиперучебник по физике
[закрыть]
скорость
В чем разница между двумя одинаковыми объектами, движущимися с разной скоростью? Почти все знают, что тот, кто движется быстрее (тот, у кого больше скорость), пройдет дальше, чем тот, кто движется медленнее, за то же время. Либо так, либо вам скажут, что тот, кто движется быстрее, доберется до места раньше, чем тот, кто медленнее. Какой бы ни была скорость, она включает в себя и расстояние, и время. «Быстрее» означает «дальше» (большее расстояние) или «скорее» (меньше времени).
Удвоение скорости означает удвоение пройденного расстояния за заданный промежуток времени. Удвоение скорости также означало бы сокращение вдвое времени, необходимого для преодоления заданного расстояния. Если вы немного разбираетесь в математике, эти утверждения будут значимыми и полезными. (Символ v используется для обозначения скорости из-за связи между скоростью и скоростью, которая будет вскоре обсуждаться.)
- Скорость прямо пропорциональна расстоянию, когда время постоянно: v ∝ с ( t константа)
- Скорость обратно пропорциональна времени при постоянном расстоянии: v ∝ 1 t ( с константа)
Объединение этих двух правил дает определение скорости в символической форме.
| v = | с |
| т |
☞ Это не окончательное определение. |
Не нравятся символы? Тогда вот еще один способ определить скорость. Скорость скорость изменения расстояния со временем.
Чтобы вычислить скорость объекта, мы должны знать, как далеко он ушел и сколько времени потребовалось, чтобы добраться туда. «Дальше» и «ранее» соответствуют «быстрее». Допустим, вы поехали на машине из Нью-Йорка в Бостон. Расстояние по дороге составляет примерно 300 км (200 миль). Если поездка занимает четыре часа, какова была ваша скорость? Применение приведенной выше формулы дает…
| v = | с | ≈ | 300 км | = 75 км/ч |
| т | 4 часа |
Это ответ, который дает нам уравнение, но насколько он верен? Было ли 75 км/ч скоростью автомобиля ? Да, конечно, это было… Ну, может быть, я думаю… Нет, это не могло быть скорости . Если только вы не живете в мире, где автомобили имеют какой-то исключительный круиз-контроль и транспортные потоки регулируются каким-то идеальным образом, ваша скорость во время этого гипотетического путешествия, безусловно, должна была варьироваться. Таким образом, число, рассчитанное выше, не равно 9.0003 скорость автомобиля, это средняя скорость за весь путь. Чтобы подчеркнуть этот момент, уравнение иногда модифицируют следующим образом…
Если только вы не живете в мире, где автомобили имеют какой-то исключительный круиз-контроль и транспортные потоки регулируются каким-то идеальным образом, ваша скорость во время этого гипотетического путешествия, безусловно, должна была варьироваться. Таким образом, число, рассчитанное выше, не равно 9.0003 скорость автомобиля, это средняя скорость за весь путь. Чтобы подчеркнуть этот момент, уравнение иногда модифицируют следующим образом…
| v = | ∆ с |
| ∆ т |
Черта между и указывает на среднее или среднее значение, а символ ∆ (дельта) указывает на изменение. Прочитайте это как «Vee bar — это дельта-эсс над дельта-тройником». Это количество мы рассчитали для нашей гипотетической поездки.
Напротив, спидометр автомобиля показывает его мгновенную скорость , то есть скорость, определяемую за очень небольшой интервал времени — мгновение. В идеале этот интервал должен быть как можно ближе к нулю, но на самом деле мы ограничены чувствительностью наших измерительных приборов. Мысленно, однако, можно представить вычисление средней скорости за все меньшие интервалы времени, пока мы не вычислим мгновенную скорость. Эта идея записывается символически как…
В идеале этот интервал должен быть как можно ближе к нулю, но на самом деле мы ограничены чувствительностью наших измерительных приборов. Мысленно, однако, можно представить вычисление средней скорости за все меньшие интервалы времени, пока мы не вычислим мгновенную скорость. Эта идея записывается символически как…
| v = |
| ∆ с | = | дс | ||
| ∆ т | дт |
или на языке исчисления скорость есть первая производная расстояние по времени.
Если вы не занимались исчислением, не парьтесь слишком сильно с этим определением. Есть и другие, более простые способы определения мгновенной скорости движущегося объекта. На графике расстояние-время скорость соответствует наклону, и, таким образом, мгновенная скорость объекта с непостоянной скоростью может быть найдена по наклону линии, касательной к его кривой.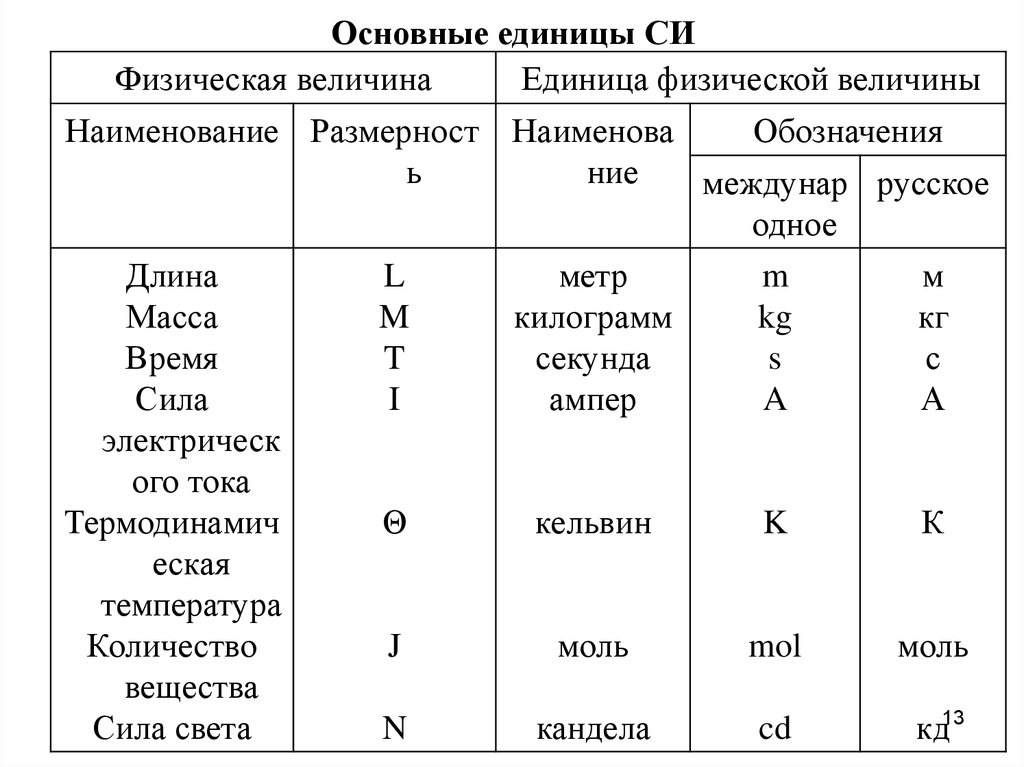 Мы займемся этим позже в этой книге.
Мы займемся этим позже в этой книге.
скорость
Чтобы вычислить скорость объекта, нам нужно знать, как далеко он ушел и сколько времени потребовалось, чтобы туда добраться. Тогда мудрый человек спросил бы…
Что вы подразумеваете под как далеко ? Вам нужно расстояние или смещение ?
Мудрый человек, когда-то давно
Ваш выбор ответа на этот вопрос определяет, что вы будете вычислять — скорость или скорость.
- Средняя скорость — это скорость изменения расстояния со временем.
- Средняя скорость — скорость изменения перемещения во времени.
А для людей, занимающихся расчетами…
- Мгновенная скорость является первой производной расстояния по времени.
- Мгновенная скорость является первой производной перемещения по времени.
Скорость и скорость связаны почти так же, как связаны расстояние и перемещение.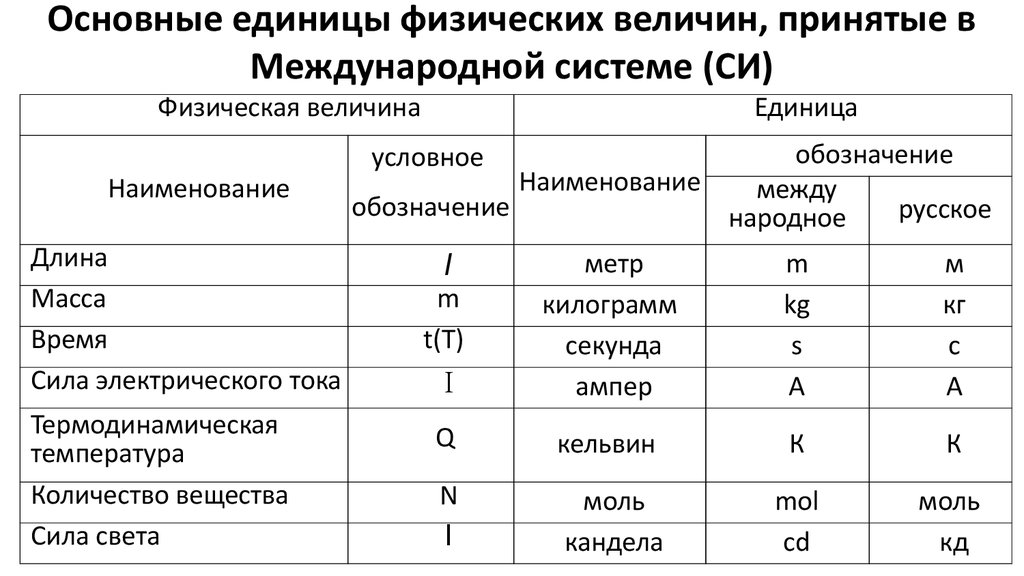 Скорость — это скаляр, а скорость — это вектор. Скорость получает символ v (курсив), а скорость получает символ v (жирный шрифт). Средние значения получают полосу над символом.
Скорость — это скаляр, а скорость — это вектор. Скорость получает символ v (курсив), а скорость получает символ v (жирный шрифт). Средние значения получают полосу над символом.
| средняя скорость |
| ||||||||||
| мгновенная скорость |
|
| средний скорость |
| ||||||||||
| мгновенная скорость |
|
Смещение измеряется по кратчайшему пути между двумя точками, и его величина всегда меньше или равна расстоянию. Величина смещения приближается к расстоянию, когда расстояние приближается к нулю. То есть расстояние и смещение фактически одинаковы (имеют одинаковую величину), когда исследуемый интервал «небольшой». Поскольку скорость основана на расстоянии, а скорость основана на смещении, эти две величины фактически одинаковы (имеют одинаковую величину), когда временной интервал «небольшой» или, говоря языком исчисления, величина средней скорости объекта приближается. его средняя скорость по мере приближения интервала времени к нулю.
Величина смещения приближается к расстоянию, когда расстояние приближается к нулю. То есть расстояние и смещение фактически одинаковы (имеют одинаковую величину), когда исследуемый интервал «небольшой». Поскольку скорость основана на расстоянии, а скорость основана на смещении, эти две величины фактически одинаковы (имеют одинаковую величину), когда временной интервал «небольшой» или, говоря языком исчисления, величина средней скорости объекта приближается. его средняя скорость по мере приближения интервала времени к нулю.
| ∆ t → 0 | ⇒ | против → | против | |
Мгновенная скорость объекта равна величине его мгновенной скорости.
v = | против |
Скорость говорит вам, насколько быстро. Скорость говорит вам, как быстро и в каком направлении.
шт.
Скорость и скорость измеряются в одних и тех же единицах измерения. Единицей расстояния и перемещения в СИ является метр. Единицей времени в СИ является секунда. Единицей скорости и скорости в СИ является отношение двух — 9.0227 метров в секунду .
Единицей времени в СИ является секунда. Единицей скорости и скорости в СИ является отношение двух — 9.0227 метров в секунду .
| ⎡ ⎢ ⎣ | м | = | м | ⎤ ⎥ ⎦ |
| с | с |
Этот прибор редко используется за пределами научных и академических кругов. Большинство людей на этой планете измеряют скорость в километров в час (км/ч или км/ч). Соединенные Штаты являются исключением в том смысле, что мы используем более старую миль в час (миль/ч или миль в час). Давайте определим коэффициенты преобразования, чтобы мы могли связать скорость, измеренную в м/с, с более привычными единицами измерения.
| 1 км/ч = | 1 км | 1000 м | 1 час | |||
| 1 час | 1 км | 3600 с | ||||
| 1 км/ч = | 0,2777… м/с ≈ ¼ м/с | |||||
| 19020= | ||||||
| 1 миля | 1609 м | 1 час | ||||
| 1 час | 1 миля | 3600 с | ||||
| 1 час в час = | 0,4469… м/с ≈ ½ м/с | |||||
Десятичные значения, показанные выше, точны до четырех значащих цифр, но дробные значения следует рассматривать только как эмпирические правила (1 км/ч на самом деле больше похож на 2 7 м/с, чем 1 4 м/с и 1 миль в час больше похоже на 4 9 м/с, чем на 1 29019).
Отношение любой единицы расстояния к любой единице времени является единицей скорости.
- Скорость кораблей, самолетов и ракет часто указывается в узлах . Один узел равен одной морской миле в час , морская миля равна 1852 метрам или 6076 футам, а час равен 3600 секундам. НАСА до сих пор сообщает скорость своих ракет в узлах и расстояние до них в морских милях. Один узел составляет примерно 0,5144 м/с.
- Самые низкие скорости измеряются в течение самых длинных периодов времени. Континентальные плиты ползут по поверхности Земли с геологически медленной скоростью 1–10 90 227 см/год 90 228 или 1–10 90 227 м/столетие 90 228 — примерно с такой же скоростью растут ногти и волосы.
- Аудиокассета движется со скоростью 1⅞ дюймов в секунду (ips). Когда магнитная лента была впервые изобретена, ее наматывали на открытые катушки, как кинопленку. Эти ранние катушечные магнитофоны воспроизводили ленту со скоростью 15 кадров в секунду.
 Более поздние модели также могли записывать с половиной этой скорости (7½ дюймов в секунду), затем с половиной этой скорости (3¾ дюймов в секунду), а затем с половиной этой скорости (1⅞ дюймов в секунду). Когда формулировался стандарт аудиокассет, было решено, что последнего из этих значений будет достаточно для нового носителя. Один дюйм в секунду по определению равен 0,0254 м/с.
Более поздние модели также могли записывать с половиной этой скорости (7½ дюймов в секунду), затем с половиной этой скорости (3¾ дюймов в секунду), а затем с половиной этой скорости (1⅞ дюймов в секунду). Когда формулировался стандарт аудиокассет, было решено, что последнего из этих значений будет достаточно для нового носителя. Один дюйм в секунду по определению равен 0,0254 м/с.
Иногда скорость объекта описывается относительно скорости чего-то другого; желательно какое-то физическое явление.
- Аэродинамика — это изучение движущегося воздуха и того, как объекты взаимодействуют с ним. В этой области скорость объекта часто измеряется относительно скорости звука . Это отношение известно как число Маха . Скорость звука составляет примерно 295 м/с (660 миль/ч) на высоте, на которой обычно летают коммерческие реактивные самолеты. Выведенный из эксплуатации сверхзвуковой Concorde British Airways и Air France двигался со скоростью 600 м/с (1340 миль в час).
 Простое деление показывает, что эта скорость примерно вдвое превышает скорость звука или 2,0 Маха, что является исключительно быстрым. Для сравнения, Боинг 777 развивает крейсерскую скорость 248 м/с (555 миль в час) или 0,8 Маха, что только кажется медленным по сравнению с Конкордом.
Простое деление показывает, что эта скорость примерно вдвое превышает скорость звука или 2,0 Маха, что является исключительно быстрым. Для сравнения, Боинг 777 развивает крейсерскую скорость 248 м/с (555 миль в час) или 0,8 Маха, что только кажется медленным по сравнению с Конкордом. - скорость света в вакууме определяется в системе СИ как 299 792 458 м/с (около миллиарда км/ч). Обычно это указывается с более разумной точностью как 3,00 × 10 8 м/с. Скорость света в вакууме обозначается символом c (курсивом) при использовании в уравнении и c (римским шрифтом) при использовании в качестве единицы измерения. Скорость света в вакууме является универсальным пределом, поэтому реальные объекты всегда движутся медленнее, чем c . Он часто используется в физике элементарных частиц и астрономии далеких объектов. Самые далекие наблюдаемые объекты — квазары; сокращение от «квазизвездные радиообъекты». Визуально они похожи на звезды (приставка «квази» означает «похожие»), но излучают гораздо больше энергии, чем любая звезда.
 Они лежат на окраинах наблюдаемой Вселенной и с невероятной скоростью уносятся от нас. Самые далекие квазары удаляются от нас почти на 0,9в. Кстати, символ c был выбран не потому, что скорость света является универсальной константой (которой она и является), а потому, что это первая буква латинского слова, обозначающего быстроту — celeritas .
Они лежат на окраинах наблюдаемой Вселенной и с невероятной скоростью уносятся от нас. Самые далекие квазары удаляются от нас почти на 0,9в. Кстати, символ c был выбран не потому, что скорость света является универсальной константой (которой она и является), а потому, что это первая буква латинского слова, обозначающего быстроту — celeritas .
| м/с | км/ч | устройство, событие, явление, процесс |
|---|---|---|
| 10 −9 ~10 −8 | континентальные пластины, рост волос, рост ногтей | |
| 10 −4 | человеческие сперматозоиды | |
| 10 −3 | улитки | |
| 0,013 | 0,045 | розлив кетчупа из бутылки |
| 10 −1 | ленивцы, черепахи, черепахи | |
| 0,65–1,29 | 2,34–4,64 | тараканы |
| 1 | 3,6 | нервные импульсы, немиелинизированные клетки |
| 1 | 3,6 | океанские течения |
| 0,06–1,14 | 0,22–4,10 | ламантины |
| 1,3 | 4,8 | человек, типичный темп ходьбы |
| 2,391 | 8. 608 608 | самый быстрый человек: плавание (Сезар Сьело) |
| 8 | 30 | максимальная комфортная скорость лифта |
| 10 | 40 | дельфины, морские свинки, киты |
| 10 | 40 | падающие капли дождя |
| 10.422 | 37.520 | самый быстрый человек: бег (Усэйн Болт) |
| 12 | 43 | волна стадиона |
| 12 | 44 | пробка для шампанского |
| 15.223 | 54.803 | самый быстрый человек: катание на коньках (Павел Кулижников) |
| 20 | 70 | кролики, зайцы, лошади, борзые, тунец, акулы |
| 30 | 100 | типичное ограничение скорости на автостраде |
| 33 | 118 | гепарды |
| 34,42 | 123,9 | самый быстрый человек: поле для софтбола (Моника Эбботт) |
| 40 | 140 | падающий град |
| 42,47 | 152,9 | самый быстрый человек: метание летающего диска (Саймон Лизотт) |
| 46,98 | 169,1 | самый быстрый человек: бейсбольное поле (Арольдис Чепмен) |
| 55 | 200 | предельная скорость типичного парашютиста |
70. 8217 8217 | 254,958 | самый быстрый человек: катание на лыжах (Иван Оригон) |
| 73,06 | 263 | самый быстрый человек: подача в теннисе (Сэм Грот) |
| 80 | 290 | сапсан в пикировании |
| 82 | 295 | очень быстрый мяч для гольфа |
| 82.211 | 296.00 | самый быстрый человек: езда на велосипеде (Дениз Коренек Мюллер) |
| 33–83 | 120–300 | ураган, максимальная устойчивая скорость ветра |
| 30–90 | 105–330 | торнадо, максимальная устойчивая скорость ветра |
| 100 | 360 | нервные импульсы, миелинизированные клетки |
| 113,2 | 407,5 | максимальный порыв приземного ветра (остров Барроу, Австралия) |
| 118,3 | 426 | самый быстрый человек: победа в бадминтоне (Мадс Пилер Колдинг) |
| 124,22 | 447,19 | самый быстрый дорожный автомобиль (Koenigsegg Agera RS) |
| 142,89 | 511.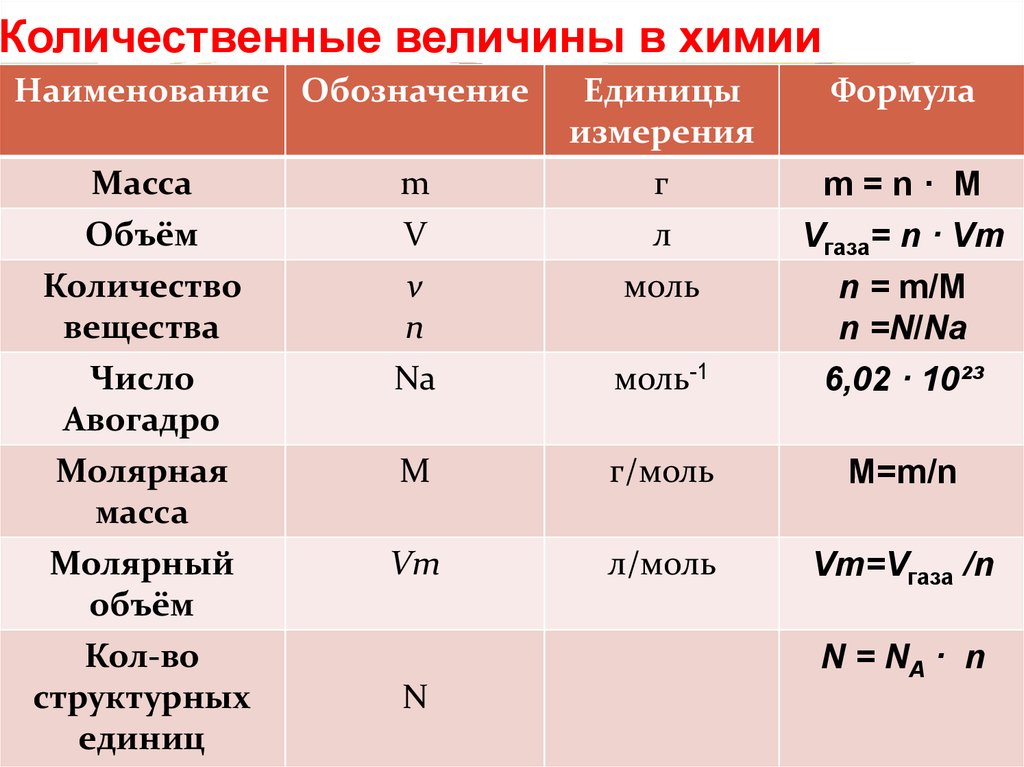 11 11 | самый быстрый корабль (Дух Австралии) |
| 159,7 | 574,8 | самый быстрый поезд (Train à Grande Vitesse) |
| 168,249 | 605,697 | самый быстрый мотоцикл (Top 1 Ack Attack) |
| 200 | 700 | цунами |
| 250 | 900 | коммерческий реактивный самолет |
| 331 | 1 190 | скорость звука в воздухе, СТП |
| 340 | 1 225 | скорость звука в воздухе на уровне моря |
| 341.4031 | 1 229,051 | самый быстрый экспериментальный автомобиль (Thrust SSC) |
| 343 | 1 235 | скорость звука в воздухе при комнатной температуре |
| 377,1 | 1 357,6 | самый быстрый человек: прыжки с парашютом (Феликс Баумгартнер) |
| 980.433 | 3 529,56 | самый быстрый самолет (SR-71 Blackbird) |
| 180–1 200 | 650–4 400 | пули |
| 1 500 | 5 400 | скорость звука в воде |
| 2 000 | 6000 | сейсмические волны |
| 6 900 | 25 000 | скорость детонации тротила |
| 8 000 | 29 000 | космический шаттл на орбите |
| 11 094 | 39 938 | самый быстрый пилотируемый космический корабль (Аполлон 10) |
| 11 180 | 40 250 | скорость убегания на поверхности Земли |
| 13 790 | 49 600 | Космический зонд New Horizons |
| 15 400 | 55 400 | Космический зонд «Вояджер-2» |
| 17 000 | 61 200 | Космический зонд «Вояджер 1» |
| 29 790 | 107 200 | Земля на орбите |
| 201 000 | 724 000 | самый быстрый беспилотный космический корабль (Parker Solar Probe) |
| 248 000 | 892 000 | Солнце движется по Млечному Пути |
| 300 000 | 1 100 000 | солнечный ветер у земли |
| 370 000 | 1 330 000 | Млечный Путь сквозь космический микроволновый фон |
| 60 000 000 | 216 000 000 | ПроектStarshot, предлагаемый межзвездный космический зонд | .
| 124 000 000 | 446 000 000 | скорость света в алмазе |
| 225 000 000 | 810 000 000 | скорость света в воде |
| 299 792 369 | 1 079 252 530 | протонов и антипротонов в Тэватроне, Фермилаб |
| 299 792 455 | 1 079 252 840 | протонов в Большом адронном коллайдере, ЦЕРН |
| 299 792 458 | 1 079 252 850 | скорость света в вакууме |
25.3: Закон преломления
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2727
- OpenStax
- OpenStax
Цели обучения
К концу этого раздела вы сможете:
- Определять показатель преломления, зная скорость света в среде.

Заглянув в аквариум, легко заметить некоторые странности. Например, вы можете увидеть одну и ту же рыбу в двух разных местах (рис. \(\PageIndex{1}\)). Это связано с тем, что свет, идущий от рыбы к нам, меняет направление, когда покидает аквариум, и в этом случае он может идти двумя разными путями, чтобы попасть к нашим глазам. Изменение направления светового луча (обобщенно называемое искривлением), когда он проходит через изменения в материи, называется преломление . Преломление отвечает за огромный спектр оптических явлений, от действия линз до передачи голоса по оптическим волокнам.
Определение: ПРЕЛОМЛЕНИЕ
Изменение направления светового луча (приблизительно называемое изгибом), когда он проходит через изменения в материи, называется преломлением.
СКОРОСТЬ СВЕТА
Скорость света \(c\) влияет не только на преломление, это одно из центральных понятий теории относительности Эйнштейна. По мере повышения точности измерений скорости света оказалось, что \(с\) не зависит от скорости источника или наблюдателя. Однако скорость света точно зависит от материала, через который он проходит. Эти факты имеют далеко идущие последствия, как мы увидим в «Специальной теории относительности». Это устанавливает связи между пространством и временем и изменяет наши ожидания, например, что все наблюдатели измеряют одно и то же время для одного и того же события. Скорость света настолько важна, что ее значение в вакууме является одной из самых фундаментальных констант в природе, а также одной из четырех основных единиц СИ.
Однако скорость света точно зависит от материала, через который он проходит. Эти факты имеют далеко идущие последствия, как мы увидим в «Специальной теории относительности». Это устанавливает связи между пространством и временем и изменяет наши ожидания, например, что все наблюдатели измеряют одно и то же время для одного и того же события. Скорость света настолько важна, что ее значение в вакууме является одной из самых фундаментальных констант в природе, а также одной из четырех основных единиц СИ.
Почему свет меняет направление при переходе из одного материала (среды) в другой? Это потому, что свет меняет скорость при переходе от одного материала к другому.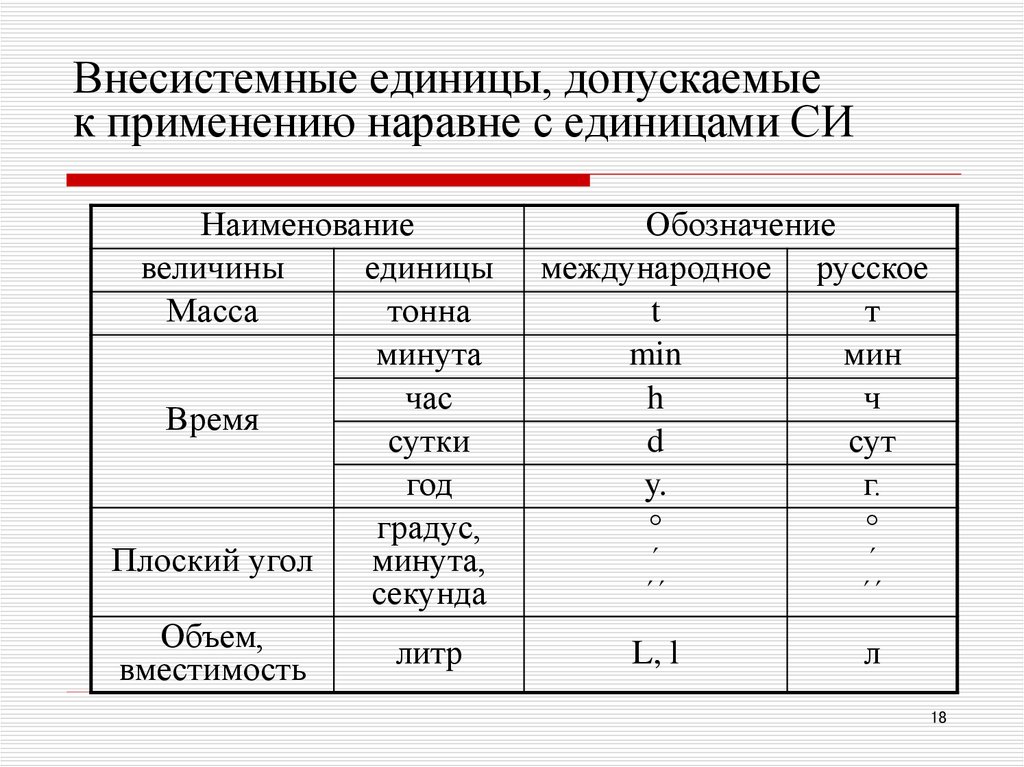 {8} м/с\) (всего 25% отличается от принятого сегодня значения). В последнее время физики измеряли скорость света различными способами и с возрастающей точностью. Один особенно прямой метод, использованный в 1887 году американским физиком Альбертом Майкельсоном (1852–1819 гг.31), показано на рисунке \(\PageIndex{2}\). Свет, отраженный от вращающегося набора зеркал, отражался от неподвижного зеркала на расстоянии 35 км и возвращался к вращающимся зеркалам. Время прохождения света можно определить по тому, как быстро должны вращаться зеркала, чтобы свет вернулся в глаз наблюдателя.
{8} м/с\) (всего 25% отличается от принятого сегодня значения). В последнее время физики измеряли скорость света различными способами и с возрастающей точностью. Один особенно прямой метод, использованный в 1887 году американским физиком Альбертом Майкельсоном (1852–1819 гг.31), показано на рисунке \(\PageIndex{2}\). Свет, отраженный от вращающегося набора зеркал, отражался от неподвижного зеркала на расстоянии 35 км и возвращался к вращающимся зеркалам. Время прохождения света можно определить по тому, как быстро должны вращаться зеркала, чтобы свет вернулся в глаз наблюдателя.
 Рассчитанное Майкельсоном значение скорости света всего на 0,04% отличалось от значения, используемого сегодня. 9{8} м/с\) используется всякий раз, когда достаточно трехзначной точности. Скорость света через вещество меньше, чем в вакууме, потому что свет взаимодействует с атомами в материале. Скорость света сильно зависит от типа материала, поскольку его взаимодействие с различными атомами, кристаллическими решетками и другими субструктурами различается.
Рассчитанное Майкельсоном значение скорости света всего на 0,04% отличалось от значения, используемого сегодня. 9{8} м/с\) используется всякий раз, когда достаточно трехзначной точности. Скорость света через вещество меньше, чем в вакууме, потому что свет взаимодействует с атомами в материале. Скорость света сильно зависит от типа материала, поскольку его взаимодействие с различными атомами, кристаллическими решетками и другими субструктурами различается.Определение: ПОКАЗАТЕЛЬ ПРЕЛОМЛЕНИЯ
Мы определяем показатель преломления \(n\) материала как
\[n = \frac{c}{v}, \label{index}\]
где \(v\) — наблюдаемая скорость света в материале. Так как скорость света всегда меньше \(с\) в веществе и равна \(с\) только в вакууме, показатель преломления всегда больше или равен единице. То есть \(n \gt 1\).
В таблице \(\PageIndex{1}\) приведены показатели преломления некоторых репрезентативных веществ. Значения указаны для определенной длины волны света, потому что они немного меняются в зависимости от длины волны.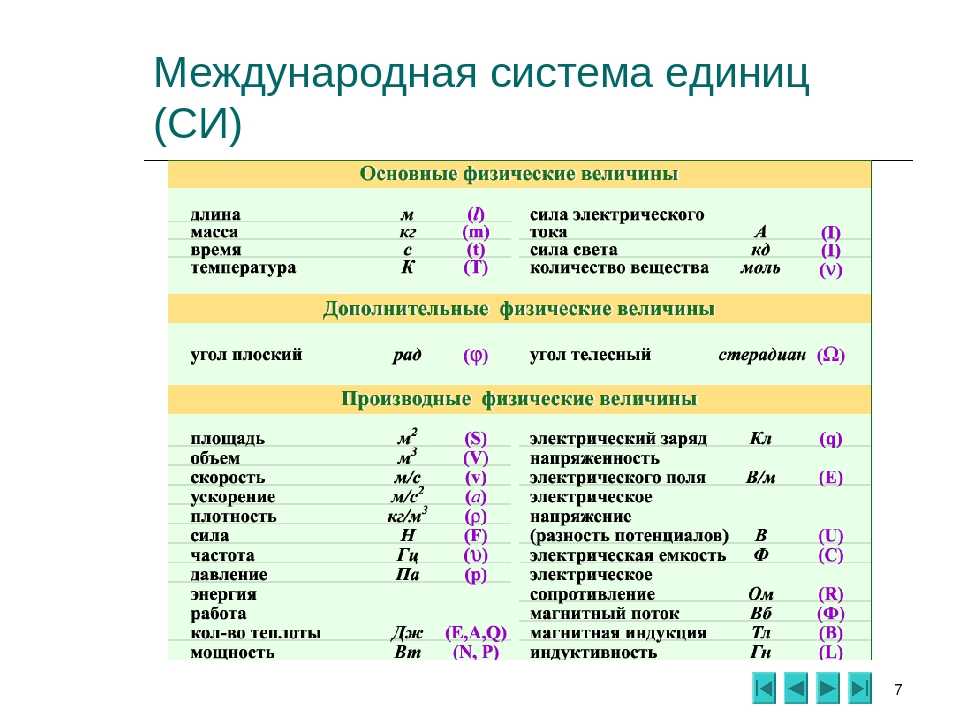 (Это может иметь важные эффекты, такие как цвета, создаваемые призмой.) Обратите внимание, что для газов \(n\) близко к 1,0. Это кажется разумным, так как атомы в газах далеко друг от друга и свет распространяется со скоростью \(с\) в вакууме между атомами. Обычно для газов принимают \(n = 1\), если не требуется большая точность. Хотя скорость света \(v\) в среде значительно отличается от ее значения \(с\) в вакууме, это все же большая скорость.
(Это может иметь важные эффекты, такие как цвета, создаваемые призмой.) Обратите внимание, что для газов \(n\) близко к 1,0. Это кажется разумным, так как атомы в газах далеко друг от друга и свет распространяется со скоростью \(с\) в вакууме между атомами. Обычно для газов принимают \(n = 1\), если не требуется большая точность. Хотя скорость света \(v\) в среде значительно отличается от ее значения \(с\) в вакууме, это все же большая скорость.
| Средний | п |
|---|---|
| Газы при \(0ºC, 1 атм\) | |
| Воздух | 1.000293 |
| Углекислый газ | 1.00045 |
| Водород | 1.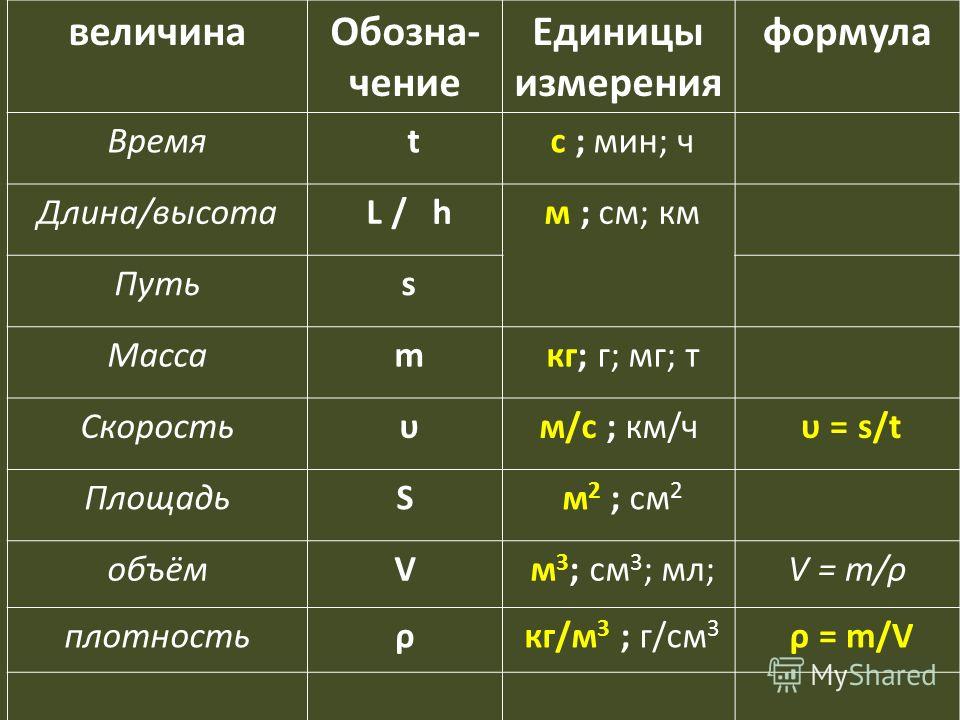 000139 000139 |
| Кислород | 1.000271 |
| Жидкости при 20ºC | |
| Бензол | 1.501 |
| Сероуглерод | 1,628 |
| Четыреххлористый углерод | 1.461 |
| Этанол | 1.361 |
| Глицерин | 1,473 |
| Вода пресная | 1,333 |
| Твердые вещества при 20ºC | |
| Алмаз | 2.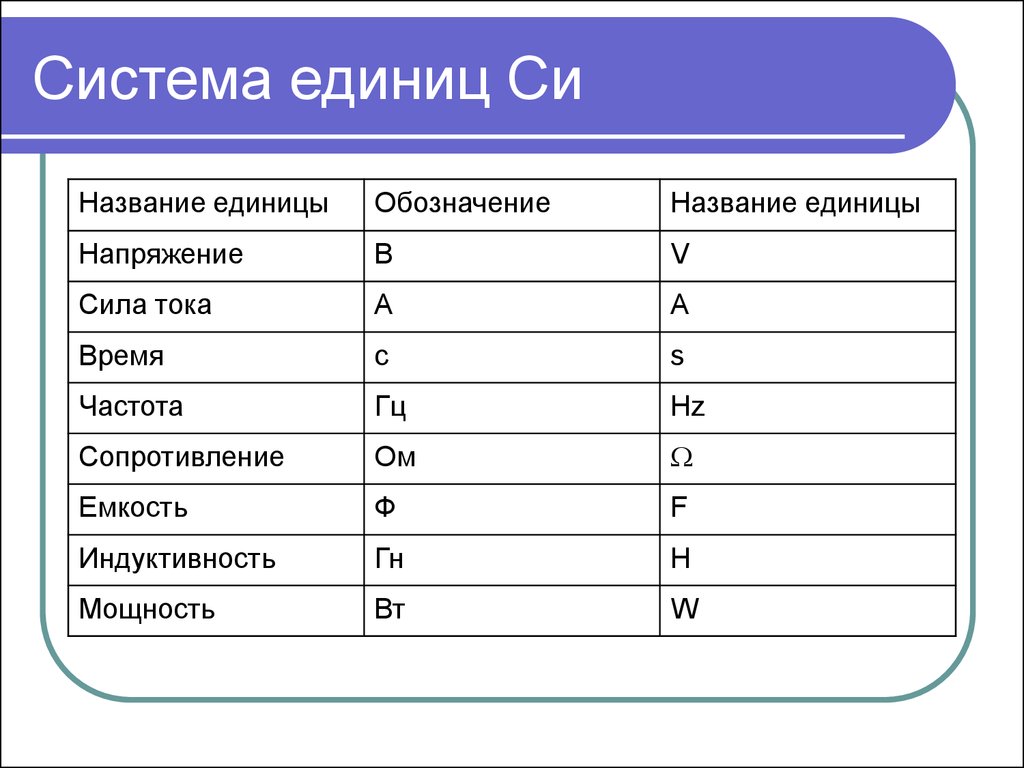 419 419 |
| Флюорит | 1.434 |
| Стекло, заводная головка | 1,52 |
| Стекло бесцветное | 1,66 |
| Лед при 20ºC | 1.309 |
| Полистирол | 1,49 |
| Оргстекло | 1,51 |
| Кварц кристаллический | 1,544 |
| Кварц, плавленый | 1,458 |
| Хлорид натрия | 1,544 |
| Циркон | 1,923 |
Пример \(\PageIndex{1}\): Скорость света в материи
Рассчитайте скорость света в цирконе, материале, используемом в ювелирных изделиях для имитации алмаза.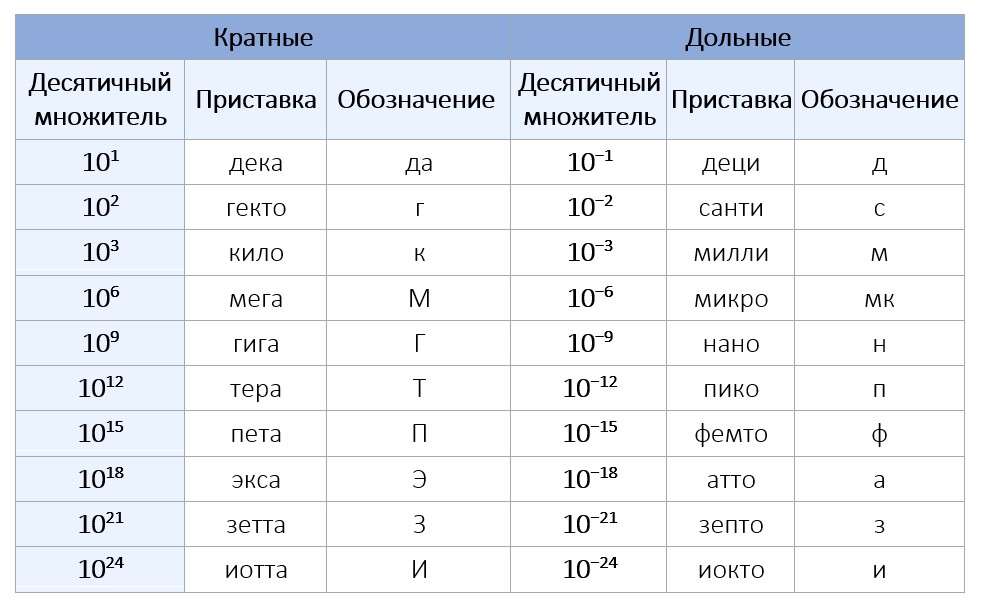
Стратегия:
Скорость света в материале \(v\) можно рассчитать по показателю преломления \(n\) материала с помощью уравнения \(n = c/v\) .
9{8} м/с. \end{align*}\]Обсуждение:
Эта скорость чуть больше половины скорости света в вакууме и все еще высока по сравнению со скоростями, с которыми мы обычно сталкиваемся. Единственное вещество, указанное в таблице \(\PageIndex{1}\), которое имеет больший показатель преломления, чем циркон, — это алмаз. Позже мы увидим, что большой показатель преломления циркона заставляет его сверкать больше, чем стекло, но меньше, чем алмаз.
Закон преломления
На рисунке \(\PageIndex{3}\) показано, как луч света меняет направление при переходе из одной среды в другую. Как и прежде, углы измеряются относительно перпендикуляра к поверхности в точке пересечения ее световым лучом. (Некоторая часть падающего света будет отражаться от поверхности, но сейчас мы сосредоточимся на проходящем свете. ) Изменение направления светового луча зависит от того, как изменяется скорость света. Изменение скорости света связано с показателями преломления соответствующих сред. В ситуациях, показанных на рисунке \(\PageIndex{3}\), среда 2 имеет больший показатель преломления, чем среда 1. Это означает, что скорость света в среде 2 меньше, чем в среде 1. Обратите внимание, что, как показано на Рисунок \(\PageIndex{3a}\), направление луча приближается к перпендикуляру, когда он замедляется. И наоборот, как показано на рисунке \(\PageIndex{3b}\), направление луча отклоняется от перпендикуляра, когда он ускоряется. Путь точно обратим. В обоих случаях вы можете себе представить, что происходит, если представить, как вы толкаете газонокосилку с тротуара на траву и наоборот. При переходе с тропинки на траву передние колеса замедляются и тянутся в сторону, как показано на рисунке. Это такое же изменение направления, как и для света, когда он переходит из быстрой среды в медленную. При переходе с травы на пешеходную дорожку передние колеса могут двигаться быстрее, и косилка меняет направление, как показано на рисунке.
) Изменение направления светового луча зависит от того, как изменяется скорость света. Изменение скорости света связано с показателями преломления соответствующих сред. В ситуациях, показанных на рисунке \(\PageIndex{3}\), среда 2 имеет больший показатель преломления, чем среда 1. Это означает, что скорость света в среде 2 меньше, чем в среде 1. Обратите внимание, что, как показано на Рисунок \(\PageIndex{3a}\), направление луча приближается к перпендикуляру, когда он замедляется. И наоборот, как показано на рисунке \(\PageIndex{3b}\), направление луча отклоняется от перпендикуляра, когда он ускоряется. Путь точно обратим. В обоих случаях вы можете себе представить, что происходит, если представить, как вы толкаете газонокосилку с тротуара на траву и наоборот. При переходе с тропинки на траву передние колеса замедляются и тянутся в сторону, как показано на рисунке. Это такое же изменение направления, как и для света, когда он переходит из быстрой среды в медленную. При переходе с травы на пешеходную дорожку передние колеса могут двигаться быстрее, и косилка меняет направление, как показано на рисунке. Это тоже то же изменение направления, что и при переходе света от медленного к быстрому.
Это тоже то же изменение направления, что и при переходе света от медленного к быстрому.
Величина, на которую луч света меняет свое направление, зависит как от угла падения, так и от величины изменения скорости. Для луча под заданным углом падения большое изменение скорости вызывает большое изменение направления и, следовательно, большое изменение угла. Точное математическое соотношение представляет собой закон преломления или «закон Снеллиуса», который выражается в виде уравнения = n_{2} \sin\theta_{2}.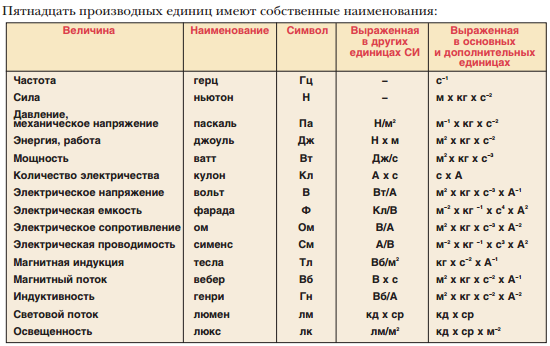 \label{25.4.2}\]
\label{25.4.2}\]
Здесь \(n_{1}\) и \(n_{2}\) — показатели преломления для сред 1 и 2, а \(\theta_{1}\) и \(\theta_{2} \) — это углы между лучами и перпендикуляром в средах 1 и 2, как показано на рисунке \(\PageIndex{3}\). Входящий луч называется падающим лучом, а выходящий луч — преломленным лучом, а связанные с ним углы — углом падения и углом преломления. Закон преломления также называют законом Снелла в честь голландского математика Виллеброрда Снелла (1591–1626), открывшего его в 1621 году. Эксперименты Снелла показали, что закон преломления соблюдается и что характеристический показатель преломления \(n\) может быть отнесены к определенному носителю. Снелл не знал, что скорость света различается в разных средах, но с помощью экспериментов он смог определить показатели преломления по тому, как световые лучи меняют направление.
ДОМАШНИЙ ЭКСПЕРИМЕНТ: СЛОМАННЫЙ КАРАНДАШ
Классическое наблюдение рефракции происходит, когда карандаш помещают в стакан, наполовину наполненный водой.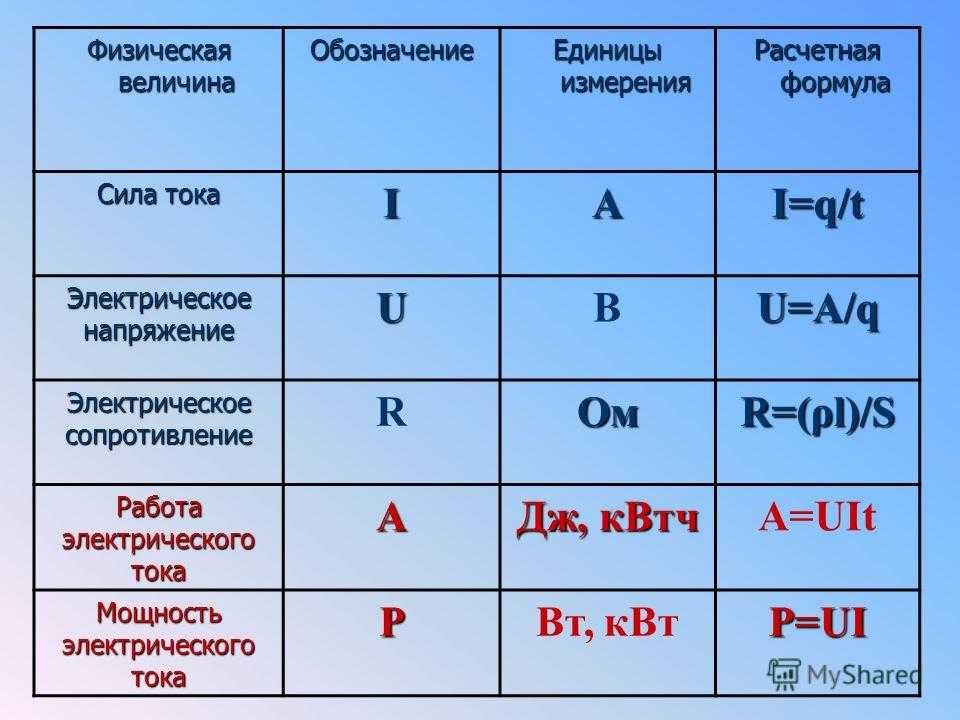 {\circ}\). 9{\circ}}} \\[5pt] &= \frac{0,500}{0,375} \\[5pt] &=1,33. \end{align*}\]
{\circ}\). 9{\circ}}} \\[5pt] &= \frac{0,500}{0,375} \\[5pt] &=1,33. \end{align*}\]
Обсуждение
Это показатель преломления воды, и Снелл мог определить его, измерив углы и выполнив этот расчет. Затем он нашел бы, что 1,33 является подходящим показателем преломления для воды во всех других ситуациях, например, когда луч проходит из воды в стекло. Сегодня мы можем проверить, что показатель преломления связан со скоростью света в среде, напрямую измерив эту скорость. 9{\circ}\). Мы можем посмотреть показатель преломления алмаза в таблице \(\PageIndex{1}\), найдя \(n_{2} = 2,419\). Единственное неизвестное в законе Снелла — это \(\theta_{2}\), которое мы хотим определить.
Решение
Решение закона Снеллиуса (уравнение \ref{25.4.2}) для \(\sin{\theta_{2}}\) дает
\[ \sin{\theta_{2}} = \ frac{n_{1}}{n_{2}}\sin{\theta_{1}}.\]
Ввод известных значений,
\[ \begin{align*} \sin{\theta_{2}} &= \фракция{1,00}{2,419{8} м/с\)
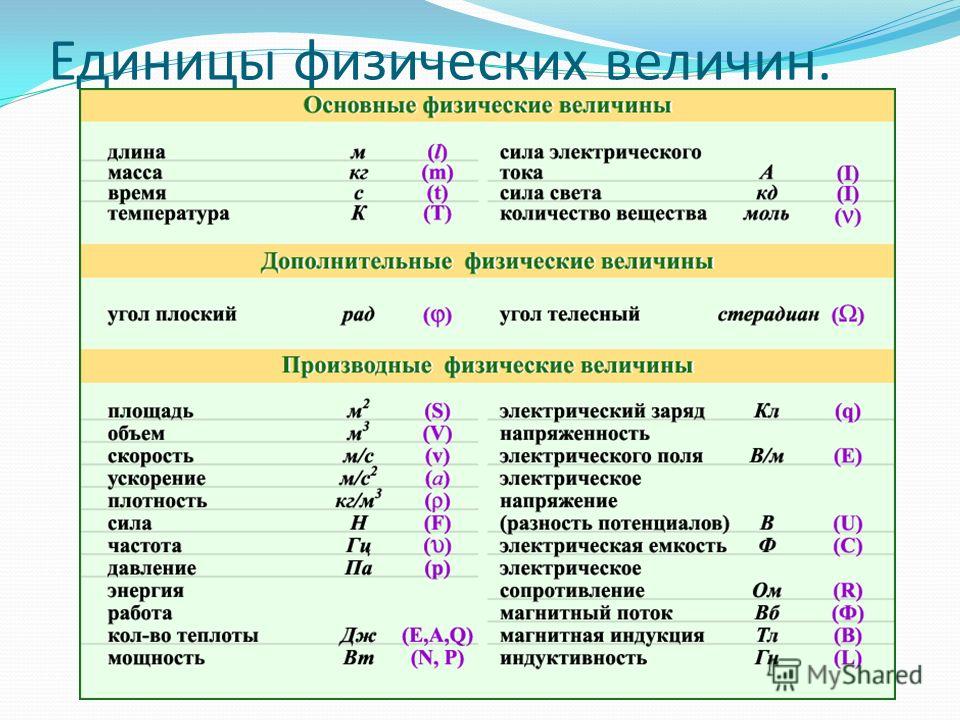
Глоссарий
- преломление
- изменение направления луча света при прохождении через изменения в материи
- показатель преломления
- для материала отношение скорости света в вакууме к скорости света в материале
Эта страница под названием 25.3: The Law of Refraction распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать оглавление
- нет
- Теги
- показатель преломления
- преломление
- Закон преломления Снеллиуса
Как рассчитать скорость света
Щелкни пальцами! За то время, которое потребовалось для этого, луч света смог пройти почти весь путь до Луны.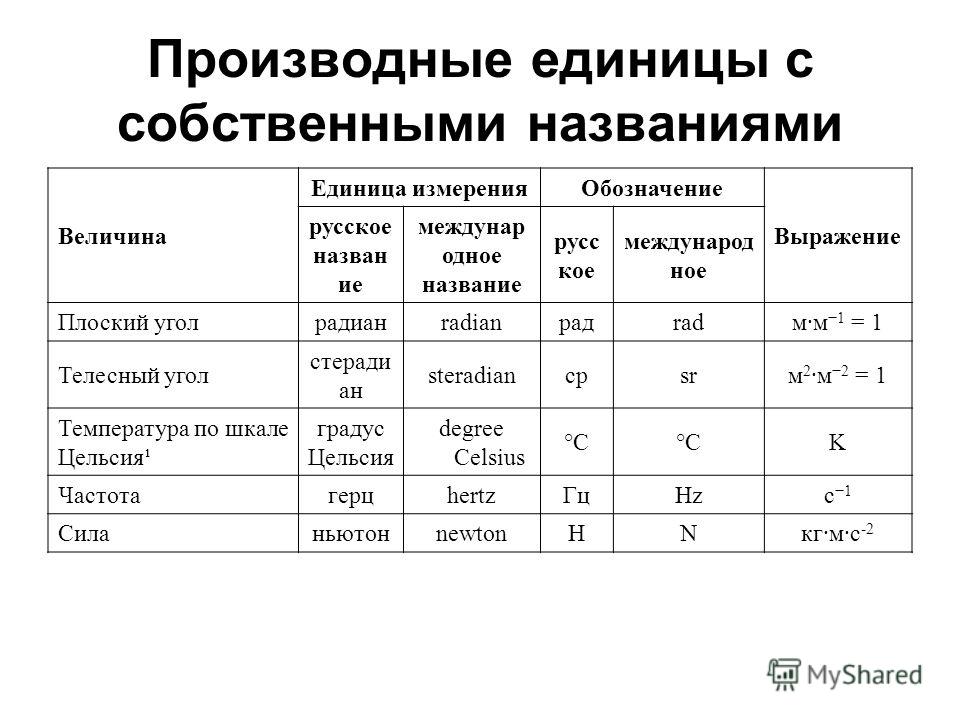 Если вы щелкнете пальцами еще раз, вы дадите лучу время завершить путешествие. Дело в том, что свет распространяется очень, очень быстро.
Если вы щелкнете пальцами еще раз, вы дадите лучу время завершить путешествие. Дело в том, что свет распространяется очень, очень быстро.
Свет распространяется быстро, но его скорость не бесконечна, как считали до XVII века. Однако скорость слишком высока, чтобы ее можно было измерить с помощью ламп, взрывов или других средств, зависящих от остроты зрения и времени реакции человека. Спросите у Галилея.
Эксперименты со светом
В 1638 году Галилей провел эксперимент с использованием фонарей, и лучшим выводом, который он смог сделать, было то, что свет «чрезвычайно быстр» (другими словами, очень, очень быстр). Он не смог придумать число, а если и смог, то даже попытался провести эксперимент. Однако он осмелился сказать, что, по его мнению, свет распространяется как минимум в 10 раз быстрее звука. На самом деле, это больше похоже на миллион раз быстрее.
Первое успешное измерение скорости света, которую физики повсеместно обозначают строчной буквой с, было сделано Оле Ремером в 1676 году. Он основывал свои измерения на наблюдениях за спутниками Юпитера. С тех пор физики использовали наблюдения за звездами, зубчатые колеса, вращающиеся зеркала, радиоинтерферометры, объемные резонаторы и лазеры для уточнения измерений. Теперь они знают c настолько точно, что Генеральный совет по мерам и весам основал на нем метр, который является основной единицей длины в системе СИ.
Он основывал свои измерения на наблюдениях за спутниками Юпитера. С тех пор физики использовали наблюдения за звездами, зубчатые колеса, вращающиеся зеркала, радиоинтерферометры, объемные резонаторы и лазеры для уточнения измерений. Теперь они знают c настолько точно, что Генеральный совет по мерам и весам основал на нем метр, который является основной единицей длины в системе СИ.
Скорость света является универсальной константой, поэтому формулы для скорости света не существует, per se . На самом деле, если бы c были другими, все наши измерения должны были бы измениться, потому что счетчик основан на них. Однако у света есть волновые характеристики, которые включают частоту ν и длину волны λ , и вы можете связать их со скоростью света с помощью следующего уравнения, которое можно назвать уравнением для скорости света:
c=\nu \lambda
Измерение скорости света с помощью астрономических наблюдений
Ремер был первым, кто придумал число для скорости света.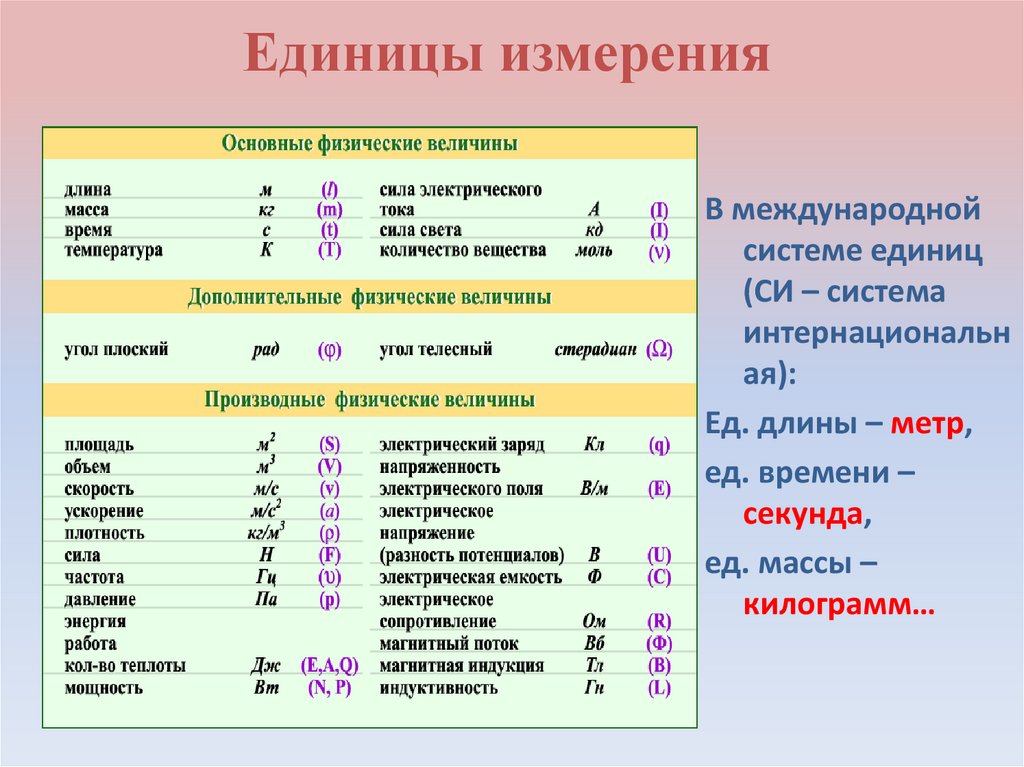 Он сделал это, наблюдая затмения спутников Юпитера, особенно Ио. Он наблюдал, как Ио исчезала за гигантской планетой, а затем замерял, сколько времени потребуется, чтобы снова появиться. Он рассудил, что это время может отличаться на 1000 секунд, в зависимости от того, насколько близко Юпитер находится к Земле. Он придумал значение скорости света 214 000 км/с, что примерно соответствует современному значению почти 300 000 км/с.
Он сделал это, наблюдая затмения спутников Юпитера, особенно Ио. Он наблюдал, как Ио исчезала за гигантской планетой, а затем замерял, сколько времени потребуется, чтобы снова появиться. Он рассудил, что это время может отличаться на 1000 секунд, в зависимости от того, насколько близко Юпитер находится к Земле. Он придумал значение скорости света 214 000 км/с, что примерно соответствует современному значению почти 300 000 км/с.
В 1728 году английский астроном Джеймс Брэдли рассчитал скорость света, наблюдая аберрации звезд, то есть их видимое изменение положения из-за движения Земли вокруг Солнца. Измерив угол этого изменения и вычтя скорость Земли, которую он мог рассчитать из данных, известных в то время, Брэдли получил гораздо более точное число. Он подсчитал, что скорость света в вакууме составляет 301 000 км/с.
Сравнение скорости света в воздухе со скоростью в воде
Следующим, кто измерил скорость света, был французский философ Арман Ипполит Физо, и он не полагался на астрономические наблюдения. Вместо этого он сконструировал аппарат, состоящий из светоделителя, вращающегося зубчатого колеса и зеркала, расположенного на расстоянии 8 км от источника света. Он мог регулировать скорость вращения колеса, позволяя лучу света проходить к зеркалу, но блокируя обратный луч. Его расчет c , который он опубликовал в 1849 году, составил 315 000 км/с, что не так точно, как у Брэдли.
Вместо этого он сконструировал аппарат, состоящий из светоделителя, вращающегося зубчатого колеса и зеркала, расположенного на расстоянии 8 км от источника света. Он мог регулировать скорость вращения колеса, позволяя лучу света проходить к зеркалу, но блокируя обратный луч. Его расчет c , который он опубликовал в 1849 году, составил 315 000 км/с, что не так точно, как у Брэдли.
Год спустя Леон Фуко, французский физик, усовершенствовал эксперимент Физо, заменив зубчатое колесо вращающимся зеркалом. Значение Фуко для c было 298 000 км / с, что было более точным, и в процессе Фуко сделал важное открытие. Вставив трубку с водой между вращающимся зеркалом и неподвижным, он определил, что скорость света в воздухе выше, чем скорость в воде. Это противоречило тому, что предсказывала корпускулярная теория света, и помогло установить, что свет представляет собой волну.
В 1881 году А. А. Майкельсон усовершенствовал измерения Фуко, сконструировав интерферометр, который мог сравнивать фазы исходного и возвращающегося лучей и отображать интерференционную картину на экране. Его результат составил 299 853 км/с.
Его результат составил 299 853 км/с.
Майкельсон разработал интерферометр для обнаружения присутствия эфира , призрачной субстанции, через которую, как считалось, распространяются световые волны. Его эксперимент, проведенный с физиком Эдвардом Морли, потерпел неудачу и привел Эйнштейна к выводу, что скорость света является универсальной константой, одинаковой во всех системах отсчета. Это послужило основой для специальной теории относительности.
Использование уравнения для скорости света
Значение Майкельсона было общепринятым, пока он сам не улучшил его в 1926 году. С тех пор это значение уточнялось рядом исследователей с использованием различных методов. Одним из таких методов является метод объемного резонатора, в котором используется устройство, генерирующее электрический ток. Это верный метод, потому что после публикации уравнений Максвелла в середине 1800-х годов физики пришли к единому мнению, что свет и электричество являются явлениями электромагнитных волн и оба распространяются с одинаковой скоростью.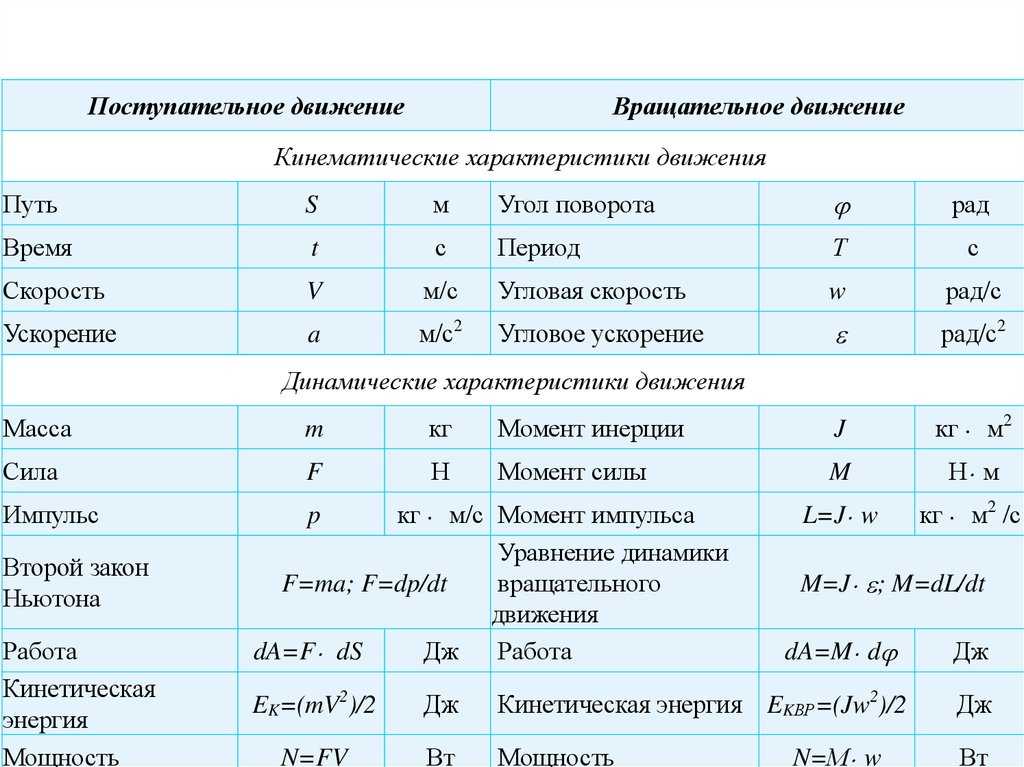
На самом деле, после того как Максвелл опубликовал свои уравнения, стало возможным измерять c косвенно, сравнивая магнитную и электрическую проницаемости свободного пространства. Два исследователя, Роза и Дорси, сделали это в 1907 году и вычислили скорость света в 299 788 км/с.
В 1950 году британские физики Луи Эссен и А.С. Гордон-Смит использовали объемный резонатор для расчета скорости света путем измерения его длины волны и частоты. Скорость света равна расстоянию, которое проходит свет d разделить на время ∆t : c = d/∆t . Учтите, что время прохождения одной длиной волны λ точки равно периоду формы волны, который является обратной величиной частоты v , и вы получите формулу скорости света:
c= \nu \lambda
Прибор, который использовали Эссен и Гордон-Смит, известен как резонансный волномер с резонатором . Он генерирует электрический ток известной частоты, и они смогли рассчитать длину волны, измерив размеры волномера. Их расчеты дали 299 792 км / с, что было самым точным определением на сегодняшний день.
Их расчеты дали 299 792 км / с, что было самым точным определением на сегодняшний день.
Современный метод измерения с использованием лазеров
Один из современных методов измерения возрождает метод разделения луча, используемый Физо и Фуко, но использует лазеры для повышения точности. В этом методе импульсный лазерный луч разделяется. Один луч идет к детектору, а другой проходит перпендикулярно к зеркалу, расположенному на небольшом расстоянии. Зеркало отражает луч обратно ко второму зеркалу, которое отклоняет его ко второму детектору. Оба детектора подключены к осциллографу, который записывает частоту импульсов.
Пики импульсов осциллографа разделены, поскольку второй луч проходит большее расстояние, чем первый. Измерив расстояние между пиками и расстояние между зеркалами, можно определить скорость светового луча. Это простой метод, и он дает довольно точные результаты. Исследователь из Университета Нового Южного Уэльса в Австралии зафиксировал значение в 300 000 км/с.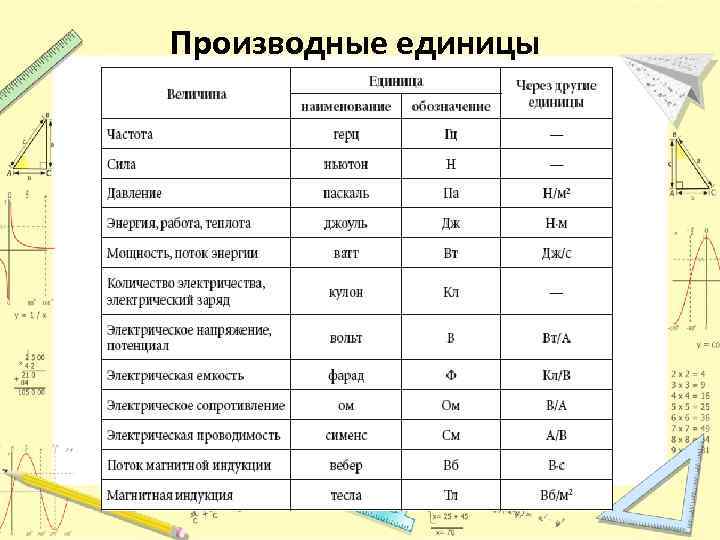
Измерение скорости света больше не имеет смысла
Измерительная линейка, используемая научным сообществом, называется метр. Первоначально он был определен как одна десятимиллионная часть расстояния от экватора до Северного полюса, а позже определение было изменено на определенное количество длин волн одной из эмиссионных линий криптона-86. В 1983 году Генеральный совет по мерам и весам отменил эти определения и принял следующее:
9 792 458 секунд, где секунда основана на радиоактивном распаде атома цезия-133.
Определение метра с точки зрения скорости света в основном фиксирует скорость света на уровне 299 792 458 м/с. Если эксперимент дает другой результат, это просто означает, что аппарат неисправен. Вместо того, чтобы проводить дополнительные эксперименты по измерению скорости света, ученые используют скорость света для калибровки своего оборудования.
Использование скорости света для калибровки экспериментального оборудования
Скорость света проявляется в различных контекстах физики, и технически возможно вычислить ее на основе других измеренных данных. Например, Планк продемонстрировал, что энергия кванта, такого как фотон, равна его частоте, умноженной на постоянную Планка (h), которая равна 6,6262 x 10 -34 Дж⋅секунда. Поскольку частота равна c/λ , уравнение Планка можно записать в терминах длины волны:
Например, Планк продемонстрировал, что энергия кванта, такого как фотон, равна его частоте, умноженной на постоянную Планка (h), которая равна 6,6262 x 10 -34 Дж⋅секунда. Поскольку частота равна c/λ , уравнение Планка можно записать в терминах длины волны:
E=h\nu = \frac{hc}{\lambda}\implies c=\frac{E\lambda}{ ч}
Облучив фотоэлектрическую пластину светом с известной длиной волны и измерив энергию выброшенных электронов, можно получить значение для c . Однако этот тип калькулятора скорости света не является необходимым для измерения с, потому что c определено как то, чем оно является. Однако его можно было использовать для проверки аппарата. Если Eλ/h не окажется равным c, что-то не так либо с измерениями энергии электрона, либо с длиной волны падающего света.
Скорость света в вакууме — универсальная константа
Имеет смысл определить метр с точки зрения скорости света в вакууме, так как это самая фундаментальная константа во Вселенной.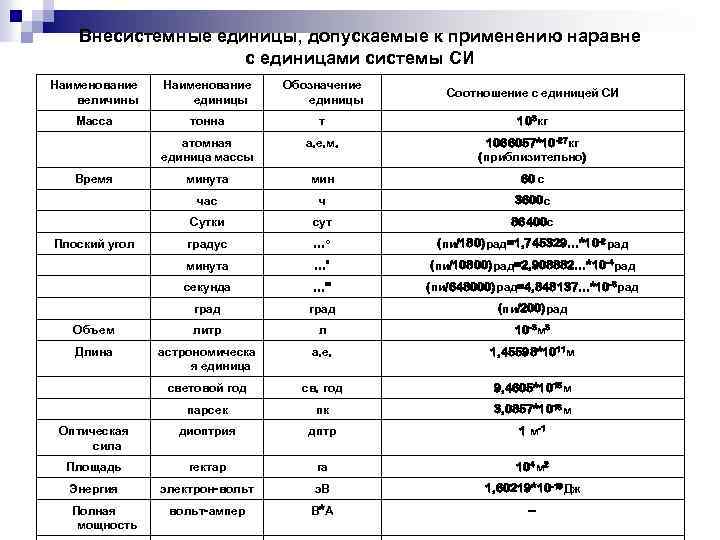 Эйнштейн показал, что она одинакова для любой точки отсчета, независимо от движения, а также это самое быстрое, что может двигаться во Вселенной — по крайней мере, все, что имеет массу. Уравнение Эйнштейна и одно из самых известных уравнений в физике: E = mc 2 92}}}
Эйнштейн показал, что она одинакова для любой точки отсчета, независимо от движения, а также это самое быстрое, что может двигаться во Вселенной — по крайней мере, все, что имеет массу. Уравнение Эйнштейна и одно из самых известных уравнений в физике: E = mc 2 92}}}
Для движущегося тела с массой m и скоростью v уравнение Эйнштейна должно быть записано E = mc 2 γ . Когда вы посмотрите на это, вы увидите, что когда v = 0, γ = 1, вы получаете E=mc 2 .
Однако, когда v = c, γ становится бесконечным, и вы должны сделать вывод, что для разгона любой конечной массы до этой скорости потребуется бесконечное количество энергии. Другой способ взглянуть на это состоит в том, что масса становится бесконечной со скоростью света.
Текущее определение метра делает скорость света стандартом для наземных измерений расстояний, но оно уже давно используется для измерения расстояний в космосе.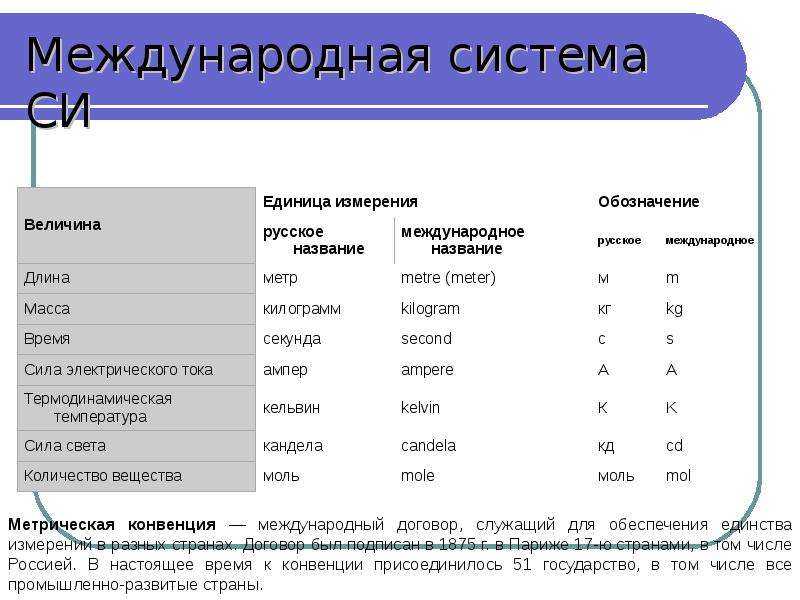 Световой год – это расстояние, которое проходит свет за один земной год, что получается 9,46×10 15 м.
Световой год – это расстояние, которое проходит свет за один земной год, что получается 9,46×10 15 м.
Это количество метров слишком много для понимания, но световой год понять легко, а поскольку скорость света постоянна во всех инерциальных системах отсчета, это надежная единица измерения расстояния. Он стал немного менее надежным из-за того, что основан на годе, а это временные рамки, которые не имеют отношения ни к кому с другой планеты.
Как быстро движется свет? | Скорость света
Скорость света — это предел скорости всего в нашей Вселенной. Или это? (Изображение предоставлено: Гетти/Юичиро Чино)Скорость света, проходящего через вакуум, составляет ровно 299 792 458 метров (983 571 056 футов) в секунду. Это около 186 282 миль в секунду — универсальная постоянная, известная в уравнениях как «с» или скорость света.
По мнению физика Альберта Эйнштейна специальной теории относительности г., на котором основана большая часть современной физики, ничто во Вселенной не может двигаться быстрее света. Теория утверждает, что по мере того, как материя приближается к скорости света, масса материи становится бесконечной. Это означает, что скорость света действует как предел скорости для всей вселенной . Скорость света настолько неизменна, что, согласно Национального института стандартов и технологий США , она используется для определения международных стандартных измерений, таких как метр (и, соответственно, миля, фут и дюйм). С помощью некоторых хитрых уравнений он также помогает определить килограмм и единицу измерения температуры 9.1998 Кельвин .
Теория утверждает, что по мере того, как материя приближается к скорости света, масса материи становится бесконечной. Это означает, что скорость света действует как предел скорости для всей вселенной . Скорость света настолько неизменна, что, согласно Национального института стандартов и технологий США , она используется для определения международных стандартных измерений, таких как метр (и, соответственно, миля, фут и дюйм). С помощью некоторых хитрых уравнений он также помогает определить килограмм и единицу измерения температуры 9.1998 Кельвин .
Но, несмотря на репутацию скорости света как универсальной константы, ученые и писатели-фантасты проводят время, размышляя о путешествиях со скоростью, превышающей скорость света. До сих пор никому не удавалось продемонстрировать настоящий варп-двигатель, но это не замедлило нашего коллективного стремления к новым историям, новым изобретениям и новым областям физики.
Родственный: Специальная теория относительности выдерживает испытание высокой энергией
Что такое световой год?
A l световой год — это расстояние, которое свет может пройти за один год — около 6 триллионов миль (10 триллионов километров). Это один из способов, которым астрономы и физики измеряют огромные расстояния в нашей Вселенной.
Это один из способов, которым астрономы и физики измеряют огромные расстояния в нашей Вселенной.
Свет проходит от луны к нашим глазам примерно за 1 секунду, что означает, что луна находится примерно в 1 световой секунде от нас. Солнечному свету требуется около 8 минут, чтобы достичь наших глаз, поэтому солнце находится на расстоянии около 8 световых минут. Свет от Альфа Центавра , ближайшая к нам звездная система, добирается до нее примерно за 4,3 года, поэтому Альфа Центавра находится на расстоянии 4,3 световых года от нас.
«Чтобы получить представление о величине светового года, возьмите окружность Земли (24 900 миль), разложите ее по прямой линии, умножьте длину линии на 7,5 (соответствующее расстояние равно одному световому -секунда), затем разместите 31,6 миллиона одинаковых строк от начала до конца», — говорится на веб-сайте Исследовательского центра Гленна НАСА .(откроется в новой вкладке). «В результате расстояние составляет почти 6 триллионов (6 000 000 000 000) миль!»
Звезды и другие объекты за пределами нашей солнечной системы находятся на расстоянии от нескольких световых лет до нескольких миллиардов световых лет. И все, что астрономы «видят» в далекой Вселенной, буквально является историей. Когда астрономы изучают объекты, находящиеся далеко, они видят свет, который показывает объекты такими, какими они существовали в то время, когда свет покинул их.
И все, что астрономы «видят» в далекой Вселенной, буквально является историей. Когда астрономы изучают объекты, находящиеся далеко, они видят свет, который показывает объекты такими, какими они существовали в то время, когда свет покинул их.
Этот принцип позволяет астрономам увидеть вселенную такой, какой она была после г. Большой взрыв г., который произошел примерно 13,8 миллиарда лет назад. Объекты, находящиеся на расстоянии 10 миллиардов световых лет от нас, кажутся астрономам такими, какими они выглядели 10 миллиардов лет назад — относительно скоро после возникновения Вселенной, — а не такими, какими они выглядят сегодня.
Связанный: Почему вселенная — это история
Как мы узнали скорость света?
Аристотель, Эмпедокл, Галилей (на фото), Оле Рёмер и бесчисленное множество других философов и физиков в истории рассматривали скорость света. (Изображение предоставлено НАСА) Еще в V веке греческие философы, такие как Эмпедокл и Аристотель, расходились во мнениях относительно природы скорости света.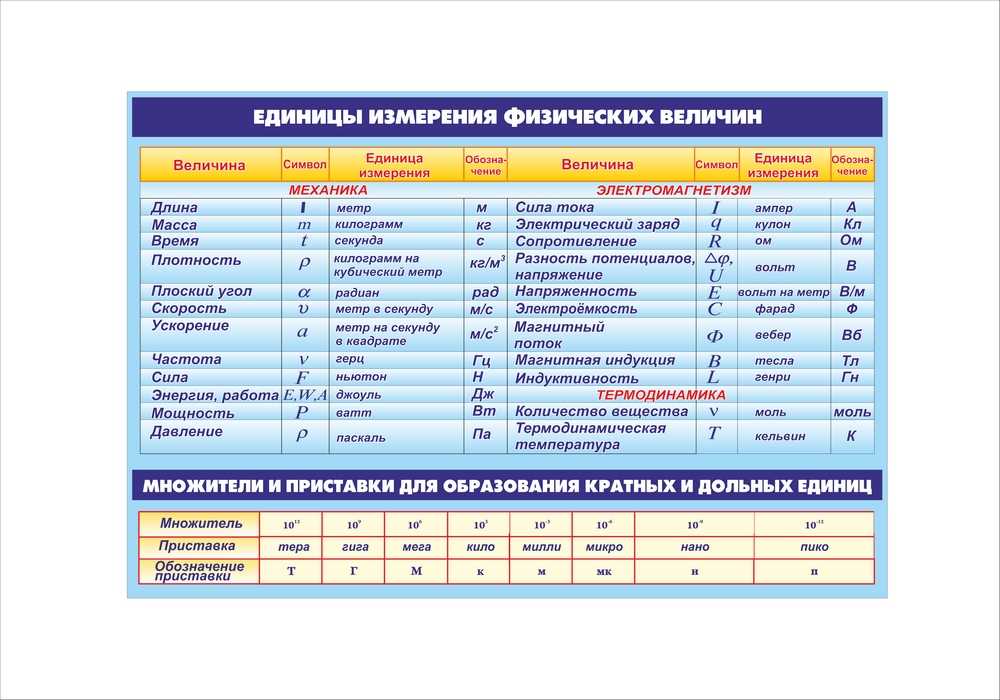 Эмпедокл предположил, что свет, из чего бы он ни состоял, должен двигаться и, следовательно, должен иметь скорость движения. Аристотель опроверг точку зрения Эмпедокла в своем собственном трактате О чувстве и чувственном , утверждая, что свет, в отличие от звука и запаха, должен быть мгновенным. Аристотель, конечно, ошибался, но чтобы доказать это, потребуются сотни лет.
Эмпедокл предположил, что свет, из чего бы он ни состоял, должен двигаться и, следовательно, должен иметь скорость движения. Аристотель опроверг точку зрения Эмпедокла в своем собственном трактате О чувстве и чувственном , утверждая, что свет, в отличие от звука и запаха, должен быть мгновенным. Аристотель, конечно, ошибался, но чтобы доказать это, потребуются сотни лет.
В середине 1600-х годов итальянский астроном Галилео Галилей поставил двух человек на холмы на расстоянии менее мили друг от друга. Каждый человек держал экранированный фонарь. Один раскрыл свой фонарь; когда другой человек увидел вспышку, он тоже раскрыл свою. Но экспериментального расстояния Галилея было недостаточно для того, чтобы его участники могли зафиксировать скорость света. Он мог только заключить, что свет движется как минимум в 10 раз быстрее звука.
В 1670-х годах датский астроном Оле Рёмер пытался создать надежное расписание для моряков в море, и согласно НАСА случайно придумало новую лучшую оценку скорости света.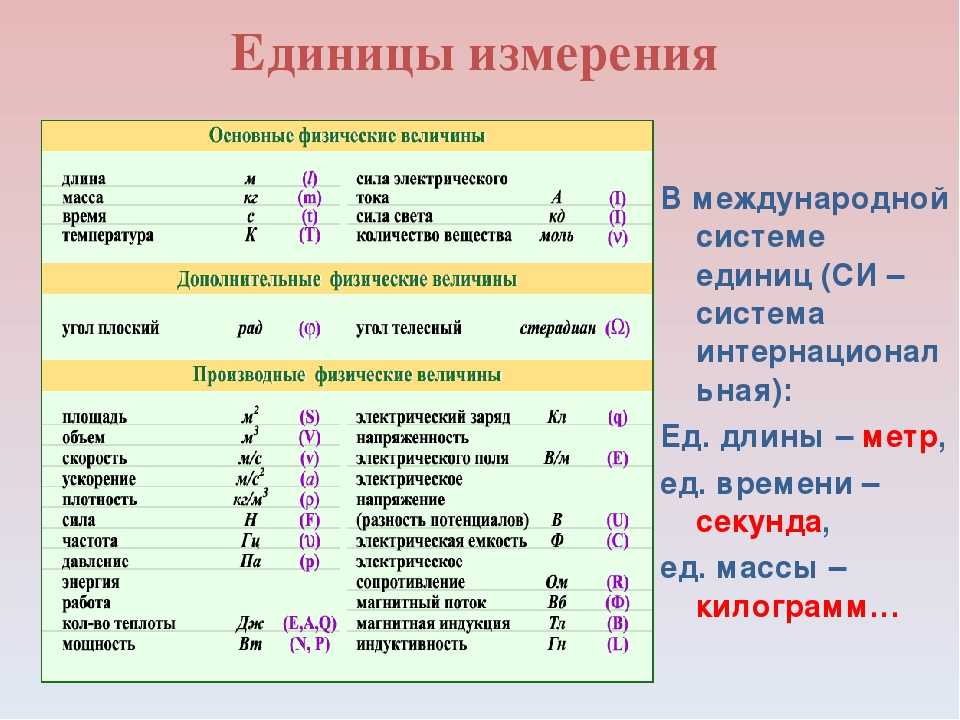 Чтобы создать астрономические часы, он записал точное время затмений луны Юпитера , Ио, от Земли . Со временем Рёмер заметил, что затмения Ио часто отличаются от его расчетов. Он заметил, что затмения, по-видимому, отставали больше всего, когда Юпитер и Земля удалялись друг от друга, появлялись раньше времени, когда планеты приближались, и происходили по расписанию, когда планеты находились в своих ближайших или самых дальних точках. Это наблюдение продемонстрировало то, что мы сегодня знаем как эффект Доплера, изменение частоты света или звука, излучаемого движущимся объектом, что в астрономическом мире проявляется как так называемый 9Красное смещение 1998 года , сдвиг в сторону «краснее», более длинные волны в объектах, удаляющихся от нас. Опираясь на интуицию, Рёмер определил, что свету требуется измеримое время, чтобы добраться от Ио до Земли.
Чтобы создать астрономические часы, он записал точное время затмений луны Юпитера , Ио, от Земли . Со временем Рёмер заметил, что затмения Ио часто отличаются от его расчетов. Он заметил, что затмения, по-видимому, отставали больше всего, когда Юпитер и Земля удалялись друг от друга, появлялись раньше времени, когда планеты приближались, и происходили по расписанию, когда планеты находились в своих ближайших или самых дальних точках. Это наблюдение продемонстрировало то, что мы сегодня знаем как эффект Доплера, изменение частоты света или звука, излучаемого движущимся объектом, что в астрономическом мире проявляется как так называемый 9Красное смещение 1998 года , сдвиг в сторону «краснее», более длинные волны в объектах, удаляющихся от нас. Опираясь на интуицию, Рёмер определил, что свету требуется измеримое время, чтобы добраться от Ио до Земли.
Рёмер использовал свои наблюдения для оценки скорости света. Поскольку размер Солнечной системы и орбита Земли еще не были точно известны, утверждалось в статье 1998 года, опубликованной в году в American Journal of Physics , он немного ошибся.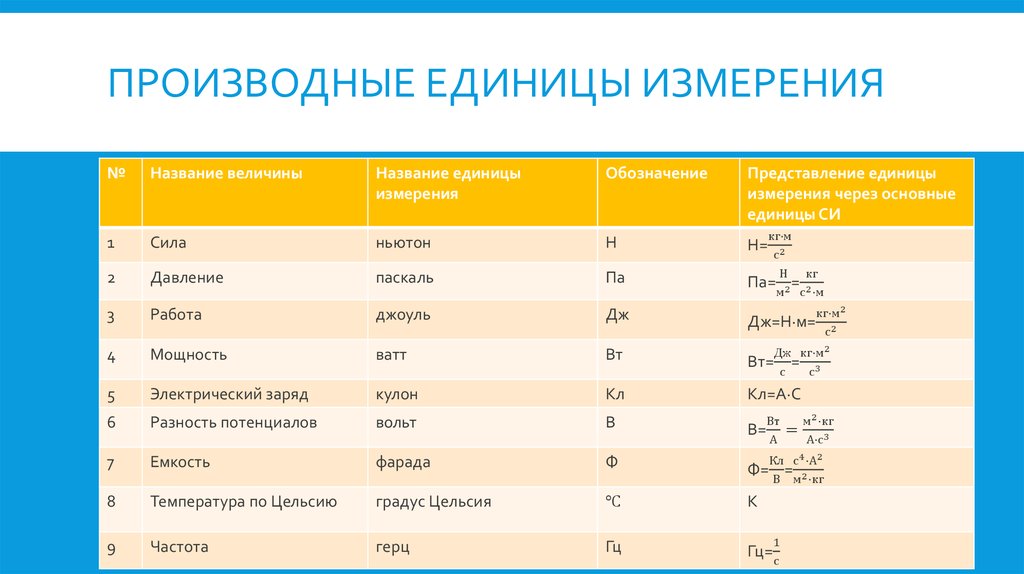 Но, наконец, у ученых появилось число, с которым можно было работать. По расчетам Ремера, скорость света составляет около 124 000 миль в секунду (200 000 км/с).
Но, наконец, у ученых появилось число, с которым можно было работать. По расчетам Ремера, скорость света составляет около 124 000 миль в секунду (200 000 км/с).
В 1728 году английский физик Джеймс Брэдли провел новый набор расчетов на основе изменения видимого положения звезд, вызванного движением Земли вокруг Солнца. Он оценил скорость света в 185 000 миль в секунду (301 000 км/с) — с точностью до 1% от реального значения, согласно Американского физического общества .
Две новые попытки в середине 1800-х вернули проблему на Землю. Французский физик Ипполит Физо направил луч света на быстро вращающееся зубчатое колесо с зеркалом, установленным на расстоянии 5 миль (8 км), чтобы отразить его обратно к источнику. Изменение скорости колеса позволило Физо рассчитать, сколько времени потребовалось свету, чтобы выйти из отверстия к соседнему зеркалу и обратно через зазор. Другой французский физик, Леон Фуко, использовал вращающееся зеркало, а не колесо, чтобы выполнить практически тот же самый эксперимент.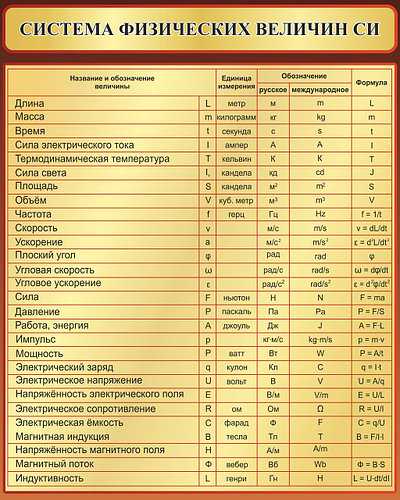 Каждый из двух независимых методов показал точность около 1000 миль в секунду (1609км/с) скорости света.
Каждый из двух независимых методов показал точность около 1000 миль в секунду (1609км/с) скорости света.
Другим ученым, который разгадал тайну скорости света, был уроженец Польши Альберт А. Майкельсон, выросший в Калифорнии в период золотой лихорадки в штате и отточивший свой интерес к физике во время учебы в Военно-морском флоте США. Академия, согласно Университет Вирджинии (открывается в новой вкладке). В 1879 году он попытался воспроизвести метод определения скорости света Фуко, но Майкельсон увеличил расстояние между зеркалами и использовал очень качественные зеркала и линзы. Результат Майкельсона 186 355 миль в секунду (299 910 км / с) считался самым точным измерением скорости света за 40 лет, пока Майкельсон не измерил его сам. Во втором раунде экспериментов Майкельсон посветил светом между двумя горными вершинами с тщательно измеренными расстояниями, чтобы получить более точную оценку. И в третьей попытке незадолго до смерти в 1931, согласно журналу Смитсоновского института Air and Space , он построил разгерметизированную трубу длиной в милю из гофрированной стальной трубы. Трубка имитировала почти вакуум, который устранял бы любое влияние воздуха на скорость света для еще более точного измерения, которое в итоге оказалось лишь немного ниже принятого сегодня значения скорости света.
Во втором раунде экспериментов Майкельсон посветил светом между двумя горными вершинами с тщательно измеренными расстояниями, чтобы получить более точную оценку. И в третьей попытке незадолго до смерти в 1931, согласно журналу Смитсоновского института Air and Space , он построил разгерметизированную трубу длиной в милю из гофрированной стальной трубы. Трубка имитировала почти вакуум, который устранял бы любое влияние воздуха на скорость света для еще более точного измерения, которое в итоге оказалось лишь немного ниже принятого сегодня значения скорости света.
Майкельсон также изучал природу самого света, написал астрофизик Итан Сигал в научном блоге Forbes, Starts With a Bang (откроется в новой вкладке). Лучшие умы физиков во время экспериментов Майкельсона разделились: был ли свет волной или частицей?
Майкельсон вместе со своим коллегой Эдвардом Морли исходил из предположения, что свет движется как волна, как и звук. И точно так же, как звуку нужны частицы для движения, рассуждали Майкельсон, Морли и другие физики того времени, свет должен иметь какую-то среду для движения.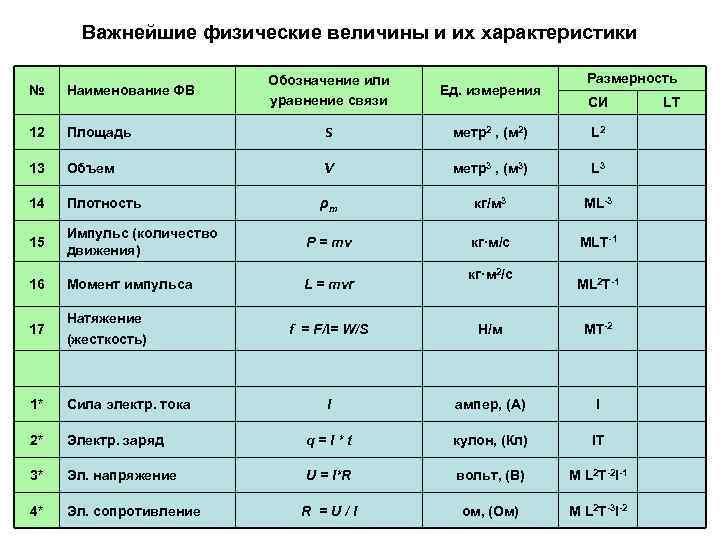 Это невидимое, необнаружимое вещество было названо «светоносным эфиром» (также известным как «эфир»).
Это невидимое, необнаружимое вещество было названо «светоносным эфиром» (также известным как «эфир»).
Хотя Майкельсон и Морли построили сложный интерферометр (самую простую версию прибора, используемого сегодня в установках LIGO ), Майкельсон не смог найти доказательств существования какого-либо светоносного эфира. Он определил, что свет может путешествовать и действительно путешествует в вакууме.
«Эксперимент — и вся работа Майкельсона — были настолько революционными, что он стал единственным человеком в истории, получившим Нобелевскую премию за очень точное отсутствие открытия чего-либо», — написал Сигал. «Сам эксперимент, возможно, был полным провалом, но то, что мы из него узнали, было большим благом для человечества и нашего понимания Вселенной, чем любой успех!» 92. Уравнение описывает взаимосвязь между массой и энергией — небольшие количества массы (m) содержат или состоят из огромного количества энергии (E). (Вот что делает ядерные бомбы такими мощными: они преобразуют массу во взрывы энергии.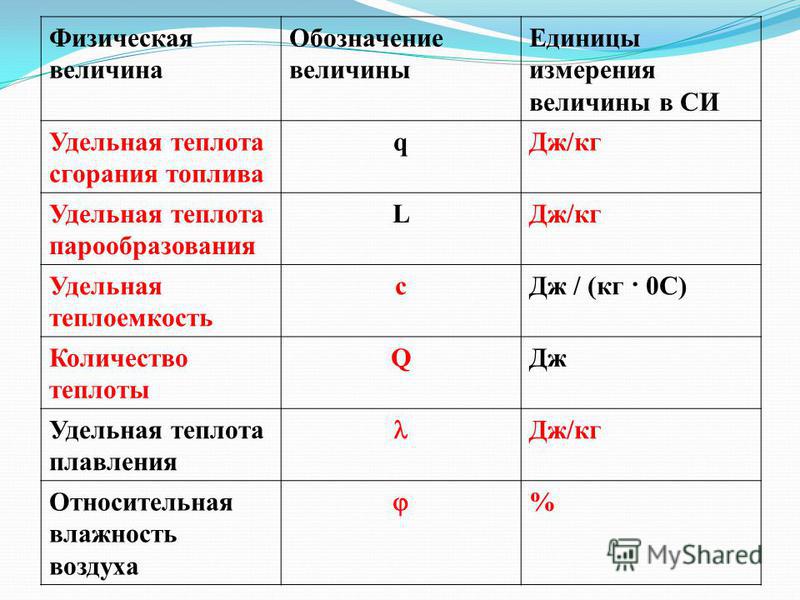 ) Поскольку энергия равна массе, умноженной на квадрат скорости света, скорость света служит коэффициентом преобразования, точно объясняющим, сколько энергии должно быть внутри материи. А поскольку скорость света — это такое огромное число, даже небольшое количество массы должно равняться огромному количеству энергии.
) Поскольку энергия равна массе, умноженной на квадрат скорости света, скорость света служит коэффициентом преобразования, точно объясняющим, сколько энергии должно быть внутри материи. А поскольку скорость света — это такое огромное число, даже небольшое количество массы должно равняться огромному количеству энергии.
Чтобы точно описать вселенную, элегантное уравнение Эйнштейна требует, чтобы скорость света была неизменной константой. Эйнштейн утверждал, что свет движется через вакуум, а не через какой-либо светоносный эфир, и таким образом, что он движется с одной и той же скоростью независимо от скорости наблюдателя.
Подумайте об этом так: наблюдатели, сидящие в поезде, могут смотреть на поезд, движущийся по параллельному пути, и думать, что его движение относительно себя равно нулю. Но наблюдатели, движущиеся почти со скоростью света, все равно будут воспринимать свет как удаляющийся от них со скоростью более 670 миллионов миль в час. (Это потому, что двигаться очень, очень быстро — один из немногих подтвержденных методов путешествие во времени — время фактически замедляется для тех наблюдателей, которые стареют медленнее и воспринимают меньше моментов, чем наблюдатель, движущийся медленно.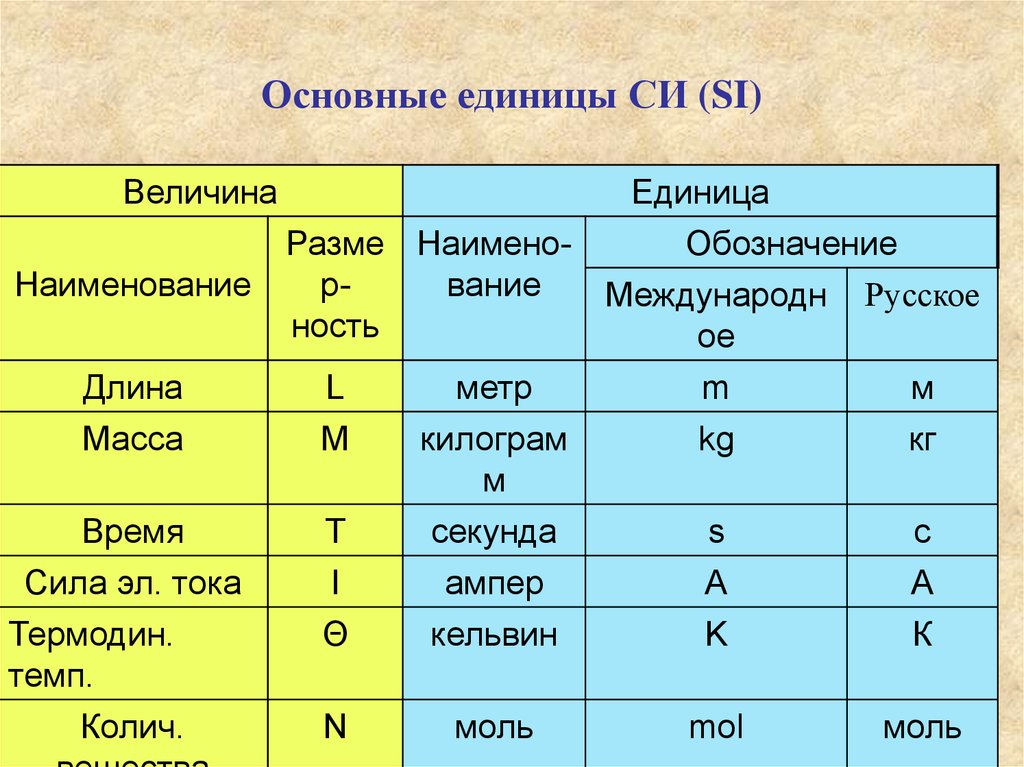 )
)
Другими словами, Эйнштейн предположил, что скорость света не зависит от времени или места. что вы его измеряете, или как быстро вы сами движетесь.
Следовательно, объекты с массой никогда не могут достичь скорости света. Если бы объект когда-нибудь достиг скорости света, его масса стала бы бесконечной. И в результате энергия, необходимая для перемещения объекта, также стала бы бесконечной: это невозможно.
Это означает, что если мы основываем наше понимание физики на специальной теории относительности (что делает большинство современных физиков), то скорость света является непреложным пределом скорости нашей Вселенной — максимальной скоростью, на которой может двигаться что-либо.
Что движется быстрее скорости света?
Хотя скорость света часто называют пределом скорости Вселенной, на самом деле Вселенная расширяется еще быстрее. Вселенная расширяется со скоростью немногим более 42 миль (68 километров) в секунду на каждый мегапарсек расстояния от наблюдателя, писал астрофизик Пол Саттер в предыдущей статье для журнала 9. 1998 Space.com . (Мегапарсек составляет 3,26 миллиона световых лет — это очень большой путь.)
1998 Space.com . (Мегапарсек составляет 3,26 миллиона световых лет — это очень большой путь.)
Другими словами, галактика, удаленная на 1 мегапарсек, удаляется от Млечного Пути со скоростью 42 мили в секунду (68 км/с). с), в то время как галактика, находящаяся на расстоянии двух мегапарсеков, удаляется со скоростью почти 86 миль в секунду (136 км/с) и так далее.
«В какой-то момент на каком-то непристойном расстоянии скорость зашкаливает и превышает скорость света, и все это от естественного, регулярного расширения пространства», — объяснил Саттер. «Кажется, это должно быть незаконно, не так ли?»
Специальная теория относительности обеспечивает абсолютный предел скорости во Вселенной, согласно Саттеру, но теория Эйнштейна 1915 года относительно общей теории относительности допускает другое поведение, когда физика, которую вы изучаете, больше не является «локальной».
«Галактика на дальней стороне вселенной? Это область общей теории относительности, а общая теория относительности говорит: какая разница! Эта галактика может иметь любую скорость, какую захочет, пока она остается далеко, а не рядом тебе в лицо», — написал Саттер.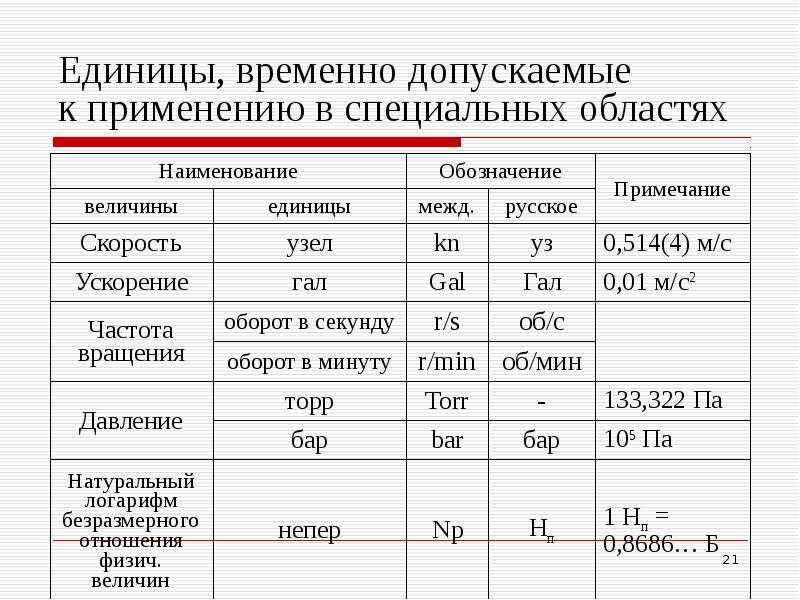 «Специальную теорию относительности не волнует скорость — сверхсветовая или какая-то другая — далекой галактики. И вам тоже не стоит».
«Специальную теорию относительности не волнует скорость — сверхсветовая или какая-то другая — далекой галактики. И вам тоже не стоит».
Свет когда-нибудь замедляется?
Свет движется медленнее в алмазе, чем в воздухе, и он движется в воздухе немного медленнее, чем в вакууме. (Изображение предоставлено Shutterstock)Обычно считается, что свет в вакууме распространяется с абсолютной скоростью, но свет, проходящий через любой материал, может быть замедлен. Величина, на которую материал замедляет свет, называется его показателем преломления. Свет изгибается при контакте с частицами, что приводит к уменьшению скорости.
Например, свет, проходящий через атмосферу Земли, движется почти так же быстро, как свет в вакууме, замедляясь всего на три десятитысячных скорости света. Но свет, проходящий через алмаз, замедляется менее чем вдвое по сравнению с обычной скоростью, сообщает PBS NOVA . Тем не менее, он движется через драгоценный камень со скоростью более 277 миллионов миль в час (почти 124 000 км/с) — достаточно, чтобы изменить ситуацию, но все же невероятно быстро.
Согласно исследованию 2001 года, опубликованному в журнале 9, свет может быть захвачен — и даже остановлен — внутри ультрахолодных облаков атомов.1998 Природа (откроется в новой вкладке). Совсем недавно в исследовании 2018 года, опубликованном в журнале Physical Review Letters , был предложен новый способ остановить свет на его пути в «исключительных точках» или местах, где два отдельных световых излучения пересекаются и сливаются в одно.
Исследователи также пытались замедлить свет, даже когда он движется в вакууме. Группа шотландских ученых успешно замедлила одиночный фотон или частицу света, даже когда он двигался в вакууме, как описано в их исследовании 2015 года, опубликованном в журнале 9.1998 Наука (открывается в новой вкладке). В их измерениях разница между замедленным фотоном и «обычным» фотоном составляла всего несколько миллионных долей метра, но это продемонстрировало, что свет в вакууме может быть медленнее, чем официальная скорость света.
Можем ли мы путешествовать быстрее света?
Истории по теме:
Научная фантастика любит идею «скорости деформации». Путешествия со скоростью, превышающей скорость света, делают возможными бесчисленные научно-фантастические франшизы, уплотняя бескрайние просторы космоса и позволяя персонажам с легкостью перемещаться между звездными системами и обратно.
Но хотя путешествия со скоростью, превышающей скорость света, не гарантированно невозможны, нам нужно использовать довольно экзотическую физику, чтобы заставить это работать. К счастью для энтузиастов научной фантастики и физиков-теоретиков, существует множество возможностей для изучения.
Все, что нам нужно сделать, это понять, как не двигаться самим — поскольку специальная теория относительности гарантирует, что мы будем уничтожены, прежде чем мы достигнем достаточно высокой скорости, — а вместо этого перемещать пространство вокруг нас. Легко, верно?
Одна из предложенных идей включает в себя космический корабль, который мог бы сворачивать вокруг себя пространственно-временной пузырь. Звучит здорово, как в теории, так и в художественной литературе.
Звучит здорово, как в теории, так и в художественной литературе.
«Если бы капитан Кирк был вынужден двигаться со скоростью наших самых быстрых ракет, ему потребовалось бы сто тысяч лет, чтобы добраться до следующей звездной системы», — сказал Сет Шостак, астроном из Поиска внеземного разума (SETI). ) Институт в Маунтин-Вью, Калифорния, в интервью 2010 года дочернему сайту Space.com LiveScience . «Поэтому научная фантастика уже давно постулировала способ преодолеть скорость светового барьера, чтобы история могла развиваться немного быстрее».
Без путешествий со скоростью, превышающей скорость света, любой «Звездный путь» (или, если уж на то пошло, «Звездная война») был бы невозможен. Если человечеству суждено когда-нибудь добраться до самых дальних и постоянно расширяющихся уголков нашей вселенной, физики будущего должны будут смело отправиться туда, куда еще не ступала нога человека.
Дополнительные ресурсы
Чтобы узнать больше о скорости света, воспользуйтесь этим забавным инструментом от Academo (открывается в новой вкладке), который позволяет визуализировать, с какой скоростью свет может перемещаться из любого места на Земле в любое другое.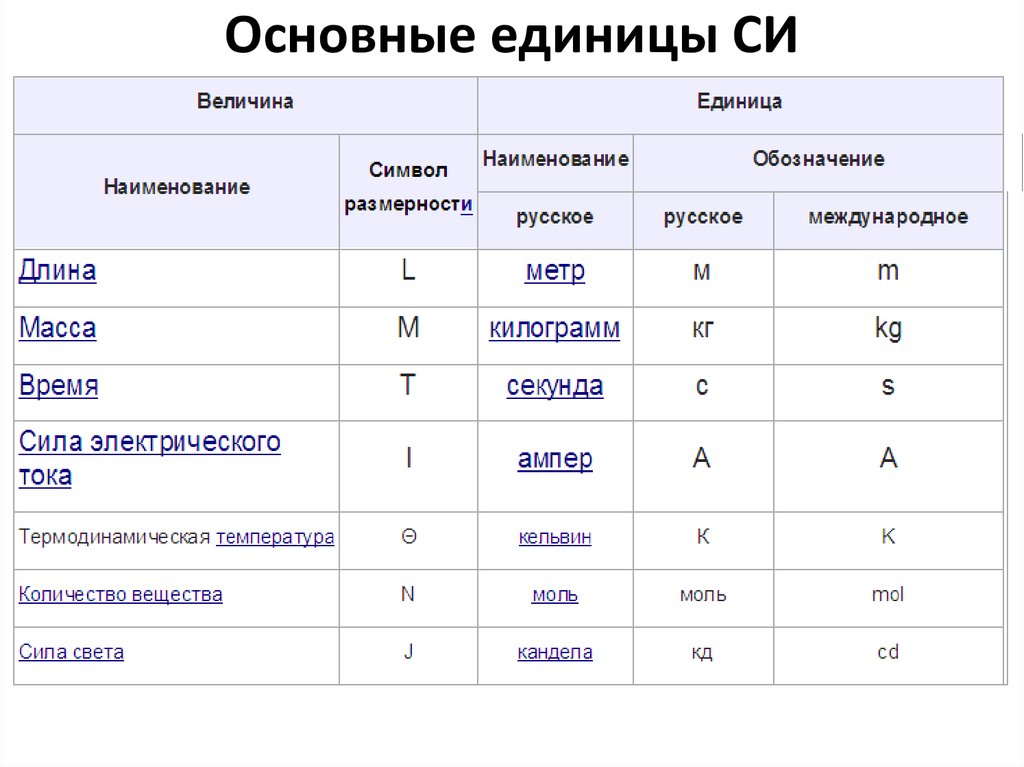 Если вас больше интересуют другие важные числа, познакомьтесь с универсальными константами, которые определяют стандартные системы измерения по всему миру с помощью 9.1998 Национальный институт стандартов и технологий (открывается в новой вкладке). А если вам интересно узнать больше об истории скорости света, ознакомьтесь с книгой «Скорость света : Призрачный эфир и гонка за измерением скорости света (откроется в новой вкладке)» (Оксфорд, 2019 г.) автора Джон Ч. Х. Спенс.
Если вас больше интересуют другие важные числа, познакомьтесь с универсальными константами, которые определяют стандартные системы измерения по всему миру с помощью 9.1998 Национальный институт стандартов и технологий (открывается в новой вкладке). А если вам интересно узнать больше об истории скорости света, ознакомьтесь с книгой «Скорость света : Призрачный эфир и гонка за измерением скорости света (откроется в новой вкладке)» (Оксфорд, 2019 г.) автора Джон Ч. Х. Спенс.
Предыдущее исследование для этой статьи предоставлено сотрудником Space.com Нолой Тейлор Редд.
Библиография
Аристотель. «О чувстве и разумном». Архив интернет-классики, 350 г. н.э. г. http://classics.mit.edu/Aristotle/sense.2.2.html г. (открывается в новой вкладке).
Д’Альто, Ник. «Трубопровод, измеривший скорость света». Smithsonian Magazine, январь 2017 г. https://www.smithsonianmag.com/air-space-magazine/18_fm2017-oo-180961669/ (открывается в новой вкладке).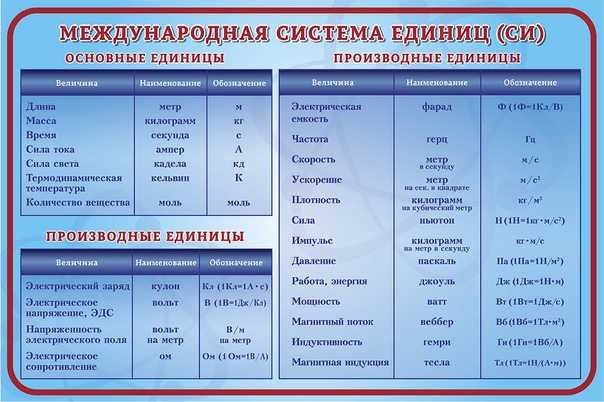
Фаулер, Майкл. «Скорость света.» Современная физика. Университет Вирджинии. По состоянию на 13 января 2022 г. https://galileo.phys.virginia.edu/classes/252/spedlite.html#Albert%20Abraham%20Michelson (откроется в новой вкладке).
Джованнини, Даниэль, Жакилин Ромеро, Вацлав Поточек, Гергели Ференци, Фиона Спейритс, Стивен М. Барнетт, Даниэле Фаччо и Майлз Дж. Пэджетт. «Пространственно структурированные фотоны, которые движутся в свободном пространстве медленнее скорости света». Science, 20 февраля 2015 г. https://www.science.org/doi/abs/10.1126/science.aaa3035 (открывается в новой вкладке).
Гольдзак, Тамар, Алексей Александрович Майлыбаев и Нимрод Моисеев. «Свет останавливается в исключительных точках». Письма о физическом обзоре 120, вып. 1 (3 января 2018 г.): 013901. https://doi.org/10.1103/PhysRevLett.120.013901 (открывается в новой вкладке).
Хазен, Роберт. «Что заставляет бриллиант сверкать?» PBS NOVA, 31 января 2000 г. https://www.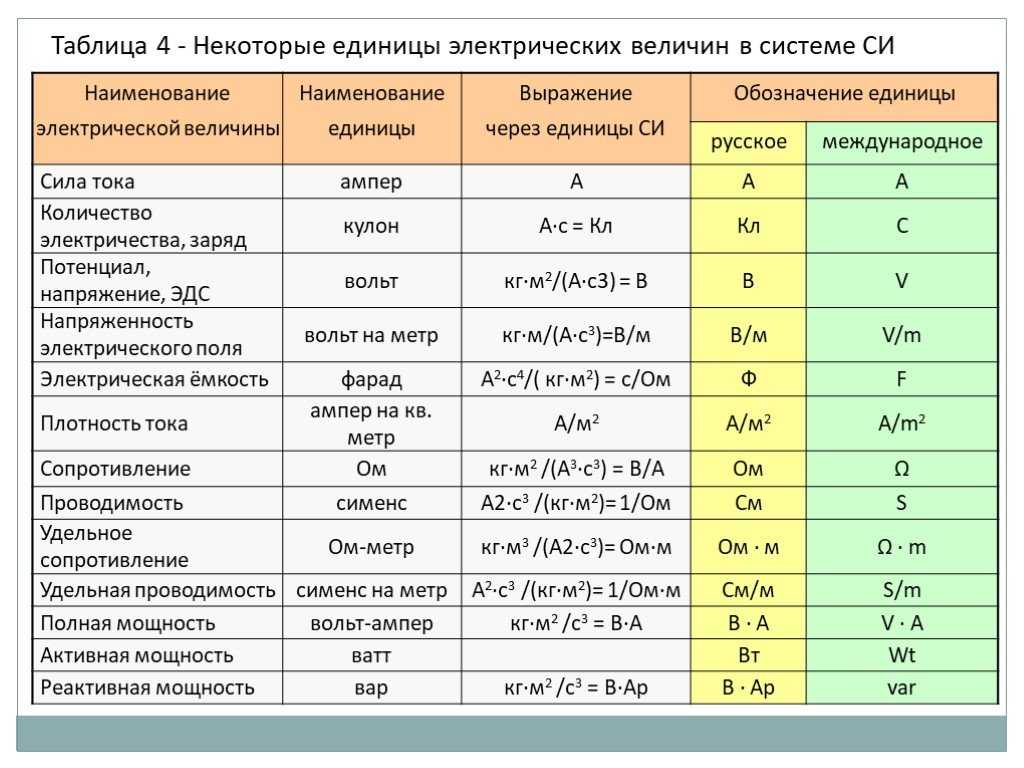 pbs.org/wgbh/nova/article/diamond-science/ (открывается в новой вкладке).
pbs.org/wgbh/nova/article/diamond-science/ (открывается в новой вкладке).
«Какой длины световой год?» Glenn Learning Technologies Project, 13 мая 2021 г. https://www.grc.nasa.gov/www/k-12/Numbers/Math/Mathematical_Thinking/how_long_is_a_light_year.htm (открывается в новой вкладке).
Новости Американского физического общества. «Июль 1849 г.: Fizeau Publishes Results of Speed of Light Experiment», июль 2010 г. http://www.aps.org/publications/apsnews/201007/physicshistory.cfm (открывается в новой вкладке).
Лю, Чиен, Закари Даттон, Сайрус Х. Бехрузи и Лене Вестергаард Хау. «Наблюдение за хранением когерентной оптической информации в атомной среде с использованием остановленных световых импульсов». Природа 409, вып. 6819 (январь 2001 г.): 490–93. https://doi.org/10.1038/35054017 (откроется в новой вкладке).
НИСТ. «Познакомьтесь с константами». 12 октября 2018 г. г. https://www.nist.gov/si-redefinition/meet-constants (открывается в новой вкладке).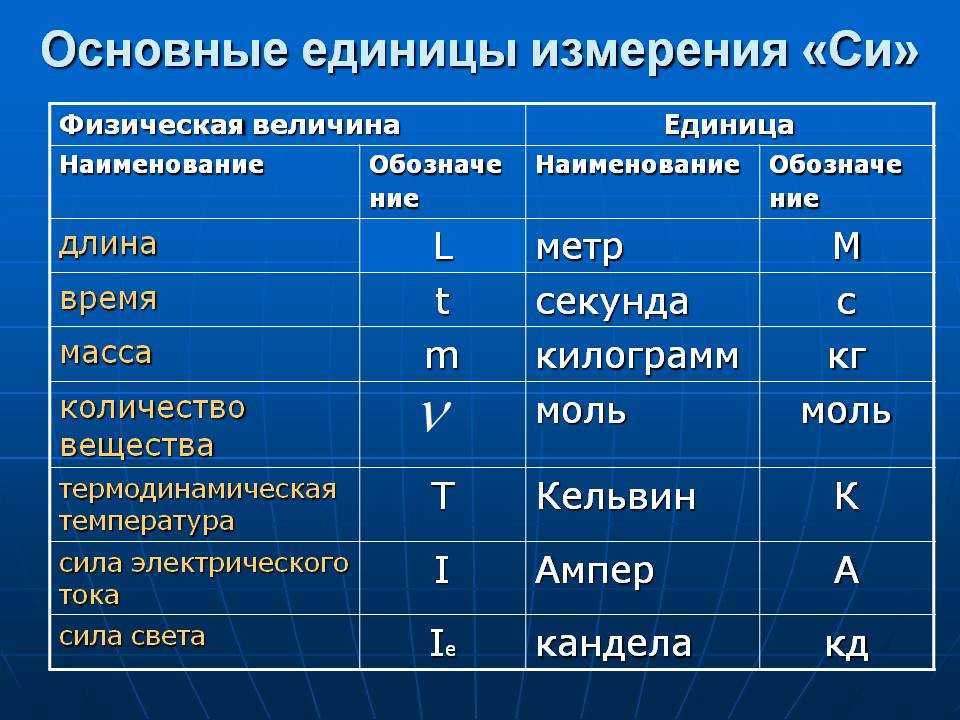
Уэллетт, Дженнифер. «Краткая история скорости света». PBS NOVA, 27 февраля 2015 г. https://www.pbs.org/wgbh/nova/article/brief-history-speed-light/ (откроется в новой вкладке).
Ши, Джеймс Х. «Оле Ро/Мер, скорость света, видимый период Ио, эффект Доплера и динамика Земли и Юпитера». Американский журнал физики 66, вып. 7 (1 июля 1998 г.): 561–69. https://doi.org/10.1119/1.19020 (открывается в новой вкладке).
Сигел, Итан. «Неудачный эксперимент, изменивший мир». Forbes, 21 апреля 2017 г. https://www.forbes.com/sites/startswithabang/2017/04/21/the-failed-experiment-that-changed-the-world/ (открывается в новой вкладке).
Стерн, Дэвид. «Рёмер и скорость света», 17 октября 2016 г. https://pwg.gsfc.nasa.gov/stargaze/Sun4Adop1.htm (открывается в новой вкладке).
Присоединяйтесь к нашим космическим форумам, чтобы продолжать обсуждать последние миссии, ночное небо и многое другое! А если у вас есть новость, исправление или комментарий, сообщите нам об этом по адресу: community@space.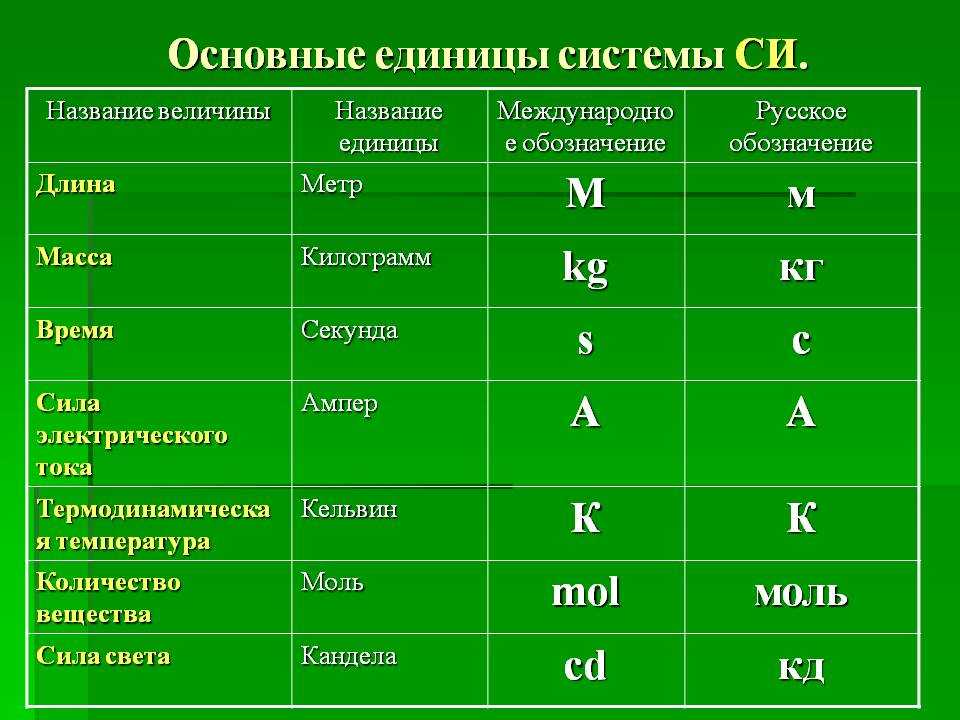


 изм. физ. вел.
изм. физ. вел.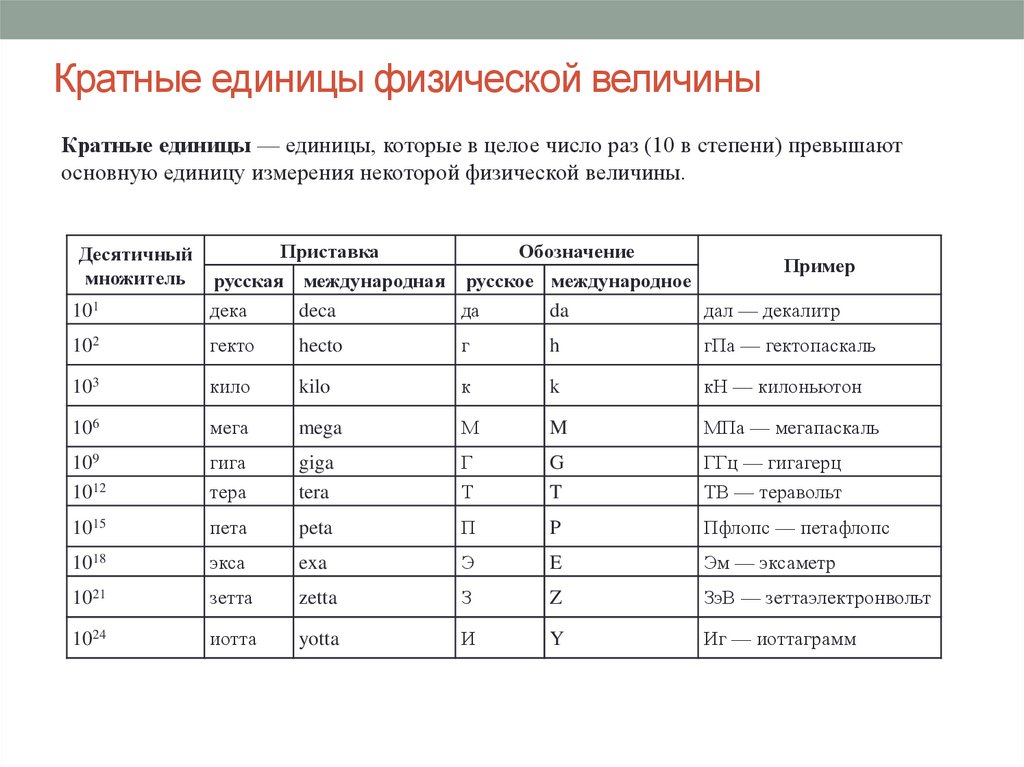






 изм. физ. вел.
изм. физ. вел.
 изм. физ. вел.
изм. физ. вел.

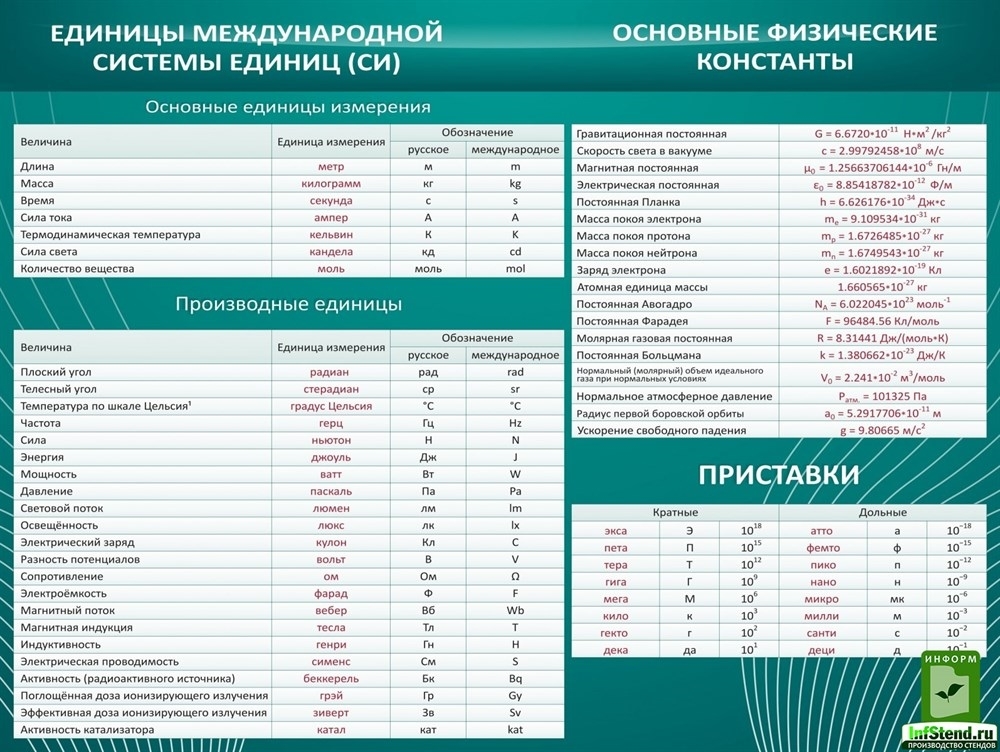


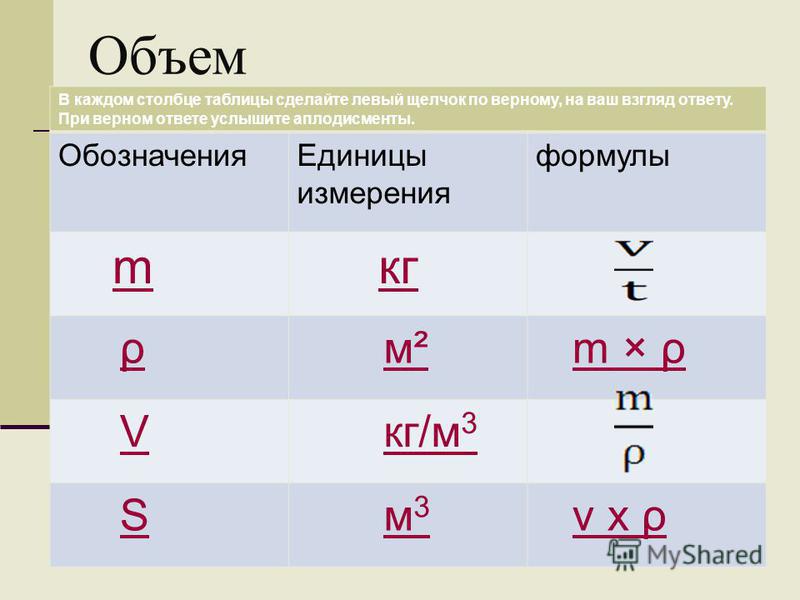 изм. физ. вел.
изм. физ. вел.
 изм. физ. вел.
изм. физ. вел.
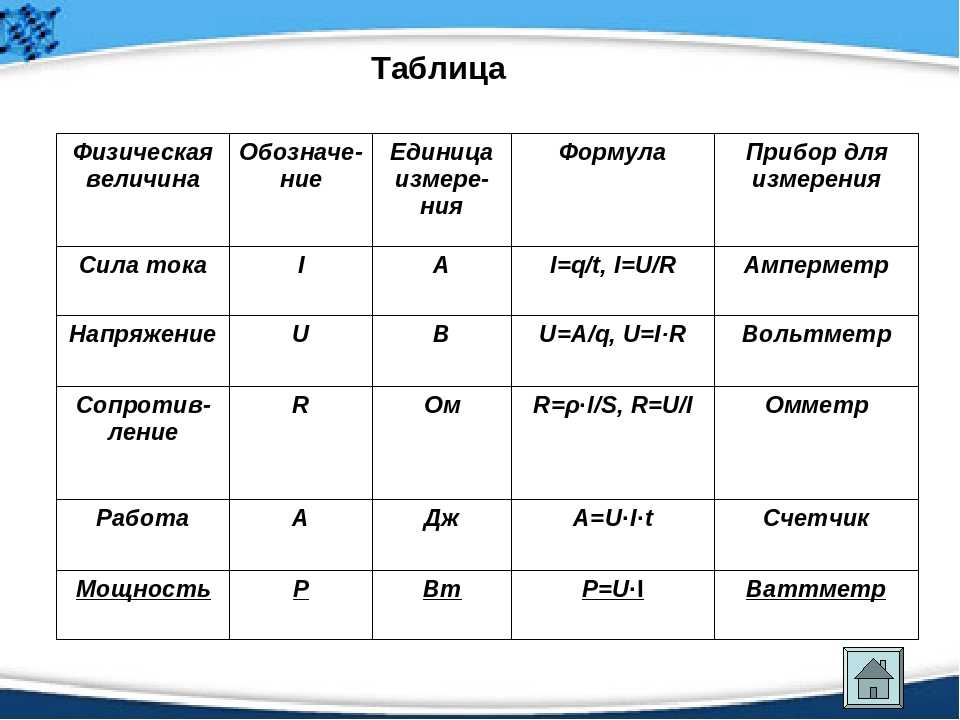

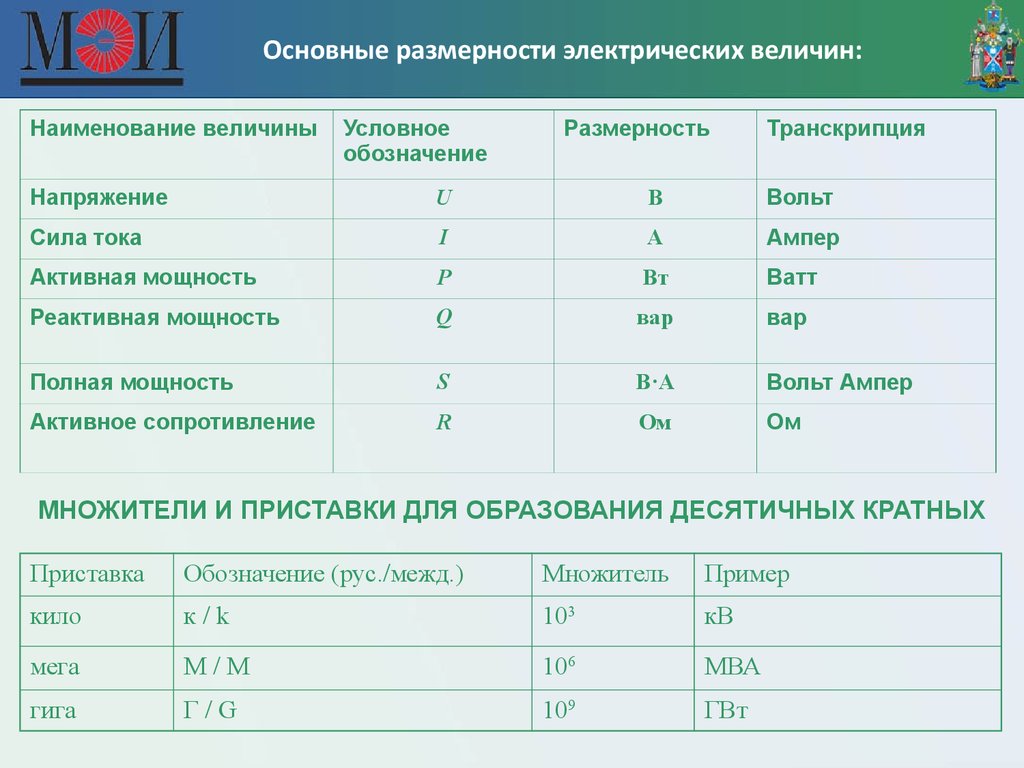 Уровень однородной жидкости в таких сосудах всегда одинаков, независимо от их формы и сечения.
Уровень однородной жидкости в таких сосудах всегда одинаков, независимо от их формы и сечения.

 д.
д. скорость: преобразования в одном и том же направлении не меняют своего характера от того, что они составлены из ускорений или даже от того, как (нашим из бесконечного числа способов) они могут состоять из ускорений.Если я иду с некоторой скоростью вдоль самого движущегося автобуса по дороге, то мое движение должно быть описано как движение по дороге с некоторой относительной скоростью, забыв об автобусе;
скорость: преобразования в одном и том же направлении не меняют своего характера от того, что они составлены из ускорений или даже от того, как (нашим из бесконечного числа способов) они могут состоять из ускорений.Если я иду с некоторой скоростью вдоль самого движущегося автобуса по дороге, то мое движение должно быть описано как движение по дороге с некоторой относительной скоростью, забыв об автобусе;
 Более поздние модели также могли записывать с половиной этой скорости (7½ дюймов в секунду), затем с половиной этой скорости (3¾ дюймов в секунду), а затем с половиной этой скорости (1⅞ дюймов в секунду). Когда формулировался стандарт аудиокассет, было решено, что последнего из этих значений будет достаточно для нового носителя. Один дюйм в секунду по определению равен 0,0254 м/с.
Более поздние модели также могли записывать с половиной этой скорости (7½ дюймов в секунду), затем с половиной этой скорости (3¾ дюймов в секунду), а затем с половиной этой скорости (1⅞ дюймов в секунду). Когда формулировался стандарт аудиокассет, было решено, что последнего из этих значений будет достаточно для нового носителя. Один дюйм в секунду по определению равен 0,0254 м/с.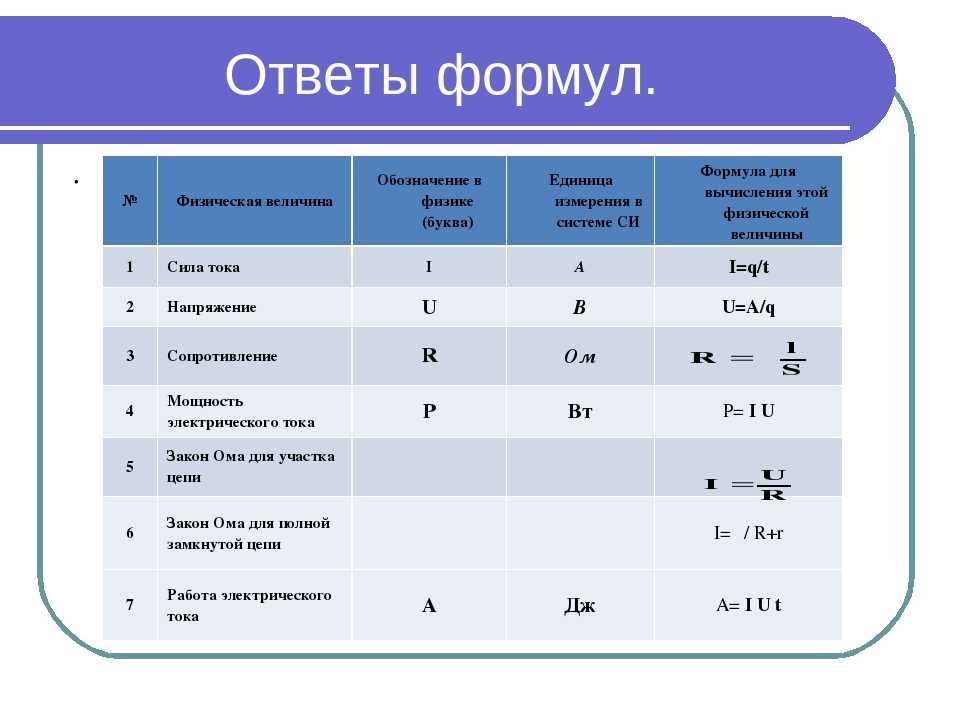 Простое деление показывает, что эта скорость примерно вдвое превышает скорость звука или 2,0 Маха, что является исключительно быстрым. Для сравнения, Боинг 777 развивает крейсерскую скорость 248 м/с (555 миль в час) или 0,8 Маха, что только кажется медленным по сравнению с Конкордом.
Простое деление показывает, что эта скорость примерно вдвое превышает скорость звука или 2,0 Маха, что является исключительно быстрым. Для сравнения, Боинг 777 развивает крейсерскую скорость 248 м/с (555 миль в час) или 0,8 Маха, что только кажется медленным по сравнению с Конкордом. Они лежат на окраинах наблюдаемой Вселенной и с невероятной скоростью уносятся от нас. Самые далекие квазары удаляются от нас почти на 0,9в. Кстати, символ c был выбран не потому, что скорость света является универсальной константой (которой она и является), а потому, что это первая буква латинского слова, обозначающего быстроту — celeritas .
Они лежат на окраинах наблюдаемой Вселенной и с невероятной скоростью уносятся от нас. Самые далекие квазары удаляются от нас почти на 0,9в. Кстати, символ c был выбран не потому, что скорость света является универсальной константой (которой она и является), а потому, что это первая буква латинского слова, обозначающего быстроту — celeritas .