В чем измеряется a: Ампер-час — Википедия – В чем измеряется a — Давление и всё о нём — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Ампер-час — Википедия

Ампе́р-час (А·ч) — внесистемная единица измерения электрического заряда, используемая главным образом для характеристики ёмкости электрических аккумуляторов.

Исходя из физического смысла, 1 ампер-час — это электрический заряд, который проходит через поперечное сечение проводника в течение одного часа при наличии в нём тока силой в 1 ампер.

Заряженный аккумулятор с заявленной ёмкостью в 1 А·ч теоретически способен обеспечить силу тока 1 ампер в течение одного часа (или, например, 10 А в течение 0,1 часа, или 0,1 А в течение 10 часов). На практике слишком большой ток разряда аккумулятора приводит к менее эффективной отдаче электроэнергии, что нелинейно уменьшает время его работы с таким током и может приводить к перегреву.

В действительности же ёмкость аккумуляторов приводят исходя из 20-часового цикла разряда до конечного напряжения. Для автомобильных аккумуляторов оно составляет 10,5 В^[1]. Например, надпись на маркировке аккумулятора «55 А·ч» означает, что он способен выдавать ток 2,75 ампера на протяжении 20 часов, и при этом напряжение на клеммах не опустится ниже 10,5 В.

Часто также применяется производная единица миллиампер-час (мА·ч, mAh), которая используется обычно для обозначения ёмкости небольших аккумуляторов.

Величину в ампер-часах можно перевести в системную единицу измерения заряда — кулон. Поскольку 1 Кл/c равен 1 А, то, переведя часы в секунды, получаем, что один ампер-час будет равен 3600 Кл.

Часто производители аккумуляторов указывают в технических характеристиках только запасаемый заряд в мА·ч (mAh), другие — только запасаемую энергию в Вт·ч (Wh). Обе характеристики можно называть термином «ёмкость» (не путать с электрической ёмкостью как мерой способности проводника накапливать заряд, измеряемой в фарадах). Вычислить запасаемую энергию по запасаемому заряду в общем случае непросто: требуется интегрирование мгновенной мощности, выдаваемой аккумулятором за всё время его разряда. Если большая точность не нужна, то вместо интегрирования можно воспользоваться средними значениями напряжения и потребляемого тока, для этого используя формулу, следующую из того, что 1 Вт = 1 В · 1 А:

1 Вт·ч = 1 В · 1 А·ч.

То есть запасаемая энергия (в ватт-часах) приблизительно равна произведению запасаемого заряда (в ампер-часах) на среднее напряжение (в вольтах):

E = q · U,

а в джоулях она будет в 3600 раз больше,

E = q · U · 3600,

Пример[править | править код]

В технической спецификации устройства указано, что «ёмкость» (запасаемый заряд) аккумулятора равна 56 А·ч, рабочее напряжение равно 15 В. Тогда «ёмкость» (запасаемая энергия) равна 56 А·ч · 15 В = 840 Вт·ч = 840 Вт · 3600 с = 3,024 МДж.

При последовательном соединении одинаковых аккумуляторов «ёмкость» в мА·ч остаётся прежней, но меняется общее напряжение аккумуляторной батареи, при параллельном же соединении «ёмкость» в мА·ч — складывается, но общее напряжение не меняется. При этом «ёмкость» в Вт·ч., у таких аккумуляторных батарей, следует считать одинаковой. Например, для двух аккумуляторов, каждый из которых обладает напряжением 3,3 В и запасаемым зарядом 1000 мА·ч, последовательное соединение создаст источник питания с напряжением 6,6 В и запасаемым зарядом 1000 мА·ч, параллельное соединение — источник с напряжением 3,3 В и запасаемым зарядом 2000 мА·ч. Ёмкость же в Ватт·час (способность проделать работу) в обоих случаях, без учёта некоторых нюансов, будет одинаковой. В современных Power Bank-ах, получивших распространение в последнее время, часто аккумуляторы внутри соединены последовательно, а общую «ёмкость» в мА·ч складывают. Это происходит из-за того что такие Power Bank имеют внутренний контроллер, который преобразует напряжение и на выходе предлагает несколько значений напряжений: 5 вольт (USB порт), 12, 15, 17 или 19 вольт для подключения ноутбуков. То есть, нет возможности указать при каком напряжении уместна та или иная «ёмкость» в мА·ч, так как она меняется в зависимости от напряжения, используемого потребителем, подключенного к такому универсальному Power Bank. Поэтому в характеристиках пишут «коммерческую» ёмкость в мА·ч, полученную как сумму последовательно соединённых аккумуляторных элементов, не указывая, при этом, напряжение при котором эта «ёмкость» в мА·ч. уместа. Также следует учитывать, что ёмкость аккумулятора и его напряжение взаимосвязанные величины, так как аккумулятор, который разряжен, теряет напряжение. Причём, измерение напряжения разряженного аккумулятора или батареи без нагрузки, может не выявить степень разряженности источника питания, так как на «холостом ходу», без нагрузки, аккумуляторная батарея способна показать высокое напряжение, которое резко упадёт, в случае если аккумулятор или батарея разряжены и если к ним подключили определённую нагрузку, в отличие от заряженных источников питания, которые сохраняют высокое значение напряжения, даже после подключения нагрузки. У разряженных аккумуляторов падение напряжения, при подключении нагрузки, происходит сильнее, чем у заряженных источников питания. Для проверки автомобильных аккумуляторов часто используют специальные «пробники», создающую стандартную нагрузку на аккумулятор.

Бурдун Г. Д., Базакуца В. А. Единицы физических величин. Справочник. — Харьков: Вища школа, 1984.

↑ ГОСТ Р МЭК 61056-1-2012

ГОСТ Р МЭК 61056-1-2012

В чем измеряется a — Давление и всё о нём

Source: electric-220.ru

Как действует напряжение

Общее понятие электрического тока заключается в направленном движении заряженных частиц. Эти частицы представляют собой электроны, перемещение которых происходит под действием электрического поля. Чем больше зарядов нужно переместить, тем большая работа совершается полем. На эту работу влияет не только сила тока, но и напряжение.

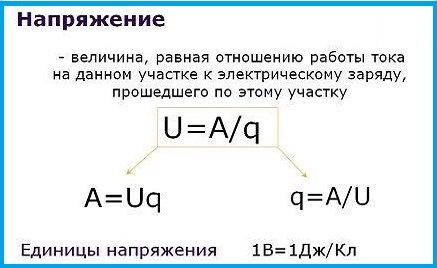
Физический смысл этой величины заключается в том, что работа тока на каком-либо участке цепи соотносится с величиной заряда, который проходит по данному участку. В процессе этой работы положительный заряд перемещается из точки, где имеется небольшой потенциал, в точку с большим значением потенциала. Таким образом, напряжение определяется в виде разности потенциалов или электродвижущей силы, а сама работа является энергией.

Работа электрического тока измеряется в джоулях (Дж), а величиной электрического заряда является кулон (Кл). В результате, напряжение представляет собой отношение 1 Дж/Кл. Полученная единица напряжения называется вольтом.

Чтобы наглядно объяснить физический смысл напряжения, нужно обратиться к примеру шланга, наполненного водой. В данном случае, объем воды будет играть роль силы тока, а ее давление будет эквивалентно напряжению. При движении воды без наконечника, она свободно и в большом количестве перемещается по шлангу, создавая невысокое давление. Если же конец шланга прижать пальцем, то произойдет уменьшение объема при одновременном повышении давления воды. Сама струя будет перемещаться на значительно большее расстояние.

В электричестве получается то же самое. Сила тока определяется количеством или объемом электронов, перемещающихся по проводнику. Значение напряжения, по сути, является силой, с которой происходит проталкивание этих электронов. Отсюда следует, что при условии одинакового напряжения, проводник, проводящий большее количество тока, должен обладать и большим диаметром.

Единица измерения напряжения

Напряжение может быть постоянным или переменным, в зависимости от тока. Эта величина может обозначаться в виде буквы В (русское обозначение) или V, соответствующее международному обозначению. Для обозначения переменного напряжения применяется значок «~», который ставится перед буквой. Для постоянного напряжения существует знак «-», однако на практике он почти не применяется.

Рассматривая вопрос, в чем измеряется напряжение, следует помнить, что для этого существуют не только вольты. Большие величины измеряются в киловольтах (кВ) и мегавольтах (мВ), что означает соответственно 1 тысячу и 1 миллион вольт.

Как измерить напряжение и ток

Атмосфера (единица измерения) — Википедия

Материал из Википедии — свободной энциклопедии

Атмосфера — внесистемная единица измерения давления, приблизительно равная атмосферному давлению на поверхности Земли на уровне Мирового океана.

Существуют две примерно равные друг другу единицы с таким названием:

Техническая атмосфера (русское обозначение: ат; международное: at) — равна давлению, производимому силой в 1 кгс, равномерно распределённой по перпендикулярной к ней плоской поверхности площадью 1 см². В свою очередь сила в 1 кгс равна силе тяжести, действующей на тело массой 1 кг при значении ускорения свободного падения 9,80665 м/с² (нормальное ускорение свободного падения): 1 кгс = 9,80665 Н. Таким образом, 1 ат = 98 066,5 Па точно^[1]^[2].
Нормальная, стандартная или физическая атмосфера (русское обозначение: атм; международное: atm) — равна давлению столба ртути высотой 760 мм на его горизонтальное основание при плотности ртути 13 595,04 кг/м³, температуре 0 °C и при нормальном ускорении свободного падения 9,80665 м/с². В соответствии с определением 1 атм = 101 325 Па = 1,033233 ат^[1]^[2].

В настоящее время Международная организация законодательной метрологии (МОЗМ) относит оба вида атмосферы к тем единицам измерения, «которые должны быть изъяты из обращения как можно скорее там, где они используются в настоящее время, и которые не должны вводиться, если они не используются»^[3].

В Российской Федерации к использованию в качестве внесистемной единицы допущена только техническая атмосфера с областью применения «все области». Существовавшее ранее ограничение срока действия допуска 2016 годом^[4] отменено в августе 2015 года^[5].

Ранее использовались также обозначения ата и ати для абсолютного и избыточного давления соответственно (выраженного в технических атмосферах). Избыточное давление — разница между абсолютным и атмосферным (барометрическим) давлением при условии, что абсолютное давление больше атмосферного: Р_изб=Р_абс-Р_атм. Разрежение (вакуум) — разница между атмосферным (барометрическим) и абсолютным давлением при условии, что абсолютное давление меньше атмосферного: Р_вак=Р_атм-Р_абс.

*Единицы давления*
	Паскаль (Pa, Па)	Бар (bar, бар)	Техническая атмосфера (at, ат)	Физическая атмосфера (atm, атм)	Миллиметр ртутного столба (мм рт. ст., mm Hg, Torr, торр)	Метр водяного столба (м вод. ст., m H₂O)	Фунт-сила на квадратный дюйм (psi)
1 Па	1 Н/м²	10⁻⁵	10,197⋅10⁻⁶	9,8692⋅10⁻⁶	7,5006⋅10⁻³	1,0197⋅10⁻⁴	145,04⋅10⁻⁶
1 бар	10⁵	1⋅10⁶дин/см²	1,0197	0,98692	750,06	10,197	14,504
1 ат	98066,5	0,980665	1 кгс/см²	0,96784	735,56	10	14,223
1 атм	101325	1,01325	1,033	1 атм	760	10,33	14,696
1 мм рт. ст.	133,322	1,3332⋅10⁻³	1,3595⋅10⁻³	1,3158⋅10⁻³	1 мм рт. ст.	13,595⋅10⁻³	19,337⋅10⁻³
1 м вод. ст.	9806,65	9,80665⋅10⁻²	0,1	0,096784	73,556	1 м вод. ст.	1,4223
1 psi	6894,76	68,948⋅10⁻³	70,307⋅10⁻³	68,046⋅10⁻³	51,715	0,70307	1 lbf/in²

Краткий словарь физических терминов / Сост. А. И. Болсун, рец. М. А. Ельяшевич. — Мн.: Высшая школа, 1979. — 416 с. — 30 000 экз.

Объём — Википедия

Материал из Википедии — свободной энциклопедии

Примеры вычисления объёмов:
Куба с помощью перемножения трех сторон^[1] Пирамиды с помощью умножения площади основания пирамиды на её высоту и делению на три^[1] Конуса с помощью умножения площади основания на треть высоты^[1] Цилиндра с помощью перемножения площади на высоту^[1] Шара с помощью перемножения четырёх третьих числа Пи на радиус шара в кубе^[1] Тетраэдра с помощью произведения длины его ребра в кубе на корень из двух и деления полученного на двенадцать^[1] Видеоурок: объём

Объём — количественная характеристика пространства, занимаемого телом или веществом.

Объём тела или вместимость сосуда определяется его формой и линейными размерами. С понятием объёма тесно связано понятие вместимость, то есть объём внутреннего пространства сосуда, упаковочного ящика и т. п..

Единица измерения объёма в СИ — кубический метр; от неё образуются производные единицы, такие как кубический сантиметр, кубический дециметр (литр) и т. д. В разных странах для жидких и сыпучих веществ используются также различные внесистемные единицы объёма — галлон, баррель.

В формулах для обозначения объёма используется заглавная латинская буква V, являющаяся сокращением от лат. volume — «объём», «наполнение».

Слово «объём» также используют в переносном значении для обозначения общего количества или текущей величины. Например, «объём спроса», «объём памяти», «объём работ». В изобразительном искусстве объёмом называется иллюзорная передача пространственных характеристик изображаемого предмета художественными методами.

На практике приблизительный объём тела, в том числе сложной формы, можно вычислить погрузив это тело в жидкость. Объём вытесненной жидкости будет равен объёму измеряемого тела.

Математически[править | править код]

Для объёмов тел простой формы имеются специальные формулы. Например, объём куба с ребром a{\displaystyle a} равен V=a3{\displaystyle V=a^{3}}, а объём прямоугольного параллелепипеда равен произведению его длины на ширину на высоту.

Объём тела сложной формы вычисляется разбиением этого тела на отдельные части простой формы и суммированием объёмов этих частей. В интегральном исчислении объёмы частей, из которых складывается объём всего тела, рассматриваются как бесконечно малые величины.

Через плотность[править | править код]

Зная массу (m) и плотность (ρ) тела объём рассчитывается по формуле: V=mρ{\displaystyle V={\frac {m}{\rho }}}

1 л = 1,76 пинты = 0,23 галлона

Английские[править | править код]

Античные[править | править код]

Древнееврейские^[2][править | править код]

Эйфа = 24,883 литра
Гин = 1/6 эйфы = 4,147 литра
Омер = 1/10 эйфы = 2,4883 литра
Кав = 1/3 гина = 1,382 литра

Русские^[3][править | править код]

Английские[править | править код]

Русские[править | править код]

Четверик = 26,24 литра (1 пуд зерна)
Гарнец = 3,28 литра
Четверть = 1/4 ведра = 3,075 литра
Штоф = 1/8 ведра = 1,54 литра
Кружка = 1/10 ведра = 1,23 литра
Бутылка (винная) = 1/16 ведра = 0,77 литра
Бутылка (пивная) = 1/20 ведра = 0,61 литра
Чарка = 1/10 кружки = 0,123 литра
Шкалик (косушка) = 1/2 чарки = 0,0615 литра

1 унция (англ.) = 2,841⋅10⁻⁵ м³
1 унция (амер.) = 2,957⋅10⁻⁵ м³
1 кубический дюйм = 1,63871⋅10⁻⁵ м³
1 кубический фут = 2,83168⋅10⁻² м³
1 кубический ярд = 0,76455 м³
1 кубическая астрономическая единица =3,348⋅10²⁴ км³
1 кубический световой год = 8,466⋅10³⁸ км³
1 кубический парсек = 2,938⋅10⁴⁰ км³
1 кубический килопарсек = 1 000 000 000 пк³ = 2,938⋅10⁴⁹ км³

Единицы измерения

Этот урок не будет новым для новичков. Все мы слышали со школы такие вещи как сантиметр, метр, километр. А когда речь заходила о массе, обычно говорили грамм, килограмм, тонна.

Сантиметры, метры и километры; граммы, килограммы и тонны носят одно общее название — единицы измерения физических величин.

В данном уроке мы рассмотрим наиболее популярные единицы измерения, но не будем сильно углубляться в эту тему, поскольку единицы измерения уходят в область физики. Сегодня мы вынуждены изучить часть физики, поскольку нам это необходимо для дальнейшего изучения математики.

Единицы измерения длины

Для измерения длины предназначены следующие единицы измерения:

миллиметры;
сантиметры;
дециметры;
метры;
километры.

Самая маленькая единица измерения это миллиметр (мм). Миллиметры можно увидеть даже воочию, если взять линейку, которой мы пользовались в школе каждый день

Подряд идущие друг за другом маленькие линии это и есть миллиметры. Точнее, расстояние между этими линиями равно одному миллиметру (1 мм):

Следующая единица измерения это сантиметр (см). На линейке каждый сантиметр обозначен числом. К примеру наша линейка, которая была на первом рисунке, имела длину 15 сантиметров. Последний сантиметр на этой линейке выделен числом 15.

В одном сантиметре 10 миллиметров. Между одним сантиметром и десятью миллиметрами можно поставить знак равенства, поскольку они обозначают одну и ту же длину:

1 см = 10 мм

Вы можете сами убедиться в этом, если посчитаете количество миллиметров на предыдущем рисунке. Вы обнаружите, что количество миллиметров (расстояний между линиями) равно 10.

Следующая единица измерения длины это дециметр (дм). В одном дециметре десять сантиметров. Между одним дециметром и десятью сантиметрами можно поставить знак равенства, поскольку они обозначают одну и ту же длину:

1 дм = 10 см

Вы можете убедиться в этом, если посчитаете количество сантиметров на следующем рисунке:

Вы обнаружите, что количество сантиметров равно 10.

Следующая единица измерения это метр (м). В одном метре десять дециметров. Между одним метром и десятью дециметрами можно поставить знак равенства, поскольку они обозначают одну и ту же длину:

1 м = 10 дм

К сожалению, метр нельзя проиллюстрировать на рисунке, потому что он достаточно великоват. Если вы хотите увидеть метр в живую, возьмите рулетку. Она есть у каждого в доме. На рулетке один метр будет обозначен как 100 см. Это потому что в одном метре десять дециметров, а в десяти дециметрах сто сантиметров:

1 м = 10 дм = 100 см

100 получается путём перевода одного метра в сантиметры. Это отдельная тема, которую мы рассмотрим чуть позже. А пока перейдём к следующей единице измерения длины, которая называется километр.

Километр считается самой большой единицей измерения длины. Есть конечно и другие более старшие единицы, такие как мегаметр, гигаметр тераметр, но мы не будем их рассматривать, поскольку для дальнейшего изучения математики нам достаточно и километра.

В одном километре тысяча метров. Между одним километром и тысячью метрами можно поставить знак равенства, поскольку они обозначают одну и ту же длину:

1 км = 1000 м

В километрах измеряются расстояния между городами и странами. К примеру, расстояние от Москвы до Санкт-Петербурга около 714 километров.

Международная система единиц СИ

Международная система единиц СИ — это некоторый набор общепринятых физических величин.

Основное предназначение международной системы единиц СИ — достижение договоренностей между странами.

Мы знаем, что языки и традиции стран мира различны. С этим ничего не поделать. Но законы математики и физики одинаково работают везде. Если в одной стране «дважды два будет четыре», то и в другой стране «дважды два будет четыре».

Основная проблема заключалась в том, что для каждой физической величины существует несколько единиц измерения. К примеру, мы сейчас узнали, что для измерения длины существуют миллиметры, сантиметры, дециметры, метры и километры. Если несколько ученых, говорящих на разных языках, соберутся в одном месте для решения какой-нибудь задачи, то такое большое многообразие единиц измерения длины может породить между этими учеными противоречия.

Один ученый будет заявлять, что в их стране длина измеряется в метрах. Второй может сказать, что в их стране длина измеряется в километрах. Третий может предложить свою единицу измерения.

Поэтому была создана международная система единиц СИ. СИ это аббревиатура от французского словосочетания Le Système International d’Unités, SI (что в переводе на русский означает — международная система единиц СИ).

В СИ приведены наиболее популярные физические величины и для каждой из них определена своя общепринятая единица измерения. К примеру, во всех странах при решении задач условились, что длину будут измерять в метрах. Поэтому, при решении задач, если длина дана в другой единице измерения (например, в километрах), то её обязательно нужно перевести в метры. О том, как переводить одну единицу измерения в другую, мы поговорим немного позже. А пока нарисуем свою международную систему единиц СИ.

Наш рисунок будет представлять собой таблицу физических величин. Каждую изученную физическую величину мы будем включать в нашу таблицу и указывать ту единицу измерения, которая принята во всех странах. Сейчас мы изучили единицы измерения длины и узнали, что в системе СИ для измерения длины определены метры. Значит наша таблица будет выглядеть так:

Единицы измерения массы

Масса – это величина, обозначающая количество вещества в теле. В народе массу тела называют весом. Обычно, когда что-либо взвешивают, говорят «это весит столько-то килограмм», хотя речь идёт не о весе, а о массе этого тела.

Вместе с тем, масса и вес это разные понятия. Вес — это сила с которой тело действует на горизонтальную опору. Вес измеряется в ньютонах. А масса это величина, показывающая количество вещества в этом теле.

Но ничего страшного нет в том, если вы назовёте массу тела весом. Даже в медицине говорят «вес человека», хотя речь идёт о массе человека. Главное быть в курсе, что это разные понятия

Для измерения массы используются следующие единицы измерения:

миллиграммы;
граммы;
килограммы;
центнеры;
тонны.

Самая маленькая единица измерения это миллиграмм (мг). Миллиграмм скорее всего вы никогда не примените на практике. Их применяют химики и другие ученые, которые работают с мелкими веществами. Для вас достаточно знать, что такая единица измерения массы существует.

Следующая единица измерения это грамм (г). В граммах принято измерять количество того или иного продукта при составлении рецепта.

В одном грамме тысяча миллиграммов. Между одним граммом и тысячью миллиграммами можно поставить знак равенства, поскольку они обозначают одну и ту же массу:

1 г = 1000 мг

Следующая единица измерения это килограмм (кг). Килограмм это общепринятая единица измерения. В ней измеряется всё что угодно. Килограмм включен в систему СИ. Давайте и мы включим в нашу таблицу СИ ещё одну физическую величину. Она у нас будет называться «масса»:

В одном килограмме тысяча граммов. Между одним килограммом и тысячью граммами можно поставить знак равенства, поскольку они обозначают одну и ту же массу:

1 кг = 1000 г

Следующая единица измерения это центнер (ц). В центнерах удобно измерять массу урожая, собранного с небольшого участка или массу какого-нибудь груза.

В одном центнере сто килограммов. Между одним центнером и ста килограммами можно поставить знак равенства, поскольку они обозначают одну и ту же массу:

1 ц = 100 кг

Следующая единица измерения это тонна (т). В тоннах обычно измеряются большие грузы и массы больших тел. Например, масса космического корабля или автомобиля.

В одной тонне тысяча килограмм. Между одной тонной и тысячью килограммами можно поставить знак равенства, поскольку они обозначают одну и ту же массу:

1 т = 1000 кг

Единицы измерения времени

Что такое время думаем объяснять не нужно. Каждый знает что из себя представляет время и зачем оно нужно. Если мы откроем дискуссию на то, что такое время и попытаемся дать ему определение, то начнем углубляться в философию, а это нам сейчас не нужно. Лучше начнём с единиц измерения времени.

Для измерения времени предназначены следующие единицы измерения:

секунды;
минуты;
часы;
сутки.

Самая маленькая единица измерения это секунда (с). Есть конечно и более маленькие единицы такие как миллисекунды, микросекунды, наносекунды, но их мы рассматривать не будем, поскольку на данный момент в этом нет смысла.

В секундах измеряются различные показатели. Например, за сколько секунд спортсмен пробежит 100 метров. Секунда включена в международную систему единиц СИ для измерения времени и обозначается как «с». Давайте и мы включим в нашу таблицу СИ ещё одну физическую величину. Она у нас будет называться «время»:

Следующая единица измерения времени это минута (м). В одной минуте 60 секунд. Между одной минутой и шестьюдесятью секундами можно поставить знак равенства, поскольку они обозначают одно и то же время:

1 м = 60 с

Следующая единица измерения это час (ч). В одном часе 60 минут. Между одним часом и шестьюдесятью минутами можно поставить знак равенства, поскольку они обозначают одно и то же время:

1 ч = 60 м

К примеру, если мы изучали этот урок один час и нас спросят сколько времени мы потратили на его изучение, мы можем ответить двумя способами: «мы изучали урок один час» или так «мы изучали урок шестьдесят минут». В обоих случаях, мы ответим правильно.

Следующая единица измерения времени это сутки. В сутках 24 часа. Между одними сутками и двадцатью четырьмя часами можно поставить знак равенства, поскольку они обозначают одно и то же время:

1 сут = 24 ч

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Единицы измерения – Tetran Translation Company

Величина	Единица
	Наименование	Обозначение
	Наименование	Международное	Русское
Плоский угол	радиан	rad	рад
Телесный угол	стерадиан	sr	ср
*Пространство и время*
Площадь	квадратный метр	m²	м²
Объем, вместимость	кубический метр	m³	м³
Скорость	метр в секунду	m/s	м/с
Ускорение	метр на секунду в квадрате	m/s²	м/с²
Угловая скорость	радиан в секунду	rad/s	рад/с
Угловое ускорение	радиан на секунду в квадрате	rad/s²	рад/с²
*Периодические явления, колебания и волны*
Период	секунда	s	с
Частота периодического процесса, частота колебаний	герц	Hz	Гц
Частота вращения	секунда в минус первой степени	s^-1	c^-1
Длина волны	метр	m	м
Волновое число	метр в минус первой степени	m^-1	м^-1
Коэффициент затухания	секунда в минус первой степени	s^-1	с^-1
Коэффициент ослабления, коэффициент фазы, коэффициент распространения	метр в минус первой степени	m^-1	м^-1
Механика
Плотность	килограмм на кубический метр	kg/m³	кг/м³
Удельный объем	кубический метр на килограмм	m³/kg	м³/кг
Количество движения	килограмм-метр в секунду	kg•m/s	кг•м/с
Момент количества движения	килограмм-метр в квадрате на секунду	kg•m²/s	кг•м²/с
Момент инерции (динамический момент инерции)	килограмм-метр в квадрате	kg•m²	кг•м²
Сила, сила тяжести (вес)	ньютон	N	Н
Момент силы, момент пары сил	ньютон-метр	N•m	Н•м
Импульс силы	ньютон-секунда	N•s	Н•с
Давление, нормальное напряжение, касательное напряжение, модуль продольной упругости, модуль сдвига, модуль объемного сжатия	паскаль	Pa	Па
Момент инерции (второй момент) площади плоской фигуры- (осевой, полярный, центробежный)	метр в четвертой степени	m⁴	м⁴
Момент сопротивления плоской фигуры	метр в третьей степени	m³	м³
Динамическая вязкость	паскаль-секунда	Pa•s	Па•с
Кинематическая вязкость	квадратный метр на секунду	m²/s	м²/с
Поверхностное натяжение	ньютон на метр	N/m	Н/м
Работа, энергия	джоуль	J	Дж
Мощность	ватт	W	Вт
*Теплота*
Температура Цельсия	градус Цельсия	°C	°С
Температурный коэффициент	кельвин в минус первой степени	К^-1	К^-1
Температурный градиент	кельвин на метр	K/m	К/м
Теплота, количество теплоты	джоуль	J	Дж
Тепловой поток	ватт	W	Вт
Поверхностная плотность теплового потока	ватт на квадратный метр	W/m²	Вт/м²
Теплопроводность	ватт на метр-кельвин	W/(m•K)	Вт/(м•К)
Коэффициент теплообмена, коэффициент теплопередачи	ватт на квадратный метр-кельвин	W/(m²•K)	Вт/(м•К)
Температуропроводность	квадратный метр на секунду	m²/s	м²/с
Теплоемкость	джоуль на кельвин	J/K	Дж/К
Удельная теплоемкость	джоуль на килограмм-кельвин	J/(kg•K)	Дж/(кг•К)
Энтропия	джоуль на кельвин	J/K	Дж/К
Удельная энтропия	джоуль на килограмм-кельвин	J/(kg•K)	Дж/(кг¹•К)
Термодинамический потенциал (внутренняя энергия, энтальпия, изохорно-изотермический потенциал, изопарно-изотермический потенциал), теплота фазового превращения, теплота химической реакции	джоуль	J	Дж
Удельное количество теплоты, удельный термодинамический потенциал, удельная теплота фазового превращения, удельная теплота химической реакции	джоуль на килограмм	J/kg	Дж/кг
*Электричество и магнетизм*
Количество электричества (электрический заряд)	кулон	С	Kл
Пространственная плотность электрического заряда	кулон на кубический метр	С/m³	Кл/м³
Поверхностная плотность электрического заряда	кулон на квадратный метр	С/m²	Кл/м²
Напряженность электрического поля	вольт на метр	V/m	В/м
Электрическое напряжение	вольт	V	В
Электрический потенциал	вольт	V	В
Разность электрических потенциалов	вольт	V	В
Электродвижущая сила	вольт	V	В
Поток электрического смещения	кулон	C	Кл
Электрическое смещение	кулон на квадратный метр	С/m²	Кл/м²
Электрическая емкость	фарад	F	Ф
Абсолютная диэлектрическая проницаемость	фарад на метр	F/m	Ф/м
Электрический момент диполя	кулон-метр	С•m	Кл•м
Плотность электрического тока	ампер на квадратный метр	А/m²	А/м²
Линейная плотность электрического тока	ампер на метр	А/m	А/м
Напряженность магнитного поля	ампер на метр	А/m	А/м
Магнитодвижущая сила, разность магнитных потенциалов	ампер	А	А
Магнитная индукция	тесла	Т	Тл
Магнитный поток	вебер	Wb	Вб
Индуктивность, взаимная индуктивность	генри	H	Гн
Абсолютная магнитная проницаемость	генри на метр	Н/m	Гн/м
Магнитный момент (амперовский)	ампер-квадратный метр	А•m²	А•м²
Магнитный момент (кулоновскнй)	вебер-метр	Wb•m	Вб•м
Намагниченность (интенсивность намагничивания)	ампер на метр	А/m	А/м
Электрическое сопротивление (активное, реактивное, полное)	Ом	Ω	Ом
Электрическая проводимость (активная, реактивная, полная)	сименс	S	См
Удельное электрическое сопротивление	Ом-метр	Ω•m	Ом•м
Удельная электрическая проводимость	сименс на метр	S/m	См/м
Магнитное сопротивление	генри в минус первой степени	H^-1	Гн^-1
Магнитная проводимость	генри	Н	Гн
Активная мощность	ватт	W	Вт
Электромагнитная энергия	джоуль	J	Дж
*Свет и другие электромагнитные излучения*
Энергия излучения	джоуль	J	Дж
Энергетическая экспозиция (лучистая экспозиция)	джоуль на квадратный метр	J/m²	Дж/м²
Поток излучения, мощность излучения	ватт	W	Вт
Поверхностная плотность потока излучения, энергетическая светимость (излучательность), энергетическая освещенность (облученность)	ватт на квадратный метр	W/m²	Вт/м²
Энергетическая сила света (сила излучения)	ватт на стерадиан	W/sr	Вт/ср
Энергетическая яркость (лучистость)	ватт на стерадиан-квадратный метр	W/(sr•m²)	Вт/(ср•м²)
Световой поток	люмен	lm	лм
Световая энергия	люмен-секунда	lm•s	лм•с
Яркость	кандела на квадратный метр	cd/m²	кд/м²
Светимость	люмен на квадратный метр	lm/m²	лм/м²
Освещенность	люкс	lx	лк
Световая экспозиция	люкс-секунда	lx•s	лк/с
*Акустика*
Период звуковых колебаний	секунда	s	с
Частота звуковых колебаний	герц	Hz	Гц
Звуковое давление, давление звука	паскаль	Pa	Па
Колебательная скорость (скорость колебания частицы)	метр в секунду	m/s	м/с
Объемная скорость	кубический метр в секунду	m³/s	м³/с
Скорость звука	метр в секунду	m/s	м/с
Звуковая энергия	джоуль	J	Дж
Плотность звуковой энергии	джоуль на кубический метр	J/m³	Дж/м³
Поток звуковой энергии	ватт	W	Вт
Звуковая мощность	ватт	W	Вт
Интенсивность звука	ватт на квадратный метр	W/m²	Вт/м²
Акустическое сопротивление	паскаль-секунда на кубический метр	Pa•s/m³	Па•с/м³
Удельное акустическое сопротивление	паскаль-секунда на метр	Pa•s/m	Па•с/м
Механическое сопротивление	ньютон-секунда на метр	N•s/m	Н•с/м
Эквивалентная площадь поглощения поверхностью или предметом	квадратный метр	m²	м²
Время реверберации	секунда	s	с
*Физическая химия и молекулярная физика*
Молярная масса	килограмм на моль	kg/mol	кг/моль
Молярный объем	кубический метр на моль	m³/mol	м³/моль
Тепловой эффект химической реакции (образования, растворения, горения, фазовых превращений и т. д.)	джоуль	J	Дж
Молярная внутренняя энергия, молярная энтальпия, химический потенциал, химическое сродство, энергия активации	джоуль на моль	J/mol	Дж/моль
Молярная теплоемкость, молярная энтропия	джоуль на моль-кельвин	J/(mol•K)	Дж/(моль•К)
Концентрация молекул	метр в минус третьей степени	m-³	м-³
Массовая концентрация	килограмм на кубический метр	kg/m³	кг/м³
Молярная концентрация	моль на кубический метр	mol/m³	моль/м³
Моляльность. удельная адсорбция	моль на килограмм	mol/kg	моль/кг
Летучесть (фугитивность)	паскаль	Pa	Па
Осмотическое давление	паскаль	Pa	Па
Коэффициент диффузии	квадратный метр на секунду	m²/s	м²/с
Скорость химической реакции	моль на кубический метр в секунду	mol/(m³•s)	моль/(м³•с)
Степень дисперсности	метр в минус первой степени	m^-1	м^-1
Удельная площадь поверхности	квадратный метр на килограмм	m²/kg	м²/кг
Поверхностная плотность	моль на квадратный метр	mol/m²	моль/м²
Электрический дипольный момент	кулон-метр	C•m	Кл•м
Поляризованность	кулон-квадратный метр на вольт	С•m²/V	Кл•м²/В
Молекулярная рефракция	кулон-квадратный метр на вольт-моль	C-m²/(V•mol)	Кл•м²/(В•моль)
Ионная сила раствора	моль на килограмм	mol/kg	моль/кг
Эквивалентная электрическая проводимость	сименс-квадратный метр на моль	S•m²/mol	См•м²/моль
Электродный потенциал	вольт	V	В
Молярная концентрация	моль на кубический метр	mol/m³	моль/м³
Подвижность ионов	квадратный метр на вольт-секунду	m²/(V•s)	м²/(В•с)
*Ионизирующие излучения*
Энергия ионизирующего излучения	джоуль	J	Дж
Поглощенная доза излучения (доза излучения), керма	грэй	Gy	Гр
Экспозиционная доза рентгеновского и гамма-излучений	кулон на килограмм	C/kg	Кл/кг
Активность нуклида в радиоактивном источнике	беккерель	Bq	Бк
*Атомная и ядерная физика*
Масса покоя частицы, атома, ядра	килограмм	kg	кг
Дефект массы	килограмм	kg	кг
Элементарный заряд	кулон	С	Кл
Магнетон ядерный	ампер-квадратный метр	A•m²	А•м²
Гиромагнитное отношение	ампер-квадратный метр на джоуль-секунду	A•m²/(J•s)	А•м²/(Дж•с)
Ядерный квадрупольный момент	квадратный метр	m²	м²
Энергия связи, ширина уровня	джоуль	J	Дж
Интенсивность излучения (плотность потока энергии)	ватт на квадратный метр	W/m²	Вт/м²
Активность нуклида (в радиоактивном источнике)	беккерель	Bq	Бк
Удельная активность	беккерель на килограмм	Bq/kg	Бк/кг
Молярная активность	беккерель на моль	Bq/mol	Бк/моль
Объемная активность	беккерель на кубический метр	Bq/m³	Бк/м³
Поверхностная активность	беккерель на квадратный метр	Bq/m²	Бк/м²
Период полураспада, средняя продолжительность жизни	секунда	s	с
Постоянная распада	секунда в минус первой степени	s^-1	с^-1
Эффективное сечение	квадратный метр	m²	м²
Дифференциальное эффективное сечение	квадратный метр на стерадиан	m²/sr	м²/ср
Подвижность	квадратный метр на вольт-секунду	m²/(V•s)	м²/(В•с)
Замедляющая способность среды	метр в минус первой степени	m^-1	м^-1
Длина замедления, длина диффузии, длина миграции	метр	m	м

Диаметр — Википедия

Материал из Википедии — свободной энциклопедии

Диа́метр в изначальном значении термина — отрезок, соединяющий две точки на окружности и проходящий через центр окружности, а также длина этого отрезка. Диаметр равен двум радиусам.

Радиус (r) и диаметр (d) окружности

Диаметр — это хорда (отрезок, соединяющий две точки) на окружности (сфере, поверхности шара), проходящая через центр этой окружности (сферы, шара). Также диаметром называют длину этого отрезка. Диаметр окружности является хордой, проходящей через её центр; такая хорда имеет наибольшую длину. По величине диаметр равен двум радиусам.

Символы со сходным начертанием: Ø · ø · ∅

Символ диаметра «⌀» (может не отображаться в некоторых браузерах) схож начертанием со строчной перечёркнутой буквой «o». В Юникоде он находится под десятичным номером 8960 или шестнадцатеричным номером 2300 (может быть введён в HTML-код как ⌀ или ⌀). Этот символ не присутствует в стандартных раскладках, поэтому для его ввода при компьютерном наборе необходимо использовать вспомогательные средства — например, приложение «Таблица символов» в Windows, программу «Таблица символов» (ранее gucharmap) в GNOME, команду «Вставка» → «Символ…» в программах Microsoft Office и т. д. В Word работает ALT+8960. Специализированные программы могут предоставлять пользователю свои способы ввода этого символа: к примеру, в САПР AutoCAD для ввода символа диаметра используется сочетание символов %%c (буква c — латинская) или \U+2205 в текстовой строке.

Во многих случаях символ диаметра может не отображаться, так как он редко включается в шрифты — например, он присутствует в Arial Unicode MS (поставляется с Microsoft Office, при установке именуется «Универсальный шрифт»), DejaVu (свободный), Code2000 (условно-бесплатный) и некоторых других.

Сопряжённые диаметры эллипса и гиперболы[править | править код]

Сопряжённые диаметры эллипса[править | править код]

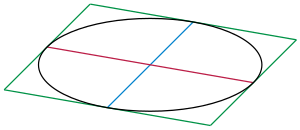Пара сопряжённых диаметров эллипса. Если в точках касания диаметра с эллипсом провести прямую, параллельную сопряжённому диаметру, то прямая будет касательной к эллипсу и четыре таких касательных ко всем четырём концам пары сопряжённых диаметров эллипса образуют описанный около эллипса параллелограмм

Диаметром эллипса называют произвольную хорду, проходящую через его центр. Сопряжёнными диаметрами эллипса называют пару его диаметров, обладающих следующим свойством: середины хорд, параллельных первому диаметру, лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру, лежат на первом диаметре.

На рисунке представлена пара сопряжённых диаметров (красный и синий). Если в точках пересечения диаметра с эллипсом провести прямую, параллельную сопряжённому диаметру, то прямая будет касательной к эллипсу, и четыре таких касательных ко всем четырём концам пары сопряжённых диаметров эллипса образуют описанный около эллипса параллелограмм (зелёные линии на рисунке).

Расстояния r1{\displaystyle r_{1}} и r2{\displaystyle r_{2}} от каждого из фокусов до данной точки на эллипсе называются фокальными радиусами в этой точке.
Радиус эллипса в данной точке (расстояние от его центра до данной точки) вычисляется по формуле r=abb2cos2⁡φ+a2sin2⁡φ=b1−e2cos2⁡φ{\displaystyle r={\frac {ab}{\sqrt {b^{2}\cos ^{2}\varphi +a^{2}\sin ^{2}\varphi }}}={\frac {b}{\sqrt {1-e^{2}\cos ^{2}\varphi }}}}, где φ{\displaystyle \varphi } — угол между радиус-вектором данной точки и осью абсцисс.

Сопряжённые диаметры гиперболы[править | править код]

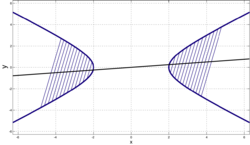$\varphi$ Диаметры гиперболы

Диаметром гиперболы, как и всякого конического сечения, является прямая, проходящая через середины параллельных хорд. Каждому направлению параллельных хорд соответствует свой сопряжённый диаметр. Все диаметры гиперболы проходят через её центр. Диаметр, соответствующий хордам, параллельным мнимой оси, есть действительная ось; диаметр соответствующий хордам, параллельным действительной оси, есть мнимая ось.
Угловой коэффициент k{\displaystyle k} параллельных хорд и угловой коэффициент k1{\displaystyle k_{1}} соответствующего диаметра связан соотношением

k⋅k1=ε2−1=b2a2{\displaystyle k\cdot k_{1}=\varepsilon ^{2}-1={\frac {b^{2}}{a^{2}}}}

$k\cdot k_{1}=\varepsilon ^{2}-1={\frac {b^{2}}{a^{2}}}$

Для произвольного угла φ показаны диаметры и сопряжённые им диаметры для окружностей и равнобочных гипербол.

Если диаметр гипербол a делит пополам хорды, параллельные диаметру b, то диаметр b делит пополам хорды, параллельные диаметру a. Такие диаметры называются взаимно сопряжёнными.
Главными диаметрами гипербол называются взаимно сопряжённые и взаимно перпендикулярные диаметры. У гиперболы есть только одна пара главных диаметров — действительная и мнимая оси.
В случае гипербол с асимптотами, образующими прямой угол, её сопряжённые гиперболы получатся при её зеркальном отражении относительно одной из асимптот. При таком зеркальном отражении её диаметр перейдет в сопряжённый диаметр, который будет просто диаметром сопряжённой гиперболы (см. рис.). Также. как наблюдается перпендикулярность сопряжённых диаметров на окружности (на рис. слева), аналогичная ортогональность наблюдается для сопряжённых диаметров гиперболы со взаимно перпендикулярными асимптотами (на рис. справа).

Понятие диаметра допускает естественные обобщения на некоторые другие геометрические и математические объекты. Если во множестве некоторых объектов определена метрика пространства, то для подмножества этих объектов может быть введено понятие диаметра множества.

Диаметром множества M{\displaystyle M}, лежащего в метрическом пространстве с метрикой ρ{\displaystyle \rho }, называется величина (supx,y∈Mρ(x,y)){\displaystyle (\sup _{x,y\in M}\rho (x,y))}.

Под диаметром метрического пространства понимается точная верхняя грань расстояний между парой любых его точек.

В частности:
- Под диаметром конического сечения понимается прямая проходящая через середины двух параллельных хорд.
- Диаметр графа — это максимальное из расстояний между парами его вершин. Расстояние между вершинами определяется как наименьшее число рёбер, которые необходимо пройти, чтобы добраться из одной вершины в другую. Иначе говоря, это расстояние измеренное в количестве рёбер между двумя вершинами графа, максимально удалёнными друг от друга.
- Максимальное расстояние Хэмминга между двумя словами равной в символах длины n{\displaystyle n} равно n{\displaystyle n}, другими словами диаметр множества слов в метрике Хэмминга равен n{\displaystyle n}.
- Диаметр геометрической фигуры — максимальное расстояние между точками этой фигуры.

Например, диаметр n-размерного гиперкуба со стороной s равен

d=s⋅n{\displaystyle d=s\cdot {\sqrt {n}}}.