2.2.3. Конденсатор в цепи синусоидального тока
Включение конденсатора в цепь переменного тока не вызывает разрыва цепи, так как ток в цепи все время поддерживается за счет заряда и разряда конденсатора. Пусть напряжение (рис. 2.8 а)
 .
.
Тогда

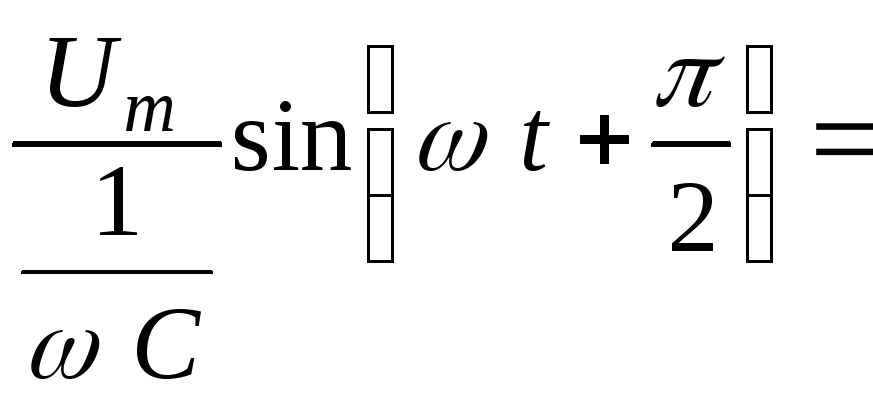
 (2.17)
(2.17)
Ф ормула
(2.17) показывает, чтоток
опережает приложенное напряжение на
угол
ормула
(2.17) показывает, чтоток
опережает приложенное напряжение на
угол 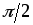
Под фазовым сдвигом тока относительно напряжения здесь, как и раньше, подразумевается разность начальных фаз напряжения и тока, т.е.
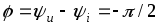 .
.
Таким образом, в отличие от цепи с
катушкой, где 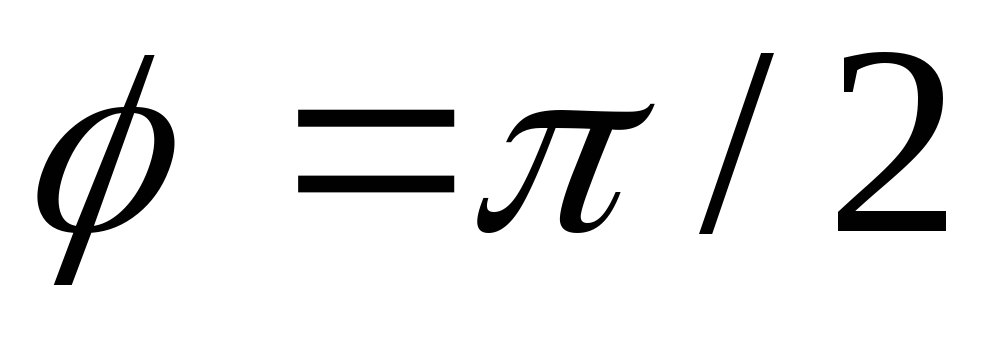
Из (2.17) видно, что амплитуды тока и напряжения связаны законом Ома
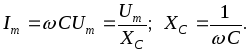 ,
,
где –емкостное сопротивление, имеющее
размерностьОм.
–емкостное сопротивление, имеющее
размерностьОм.
Мгновенная мощность, поступающая в конденсатор
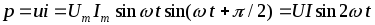 ,
,
колеблется
синусоидально с угловой частотой 2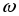
 (рис. 2.8 г). Поступая от источника, энергия
временно запасается в электрическом
поле конденсатора, затем возвращается
источнику при исчезновении электрического
поля. Таким образом, здесь, как и в цепи
с катушкой, происходит колебание энергии
между источником и конденсатором, причем
активная мощность
(рис. 2.8 г). Поступая от источника, энергия
временно запасается в электрическом
поле конденсатора, затем возвращается
источнику при исчезновении электрического
поля. Таким образом, здесь, как и в цепи
с катушкой, происходит колебание энергии
между источником и конденсатором, причем
активная мощность = 0. Амплитуду колебания мощности в
цепи с конденсатором называютреактивной
(емкостной) мощностью
= 0. Амплитуду колебания мощности в
цепи с конденсатором называютреактивной
(емкостной) мощностью 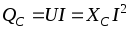 .
.
2.3. Анализ цепей синусоидального тока с помощью векторных диаграмм
Совокупность векторов, изображающих синусоидальные ЭДС, напряжения и токи одной частоты и построенных на плоскости с соблюдением их ориентации друг относительно друга, называют векторной диаграммой. Векторные диаграммы широко применяются при анализе режимов работы цепей синусоидального тока, что делает расчет цепи наглядным.
2.3.1. Цепь, содержащая резистор и индуктивную катушку
Реальная катушка в цепи переменного
тока представляет сочетание активной
и индуктивной составляющих сопротивления.
Схема замещения индуктивной катушки
представлена на рис 2.9 а. Пусть по катушке
протекает ток 
Рис. 2.9
В соответствии со вторым законом Кирхгофа для мгновенных значений
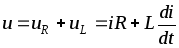 ,
(2.18)
,
(2.18)
где  –
напряжение на активном сопротивлении;
–
напряжение на активном сопротивлении; – напряжение на индуктивном
сопротивлении.
– напряжение на индуктивном
сопротивлении.
Для действующих значений уравнение (2.18) можно записать
 .
(2.19)
.
(2.19)
Построим векторную
диаграмму в соответствии с (2.19) в такой
последовательности. Изобразим вектор
тока  (основной вектор) на координатной
плоскости
(основной вектор) на координатной
плоскости –
– (рис. 2.9 б). Затем строим вектор напряжения
на активной составляющей сопротивления
(рис. 2.9 б). Затем строим вектор напряжения
на активной составляющей сопротивления
 опережает вектор тока на 90°. Сумма двух
векторов дает вектор напряжения
источника, который опережает вектор
тока на угол
опережает вектор тока на 90°. Сумма двух
векторов дает вектор напряжения
источника, который опережает вектор
тока на угол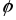 .
Из векторной диаграммы следует
.
Из векторной диаграммы следует 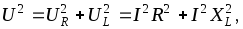
отсюда
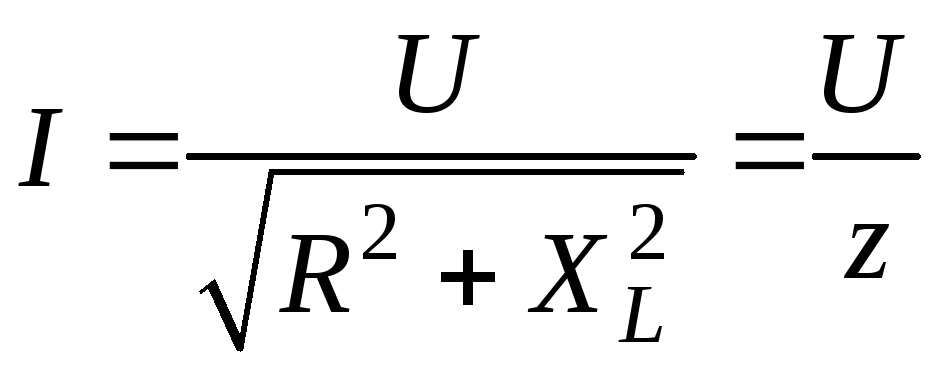
 . (2.20)
. (2.20)где z – полное сопротивление цепиR,L.
Треугольник ОАВ(рис. 2.9 б) назовемтреугольником напряжений. Составляющая
напряжения, находящаяся в фазе с током,
называетсяактивнойсоставляющей
напряжения
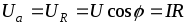 .
(2.21)
.
(2.21)
Составляющая напряжения, перпендикулярная вектору тока, называется
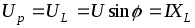 .
(2.22)
.
(2.22)
Если стороны треугольника напряжений (рис. 2.9 б) разделить на действующее значение тока, то получим треугольник сопротивлений (рис. 2.9 в). Из треугольника сопротивлений получают соотношения для угла сдвига фаз, а также связь между параметрами цепи
 ;
;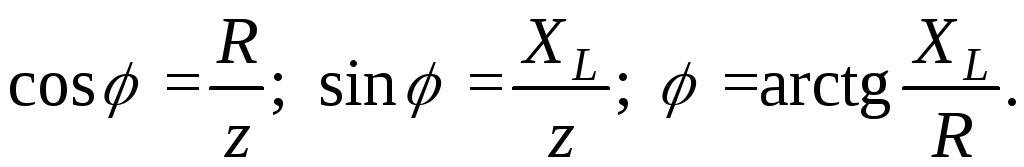
Цепь имеет индуктивный
характер, если 0< <
< .
Крайние значения
.
Крайние значения = 0 и
= 0 и =
=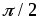 соответствуют чисто активной и чисто
индуктивному характеру нагрузки.
соответствуют чисто активной и чисто
индуктивному характеру нагрузки.
Конденсатор в цепи синусоидального тока
⇐ ПредыдущаяСтр 4 из 4
Конденсатор представляет собой две металлические пластины (обкладки), разделённые диэлектриком. Если приложить к конденсатору постоянное напряжение, на его обкладки поступит электрический заряд, как показано на рис. 53. Полученный заряд может сохраняться на обкладках долгое время. Заряды со знаком «плюс» и «минус» притягиваются друг к другу и не могут уйти с обкладок. В то же время они не могут и соединиться, нейтрализовав друг друга, т.к. этому препятствует диэлектрик (изоляция) между обкладками. Таким образом, конденсатор это устройство, предназначенное для накопления и хранения электрического заряда. (Поскольку изоляция между обкладками неидеальна, рано или поздно конденсатор разрядится – потеряет заряд)

Рис. 53. Конденсатор хранит заряд на своих обкладках
Постоянный ток не может проходить через конденсатор. Этому препятствует диэлектрик между обкладками.

Рис. 54. В цепи переменного напряжения через конденсатор протекает ток.
Как ни странно, переменный ток может проходить в цепи с конденсатором, несмотря на наличие изоляции между обкладками.
При переменном напряжении конденсатор, при смене полупериода, вынужден постоянно перезаряжаться. При этом меняется полярность и величина заряда на обкладках конденсатора (см. рис. 54).
В положительный полупериод синусоиды на верхнюю обкладку конденсатора поступает положительный заряд, а на нижнюю – отрицательный.
В отрицательный полупериод (его полярность показана в скобках) заряд на обкладках меняется на противоположный.
При работе в цепях синусоидального тока конденсатор постоянно перезаряжается. В проводниках, подводящих напряжение к конденсатору, происходит перемещение заряда. Это означает, что в цепи протекает ток.
Вместо термина «конденсатор» часто используется термин «емкость». Это слово имеет в электротехнике два значения:
— параметр конденсатора, характеризующий его величину заряда, который он способен накапливать;
— собственно конденсатор.
Конденсатор оказывает сопротивление проходящему току. Это сопротивление называется ёмкостным, обозначается XCи определяется по формуле:
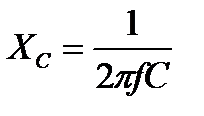
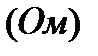 , где:
, где:
f — частота приложенного напряжения;
С — ёмкость конденсатора (Фарад).
Ёмкостное сопротивление зависит от частоты. С ее увеличением емкостное сопротивление уменьшается. Соответственно, ток в цепи с конденсатором увеличивается:
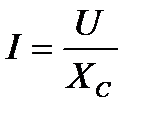
В конденсаторе ток опережает напряжение на угол  радиан (90 градусов).
радиан (90 градусов).

Рис. 55. В конденсаторе ток опережает по фазе приложенное напряжение
Конденсатор, как и катушка индуктивности, относится к реактивным элементам. В реактивных элементах происходит обратимое преобразование энергии. Конденсатор сначала забирает энергию от источника напряжения, накапливает энергию в своём электрическом поле, а затем отдает ее генератору. Затем процесс повторяется.
В конденсаторе выделяется реактивная мощность:
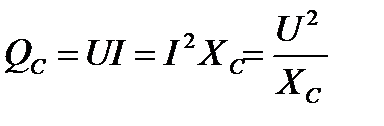
 ,
,
Пример 12. Идеальный конденсатор в цепи синусоидального тока.
 К конденсатору емкостью С = 63,7 мкФ приложено напряжение u=141sin314t, В. Определить действующее значение тока и реактивную мощность конденсатора.
К конденсатору емкостью С = 63,7 мкФ приложено напряжение u=141sin314t, В. Определить действующее значение тока и реактивную мощность конденсатора.
Решение.
Идеальный конденсатор обладает только одним параметром – ёмкостью. Влияние сопротивления изоляции между обкладками не учитывается.
В условии задачи приведено уравнение напряжения, действующего на входе цепи, имеющее вид: u = Um sinwt. Из этого уравнения можно узнать амплитуду приложенного напряжения Um =141В и угловую частоту w = 314рад/сек.
Зная амплитуду Um, приложенного напряжения, находим действующее значение напряжения U=Um/1,41=141/1,41=100B.
Зная, что угловая частота w = 2pf, находим частоту приложенного к конденсатору напряжения f = w/2p =314/6,28=50Гц.
Емкостное сопротивление конденсатора
Xc=1/2pfC=1 / 6,28·50·63,7·10-6=50 Ом.
В этой формуле ёмкость конденсатора выражена в фарадах, для чего, предварительно, был сделан перевод ёмкости конденсатора из микрофарад, приведённых в условии задачи, в фарады. Приставка «микро» обозначает одну миллионную долю, следовательно:
63,7мкФ = 63,7/1000000 Ф = 63,7·10-6 Ф.
Ток в цепи, по закону Ома
I = U /Xс = 100/50 = 2 А.
Реактивная мощность
Qc = UI = 100 • 2 = 200 вар.
Рекомендуемые страницы:
3). Цепь синусоидального тока с идеальным конденсатором.
Конденсатор – элемент электрической цепи, предназначенный для использования его ёмкости. В конденсаторе накапливается энергия электрического поля. Свойство элемента запасать электрический заряд характеризует ёмкость. Этот параметр является коэффициентом пропорциональности между зарядом q и прикладываемым напряжением u
q = C·u,
где q – выражается в кулонах [Кл], С – в фарадах [Ф], u – в вольтах [B].
При изменении напряжения на конденсаторе изменяется заряд и возникает электрический ток

Идеализированный конденсатор обладает только параметром С.
Рассмотрим электрические процессы в цепи с идеальным ёмкостным элементом, рис., а.
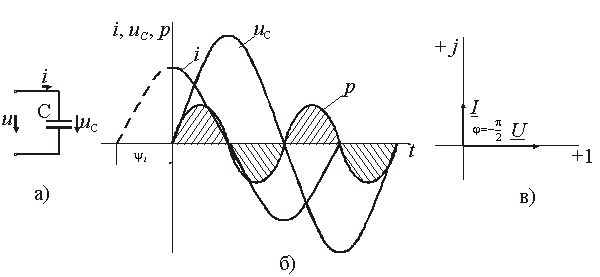
Пусть напряжение источника изменяется по закону
u = Um·sinω·t, (ψu = 0).
В цепи возникает ток
Из полученного выражения видно, что начальная фаза тока ψi = π/2. Угол сдвига фаз между напряжением и током составляет
φ = ψu – ψi = 0 – π/2 = — π/2.
Следовательно, синусоида напряжения на емкости отстаёт от синусоиды тока на угол π/2, рис. 3.6, б, в. На практике, если в электрической цепи напряжение отстаёт по фазе от тока, говорят об ёмкостном характере нагрузки.
Амплитуда тока
Im = ω·C·Um,
действующее значение

Это выражение представляет закон Ома. Величину 1/ω·C называют ёмкостным сопротивлением конденсатора и измеряют в [Ом]
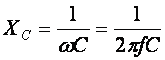 .
.
Ёмкостное сопротивление имеет место только в том случае, когда происходит изменение напряжения на обкладках конденсатора. При постоянном напряжении (f = 0) ёмкостное сопротивление равно бесконечности (т. е. В цепи будет разрыв).
Мгновенная мощность ёмкостного элемента
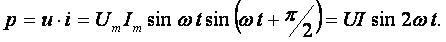
Амплитуда мгновенной мощности равна реактивной мощности
QC = U·I = XC·I2.
Активная мощность (средняя за период) равна нулю, рис., б.
С энергетической точки зрения график мгновенной мощности отражает накопление энергии в электрическом поле конденсатора (когда мощность положительная) и возврат её источнику питания (когда мощность отрицательная). Следовательно, ёмкостной элемент является реактивной нагрузкой.
Выразим электрические величины в комплексной форме. Напряжение и ток (действующие значения) в цепи имеют вид
U = U·ej·ψu, I = I·ej·ψi , ψu = 0, ψi = π/2, φ = — π/2.
Комплексное сопротивление цепи
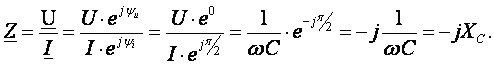
Ёмкостное сопротивление является отрицательным мнимым числом.
Последовательное соединение активного, индуктивного и ёмкостного элементов.
Рассмотрим процессы, происходящие в цепи, содержащей индуктивную катушку с параметрами L, R и конденсатор с параметром С. Схема замещения цепи показана на рисунке.
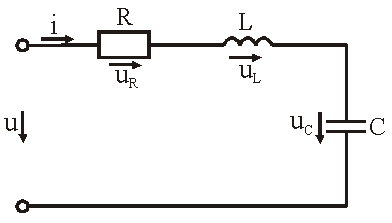
Для последовательной цепи общим является ток. Согласно второму закону Кирхгофа для мгновенных значений напряжение на входе цепи определяется выражением
u = uR + uL + uC.
Запишем это уравнение в комплексной форме
U = UR + UL + UC.
Представим это уравнение векторной диаграммой, рис. 3.8, а.
Построение векторной диаграммы начинаем с отложения на комплексной плоскости вектора тока I, который является общим для всех элементов цепи. Причём направление вектора выбираем произвольно. На рис 3.8, а вектор тока I выбран совпадающим с положительным направлением действительной оси. Вектор напряжения на активном сопротивлении UR совпадает по направлению с вектором тока, его называют активной составляющей напряжения, UR = R∙I. Вектор напряжения на индуктивности катушки UL = jXL∙I опережает вектор тока на угол 90°. Вектор напряжения на ёмкости UC = — jXC∙I отстаёт от вектора тока на угол 90°.
Геометрическая сумма трех векторов напряжения даёт вектор напряжения U, приложенного к цепи. Результирующий вектор напряжения U опережает вектор тока I на угол φ.
При построении диаграммы условно принято UL > UC. В построенной диаграмме можно выделить треугольник ОАВ, называемый треугольником напряжений. Сторона треугольника
АВ = UХ = UL + UC = j(XL – XC)·I
называется реактивной составляющей напряжения. Из треугольника напряжений можно найти модуль напряжения на зажимах в цепи

Заменяя напряжения на элементах произведением тока на соответствующие сопротивления, получаем
U = R·I + jXL·I – jXC · I = I·[R + j(XL – XC)] = Z·I,
где Z – полное комплексное сопротивление цепи,
Z = R + j(XL – XC).
Из треугольника сопротивлений можно определить модуль полного сопротивления и угол φ
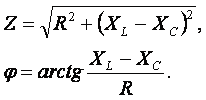
Мощность однофазной цепи синусоидального тока.
Активная мощность определяется выражением
P = U·I·cosφ = R·I2 [Вт].
Она характеризует интенсивность необратимого преобразования электрической энергии в другие виды энергии.
Реактивная мощность определяется выражением
Q = U·I·sinφ = X·I2 [Bap].
Она характеризует интенсивность колебательного обмена энергией между источником и реактивными элементами приемника без её преобразования.
Полная мощность определяется выражением
S = U·I = Z·I2 [B·A].
Она характеризует амплитуду колебания мощности в цепи.
Комплексная мощность определяется выражением

где 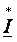 —
сопряженный вектор.
—
сопряженный вектор.
Умножив все стороны треугольника напряжений на ток, получаем треугольник мощностей, рис. 3.8, в.
Модуль полной мощности равен
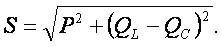
ТРЕХФАЗНЫЕ ЦЕПИ.
Трехфазная система ЭДС.
Трехфазные электрические цепи представляют собой частный случай многофазных цепей.
Трехфазные цепи — это совокупность трех однофазных цепей, в которых действуют синусоидальные э. д. с. одной и той же частоты, сдвинутые по фазе друг относительно друга на угол 2π / 3. Передача электрической энергии на дальние расстояния по трехфазным цепям более выгодна, чем передача энергии по однофазным цепям; кроме того, трехфазные синхронные генераторы и двигатели, трехфазные асинхронные двигатели и трансформаторы более просты в производстве, экономичны и надежны в эксплуатации. В трехфазных системах достаточно просто получить вращающееся магнитное поле, воздействие которого на проводники с током положено в основу принципа работы асинхронных и синхронных электродвигателей.
Источником электрической энергии в трехфазной цепи является синхронный генератор, в трех обмотках которого, конструктивно сдвинутых друг относительно друга на угол 2π / 3 и называемых фазами, индуцируются три э. д. с., фазы которых, в свою очередь, также сдвинуты относительно друг друга на угол 2π / 3.

Мгновенные значения ЭДС трехфазного источника
eA = Em∙sinωt, eB = Em∙sin(ωt — 120°), eC = Em∙sin(ωt + 120°),
где начальные фазы соответственно равны
ψeA = 0; ψeB = — 120°; ψeC = 120°.
Такая система называется симметричной. Временная и векторная диаграммы показаны на рис. 4.2 а, б. Векторная диаграмма токов и напряжений строится на комплексной плоскости, оси которой +1, +j повернуты на 90° против направления часовой стрелки. Такое направление осей часто принимается при расчете трехфазных цепей (исключительно для удобства).
Часть трехфазной системы, в которой может протекать один из её токов, называется фазой (фазы А, В, С).
Обмотки трехфазного источника питания могут быть соединены в звезду или в треугольник. При соединении обмоток звездой концы обмоток всех фаз (X, Y, Z) объединяют в одну общую точку N, называемую нейтральной рис. 4.3, а. От начал обмоток (А, В, С) и нейтральной точки N выводят провода, по которым энергия подаётся потребителям (приёмникам). Провода, соединяющие начала обмоток источника и приёмника, называются линейными. Провод, соединяющий нейтральные точки источника и приёмника, называется нейтральным (нулевым).
 Рис.
4.3 – Схемы соединения обмоток трехфазного
источника:
а) звезда; б) треугольник
Рис.
4.3 – Схемы соединения обмоток трехфазного
источника:
а) звезда; б) треугольник
Напряжения
между линейными проводами UAB, UBC, UCA называют линейными напряжениями.
Напряжения между нейтральным проводом
и соответствующим линейным проводом UA, UB, UC называют фазными напряжениями. Можно
показать, что при соединении обмоток в
звезду фазное напряжение меньше линейного
в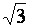 ,
а фазные токи равны линейным.
,
а фазные токи равны линейным.
Временная и векторная диаграммы напряжений имеют тот же вид, что и диаграммы ЭДС.
За условное положительное направление токов в линейных проводах принято направление в сторону потребителей, а в нейтральном – в сторону источника.
При соединении обмоток источника (генератора, трансформатора) треугольником объединяют в одну общую точку начало и конец соответствующих фаз Х и В, У и С. Z и А (рис. 4.2, б). При таком соединении фазные напряжения равны линейным, а фазные токи меньше линейных в √3 (IА, IВ, IС – линейные токи; IАВ, IВС, IСА – фазные токи)

Широкое распространение в энергетике получили трехфазная четырехпроводная система и трехфазная трехпроводная система.
1. Схема «звезда». Векторные диаграммы для различных схем при неравномерной однородной нагрузке.
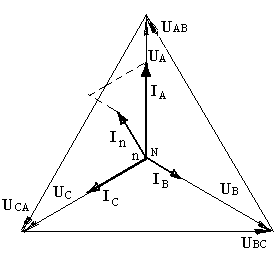
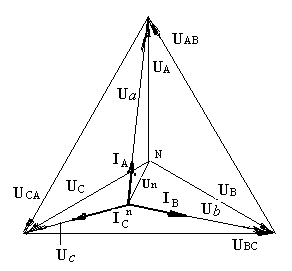
а).Четырёхпроводная схема. б). Трёхпроводная схема
2. Схема «треугольник». Векторная диаграмма при равномерной неоднородной нагрузке.

Электроника.
Физические основы работы полупроводниковых приборов.
К полупроводникам относят материалы, занимающие по своему удельному сопротивлению промежуточное положение между проводниками и диэлектриками. При производстве полупроводниковых приборов наибольшее применение нашли германий Ge и кремний Si. У идеальных кристаллов германия и кремния, относящихся к четвертой группе периодической системы Менделеева, все валентные электроны образуют связанную пару. Такие идеальные кристаллы не проводят электрический ток.
При добавлении в кристалл кремния элементов из пятой группы, например сурьмы Sb или фосфора P появляется несвязанный, свободный электрон. Таким образом, в кристалле кремния возникает электронная проводимость, а полупроводник называется n – типа. Примесь, образующая электронную проводимость, называется донорной.
Добавление в кремний трехвалентной примеси, например, галлия Ga или индия In приводит к тому, что три валентных электрона индия участвуют в образовании ковалентных связей с атомом кремния, а одна связь остается свободной. Таким образом, для образования четвертой ковалентной связи примесным атомам не хватает по одному электрону. В кристалле кремния образуется «дырка», способная присоединить свободный электрон. Такой полупроводник называется полупроводником с дырочной проводимостью или полупроводником p — типа, а соответствующая примесь называется акцепторной.
Принцип действия большинства полупроводниковых приборов основан на явлениях, происходящих на границе двух полупроводников с различными видами проводимости. Электронно-дырочный переход или р — n – переход.
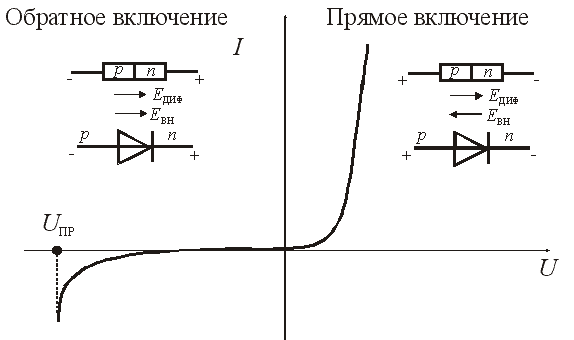
Выпрямительные диоды предназначены для преобразования переменного тока в постоянный ток. Выпрямление переменного тока основано на односторонней проводимости диода. Вольтамперная характеристика р — n перехода, изображенная на рисунке, является характеристикой диода. При включении диода в прямом направлении сопротивление его электрическому току очень мало. При обратном включении – сопротивление диода велико и он практически не пропускает электрический ток. Выпрямление переменного напряжения (тока) показано на рис.6.3. При действии положительной полуволны входного напряжения U1 диод включен в прямом направлении, сопротивление его мало и на сопротивлении нагрузки Rн падение напряжения U2 практически равно входному напряжению.
Выпрямители присутствуют во всех электронных устройствах, питающихся от сети переменного тока. Схема нестабилизированного выпрямителя содержит :силовой трансформатор, предназначенный для преобразования напряжения питающей сети в напряжение, необходимое для получения заданного значения выпрямленного напряжения на выходе выпрямителя; полупроводниковые диоды (вентили), предназначенные для преобразования переменного напряжения в постоянное; сглаживающий фильтр для уменьшения пульсаций выпрямленного напряжения.
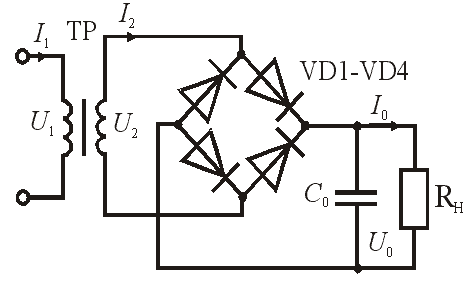
В зависимости от мощности, напряжения, допустимых пульсаций и т. д. применяются различные схемы выпрямления.
Однофазная мостовая схема находит наибольшее применение при питании от однофазной сети, рис.6.7. Обратное напряжение, приходящееся на один диод и напряжение вторичной обмотки трансформатора при этой схеме примерно в 2 раза меньше, чем в двухполупериодной схеме.
Точный аналитический расчет выпрямителей представляет определенные трудности, в связи с тем, что полупроводниковые приборы, применяемые в качестве преобразователей переменного напряжения в постоянное напряжение, являются нелинейными элементами. Расчет таких электрических цепей проводится по приближенным формулам с использованием графических зависимостей.
2.2. Резистор, индуктивная катушка и конденсатор в цепи синусоидального тока
Составными элементами цепей синусоидального тока являются резистор, индуктивная катушка и конденсатор. Для упрощения исследования процессов в реальной электрической цепи переменного тока эту цепь, как и цепь постоянного тока, представляют схемой замещения, составленной из этих элементов. Элементы цепи переменного тока, в которых энергия выделяется в виде теплоты, называются активными. Элементы цепи, в которых периодически запасается энергия в электрическом или магнитном поле, называются реактивными, а сопротивления, оказываемые ими переменному току –реактивными сопротивлениями. Реактивные сопротивления имеют катушки и конденсаторы.
Рассмотрим соотношения между токами и напряжениями в простейших цепях.
2.2.1. Резистор в цепи синусоидального тока
Если синусоидальное напряжение 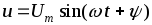 (рис. 2.6 а) подключить к резистору с
сопротивлением
(рис. 2.6 а) подключить к резистору с
сопротивлением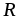 ,
то через него будет протекать
синусоидальный ток
,
то через него будет протекать
синусоидальный ток
 (2.7)
(2.7)
Следовательно, напряжение на зажимах и ток, проходящий через резистор, имеют одинаковую начальную фазу, или, как говорят, совпадают по фазе– они одновременно достигают своих амплитудных значений и соответственно одновременно проходят через нуль (рис. 2.6 б, в).
Разность начальных фаз двух синусоид называют углом сдвига фаз. В данном случае угол сдвига фаз между напряжением и током равен нулю
 .
(2.8)
.
(2.8)
Амплитуды и действующие значения тока и напряжения связаны законом Ома
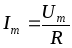 ;
;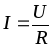 .
.
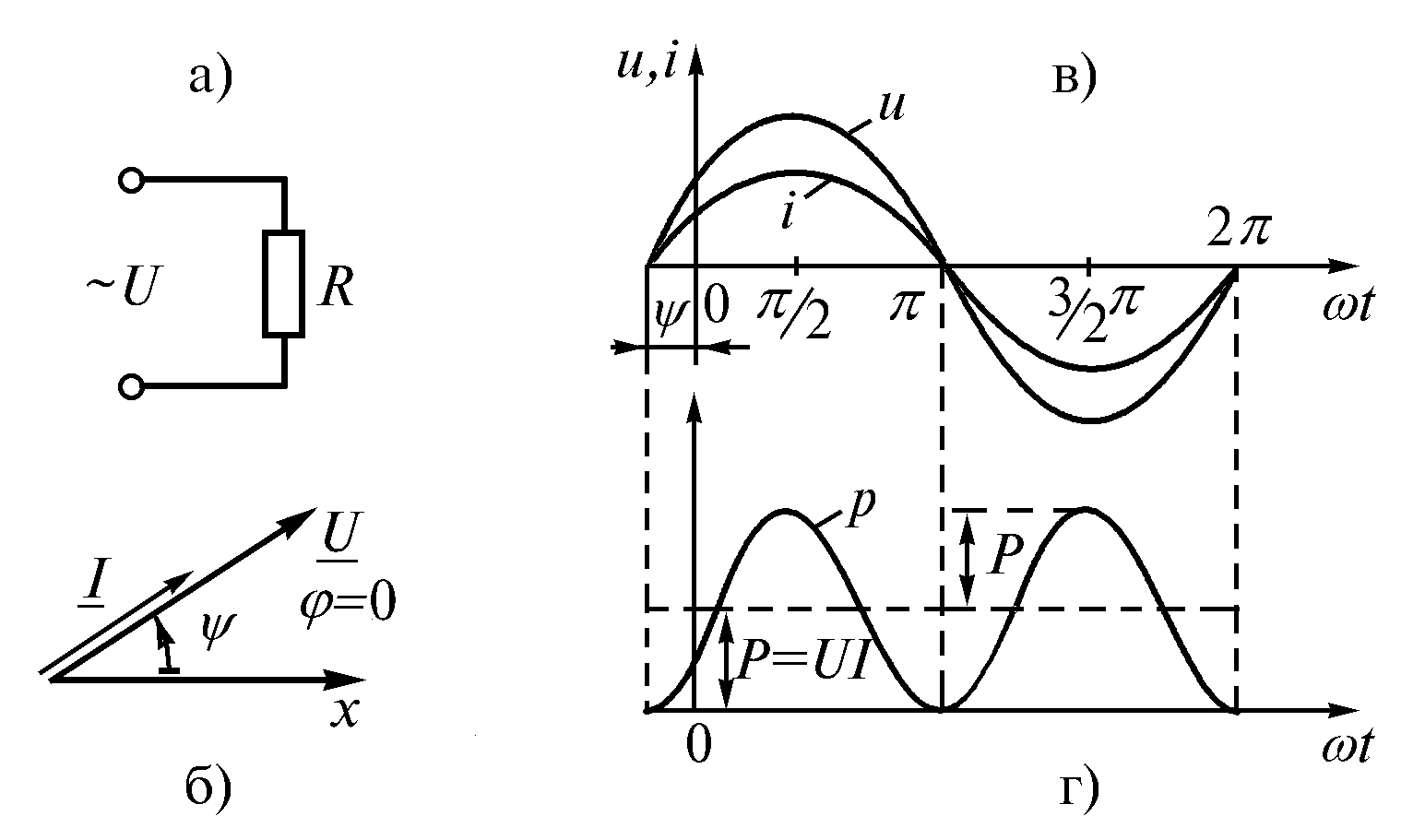
Рис. 2.6
Протекание тока через резистор сопровождается потреблением энергии от источников. Скорость поступления энергии характеризуется мощностью. Мгновенная мощность, потребляемая резистором
 ,
(2.9)
,
(2.9)
изменяется с угловой частотой, удвоенной
по сравнению с частотой напряжения и
тока. Мгновенная мощность имеет постоянную
составляющую 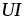 и составляющую
и составляющую ,
изменяющуюся с частотой
,
изменяющуюся с частотой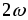 (рис. 2.6 г). Так как
(рис. 2.6 г). Так как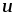 и
и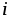 совпадают по фазе, т.е. всегда имеют
одинаковый знак, то их произведение
всегда положительно, следовательно,
совпадают по фазе, т.е. всегда имеют
одинаковый знак, то их произведение
всегда положительно, следовательно,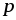 >
0.
>
0.
Среднее значение мгновенной мощности за период
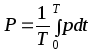 (2.10)
(2.10)
называется активной мощностьюи измеряется в ваттах. В данном случае активная мощность
 .
(2.11)
.
(2.11)
Отсюда активное сопротивление
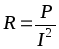 .
(2.12)
.
(2.12)
Известно, что сопротивление проводника переменному току больше, чем постоянному, вследствие явления поверхностного эффекта.
2.2.2. Индуктивная катушка в цепи синусоидального тока
Индуктивная катушка как элемент схемы
замещения реальной цепи синусоидального
тока дает возможность учитывать при
расчете явление самоиндукции и
явление накопления энергии в ее магнитном
поле. Пусть в цепь переменного тока
(рис 2.7 а) включена катушка с бесконечно
малым сопротивлением провода = 0. Непрерывное во времени изменение
тока вызывает
появление в витках катушки ЭДС
самоиндукции. В соответствии с
правилом Ленца эта ЭДС противодействует
изменению тока.
= 0. Непрерывное во времени изменение
тока вызывает
появление в витках катушки ЭДС
самоиндукции. В соответствии с
правилом Ленца эта ЭДС противодействует
изменению тока.
Допустим, ток через катушку изменяется по закону
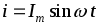 .
(2.13)
.
(2.13)
В этом случае ЭДС самоиндукции
 .
(2.14)
.
(2.14)
Поэтому напряжение на катушке
 .
(2.15)
.
(2.15)
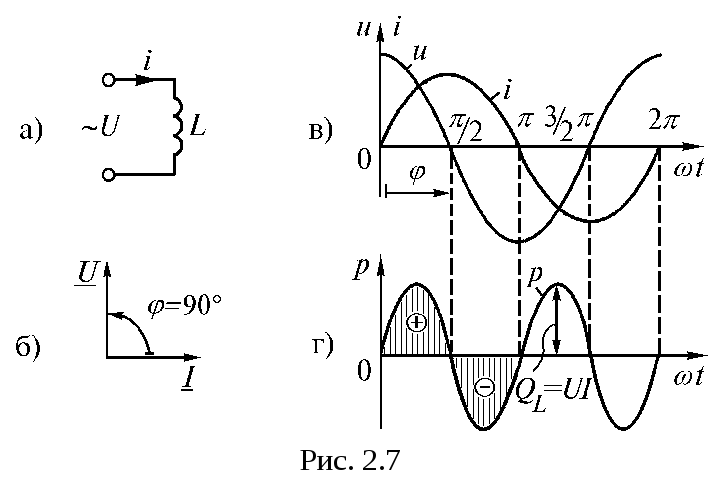 Сравнивая
формулы (2.13) и (2.15), можно сделать вывод
о том, чтонапряжение на катушке
опережает ток на угол
Сравнивая
формулы (2.13) и (2.15), можно сделать вывод
о том, чтонапряжение на катушке
опережает ток на угол 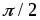 или ток отстает от напряжения по фазе
на угол
или ток отстает от напряжения по фазе
на угол (рис 2.7 б). Угол сдвига фаз в этом случае
положительный (рис. 2.7 в)
(рис 2.7 б). Угол сдвига фаз в этом случае
положительный (рис. 2.7 в)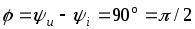 .
.
Параметр цепи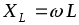 –индуктивное сопротивление, имеющее
размерностьОм. Оно зависит от
частоты и представляет собой величину,
с помощью которой учитывается явление
самоиндукции.
–индуктивное сопротивление, имеющее
размерностьОм. Оно зависит от
частоты и представляет собой величину,
с помощью которой учитывается явление
самоиндукции.
Из анализа (2.14) видно, что амплитуды напряжения и тока связаны законом Ома:
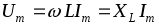 .
.
Аналогично для действующих значений
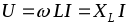 .
.
Мгновенная мощность цепи с катушкой
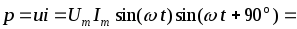
 .
(2.16)
.
(2.16)
Из графика (рис 2.7 г), построенного по
уравнению (2.16), видно, что за первую
четверть периода, когда 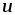 > 0 и
> 0 и > 0, площадь, ограниченная кривой
> 0, площадь, ограниченная кривой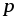 и осью абсцисс, пропорциональна энергии,
потребляемой катушкой на создание
магнитного поля. Во вторую четверть
периода (ток убывает от максимума до
нуля) энергия магнитного поля катушки
передается источнику питания. При этом
мгновенная мощность отрицательна,
а процесс повторяется. Таким образом,
происходит колебание энергии между
источником и катушкой, причемактивная
мощность, поступающая в катушку, равна
нулю. Амплитуду колебания мгновенной
мощности в цепи с катушкой называютреактивной (индуктивной) мощностью
и осью абсцисс, пропорциональна энергии,
потребляемой катушкой на создание
магнитного поля. Во вторую четверть
периода (ток убывает от максимума до
нуля) энергия магнитного поля катушки
передается источнику питания. При этом
мгновенная мощность отрицательна,
а процесс повторяется. Таким образом,
происходит колебание энергии между
источником и катушкой, причемактивная
мощность, поступающая в катушку, равна
нулю. Амплитуду колебания мгновенной
мощности в цепи с катушкой называютреактивной (индуктивной) мощностью
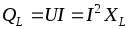 .
.
Реактивную мощность в отличие от активной мощности измеряют в вар(вольт-ампер реактивный).
2.7. Емкостный элемент в цепи синусоидального тока
Лекция 7
Емкостный элемент представляет собой идеальный конденсатор, между обкладками которого содержится идеальный диэлектрик, т. е. диэлектрик, в котором отсутствует ток проводимости и, следовательно, не существует тепловых потерь. К зажимам электрической цепи, содержащей емкостный элемент (рис. 2.12, а), приложено синусоидальное напряжение
 (2.43)
(2.43)
Ток в такой цепи есть движение зарядов к обкладкам конденсатора
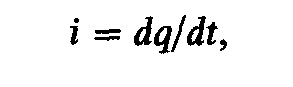 (2.44)
(2.44)
но так как то
то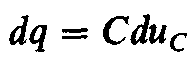 и,
следовательно,
и,
следовательно,
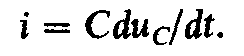 (2.45)
(2.45)
При синусоидальном напряжении в цепи ток
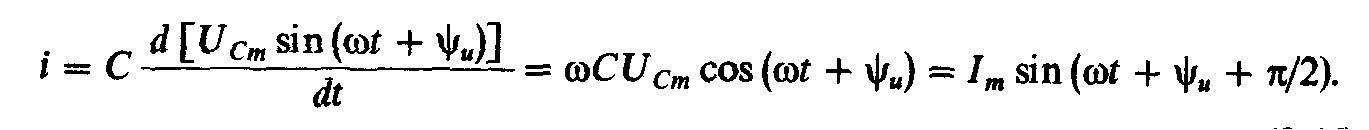
Таким образом, ток
в цепи с идеальным конденсатором, как
и напряжение на емкости, изменяется
по синусоидальному закону, причем ток
опережает напряжение по фазе на угол Иначе
напряжение отстает от тока по фазе на
угол
Иначе
напряжение отстает от тока по фазе на
угол что
видно из векторной диаграммы (рис. 2.12,
6) и графика мгновенных значений (рис.
2.12, в).
что
видно из векторной диаграммы (рис. 2.12,
6) и графика мгновенных значений (рис.
2.12, в).
Следует помнить, что постоянный ток в цепи с идеальным конденсатором существовать не может, так как явления протекания тока в такой цепи связаны с существованием тока смещения, поэтому конденсатор в цепи постоянного тока разрывает цепь.
Амплитуда тока цепи с емкостным элементом
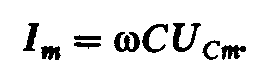
Действующее
значение тока (закон Ома цепи с емкостью)
имеет вид  (2.47)
(2.47)
где —
реактивное сопротивление емкости, или
просто емкостное сопротивление, которое
учитывает реакцию электри-ческой цепи
на изменение электрического поля в
конденсаторе, причем значение этого
сопротивления обратно пропорционально
частоте.
—
реактивное сопротивление емкости, или
просто емкостное сопротивление, которое
учитывает реакцию электри-ческой цепи
на изменение электрического поля в
конденсаторе, причем значение этого
сопротивления обратно пропорционально
частоте.
Мгновенная мощность p в цепи с емкостным элементом
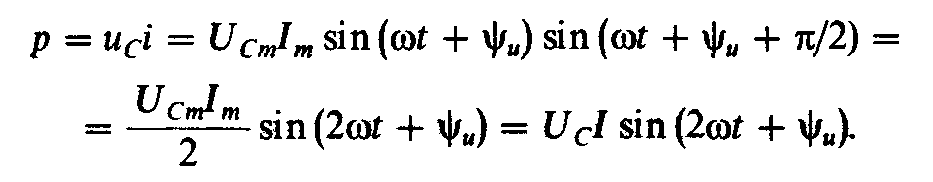
(2.48)
Из выражения (2.48) следует, что мгновенная мощность изменяется по синусоидальному закону с удвоенной частотой по сравнению с током.
Среднее значение мощности за период для цепи с идеальным конденсатором, как видно из графика рис. 2.12, в, равно нулю:
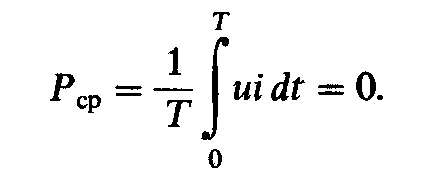
Р ассмотрим,
как протекают процессы в цепи с емкостным
элементом. Из рис. 2.12, в (для случая,
когда начальная фаза напряжения равна
нулю) видно, что в первую четверть периода
напряжение на конденсаторе возрастает,
ток положителен — происходит зарядка
конденсатора, т. е. накопление энергии
в электрическом поле конденсатора за
счет электрической энергии сети,
поступающей к конденсатору. Накопленная
в конденсаторе за первую четверть
периода энергия электрического поля
равна
ассмотрим,
как протекают процессы в цепи с емкостным
элементом. Из рис. 2.12, в (для случая,
когда начальная фаза напряжения равна
нулю) видно, что в первую четверть периода
напряжение на конденсаторе возрастает,
ток положителен — происходит зарядка
конденсатора, т. е. накопление энергии
в электрическом поле конденсатора за
счет электрической энергии сети,
поступающей к конденсатору. Накопленная
в конденсаторе за первую четверть
периода энергия электрического поля
равна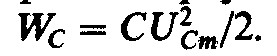 В
течение второй четверти периода
напряжение на конденсаторе убывает,
ток и мощность отрицательны — происходит
разрядка конденсатора и энергия
электрического поля отдается в сеть.
Следовательно, в цепи с идеальным
конденсатором происходит непрерывный
периодический процесс обмена энергией
между конденсатором и сетью, причем
процесс идет без потерь энергии.
В
течение второй четверти периода
напряжение на конденсаторе убывает,
ток и мощность отрицательны — происходит
разрядка конденсатора и энергия
электрического поля отдается в сеть.
Следовательно, в цепи с идеальным
конденсатором происходит непрерывный
периодический процесс обмена энергией
между конденсатором и сетью, причем
процесс идет без потерь энергии.
Амплитуду колебания мощности в цепи с емкостью называют реактивной емкостной мощностью:
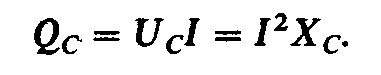 (2.49)
(2.49)
Реактивную емкостную мощность выражают в вольт-амперах реактивных (ВАр).
Запишем для участка
цепи с идеальным конденсатором закон
Ома в комплексной форме, для чего вначале
представим напряжение и ток в комплексной
форме:
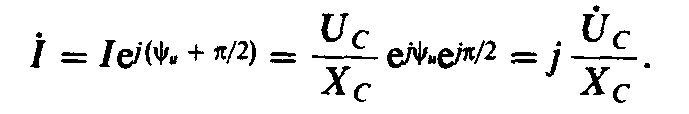
Закон Ома для цепи с идеальным конденсатором имеет вид
 (2.50)
(2.50)
где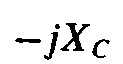 —
комплекс емкостного сопротивления.
—
комплекс емкостного сопротивления.
На рис. 2.12, г
построены векторы действующих значений
напряжения и тока на идеальном
конденсаторе, когда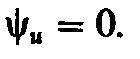
Емкость в цепи синусоидального тока
Емкостный элемент — это идеализированный схемный элемент, позволяющий учесть протекание токов смещения и явление накопления энергии в электрическом поле реальных элементов электрической цепи. Его характеризует зависимость заряда q от напряжения U (кулон-вольтная характеристика) или емкость C=q/U Графическое изображение емкостного элемента такое же, что и изображение конденсатора — рис. 3.7, а. Положительные направления отсчета U и i совпадают. Если приложенное к конденсатору напряжение U не изменяется во времени, то заряд q=CU на одной его обкладке и заряд —q на другой (С — емкость конденсатора) неизменны, и ток через конденсатор не проходит (i=dq/dt=0) Если же напряжение на конденсаторе изменяется во времени, например по синусоидальному закону (рис. 3.7, а):
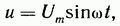
то
по синусоидальному закону будет меняться
и заряд q конденсатора: q=CU=C т.
е. конденсатор будет периодически
перезаряжаться. Периодическая перезарядка
конденсатора сопровождается протеканием
через него зарядного тока:
т.
е. конденсатор будет периодически
перезаряжаться. Периодическая перезарядка
конденсатора сопровождается протеканием
через него зарядного тока:
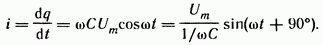 (3.19а)
(3.19а)
Из сопоставления (3.19) и (3.19а) видно, что ток через конденсатор опережает по фазе напряжение на конденсаторе на 90°. Поэтому на векторной диаграмме (рис. 3.7, б) вектор Im опережает вектор напряжения Um на 90°. Амплитуда тока Im равна амплитуде напряженияUm деленной на емкостное сопротивление:
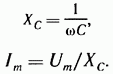
Емкостное сопротивление обратно пропорционально частоте. Единица емкостного сопротивления — Ом. Графики мгновенных значений u,i,p изображены на рис. 3.7, в. Мгновенная мощность
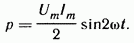
За первую четверть периода конденсатор потребляет от источника питания энергию, которая идет на создание электрического поля в нем.
Во вторую четверть периода напряжение на конденсаторе уменьшается от максимума до нуля, и запасенная в электрическом поле энергия отдается источнику (мгновенная мощность отрицательна). За третью четверть периода энергия снова запасается, за четвертую отдается и т. д.
Если проинтегрировать по времени обе части равенства
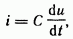
то получим
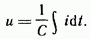 (3.24)
(3.24)
Равенство (3.24) позволяет определить напряжение на конденсаторе через ток по конденсатору. Ток через реальный конденсатор, пластины которого разделены твердым или жидким диэлектриком, в котором имеются тепловые потери, обусловленные вязким трением дипольных молекул и другими причинами, в радчете. можно учесть по схеме (рис. 3.7, г). Результирующий ток I=I1+I2
Ток I1 опережает U на 90°, а ток I2 совпадает с U по фазе (рис. 3.7, (9). Угол б называют углом потерь; tgб=1/Qc где Qc — добротность конденсатора, tgб зависит от типа диэлектрика и от частоты и изменяется от нескольких секунд до нескольких градусов.
Емкость в цепи синусоидального тока
Емкостный элемент — это идеализированный схемный элемент, позволяющий учесть протекание токов смещения и явление накопления энергии в электрическом поле реальных элементов электрической цепи. Его характеризует зависимость заряда q от напряжения U (кулон-вольтная характеристика) или емкость C=q/U Графическое изображение емкостного элемента такое же, что и изображение конденсатора — рис. 3.7, а. Положительные направления отсчета U и i совпадают. Если приложенное к конденсатору напряжение U не изменяется во времени, то заряд q=CU на одной его обкладке и заряд —q на другой (С — емкость конденсатора) неизменны, и ток через конденсатор не проходит (i=dq/dt=0) Если же напряжение на конденсаторе изменяется во времени, например по синусоидальному закону (рис. 3.7, а):
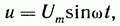
то
по синусоидальному закону будет меняться
и заряд q конденсатора: q=CU=C т.
е. конденсатор будет периодически
перезаряжаться. Периодическая перезарядка
конденсатора сопровождается протеканием
через него зарядного тока:
т.
е. конденсатор будет периодически
перезаряжаться. Периодическая перезарядка
конденсатора сопровождается протеканием
через него зарядного тока:
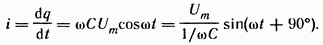 (3.19а)
(3.19а)
Из сопоставления (3.19) и (3.19а) видно, что ток через конденсатор опережает по фазе напряжение на конденсаторе на 90°. Поэтому на векторной диаграмме (рис. 3.7, б) вектор Im опережает вектор напряжения Um на 90°. Амплитуда тока Im равна амплитуде напряженияUm деленной на емкостное сопротивление:

Емкостное сопротивление обратно пропорционально частоте. Единица емкостного сопротивления — Ом. Графики мгновенных значений u,i,p изображены на рис. 3.7, в. Мгновенная мощность
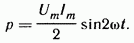
За первую четверть периода конденсатор потребляет от источника питания энергию, которая идет на создание электрического поля в нем.
Во вторую четверть периода напряжение на конденсаторе уменьшается от максимума до нуля, и запасенная в электрическом поле энергия отдается источнику (мгновенная мощность отрицательна). За третью четверть периода энергия снова запасается, за четвертую отдается и т. д.
Если проинтегрировать по времени обе части равенства

то получим
 (3.24)
(3.24)
Равенство (3.24) позволяет определить напряжение на конденсаторе через ток по конденсатору. Ток через реальный конденсатор, пластины которого разделены твердым или жидким диэлектриком, в котором имеются тепловые потери, обусловленные вязким трением дипольных молекул и другими причинами, в радчете. можно учесть по схеме (рис. 3.7, г). Результирующий ток I=I1+I2
Ток I1 опережает U на 90°, а ток I2 совпадает с U по фазе (рис. 3.7, (9). Угол б называют углом потерь; tgб=1/Qc где Qc — добротность конденсатора, tgб зависит от типа диэлектрика и от частоты и изменяется от нескольких секунд до нескольких градусов.

