Введение в алгоритм A* / Habr

При разработке игр нам часто нужно находить пути из одной точки в другую. Мы не просто стремимся найти кратчайшее расстояние, нам также нужно учесть и длительность движения. Передвигайте звёздочку (начальную точку) и крестик (конечную точку), чтобы увидеть кратчайший путь. [Прим. пер.: в статьях этого автора всегда много интерактивных вставок, рекомендую сходить в оригинал статьи.]
Для поиска этого пути можно использовать алгоритм поиска по графу, который применим, если карта представляет собой граф. A* часто используется в качестве алгоритма поиска по графу. Поиск в ширину — это простейший из алгоритмов поиска по графу, поэтому давайте начнём с него и постепенно перейдём к A*.

Представление карты

Первое, что нужно при изучении алгоритма — понять данные. Что подаётся на вход? Что мы получаем на выходе?

Вход: алгоритмы поиска по графу, в том числе и A*, получают в качестве входных данных граф. Граф — это набор точек («узлов») и соединений («рёбер») между ними. Вот граф, который я передал A*:

A* не видит ничего другого. Он видит только граф. Он не знает, находится ли что-то в помещении или за его пределами, дверь это или комната, насколько велика область. Он видит только граф! Он не понимает никакой разницы между картой сверху и вот этой:

Выход: определяемый A* путь состоит из узлов и рёбер. Рёбра — это абстрактное математическое понятие. A* сообщает нам, что нужно перемещаться из одной точки в другую, но не сообщает, как это нужно делать. Помните, что он ничего не знает о комнатах или дверях, он видит только граф. Вы сами должны решить, чем будет являться ребро графа, возвращённое A* — перемещением с тайла на тайл, движением по прямой линии, открытием двери, бегом по кривому пути.

Компромиссы: для каждой игровой карты есть множество разных способов передачи графа поиска пути алгоритму A*. Карта на рисунке выше превращает двери в узлы.

А что, если мы превратим двери в рёбра?

А если мы применим сетку для поиска пути?

Граф поиска пути не обязательно должен быть тем же, что используется в вашей игровой карте. В карте на основе сеток можно использовать граф поиска пути без сеток, и наоборот. A* выполняется быстрее с наименьшим количеством узлов графа. С сетками часто проще работать, но в них получается множество узлов. В этой статье рассматривается сам алгоритм A*, а не дизайн графов. Подробнее о графах можно прочитать на моей другой странице. Для объяснений я в дальнейшем

буду использовать сетки, потому что так проще визуализировать концепции.

Алгоритмы

Существует множество алгоритмов, работающих с графами. Я рассмотрю следующие:

Поиск в ширину выполняет исследование равномерно во всех направлениях. Это невероятно полезный алгоритм, не только для обычного поиска пути, но и для процедурной генерации карт, поиска путей течения, карт расстояний и других типов анализа карт.

Алгоритм Дейкстры (также называемый поиском с равномерной стоимостью) позволяет нам задавать приоритеты исследования путей. Вместо равномерного исследования всех возможных путей он отдаёт предпочтение путям с низкой стоимостью. Мы можем задать уменьшенные затраты, чтобы алгоритм двигался по дорогам, повышенную стоимость, чтобы избегать лесов и врагов, и многое другое. Когда стоимость движения может быть разной, мы используем его вместо поиска в ширину.

A* — это модификация алгоритма Дейкстры, оптимизированная для единственной конечной точки. Алгоритм Дейкстры может находить пути ко всем точкам, A* находит путь к одной точке. Он отдаёт приоритет путям, которые ведут ближе к цели.

Я начну с самого простого — поиска в ширину, и буду добавлять функции, постепенно превращая его в A*.

Поиск в ширину

Ключевая идея всех этих алгоритмов заключается в том, что мы отслеживаем состояние расширяющегося кольца, которое называется границей. В сетке этот процесс иногда называется заливкой (flood fill), но та же техника применима и для карт без сеток. Посмотрите анимацию расширения границы:

Как это реализовать? Повторяем эти шаги, пока граница не окажется пустой:

1. Выбираем и удаляем точку из границы.
2. Помечаем точку как посещённую, чтобы знать, что не нужно обрабатывать её повторно.
3. Расширяем границу, глядя на её соседей. Всех соседей, которых мы ещё не видели, добавляем к границе.

Давайте рассмотрим это подробнее. Тайлы нумеруются в порядке их посещения:

Алгоритм описывается всего в десяти строках кода на Python:

frontier = Queue()
frontier.put(start )
visited = {}
visited[start] = True

while not frontier.empty():
   current = frontier.get()
   for next in graph.neighbors(current):
      if next not in visited:
         frontier.put(next)
         visited[next] = True

В этом цикле заключается вся сущность алгоритмов поиска по графу этой статьи, в том числе и A*. Но как нам найти кратчайший путь? Цикл на самом деле не создаёт путей, он просто говорит нам, как посетить все точки на карте. Так получилось потому, что поиск в ширину можно использовать для гораздо большего, чем просто поиск путей. В этой статье я показываю, как он применяется в играх tower defense, но его также можно использовать в картах расстояний, в процедурной генерации карт и многом другом. Однако здесь мы хотим использовать его для поиска путей, поэтому давайте изменим цикл так, чтобы отслеживать,

откуда мы пришли для каждой посещённой точки, и переименуем visited в came_from:

frontier = Queue()
frontier.put(start )
came_from = {}
came_from[start] = None

while not frontier.empty():
   current = frontier.get()
   for next in graph.neighbors(current):
      if next not in came_from:
         frontier.put(next)
         came_from[next] = current 

Теперь came_from для каждой точки указывает на место, из которого мы пришли. Это похоже на «хлебные крошки» из сказки. Нам этого достаточно для воссоздания целого пути. Посмотрите, как стрелки показывают обратный путь к начальной позиции.

Код воссоздания путей прост: следуем по стрелкам обратно от цели к началу. Путь — это последовательность рёбер, но иногда проще хранить только узлы:

current = goal 
path = [current]
while current != start: 
   current = came_from[current]
   path.append(current)
path.append(start) # optional
path.reverse() # optional 

Таков простейший алгоритм поиска путей. Он работает не только в сетках, как показано выше, но и в любой структуре графов. В подземелье точки графа могут быть комнатами, а рёбра — дверями между ними. В платформере узлы графа могут быть локациями, а рёбра — возможными действиями: переместиться влево, вправо, подпрыгнуть, спрыгнуть вниз. В целом можно воспринимать граф как состояния и действия, изменяющие состояние. Подробнее о представлении карт я написал здесь. В оставшейся части статьи я продолжу использовать примеры с сетками, и расскажу о том, для чего можно применять разновидности поиска в ширину.

Ранний выход

Мы нашли пути из одной точки во все другие точки. Часто нам не нужны все пути, нам просто нужен путь между двумя точками. Мы можем прекратить расширять границу, как только найдём нашу цель. Посмотрите, как граница перестаёт расширятся после нахождения цели.

Код достаточно прямолинеен:

frontier = Queue()
frontier.put(start )
came_from = {}
came_from[start] = None

while not frontier.empty():
   current = frontier.get()

   if current == goal: 
      break           

   for next in graph.neighbors(current):
      if next not in came_from:
         frontier.put(next)
         came_from[next] = current

Стоимость перемещения

Пока мы делали шаги с одинаковой стоимостью. В некоторых случаях поиска путей у разных типов движения есть разная стоимость. Например, в Civilization движение через равнины или пустыню может стоить 1 очко движения, а движение через лес — 5 очков движения. На карте в самом начале статьи прохождение через воду стоит в 10 раз дороже, чем движение по траве. Ещё одним примером является диагональное движение в сетке, которое стоит больше, чем движение по осям. Нам нужно, чтобы поиск пути учитывал эту стоимость. Давайте сравним количество шагов от начала с расстоянием от начала:

Для этого нам нужен алгоритм Дейкстры (также называемый поиском с равномерной стоимостью). Чем он отличается от поиска в ширину? Нам нужно отслеживать стоимость движения, поэтому добавим новую переменную

cost_so_far, чтобы следить за общей стоимостью движения с начальной точки. При оценке точек нам нужно учитывать стоимость передвижения. Давайте превратим нашу очередь в очередь с приоритетами. Менее очевидно то, что у нас может получиться так, что одна точка посещается несколько раз с разной стоимостью, поэтому нужно немного поменять логику. Вместо добавления точки к границе в случае, когда точку ни разу не посещали, мы добавляем её, если новый путь к точке лучше, чем наилучший предыдущий путь.

frontier = PriorityQueue()
frontier.put(start, 0)
came_from = {}
cost_so_far = {}
came_from[start] = None
cost_so_far[start] = 0

while not frontier.empty():
   current = frontier.get()

   if current == goal:
      break
   
   for next in graph.neighbors(current):
      new_cost = cost_so_far[current] + graph.cost(current, next)
      if next not in cost_so_far or new_cost < cost_so_far[next]:
         cost_so_far[next] = new_cost
         priority = new_cost
         frontier.put(next, priority)
         came_from[next] = current 

Использование очереди с приоритетами вместо обычной очереди изменяет способ расширения границы. Контурные линии позволяют это увидеть. Посмотрите видео, чтобы понаблюдать, как граница расширяется медленнее через леса, и поиск кратчайшего пути выполняется вокруг центрального леса, а не сквозь него:

Стоимость движения, отличающаяся от 1, позволяет нам исследовать более интересные графы, а не только сетки. На карте в начале статьи стоимость движения основана на расстоянии между комнатами. Стоимость движения можно также использовать, чтобы избегать или предпочитать области на основании близости врагов или союзников. Интересная деталь реализации: обычная очередь с приоритетами поддерживает операции вставки и удаления, но в некоторых версиях алгоритма Дейкстры используется и третья операция, изменяющая приоритет элемента, уже находящегося в очереди с приоритетами. Я не использую эту операцию, и объясняю это на странице реализации алгоритма.

Эвристический поиск

В поиске в ширину и алгоритме Дейкстры граница расширяется во всех направлениях. Это логичный выбор, если вы ищете путь ко всем точкам или ко множеству точек. Однако обычно поиск выполняется только для одной точки. Давайте сделаем так, чтобы граница расширялась к цели больше, чем в других направлениях. Во-первых, определим эвристическую функцию, сообщающую нам, насколько мы близки к цели:

def heuristic(a, b):
   # Manhattan distance on a square grid
   return abs(a.x - b.x) + abs(a.y - b.y)

В алгоритме Дейкстры для порядка очереди с приоритетами мы использовали расстояние от начала. В жадном поиске по первому наилучшему совпадению для порядка очереди с приоритетами мы вместо этого используем оцененное расстояние до цели. Точка, ближайшая к цели, будет исследована первой. В коде используется очередь с приоритетами из поиска в ширину, но не применяется cost_so_far из алгоритма Дейкстры:

frontier = PriorityQueue()
frontier.put(start, 0)
came_from = {}
came_from[start] = None

while not frontier.empty():
   current = frontier.get()

   if current == goal:
      break
   
   for next in graph.neighbors(current):
      if next not in came_from:
         priority = heuristic(goal, next)
         frontier.put(next, priority)
         came_from[next] = current

Давайте посмотрим, как это работает:

Ого! Потрясающе, правда? Но что случится на более сложной карте?

Эти пути не являются кратчайшими. Итак, этот алгоритм работает быстрее, когда препятствий не очень много, но пути не слишком оптимальны. Можно ли это исправить? Конечно.

Алгоритм A*

Алгоритм Дейкстры хорош в поиске кратчайшего пути, но он тратит время на исследование всех направлений, даже бесперспективных. Жадный поиск исследует перспективные направления, но может не найти кратчайший путь. Алгоритм A* использует и подлинное расстояние от начала, и оцененное расстояние до цели.

Код очень похож на алгоритм Дейкстры:

frontier = PriorityQueue()
frontier.put(start, 0)
came_from = {}
cost_so_far = {}
came_from[start] = None
cost_so_far[start] = 0

while not frontier.empty():
   current = frontier.get()

   if current == goal:
      break
   
   for next in graph.neighbors(current):
      new_cost = cost_so_far[current] + graph.cost(current, next)
      if next not in cost_so_far or new_cost < cost_so_far[next]:
         cost_so_far[next] = new_cost
         priority = new_cost + heuristic(goal, next)
         frontier.put(next, priority)
         came_from[next] = current

Сравните алгоритмы: алгоритм Дейкстры вычисляет расстояние от начальной точки. Жадный поиск по первому наилучшему совпадению оценивает расстояние до точки цели. A* использует сумму этих двух расстояний.

Попробуйте в оригинале статьи делать отверстия в разных местах стены. Вы обнаружите, что жадный поиск находит правильный ответ, A* тоже его находит, исследуя ту же область. Когда жадный поиск по первому наилучшему находит неверный ответ (более длинный путь), A* находит правильный, как и алгоритм Дейкстры, но всё равно исследует меньше, чем алгоритм Дейкстры.

A* берёт лучшее от двух алгоритмов. Поскольку эвристика не оценивает расстояния повторно, A* не использует эвристику для поиска подходящего ответа. Он находит оптимальный путь, как и алгоритм Дейкстры. A* использует эвристику для изменения порядка узлов, чтобы повысить вероятность более раннего нахождения узла цели.

И… на этом всё! В этом и заключается алгоритм A*.

Дополнительное чтение

Вы готовы реализовать его? Попробуйте использовать готовую библиотеку. Если вы хотите реализовать его самостоятельно, то у меня есть инструкция по пошаговой реализации графов, очередей и алгоритмов поиска пути на Python, C++ и C#.

Какой алгоритм стоит использовать для поиска путей на игровой карте?

• Если вам нужно найти пути из или ко всем точкам, используйте поиск в ширину или алгоритм Дейкстры. Используйте поиск в ширину, если стоимость движения одинакова. Используйте алгоритм Дейкстры, если стоимость движения изменяется.
• Если нужно найти пути к одной точке, используйте жадный поиск по наилучшему первому или A*. В большинстве случаев стоит отдать предпочтение A*. Когда есть искушение использовать жадный поиск, то подумайте над применением A* с «недопустимой» эвристикой.

А что насчёт оптимальных путей? Поиск в ширину и алгоритм Дейкстры гарантированно найдут кратчайший путь по графу. Жадный поиск не обязательно его найдёт. A* гарантированно найдёт кратчайший путь, если эвристика никогда не больше истинного расстояния. Когда эвристика становится меньше, A* превращается в алгоритм Дейкстры. Когда эвристика становится больше, A* превращается в жадный поиск по наилучшему первому совпадению.

А как насчёт производительности? Лучше всего устранить ненужные точки графа. Если вы используете сетку, то прочитайте это. Уменьшение размера графа помогает всем алгоритмам поиска по графам. После этого используйте простейший из возможных алгоритмов. Простые очереди выполняются быстрее. Жадный поиск обычно выполняется быстрее, чем алгоритм Дейкстры, но не обеспечивает оптимальных путей. Для большинства задач по поиску путей оптимальным выбором является A*.

А что насчёт использования не на картах? Я использовал в статье карты, потому что думаю, что на них проще объяснить работу алгоритма. Однако эти алгоритмы поиска по графам можно использовать на любых графах, не только на игровых картах, и я пытался представить код алгоритма в виде, не зависящем от двухмерных сеток. Стоимость движения на картах превращается в произвольные веса рёбер графа. Эвристики перенести на произвольные карты не так просто, необходимо создавать эвристику для каждого типа графа. Для плоских карт хорошим выбором будут расстояния, поэтому здесь мы использовали их.

Я написал ещё много всего о поиске путей здесь. Не забывайте, что поиск по графам — это только одна часть того, что вам нужно. Сам по себе A* не обрабатывает такие аспекты, как совместное движение, перемещение препятствий, изменение карты, оценку опасных областей, формации, радиусы поворота, размеры объектов, анимацию, сглаживание путей и многое другое.

Простое объяснение алгоритмов поиска пути и A* / Habr

Часть 1. Общий алгоритм поиска

Введение

Поиск пути — это одна из тех тем, которые обычно представляют самые большие сложности для разработчиков игр. Особенно плохо люди понимают алгоритм A*, и многим кажется, что это какая-то непостижимая магия.

Цель данной статьи — объяснить поиск пути в целом и A* в частности очень понятным и доступным образом, положив таким образом конец распространённому заблуждению о том, что эта тема сложна. При правильном объяснении всё достаточно просто.

Учтите, что в статье мы будем рассматривать поиск пути для игр; в отличие от более академических статей, мы опустим такие алгоритмы поиска, как поиск в глубину (Depth-First) или поиск в ширину (Breadth-First). Вместо этого мы постараемся как можно быстрее дойти от нуля до A*.

В первой части мы объясним простейшие концепции поиска пути. Разобравшись с этими базовыми концепциями, вы поймёте, что A* на удивление очевиден.

Простая схема

Хотя вы сможете применять эти концепции и к произвольным сложным 3D-средам, давайте всё-таки начнём с чрезвычайно простой схемы: квадратной сетки размером 5 x 5. Для удобства я пометил каждую ячейку заглавной буквой.
Простая сетка.

Самое первое, что мы сделаем — это представим эту среду в виде графа. Я не буду подробно объяснять, что такое граф; если говорить просто, то это набор кружков, соединённых стрелками. Кружки называются «узлами», а стрелки — «рёбрами».

Каждый узел представляет собой «состояние», в котором может находиться персонаж. В нашем случае состояние персонажа — это его позиция, поэтому мы создаём по одному узлу для каждой ячейки сетки:

Узлы, обозначающие ячейки сетки.

Теперь добавим рёбра. Они обозначают состояния, которых можно «достичь» из каждого заданного состояния; в нашем случае мы можем пройти из любой ячейки в соседнюю, за исключением заблокированных:

Дуги обозначают допустимые перемещения между ячейками сетки.

Если мы можем добраться из A в B, то говорим, что B является «соседним» с A узлом.

Стоит заметить, что рёбра имеют направление; нам нужны рёбра и из A в B, и из B в A. Это может показаться излишним, но не тогда, когда могут возникать более сложные «состояния». Например, персонаж может упасть с крыши на пол, но не способен допрыгнуть с пола на крышу. Можно перейти из состояния «жив» в состояние «мёртв», но не наоборот. И так далее.

Пример

Допустим, мы хотим переместиться из A в T. Мы начинаем с A. Можно сделать ровно два действия: пройти в B или пройти в F.

Допустим, мы переместились в B. Теперь мы можем сделать два действия: вернуться в A или перейти в C. Мы помним, что уже были в A и рассматривали варианты выбора там, так что нет смысла делать это снова (иначе мы можем потратить весь день на перемещения A → B → A → B…). Поэтому мы пойдём в C.

Находясь в C, двигаться нам некуда. Возвращаться в B бессмысленно, то есть это тупик. Выбор перехода в B, когда мы находились в A, был плохой идеей; возможно, стоит попробовать вместо него F?

Мы просто продолжаем повторять этот процесс, пока не окажемся в T. В этот момент мы просто воссоздадим путь из A, вернувшись по своим шагам. Мы находимся в T; как мы туда добрались? Из O? То есть конец пути имеет вид O → T. Как мы добрались в O? И так далее.

Учтите, что на самом деле мы не движемся; всё это было лишь мысленным процессом. Мы продолжаем стоять в A, и не сдвинемся из неё, пока не найдём путь целиком. Когда я говорю «переместились в B», то имею в виду «представьте, что мы переместились в B».

Общий алгоритм

Этот раздел — самая важная часть всей статьи. Вам абсолютно необходимо понять его, чтобы уметь реализовывать поиск пути; остальное (в том числе и A*) — это просто детали. В этом разделе вы будете разбираться, пока не поймёте смысл.

К тому же этот раздел невероятно прост.

Давайте попробуем формализовать наш пример, превратив его в псевдокод.

Нам нужно отслеживать узлы, которых мы знаем как достичь из начального узла. В начале это только начальный узел, но в процессе «исследования» сетки мы будем узнавать, как добираться до других узлов. Давайте назовём этот список узлов reachable:

reachable = [start_node]

Также нам нужно отслеживать уже рассмотренные узлы, чтобы не рассматривать их снова. Назовём их explored:

explored = []

Дальше я изложу ядро алгоритма: на каждом шаге поиска мы выбираем один из узлов, который мы знаем, как достичь, и смотрим, до каких новых узлов можем добраться из него. Если мы определим, как достичь конечного (целевого) узла, то задача решена! В противном случае мы продолжаем поиск.

Так просто, что даже разочаровывает? И это верно. Но из этого и состоит весь алгоритм. Давайте запишем его пошагово псевдокодом.

Мы продолжаем искать, пока или не доберёмся до конечного узла (в этом случае мы нашли путь из начального в конечный узел), или пока у нас не закончатся узлы, в которых можно выполнять поиск (в таком случае между начальным и конечным узлами пути нет).

while reachable is not empty:

Мы выбираем один из узлов, до которого знаем, как добраться, и который пока не исследован:

    node = choose_node(reachable)

Если мы только что узнали, как добраться до конечного узла, то задача выполнена! Нам просто нужно построить путь, следуя по ссылкам previous обратно к начальному узлу:

    if node == goal_node:
       path = []
       while node != None:
            path.add(node)
            node = node.previous
        
        return path

Нет смысла рассматривать узел больше одного раза, поэтому мы будем это отслеживать:

    reachable.remove(node)
    explored.add(node)

Мы определяем узлы, до которых не можем добраться отсюда. Начинаем со списка узлов, соседних с текущим, и удаляем те, которые мы уже исследовали:

    new_reachable = get_adjacent_nodes(node) - explored

Мы берём каждый из них:

    for adjacent in new_reachable:

Если мы уже знаем, как достичь узла, то игнорируем его. В противном случае добавляем его в список reachable, отслеживая, как в него попали:

        if adjacent not in reachable:
            adjacent.previous = node  # Remember how we got there.
            reachable.add(adjacent)

Нахождение конечного узла — это один из способов выхода из цикла. Второй — это когда reachable становится пустым: у нас закончились узлы, которые можно исследовать, и мы не достигли конечного узла, то есть из начального в конечный узел пути нет:

return None

И… на этом всё. Это весь алгоритм, а код построения пути выделен в отдельный метод:

function find_path (start_node, end_node):
    reachable = [start_node]
    explored = []

    while reachable is not empty:
        # Choose some node we know how to reach.
        node = choose_node(reachable)

        # If we just got to the goal node, build and return the path.
        if node == goal_node:
            return build_path(goal_node)

        # Don't repeat ourselves.
        reachable.remove(node)
        explored.add(node)

        # Where can we get from here?
        new_reachable = get_adjacent_nodes(node) - explored
        for adjacent in new_reachable:
            if adjacent not in reachable
                adjacent.previous = node  # Remember how we got there.
                reachable.add(adjacent)

    # If we get here, no path was found :(
    return None

Вот функция, которая строит путь, следуя по ссылкам previous обратно к начальному узлу:

function build_path (to_node):
    path = []
    while to_node != None:
        path.add(to_node)
        to_node = to_node.previous
    return path

Вот и всё. Это псевдокод каждого алгоритма поиска пути, в том числе и A*.

Перечитывайте этот раздел, пока не поймёте, как всё работает, и, что более важно, почему всё работает. Идеально будет нарисовать пример вручную на бумаге, но можете и посмотреть интерактивное демо:

Интерактивное демо

Вот демо и пример реализации показанного выше алгоритма (запустить его можно на странице оригинала статьи). choose_node просто выбирает случайный узел. Можете запустить алгоритм пошагово и посмотреть на список узлов reachable и explored, а также на то, куда указывают ссылки previous.
Заметьте, что поиск завершается, как только обнаруживается путь; может случиться так, что некоторые узлы даже не будут рассмотрены.

Заключение

Представленный здесь алгоритм — это общий алгоритм для любого алгоритма поиска пути.

Но что же отличает каждый алгоритм от другого, почему A* — это A*?

Вот подсказка: если запустить поиск в демо несколько раз, то вы увидите, что алгоритм на самом деле не всегда находит один и тот же путь. Он находит какой-то путь, и этот путь необязательно является кратчайшим. Почему?

Часть 2. Стратегии поиска

Если вы не полностью поняли описанный в предыдущем разделе алгоритм, то вернитесь к нему и прочтите заново, потому что он необходим для понимания дальнейшей информации. Когда вы в нём разберётесь, A* покажется вам совершенно естественным и логичным.

Секретный ингредиент

В конце предыдущей части я оставил открытыми два вопроса: если каждый алгоритм поиска использует один и тот же код, почему A* ведёт себя как A*? И почему демо иногда находит разные пути?

Ответы на оба вопроса связаны друг с другом. Хоть алгоритм и хорошо задан, я оставил нераскрытым один аспект, и как оказывается, он является ключевым для объяснения поведения алгоритмов поиска:

node = choose_node(reachable)

Именно эта невинно выглядящая строка отличает все алгоритмы поиска друг от друга. От способа реализации choose_node зависит всё.

Так почему же демо находит разные пути? Потому что его метод choose_node выбирает узел случайным образом.

Длина имеет значение

Прежде чем погружаться в различия поведений функции choose_node, нам нужно исправить в описанном выше алгоритме небольшой недосмотр.

Когда мы рассматривали узлы, соседние с текущим, то игнорировали те, которые уже знаем, как достичь:

if adjacent not in reachable:
    adjacent.previous = node  # Remember how we got there.
    reachable.add(adjacent)

Это ошибка: что если мы только что обнаружили лучший способ добраться до него? В таком случае необходимо изменить ссылку previous узла, чтобы отразить этот более короткий путь.

Чтобы это сделать, нам нужно знать длину пути от начального узла до любого достижимого узла. Мы назовём это стоимостью (cost) пути. Пока примем, что перемещение из узла в один из соседних узлов имеет постоянную стоимость, равную 1.

Прежде чем начинать поиск, мы присвоим значению cost каждого узла значение infinity; благодаря этому любой путь будет короче этого. Также мы присвоим cost узла start_node значение 0.

Тогда вот как будет выглядеть код:

if adjacent not in reachable:
    reachable.add(adjacent)

# If this is a new path, or a shorter path than what we have, keep it.
if node.cost + 1 < adjacent.cost:
    adjacent.previous = node
    adjacent.cost = node.cost + 1

Одинаковая стоимость поиска

Давайте теперь рассмотрим метод choose_node. Если мы стремимся найти кратчайший возможный путь, то выбирать узел случайным образом — не самая лучшая идея.

Лучше выбирать узел, которого мы можем достичь из начального узла по кратчайшему пути; благодаря этому мы в общем случае будем предпочитать длинным путям более короткие. Это не значит, что более длинные пути не будут рассматриваться вовсе, это значит, что более короткие пути будут рассматриваться первыми. Так как алгоритм завершает работу сразу после нахождения подходящего пути, это должно позволить нам находить короткие пути.

Вот возможный пример функции choose_node:

function choose_node (reachable):
    best_node = None

    for node in reachable:
        if best_node == None or best_node.cost > node.cost:
            best_node = node
    
    return best_node

Интуитивно понятно, что поиск этого алгоритма расширяется «радиально» от начального узла, пока не достигнет конечного. Вот интерактивное демо такого поведения:

Заключение

Простое изменение в способе выбора рассматриваемого следующим узла позволило нам получить достаточно хороший алгоритм: он находит кратчайший путь от начального до конечного узла.

Но этот алгоритм всё равно в какой-то степени остаётся «глупым». Он продолжает искать повсюду, пока не наткнётся на конечный узел. Например, какой смысл в показанном выше примере выполнять поиск в направлении A, если очевидно, что мы отдаляемся от конечного узла?

Можно ли сделать choose_node умнее? Можем ли мы сделать так, чтобы он направлял поиск в сторону конечного узла, даже не зная заранее правильного пути?

Оказывается, что можем — в следующей части мы наконец-то дойдём до choose_node, позволяющей превратить общий алгоритм поиска пути в A*.

Часть 3. Снимаем завесу тайны с A*

Полученный в предыдущей части алгоритм достаточно хорош: он находит кратчайший путь от начального узла до конечного. Однако, он тратит силы впустую: рассматривает пути, которые человек очевидно назовёт ошибочными — они обычно удаляются от цели. Как же этого можно избежать?

Волшебный алгоритм

Представьте, что мы запускаем алгоритм поиска на особом компьютере с чипом, который может творить магию. Благодаря этому потрясающему чипу мы можем выразить choose_node очень простым способом, который гарантированно создаст кратчайший путь, не теряя времени на исследование частичных путей, которые никуда не ведут:

function choose_node (reachable):
    return magic(reachable, "любой узел, являющийся следующим на кратчайшем пути")

Звучит соблазнительно, но магическим чипам всё равно требуется какой-то низкоуровневый код. Вот какой может быть хорошая аппроксимация:

function choose_node (reachable):
    min_cost = infinity
    best_node = None

    for node in reachable:
        cost_start_to_node = node.cost
        cost_node_to_goal = magic(node, "кратчайший путь к цели")
        total_cost = cost_start_to_node + cost_node_to_goal

        if min_cost > total_cost:
            min_cost = total_cost
            best_node = node

    return best_node

Это отличный способ выбора следующего узла: вы выбираем узел, дающий нам кратчайший путь от начального до конечного узла, что нам и нужно.

Также мы минимизировали количество используемой магии: мы точно знаем, какова стоимость перемещения от начального узла к каждому узлу (это node.cost), и используем магию только для предсказания стоимости перемещения от узла к конечному узлу.

Не магический, но довольно потрясающий A*

К сожалению, магические чипы — это новинка, а нам нужна поддержка и устаревшего оборудования. БОльшая часть кода нас устраивает, за исключением этой строки:

# Throws MuggleProcessorException
cost_node_to_goal = magic(node, "кратчайший путь к цели")

То есть мы не можем использовать магию, чтобы узнать стоимость ещё не исследованного пути. Ну ладно, тогда давайте сделаем прогноз. Будем оптимистичными и предположим, что между текущим и конечным узлами нет ничего, и мы можем просто двигаться напрямик:

cost_node_to_goal = distance(node, goal_node)

Заметьте, что кратчайший путь и минимальное расстояние разные: минимальное расстояние подразумевает, что между текущим и конечным узлами нет совершенно никаких препятствий.

Эту оценку получить достаточно просто. В наших примерах с сетками это расстояние городских кварталов между двумя узлами (то есть abs(Ax - Bx) + abs(Ay - By)). Если бы мы могли двигаться по диагонали, то значение было бы равно sqrt( (Ax - Bx)^2 + (Ay - By)^2 ), и так далее. Самое важное то, что мы никогда не получаем слишком высокую оценку стоимости.

Итак, вот немагическая версия choose_node:

function choose_node (reachable):
    min_cost = infinity
    best_node = None

    for node in reachable:
        cost_start_to_node = node.cost
        cost_node_to_goal = estimate_distance(node, goal_node)
        total_cost = cost_start_to_node + cost_node_to_goal

        if min_cost > total_cost:
            min_cost = total_cost
            best_node = node

    return best_node

Функция, оценивающая расстояние от текущего до конечного узла, называется эвристикой, и этот алгоритм поиска, леди и джентльмены, называется … A*.

Интерактивное демо

Пока вы оправляетесь от шока, вызванного осознанием того, что загадочный A* на самом деле настолько прост, можете посмотреть на демо (или запустить его в оригинале статьи). Вы заметите, что в отличие от предыдущего примера, поиск тратит очень мало времени на движение в неверном направлении.

Заключение

Наконец-то мы дошли до алгоритма A*, который является не чем иным, как описанным в первой части статьи общим алгоритмом поиска с некоторыми усовершенствованиями, описанными во второй части, и использующим функцию choose_node, которая выбирает узел, который по нашей оценке приближает нас к конечному узлу. Вот и всё.

Вот вам для справки полный псевдокод основного метода:

function find_path (start_node, end_node):
    reachable = [start_node]
    explored = []

    while reachable is not empty:
        # Choose some node we know how to reach.
        node = choose_node(reachable)

        # If we just got to the goal node, build and return the path.
        if node == goal_node:
            return build_path(goal_node)

        # Don't repeat ourselves.
        reachable.remove(node)
        explored.add(node)

        # Where can we get from here that we haven't explored before?
        new_reachable = get_adjacent_nodes(node) - explored
        for adjacent in new_reachable:
            # First time we see this node?
            if adjacent not in reachable:
                reachable.add(adjacent)
        
            # If this is a new path, or a shorter path than what we have, keep it.
            if node.cost + 1 < adjacent.cost:
                adjacent.previous = node
                adjacent.cost = node.cost + 1

    # If we get here, no path was found :(
    return None

Метод build_path:

function build_path (to_node):
    path = []
    while to_node != None:
        path.add(to_node)
        to_node = to_node.previous
    return path

А вот метод choose_node, который превращает его в A*:

function choose_node (reachable):
    min_cost = infinity
    best_node = None

    for node in reachable:
        cost_start_to_node = node.cost
        cost_node_to_goal = estimate_distance(node, goal_node)
        total_cost = cost_start_to_node + cost_node_to_goal

        if min_cost > total_cost:
            min_cost = total_cost
            best_node = node

    return best_node

Вот и всё.

А зачем же нужна часть 4?

Теперь, когда вы поняли, как работает A*, я хочу рассказать о некоторых потрясающих областях его применения, которые далеко не ограничиваются поиском путей в сетке ячеек.

Часть 4. A* на практике

Первые три части статьи начинаются с самых основ алгоритмов поиска путей и заканчиваются чётким описанием алгоритма A*. Всё это здорово в теории, но понимание того, как это применимо на практике — совершенно другая тема.

Например, что будет, если наш мир не является сеткой?

Что если персонаж не может мгновенно поворачиваться на 90 градусов?

Как построить граф, если мир бесконечен?

Что если нас не волнует длина пути, но мы зависим от солнечной энергии и нам как можно больше нужно находиться под солнечным светом?

Как найти кратчайший путь к любому из двух конечных узлов?

Функция стоимости

В первых примерах мы искали кратчайший путь между начальным и конечным узлами. Однако вместо того, чтобы хранить частичные длины путей в переменной length, мы назвали её cost. Почему?

Мы можем заставить A* искать не только кратчайший, но и лучший путь, причём определение «лучшего» можно выбирать, исходя из наших целей. Когда нам нужен кратчайший путь, стоимостью является длина пути, но если мы хотим минимизировать, например, потребление топлива, то нужно использовать в качестве стоимости именно его. Если мы хотим по максимуму увеличить «время, проводимое под солнцем», то затраты — это время, проведённое без солнца. И так далее.

В общем случае это означает, что с каждым ребром графа связаны соответствующие затраты. В показанных выше примерах стоимость задавалась неявно и считалась всегда равной 1, потому что мы считали шаги на пути. Но мы можем изменить стоимость ребра в соответствии с тем, что мы хотим минимизировать.

Функция критерия

Допустим, наш объект — это автомобиль, и ему нужно добраться до заправки. Нас устроит любая заправка. Требуется кратчайший путь до ближайшей АЗС.

Наивный подход будет заключаться в вычислении кратчайшего пути до каждой заправки по очереди и выборе самого короткого. Это сработает, но будет довольно затратным процессом.

Что если бы мы могли заменить один goal_node на метод, который по заданному узлу может сообщить, является ли тот конечным или нет. Благодаря этому мы сможем искать несколько целей одновременно. Также нам нужно изменить эвристику, чтобы она возвращала минимальную оцениваемую стоимость всех возможных конечных узлов.

В зависимости от специфики ситуации мы можем и не иметь возможности достичь цели идеально, или это будет слишком много стоить (если мы отправляем персонажа через половину огромной карты, так ли важна разница в один дюйм?), поэтому метод is_goal_node может возвращать true, когда мы находимся «достаточно близко».

Полная определённость не обязательна

Представление мира в виде дискретной сетки может быть недостаточным для многих игр. Возьмём, например, шутер от первого лица или гоночную игру. Мир дискретен, но его нельзя представить в виде сетки.

Но есть проблема и посерьёзней: что если мир бесконечен? В таком случае, даже если мы сможем представить его в виде сетки, то у нас просто не будет возможности построить соответствующий сетке граф, потому что он должен быть бесконечным.

Однако не всё потеряно. Разумеется, для алгоритма поиска по графам нам определённо нужен граф. Но никто не говорил, что граф должен быть исчерпывающим!

Если внимательно посмотреть на алгоритм, то можно заметить, что мы ничего не делаем с графом, как целым; мы исследуем граф локально, получая узлы, которых можем достичь из рассматриваемого узла. Как видно из демо A*, некоторые узлы графа вообще не исследуются.

Так почему бы нам просто не строить граф в процессе исследования?

Мы делаем текущую позицию персонажа начальным узлом. При вызове get_adjacent_nodes она может определять возможные способы, которыми персонаж способен переместиться из данного узла, и создавать соседние узлы на лету.

За пределами трёх измерений

Даже если ваш мир действительно является 2D-сеткой, нужно учитывать и другие аспекты. Например, что если персонаж не может мгновенно поворачиваться на 90 или 180 градусов, как это обычно и бывает?

Состояние, представляемое каждым узлом поиска, не обязательно должно быть только позицией; напротив, оно может включать в себя произвольно сложное множество значений. Например, если повороты на 90 градусов занимают столько же времени, сколько переход из одной ячейки в другую, то состояние персонажа может задаваться как [position, heading]. Каждый узел может представлять не только позицию персонажа, но и направление его взгляда; и новые рёбра графа (явные или косвенные) отражают это.

Если вернуться к исходной сетке 5×5, то начальной позицией поиска теперь может быть [A, East]. Соседними узлами теперь являются [B, East] и [A, South] — если мы хотим достичь F, то сначала нужно скорректировать направление, чтобы путь обрёл вид [A, East], [A, South], [F, South].

Шутер от первого лица? Как минимум четыре измерения: [X, Y, Z, Heading]. Возможно, даже [X, Y, Z, Heading, Health, Ammo].

Учтите, что чем сложнее состояние, тем более сложной должна быть эвристическая функция. Сам по себе A* прост; искусство часто возникает благодаря хорошей эвристике.

Заключение

Цель этой статьи — раз и навсегда развеять миф о том, что A* — это некий мистический, не поддающийся расшифровке алгоритм. Напротив, я показал, что в нём нет ничего загадочного, и на самом деле его можно довольно просто вывести, начав с самого нуля.

Дальнейшее чтение

У Амита Патела есть превосходное «Введение в алгоритм A*» [перевод на Хабре] (и другие его статьи на разные темы тоже великолепны!).

Что такое алгоритм — Викиучебник

Исходная версия статьи (Ворожцов А. В., «Что такое алгоритм?») была опубликована в журнале «Потенциал»

Геометрия развивает геометрическое мышление, математика — абстрактное математическое, логика — логическое, физика — физическое… А какое мышление развивает информатика? Информатика есть наука, служащая информационным технологиям. Но фундаментальными достижениями этой науки оказались не сами технологии, а общие методы построения систем и решения сложных задач. Базисом этих методов являются алгоритмы и системный подход к решению задач. Поэтому информатика развивает алгоритмическое мышление и учит системному подходу к решению задач.

Сегодня мы познакомимся с понятиями алгоритма и исполнителя. Оказывается, не так-то просто понять, чем определяется сущность алгоритма.

Понятие алгоритма[править]

Понятие алгоритма — одно из основных в программировании и информатике^[1]. Это последовательность команд, предназначенная исполнителю, в результате выполнения которой он должен решить поставленную задачу. Алгоритм должен описываться на формальном языке, исключающем неоднозначность толкования. Исполнитель может быть человеком или машиной. Исполнитель должен уметь выполнять все команды, составляющие алгоритм. Множество возможных команд конечно и изначально строго задано. Действия, выполняемые по этим командам, называются элементарными.

Запись алгоритма на формальном языке называется программой. Иногда само понятие алгоритма отождествляется с его записью, так что слова «алгоритм» и «программа» — почти синонимы. Небольшое различие заключается в том, что под алгоритмом, как правило, понимают основную идею его построения. Программа же всегда связана с записью алгоритма на конкретном формальном языке.

Приведём для примера простой алгоритм действия пешехода, который позволит ему безопасно перейти улицу:

1. Подойти к дороге.
2. Дождаться зелёного сигнала светофора.
3. Перейти дорогу.
4. Если впереди есть ещё одна дорога, то перейти к шагу 1.

Алгоритмы обладают свойством детерминированности (определённости): каждый шаг и переход от шага к шагу должны быть точно определены так, чтобы его мог выполнить любой другой человек или механическое устройство.

Кроме детерминированности, алгоритмы также должны обладать свойством конечности и массовости:

Конечность

Алгоритм всегда должен заканчиваться за конечное число шагов, но это число не ограничено сверху.

Массовость

Алгоритм применяется к некоторому классу входных данных (чисел, пар чисел, набору букв и тому подобному). Не имеет смысла строить алгоритм нахождения наибольшего общего делителя только для одной пары чисел 10 и 15.

Поясним эти свойства на простом примере. Рассмотрим следующую формулу вычисления числа π{\displaystyle \pi }: π=4(1−13+15−17+…)=4∑i=0∞(−1)i2i+1{\displaystyle \pi =4\left(1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\dots \right)=4\sum _{i=0}^{\infty }{\frac {(-1)^{i}}{2i+1}}}.

Является ли эта формула алгоритмом вычисления числа π{\displaystyle \pi }? Ответ на этот вопрос — «нет», так как здесь нет ни свойства массовости (нет входных данных), ни свойства конечности (сумма бесконечного количества чисел)^[2].

Операция суммирования бесконечного ряда не является элементарной ни для современных компьютеров, ни для человека, а если разложить эту операцию на отдельные шаги сложения, то получим бесконечное число шагов. Алгоритмы же по определению должны выполняться за конечное число шагов и через конечное число шагов предоставлять результат вычислений.

Понятие элементарных объектов и элементарных действий[править]

Алгоритмы по определению должны сводиться к последовательности элементарных действий над элементарными объектами. Какие действия и объекты элементарны, а какие — нет, зависит от исполнителя (вычислительной машины). Набор элементарных действий и элементарных объектов для каждого исполнителя чётко зафиксирован. Элементарные действия оперируют с небольшим числом элементарных объектов. Все остальные объекты и действия являются совокупностью элементарных. В современных компьютерах рациональные числа и иррациональные числа не являются элементарными объектами^[3]. Элементарным объектом в современных компьютерах является бит — это ячейка памяти, в которую может быть записано число 0 или 1. С помощью набора бит можно записывать целые и действительные числа. В частности, существует простой способ представить целые числа от 0{\displaystyle 0} до 28−1=255{\displaystyle 2^{8}-1=255} в виде последовательности 8 бит:

0	→ 00000000
1	→ 00000001
2	→ 00000010
3	→ 00000011
4	→ 00000100
5	→ 00000101
…	→ …
250	→ 11111010
251	→ 11111011
252	→ 11111100
253	→ 11111101
254	→ 11111110
255	→ 11111111

Указанный способ представления натуральных чисел в виде последовательности нулей и единиц называется двоичной записью числа. Каждому биту в этом представлении соответствует степень двойки. Самому правому биту соответствует 1=20{\displaystyle 1=2^{0}}, второму справа — 2=21{\displaystyle 2=2^{1}}, третьему справа — 4=22{\displaystyle 4=2^{2}}, и так далее. Двоичная запись соответствует разложению числа в сумму неповторяющихся степеней двойки. Например:

Задача 1

Докажите, что каждое натуральное число единственным образом представляется в виде суммы неповторяющихся степеней двойки. Подсказка: для данного числа n{\displaystyle n} найдите максимальную степень двойки 2m{\displaystyle 2^{m}}, которая меньше n{\displaystyle n}. Рассмотрите число n′=n−2m{\displaystyle n’=n-2^{m}}. Воспользуйтесь методом математической индукции.

Конечный набор элементарных объектов может принимать лишь конечное число значений. Так, например, упорядоченный набор 8 бит (один байт) имеет 256 возможных значений. Из этого простого факта следует очень важное утверждение: среди команд исполнителя не может быть команд сложения или умножения произвольных натуральных (действительных) чисел.

При изучении языка программирования, вы встретитесь с таким явлением, как переполнение — ситуация, когда результат элементарной арифметической операции выходит за пределы подмножества чисел, которые можно записать в выбранном машинном представлении.

Итак, для компьютеров лишь некоторые действительные числа являются элементарными объектами^[4]Множество этих чисел конечно. Какие именно действительные числа элементарны, зависит от используемого машинного представления. Многие современные процессоры поддерживают несколько типов машинного представления действительных чисел. Целые числа практически везде представляются одинаковым образом. В процессорах с 32-битной архитектурой большая часть команд связана с числами, записанными в 32 битах. При представлении неотрицательных чисел в 32 бита помещается просто двоичная запись. Множество представимых таким образом чисел — это все неотрицательные числа меньше 232{\displaystyle 2^{32}}. Этому машинному представлению в языке Си соответствует тип данных unsigned int. Если мы попытаемся сложить с помощью команды процессора два числа типа unsigned int, сумма которых больше либо равна 232{\displaystyle 2^{32}}, то возникнет переполнение — старший 33-й бит результата будет утерян.

При представлении отрицательных чисел в виде 32 бит один бит необходимо выделить под знак — «плюс» или «минус». Неотрицательные числа, меньшие 231{\displaystyle 2^{31}}, записываются обычным образом в виде двоичной записи. Старший бит у них равен нулю. Отрицательное число −a{\displaystyle -a}, модуль a{\displaystyle a} которого меньше либо равен 231{\displaystyle 2^{31}}, записывается в 32 битах как двоичная запись числа 232−a{\displaystyle 2^{32}-a}. Старший бит для отрицательных чисел равен 1. Этому машинному представлению соответствует тип int. Представимые таким образом числа — это числа на отрезке [−231,231−1]{\displaystyle [-2^{31},\;2^{31}-1]}.

Подведём итоги:

У каждого исполнителя есть конечный набор элементарных команд (действий), оперирующих элементарными объектами, которых также конечное число.

Входом алгоритма является конечный набор элементарных объектов. Во время работы алгоритма выполняется конечное число элементарных действий и результат алгоритма также является конечным набором элементарных объектов.

В компьютерах элементарным объектом является бит. Есть несколько стандартных способов записи чисел (действительных, целых, и целых неотрицательных) в виде последовательности бит фиксированной длины.

Алгоритм входным данным сопоставляет выходные данные и этим он чем-то похож на обыкновенную функцию. Но главной особенностью алгоритма является то, что он содержит описание того, как это сделать. Функция может быть задана неявно, а алгоритм — нет. Алгоритм описывает, что нужно сделать с входными данными, чтобы получить результат. При этом предполагается, что инструкции алгоритма выполняет исполнитель с ограниченными способностями: собственная память исполнителя конечна, также конечен и чётко зафиксирован набор инструкций, которые он может исполнять. В большинстве классических исполнителей присутствует внешняя память, которая в принципе не ограничена. Например у человека под рукой есть сколь угодно много листов бумаги, уложенных в бесконечный ряд (ячеек памяти), которые он может использовать. Заметьте, что информация о том, что на каком листке записано в какой-то момент может не поместиться в конечную память исполнителя и эту информацию ему также нужно будет записывать на листах.

Способы записи алгоритмов[править]

Алгоритмы можно описывать человеческим языком — словами. Так и в математике — все теоремы и утверждения можно записывать без специальных обозначений. Но специальный формальный язык записи утверждений сильно облегчает жизнь математикам: исчезает неоднозначность, появляются краткость и ясность изложения. Всё это позволяет математикам говорить и писать на одном языке и лучше понимать друг друга.

Большинство используемых в программировании алгоритмических языков имеют общие черты. В то же время, не всегда целесообразно пользоваться каким-либо конкретным языком программирования и загромождать изложение несущественными деталями. Здесь мы будем использовать псевдокод, который похож на язык Pascal, но не является таким строгим.

Разницу между программой и алгоритмом можно пояснить следующим образом. Алгоритм — это метод, схема решения какой-то задачи. А программа — это конкретная реализация алгоритма, которая может быть скомпилирована и выполнена на компьютере. Алгоритм, в свою очередь, является реализацией идеи решения. Это можно проиллюстрировать следующей схемой:

Идея решения → Алгоритм → Программа

Стрелка означает переход к следующему этапу решения задачи с повышением уровня подробности описания метода решения.

Алгоритм Евклида[править]

Описание алгоритма:

1. Если a=b{\displaystyle a=b}, то НОД (наибольший общий делитель) =a=b{\displaystyle =a=b} и заканчиваем вычисления.
2. Если a>b{\displaystyle a>b}, то из a{\displaystyle a} вычитаем b{\displaystyle b} (a←a−b{\displaystyle a\gets a-b}). Переходим к 1.
3. Если же b>a{\displaystyle b>a}, то из b{\displaystyle b} вычитаем a{\displaystyle a} (b←b−a{\displaystyle b\gets b-a}). Переходим к 1.

Запишем этот алгоритм с помощью псевдокода.

Псевдокод 1. Алгоритм Евклида

 1 Function НОД(a, b)
 2   While a≠b{\displaystyle a\neq b}
 3     If a>b{\displaystyle a>b}
 4       a←a−b{\displaystyle a\gets a-b}
 5     Else
 6       b←b−a{\displaystyle b\gets b-a}
 7     End If
 8   End While
 9   Return a
10 End Function

Конструкция While(A) B End While псевдокода означает «повторять последовательность операций B, записанных в теле оператора While, пока выполнено условие A». Тело оператора While — это все инструкции между While(A) и End While. Если условие A не выполнено в самом начале, то тело оператора While не выполняется ни разу. Один шаг выполнения тела цикла называется итерацией цикла.

Конструкция If(A) B Else C End If» псевдокода означает «если верно A, то выполнить инструкции B, иначе выполнить инструкции C».

Инструкция return a означает «вернуть как результат вычислений объект a».

Покажем, что наш алгоритм нахождения НОДа чисел a{\displaystyle a} и b{\displaystyle b}.

Действительно, НОД(a,b)={\displaystyle (a,\;b)=\;}НОД(a−b,b){\displaystyle (a-b,\;b)} при a>b{\displaystyle a>b}, поэтому, несмотря на то, что на каждом шаге меняется одно из чисел, значение НОД(a,b){\displaystyle (a,\;b)} остаётся неизменным. Максимальное из чисел a{\displaystyle a} и b{\displaystyle b} с каждым шагом уменьшается, и в какой-то момент они становятся равны друг другу и равны искомому значениюЗадача 2

Докажите, что НОД(a,b)={\displaystyle (a,\;b)=\;}НОД(a−b,b){\displaystyle (a-b,\;b)} для любых неотрицательных целых a{\displaystyle a} и b{\displaystyle b}, таких что a>b{\displaystyle a>b}.

Алгоритм вычисления чисел Фибоначчи[править]

В математике для описания функций часто используются рекуррентные соотношения, в которых значение функции определяется через её значение при других (обычно меньших) аргументах. Наиболее известным примером является последовательность Фибоначчи 1, 1, 2, 3, 5, 8, 13, …, определяемая следующими соотношениями:

F1=1,F2=1,Fn=Fn−1+Fn−2{\displaystyle F_{1}=1,\quad F_{2}=1,\quad F_{n}=F_{n-1}+F_{n-2}}.

Используя это рекуррентное соотношение, можно построить рекурсивный алгоритм вычисления чисел Фибоначчи:

Псевдокод 2. Числа Фибоначчи

1 Function Fibo(n)
2   If n = 1 Or n = 2
3     Return 1
4   End If
5   Return Fibo(n - 1) + Fibo(n - 2)
6 End Function

При анализе рекурсивной функции обычно возникает два вопроса: почему функция работает правильно и почему она завершает работу? Ответ на первый вопрос обычно прост, — если рекуррентные отношения правильны и интерпретатор (компилятор) сработал правильно, то единственное значение, которое может вернуть программа, — правильное. Но есть ещё другая альтернатива — программа может не закончить свою работу^[5].

Наибольший интерес в этом алгоритме представляет строчка 5:

Return Fibo(n - 1) + Fibo(n - 2)

Она означает следующее: «Запустить процесс вычисления Fibo(n - 1), затем запустить процесс вычисления Fibo(n - 2), результаты вычислений сложить и вернуть в качестве результата». Можно считать что в этой строчке исполнитель нашего алгоритма просит другого исполнителя вычислить Fibo(n - 1), а сам ждёт, когда тот закончит вычисления. Узнаёт у него результат, просит вычислить Fibo(n - 2) и снова ждёт результата. Два полученных результата складывает, возвращает значение суммы как результат и заканчивает работу. Интерес заключается в том, что этот дополнительный исполнитель действует по такому же алгоритму — если его аргумент больше 1, он также вызывает очередного исполнителя для вычисления нужных ему значений. Получается серия вызовов, которые выстраиваются в дерево рекурсивных вызовов.

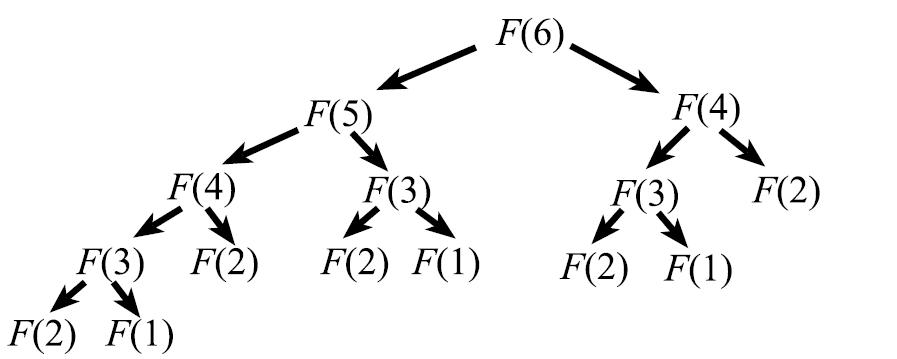Рис. 1. Дерево рекурсивных вызовов для F6{\displaystyle F_{6}}.

На рисунке 1 изображено дерево рекурсивных вызовов, возникающее при вычислении F6{\displaystyle F_{6}}. Это дерево демонстрирует как функция сама себя использует при вычислении. Например, при вычислении F6{\displaystyle F_{6}} были вызваны функции вычисления F5{\displaystyle F_{5}} и F4{\displaystyle F_{4}}. Для вычисления F5{\displaystyle F_{5}} понадобились F4{\displaystyle F_{4}} и F3{\displaystyle F_{3}}, и так далее.

Для того, чтобы рекурсивный алгоритм заканчивал свою работу, необходимо, чтобы дерево рекурсивных вызовов при любых входных данных обрывалось и было конечным. В данном примере дерево рекурсивных вызовов обрывается на F1{\displaystyle F_{1}} и F2{\displaystyle F_{2}}, для вычисления которых не используются рекурсивные вызовы.

Довольно часто «зависание» компьютеров связано с использованием плохо реализизованных рекурсивных идей. Наш пример тоже плох — попробуйте подставить отрицательный аргумент n{\displaystyle n}.

Пользоваться рекурсивными алгоритмами нужно осторожно, так как они могут быть очень неэффективными с точки зрения времени работы. К сожалению рекурсивные алгоритмы не всегда являются хорошими. Попробуем оценить количество операций, необходимых для того, чтобы вычислить n{\displaystyle n}-й член последовательности Фибоначчи (здесь под операцией мы понимаем строчку в программе). Обозначим это число как T(n){\displaystyle T(n)}.

Для вычисления Fibo(n) нам потребуется вызвать Fibo(n - 1) и Fibo(n - 2), поэтому T(n)≥T(n−1)+T(n−2){\displaystyle T(n)\geq T(n-1)+T(n-2)}. Используя это соотношение и то, что T(1)=T(2)>1{\displaystyle T(1)=T(2)>1}, можно по индукции доказать, что T(n)≥Fn{\displaystyle T(n)\geq F_{n}}. Но числа Фибоначчи возрастают достаточно быстро (F50=20365011074{\displaystyle F_{50}=20365011074}). Поэтому даже на мощном компьютере с помощью этого алгоритма нам не удастся вычислить больше, чем первые несколько десятков членов последовательности Фибоначчи. Вы, наверное, уже догадываетесь, в чём здесь проблема. В нашей программе очень много избыточных вызовов — в дереве рекурсивных вызовов много повторений. Например Fibo(n - 2) будет вызвана два раза: сначала из Fibo(n), а потом из Fibo(n - 1), и оба раза будут проводится одни и те же вычисления. Простой «человеческий» алгоритм вычисления чисел Фибоначчи работает существенно быстрее: нужно помнить последние два числа Фибоначчи, вычислять следующее число и повторять этот шаг нужное число раз. Приведём его описание на псевдокоде (см. псевдокод 3).

Алгоритм 3 для вычисления Fn{\displaystyle F_{n}} выполнит n−2{\displaystyle n-2} итераций цикла While. Видно, что время работы алгоритма растёт линейно с n{\displaystyle n} (увеличение n{\displaystyle n} в k{\displaystyle k} раз приведёт к тому, что время работы алгоритма тоже увеличится примерно в k{\displaystyle k} раз).

Как мы видим, в данном случае рекурсивный алгоритм оказался существенно менее эффективным (дольше работающим при больших n{\displaystyle n}), нежели нерекурсивный алгоритм.

Но это не значит, что использовать рекурсию не надо. Рекурсия очень важный и удобный инструмент программирования. С помощью рекурсии успешно реализуют важный подход к решению задач: разделяй и властвуй.

Лучший способ решить сложную задачу — это разделить её на несколько простых и «разделаться» с ними по отдельности. По сути, это один из важных инструментов мышления при решении задач.

Псевдокод 3. Числа Фибоначчи: нерекурсивный алгоритм

 1 Function FiboNR(n)
 2   If n<3{\displaystyle n<3} Then
 3     Return 1
 4   Else
 5     b←1{\displaystyle b\gets 1}         \\ Предпоследнее вычисленное число Фибоначчи
 6     a←1{\displaystyle a\gets 1}         \\ Последнее вычисленное число Фибоначчи
 7     For i∈3…n{\displaystyle i\in 3\ldots n}
 8       c←a+b{\displaystyle c\gets a+b}    \\ Вычисляем следующее число Фибоначчи
 9       b←a{\displaystyle b\gets a}       \\ Старое последнее число стало предпоследним
10       a←c{\displaystyle a\gets c}       \\ Новое вычисленное число стало последним
11     End For
12     Return c
13   End If
14 End Function

От экспоненциального роста времени вычисления рекурсивных алгоритмов легко избавится с помощью запоминания вычисленных значений. А именно, в памяти хранят вычисленные значения, а в начале функции помещается проверка на то, что требуемое значение уже вычислено и хранится в памяти. Если это так, то это значение возвращается как результат, а вычисления и рекурсивные вызовы осуществляются лишь в том случае, когда функция с такими аргументами ещё ни разу не вызывалась. Подробнее этот метод мы рассмотрим при изучении динамического программирования.

Задача «Ханойские башни»[править]

Рассмотрим ещё один классический пример на рекурсивные алгоритмы — игру «Ханойские башни», придуманную ещё в 1883 году Эдуардом Люка. Есть три стержня и 64 кольца́, нанизанных на них. В начале все ко́льца находятся на первом стержне, причём все ко́льца разного диаметра, и меньшие ко́льца лежат на бо́льших. За ход разрешается взять верхнее кольцо с любого стержня и положить на другой стержень сверху, при этом запрещается класть большее кольцо на меньшее. Цель игры состоит в том, чтобы переместить всю пирамиду с первого стержня на второй.

Заметим, что для того, чтобы переместить пирамиду, нам надо будет переместить и самое нижнее большое кольцо. Для этого нам нужно будет, чтобы все остальные ко́льца были на третьем штыре. Значит, чтобы переместить N{\displaystyle N} колец, нам сначала нужно переместить столбик из верхних N−1{\displaystyle N-1} колец на третий стержень, затем переместить самое большое кольцо с первого на второй и, наконец, переместить столбик из N−1{\displaystyle N-1} колец с третьего стержня на второй.

Псевдокод 4. Ханойские башни

1 Function Move(n, x, y)
2   If n = 1 Then
3     передвинуть кольцо с стержня x на стержень y
4   End If
5   Move(n - 1, x        , 6 - x - y)
6   Move(1    , x        , y        )
7   Move(n - 1, 6 - x - y, y        )
8 End Function

Итак, мы опять получили рекурсивный алгоритм: для того, чтобы решить задачу для пирамиды из N{\displaystyle N} колец, достаточно решить её для пирамиды из N−1{\displaystyle N-1} колец. Посчитаем теперь количество действий, необходимое для проведения всей операции. Пусть f(N){\displaystyle f(N)} — необходимое число действий, для переноса пирамиды из n{\displaystyle n} колец. Для одного кольца ответ равен единице: f(1)=1{\displaystyle f(1)=1}, для N{\displaystyle N} ответ будет f(N)=f(N−1)+1+f(N−1)=2f(

Список алгоритмов — Википедия

Материал из Википедии — свободной энциклопедии

Ниже приводится список алгоритмов, группированный по категориям. Более детальные сведения приводятся в списке структур данных и списке основных разделов теории алгоритмов^[1]

Общие комбинаторные алгоритмы[править | править код]

Генерация комбинаторных объектов[править | править код]

Алгоритмы на графах[править | править код]

Алгоритмы нахождения максимального потока[править | править код]

n{\displaystyle n} — число вершин, m{\displaystyle m} — число рёбер, U{\displaystyle U} — наибольшая величина максимальной пропускной способности сети.

Алгоритмы нахождения максимального паросочетания[править | править код]

Алгоритмы поиска[править | править код]

Алгоритмы на строках[править | править код]

Алгоритмы поиска строки[править | править код]

Алгоритмы вычисления расстояния между строками[править | править код]

Алгоритмы приближенного сравнения строк с шаблоном[править | править код]

Вычисление характеристических паттернов[править | править код]

Примерное соответствие[править | править код]

Индексы подстрок[править | править код]

Алгоритмы сортировки[править | править код]

• Bogosort
• Stooge sort
• Timsort — гибридный алгоритм сортировки, сочетающий сортировку вставками и сортировку слиянием
• Наивная сортировка — генерация всех n!{\displaystyle n!} возможных перестановок и проверка на отсортированность
• Блинная сортировка
• Блочная сортировка (также известен как корзинная сортировка), ср. с поразрядной
• Быстрая сортировка — с разбиением исходного набора данных на две половины так, что любой элемент первой половины упорядочен относительно любого элемента второй половины; затем алгоритм применяется рекурсивно к каждой половине
• Гномья сортировка — имеет общее с сортировкой пузырьком и сортировкой вставками. Сложность алгоритма — O(n2){\displaystyle O(n^{2})}.
• Пирамидальная сортировка (Сортировка кучей) — превращаем список в кучу, берём наибольший элемент и добавляем его в конец списка
• Плавная сортировка
• Поразрядная сортировка — сортирует строки буква за буквой.
• Сортировка Бентли — Седжвика (англ. BeSe sort) — модификация быстрой сортировки для составных ключей, заключающаяся в делении не пополам, а на три части — в третью попадают одинаковые (по текущему символу) ключи
• Сортировка с помощью двоичного дерева (англ. Tree sort)
• Сортировка методом вставок — определяем, где текущий элемент должен находиться в отсортированном списке, и вставляем его туда
• Сортировка методом выбора — наименьшего или наибольшего элемента и помещения его в начало или конец отсортированного списка
• Сортировка перемешиванием (Сортировка коктейлем)
• Сортировка подсчётом — используется диапазон входных данных, подсчитывается число одинаковых элементов (3 варианта)
• Сортировка пузырьком
• Сортировка расчёской
• Сортировка слиянием — сортируем первую и вторую половину списка отдельно, а затем — сливаем отсортированные списки
• Сортировка Шелла — попытка улучшить сортировку вставками
• Топологическая сортировка
• Хитрая сортировка — извлекает из исходной последовательности отсортированные подпоследовательности, производя их слияние с уже извлечёнными данными
• Цифровая сортировка — то же, что и Поразрядная сортировка.

Алгоритмы слияния[править | править код]

Минимизация булевых функций[править | править код]

Алгоритмы сжатия без потерь[править | править код]

• Преобразование Барроуза — Уилера (также известен как англ. BWT) — предварительная обработка данных для улучшения сжатия без потерь
• Преобразование Шиндлера (англ.  ST) — модификация преобразования Барроуза — Уилера
• Алгоритм DEFLATE — популярный свободный алгоритм сжатия (используется в библиотеке zlib)
• Дельта-кодирование — эффективно для сжатия данных с часто повторяющимися последовательностями
• Инкрементное кодирование — дельта-кодирование, применяемое к последовательности строк
• Семейство алгоритмов словарного сжатия Лемпеля — Зива:
  • LZ77 — родоначальник семейства LZ77-алгоритмов
  • LZ78 — родоначальник семейства LZ78-алгоритмов
  • LZMA — сокращение от англ. Lempel-Ziv-Markov chain-Algorithm
  • LZO — алгоритм сжатия, ориентированный на скорость
• Алгоритм сжатия PPM
• Кодирование длин серий (Групповое кодирование, также известен как англ. RLE) — последовательная серия одинаковых элементов заменяется на два символа: элемент и число его повторений
• Алгоритм SEQUITUR (англ.) — сжатие без потерь, автоматическое адаптивное построение контекстно-свободной грамматики для обрабатываемых данных
• Вейвлет-кодирование на основе вложенных нуль-деревьев (англ.) (EZW-кодирование)
• Энтропийное кодирование — схема кодирования, которая присваивает коды символам таким образом, чтобы соотнести длину кодов с вероятностью появления символов
• Энтропийное кодирование с известными характеристиками
  • Унарное кодирование — код, который представляет число n{\displaystyle n} в виде n{\displaystyle n} единиц с замыкающим нулём
  • дельта|гамма|омега-кодирование Элиаса (англ. Elias coding) — универсальный код, кодирующий положительные целые числа
  • Кодирование Фибоначчи — универсальный код, который кодирует положительные целые числа в двоичные кодовые слова
  • Кодирование Голомба — форма энтропийного кодирования, которая оптимальна для алфавитов с геометрическим распределением
  • Кодирование Райса — форма энтропийного кодирования, которая оптимальна для алфавитов с геометрическим распределением

Алгоритмы сжатия с потерями[править | править код]

Для чего нужны алгоритмы? Основные алгоритмы программирования

Алгоритмы и структуры данных → Полезные материалы по алгоритмам

Теги: программирование, разработка, алгоритмы, алгоритм, rsa, быстрая сортировка, пирамидальная сортировка, сортировка слиянием, преобразование фурье, алгоритм дейкстры, алгоритм безопасного хэширования, анализ связей, пропорционально-интегрально-дифференцирующий алгоритм, сжатие данных, генерация случайных чисел

Каждый программист знает о важности использования алгоритмов. В этой статье мы поговорим о том, что такое алгоритм и какими характеристиками он обладает. А самое главное — составим список алгоритмов, которые широко применяются в программировании и, стало быть, будут полезны для программиста.

Алгоритм — что это?

Если говорить неофициально, то алгоритмом можно назвать любую корректно определённую вычислительную процедуру, когда на вход подаётся какая-нибудь величина либо набор величин, а результатом выполнения становится выходная величина либо набор значений. Можно сказать, что алгоритм — это некая последовательность вычислительных шагов, благодаря чему происходит преобразование входных данных в выходные.

Также нужно понимать, что алгоритм как последовательность шагов позволяет решать конкретную задачу и должен: 1. Работать за конечный объём времени. Если алгоритм не способен разобраться с проблемой за конечное количество времени, можно сказать, что этот алгоритм бесполезен. 2. Иметь чётко определённые инструкции. Любой шаг алгоритма должен точно определяться. При этом его инструкции должны быть однозначны для любого случая. 3. Быть пригоден к использованию. Речь идёт о том, что алгоритм должен быть способен решить проблему, для устранения которой его создавали.

Сегодня алгоритмы используются как в информатике и программировании, так и в математике. Кстати, наиболее ранними математическими алгоритмами называют разложение на простые множители и извлечение квадратного корня — их использовали в древнем Вавилоне ещё в 1600 г. до н. э. Но мы не будем уходить далеко в прошлое, а рассмотрим, как и обещали, основные алгоритмы программирования на сегодняшний день.

Алгоритмы сортировки (пирамидальная, быстрая, слиянием)

Какой алгоритм сортировки считают лучшим? Здесь нет однозначного ответа, ведь всё зависит от ваших предпочтений и поставленных перед вами задач. Рассмотрим каждый из алгоритмов: 1. Сортировка слиянием. Важнейший на сегодня алгоритм. Базируется на принципе сравнения элементов и задействует подход «разделяй и властвуй», позволяя более эффективно решать проблемы, которые когда-то решались за время O (n^2). Сортировка слиянием была изобретена математиком Джоном фон Нейманом в далёком 1945 году. 2. Быстрая сортировка. Это уже другой подход к сортировке. Тут алгоритм базируется, как на in-place разделении, так и на принципе «разделяй и властвуй». Однако эта сортировка нестабильна, что и является её проблемой. Зато алгоритм эффективен при сортировке массивов в оперативной памяти. 3. Пирамидальная сортировка. Алгоритм in-place который использует приоритетную очередь (за счёт этой очереди сокращается время поиска данных).

Считается, что вышеописанные алгоритмы лучше, если сравнивать их с другими, например, сортировкой пузырьком. Можно сказать, что именно благодаря алгоритмам сортировки у нас сегодня есть искусственный интеллект, глубинный анализ данных и даже интернет.

Преобразование Фурье. Быстрое преобразование Фурье

Электронно-вычислительные устройства используют алгоритмы для функционирования, в том числе и алгоритм преобразования Фурье. И телефон, и смартфон, и компьютер, и маршрутизатор, и интернет — всё это не может работать без алгоритмов для функционирования, запомните это.

Алгоритм Дейкстры

Без этого алгоритма, опять же, не сможет эффективно работать тот же интернет. С его помощью решаются задачи, в которых проблема представляется в виде графа, обеспечивающего поиск наикратчайшего пути между 2-мя узлами. Даже сегодня, когда у нас есть решения и получше, программисты по-прежнему используют поиск кратчайшего пути, если речь идёт о системах, требующих повышенной стабильности.

Алгоритм RSA

Это алгоритм пришёл к нам из криптографии. Он сделал криптографию доступной всем, предопределив её будущее. Вообще, RSA-алгоритм сделан для решения простой задачи с неочевидным решением. Он позволяет делиться открытыми ключами между конечными пользователями и независимыми платформами таким образом, чтобы можно было применять шифрование.

Алгоритм безопасного хэширования

Ну, это не совсем алгоритм. Скорее, его можно назвать семейством криптографических хэш-функций (SHA-1, SHA-2 и т.д.), которые разработаны в США и имеют важнейшее значение для всего мира. Антивирусы, электронная почта, магазины приложений, браузеры и т. п. — во всём этом используются алгоритмы безопасного хэширования (на деле хэш является результатом их работы). Алгоритм нужен для определения, удалось ли вам загрузить то, что хотели, а также не подверглись ли вы фишингу или атаке «человек посередине».

Анализ связей

Идея алгоритма анализа связей проста. Например, вы легко сможете представить график в виде матрицы, что сведёт задачу к проблеме уровня собственной значимости каждого узла. Данный подход к структуре графа позволит оценить относительную важность каждого объекта, который включён в систему.

Алгоритм был создан в далёком 1976 году и используется сегодня при ранжировании страниц в процессе поиска в Google, при генерации ленты новостей, при составлении списка возможных друзей на Facebook, при работе с контактами в LinkedIn и во многих других случаях. Любой из перечисленных сервисов работает с различными объектами и параметрами и объектами, однако сама математика по сути не меняется.

Пропорционально-интегрально-дифференцирующий алгоритм

Пользовались ли вы автомобилем, самолётом, сотовой связью? Видели ли вы робота в работе? Во всех этих случаях вы можете сказать, что видели данный алгоритм в действии.

Пропорционально-интегрально-дифференцирующий алгоритм обычно применяет замкнутый механизм обратной связи для контура управления. Это необходимо для минимизации ошибки между реальным выходным сигналом и желаемым выходным сигналом. Алгоритм задействуется там, где необходимо создать систему для обработки сигнала либо для управления гидравлическими, механическими и тепловыми механизмами автоматизированного типа.

Алгоритмы сжатия данных

Сложно сказать, какой алгоритм для сжатия наиболее важен, ведь в зависимости от поставленных задач он может меняться от zip до mp3 либо от JPEG до MPEG-2. Но эти алгоритмы важны почти для всех сфер деятельности.

Алгоритм сжатия — это не только очередной заархивированный документ. Он позволяет выполнять сжатие данных на веб-странице при их загрузке на компьютер. Или задействуется в базах данных, видео, музыке, облачных вычислениях. По сути алгоритмы сжатия данных делают системы дешевле и эффективнее.

Алгоритм генерации случайных чисел

На самом деле не существует «настоящего» генератора случайных чисел, и мы уже об этом говорили. Зато у нас существуют генераторы псевдослучайных чисел, которые прекрасно с этим справляются. Они имеют расширенную вариативность использования: программные приложения в программировании, криптография, алгоритмы хэширования, видеоигры, искусственный интеллект, тесты при разработке программ и т. д.

Узнать больше можно на курсе «Алгоритмы для разработчиков». Ждём вас!

Значение слова АЛГОРИТМ. Что такое АЛГОРИТМ?

Алгори́тм — набор инструкций, описывающих порядок действий исполнителя для достижения некоторого результата. В старой трактовке вместо слова «порядок» использовалось слово «последовательность», но по мере развития параллельности в работе компьютеров слово «последовательность» стали заменять более общим словом «порядок». Независимые инструкции могут выполняться в произвольном порядке, параллельно, если это позволяют используемые исполнители.

Ранее в русском языке писали «алгорифм», сейчас такое написание используется редко, но, тем не менее, имеет место исключение (нормальный алгорифм Маркова).

Часто в качестве исполнителя выступает компьютер, но понятие алгоритма необязательно относится к компьютерным программам, так, например, чётко описанный рецепт приготовления блюда также является алгоритмом, в таком случае исполнителем является человек (а может быть и некоторый механизм, ткацкий станок, и пр.).

Можно выделить алгоритмы вычислительные (о них в основном идет далее речь), и управляющие. Вычислительные по сути преобразуют некоторые начальные данные в выходные, реализуя вычисление некоторой функции. Семантика управляющих алгоритмов существенным образом может отличаться и сводиться к выдаче необходимых управляющих воздействий либо в заданные моменты времени, либо в качестве реакции на внешние события (в этом случае, в отличие от вычислительного алгоритма, управляющий может оставаться корректным при бесконечном выполнении).

Понятие алгоритма относится к первоначальным, основным, базисным понятиям математики. Вычислительные процессы алгоритмического характера (арифметические действия над целыми числами, нахождение наибольшего общего делителя двух чисел и т. д.) известны человечеству с глубокой древности. Однако в явном виде понятие алгоритма сформировалось лишь в начале XX века.

Частичная формализация понятия алгоритма началась с попыток решения проблемы разрешения (нем. Entscheidungsproblem), которую сформулировал Давид Гильберт в 1928 году. Следующие этапы формализации были необходимы для определения эффективных вычислений или «эффективного метода»; среди таких формализаций — рекурсивные функции Геделя — Эрбрана — Клини 1930, 1934 и 1935 гг., λ-исчисление Алонзо Чёрча 1936 г., «Формулировка 1» Эмиля Поста 1936 года и машина Тьюринга. В методологии алгоритм является базисным понятием и получает качественно новое понятие как оптимальности по мере приближения к прогнозируемому абсолюту. В современном мире алгоритм в формализованном выражении составляет основу образования на примерах, по подобию.

АЛГОРИТМ | Энциклопедия Кругосвет

Содержание статьи

АЛГОРИТМ – система правил, сформулированная на понятном исполнителю языке, которая определяет процесс перехода от допустимых исходных данных к некоторому результату и обладает свойствами массовости, конечности, определенности, детерминированности.

Слово «алгоритм» происходит от имени великого среднеазиатского ученого 8–9 вв. Аль-Хорезми (Хорезм – историческая область на территории современного Узбекистана). Из математических работ Аль-Хорезми до нас дошли только две – алгебраическая (от названия этой книги родилось слово алгебра) и арифметическая. Вторая книга долгое время считалась потерянной, но в 1857 в библиотеке Кембриджского университета был найден ее перевод на латинский язык. В ней описаны четыре правила арифметических действий, практически те же, что используются и сейчас. Первые строки этой книги были переведены так: «Сказал Алгоритми. Воздадим должную хвалу Богу, нашему вождю и защитнику». Так имя Аль-Хорезми перешло в Алгоритми, откуда и появилось слово алгоритм. Термин алгоритм употреблялся для обозначения четырех арифметических операций, именно в таком значении он и вошел в некоторые европейские языки. Например, в авторитетном словаре английского языка Webster’s New World Dictionary, изданном в 1957, слово алгоритм снабжено пометкой «устаревшее» и объясняется как выполнение арифметических действий с помощью арабских цифр.

Слово «алгоритм» вновь стало употребительным с появлением электронных вычислительных машин для обозначения совокупности действий, составляющих некоторый процесс. Здесь подразумевается не только процесс решения некоторой математической задачи, но и кулинарный рецепт и инструкция по использованию стиральной машины, и многие другие последовательные правила, не имеющие отношения к математике, – все эти правила являются алгоритмами. Слово «алгоритм» в наши дни известно каждому, оно настолько уверенно шагнуло в разговорную речь, что сейчас нередко на страницах газет, в выступлениях политиков встречаются выражения «алгоритм поведения», «алгоритм успеха» и т.д.

Проблема определения понятия «алгоритм».

На протяжении многих веков понятие алгоритма связывалось с числами и относительно простыми действиями над ними, да и сама математика была, по большей части, наукой о вычислениях, наукой прикладной. Чаще всего алгоритмы представлялись в виде математических формул. Порядок элементарных шагов алгоритма задавался расстановкой скобок, а сами шаги заключались в выполнении арифметических операций и операций отношения (проверки равенства, неравенства и т.д.). Часто вычисления были громоздкими, а вычисления вручную – трудоемкими, но суть самого вычислительного процесса оставалась очевидной. У математиков не возникала потребность в осознании и строгом определении понятия алгоритма, в его обобщении. Но с развитием математики появлялись новые объекты, которыми приходилось оперировать: векторы, графы, матрицы, множества и др. Как определить для них однозначность или как установить конечность алгоритма, какие шаги считать элементарными? В 1920-х задача точного определения понятия алгоритма стала одной из центральных проблем математики. В то время существовало две точки зрения на математические проблемы:

Все проблемы алгоритмически разрешимы, но для некоторых алгоритм еще не найден, поскольку еще не развиты соответствующие разделы математики.

Есть проблемы, для которых алгоритм вообще не может существовать.

Идея о существовании алгоритмически неразрешимых проблем оказалась верной, но для того, чтобы ее обосновать, необходимо было дать точное определение алгоритма. Попытки выработать такое определение привели к возникновению теории алгоритмов, в которую вошли труды многих известных математиков – К.Гедель, К.Черч, С.Клини, А.Тьюринг, Э.Пост, А.Марков, А.Колмогоров и многие другие.

Точное определение понятия алгоритма дало возможность доказать алгоритмическую неразрешимость многих математических проблем.

Появление первых проектов вычислительных машин стимулировало исследование возможностей практического применения алгоритмов, использование которых, ввиду их трудоемкости, было ранее недоступно. Дальнейший процесс развития вычислительной техники определил развитие теоретических и прикладных аспектов изучения алгоритмов.

Понятие «алгоритма».

В повседневной жизни каждый человек сталкивается с необходимостью решения задач самой разной сложности. Некоторые из них трудны и требуют длительных размышлений для поиска решений (а иногда его так и не удается найти), другие же, напротив, столь просты и привычны, что решаются автоматически. При этом выполнение даже самой простой задачи осуществляется в несколько последовательных этапов (шагов). В виде последовательности шагов можно описать процесс решения многих задач, известных из школьного курса математики: приведение дробей к общему знаменателю, решение системы линейных уравнений путем последовательного исключения неизвестных, построение треугольника по трем сторонам с помощью циркуля и линейки и т.д. Такая последовательность шагов в решении задачи называется алгоритмом. Каждое отдельное действие – это шаг алгоритма. Последовательность шагов алгоритма строго фиксирована, т.е. шаги должны быть упорядоченными. Правда, существуют параллельные алгоритмы, для которых это требование не соблюдается.

Понятие алгоритма близко к другим понятиям, таким, как метод (метод Гаусса решения систем линейных уравнений), способ (способ построения треугольника по трем сторонам с помощью циркуля и линейки). Можно сформулировать основные особенности именно алгоритмов.

Наличие исходных данных и некоторого результата.

Алгоритм – это точно определенная инструкция, последовательно применяя которую к исходным данным, можно получить решение задачи. Для каждого алгоритма есть некоторое множество объектов, допустимых в качестве исходных данных. Например, в алгоритме деления вещественных чисел делимое может быть любым, а делитель не может быть равен нулю.

Массовость, т.е. возможность применять многократно один и тот же алгоритм. Алгоритм служит, как правило, для решения не одной конкретной задачи, а некоторого класса задач. Так алгоритм сложения применим к любой паре натуральных чисел.

Детерминированность.

При применении алгоритма к одним и тем же исходным данным должен получаться всегда один и тот же результат, поэтому, например, процесс преобразования информации, в котором участвует бросание монеты, не является детерминированным и не может быть назван алгоритмом.

Результативность.

Выполнение алгоритма должно обязательно приводить к его завершению. В то же время можно привести примеры формально бесконечных алгоритмов, широко применяемых на практике. Например, алгоритм работы системы сбора метеорологических данных состоит в непрерывном повторении последовательности действий («измерить температуру воздуха», «определить атмосферное давление»), выполняемых с определенной частотой (через минуту, час) во все время существования данной системы.

Определенность.

На каждом шаге алгоритма у исполнителя должно быть достаточно информации, чтобы его выполнить. Кроме того, исполнителю нужно четко знать, каким образом он выполняется. Шаги инструкции должны быть достаточно простыми, элементарными, а исполнитель должен однозначно понимать смысл каждого шага последовательности действий, составляющих алгоритм (при вычислении площади прямоугольника любому исполнителю нужно уметь умножать и трактовать знак «x» именно как умножение). Поэтому вопрос о выборе формы представления алгоритма очень важен. Фактически речь идет о том, на каком языке записан алгоритм.

Формы представления алгоритмов.

Для записи алгоритмов необходим некоторый язык, при этом очень важно, какой именно язык выбран. Записывать алгоритмы на русском языке (или любом другом естественном языке) громоздко и неудобно.

Например, описание алгоритма Евклида нахождения НОД (наибольшего общего делителя) двух целых положительных чисел может быть представлено в виде трех шагов. Шаг 1: Разделить m на n. Пусть p – остаток от деления.

Шаг 2: Если p равно нулю, то n и есть исходный НОД.

Шаг 3: Если p не равно нулю, то сделаем m равным n, а n равным p. Вернуться к шагу 1.

Приведенная здесь запись алгоритма нахождения НОД очень упрощенная. Запись, данная Евклидом, представляет собой страницу текста, причем последовательность действий существенно сложней.

Одним из распространенных способов записи алгоритмов является запись на языке блок-схем. Запись представляет собой набор элементов (блоков), соединенных стрелками. Каждый элемент – это «шаг» алгоритма. Элементы блок-схемы делятся на два вида. Элементы, содержащие инструкцию выполнения какого-либо действия, обозначают прямоугольниками, а элементы, содержащие проверку условия – ромбами. Из прямоугольников всегда выходит только одна стрелка (входить может несколько), а из ромбов – две (одна из них помечается словом «да», другая – словом «нет», они показывают, соответственно, выполнено или нет проверяемое условие).

На рисунке представлена блок-схема алгоритма нахождения НОД:

Построение блок-схем из элементов всего лишь нескольких типов дает возможность преобразовать их в компьютерные программы и позволяет формализовать этот процесс.

Формализация понятия алгоритмов. Теория алгоритмов.

Приведенное определение алгоритма нельзя считать представленным в привычном математическом смысле. Математические определения фигур, чисел, уравнений, неравенств и многих других объектов очень четки. Каждый математически определенный объект можно сравнить с другим объектом, соответствующим тому же определению. Например, прямоугольник можно сравнить с другим прямоугольником по площади или по длине периметра. Возможность сравнения математически определенных объектов – важный момент математического изучения этих объектов. Данное определение алгоритма не позволяет сравнивать какие-либо две таким образом определенные инструкции. Можно, например, сравнить два алгоритма решения системы уравнений и выбрать более подходящий в данном случае, но невозможно сравнить алгоритм перехода через улицу с алгоритмом извлечения квадратного корня. С этой целью нужно формализовать понятие алгоритма, т.е. отвлечься от существа решаемой данным алгоритмом задачи, и выделить свойства различных алгоритмов, привлекая к рассмотрению только его форму записи. Задача нахождения единообразной формы записи алгоритмов, решающих различные задачи, является одной из основных задач теории алгоритмов. В теории алгоритмов предполагается, что каждый шаг алгоритма таков, что его может выполнить достаточно простое устройство (машина), Желательно, чтобы это устройство было универсальным, т.е. чтобы на нем можно было выполнять любой алгоритм. Механизм работы машины должен быть максимально простым по логической структуре, но настолько точным, чтобы эта структура могла служить предметом математического исследования. Впервые это было сделано американским математиком Эмилем Постом в 1936 (машина Поста) еще до создания современных вычислительных машин и (практически одновременно) английским математиком Аланом Тьюрингом (машина Тьюринга).

История конечных автоматов: машина Поста и машина Тьюринга.

Машина Поста – абстрактная вычислительная машина, предложенная Постом (Emil L.Post), которая отличается от машины Тьюринга большей простотой. Обе машины «эквивалентны» и были созданы для уточнения понятия «алгоритм».

В 1935 американский математик Пост опубликовал в «Журнале символической логики» статью Финитные комбинаторные процессы, формулировка 1. В этой статье и появившейся одновременно в Трудах Лондонского математического общества статье английского математика Тьюринга О вычислимых числах с приложением к проблеме решения были даны первые уточнения понятия «алгоритм». Важность идей Поста состоит в том, что был предложен простейший способ преобразования информации, именно он построил алгоритмическую систему (алгоритмическая система Поста). Пост доказал, что его система обладает алгоритмической полнотой. В 1967 профессор В.Успенский пересказал эти статьи с новых позиций. Он ввел термин «машина Поста». Машина Поста – абстрактная машина, которая работает по алгоритмам, разработанным человеком, она решает следующую проблему: если для решения задачи можно построить машину Поста, то она алгоритмически разрешима. В 1970 машина Поста была разработана в металле в Симферопольском университете. Машина Тьюринга была построена в металле в 1973 в Малой Крымской Академии Наук.

Абстрактная машина Поста представляет собой бесконечную ленту, разделенную на одинаковые клетки, каждая из которых может быть либо пустой, либо заполненной меткой «V». У машины есть головка, которая может перемещаться вдоль ленты на одну клетку вправо или влево, наносить в клетку ленты метку, если этой метки там ранее не было, стирать метку, если она была, либо проверять наличие в клетке метки. Информация о заполненных метками клетках ленты характеризует состояние ленты, которое может меняться в процессе работы машины. В каждый момент времени головка находится над одной из клеток ленты и, как говорят, обозревает ее. Информация о местоположения головки вместе с состоянием ленты характеризует состояние машины Поста. Работа машины Поста заключается в том, что головка передвигается вдоль ленты (на одну клетку за один шаг) влево или вправо, наносит или стирает метки, а также распознает, есть ли метка в клетке в соответствии с заданной программой, состоящей из отдельных команд.

Машина Тьюринга состоит из счетной ленты (разделенной на ячейки и ограниченной слева, но не справа), читающей и пишущей головки, лентопротяжного механизма и операционного исполнительного устройства, которое может находиться в одном из дискретных состояний q0, q1, …, qs , принадлежащих некоторой конечной совокупности (алфавиту внутренних состояний), при этом q0 называется начальным состоянием. Читающая и пишущая головка может читать буквы рабочего алфавита A = {a0, a1, …, at }, стирать их и печатать. Каждая ячейка ленты в каждый момент времени занята буквой из множества А. Чаще всего встречается буква а0 – «пробел». Головка находится в каждый момент времени над некоторой ячейкой ленты – текущей рабочей ячейкой. Лентопротяжный механизм может перемещать ленту так, что головка оказывается над соседней ячейкой ленты, при этом возможна ситуация выхода за левый край ленты, которая является аварийной (недопустимой), или машинного останова, когда машина выполняет предписание об остановке.

Современный взгляд на алгоритмизацию.

Теория алгоритмов строит и изучает конкретные модели алгоритмов. С развитием вычислительной техники и теории программирования возрастает необходимость построения новых экономичных алгоритмов, изменяются способы их построения, способы записи алгоритмов на языке, понятном исполнителю. Особый тип исполнителя алгоритмов – компьютер, поэтому необходимо создавать специальные средства, позволяющие, с одной стороны, разработчику в удобном виде записывать алгоритмы, а с другой – дающие компьютеру возможность понимать написанное. Такими средствами являются языки программирования или алгоритмические языки.

Анна Чугайнова