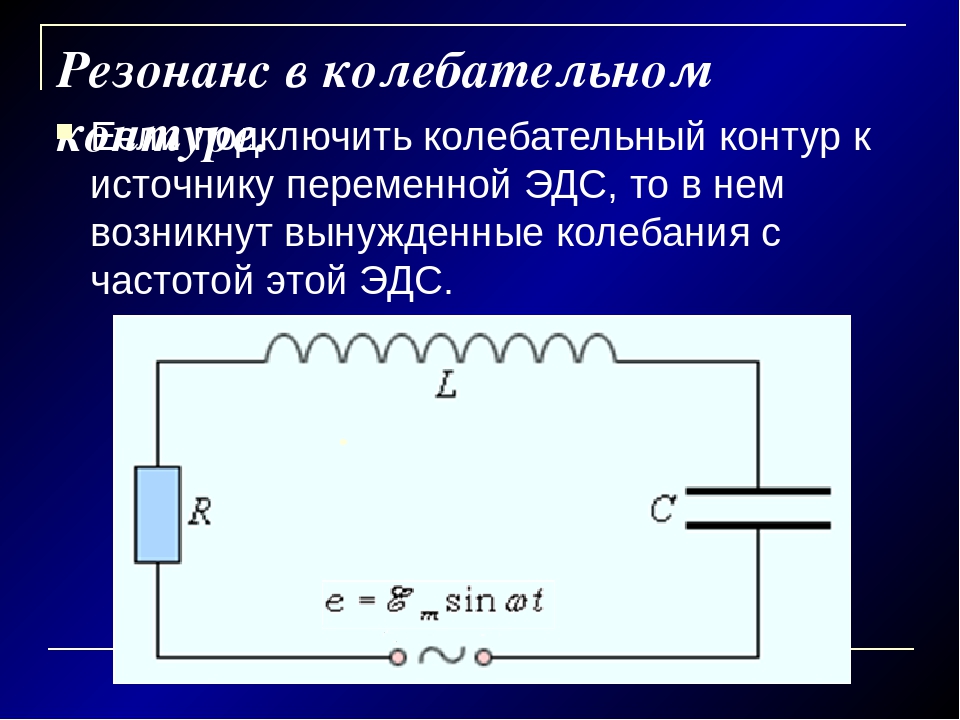
Условия возникновения резонанса в электрической цепи. Резонанс напряжений

Резонанс токов возникает в электрических цепях переменного тока при параллельном соединении ветвей с разнохарактерными (индуктивными и емкостными) реактивными сопротивлениями. В режиме резонанса токов реактивная индуктивная проводимость цепи оказывается равной ее реактивной емкостной проводимости, т.е. B L =B C .

Простейшей электрической цепью, в которой может наблюдаться резонанс токов, является цепь с параллельным соединением катушки индуктивности и конденсатора. Данная схема соответствует цепи, представленной на рис. 8, а , для которойR 2 = 0, а R 1 =R к (здесьR к – активное сопротивление катушки индуктивности). Полная проводимость такой цепиY =.

Условие резонанса токов (B L =B C) можно записать через соответствующие параметры электрической цепи. Так как реактивная проводимость катушки, имеющей активное сопротивлениеR к, определяется выражениемB L =X L /=L /(R к 2 + 2

L 2), а пр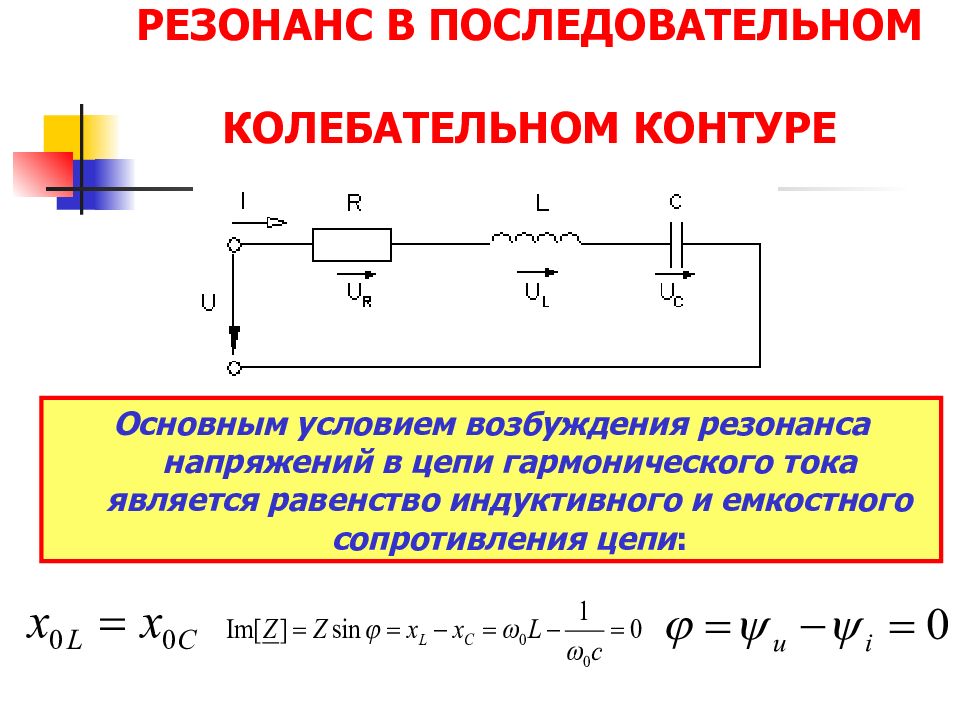оводимость конденсатора без учета его активного сопротивления (R C = 0)B C =X C /= 1/X C =C , то условие резонанса может быть записано в виде

L /(+ 2 L 2) = C .

Из этого выражения следует, что резонанс токов в такой цепи можно получить при изменении одного из параметров R к,L ,C ипри постоянстве других. При некоторых условиях в подобных цепях резонанс может возникать и при одновременном изменении указанных параметров.

Простейшие резонансные цепи, состоящие из параллельно соединенных между собой катушки индуктивности и конденсатора, широко применяются в радиоэлектронике в качестве колебательных контуров, резонанс токов в которых достигается при некоторой определенной частоте поступающего на вход соответствующего устройства сигнала.

В лабораторных условиях наиболее часто резонанс токов достигается при неизменной индуктивности катушки L , путем изменения емкостиС батареи конденсаторов. С изменением емкостной проводимостиB C =C , пропорциональной емкости конденсатора, происходит изменение полной проводимостиY , общего токаI и коэффициента мощности cos. Указанные зависимости приведены на рис.

10,a . Анализ этих зависимостей показывает, что при увеличении емкости от нуля полная проводимость электрической цепи сначала уменьшается, достигает при (B L =B C) своего минимума, а затем возрастает с увеличениемС , в пределе стремясь к бесконечности. Общий токI =YU , потребляемый цепью, пропорционален полной проводимости. Поэтому характер его изменения подобен характеру изменения проводимости.

Коэффициент мощности cosс увеличением емкости сначала возрастает, а затем уменьшается, в пределе стремясь к нулю, так как cos=G /Y . В результате анализа указанных зависимостей можно установить, что резонанс токов характеризуется следующими явлениями.

a) б)

1. При резонансе токов полная проводимость всей электрической цепи приобретает минимальное значение и становится равной активной ее составляющей:

Y = =G .

2. Минимальное значение проводимости обусловливает минимальное значение тока цепи:

I = YU = GU .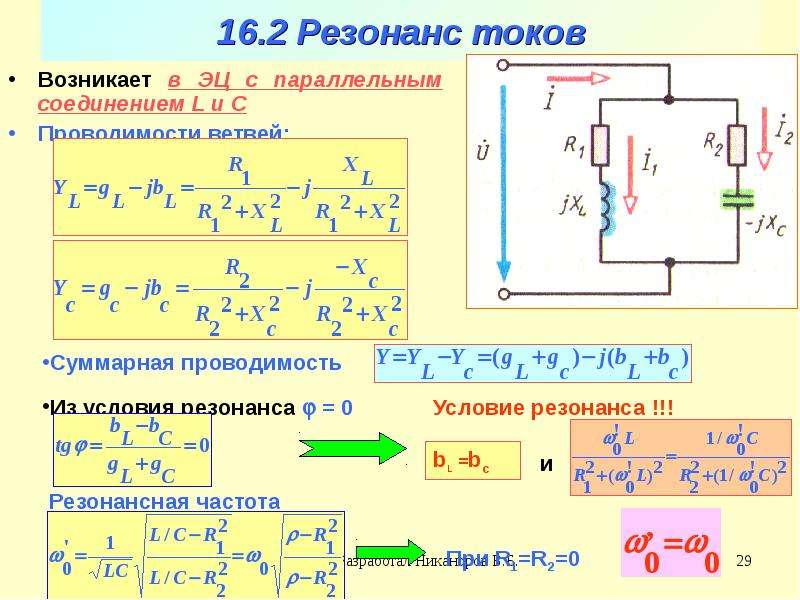

3. Емкостный ток I C и индуктивная составляющаяI L тока катушкиI к оказываются при этом равными по величине, а активная составляющая тока катушкиI а1 становится равной току

I , потребляемому из сети:

I р1 = I L = B L U = B C U = I C = I р2 ; I а = I а1 =GU = YU =I .

При этом реактивные составляющие токов I L иI C в зависимости от значений реактивных проводимостей могут приобретать теоретически весьма большие значения и намного превышать токI , потребляемый электрической цепью из сети.

4. Реактивная составляющая полной мощности цепи при B L =B C оказывается равной нулю:

Q = B L U 2  B C U 2 = Q L  Q C = 0.

При этом индуктивная и емкостная составляющие реактивной мощности также могут приобретать весьма большие значения, оставаясь равными друг другу.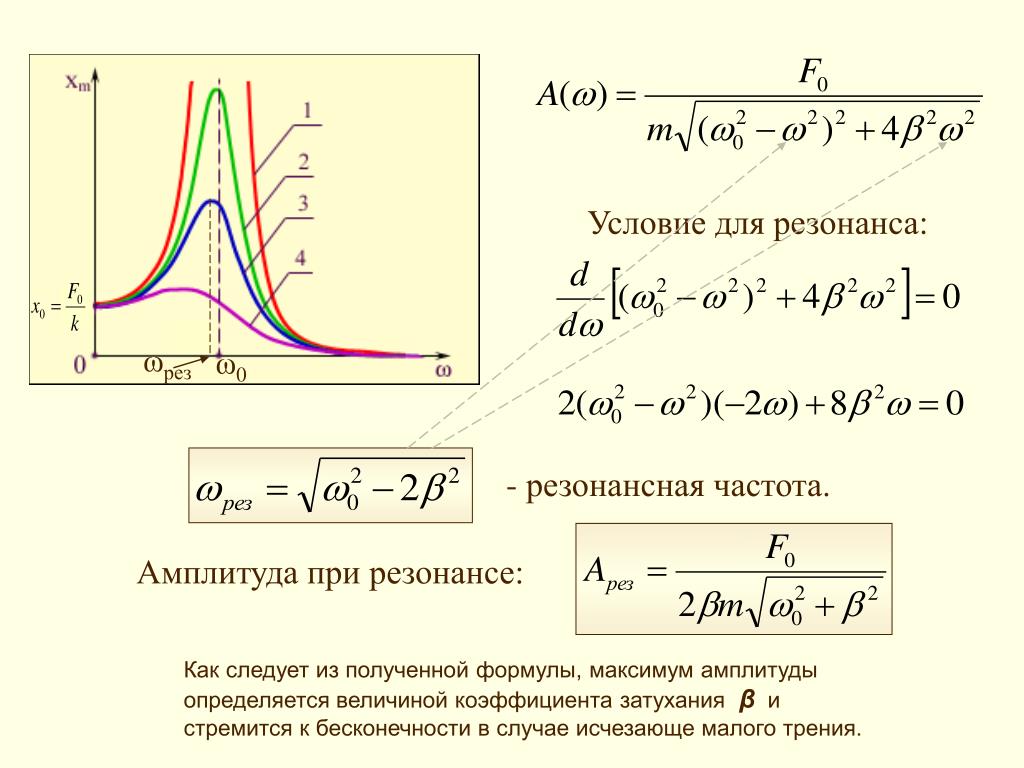

5. Полная мощность цепи при резонансе равна ее активной составляющей:

S = YU 2 = GU 2 = P .

6. Коэффициент мощности всей цепи при резонансе:

cos = P /S = GU 2 /YU 2 = 1.

Напряжение и ток электрической цепи при резонансе токов совпадают по фазе. Векторная диаграмма, построенная для условий резонанса токов и применительно к рассматриваемой цепи, представлена на рис. 10, б . В табл. 2 методических указаний по выполнению работы обозначениямI L , I K , I C соответствуют обозначения

I р1 , I 1 , I р2 на векторной диаграмме токов (рис. 10,б ).

Резонанс токов находит широкое применение в силовых электрических цепях для повышения коэффициента мощности, так как это имеет большое технико-экономическое значение. Большинство промышленных потребителей переменного тока имеют активно-индуктивный характер; некоторые из них работают с низким коэффициентом мощности и потребляют значительную реактивную мощность.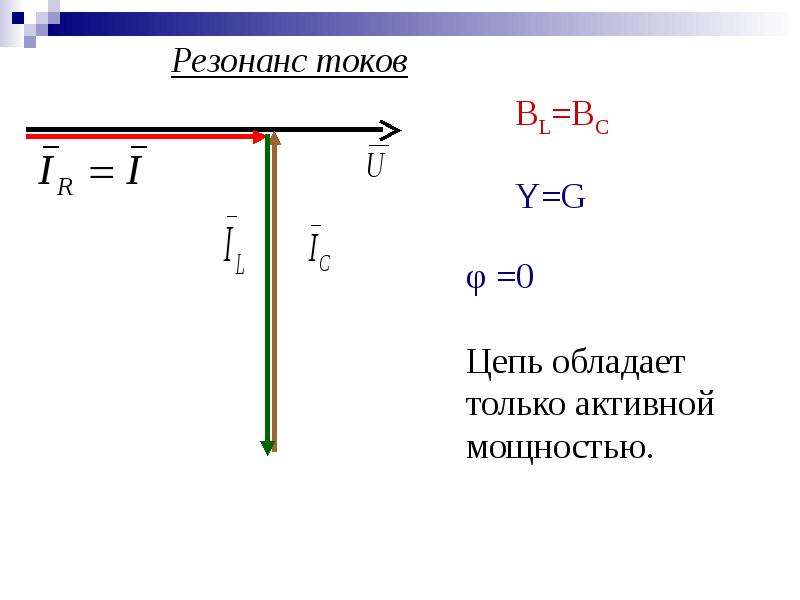 К таким потребителям могут быть отнесены асинхронные двигатели (особенно работающие с неполной нагрузкой), установки электрической сварки, высокочастотной закалки и т.д. Для уменьшения реактивной мощности и повышения коэффициента мощности параллельно потребителю включают батарею конденсаторов. Реактивная мощность конденсаторной батарей снижает общую реактивную мощность установки и тем самым увеличивает коэффициент мощности. Повышение коэффициента мощности приводит к уменьшению тока в проводах за счет снижения его реактивной составляющей и, соответственно, к уменьшению потерь энергии в генераторе и подводящих проводах.

Явление резонанса токов и напряжений наблюдается в цепях индуктивно-емкостного характера. Это явление нашло применение в радиоэлектронике, став основным способов настройки приемника на определенную волну. К сожалению, резонанс может нанести вред электрооборудованию и кабельным линиям. В физике резонансом является совпадение частот нескольких систем. Давайте рассмотрим, что такое резонанс напряжений и токов, какое значение он имеет и где используется в электротехнике.

Реактивные сопротивления индуктивности и емкости

Индуктивностью называется способность тела накапливать энергию в магнитном поле. Для нее характерно отставание тока от напряжения по фазе. Характерные индуктивные элементы — дросселя, катушки, трансформаторы, электродвигатели.

Емкостью называются элементы, которые накапливают энергию с помощью электрического поля. Для емкостных элементов характерно отставание по фазе напряжения от тока. Емкостные элементы: конденсаторы, варикапы.

Приведены их основные свойства, нюансы в пределах этой статьи во внимание не берутся.

Кроме перечисленных элементов другие также имеют определенную индуктивность и емкость, например в электрических кабелях распределенные по его длине.

Емкость и индуктивность в цепи переменного тока

Если в цепях постоянного тока емкость в общем смысле представляет собой разорванный участок цепи, а индуктивность — проводник, то в переменном конденсаторы и катушки представляют собой реактивный аналог резистора.

Реактивное сопротивление катушки индуктивности определяется по формуле:

Векторная диаграмма:

Реактивное сопротивление конденсатора:

Здесь w — угловая частота, f — частота в цепи синусоидального тока, L — индуктивность, C — емкость.

Векторная диаграмма:

Стоит отметить, что при расчете соединенных последовательно реактивных элементов используют формулу:

Обратите внимание, что емкостная составляющая принимается со знаком минус. Если в цепи присутствует еще и активная составляющая (резистор), то складывают по формуле теоремы Пифагора (исходя из векторной диаграммы):

От чего зависит реактивное сопротивление? Реактивные характеристики зависят от величины емкости или индуктивности, а также от частоты переменного тока.

Если посмотреть на формулу реактивной составляющей, то можно заметить, что при определенных значениях емкостной или индуктивной составляющей их разность будет равна нулю, тогда в цепи останется только активное сопротивление. Но это не все особенности такой ситуации.

Резонанс напряжений

Если последовательно с генератором соединить конденсатор и катушку индуктивности, то, при условии равенства их реактивных сопротивлений, возникнет резонанс напряжений. При этом активная часть Z должно быть как можно меньшей.

Стоит отметить, что индуктивность и емкость обладает только реактивными качествами лишь в идеализированных примерах. В реальных же цепях и элементах всегда присутствует активное сопротивление проводников, хоть оно и крайне мало.

При резонансе происходит обмен энергией между дросселем и конденсатором. В идеальных примерах при первоначальном подключении источника энергии (генератора) энергия накапливается в конденсаторе (или дросселе) и после его отключения происходят незатухающие колебания за счет этого обмена.

Напряжения на индуктивности и емкости примерно одинаковы, согласно :

Где X — это Xc емкостное или XL индуктивное сопротивление соответственно.

Цепь, состоящую из индуктивности и емкости, называют колебательным контуром. Его частота вычисляется по формуле:

Период колебаний определяется по формуле Томпсона:

Так как реактивное сопротивление зависит от частоты, то сопротивление индуктивности с ростом частоты увеличивается, а у ёмкости падает. Когда сопротивления равны, то общее сопротивление сильно снижается, что отражено на графике:

Основными характеристиками контура являются добротность (Q) и частота. Если рассмотреть контур в качестве четырехполюсника, то его коэффициент передачи после несложных вычислений сводится к добротности:

А напряжение на выводах цепи увеличивается пропорционально коэффициенту передачи (добротности) контура.

Uк=Uвх*Q

При резонансе напряжений, чем выше добротность, тем больше напряжение на элементах контура будет превышать напряжение подключенного генератора. Напряжение может повышаться в десятки и сотни раз. Это отображено на графике:

Потери мощности в контуре обусловлены только наличием активного сопротивления. Энергия из источника питания берется только для поддержания колебаний.

Коэффициент мощности будет равен:

Эта формула показывает, что потери происходят за счет активной мощности:

S=P/Cosф

Резонанс токов наблюдается в цепях, где индуктивность и емкость соединены параллельно.

Явление заключается в протекании токов большой величины между конденсатором и катушкой, при нулевом токе в неразветвленной части цепи. Это объясняется тем, что при достижении резонансной частоты общее сопротивление Z возрастает. Или простым языком звучит так – в точке резонанса достигается максимальное общее значение сопротивления Z, после чего одно из сопротивлений увеличивается, а другое снижается в зависимости от того растет или снижается частота. Это наглядно отображено на графике:

В общем, всё аналогично предыдущему явлению, условия возникновения резонанса токов следующие:

1. Частота питания аналогична резонансной у контура.
2. Проводимости у индуктивности и ёмкости по переменному току равны BL=Bc, B=1/X.

Применение на практике

Рассмотрим, какая польза и вред резонанса токов и напряжений. Наибольшую пользу явления резонанса принесли в радиопередающей аппаратуре. Простыми словами, а схеме приемника установлены катушка и конденсатор, подключенные к антенне. С помощью изменения индуктивности (например, перемещая сердечник) или величины емкости (например, воздушным переменным конденсатором) вы настраиваете резонансную частоту. В результате чего напряжение на катушке повышается и приемник ловит определенную радиоволну.

Вред эти явления могут на нести в электротехнике, например, на кабельных линиях. Кабель представляет собой распределенную по длине индуктивность и емкость, если на длинную линию подать напряжение в режиме холостого хода (когда на противоположном от источника питания конце кабеля нагрузка не подключена). Поэтому есть опасность того, что произойдет пробой изоляции, во избежание этого подключается нагрузочный балласт. Также аналогичная ситуация может привести к выходу из строя электронных компонентов, измерительных приборов и другого электрооборудования – это опасные последствия возникновения этого явления. (1/2)

1. Как устранить явление?

Увеличив активное сопротивление в цепи или изменив частоту.

Теперь вы знаете, что такое резонанс токов и напряжений, каковы условия его возникновения и варианты применения на практике. Для закрепления материала рекомендуем просмотреть полезное видео

Резонансом называют режим, когда в цепи, содержащей индуктивности и емкости, ток совпадает по фазе с напряжением . Входные реактивные сопротивление и проводимость равны нулю:
x = ImZ = 0 и B = ImY = 0. Цепь носит чисто активный характер:
Z = R ; сдвиг фаз отсутствует (j = 0).

Напряжения на индуктивности и емкости в этом режиме равны по величине и, находясь в противофазе, компенсируют друг друга. Все приложенное к цепи напряжение приходится на ее активное сопротивление (рис. 2.42, а ).

Рис. 2.42. Векторные диаграммы при резонансе напряжений (а) и токов (б)

Напряжения на индуктивности и емкости могут значительно превышать напряжения на входе цепи. Их отношение, называемое добротностью контура Q , определяется величинами индуктивного (или емкостного) и активного сопротивлений

.

Добротность показывает, во сколько раз напряжения на индуктивности и емкости при резонансе превышают напряжение, приложенное к цепи. В радиотехнических цепях она может достигать нескольких сотен единиц.

Из условия (2.33) следует, что резонанса можно достичь, изменяя любой из параметров – частоту, индуктивность, емкость. При этом меняются реактивное и полное сопротивления цепи, а вследствие этого – ток, напряжение на элементах и сдвиг фаз. Не приводя анализа формул, показываем графические зависимости некоторых из этих величин от емкости (рис. 2.43). Емкость , при которой наступает резонанс, можно определить из формулы (2.33):

.

Если, например, индуктивность контура L = 0,2 Гн, то при частоте 50 Гц, резонанс наступит при емкости

Рис. 2.43. Зависимости параметров режима от емкости

Аналогичные рассуждения можно провести и для цепи, состоящей из параллельно соединенных R , L и C (рис. 2.31, а ). Векторная диаграмма ее резонансного режима приведена на рис. 2.42, б .

Рассмотрим теперь более сложную цепь с двумя параллельными ветвями, содержащими активные и реактивные сопротивления
(рис. 2.44, а ).

Рис. 2.44. Разветвленная цепь (а ) и ее эквивалентная схема (б )

Для нее условием резонанса является равенство нулю ее реактивной проводимости: ImY = 0 . Это равенство означает, что мы должны мнимую часть комплексного выражения Y приравнять к нулю.

Определяем комплексную проводимость цепи. Она равна сумме комплексных проводимостей ветвей:

Приравнивая к нулю выражение, стоящее в круглых скобках, получаем:

или . (2.34)

Левая и правая части последнего выражения представляют собой не что иное, как реактивные проводимости первой и второй ветвей B 1 и B 2 . Заменяя схему на рис. 2.44, а эквивалентной (рис. 2.44, б ), параметры которой вычисляем по формуле (2. 31), и используя условие резонанса(B = B 1 – B 2 = 0), снова приходим к выражению (2.34).

Схеме на рис. 2.44, б соответствует векторная диаграмма, приведенная на рис. 2.45.

Резонанс в разветвленной цепи называется резонансом токов . Реактивные составляющие токов параллельных ветвей противоположны по фазе, равны по величине и компенсируют друг друга, а сумма активных составляющих токов ветвей дает общий ток.

Рис. 2.45. Векторная диаграмма резонансного режима разветвленной цепи

Пример 2.23. Считая R 2 и x 3 известными, определить величину x 1 , при которой в цепи наступит резонанс напряжений (рис. 2.46, а ). Для резонансного режима построить векторную диаграмму.

САМАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ

Электрические цепи переменного тока Явление резонанса.

Выполнил:

Антропов А. И.

Проверила:

Бородина А. В.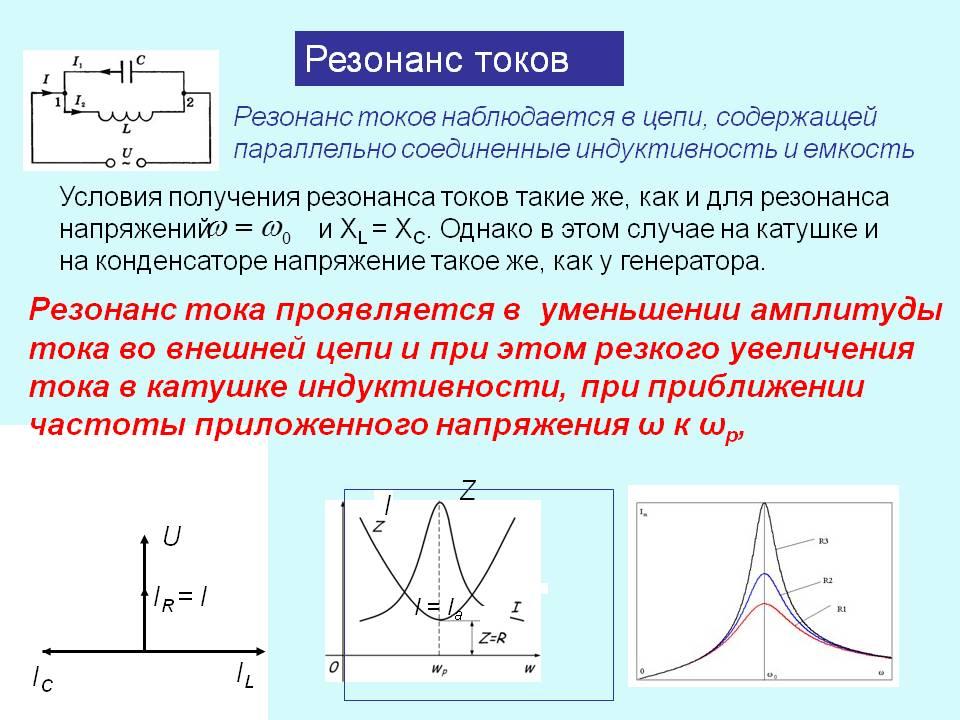

Самара 2009

Электрические цепи переменного тока. Явление резонанса

Явление резонанса относится к наиболее важным с практической точки зрения свойствам электрических цепей. Оно заключается в том, что электрическая цепь, имеющая реактивные элементы обладает чисто резистивным сопротивлением .

Общее условие резонанса для любого двухполюсника можно сформулировать в виде Im[Z ]=0 или Im[Y ]=0, где Z и Y комплексное сопротивление и проводимость двухполюсника. Следовательно, режим резонанса полностью определяется параметрами электрической цепи и не зависит от внешнего воздействия на нее со стороны источников электрической энергии.

Для определения условий возникновения режима резонанса в электрической цепи нужно:

· найти ее комплексное сопротивление или проводимость;

· выделить мнимую часть и приравнять нулю.

Все параметры электрической цепи, входящие в полученное уравнение, будут в той или иной степени влиять на характеристики явления резонанса.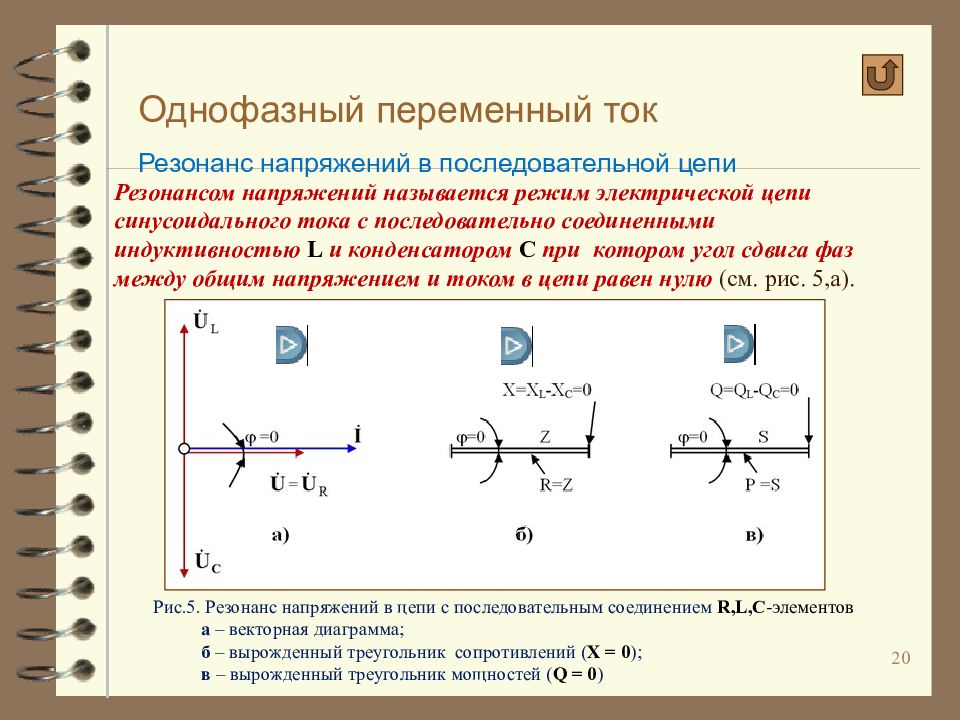

Уравнение Im[Z ]=0 может иметь несколько корней решения относительно какого-либо параметра. Это означает возможность возникновения резонанса при всех значениях этого параметра, соответствующих корням решения и имеющих физический смысл.

В электрических цепях резонанс может рассматриваться в задачах:

· анализа этого явления при вариации параметров цепи;

· синтеза цепи с заданными резонансными параметрами.

Электрические цепи с большим количеством реактивных элементов и связей могут представлять значительную сложность при анализе и почти никогда не используются для синтеза цепей с заданными свойствами, т.к. для них не всегда возможно получить однозначное решение. Поэтому на практике исследуются простейшие двухполюсники и с их помощью создаются сложные цепи с требуемыми параметрами.

Сдвиг фаз между током и напряжением. Понятие двухполюсника

Простейшими электрическими цепями, в которых может возникать резонанс, являются последовательное и параллельное соединения резистора, индуктивности и емкости. Соответственно схеме соединения, эти цепи называются последовательным и параллельным резонансным контуром . Наличие резистивного сопротивления в резонансном контуре по определению не является обязательным и оно может отсутствовать как отдельный элемент (резистор). Однако при анализе резистивным сопротивлением следует учитывать по крайней мере сопротивления проводников.

Последовательный резонансный контур представлен на рис. 1 а). Комплексное сопротивление цепи равно

Условием резонанса из выражения (1) будет

Таким образом, резонанс в цепи наступает независимо от значения резистивного сопротивления R когда индуктивное сопротивление x L = wL равно емкостному x C = 1/(wC ) . Как следует из выражения (2), это состояние может быть получено вариацией любого их трех параметров — L , C и w , а также любой их комбинацией. При вариации одного из параметров условие резонанса можно представить в виде

Все величины, входящие в выражение (3) положительны, поэтому эти условия выполнимы всегда, т. е. резонанс в последовательном контуре можно создать

· изменением индуктивности L при постоянных значениях C и w ;

· изменением емкости C при постоянных значениях L и w ;

· изменением частоты w при постоянных значениях L и C .

Наибольший интерес для практики представляет вариация частоты. Поэтому рассмотрим процессы в контуре при этом условии.

При изменении частоты резистивная составляющая комплексного сопротивления цепи Z остается постоянной, а реактивная изменяется. Поэтому конец вектора Z на комплексной плоскости перемещается по прямой параллельной мнимой оси и проходящей через точку R вещественной оси (рис. 1 б)). В режиме резонанса мнимая составляющая Z равна нулю и Z = Z = Z min = R , j = 0 , т.е. полное сопротивление при резонансе соответствует минимальному значению .

Индуктивное и емкостное сопротивления изменяются в зависимости от частоты так, как показано на рис. 2. При частоте стремящейся к нулю x C ®µ , x L ® 0 , и j® — 90° (рис. 1 б)). При бесконечном увеличении частоты — x L ®µ , x C ® 0 , а j® 90° . Равенство сопротивлений x L и x C наступает в режиме резонанса при частоте w 0 .

Рассмотрим теперь падения напряжения на элементах контура. Пусть резонансный контур питается от источника, обладающего свойствами источника ЭДС, т.е. напряжение на входе контура u = const, и пусть ток в контуре равен i =I m sinwt . Падение напряжения на входе уравновешивается суммой напряжений на элементах

Переходя от амплитудных значений к действующим, из выражения (4) получим напряжения на отдельных элементах контура

А при резонансной частоте

величина, имеющая размерность сопротивления и называемая волновым или характеристическим сопротивлением контура.

Следовательно, при резонансе

· напряжение на резисторе равно напряжению на входе контура;

· напряжения на реактивных элементах одинаковы и пропорциональны волновому сопротивлению контура;

· соотношение напряжения на входе контура (на резисторе) и напряжений на реактивных элементах определяется соотношением резистивного и волнового сопротивлений.

Отношение волнового сопротивления к резистивному r /R = Q , называется добротностью контура , а величина обратная D =1/Q — затуханием . Таким образом, добротность числено равна отношению напряжения на реактивном элементе контура к напряжению на резисторе или на входе в режиме резонанса. Добротность может составлять несколько десятков единиц и во столько же раз напряжение на реактивных элементах контура будет превышать входное. Поэтому резонанс в последовательном контуре называется резонансом напряжений .

Рассмотрим зависимости напряжений и тока в контуре от частоты. Для возможности обобщенного анализа перейдем в выражениях (5) к относительным единицам, разделив их на входное напряжение при резонансе

U =RI 0

где i =I /I 0 , u k =U k /U , v = w /w 0 — соответственно ток, напряжение и частота в относительных единицах, в которых в качестве базовых величин приняты ток I 0 , напряжение на входе U и частота w 0 в режиме резонанса.

Абсолютный и относительный ток в контуре равен

Из выражений (7) и (8) следует, что характер изменения всех величин при изменении частоты зависит только от добротности контура. Графическое представление их при Q =2 приведено на рис. 3 в логарифмическом (а) и линейном (б) масштабах оси абсцисс.

На рис. 3 кривые A (v), B (v) и C (v) соответствуют напряжению на индуктивности, емкости и резисторе или току в контуре. Кривые A (v)=u L (v) и B (v)=u C (v) имеют максимумы, напряжения в которых определяются выражением

, (9)

а относительные частоты максимумов равны

(10)

При увеличении добротности Q ®µA max = B max ®Q , а v 1 ®1.0 и v 2 ®1.0.

С уменьшением добротности максимумы кривых u L (v) и u С (v) смещаются от резонансной частоты, а при Q 2

Напряжение на резисторе и ток в контуре имеют при резонансной частоте максимум равный 1,0. Если на оси ординат отложить абсолютные значения тока или напряжения на резисторе, то для различных значений добротности они будут иметь вид, показанный на рис. 4. В целом они дают представление о характере изменения величин, но удобнее делать сопоставление в относительных единицах.

На рис. 5 представлены кривые рис. 4 в относительных единицах. Здесь видно, что увеличение добротности влияет на скорость изменения тока при изменении частоты.

Можно показать, что разность относительных частот, соответствующих значениям относительного тока

, равна затуханию контура D =1/Q =v 2 -v 1 .

Перейдем теперь к анализу зависимости фазового сдвига между током и напряжением на входе контура от частоты. Из выражения (1) угол j равен

При протекании электроэнергии по элементам электрической схемы возможно возникновение различных режимов; совпадение по фазе вектора токов и напряжений в цепях с емкостью и индуктивностью называют явлением электрического резонанса.

При нем исчезает реактивный характер нагрузки и выполняются все соотношения для активного сопротивления , когда Х=I m ∙Z, В= I m ∙Y, R=Z, φ=0 .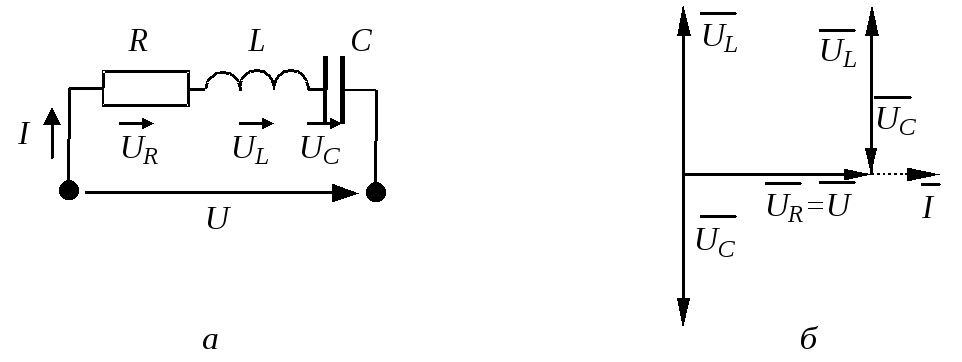

В электротехнике при последовательном соединении элементов индуктивной и емкостной нагрузки возможен резонанс напряжений. Рассмотрим его проявление для простейшей цепи с последовательно образованным контуром, когда резонанс проявится при случае Х=Х L -Х C =0 . Выразим Х L =Х C , а после подстановки их выражений получим соотношение:

φL=1/φC .

У индуктивности и емкости для рассматриваемого случая вектора напряжений находятся в противоположных фазах, уравновешивают друг друга. При этом, все напряжение, которое приложено на электрическую схему, воздействует на активное сопротивление. Диаграмма векторов представлена следующим видом:

Диаграмма демонстрирует, что величины напряжений на реактивных нагрузках при резонансе могут весьма значительно превышать входное напряжение схемы. Для оценки этого параметра введено термин добротности контура Q .

Q=U L /U=U C /U=x Lрез /R=x Cрез /R .

Она зависит от частоты, величины емкости или индуктивности. Изменяя любой из перечисленных параметров можно регулировать величину добротности. В радиотехнике она нашла широкое применение, где ее величина доводится до больших значений в несколько сотен единиц во время резонанса напряжений.

При этом возникают изменения реактивного и полного сопротивлений в схеме, следствием чего проявляются изменения токов, напряжений, углов сдвига фаз на различных приемниках электроэнергии.

Зависимость параметров электрической схемы при изменении значений емкости С O для создания резонанса демонстрирует график:

Величину С O выражает соотношение: С O =1/(ω2L) .

Вполне допустимо рассмотреть случай параллельного соединения нагрузок R, L и C . Для него будет справедлива векторная диаграмма вида:

На практике приходится иметь дело с более сложными соединениями элементов. Для примера можно взять разветвленную схему с 2-мя параллельными ветвями, включающими как активные, так и реактивные нагрузки.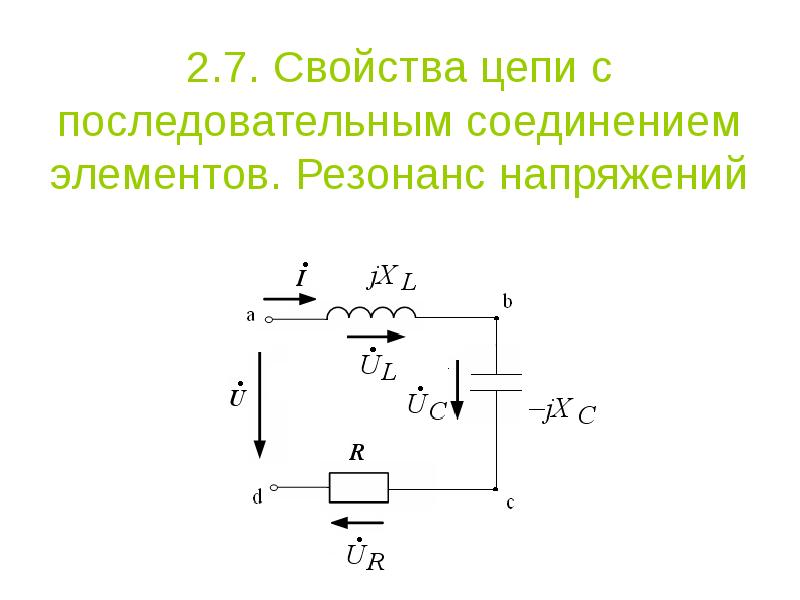

У данной цепи резонанс наступает при равенстве нулю составляющей ее реактивной проводимости, когда I m ∙Y=0 . То есть, при рассматриваемом случае мнимая часть у комплексного выражения Y приравнена к нулю.

Найдем значение комплексной проводимости для схемы, которая выразится суммой всех проводимостей в ветвях.

Y=Y1+Y2=1/Z1+1/Z2=1/(R1+jx1)+1/(R2-jx2)=(R1-jx1)/(R 2 1+x 2 1)+(R2+jx2)/(R 2 2+x 2 2)=
R1/(R 2 1+x 2 1)+R2/(R 2 2+x 2 2)-j(x1/(R 2 1+x 2 1)-x2/(R 2 2+x 2 2)) .

Выражение, выделенное круглыми скобками, приравниваем к нулю и получаем соотношение:

x1/(R 2 1+x 2 1)=x2/(R 2 2+x 2 2) .

Данное соотношение может быть представлено развернутым видом:

φL/(R 2 1+(φL) 2)=(1/φC)/(R 2 2+(1/φC) 2) .

Мы получили выражение, не похожее на реактивные проводимости для 1-й и 2-й ветвей цепи с В1 и В2 . Сделаем замену рассматриваемой нами схемы на эквивалентную. У нее значения параметров определены расчетом для условий резонанса, когда В=В1-В2=0 :

Таким способом мы пришли к искомому выражению. Векторная диаграмма для полученной схемы разветвленной цепи может быть выражена так:

В разветвленных схемах возникает явление резонанса токов, когда реактивные части токов для противоположных ветвей направлены в противоположных направлениях и уравновешены между собой по величине. Общий ток в схеме формируется суммой составляющих активных токов в ветвях.

Резонанс напряжений, условие возникновения

Резонанс токов (параллельный резонанс) — резонанс, происходящий в параллельном колебательном контуре при его подключении к источнику напряжения, частота которого совпадает c резонансной частотой контура.

Блок: 1/9 | Кол-во символов: 208
Источник: https://ru.wikipedia.org/wiki/%D0%A0%D0%B5%D0%B7%D0%BE%D0%BD%D0%B0%D0%BD%D1%81_%D1%82%D0%BE%D0%BA%D0%BE%D0%B2

Что это такое

Резонанс токов — разновидность состояния электрической цепи, когда общий вид токовых показателей совпадает по фазам уровню напряжения, а мощность реактивного вида равна нулю или же она представлена в активном виде.

. Резонанс токов

Этот вариант развития событий характерен для переменного тока и имеет не только положительные свойства, но и некоторые нежелательные последствия. Так, благодаря резонансу работает радиотехника, автоматика и проволочная телефония, но в то же время возникают перенапряжения и сбои в работе электрической системы.

Определение из учебного пособия

Блок: 2/6 | Кол-во символов: 589
Источник: https://rusenergetics.ru/ustroistvo/rezonans-tokov

При каких условиях возникает

Условием того, чтобы возникло это явление, является равные показатели проводниковой частоты, где BL=BC. То есть емкостная с индуктивной проводимостью должна быть равна. Только тогда подобное явление резонанса токов наблюдается в электрической цепи. Он при этом может быть как положительным, так и отрицательным. В любом радиоприемнике есть колебательный контур, который из-за индуктивного или емкостного изменения, настраивается на нужный сигнал радиоволны. В другом случае, это ведет к тому, что появляются скачки напряжения или ток в цепи и появляется аварийная ситуация.

В условиях лаборатории, он возникает во время, когда изменяется емкость и не изменяется индуктивность катушки L. В таком случае формула выглядит как Bc=C

При каких условиях возникает

Блок: 3/6 | Кол-во символов: 786
Источник: https://rusenergetics.ru/ustroistvo/rezonans-tokov

Собственная частота резонансного контура

Емкость конденсатора (С) в совокупности с индуктивностью катушки (L) определяют собственную частоту контура (Wc). Для приблизительных расчетов пользуются формулой Wc=1/√L*C. В этом случае речь идет об идеальных условиях, когда потерями пренебрегают по причине минимальных значений.

Для повышения точности применяют коэффициент затухания (Кз). С учетом этого фактора можно привести следующую зависимость между собственной и резонансной частотами:

Wo=√Wc2-2*Кз2.

Блок: 3/12 | Кол-во символов: 502
Источник: https://amperof.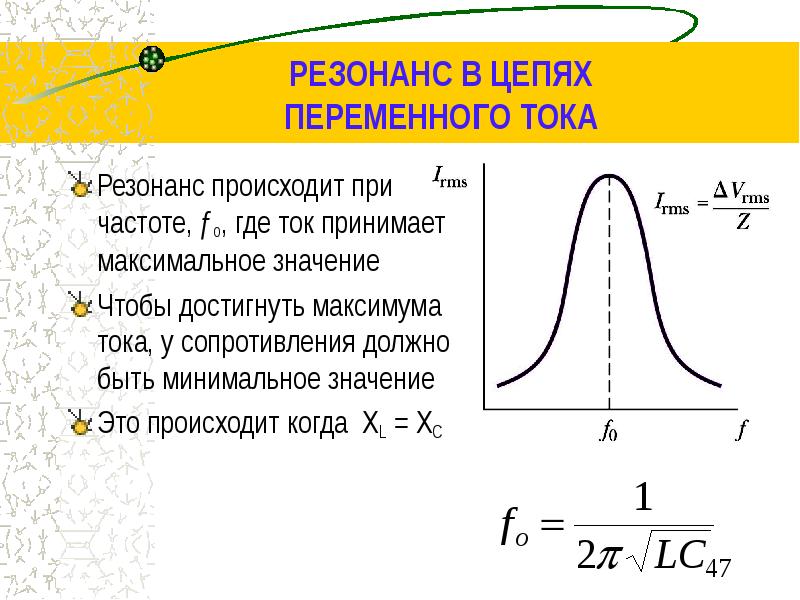 ru/bezopasnost/usloviya-rezonansa.html

Использование резонанса напряжений для передачи радиосигнала

Колебательный контур этого типа создают из последовательной комбинации трех базовых компонентов: резистор, конденсатор, индуктивность. Подходящим для резонанса условием является нулевое сопротивление цепи (комплексное). Для решения такой задачи следует изучить основные формулы.

Комплексное сопротивление Rк=R+j(wL-1/wC). Постоянный резистор (R) не зависит от частоты (w). Значит, придется оперировать с индукционными и емкостными элементами. Резонансный эффект получают при (wL-1/wC)=0. Для вычисления необходимых значений пользуются следующими расчетами:

• Lп=1/w2*C;
• Сп=1/w2*L;
• Wп=1/√L*C.

Из приведенных данных понятно, что корректировать можно любой из параметров при одновременном сохранении двух других. В практической схемотехнике удобнее работать с частотой, поэтому рассмотрим подробнее применение такого варианта.

Последовательный контур с графиками

На рисунках показаны условия возникновения резонанса напряжений. В точке, обозначенной w0, наблюдается равенство индуктивной и емкостной составляющих на определенной частоте. Небольшой сдвиг влево по оси обусловлен резистивным компонентом цепи.

Напряжение на конденсаторе (Uc) при частоте резонанса (W0) равно волновому сопротивлению колебательного контура (p=√L/C). Аналогичная разница потенциалов будет на клеммах катушки при частоте W0. Данная особенность объясняет особое название процесса – «резонанс напряжений». Также в электротехнических расчетах применяют следующие определения:

• Добротность – Q=p/R;
• Затухание – 1/Q.

Отмеченные свойства используют в радиоприемной и передающей аппаратуре. Выделение контуром определенного диапазона позволяет выполнять настройку станции на определенную частоту с определенной параметрами цепи погрешностью. Для контроля избирательности оценивают амплитуду сигнала относительно резонансной частоты. Уровень отклонения на 3 дБ в обе стороны (0,7 от максимума) называют полосой пропускания.

Амплитудно-частотная характеристика (АЧХ) и полоса пропускания

Блок: 2/12 | Кол-во символов: 2012
Источник: https://amperof.ru/bezopasnost/usloviya-rezonansa.html

Примеры применения на практике

Классическим примером применения резонанса колебательных контуров является настройка радиоприёмника на частоту соответствующей радиостанции. В качестве рабочего элемента настроечного узла используется конденсатор с регулируемой ёмкостью. Вращение ручки настройки изменяет ёмкость конденсатора, а значит и резонансную частоту контура.

В момент совпадения резонансной частоты с рабочей частотой какой-либо радиостанции возникает резонанс напряжений, в результате которого резко возрастает амплитуда колебаний принятой радиоприёмником частоты. Специальные фильтры отделяют эти колебания от несущих радиочастот, а усилители усиливают полученные сигналы. В динамике появляются звуки, генерируемые передатчиком радиостанции.

Колебательные контуры, построенные на принципе последовательного соединения LC-элементов, применяются в цепях питания высокоомных нагрузок, потребляющих токи повышенного напряжения. Такие же устройства применяют в полосовых фильтрах.

Последовательный резонанс применяют при пониженных напряжениях сети. В этом случае используют реактивную энергию обмоток трансформатора, соединённых последовательно.

Конденсаторы и различные катушки индуктивности (рис. 5) входят в конструкцию практически всех аналоговых устройств. Они используются для настройки фильтров или для управления токами в отдельных узлах.

Катушки индуктивности

Важно знать, что резонансные контуры не увеличивают количество электрической энергии в цепях. Они лишь могут повышать напряжения, иногда до опасных значений. Постоянный ток не причиной резонансных явлений.

Наряду с полезными свойствами резонансных явлений, в практической электротехнике часто возникают ситуации, когда резонанс напряжений приносит вред. В основном это связано с нежелательным повышением параметров тока на участках цепей. Примером могут служить опасное резонансные явления в кабельных линиях без нагрузки, что может привести к пробоям изоляции. Чтобы этого не случилось, на концевых участках таких линий устанавливают балластные нагрузочные элементы.

Блок: 3/3 | Кол-во символов: 2059
Источник: https://www.asutpp.ru/rezonans-napryazheniy.html

Замечания

• Колебательный контур, работающий в режиме резонанса токов, не является усилителем мощности. Он является усилителем тока.

Большие токи, циркулирующие в контуре, возникают за счет мощного импульса тока от генератора в момент включения, когда заряжается конденсатор. При значительном отборе мощности от контура эти токи «расходуются», и генератору вновь приходится отдавать значительный ток подзарядки. Поэтому внутри контура сопротивление должно быть сведено к минимуму чтобы уменьшить потери.

• Если генератор слабый, большой ток подзарядки в момент его включения на колебательный контур может сжечь его. Выйти из положения можно, постепенно повышая напряжение на клеммах генератора (постепенно «раскачивая» контур).

• Колебательный контур с низкой добротностью и катушкой небольшой индуктивности слишком плохо «накачивается» энергией (запасает мало энергии), что понижает КПД системы. Также катушка с маленькой индуктивностью и на низких частотах обладает малым индуктивным сопротивлением, что может привести к «короткому замыканию» генератора по катушке, и вывести генератор из строя.

• Добротность колебательного контура пропорциональна L/C, колебательный контур с низкой добротностью плохо «запасает» энергию. Для повышения добротности колебательного контура используют несколько путей:

1. Повышение рабочей частоты;
2. По возможности увеличить L и уменьшить C. Если увеличить L с помощью увеличения витков катушки или увеличения длины провода не представляется возможным, используют ферромагнитные сердечники или ферромагнитные вставки в катушку; катушка обклеивается пластинками из ферромагнитного материала и т п.

• При расчёте колебательного контура с катушкой небольшой индуктивности, нужно учитывать индуктивность соединительных шин (от катушки к конденсатору), соединительные провода конденсаторной батареи. Индуктивность соединительных шин может быть намного больше индуктивности катушки и серьёзно понизить частоту колебательного контура.

• При реализации резонанса токов на трансформаторах, первичная и вторичная обмотки должны располагаться на разных кернах на магнитопроводе, иначе электромагнитные наводки от вторичной обмотки будут мешать резонансу. Поэтому годятся трансформаторы с П образным или Ш образным сердечником. В противном случае обмотки тщательно экранируют друг от друга фольгой.

Блок: 4/9 | Кол-во символов: 2298
Источник: https://ru.wikipedia.org/wiki/%D0%A0%D0%B5%D0%B7%D0%BE%D0%BD%D0%B0%D0%BD%D1%81_%D1%82%D0%BE%D0%BA%D0%BE%D0%B2

Как используется

Резонансные токи используются сегодня в некоторых фильтрующих системах, радиотехнике, электричестве, радиостанциях, асинхронных двигателях, высокоточных электрических сварных установках, колебательных генераторных электрических контурах и высокочастотных приборах. Нередко, когда они применяются, чтобы снизить генераторную нагрузку.

Обратите внимание! Простейшая цепь, где наблюдаются они, это параллельного вида колебательный контур. Такие контуры используются в современном промышленном индукционном котловом оборудовании и улучшают показатели КПД.

Сфера применения

Блок: 4/6 | Кол-во символов: 590
Источник: https://rusenergetics.ru/ustroistvo/rezonans-tokov

Последовательно-параллельный резонанс

Параллельно-последовательный резонанс выполненый на основе трансформаторов.

Параллельно-последовательный резонанс.

Кроме параллельного и последовательного резонанса существует также комбинированный, а точнее параллельно-последовательный. В простейшем варианте это две катушки с одинаковой индуктивностью соединённые последовательно. На одной из катушек реализован колебательный контур. При этом на половину проявляется эффект от параллельного резонанса и на половину проявляется эффект от последовательного резонанса.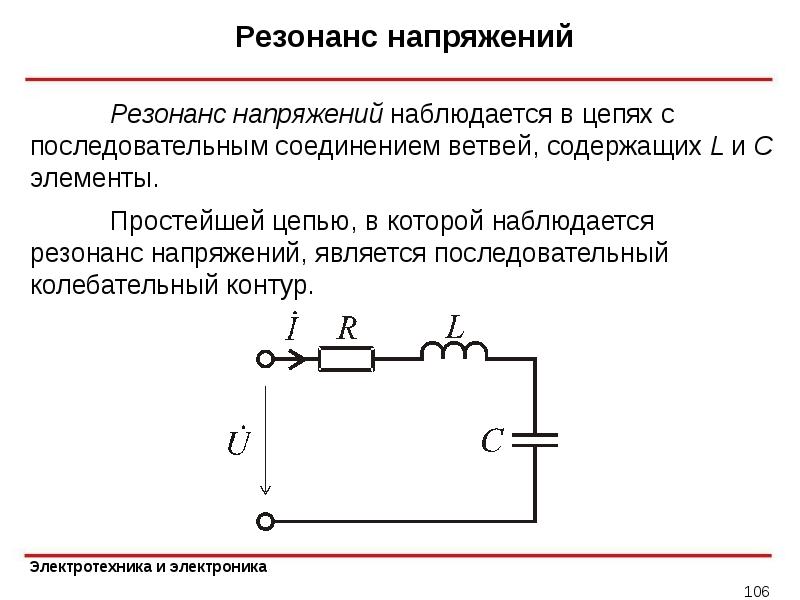 Поэтому при этом происходит частичное увеличение напряжения. Этот способ уместно применять в тех случаях когда генератор не может выдать нужное напряжение или напряжение в сети проседает. Но применяется такой способ только к тем потребителям, у которых нагрузка постоянная, потому что если нагрузка будет меняться, то резонанс будет сбиваться. Для такой схемы годятся не любые трансформаторы, а только те у которых обмотки не накладываются друг на друга и располагаются на разных кернах на против друг друга на сердечнике. Если вторичная обмотка намотана поверх первичной, то на таком трансформаторе параллельный резонанс не работает. Кроме этого существуют и более сложные схемы последовательно-параллельного резонанса использующие полупроводники, такие как транзисторы.

Блок: 3/9 | Кол-во символов: 1329
Источник: https://ru.wikipedia.org/wiki/%D0%A0%D0%B5%D0%B7%D0%BE%D0%BD%D0%B0%D0%BD%D1%81_%D1%82%D0%BE%D0%BA%D0%BE%D0%B2

Принцип действия

Токовый резонанс можно заметить во внутренней поверхности электрической цепи, которая имеет параллельное катушечное, резисторное и конденсаторное подсоединение. Главный принцип того, как работает стандартный аппарат, не сложен в понимании.

Когда включается электрическое питание, внутри конденсаторной установки накапливается заряд до номинального напряжения. В этом время отключается питающий источник и замыкается цепь в контур. Этот момент сопровождается переносом разряда на часть катушки. Далее показатели тока, которые проходят по катушке, генерируют магнитное поле. Создается электродвижущая самостоятельная индукционная сила по направлению встречному току. При полном конденсаторном разряде максимально увеличиваются токовые показатели. Объем энергии становится магнитным индукционным полем. В результате данный цикл повторяется, и катушечное поле преобразовывается в конденсаторный заряд.

Принцип работы

Блок: 5/6 | Кол-во символов: 930
Источник: https://rusenergetics.ru/ustroistvo/rezonans-tokov

Как правильно рассчитать

Токовый резонанс очень важно правильно рассчитать, если есть параллельное соединение, предотвращающая появление помех около системы. Для правильного расчета необходимо понять, какие показатели мощности в электросети. Средняя стандартная мощность, рассеивающаяся при резонансном контуре, выражается при помощи среднеквадратичных токовых показателей и напряжения. При резонансе мощностный коэффициент равен единице и формула имеет вид, как на картинке.

Формула расчета

Чтобы правильно определить нулевой импеданс, понадобиться воспользоваться стандартной формулой, которая дана ниже.

Формула резонансных кривых

Что касается аппроксимирования резонанса колебательных частот, это можно выяснить по следующей формуле.

Расчет колебательного контура

Обратите внимание! Для получения максимально точных данных по приведенным формулам, округлять данные не нужно. Благодаря этому получится грамотный расчет, который приведет к достойной экономии переменного тока, если речь идет о подсчете в целях снижения счетов.

В целом, резонанс токов — это то, что происходит в части параллельного колебательного контура, в случае его подключения к источнику напряжения, частота какого может совпадать с контурной. Возникает при условиях, когда цепь, имеющая параллельное соединение резисторной катушки и конденсатора, равна проводимости BL=BC. Правильно сделать весь необходимый подсчет можно по специальной формуле или, прибегая к использованию специальных измерительных инструментов в виде мультиметра.

Блок: 6/6 | Кол-во символов: 1511
Источник: https://rusenergetics.ru/ustroistvo/rezonans-tokov

Резонанс в линейных системах с одной степенью свободы

К этой группе можно причислить рассмотренные последовательные и параллельные электрические схемы. Механический пример – пружина с грузом, который способен перемещаться только по вертикальной прямой. Исключены порывы ветра, вибрации, другие «паразитные» внешние воздействия. В подобных условиях можно применять типовые формулы для систем линейного типа.

Отмеченная выше добротность является определяющим фактором для избирательности по частоте. Сужение ширины резонансного диапазона помогает улучшить характеристики приемных и передающих устройств. Кроме экономного расходования электроэнергии, при правильном расчете схемы существенно улучшается помехозащищенность.

Блок: 6/12 | Кол-во символов: 720
Источник: https://amperof.ru/bezopasnost/usloviya-rezonansa.html

Литература

• Власов В. Ф. Курс радиотехники. М.: Госэнергоиздат, 1962. С. 928.
• Изюмов Н. М., Линде Д. П. Основы радиотехники. М.: Госэнергоиздат, 1959. С. 512.

Блок: 8/9 | Кол-во символов: 157
Источник: https://ru.wikipedia.org/wiki/%D0%A0%D0%B5%D0%B7%D0%BE%D0%BD%D0%B0%D0%BD%D1%81_%D1%82%D0%BE%D0%BA%D0%BE%D0%B2

Ссылки

Резонанс токов

Circuits. A/C Circuits. Parallel Resonance

Частотно-модулированный преобразователь с последовательно- параллельным резонансом

Блок: 9/9 | Кол-во символов: 148
Источник: https://ru.wikipedia.org/wiki/%D0%A0%D0%B5%D0%B7%D0%BE%D0%BD%D0%B0%D0%BD%D1%81_%D1%82%D0%BE%D0%BA%D0%BE%D0%B2

Резонанс в реальных цепях

Для изучения описанных процессов надо собрать контур из соответствующих компонентов. Придется подготовить генератор с изменяющейся частотой выходного сигнала, осциллограф и другие измерительные инструменты. Чтобы получить достоверные результаты без лишних трудностей, пользуются специализированным программным обеспечением.

Теория и практика

В левой части рисунка размещены схема и амплитуда сигнала на выходе при подключении к выводам конденсатора параллельного контура. В правой – снимок экрана измерительной аппаратуры. Несложно убедиться в идентичности колебаний.

К сведению. С помощью ПО выполняют десятки экспериментов быстро и точно в обычных домашних условиях. Этот способ значительно упрощает создание электрических схем с оптимальными параметрами.

Блок: 9/12 | Кол-во символов: 785
Источник: https://amperof.ru/bezopasnost/usloviya-rezonansa.html

Частотные характеристики контура

Для любой схемы определить выходные параметры можно по параметрам входного сигнала, значениям емкости (индуктивности). Также применяют расчет по добротности контура:

• параллельный: Q=1/w*L*C;
• последовательный: Q= 1/w*C*R=wL/R.

Блок: 10/12 | Кол-во символов: 259
Источник: https://amperof.ru/bezopasnost/usloviya-rezonansa.html

Резонанс в линейных колебательных системах с несколькими степенями свободы

Такие расчеты понадобятся при конструировании двух последовательных контуров с индуктивной связью. В этом случае переменные колебательные процессы оказывают взаимное влияние. Фактически речь идет о распределенной системе.

Кроме схемотехники, в подобных ситуациях отдельно изучают коэффициент связи (Кс). При работе с трансформатором его вычисляют делением напряжений на первичной (вторичной) катушке, соответственно. Следует учесть реактивные характеристики, которые преобладают в рабочем диапазоне частот.

Узнав, что такое резонанс напряжений и токов, можно самостоятельно реализовать различные проекты. Тщательная предварительная подготовка необходима для создания схемы с хорошими эксплуатационными параметрами. Начинают с чертежей и расчетной части. Теоретические изыскания дополняют изготовлением макета и практическими испытаниями. Ускоряют подготовку конструкторской документации, а также выполняют эксперименты с применением программного обеспечения. В наиболее сложных ситуациях обращаются к опытным специалистам.

Блок: 11/12 | Кол-во символов: 1098
Источник: https://amperof.ru/bezopasnost/usloviya-rezonansa.html

Видео

Блок: 12/12 | Кол-во символов: 6
Источник: https://amperof.ru/bezopasnost/usloviya-rezonansa.html

Кол-во блоков: 23 | Общее кол-во символов: 16179
Количество использованных доноров: 5
Информация по каждому донору:

1. https://rusenergetics.ru/ustroistvo/rezonans-tokov: использовано 5 блоков из 6, кол-во символов 4406 (27%)
2. https://ru.wikipedia.org/wiki/%D0%A0%D0%B5%D0%B7%D0%BE%D0%BD%D0%B0%D0%BD%D1%81_%D1%82%D0%BE%D0%BA%D0%BE%D0%B2: использовано 5 блоков из 9, кол-во символов 4140 (26%)
3. https://www.asutpp.ru/rezonans-napryazheniy.html: использовано 1 блоков из 3, кол-во символов 2059 (13%)
4. https://amperof.ru/bezopasnost/usloviya-rezonansa.html: использовано 7 блоков из 12, кол-во символов 5382 (33%)
5. https://remont220.ru/stati/728-rezonans-napryazheniy-uslovie-vozniknoveniya/: использовано 3 блоков из 5, кол-во символов 192 (1%)

Резонансные явления в электрических сетях

Идеальное активное сопротивление от частоты не зависит, индуктивное сопротивление линейно зависит от частоты, емкостное сопротивление зависит от частоты по гиперболическому закону:

Резонанс напряжений

Резонансом в электрических цепях называется режим участка электрической цепи, содержащей индуктивный и емкостной элементы, при котором разность фаз между напряжением и током равна нулю . Режим резонанса может быть получен при изменении частоты питающего напряжения или изменением параметров элементов L и С.
При последовательном соединении возникает резонанс напряжения.

Последовательное соединение R, L, C.

Знаменатель данного выражения есть модуль комплексного сопротивления, который зависит от частоты. При достижении некоторой частоты реактивная составляющая сопротивления исчезает, модуль сопротивления становится минимальным, ток в данной схеме возрастает до максимального значения, причем вектор тока совпадает с вектором напряжения по фазе:

Максимальная амплитуда силы тока достигается при условии минимума полного сопротивления, т. е. при

где
— резонансная частота напряжения, определяемая из условия

При последовательном соединении в цепь конденсатора и соленоида силы токов в каждом из участков цепи, как известно, равны. Поэтому, умножив левую и правую части последнего соотношения на силу тока Im, получим

В этом выражении слева — амплитуда напряжения на концах соленоида, а справа — амплитуда напряжения на обкладках конденсатора.
Мы видим, что . Отсюда получаем

Знак минус указывает на то, что колебания напряжения на участках с индуктивностью и емкостью происходят в противофазе.
Режим электрической цепи при последовательном соединении индуктивности и емкости, характеризующийся равенством напряжений на индуктивности и емкости, называют резонансом напряжений.

 

Волновое или характеристическое сопротивление последовательного контура

Отношение напряжения на индуктивности или емкости к напряжению на входе в режиме резонанса называется добротностью контура:

Добротность контура представляет собой коэффициент усиления по напряжению и в катушках индуктивности может достигать сотен единиц:

При напряжение на индуктивности (или емкости) может быть гораздо больше напряжения на входе, что широко используется в радиотехнике. В промышленных сетях резонанс напряжений является аварийным режимом, так как увеличение напряжения на конденсаторе может привести к его пробою, а рост тока — к нагреву проводов и изоляции.

Резонанс токов

При параллельном соединении конденсатора и соленоида (смотри рисунок), так же как и при последовательном, сила тока в цепи зависит от значений емкости и индуктивности. При изменении емкости и индуктивности при определенном их соотношении сила тока в неразветвленном участке цепи оказывается минимальной (практически близкой к нулю).
В этом случае:

Параллельное соединение реактивных элементов

тогда

При определенной частоте, называемой резонансной, реактивные составляющие проводимости могут сравняться по модулю и суммарная проводимость будет минимальной. Общее сопротивление при этом становится максимальным, общий ток минимальным, вектор тока совпадает с вектором напряжения. Такое явление называется резонансом токов.
Волновая проводимость

При ток в ветви с индуктивностью гораздо больше общего тока, поэтому такое явление называется резонансом токов и широко используется в силовых сетях промышленных предприятий для компенсации реактивной мощности.
Резонансную частоту тока найдем из условия равенства реактивных проводимостей ветвей.

После ряда преобразований получим:

Из формулы следует, что:

1) резонансная частота зависит от параметров не только реактивных сопротивлений, но и активных;
2) резонанс возможен, если и больше или меньше ρ, в противном случае частота будет мнимой величиной и резонанс невозможен;
3) если , то частота будет иметь неопределенное значение, что означает возможность существования резонанса на любой частоте при совпадении фаз напряжения питания и общего тока;
4) при резонансная частота напряжения равна резонансной частоте тока.

Энергетические процессы в цепи при резонансе токов аналогичны процессам, происходящим при резонансе напряжений.
Реактивная энергия циркулирует внутри цепи: в одну часть периода энергия магнитного поля индуктивности переходит в энергию электрического поля емкости, в следующую часть периода происходит обратный процесс.
При резонансе токов реактивная мощность равна нулю.
Большинство промышленных потребителей переменного тока носит активно-индуктивный характер и, следовательно, потребляет реактивную мощность. К таким потребителям относятся асинхронные двигатели, установки электрической сварки и т.д.
Для уменьшения реактивной мощности и повышения коэффициента мощности параллельно потребителю включают батарею конденсаторов, что приводит к уменьшению тока в проводах, соединяющих потребителя с источником энергии.

Резонанс напряжений — Справочник химика 21

    Условие для резонанса напряжения [c.323]

    Изменение энтальпии химической реакции является, по существу, разностью энергий связей реагентов и продуктов, включая энергию сопряжения (резонанса), напряжения, например в цикле, сольватации. [c.84]

    Двухполюсники, элементы которых обладают одинаковой колебательной скоростью (рис. 1.77, в), называют соединенными узлом, что соответствует последовательному соединению на эквивалентной схеме (рис. 1.77, г). В этом случае на элементы двухполюсника действуют разные силы. Резонанс в механическом двухполюснике т. К, К с элементами, соединенными узлом, именуют резонансом сил. Это соответствует резонансу напряжений в [c.118]

    На рис. 3.40, а представлена схема последовательного резонансного контура, в котором наблюдается резонанс напряжений. Аналогично рассмотренному примеру для измерений может быть использован и параллельный резонансный контур, в котором наблюдается резонанс токов. [c.458]

    При резонансе напряжение на образцовом конденсаторе Со, определяемое по показаниям вольтметра PV, равно  [c.462]

    Куметры работают на принципе резонанса, и поэтому все показания отсчитываются только в момент резонанса. Принципиально в приборах может быть использован как резонанс напряжений, так и резонанс токов. При применении в приборах последовательного резонансного контура с параметрами г, Ь, С, питаемого напряжением С/о> добротность контура Q можно определить, используя следующие известные соотношения  [c.463]

    Регистрация резонанса осуществлялась с помощью лампового вольтметра, измеряющего напряжение на излучающем пьезоэлементе, в некоторых схемах — по измерению анодного тока генератора. При резонансе напряжение на излучателе максимально, а ток генератора минимален. [c.103]

    На рис. 2-5 представлена, например, кривая отклика электрического колебательного контура в области резонанса. Напряжение на клеммах С-контура максимально при резонансной ча- [c.35]

    Объяснение этой непонятной аксиомы подсказывается, однако, сочетанием теории напряжения Байера с принципами резонанса. Напряжение кольца представляет собою разрушающее влияние и действует, таким образом, против стабилизирующего влияния резонанса. Резонансная энергия бензола более чем достаточна для преодоления напряжения кольца, и три электронные пары (секстет) вступают в резонанс. В циклооктатетраене копланарность восьми углеродных атомов, являющаяся необходимым условием для резонанса, ведет, очевидно, к достаточно большому напряжению кольца, чтобы преодолеть эффект резонанса поэтому ароматический октет и не разрешен. В циклопентадиене, где имеется лишь квартет электронов, возможен только ограниченный резонанс однако образование отрицательного иона создает ароматический секстет и увеличивает воз.можность резонанса. Более того, напряжение кольца в пятичленном цикле минимально. Эти соображения легко распространить на фуран, тиофен, пиридин и т. п., и при этом в каждом отдельном случае окажется, что для максимального эффекта необходим именно секстет вступающих в резонанс электронов. [c.187]

    В момент резонанса напряжение на контуре без датчика с раствором равно  [c.22]

    Как видно из рис. 106, на котором в увеличенном масштабе изображена кривая 9 (рис. 105), при частоте около 1 200 гц наступает резонанс напряжений, после чего внутреннее сопротивление аккумулятора приобретает индуктивный характер. [c.205]

    Для иллюстрации на рис. 128 показаны типичные кривые частотной зависимости внутреннего сопротивления заряженной батареи 6СТ-54 при различных температурах. В интервале температур от О до 20° С уже при частоте 1 600 гц наступает резонанс напряжений. [c.252]

    Для первого аккумулятора резонанс напряжения наступает при 800 гц, для второго — при 250 гц, а для третьего, если он и наступает, то при частотах значительно меньших 50 гц. [c.253]

    При постоянной частоте электромагнитного облучения в случае ядерного резонанса напряженность приложенного магнитного поля непосредственно характеризует магнитное поле, действующее на данный протон, и зависит от структуры остальной части молекулы. Помимо химического сдвига, т. е. положения резонансного сигнала в т-шкале, ценную информацию содержит также тонкая структура каждого сигнала. Например, протон Но будет давать дублет, если рядом расположен второй, неэквивалентный ему протон Нр. Причина этого явления состоит в том, что при наложении внешнего магнитного поля половина протонов Нр имеет спин, параллельный [c.134]

    Емкость компенсирует часть индуктивного сопротивления обмотки автотрансформатора, ток, проходящий через нее, возрастает, и напряжение на выходе автотрансформатора повышается, что характерно для случая резонанса напряжений. При повышении напряжения сети ток, проходящий через обмотку дросселя, возрастает и индуктивность дросселя падает. Емкость конденсатора подобрана таки м образом, что в контуре, состоящем из дросселя и конденсатора, наступает резонанс токов, при котором сопротивление контура становится максимальным, а ток, поступающий из сети к обмотке автотрансформатора,—минимальным. Постепенное повышение сопротивления контура до наступления резонанса при повышении напряжения сети обеспечивает стабильность напряжения на обмотке автотрансформатора (рис. II. 18) при изменении напряжения сети в больших пределах. [c.96]

    Емкость компенсирует часть индуктивного сопротивления обмотки автотрансформатора, ток, проходящий через нее, возрастает, и напрян на выходе автотрансформатора повышается, что характерно для случая резонанса напряжений. [c.63]

    В качестве реперной точки для измерения химического сдвига у ксенона в случае опытов с двойным резонансом используется линия HF. В наиболее характерных экспериментах с двойным резонансом напряженность магнитного лоля доводится до величины, при которой наблюдается, например, [c.356]

    Напряжение на конденсаторах может несколько превышать напряжение на полюсах индуктора вследствие местного резонанса напряжений в цепи, образованной [c.237]

    Последовательный контур. Резонанс напряжений. Для цепи аЬ из последовательно включенных индуктивности Ьз, емкости С и активного сопротивления Дв (рис. А, А) модуль полного сопротивления [c.16]

    При Хь — Хс = О наблюдается резонанс напряжений, при котором напряжение на индуктивности колебательного контура равно напряжению на конденсаторе этого же контура, т. е. [c.17]

    При продолжительной работе на резонансе или вблизи резонанса напряжения в колеблющихся деталях иногда достигают столь большой величины, что случаются поломки деталей, чаще всего усталостного характера. Поэтому в процессе запуска или выбега машины стараются работать вдали от резонанса или же поскорее пройти его. Однако реальное уменьшение резонансной амплитуды при нестационарном режиме достигается только при очень быстром относительном изменении частоты возбуждения (при большом угловом ускорении е главного вала, т. е. когда е > 10 ), осуществляемом лишь в поршневых машинах и в очень тихоходных турбомашинах. Параметр е может быть определен при наблюдениях запуска или выбега машины по соотношению [c.352]

    Для смешанного сопротивления (рис. 23,а) активное сопротивление г равно величине 2 в области резонанса напряжений. Емкостная составляющая находится из левой ветви кривой, а индуктивная — из правой нижеизложенными способами. [c.50]

    Как видно из рис. 122, на котором в увеличенном масштабе изображена кривая 9 (рис. 121), при частоте около 1200 Гц наступает резонанс напряжений, после чего внутреннее сопротивление аккумулятора приобретает индуктивный характер. Дальнейший разряд аккумулятора, вплоть до его окончания, практически не влияет на вид частотной зависимости внутреннего сопротивления. [c.155]

    Для аккумулятора С-1 резонанс напряжений наступает при 800 Гц, для С-6 — при 250 Гц, а для С-24, [c.184]

    Явление здесь сходно с резонансом. В контуре рис. 112,а случай (1), когда ток максимален, принято называть резонансом напряжений, так как на. конденсаторе и катушке получаются большие напряжения (по сравнению с общим напряжением на клеммах). В случае же пробки (рис. 112,6) говорят о резонансе токов, потому что ток в контуре ЬС имеет при условии (1) большую амплитуду (по сравнению с током в общей цепи). Эта теория очень проста, но простота куплена ценой отказа от рассмотрения [c.271]

    Изменение энтальпии реакции является, по существу, разностью энергий связей реагентов и продуктов, включая энергию резонанса, напряжения и сольватации. Изменение энтальпии можно рассчитать, суммируя энергии всех разрывающихся связей и вычитая из этой суммы энергии всех образующихся связей, прибавив все изменения в энергии резонанса, напряжения или сольватации. Изменение энтропии совершенно иное, оно относится к разупорядочиванию системы. Чем менее упорядочена система, тем больше ее энтропия. Природа предпочитает такие условия, при которых энтальпия низка, а энтропия высока-, в соответствии с этим принципом в реаги- [c.274]

    В основу действия Q-мeтpa положен резонанс напряжений, при котором напряжение на емкости или на индуктивности ( /с, UL) Q раз больше приложенного к контуру напряжения. [c.208]

    Конденсаторная батарея КВ в настоящее бремя включается параллельно с индуктором печи по схеме резонанса токов, так как при последовательном соединении (т. е. при резонансе напряжений) наеряжение на индукторе и конденсаторной батарее будет более высоким, чем напряжение питающей сети это потребует соответствующей изоляции и удорожит установку. [c.278]

    Из произведенного анализа следует, что ВЧ-генератор с малым должен включаться для возбуждения резонанса напряжения в контуре последовательно с ним, а ВЧ-генератор с больпшм 7 может быть включен лишь параллельно контуру для возбуждения в нем резонанса токов. [c.47]

---

причины возникновения, способы использования и возможный вред, цепь переменного тока

Резонанс напряжений происходит в электрической цепи, включающей в себя несколько элементов: источник электроэнергии, катушку индуктивности и конденсатор. Перечисленные элементы соединяются последовательно. При этом источник напряжения имеет такую частоту, которая совпадает с внутренним контуром. Это часто применяется в полосовых фильтрах.

Последовательное соединение

Катушка индуктивности и последовательно включенный в цепь конденсатор вместе особенным образом воздействуют на генератор, от которого запитана цепь. Также они влияют на фазовые соотношения напряжения и тока:

1. Первый элемент сдвигает фазу, при этом напряжение начинает обгонять ток примерно на четверть периода.
2. Второй элемент действует иначе. Он заставляет ток обгонять напряжение также на одну четвертую часть периода фазы.

Индуктивное сопротивление действует на смещение фаз, из-за чего его можно считать противоположным работе емкостного сопротивления. В результате итоговый сдвиг фаз между напряжением и током в цепи зависит от суммарного действия индуктивного и емкостного сопротивлений, а также соотношения между ними. От этого тоже зависит характер цепи.

Если одноимённая величина превосходит противоположную, то систему можно считать емкостной, ведь ток превосходит по фазе. При иной ситуации характер цепи считается индуктивным, ведь напряжение доминирует.

Общее реактивное сопротивление определить просто. Необходимо сложить два показателя сопротивления:

1. Индуктивное от катушки.
2. Емкостное от конденсатора.

Из-за того, что они оказывают противоположное воздействие, одному из них присваивается отрицательный знак (обычно ёмкостному сопротивлению конденсатора). Тогда общее реактивное сопротивление можно найти так: из показателя катушки вычесть конденсатор. Если общее напряжение разделить на найденный параметр, то по закону Ома получится сила тока. Эту формулу можно легко изменить, переведя на напряжение. Оно будет равно произведению силы тока и разности двух сопротивлений (индуктивное берется с катушки, а емкостное — с конденсатора).

Если раскрыть скобку, то первое значение отразит действительный показатель части общего напряжения, которая старается преодолеть сопротивление. Второе — слагающая всего напряжения, которая пытается преодолеть емкостный параметр. Так, общее напряжение можно рассматривать как сумму этих слагаемых.

Обычно значением активного сопротивления можно пренебречь. Если оно слишком велико, учитывать его все же нужно.

Для определения этого значения нужно вычислить квадратный корень из суммы двух частей:

1. Общее активное сопротивление, возведенное в квадрат.
2. Квадрат разности индуктивного и емкостного сопротивлений, то есть общее реактивное.

Очевиден переход к закону Ома. Если разделить силу тока на найденное значение, то можно получить напряжение.

Цепь переменного тока

Если соединить катушку с конденсатором последовательно, происходит меньшее смещение по фазе, чем если бы эти элементы были включены отдельно. Это связано с тем, что эти элементы действуют на цепь совершенно иначе, сдвигая баланс в разные стороны. Они компенсируют фазовый сдвиг, усредняют его значение.

Возможен и равный баланс. Полная компенсация соотношения между напряжением и током произойдет, если сопротивление катушки и конденсатора будут равны друг другу. В этом случае цепь будет вести себя так, будто бы в нее не включены эти элементы. Действие системы сведется к чистому активному сопротивлению, образованному соединительными проводами и катушкой. Сила действующего тока достигнет максимального значения, его можно будет вычислить по стандартному закону Ома.

Понятие резонанса

При описанной ситуации действующие напряжения на катушке и конденсаторе сравняются, а также достигнут максимального значения. Если активное сопротивление в этой цепи минимальное, то локальные показатели будут в несколько раз превышать общее напряжение. Такое явление принято называть резонансом напряжений.

Важно понимать, что местные сопротивления напрямую зависят от показателей тока. Если частоту тока уменьшить, то индуктивное значение снизится, а емкостное — возрастет. Помимо активного сопротивления, в сети также возникнет реактивное, из-за чего резонанс сойдет на нет. Это случится и в том случае, если изменить значения индуктивности или емкости.

Если в цепи возникает резонанс, то энергия источника расходуется исключительно на нагрев проводов, то есть преодоление активного сопротивления, так как катушка перекидывает ток на конденсатор и обратно без усилий генератора. Ведь в цепи с одним из элементов ток колеблется, периодически переходя от истока в магнитное поле. Это касается катушки. В случае с конденсатором наблюдается аналогичная ситуация, только участвует электрическое поле. Если эти два элемента объединены, а также наблюдается резонанс, то энергия циклично движется от катушки к конденсатору и обратно. При этом она тратится в большей степени только из-за сопротивления проводника.

При нарушении резонанса количество энергии, требуемой первому и второму элементу, не совпадает. Возникнет избыток, который будет покрываться усилиями генератора. Этот процесс можно сравнить с механизмом часов с маятником. Если бы силы трения не было, он мог колебаться без использования дополнительного груза или пружины в механизме. Но эти элементы, когда необходимо, передают часть своей энергии маятнику, из-за чего тот преодолевает силу трения и движется непрерывно. При резонансе в электроцепи количество энергии, которую необходимо сообщить для поддержания колебаний, минимально.

Цепь считается колебательным контуром, если соблюдено несколько условий. Во-первых, ток должен быть переменным. Во-вторых, в систему должны входить генератор, конденсатор и катушка индуктивности. В-третьих, элементы должны быть соединены последовательно. В-четвертых, показатели внутренних сопротивлений должны быть равны.

Но резонанс невозможен, если частота генератора, емкость и индуктивность цепи не будут соответствовать значениям, зависящим от других параметров цепи. Все они вычисляются по специальным несложным формулам.

Польза и вред

Резонанс часто используют с пользой. Один из ярких бытовых примеров — починка радиоприемника. Электрика устройства настраивается таким образом, чтобы возник резонанс. Благодаря этому напряжение на катушке повышается и превосходит значение в цепи, созданной антенной. Это необходимо для нормальной работы приемника.

Но иногда действие резонанса сказывается на технике исключительно пагубно. Рост напряжения на некоторых участках может привести к их порче. Из-за того, что локальные значения не соответствуют генератору, отдельные детали или измерительные приборы могут выйти из строя.

Назовите характерные признаки резонанса напряжений резонанса токов

1. Ток и напряжение, приложенное к цепи, совпадают по фазе j = 0.

2. Сопротивление контура минимальное и чисто активное Z = R.

3. Ток в цепи максимален, т. к.

→ I_max

4. Падение напряжения на активном сопротивлении равно приложенному к контуру напряжению, а именно: U_R= IR = IZ = U.

5. Падения напряжений на индуктивности и ёмкости равны по амплитуде, противоположны по фазе и больше (или значительно больше) приложенного напряжения:

При этом коэффициент усиления по напряжению:

,

где

— характеристическое волновое сопротивление контура;

Q=K_U — качество, или добротность контура.

Возникновение резонанса напряжений в электрических цепях (сильно-точных) нежелательно. Чрезмерное повышение напряжений на ёмкостном и индуктивном элементах при резонансе может вывести их из строя.

В слаботочных (электронных, радиотехнических) цепях явление резонанса напряжений находит широкое применение. Благодаря усилению на реактивных элементах последовательной радиотехнической цепи (последовательный колебательный контур) при резонансе можно выделять напряжение, частота которого равна резонансной частоте цепи. Это позволяет осуществить прием и использование данного напряжения в системах радио-, телевизионного и радиолокационного приема.

Дата добавления: 2015-03-03 ; просмотров: 7113 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Читайте также:

1. Алгоритм метода частичных потоков
2. Биофизические принципы исследования электрических полей в организме. Понятие о токовом диполе.
3. В любом узле электрической цепи алгебраическая сумма токов равна нулю.
4. Векторная диаграмма токов при параллельном соединении R, L и С.
5. Виды денежных потоков
6. Виды и оценка денежных потоков предприятия
7. Виды финансовых потоков.
8. ВИМУШЕНІ КОЛИВАННЯ. РЕЗОНАНС, ЙОГО ВИКОРИСТАННЯ ТА УСУНЕННЯ В ТЕХНІЦІ
9. ВИХРЕТОКОВЫЙ МЕТОД
10. Власть информации связана с индивидуальными способностями и умением лидера соединять на своем уровне несоединяемые внизу концы, информационных потоков.
11. Вопрос 2: Методы защиты от прикосновения к токоведущим частям и технологическому оборудованию, оказавшемуся под напряжением.
12. Вынужденные колебания в электрическом колебательном контуре. Резонанс. Резонансные кривые.

Резонанс токов – это явление в цепи с параллельным колебательным контуром, ко­гда ток в неразветвленной части цепи совпадает по фазе с напряжением источника.

На рис. 12 представлена схема параллельного колебательного контура. Сопротивление R в индуктив­ной ветви обусловлено тепловыми потерями на актив­ном сопротивлении катушки. Потерями в емкостной ветви можно пренебречь.

Условие резонанса токов: равенство нулю реактивной проводимости контура b=0.

Для выяснения признаков резонанса токов постро­им векторную диаграмму.

Для того чтобы ток I в неразветвленной части цепи совпадал по фазе с напряжением, реактивная составляющая тока индуктивной ветви I_Lp должна быть равна по модулю току емкостной ветви I_C (рис. 12,б). Активная составляющая тока индуктивной ветви I_L, оказывается равной току источника I_C .

Рис. 12. Схема параллельного колебательного контура и векторная

диаграмма при резонансе токов

Признаки резонанса токов:

а) сопротивление контура

максимальное и чисто активное;

б) ток в неразветвленной части цепи совпадает по фазе с напряжением источника и достигает практи­чески минимального значения;

в) реактивная составляющая тока в катушке равна емкостному току, причем эти токи могут во много раз превышать ток источника.

Физически это объясняется тем, что при малых потерях в контуре (при малом R) ток источника тре­буется только для покрытия этих потерь. Ток в кон­туре обусловлен обменом энергией между катушкой и конденсатором. В идеальном случае (контур без по­терь) ток источника отсутствует.

Критерием возникновения резонансного явления в цепи, содержащей индуктивные и емкостные элементы, является…

1. равенство нулю угла сдвига фаз φ между напряжением и током на входе цепи

2. равенство 90° угла сдвига фаз φ между напряжением и током на входе цепи

3. равенство 180° угла сдвига фаз φ между напряжением и током на входе цепи

4. равенство 270° угла сдвига фаз φ между напряжением и током на входе цепи

Режим резонанса напряжений может быть установлен в цепи…

1.

2.

3.

4.

К возникновению режима резонанса напряжений ведет выполнение условия…

1.

2.

3.

4.

Для случая, соответствующего приведенной векторной диаграмме, характер сопротивления пассивной электрической цепи…

Характер сопротивления пассивной электрической цепи для случая, соответствующего приведенной векторной диаграмме…

1.

активно-емкостной

Если величина начальной фазы синусоидального тока

, а величина начальной фазы синусоидального напряжения , то угол сдвига фаз между напряжением и током составляет…

1.

2.

3.

4.

Полное сопротивление Z приведенной цепи при

Ом и Ом составляет…

1.

50 Ом

Вывод по третьему вопросу: в заключение необходимо отметить, что явление резонанса токов сложнее и многообразнее явления резонанса напряжений. Фактически был рассмотрен только частный случай радиотехнического резонанса. Резонансы токов и напряжений широко используются в радиотехнических цепях (установках автоматики, телемеханики, связи). Резонанс токов позволяет улучшить коэффициент мощности электроустановок промпредприятий.

Дата добавления: 2014-01-06 ; Просмотров: 7047 ; Нарушение авторских прав? ;

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

В физике резонансом называется явление, при котором в колебательном контуре частота свободных колебаний совпадает с частотой вынужденных колебаний. В электричестве аналогом колебательного контура служит цепь, состоящая из сопротивления, ёмкости и индуктивности. В зависимости от того как они соединены различают резонанс напряжений и резонанс токов.

Резонанс напряжений

Резонанс напряжений возникает в последовательной RLC-цепи.

Условием возникновения резонанса является равенство частоты источника питания резонансной частоте w=w_р, а следовательно и индуктивного и емкостного сопротивлений x_L=x_C. Так как они противоположны по знаку, то в результате реактивное сопротивление будет равно нулю. Напряжения на катушке U_L и на конденсаторе U_C будет противоположны по фазе и компенсировать друг друга. Полное сопротивление цепи при этом будет равно активному сопротивлению R, что в свою очередь вызывает увеличение тока в цепи, а следовательно и напряжение на элементах.

При резонансе напряжения U_C и U_L могут быть намного больше, чем напряжение источника, что опасно для цепи.

С увеличением частоты сопротивление катушки увеличивается, а конденсатора уменьшается. В момент времени, когда частота источника будет равна резонансной, они будут равны, а полное сопротивление цепи Z будет наименьшим. Следовательно, ток в цепи будет максимальным.

Из условия равенства индуктивного и емкостного сопротивлений найдем резонансную частоту

Исходя из записанного уравнения, можно сделать вывод, что резонанса в колебательном контуре можно добиться изменением частоты тока источника (частота вынужденных колебаний) или изменением параметров катушки L и конденсатора C.

Следует знать, что в последовательной RLC-цепи, обмен энергией между катушкой и конденсатором осуществляется через источник питания.

Резонанс токов

Резонанс токов возникает в цепи с параллельно соединёнными катушкой резистором и конденсатором.

Условием возникновения резонанса токов является равенство частоты источника резонансной частоте w=w_р, следовательно проводимости B_L=B_C. То есть при резонансе токов, ёмкостная и индуктивная проводимости равны.

Для наглядности графика, на время отвлечёмся от проводимости и перейдём к сопротивлению. При увеличении частоты полное сопротивление цепи растёт, а ток уменьшается. В момент, когда частота равна резонансной, сопротивление Z максимально, следовательно, ток в цепи принимает наименьшее значение и равен активной составляющей.

Выразим резонансную частоту

Как видно из выражения, резонансная частота определяется, как и в случае с резонансом напряжений.

Явление резонанса может носить как положительный, так и отрицательный характер. Например, любой радиоприемник имеет в своей основе колебательный контур, который с помощью изменения индуктивности или емкости настраивают на нужную радиоволну. С другой стороны, явление резонанса может привести к скачкам напряжения или тока в цепи, что в свою очередь приводит к аварии.

Условия резонанса: явление резонанса напряжений

Резонанс электрического тока и напряжения чаще всего проявляется в сетях индуктивного и емкостного характеров. Он стал очень популярным в радиоэлектронике и активно используется как один из методов конфигурирования радиоприемника на определенную частоту волны. Несмотря на его пользу, резонанс обычно несет существенный вред электрическому оборудованию и проводам. В этом материале рассмотрено, что такое резонансное напряжение, как его используют и при каких условиях оно возникает.

Что такое резонансное напряжение

Если в сеть с переменным электротоком последовательно подключены дроссель и конденсаторный элемент, они способны по-своему воздействовать на генератор, который питает всю схему. Также они влияют на фазовые отношения тока и напряженности. Индуктивная катушка привносит в цепь сдвиг фаз, который заставляет электроток отставать от напряжения на четверть периода. Конденсирующий элемент, наоборот, работает так, что U отстает от тока на четверть по фазе.

Процесс резонирования, основанный на использовании трансформатора

Это означает, что сопротивляемость индуктивного типа, которое работает на сдвижение фазы напряжения и тока в сети, функционирует противоположно силе емкостного сопротивления.

Основная формула резонанса электрической цепи

К сведению! Данный процесс приводит к тому, что общий сдвиг по фазе между силой тока и напряженностью в сети всегда зависит от отношения величины индуктивной и емкостной сопротивляемостей.

Резонирование токов

Если емкостное R в сети больше индуктивного, то все соединение является емкостным. Это значит, что напряжение характеризуется разностью фаз по току. Иногда бывает и обратная ситуация, индуктивное сопротивление сети получается большим, чем емкостное. В этом случае вся сеть становится индуктивной.

При каких условиях возникает явление: основные условия

Резонанс электротоков и напряжений появляется в результате сохранения тождества реактивных характеристик сопротивляемости сети. Несмотря на это, в ней должна быть и активная характеристика хотя бы минимального значения. Частота же генератора питания соединения всегда должна совпадать с частотой резонанса контура индуктивно-емкостной сети.

Обратите внимание! Условие работы сопротивления активного типа в реальных действующих схемах выполняется практически всегда. Одна лишь реактивная характеристика емкости и индуктивности возможна только в изолированных и теоретических примерах.

График и векторная диаграмма возникновения резонирования

Во время резонанса дроссель и конденсатор обмениваются накопленной энергией. В теоретических примерах, когда происходит первое подключение электрогенератора (в качестве питательного источника), энергия копится в катушке индуктивности или конденсаторе. После выключения электрогенератора из сети возникают колебания незатухающего характера, возникшие в результате этого обмена.

Для чего используется резонанс

Как явление, резонанс напряжений часто используется в различных фильтрах электрического типа. Например, если есть необходимость устранения из сигнала передачи некоторой составляющей тока определенной частоты, то к приемнику параллельно подключают катушку и конденсатор, которые по отношению друг к другу соединены последовательно. В результате подобных действий электроток определенной резонансной частоты замкнется через цепочку дроссель-конденсатор и не попадет на приемник.

Колебательный контур

Важно! Сам по себе резонанс напряженности в электричестве — явление негативное, так как он способствует появлению перенапряжений на некоторых участках соединения и выводит из строя приборы.

Принцип работы резонанса

Если сопротивление емкости и индуктивности подключить последовательно, то они вызовут в переменной цепи гораздо меньший сдвиг фаз, чем при отдельном включении. Говоря иначе, одновременное воздействие индуктивности и емкости создает компенсационные силы сдвига фаз. Полностью сдвиг компенсируется лишь в том случае уравнивания индуктивного и емкостного сопротивления, когда ωL = 1 / ωС.

Обратите внимание! Такая схема будет полностью характеризоваться активным R, то есть вести себя так, как будто в нее не подключены дроссель и конденсатор. Эта сопротивляемость будет равна сумме всех активных характеристик катушки и проводов соединения.

Вместе с этим рабочие напряжения дросселя и конденсатора будут равными и максимальными для данных условий. Если при маленьком активном сопротивлении данные характеристики значительно превысят общую напряженность цепи, то напряжения начнут резонировать.

Как правильно рассчитать резонансный контур

Колебательный контур — это цепь, которая характеризуется появлением в ней колебаний определенной частоты, зависящих от параметров этой цепи. Самый простой контур включает в себя последовательно или параллельно соединенные дроссель и конденсатор. Для расчета ƒ резонанса в контуре используют формулу ƒ = 1/(2π √LC), где L — индуктивность, а C — емкость.

Калькуляторы точного расчета резонансного контура

Таким образом, было рассмотрено, при каких условиях возникает явление резонанса напряжений и что это такое. Наблюдается оно только в схемах, которые характеризуются емкостью и индуктивностью, где активное R крайне мало.

Резонансные цепи RLC

Резонансные цепи используются для избирательного реагирования на сигналы заданной частоты при одновременном различении сигналов разных частот. Если характеристика схемы имеет более узкий пик около выбранной частоты, мы говорим, что схема имеет более высокую «избирательность». «Фактор качества» Q, как описано ниже, является мерой этой избирательности, и мы говорим о схеме, имеющей «высокую добротность», если она является более узкоселективной. Примером применения резонансных цепей является выбор AM-радиостанций радиоприемником.Избирательность настройки должна быть достаточно высокой, чтобы четко различать станции выше и ниже по несущей частоте, но не настолько высокой, чтобы различать «боковые полосы», создаваемые наложением сигнала амплитудной модуляцией. Селективность цепи зависит от величины сопротивления в цепи. Варианты последовательного резонансного контура справа следуют примеру Serway & Beichner. Чем меньше сопротивление, тем выше «Q» для данных значений L и C.Параллельный резонансный контур чаще используется в электронике, но алгебра, необходимая для описания резонанса, гораздо сложнее. Используя те же параметры схемы, на рисунке слева показана мощность, рассеиваемая в цепи, как функция частоты. Поскольку эта мощность зависит от квадрата тока, эти резонансные кривые кажутся круче и уже, чем резонансные пики для тока, указанные выше. Добротность Q определяется по , где Δω — ширина резонансной кривой мощности на половине высоты. Поскольку эта ширина оказывается равной Δω = R / L, значение Q также можно выразить как Q — это обычно используемый параметр в электронике, значения которого обычно находятся в диапазоне от Q = 10 до 100 для схемных приложений.

Index AC Circuits Reference Serway & Beichner Ch 33

Что такое последовательный резонанс? — его эффекты

В последовательной цепи RLC, когда ток схемы находится в фазе с приложенным напряжением, цепь считается находящейся в последовательном резонансе . Состояние резонанса возникает в последовательной цепи RLC, когда индуктивное реактивное сопротивление равно емкостному реактивному сопротивлению.

X _L = X _C или (X _L — X _C = 0)

Последовательный резонансный контур может потреблять большой ток и мощность от сети; она также называется цепью приемника . Цепь последовательного резонанса RLC показана на рисунке ниже:

В резонансе: X _L — X _C = 0 или X _L = X _C

Импеданс будет:

Где Zr — резонансное сопротивление цепи.

Подставляя значение X _L — X _C = 0 в уравнение (1), мы получим:

Zr =

рэнд

Ток I = V / Zr = V / R

Так как при резонансе противодействием току является только сопротивление (R) цепи. В этом состоянии схема потребляет максимальный ток.

См. Также : Что такое резонансная частота?

Эффекты последовательного резонанса

Следующие эффекты условия последовательного резонанса приведены ниже:

• В условиях резонанса, XL = XC, полное сопротивление цепи минимально и сводится к сопротивлению цепи.т.е. Zr = R
• В условиях резонанса, поскольку полное сопротивление цепи минимально, ток в цепи максимален. т.е. Ir = V / Zr = V / R
• Поскольку значение резонансного тока Ir является максимальным, следовательно, мощность, потребляемая цепью, также максимальна. т.е. Pr = I ² Rr
• В условиях резонанса ток, потребляемый цепью, очень велик, или мы можем сказать, что ток потребляется максимальным. Следовательно, падение напряжения на индуктивности L ie (V _L = IX _L = I x 2πfrL) и емкости C i.e (V _C = IX _C = I x I / 2πfrC) также будет очень большим.

В энергосистеме в условиях резонанса чрезмерное напряжение, создаваемое на индуктивных и емкостных компонентах цепи, таких как автоматический выключатель, реакторы и т. Д., Может вызвать повреждение. Таким образом, в энергосистеме избегается состояние последовательного резонанса.

Однако в некоторых электронных устройствах, таких как антенная цепь радио и ТВ-приемника, схема настройки и т. Д.Условие последовательного резонанса используется для увеличения напряжения сигнала и тока на желаемой частоте (fr).

Увеличение напряжения

• • Опишите увеличение напряжения и коэффициент добротности в цепях серии LCR.
• • Рассчитайте увеличение напряжения, используя соответствующие формулы.

В отвечает на вычисления в примере 9.2.2 должно быть заметно, что на резонансной частоте схемы _r 107 кГц, реактивные напряжения на L и C равны, и каждое из них больше, чем напряжение питания схемы V _S , равное 100 В.

Это возможно, потому что в резонансе напряжение (В _C = 199,56 В) на конденсаторе находится в противофазе к напряжению (В _L = 199,56 В) на индуктивности. Поскольку эти два напряжения равны и противоположны по фазе, они полностью компенсируют друг друга, оставляя только напряжение питания, развиваемое на импедансе цепи, которое в резонансе совпадает с общим сопротивлением 320 + 18 = 338 Ом.

На резонансной частоте ток в цепи имеет максимальное значение около 296 мА. Из-за эффекта компенсации фазы при резонансе два реактивных напряжения V _C и V _L «исчезли»! Это оставляет ток питания I _S , эффективно протекающий через R, и сопротивление индуктора R _L последовательно.

В этом примере влияние внутреннего сопротивления катушки индуктивности 18 Ом на V _L очень мало (0.03V) считается незначительным, а значение V _{L TOT} совпадает с значением V _L при приблизительно 199,6 В. .

Поскольку полное сопротивление цепи меньше, чем емкостное или индуктивное реактивное сопротивление при резонансе, напряжение питания 100 В (развиваемое на сопротивлении цепи) меньше любого из противоположных реактивных напряжений V _C или V _L . Этот эффект, когда реактивные напряжения внутренних компонентов больше, чем напряжение питания, называется УВЕЛИЧЕНИЕМ НАПРЯЖЕНИЯ.

Это может быть очень полезным свойством и используется, например, в антенных каскадах радиоприемников, где последовательная цепь, резонирующая на частоте принимаемой передачи, используется для увеличения амплитуды напряжения принимаемого сигнала напряжения перед тем, как оно подается на любые транзисторные усилители в схеме.

Увеличение напряжения, которое происходит при резонансе, обозначается символом Q, а «Q Factor» (увеличение напряжения) цепей полосового фильтра LC и полосового фильтра, например, управляет «отклонением», отношением желаемого к нежелательному. частоты, которые могут быть достигнуты схемой.

Эффекты увеличения напряжения особенно полезны, поскольку они могут обеспечить увеличение напряжений сигналов переменного тока с использованием только пассивных компонентов, то есть без необходимости в каком-либо внешнем источнике питания.

В некоторых случаях увеличение напряжения также может быть опасным. В оборудовании, работающем от высоковольтной сети (линии), имеющем индуктивность и емкость, при проектировании необходимо соблюдать осторожность, чтобы гарантировать, что цепь не резонирует на частотах, слишком близких к частоте сети (линии).Если это произойдет, в оборудовании могут возникнуть чрезвычайно высокие реактивные напряжения, что приведет к катастрофическим последствиям для схемы и / или пользователя.

Коэффициент добротности можно рассчитать по простой формуле. Отношение напряжения питания V _S к любому из (равных) реактивных напряжений V _C или V _L будет в том же соотношении, что и полное сопротивление цепи (R) к любому из реактивных сопротивлений (X _C или X _L ) в резонансе.Отношение реактивного напряжения V _L к напряжению питания V _S является коэффициентом увеличения Q.

Формула для определения Q (увеличения напряжения) использует отношение индуктивного реактивного сопротивления к общему сопротивлению цепи.

Где X _L — это индуктивное реактивное сопротивление при резонансе , равное 2πƒ _r L, а R — ОБЩЕЕ сопротивление цепи. Обратите внимание, что Q не имеет единиц измерения (вольт, ом и т. Д.), Так как это ОТНОШЕНИЕ

Цепи переменного тока серии

RLC | Физика

Цели обучения

К концу этого раздела вы сможете:

• Рассчитайте полное сопротивление, фазовый угол, резонансную частоту, мощность, коэффициент мощности, напряжение и / или ток в последовательной цепи RLC.
• Нарисуйте принципиальную схему последовательной цепи RLC.
• Объясните значение резонансной частоты.

Когда один в цепи переменного тока, все катушки индуктивности, конденсаторы и резисторы препятствуют току. Как они себя ведут, когда все три встречаются вместе? Интересно, что их индивидуальные сопротивления в Ом не складываются просто так. Поскольку катушки индуктивности и конденсаторы ведут себя противоположным образом, они частично полностью нейтрализуют влияние друг друга. На рисунке 1 показана последовательная цепь RLC с источником переменного напряжения, поведение которой является предметом этого раздела.Суть анализа цепи RLC — это частотная зависимость X _L и X _C , а также их влияние на фазу зависимости напряжения от тока (установлено в предыдущий раздел). Это приводит к частотной зависимости схемы с важными «резонансными» характеристиками, которые лежат в основе многих приложений, таких как радиотюнеры.

Рисунок 1. Последовательная цепь RLC с источником переменного напряжения.

Комбинированный эффект сопротивления R , индуктивного реактивного сопротивления X _L и емкостного реактивного сопротивления X _C определяется как полное сопротивление , аналог сопротивления в цепи постоянного тока по переменному току. Ток, напряжение и импеданс в цепи RLC связаны версией закона Ома для переменного тока:

[латекс] {I} _ {0} = \ frac {{V} _ {0}} {Z} \ text {или} {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} \\ [/ latex].

Здесь I ₀ — пиковый ток, V ₀ — пиковое напряжение источника и Z — полное сопротивление цепи. Единицы измерения импеданса — омы, и его влияние на схему такое, как и следовало ожидать: чем больше импеданс, тем меньше ток. Чтобы получить выражение для Z через R , X _L и X _C , мы теперь рассмотрим, как напряжения на различных компонентах связаны с источником. Напряжение.Эти напряжения обозначены как V _R , V _L и V _C на рисунке 1. Для сохранения заряда ток должен быть одинаковым в каждой части цепи. всегда, так что мы можем сказать, что токи в R , L и C равны и синфазны. Но из предыдущего раздела мы знаем, что напряжение на катушке индуктивности В _L опережает ток на одну четверть цикла, напряжение на конденсаторе В _C следует за током на единицу. -четвертая часть цикла, и напряжение на резисторе В, _R точно совпадает по фазе с током.На рисунке 2 показаны эти отношения на одном графике, а также показано общее напряжение в цепи В = В _R + В _L + V _C , где все четыре напряжения — мгновенные значения. Согласно правилу петли Кирхгофа, полное напряжение вокруг цепи В, также является напряжением источника. Из рисунка 2 видно, что в то время как V _R находится в фазе с током, V _L опережает 90º, а V _C следует на 90º.Таким образом, V _L и V _C сдвинуты по фазе на 180º (от пика до впадины) и имеют тенденцию к аннулированию, хотя и не полностью, если они не имеют одинаковой величины. Поскольку пиковые напряжения не выровнены (не совпадают по фазе), пиковое напряжение В ₀ источника не равно сумме пиковых напряжений на R , L и C . {2}} \\ [/ latex],

, который является сопротивлением цепи переменного тока серии RLC .Для схем без резистора принять R = 0; для тех, у кого нет индуктора, возьмите X _L = 0; а для тех, у кого нет конденсатора, возьмите X _C = 0.

Рис. 2. На этом графике показаны отношения напряжений в цепи RLC к току. Напряжения на элементах схемы складываются, чтобы равняться напряжению источника, которое, как видно, не совпадает по фазе с током.

Пример 1.Расчет импеданса и тока

Последовательная цепь RLC имеет резистор 40,0 Ом, индуктивность 3,00 мГн и конденсатор 5,00 мкФ. (a) Найдите полное сопротивление цепи при 60,0 Гц и 10,0 кГц, отметив, что эти частоты и значения для L и C такие же, как в Примере 1 и Примере 2 из раздела Реактивное, индуктивное и емкостное. (b) Если источник напряжения имеет В _{среднеквадратичное значение} = 120 В, что будет I _{среднеквадратичное значение} на каждой частоте?

Стратегия

Для каждой частоты мы используем [latex] Z = \ sqrt {{R} ^ {2} + \ left ({X} _ {L} — {X} _ {C} \ right) ^ {2}} \ \ [/ latex], чтобы найти импеданс, а затем закон Ома, чтобы найти ток. { 2}} \\ & = & \ sqrt {\ left (40.{2}} \\ & = & 190 \ text {} \ Omega \ text {at} 10.0 \ text {kHz} \ end {array} \\ [/ latex]

Обсуждение для (а)

В обоих случаях результат почти такой же, как и наибольшее значение, и импеданс определенно не является суммой отдельных значений. Ясно, что X _L доминирует на высокой частоте, а X _C доминирует на низкой частоте.

Решение для (b)

Текущее значение I _{среднеквадратичное значение} можно найти, используя версию закона Ома по переменному току в уравнении I _{среднеквадратичное значение} = В _{среднеквадратичное значение} / Z :

[латекс] {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} = \ frac {120 \ text {V}} {531 \ text { } \ Omega} = 0.226 \ text {A} \\ [/ latex] при 60,0 Гц

Наконец, на частоте 10,0 кГц мы находим

[латекс] {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} = \ frac {120 \ text {V}} {190 \ text { } \ Omega} = 0,633 \ text {A} \\ [/ latex] при 10,0 кГц

Обсуждение для (а)

Ток при 60,0 Гц является таким же (до трех цифр), который был найден для одного только конденсатора в Примере 2 из раздела «Реактивное сопротивление, индуктивность и емкость». Конденсатор преобладает на низкой частоте. Ток на частоте 10,0 кГц лишь незначительно отличается от того, который был обнаружен для одной катушки индуктивности в примере 1 из раздела «Реактивное сопротивление, индуктивность и емкость».{2}}} \\ [/ latex]

Реактивные сопротивления изменяются в зависимости от частоты: X _L большие на высоких частотах и ​​ X _C большие на низких частотах, как мы видели в трех предыдущих примерах. На некоторой промежуточной частоте f ₀ реактивные сопротивления будут равны и уравновешены, давая Z = R — это минимальное значение для импеданса и максимальное значение для I _{среднеквадратичное значение} результатов .Мы можем получить выражение для f ₀ , взяв

X _L = X _C .

Замена определений X _L и X _C ,

[латекс] 2 \ pi f_ {0} L = \ frac {1} {2 \ pi f_ {0} C} \\ [/ latex].

Решение этого выражения для f ₀ дает

[латекс] {f} _ {0} = \ frac {1} {2 \ pi \ sqrt {LC}} \\ [/ latex],

, где f ₀ — резонансная частота последовательной цепи RLC .Это также собственная частота , на которой цепь будет колебаться, если не будет управляться источником напряжения. При f ₀ влияние катушки индуктивности и конденсатора компенсируется, так что Z = R и I _{среднеквадратичное значение} является максимальным.

Резонанс в цепях переменного тока аналогичен механическому резонансу, где резонанс определяется как вынужденное колебание — в данном случае вызываемое источником напряжения — на собственной частоте системы.Приемник в радиоприемнике представляет собой схему RLC , которая лучше всего колеблется на ее f ₀ . Переменный конденсатор часто используется для настройки f ₀ , чтобы получить желаемую частоту и отклонить другие. На рисунке 3 представлен график зависимости тока от частоты, иллюстрирующий резонансный пик в I _{среднеквадратичное значение} при f ₀ . Две кривые относятся к двум разным схемам, которые различаются только величиной сопротивления в них.Пик ниже и шире для цепи с более высоким сопротивлением. Таким образом, цепь с более высоким сопротивлением не так сильно резонирует и, например, не будет такой избирательной в радиоприемнике.

Рис. 3. График зависимости тока от частоты для двух последовательных цепей RLC, различающихся только величиной сопротивления. Оба имеют резонанс при f ₀ , но для более высокого сопротивления он ниже и шире. Источник управляющего переменного напряжения имеет фиксированную амплитуду В ₀ .

Пример 2. Расчет резонансной частоты и тока

Для той же последовательной цепи RLC , имеющей резистор 40,0 Ом, индуктивность 3,00 мГн и конденсатор 5,00 мкФ: (a) Найдите резонансную частоту. (b) Рассчитайте I _{среднеквадратичное значение} при резонансе, если В _{среднеквадратичное значение} равно 120 В.

Стратегия

Резонансная частота находится с помощью выражения в [latex] {f} _ {0} = \ frac {1} {2 \ pi \ sqrt {LC}} \\ [/ latex].{-6} \ text {F} \ right)}} = 1,30 \ text {кГц} \ end {array} \\ [/ latex]

Обсуждение для (а)

Мы видим, что резонансная частота находится между 60,0 Гц и 10,0 кГц, двумя частотами, выбранными в предыдущих примерах. Этого и следовало ожидать, поскольку конденсатор преобладает на низкой частоте, а катушка индуктивности — на высокой. Их эффекты такие же на этой промежуточной частоте.

Решение для (b)

Ток определяется законом Ома.В резонансе два реактивных сопротивления равны и компенсируются, так что полное сопротивление равно только сопротивлению. Таким образом,

[латекс] {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} = \ frac {120 \ text {V}} {40.0 \ text { } \ Omega} = 3,00 \ text {A} \\ [/ latex].

Обсуждение для (б)

В резонансе ток больше, чем на более высоких и более низких частотах, рассмотренных для той же цепи в предыдущем примере.

Питание в цепях переменного тока серии

RLC

Если ток изменяется в зависимости от частоты в цепи RLC , то мощность, подаваемая на нее, также зависит от частоты.Но средняя мощность — это не просто ток, умноженный на напряжение, как в чисто резистивных цепях. Как видно на рисунке 2, напряжение и ток в цепи RLC не совпадают по фазе. Существует фазовый угол ϕ между напряжением источника В и током I , который можно найти из

[латекс] \ cos \ varphi = \ frac {R} {Z} \\ [/ latex]

Например, на резонансной частоте или в чисто резистивной цепи Z = R , так что [latex] \ text {cos} \ varphi = 1 \\ [/ latex].Это означает, что ϕ = 0º и что напряжение и ток синфазны, как и ожидалось для резисторов. На других частотах средняя мощность меньше, чем на резонансе. Причина в том, что напряжение и ток не совпадают по фазе, а также потому, что I _{действующее значение} ниже. Тот факт, что напряжение и ток источника не совпадают по фазе, влияет на мощность, подаваемую в цепь. Можно показать, что средняя мощность равна

[латекс] {P} _ {\ text {ave}} = {I} _ {\ text {rms}} {V} _ {\ text {rms}} \ cos \ varphi \\ [/ latex],

Таким образом, cos ϕ называется коэффициентом мощности , который может находиться в диапазоне от 0 до 1.Например, при разработке эффективного двигателя желательны коэффициенты мощности, близкие к 1. На резонансной частоте cos ϕ = 1.

Пример 3. Расчет коэффициента мощности и мощности

Для той же последовательной цепи RLC , имеющей резистор 40,0 Ом, индуктивность 3,00 мГн, конденсатор 5,00 мкФ и источник напряжения с В _{среднеквадратичное значение} 120 В: (a) Рассчитайте коэффициент мощности и фазу угол для f = 60,0 Гц. (б) Какая средняя мощность при 50.0 Гц? (c) Найдите среднюю мощность на резонансной частоте цепи.

Стратегия и решение для (а)

Коэффициент мощности при 60,0 Гц находится из

.

[латекс] \ cos \ varphi = \ frac {R} {Z} \\ [/ latex].

Мы знаем Z = 531 Ом из Пример 1: Расчет импеданса и тока , так что

[латекс] \ cos \ varphi = \ frac {40.0 \ text {} \ Omega} {531 \ text {} \ Omega} = 0,0753 \ text {at} 60.0 \ text {Hz} \\ [/ latex].

Это небольшое значение указывает на то, что напряжение и ток значительно не совпадают по фазе.{-1} 0,0753 = \ text {85,7º} \ text {at} 60,0 \ text {Hz} \\ [/ latex].

Обсуждение для (а)

Фазовый угол близок к 90 °, что согласуется с тем фактом, что конденсатор доминирует в цепи на этой низкой частоте (чистая цепь RC имеет напряжение и ток, сдвинутые по фазе на 90 °).

Стратегия и решение для (b)

Средняя мощность при 60,0 Гц —

P _средн. = I _rms V _rms cos ϕ .

I _{среднеквадратичное значение} оказалось равным 0,226 А в Пример 1: Расчет импеданса и тока . Ввод известных значений дает

P _средн. = (0,226 A) (120 В) (0,0753) = 2,04 Вт при 60,0 Гц.

Стратегия и решение для (c)

На резонансной частоте мы знаем, что cos ϕ = 1, и I _{среднеквадратичное значение} оказалось равным 6,00 A в Пример 3: Расчет резонансной частоты и тока .Таким образом, P _средн. = (3,00 A) (120 В) (1) = 360 Вт при резонансе (1,30 кГц)

Обсуждение

Как ток, так и коэффициент мощности больше в резонансе, производя значительно большую мощность, чем на более высоких и низких частотах.

Мощность, подаваемая в цепь переменного тока серии RLC , рассеивается только за счет сопротивления. Катушка индуктивности и конденсатор имеют входную и выходную энергию, но не рассеивают ее из цепи. Скорее они передают энергию туда и обратно друг другу, а резистор рассеивает именно то, что источник напряжения вводит в цепь.Это предполагает отсутствие значительного электромагнитного излучения от катушки индуктивности и конденсатора, например радиоволн. Такое излучение может происходить и даже быть желательным, как мы увидим в следующей главе об электромагнитном излучении, но оно также может быть подавлено, как в случае в этой главе. Схема аналогична колесу автомобиля, движущегося по рифленой дороге, как показано на рисунке 4. Ровные неровности дороги аналогичны источнику напряжения, приводящему колесо в движение вверх и вниз. Амортизатор аналогичен демпфирующему сопротивлению и ограничивающему амплитуду колебаний.Энергия внутри системы перемещается между кинетической (аналогично максимальному току и энергии, хранящейся в индукторе) и потенциальной энергией, хранящейся в автомобильной пружине (аналогично отсутствию тока и энергии, хранящейся в электрическом поле конденсатора). Амплитуда движения колес максимальна, если неровности дороги встречаются на резонансной частоте.

Рис. 4. Вынужденное, но демпфированное движение колеса на автомобильной пружине аналогично цепи переменного тока серии RLC .Амортизатор гасит движение и рассеивает энергию, аналогично сопротивлению в цепи RLC . Масса и пружина определяют резонансную частоту.

Чистый контур LC с незначительным сопротивлением колеблется на f ₀ , той же резонансной частоте, что и контур RLC . Он может служить эталоном частоты или схемой часов — например, в цифровых наручных часах. При очень маленьком сопротивлении требуется лишь очень небольшая подводимая энергия для поддержания колебаний.Схема аналогична автомобилю без амортизаторов. Как только он начинает колебаться, он некоторое время продолжает работать на своей собственной частоте. На рисунке 5 показана аналогия между цепью LC и грузом на пружине.

Рис. 5. LC-контур аналогичен массе, колеблющейся на пружине без трения и без движущей силы. Энергия движется вперед и назад между катушкой индуктивности и конденсатором, точно так же, как она движется от кинетической к потенциальной в системе масса-пружина.

Исследования PhET: комплект для конструирования цепей (AC + DC), виртуальная лаборатория

Создавайте цепи с конденсаторами, катушками индуктивности, резисторами и источниками переменного или постоянного напряжения и проверяйте их с помощью лабораторных инструментов, таких как вольтметры и амперметры.

Щелкните, чтобы загрузить симуляцию. Запускать на Java.

Сводка раздела

• Аналогом сопротивления переменного тока является сопротивление Z , комбинированное действие резисторов, катушек индуктивности и конденсаторов, определяемое версией закона Ома для переменного тока:

  [латекс] {I} _ {0} = \ frac {{V} _ {0}} {Z} \ text {или} {I} _ {\ text {rms}} = \ frac {{V} _ {\ text {rms}}} {Z} \\ [/ latex],

  , где I _o — пиковый ток, а В _o — пиковое напряжение источника.{2}} \\ [/ латекс].

• Резонансная частота f ₀ , при которой X _L = X _C , составляет

  [латекс] {f} _ {0} = \ frac {1} {2 \ pi \ sqrt {LC}} \\ [/ latex]

• В цепи переменного тока существует фазовый угол ϕ между напряжением источника В и током I , который можно найти из

  [латекс] \ text {cos} \ varphi = \ frac {R} {Z} \\ [/ latex],

• ϕ = 0º для чисто резистивной цепи или цепи RLC в резонансе.
• Средняя мощность, подаваемая в цепь RLC , зависит от фазового угла и определяется выражением

  [латекс] {P} _ {\ text {ave}} = {I} _ {\ text {rms}} {V} _ {\ text {rms}} \ cos \ varphi \\ [/ latex],

  cos ϕ называется коэффициентом мощности, который находится в диапазоне от 0 до 1.

Концептуальные вопросы

1. Зависит ли резонансная частота цепи переменного тока от пикового напряжения источника переменного тока? Объясните, почему да или почему нет.

2. Предположим, у вас есть двигатель с коэффициентом мощности значительно меньше 1.Объясните, почему было бы лучше улучшить коэффициент мощности как метод улучшения выходной мощности двигателя, чем увеличивать входное напряжение.

Задачи и упражнения

1. Цепь RL состоит из резистора 40,0 Ом и катушки индуктивности 3,00 мГн. (a) Найдите его полное сопротивление Z при 60,0 Гц и 10,0 кГц. (b) Сравните эти значения Z со значениями, найденными в Пример 1: Расчет импеданса и тока , в котором также был конденсатор.

2. Схема RC состоит из резистора 40,0 Ом и конденсатора 5,00 мкФ. (а) Найдите его полное сопротивление при 60,0 Гц и 10,0 кГц. (b) Сравните эти значения Z со значениями, найденными в Пример 1: Расчет импеданса и тока , в котором также была катушка индуктивности.

3. Цепь LC состоит из индуктора 3,00 мГн и конденсатора 5,00 мкФ. (а) Найдите его полное сопротивление при 60,0 Гц и 10,0 кГц. (b) Сравните эти значения Z со значениями, найденными в Пример 1: Расчет импеданса и тока , в котором также был резистор.

4. Какова резонансная частота индуктора 0,500 мГн, подключенного к конденсатору 40,0 мкФ?

5. Для приема AM-радио вам нужна цепь RLC , которая может резонировать на любой частоте от 500 до 1650 кГц. Это достигается с помощью фиксированной катушки индуктивности 1,00 мкГн, подключенной к конденсатору переменной емкости. Какой диапазон емкости нужен?

6. Предположим, у вас есть запас индукторов от 1,00 нГн до 10,0Гн и конденсаторов от 1.От 00 пФ до 0,100 F. Каков диапазон резонансных частот, который может быть достигнут при сочетании одной катушки индуктивности и одного конденсатора?

7. Какая емкость необходима для получения резонансной частоты 1,00 ГГц при использовании катушки индуктивности 8,00 нГн?

8. Какая индуктивность необходима для получения резонансной частоты 60,0 Гц при использовании конденсатора 2,00 мкФ?

9. Самая низкая частота в диапазоне FM-радио — 88,0 МГц. (а) Какая индуктивность необходима для создания этой резонансной частоты, если она подключена к 2.Конденсатор 50 пФ? (b) Конденсатор регулируемый, что позволяет регулировать резонансную частоту до 108 МГц. Какой должна быть емкость на этой частоте?

10. Последовательная цепь RLC имеет резистор 2,50 Ом, индуктивность 100 мкГн и конденсатор 80,0 мкФ. (A) Найдите полное сопротивление цепи при 120 Гц. (b) Найдите полное сопротивление цепи на частоте 5,00 кГц. (c) Если источник напряжения имеет В _{среднеквадратичное значение} = 5,60 В, что будет I _{среднеквадратичное значение} на каждой частоте? (d) Какова резонансная частота контура? (e) Что такое I _RMS в резонансе?

11.Последовательная цепь RLC имеет резистор 1,00 кОм, индуктивность 150 мкГн и конденсатор 25,0 нФ. (а) Найдите полное сопротивление цепи при 500 Гц. (b) Найдите полное сопротивление цепи на частоте 7,50 кГц. (c) Если источник напряжения имеет В _{среднеквадратичное значение} = 408 В, что будет I _{среднеквадратичное значение} на каждой частоте? (d) Какова резонансная частота контура? (e) Что такое I _RMS в резонансе?

12. Последовательная цепь RLC имеет 2.Резистор 50 Ом, катушка индуктивности 100 мкГн и конденсатор 80,0 мкФ. (а) Найдите коэффициент мощности при f = 120 Гц. (б) Каков фазовый угол при 120 Гц? (c) Какая средняя мощность при 120 Гц? (d) Найдите среднюю мощность на резонансной частоте цепи.

13. Последовательная цепь RLC имеет резистор 1,00 кОм, индуктивность 150 мкГн и конденсатор 25,0 нФ. (a) Найдите коэффициент мощности при f = 7,50 Гц. б) Каков фазовый угол на этой частоте? (c) Какая средняя мощность на этой частоте? (d) Найдите среднюю мощность на резонансной частоте цепи.

14. Последовательная цепь RLC имеет резистор 200 Ом и катушку индуктивности 25,0 мГн. {2}} \\ [/ latex]

резонансная частота:

— частота, при которой полное сопротивление в цепи минимально, а также частота, с которой цепь будет колебаться, если не будет управляться источником напряжения; рассчитывается по [latex] {f} _ {0} = \ frac {1} {2 \ pi \ sqrt {\ text {LC}}} \\ [/ latex]

фазовый угол:

обозначается как ϕ , величина, на которую напряжение и ток не совпадают по фазе друг с другом в цепи

Коэффициент мощности:

— величина, на которую мощность, передаваемая в цепи, меньше теоретического максимума цепи из-за того, что напряжение и ток не совпадают по фазе; рассчитывается по cos ϕ

Избранные решения проблем и упражнения

1.(a) 40,02 Ом при 60,0 Гц, 193 Ом при 10,0 кГц (b) При 60 Гц, с конденсатором, Z = 531 Ом, что в 13 раз больше, чем без конденсатора. Конденсатор имеет большое значение на низких частотах. На 10 кГц, с конденсатором Z = 190 Ом, примерно так же, как без конденсатора. Конденсатор оказывает меньшее влияние на высоких частотах.

3. (a) 529 Ом при 60,0 Гц, 185 Ом при 10,0 кГц (b) Эти значения близки к значениям, полученным в Пример 1: Расчет импеданса и тока , поскольку на низкой частоте преобладает конденсатор, а на высокой — индуктор доминирует.Таким образом, в обоих случаях резистор вносит небольшой вклад в общий импеданс.

5. От 9,30 нФ до 101 нФ

7. 3,17 пФ

9. (а) 1,31 мкГн (б) 1,66 пФ

11. (a) 12,8 кОм (b) 1,31 кОм (c) 31,9 мА при 500 Гц, 312 мА при 7,50 кГц (d) 82,2 кГц (e) 0,408 A

13. (а) 0,159 (б) 80,9º (в) 26,4 Вт (г) 166 Вт

15. 16.0 Вт

Поставщики и ресурсы беспроводной связи RF

О мире беспроводной связи RF

Веб-сайт RF Wireless World является домом для поставщиков и ресурсов радиочастотной и беспроводной связи.На сайте представлены статьи, руководства, поставщики, терминология, исходный код (VHDL, Verilog, MATLAB, Labview), тестирование и измерения, калькуляторы, новости, книги, загрузки и многое другое.

Сайт RF Wireless World охватывает ресурсы по различным темам, таким как RF, беспроводная связь, vsat, спутник, радар, оптоволокно, микроволновая печь, wimax, wlan, zigbee, LTE, 5G NR, GSM, GPRS, GPS, WCDMA, UMTS, TDSCDMA, Bluetooth, Lightwave RF, z-wave, Интернет вещей (IoT), M2M, Ethernet и т. Д. Эти ресурсы основаны на стандартах IEEE и 3GPP.Он также имеет академический раздел, который охватывает колледжи и университеты по инженерным дисциплинам и MBA.

Статьи о системах на основе Интернета вещей

Система обнаружения падений для пожилых людей на основе Интернета вещей : В статье рассматривается архитектура системы обнаружения падений, используемой для пожилых людей. В нем упоминаются преимущества или преимущества системы обнаружения падений Интернета вещей. Читать дальше➤
Также обратитесь к другим статьям о системах на основе Интернета вещей следующим образом:
• Система очистки туалетов самолета. • Система измерения столкновений • Система отслеживания скоропортящихся продуктов и овощей • Система помощи водителю • Система умной торговли • Система мониторинга качества воды. • Система Smart Grid • Система умного освещения на базе Zigbee • Умная система парковки на базе Zigbee • Система умной парковки на основе LoRaWAN

---

RF Статьи о беспроводной связи

В этом разделе статей представлены статьи о физическом уровне (PHY), уровне MAC, стеке протоколов и сетевой архитектуре на основе WLAN, WiMAX, zigbee, GSM, GPRS, TD-SCDMA, LTE, 5G NR, VSAT, Gigabit Ethernet на основе IEEE / 3GPP и т. Д. .стандарты. Он также охватывает статьи, относящиеся к испытаниям и измерениям, по тестированию на соответствие, используемым для испытаний устройств на соответствие RF / PHY. УКАЗАТЕЛЬ СТАТЬИ ДЛЯ ССЫЛКИ >>.

---

Физический уровень 5G NR : Обработка физического уровня для канала 5G NR PDSCH и канала 5G NR PUSCH рассмотрена поэтапно. Это описание физического уровня 5G соответствует спецификациям физического уровня 3GPP. Читать дальше➤

---

Основы повторителей и типы повторителей : В нем объясняются функции различных типов ретрансляторов, используемых в беспроводных технологиях.Читать дальше➤

---

Основы и типы замирания : В этой статье рассматриваются мелкомасштабные замирания, крупномасштабные замирания, медленные, быстрые и т. Д., Используемые в беспроводной связи. Читать дальше➤

---

Архитектура сотового телефона 5G : В этой статье рассматривается блок-схема сотового телефона 5G с внутренними модулями 5G. Архитектура сотового телефона. Читать дальше➤

---

Основы помех и типы помех: В этой статье рассматриваются помехи в соседнем канале, помехи в совмещенном канале, Электромагнитные помехи, ICI, ISI, световые помехи, звуковые помехи и т. Д.Читать дальше➤

---

5G NR Раздел

В этом разделе рассматриваются функции 5G NR (New Radio), нумерология, диапазоны, архитектура, развертывание, стек протоколов (PHY, MAC, RLC, PDCP, RRC) и т. Д. 5G NR Краткий указатель ссылок >>
• Мини-слот 5G NR • Часть полосы пропускания 5G NR • 5G NR CORESET • Форматы DCI 5G NR • 5G NR UCI • Форматы слотов 5G NR • IE 5G NR RRC • 5G NR SSB, SS, PBCH • 5G NR PRACH • 5G NR PDCCH • 5G NR PUCCH • Эталонные сигналы 5G NR • 5G NR m-последовательность • Золотая последовательность 5G NR • 5G NR Zadoff Chu Sequence • Физический уровень 5G NR • Уровень MAC 5G NR • Уровень 5G NR RLC • Уровень 5G NR PDCP

---

Учебные пособия по беспроводным технологиям

В этом разделе рассматриваются учебные пособия по радиочастотам и беспроводной связи.Он охватывает учебные пособия по таким темам, как сотовая связь, WLAN (11ac, 11ad), wimax, bluetooth, zigbee, zwave, LTE, DSP, GSM, GPRS, GPS, UMTS, CDMA, UWB, RFID, радар, VSAT, спутник, WLAN, волновод, антенна, фемтосота, тестирование и измерения, IoT и т. Д. См. УКАЗАТЕЛЬ >>

---

Учебное пособие по 5G — В этом руководстве по 5G также рассматриваются следующие подтемы по технологии 5G:
Учебное пособие по основам 5G. Частотные диапазоны руководство по миллиметровым волнам Волновая рама 5G мм Зондирование волнового канала 5G мм 4G против 5G Испытательное оборудование 5G Сетевая архитектура 5G Сетевые интерфейсы 5G NR канальное зондирование Типы каналов 5G FDD против TDD Разделение сети 5G NR Что такое 5G NR Режимы развертывания 5G NR Что такое 5G TF

---

В этом учебном пособии GSM рассматриваются основы GSM, сетевая архитектура, сетевые элементы, системные спецификации, приложения, Типы пакетов GSM, структура или иерархия кадров GSM, логические каналы, физические каналы, Физический уровень GSM или обработка речи, вход в сеть мобильного телефона GSM, установка вызова или процедура включения питания, MO-вызов, MT-вызов, VAMOS, AMR, MSK, модуляция GMSK, физический уровень, стек протоколов, основы работы с мобильным телефоном, Планирование RF, нисходящая линия связи PS и восходящая линия связи PS.
➤Подробнее.

LTE Tutorial , охватывающий архитектуру системы LTE, охватывающий основы LTE EUTRAN и LTE Evolved Packet Core (EPC). Он обеспечивает связь с обзором системы LTE, радиоинтерфейсом LTE, терминологией LTE, категориями LTE UE, структурой кадра LTE, физическим уровнем LTE, Стек протоколов LTE, каналы LTE (логические, транспортные, физические), пропускная способность LTE, агрегация несущих LTE, передача голоса по LTE, расширенный LTE, Поставщики LTE и LTE vs LTE продвинутые.➤Подробнее.

---

RF Technology Stuff

Эта страница мира беспроводной радиосвязи описывает пошаговое проектирование преобразователя частоты RF на примере преобразователя RF UP от 70 МГц до диапазона C. для микрополосковой платы с использованием дискретных радиочастотных компонентов, а именно. Смесители, гетеродин, MMIC, синтезатор, опорный генератор OCXO, колодки аттенюатора. ➤Подробнее.
➤Проектирование и разработка радиочастотного трансивера ➤Конструкция RF-фильтра ➤Система VSAT ➤Типы и основы микрополосковой печати ➤ОсновыWaveguide

---

Секция испытаний и измерений

В этом разделе рассматриваются контрольно-измерительные ресурсы, испытательное и измерительное оборудование для тестирования DUT на основе Стандарты WLAN, WiMAX, Zigbee, Bluetooth, GSM, UMTS, LTE.УКАЗАТЕЛЬ испытаний и измерений >>
➤Система PXI для T&M. ➤ Генерация и анализ сигналов ➤Измерения слоя PHY ➤Тест устройства на соответствие WiMAX ➤ Тест на соответствие Zigbee ➤ Тест на соответствие LTE UE ➤Тест на соответствие TD-SCDMA

---

Волоконно-оптическая технология

Оптоволоконный компонент , основы, включая детектор, оптический соединитель, изолятор, циркулятор, переключатели, усилитель, фильтр, эквалайзер, мультиплексор, разъемы, демультиплексор и т. д.Эти компоненты используются в оптоволоконной связи. Оптические компоненты INDEX >>
➤Учебник по оптоволоконной связи ➤APS в SDH ➤SONET основы ➤SDH Каркасная конструкция ➤SONET против SDH

---

Поставщики, производители радиочастотной беспроводной связи

Сайт RF Wireless World охватывает производителей и поставщиков различных радиочастотных компонентов, систем и подсистем для ярких приложений, см. ИНДЕКС поставщиков >>.

Поставщики радиочастотных компонентов, включая радиочастотный изолятор, радиочастотный циркулятор, радиочастотный смеситель, радиочастотный усилитель, радиочастотный адаптер, радиочастотный разъем, радиочастотный модулятор, радиочастотный трансивер, PLL, VCO, синтезатор, антенну, генератор, делитель мощности, сумматор мощности, фильтр, аттенюатор, диплексор, дуплексер, микросхема резистора, микросхема конденсатора, индуктор микросхемы, ответвитель, оборудование ЭМС, программное обеспечение для проектирования радиочастот, диэлектрический материал, диод и т. д.Производители радиокомпонентов >>
➤Базовая станция LTE ➤RF Циркулятор ➤RF Изолятор ➤Кристаллический осциллятор

---

MATLAB, Labview, встроенные исходные коды

Раздел исходного кода RF Wireless World охватывает коды, связанные с языками программирования MATLAB, VHDL, VERILOG и LABVIEW. Эти коды полезны для новичков в этих языках. ИНДЕКС ИСХОДНОГО КОДА >>
➤3-8 декодер кода VHDL ➤Код MATLAB для дескремблера ➤32-битный код ALU Verilog ➤T, D, JK, SR триггеры labview коды

* Общая информация о здоровье населения *

Выполните эти пять простых действий, чтобы остановить коронавирус (COVID-19).
СДЕЛАЙТЕ ПЯТЬ
1. РУКИ: часто мойте их.
2. КОЛЕНО: Откашляйтесь
3. ЛИЦО: не трогайте его
4. НОГИ: держитесь на расстоянии более 3 футов (1 м) друг от друга
5. ЧУВСТВОВАТЬ: Болен? Оставайся дома

Используйте технологию отслеживания контактов >>, соблюдайте >> рекомендации по социальному дистанцированию и установить систему видеонаблюдения >> чтобы спасти сотни жизней. Использование концепции телемедицины стало очень популярным в таким странам, как США и Китай, чтобы остановить распространение COVID-19, поскольку это заразное заболевание.

---

RF Беспроводные калькуляторы и преобразователи

Раздел «Калькуляторы и преобразователи» охватывает ВЧ-калькуляторы, беспроводные калькуляторы, а также преобразователи единиц измерения. Сюда входят такие беспроводные технологии, как GSM, UMTS, LTE, 5G NR и т. Д. СПРАВОЧНЫЕ КАЛЬКУЛЯТОРЫ Указатель >>.
➤ Калькулятор пропускной способности 5G NR ➤5G NR ARFCN против преобразования частоты ➤Калькулятор скорости передачи данных LoRa ➤LTE EARFCN для преобразования частоты ➤ Калькулятор антенн Яги ➤ Калькулятор времени выборки 5G NR

---

IoT-Интернет вещей Беспроводные технологии

Раздел IoT охватывает беспроводные технологии Интернета вещей, такие как WLAN, WiMAX, Zigbee, Z-wave, UMTS, LTE, GSM, GPRS, THREAD, EnOcean, LoRa, SIGFOX, WHDI, Ethernet, 6LoWPAN, RF4CE, Bluetooth, Bluetooth Low Power (BLE), NFC, RFID, INSTEON, X10, KNX, ANT +, Wavenis, Dash7, HomePlug и другие.Он также охватывает датчики Интернета вещей, компоненты Интернета вещей и компании Интернета вещей.
См. Главную страницу IoT >> и следующие ссылки.
➤ НИТЬ ➤EnOcean ➤Учебник по LoRa ➤Учебник по SIGFOX ➤WHDI ➤6LoWPAN ➤Zigbee RF4CE ➤NFC ➤Lonworks ➤CEBus ➤UPB

СВЯЗАННЫЕ ЗАПИСИ

RF Wireless Учебники

Различные типы датчиков

Поделиться страницей

Перевести страницу

Гармонический резонанс в энергосистемах — нарушение напряжения

Гармонические токи, создаваемые нелинейными электронными нагрузками, являются вводится в сеть энергосистемы.Эффект от инъекции большой величины гармонического тока в сети зависит от реакции электросети на различные вводимые гармонические частоты. В зависимости от ответа сети, подаваемый ток может просто безвредно течь в сеть или создавать резонанс системы электропитания, приводящий к повреждению от перенапряжения или условия перегрузки по току. Характеристики системы, определяющие реакция сети на гармоники энергосистемы:

* Полное сопротивление системы каждой гармонической частоте

* Наличие конденсаторных батарей

* Количество резистивных нагрузок

Повреждение конденсатора из-за резонанса

Есть некоторые ключевые идеи, которые следует понять, пытаясь углубиться в понимание электрических Гармонический резонанс энергосистемы.Их:

Нелинейный нагрузки производят гармонический ток, который затем вводится в электросеть.

Текущее поступление к источнику (сети) вызывает падение напряжения, пропорциональное импеданс, предлагаемый этой конкретной гармонической частотной составляющей.

Если индуктивность и емкость источника образуют последовательный или параллельный резонансный контур, тогда введенный ток может вызвать очень сильные искажения тока и напряжения.

Каждая система с конденсаторами будет иметь параллельную резонансную точку.Важно определить, близка ли эта резонансная точка к одной из гармонических частот вводится системой нагрузок.

Симптомы и характеристика гармонического резонанса

Самокорректирующийся : Большинство проблем гармонического резонанса обычно самокорректируются, что означает, что резонансное состояние вызовет достаточно ток / напряжение в системе, которые могут либо перегореть предохранители, либо выйти из строя конденсатор (выходящий из резонанса) или другое повреждение системы, которое вызывает система больше не резонансная.Обратите внимание, что резонанс системы низкого уровня может по-прежнему остаются незамеченными в течение долгого времени, и многие из них не вызывают сбоев, которые внимание к проблеме немедленно.

Перегорел предохранитель конденсатора : Обычно возникает резонансное состояние при больших токах конденсаторов и срабатывании предохранителей.

Неисправность конденсатора : Конденсатор также может быть поврежден из-за к перегреву или повреждению изоляционных слоев внутри банка напряжением.

Искажение напряжения : Для резонансного состояния искажение будет происходить из-за одного или двух близко расположенных гармонических порядков.Анализируя ток и напряжение на анализаторе качества электроэнергии, порядок гармоник Причина резонанса обычно может быть идентифицирована.

Неисправность оборудования : Возможен низкий резонанс незамеченным долгое время. Обычно симптомы необъяснимы. чувствительные источники питания, электронные нагрузки, перегрев трансформатора и т. д.

Состояние устойчивого состояния: Гармонический резонанс считается явление устойчивого состояния. Хотя переключение индуцированного переходного резонанса возможно, это решается с помощью программы моделирования переходных процессов и обычно требует различные методы смягчения.

11-й гармонический резонанс

Индуктивный импеданс

Система питания сопротивление в основном индуктивное при номинальной частоте (50/60 Гц). В сопротивление меняется в зависимости от частоты гармоники. Для индуктивности «L» полное сопротивление Z на частоте f равно

Емкостное сопротивление

Система питания конденсаторы могут быть конденсаторами коррекции коэффициента мощности, емкостью кабеля, емкость выключателя и т. д. Полное сопротивление изменяется обратно пропорционально в зависимости от гармоники. частота.Для конденсатора «C» полное сопротивление Z на частоте f равно

.

Импеданс индуктивность обратно пропорциональна частоте. Для гармоник более высокого порядка (большое f), импеданс будет пропорционально ниже.

Когда система индуктивное сопротивление и емкостное реактивное сопротивление становятся равными, резонансное состояние может развиваться. Это может быть:

Параллельный резонанс

Резонанс серии

Параллельный резонанс в энергосистеме

Ниже представлена ​​система, которая может дрейфовать до параллельного резонанса.Этот может ли крупный промышленный объект, где несколько низковольтных подстанций вводить гармонический ток в шине установки среднего напряжения. Потенциальная параллель Резонансное состояние может возникнуть между средним или низким напряжением установки. коэффициент конденсаторной батареи и индуктивность источника X _с .

Цепь с потенциалом для состояния параллельного резонанса

Резонансный частота определяется по формуле:

При параллельном резонансе частота, эффективное сопротивление цепи станет очень высоким.Примечание что при резонансе Xs = Xc. Для показанной схемы

Q известен как добротность и определяет резкость частотная характеристика. Для системы распределения Q может быть 5 и может быть 30 на вторичной обмотке большого распределительного трансформатора. Значение Q отличается для последовательного резонансного и параллельного резонансного контура.

Напряжение на конденсатор

При параллельном резонансе очень высокое напряжение на конденсаторе, выданном.

Поскольку значения QX _s очень высоки, небольшая гармоника ток (Ip) может вызвать падение большого напряжения на конденсаторе.

Ток через конденсатор

В условиях параллельного резонанса ток, протекающий в конденсатора и трансформатора, увеличивается в Q раз гармонического тока инъекционный (Ip).

Текущий увеличение может вызвать выход из строя конденсатора, нагрев трансформатора, перегорание предохранителя. Размер шунтирующей конденсаторной батареи относительно источника MVA определяет параллельную резонансную точку настройки . Параллельная резонансная частота для системы с шунтирующими батареями конденсаторов во вторичной обмотке силового трансформатора выдает:

Где

h _p — порядок параллельной резонансной частоты

MVA _3øsc — трехфазное короткое замыкание MVA

X _s — реактивное сопротивление короткого замыкания системы

X _c — реактивное сопротивление звезды, эквивалентное конденсаторная батарея

Q _cap — размер конденсаторной батареи в МВАр

.

MVA _3øsc — эффективный MVA короткого замыкания в интересующей точке.Для большинства приложений быстрая оценка MVA _3øsc может быть сделана путем определения номинальной мощности трансформатора на входе в кВА и% импеданса. Это связано с тем, что полное сопротивление трансформатора преобладает над полным сопротивлением системы и, следовательно, имеет наибольшее влияние на эффективное значение MVA короткого замыкания. Обратите внимание, что включение импеданса сетевого источника, если оно доступно, приведет к более точным результатам.

Чтение: Расчет импеданса источника в энергосистеме

Сканирование гармонического импеданса с батареей конденсаторов и без нее

Пример : Рассмотрим систему, питающуюся от трансформатора 1000 кВА с % импеданс 5.65. Конденсаторная батарея, подключенная к низковольтной стороне трансформатор 350 кВАр или 0,350 МВАр. Доминирующие гармоники, генерируемые в объекта 5 ^-й и 7 ^-й . Определить системную параллель резонансной частоты и определить, существует ли какая-либо потенциальная проблема.

Ответ : С трансформатором 1000 кВА и импедансом 5,65% эффективное короткое замыкание источника MVA может быть приблизительно равно 1000 / 0,0565 = 17,7 МВА _3øsc.

Параллельная резонансная частота определяется выражением:

Система имеет параллельную резонансную точку 7.1, который опасно близка к доминирующей 7 ^{-й гармонике} , генерируемой в средство. Одним из решений здесь будет уменьшение размера конденсатора для перемещения резонансная точка. Если мы выберем банк 250 кВАр, новая резонансная точка будет 8,4. что достаточно далеко от заказа 7 ^th . Другое решение было бы быть использовать отстроенную батарею конденсаторов.

Резонанс серии

в системе питания Резонанс серии

может возникнуть, когда последовательная комбинация индуктивность трансформатора объекта и батарея шунтирующих конденсаторов на объекте резонирует на гармонической частоте, которая вводится из распределения система. В этом сценарии объект сам по себе не может быть значительным генератором гармонических токов, но все же может испытать гармонические эффекты резонанса из-за последовательной комбинации LC «Отвод» значительного гармонического тока из вышестоящей распределительной системы. Ниже приведен пример системы, которая потенциально может быть включена в серию резонанс.

Цепь с потенциалом для условия последовательного резонанса

Напряжение на конденсаторе увеличивается и искажается и можно представить как:

Где V _h — гармоническое напряжение, присутствующее в системе.R — внутреннее последовательное сопротивление указанной выше цепи и не показано на рисунке. Обратите внимание, что при резонансе значения Xt и Xc будут равны и противоположны по величине, следовательно, компенсируют друг друга.

Последовательный и параллельный резонанс в практическом применении энергосистем

Практически говоря, резонансное состояние серии также будет имеют состояние параллельного резонанса из-за топологии цепи. На рисунке ниже, X _t — реактивное сопротивление трансформатора объекта, а X _c — реактивное сопротивление конденсаторной батареи объекта.Реактивное сопротивление источника равно X _s .

Гармонический резонанс энергосистемы

Система, как показано, будет имеют свою первую резонансную точку серии, определяемую Xc и Xt, и первую параллельную резонансная точка, определяемая Xc, Xt и Xs.

Из уравнения для последовательного и параллельного резонанса можно заметил, что параллельный резонансный точка всегда ниже, чем точка последовательного резонанса в практической мощности установка системы.

Последовательный и параллельный резонанс в энергосистеме

Разница между Последовательный и параллельный резонанс в энергосистеме — это серия резонанс создает низкий импеданс (потребляет максимальный ток в системе) тогда как параллельный резонанс создает большой импеданс , который даже при небольшом токе может создать большое падение гармонического напряжения и, как следствие, повреждения, связанные с напряжением.

Калькулятор, приведенный ниже, можно использовать для определения последовательной и параллельной резонансной частоты для простой системы.

Фильтр гармоник Резонанс

Важное наблюдение можно увидеть, наблюдая за графиком выше. То, что обсуждается о последовательном и параллельном резонансе, также может быть применено. к шунтирующему фильтру гармоник. Если размер фильтра соответствует приложения, последовательная резонансная точка будет гармоническим порядком, который требует фильтрация, в то время как параллельная резонансная точка будет в точке, удаленной от любого система генерирует гармонические частоты.Теперь предположим, что некоторые из конденсаторов в фильтр не работает. Потеря емкости (увеличение Xc) приводит к перемещению серии и параллельная резонансная точка, которая до отказа находилась в «безопасных» местах но, возможно, переместился в более проблемные области после отказа конденсатора. В результирующий фильтр может потреблять чрезмерный гармонический ток (последовательный резонанс) и выходят из строя или создают искажения высокого напряжения (параллельный резонанс).

Влияние цепи сопротивление при подавлении резонанса

Демпфирование, создаваемое сопротивлениями в энергосистеме, составляет помогает снизить катастрофические последствия резонанса энергосистемы. Даже 10% резистивная нагрузка может иметь значительное положительное влияние на пиковое сопротивление. Обратите внимание, что сопротивление цепи не удаляет гармоники, а только уменьшает (смягчает) разрушительные последствия, вызванные резонанс. Коммунальные предприятия в этом отношении имеют преимущество, поскольку могут физически изменить расположение фильтров гармоник, конденсаторных батарей на место, обеспечивающее дополнительное последовательное линейное сопротивление. Промышленные установки делают не имеют этой роскоши и обычно имеют ограниченные возможности при установке конденсаторные батареи или фильтры.

Резистивная нагрузка и ее влияние на пик параллельного резонанса

Конденсаторные батареи обычно устанавливается на шине подстанции низкого напряжения сразу после подстанции трансформатор. Отношение X / R в таком месте имеет тенденцию быть высоким или в другом месте. словами сопротивление в этом месте относительно меньше и, следовательно, параллельно резонансный пик будет очень резким и высоким. Применение конденсаторных батарей при такое расположение необходимо проверить, чтобы определить, где находится точка резонанса (используйте указанный выше калькулятор в качестве предварительной проверки перед использованием инженерных программное обеспечение для моделирования).Если резонансная точка системы лежит близко к одной из доминирующие гармоники, производимые на объекте (скажем, 5 ^-я , 7 ^-я и т. д.) то у нас возникла проблема. г. решением будет либо изменить размер банка, либо использовать «расстроенный» конденсаторная батарея.

Малогабаритные двигатели HP немного помогают с системой демпфирования резонанс, поскольку их кажущееся отношение X / R низкое. С другой стороны, больший HP двигатели имеют высокое отношение X / R и могут делать наоборот. Очень большие двигатели также имеют тенденцию влиять на частотную характеристику системы и может сместить систему резонансная точка.В инженерный анализ необходимо включить такие большие (> 500 л.с.) нагрузки двигателя.

Вывод: Гармонический резонанс — это мощность проблема качества, которую трудно визуализировать, так как ущерб, причиненный из-за резонанс вывел бы систему из резонанса (самокоррекции) время, когда инженер выполняет измерение или анализ. Отсюда важное Шаги в диагностике гармонического резонанса заключаются в том, чтобы сначала определить, конфигурация может перейти в состояние последовательного или параллельного резонанса, как подробно в этой статье.Подробный компьютерный гармонический анализ может обычно определяют состояние резонанса.

Другие статьи по теме: Калькулятор коэффициента мощности, Калькулятор резонанса, Калькулятор фильтра гармоник, Соединение конденсаторов звездой и треугольником, Расчет КВАр-Ампер

Резонанс в цепях RLC

Резонанс — это тенденция системы к колебаниям с большей амплитудой на одних частотах, чем на других. Частоты, при которых амплитуда отклика является относительным максимумом, известны как резонансные частоты системы.2}} $,

, где I _rms и V _rms — среднеквадратичные значения тока и напряжения соответственно. Реактивные сопротивления изменяются в зависимости от частоты $ \ nu $, при этом X _L большое на высоких частотах и ​​X _C большое на низких частотах, определяемое как:

$ X_L = 2 \ pi \ nu L, X_C = \ frac {1} {2 \ pi \ nu C} $.

При некоторой промежуточной частоте $ \ nu_0 $ реактивные сопротивления будут равны и отменены, давая Z = R — это минимальное значение для импеданса, а максимальное значение для I _rms результатов.Мы можем получить выражение для $ \ nu_0 $, взяв X _L = X _C . Подстановка определений X _L и X _C дает:

$ \ nu_0 = \ frac {1} {2 \ pi \ sqrt {LC}} $.

$ \ nu_0 $ — резонансная частота последовательного контура RLC. Это также собственная частота, на которой цепь будет колебаться, если не будет управляться источником напряжения. При $ \ nu_0 $ влияние катушки индуктивности и конденсатора компенсируется, так что Z = R, а I _{среднеквадратичное значение} является максимальным.Резонанс в цепях переменного тока аналогичен механическому резонансу, где резонанс определяется как вынужденные колебания (в данном случае вызванные источником напряжения) на собственной частоте системы.

Приемник в радиостанции представляет собой схему RLC, которая лучше всего генерирует колебания на своем $ \ nu_0 $. Переменный конденсатор часто используется для регулировки резонансной частоты, чтобы получить желаемую частоту и отклонить другие. представляет собой график зависимости тока от частоты, иллюстрирующий резонансный пик в I _rms при $ \ nu_0 = f_0 $.Две кривые относятся к двум разным схемам, которые различаются только величиной сопротивления в них. Пик ниже и шире для цепи с более высоким сопротивлением. Таким образом, цепи с более высоким сопротивлением не резонируют так сильно, и, например, в радиоприемнике они не будут такими избирательными.

Зависимость тока от частоты

График зависимости тока от частоты для двух цепей серии RLC, различающихся только величиной сопротивления. Оба имеют резонанс при f0, но для более высокого сопротивления он ниже и шире.