Законы Кирхгофа для электрической цепи

Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Главная Справочник Физика Законы Кирхгофа для электрической цепи

Правильнее было бы говорить правила Кирхгофа для расчетов сложных электрических цепей постоянного тока. Электрическая цепь на практике может состоять из нескольких резисторов и источников тока. Такие цепи называют разветвленными. Уравнения позволяющие провести расчеты, например, сил токов, текущих в сопротивлениях, в любых сетях можно составить, воспользовавшись законом Ома и законом сохранения заряда.

Правила Кирхгофа являются следствиями вышеназванных законов и принципиально нового ни чего не привносят, однако, с их помощью можно упростить процедуру написания необходимых уравнений. Существует два правила Кирхгофа для электрических цепей постоянного тока. Одно правило называют правилом узлов, так как оно связывает в одно уравнение токи, сходящиеся в узле. Второе правило касается замкнутых контуров, которые можно выделить в сложной цепи.

Первый закон (правило) Кирхгофа

В электрической цепи в одной точке могут сходиться более двух проводников с токами, тогда такую точку цепи называют узлом (разветвлением). Учитывая, что сила тока алгебраическая величина для любого узла:

   

где N – число токов, которые сходятся в узле. Выражение (1) называют первым правилом Кирхгофа (правило узлов): сумма токов, текущих через сопротивления в цепи постоянного тока, с учетом их знака, сходящихся в узле, равна нулю.

Знак у тока (плюс или минус) выбирают произвольно, но при этом следует считать, что все входящие в узел токи имеют одинаковые знаки, а все исходящие из узла токи имеют противоположные входящим, знаки.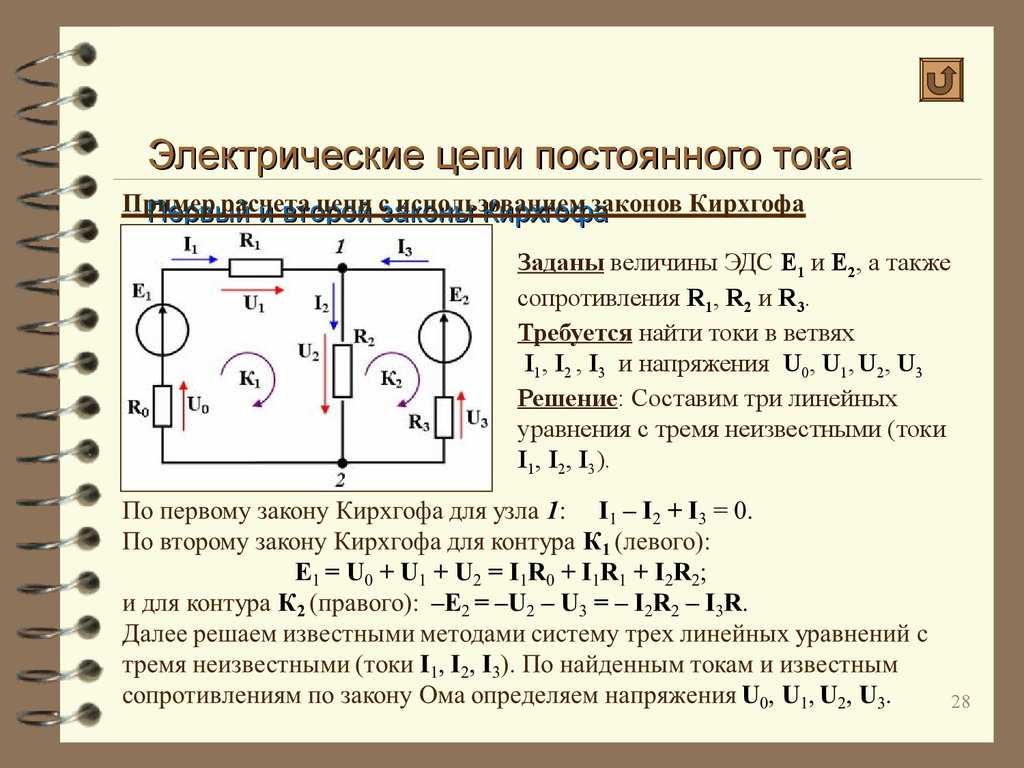 Допустим, все входящие токи мы примем за положительные, тогда все исходящие их этого узла токи будут отрицательными.

Первое правило Кирхгофа дает возможность составить независимое уравнение, если в цепи k узлов.

Первое правило Кирхгофа является следствием закона сохранения заряда.

Второй закон (правило) Кирхгофа

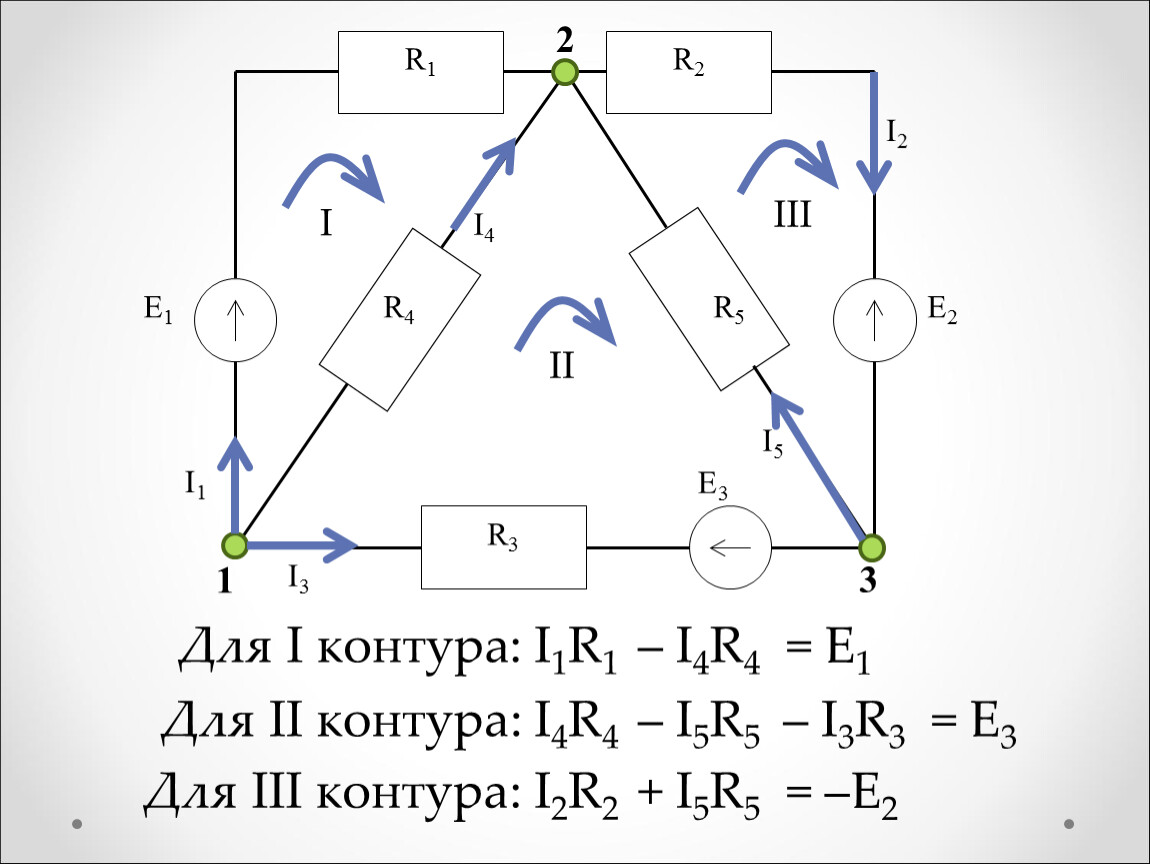
Во втором правиле Кирхгофа рассматриваются замкнутые контуры, поэтому оно носит название правила контуров: Суммы произведений алгебраических величин сил тока на внешние и внутренние сопротивления всех участков замкнутого контура равны алгебраической сумме величин сторонних электродвижущих сил (ЭДС) (), которые входят в рассматриваемый контур. В математическом виде второй закон Кирхгофа записывают как:

   

Величины называют падениями напряжения. До применения второго закона Кирхгофа выбирают положительное направление обхода контура. Это направление берется произвольно, либо по часовой стрелке, либо против нее. Если направление обхода совпадает с направлением течения тока в рассматриваемом элементе контура, то падение напряжения в формулу второго правила для данного контура входит со знаком плюс. ЭДС считают положительной, если при движении по контуру (в избранном направлении) первым встречается отрицательный полюс источника. Более правильно было бы сказать, что ЭДС считают положительной, если работа сторонних сил по перемещению единичного положительного заряда на рассматриваемом участке цепи в заданном направлении обхода контура является положительной величиной.

Второе правило Кирхгофа является следствием закона Ома.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

Задача на закон Кирхгофа — Электрические цепи — Спроси!

Dayana (Deya)

01.Март.2023 12:39:36

1

Нужно найти I2, I3. Вообще не понимаю, как составлять систему уравнений по закону Кирхгофа.

1 лайк

Kirill_Chumikov (Kirill Chumikov) 01.Март.2023 12:49:01

2

Иродов элекромагнетизм
Прочитай и проанализируй §5.4

Подсказка

Токи у тебя уже направлены,поэтому правило узлов (1 правило Кирхгофа) записать,думаю, сможешь.
Разбей цепь на контуры и выбери положительное направление обхода контуров произвольно.
Количество неизвестных равно количеству уравнений.

4 лайка

NurassylL (Nurassyl Mirkamalov) 01.Март.2023 13:02:31

3

Могу порекомендовать Урок 263. Правила Кирхгофа — YouTube

1 лайк

MegaBit 01.Март.2023 13:09:19

4

Думаю все понятно

1 лайк

ernur045 (Yernur Kairollayev) 01.Март.2023 14:04:40

5

MegaBit:

Думаю все понятно

Не факт, что человек взглянувший на решение без комментариев, поймёт его. Для такого нужно иметь пару попыток решения задачи, или успешное прорешивание. В данном же случае просят объяснить как составлять законы Кирхгофа, значит стоит уделить отдельное внимание объяснению этого момента

5 лайков

Dayana (Deya) 01.

Март.2023 14:17:22

6

В принципе, кажется, поняла. Но все же и не совсем)))
Спасибо большое!

MegaBit 01.Март.2023 14:18:18

7

Посмотри в интернете, достаточно много информации в интернете есть на эту тему

1 лайк

Dayana (Deya) 01.Март.2023 14:18:24

8

Я пыталась решить это много раз, но не понимаю именно механизм составления уравнений Кирхгофа

Alisher (Alisher Yerkebayev) 01. Март.2023 15:54:54

9

Deya:

механизм составления уравнений Кирхгофа

Вы знакомы с понятием “обход контура”?

Dayana (Deya) 01.Март.2023 16:18:03

10

Я примерно понимаю, что это такое, но была бы очень благодарна, если поглубже объясните)

Alisher (Alisher Yerkebayev) 01.Март.2023 16:28:34

11

Это просто понятие, которое вводится, чтобы понять смысл нижеследующей записи второго правила Кирхгофа:

\sum_i\xi_i = \sum_i I_i R_i.

По левой части “суммируются” все эдс, что есть в контуре, по правой части суммируются все напряжения на резисторах. Положительным эдс считается при обходе контура от минуса к плюсу, а напряжение резистора положительно при направлении силы тока, совпадающем с обходом контура. Направление контура можно брать произвольно, так как при смене направления просто добавятся дополнительные минусы по обе части, что никак не влияют на уравнения. Например, из решения @MegaBit второе правило Кирхгофа записано в 1 и 5 строчках:

\xi_3-\xi_2 = I_3\cdot(2+1)+I_2\cdot2,\\ \xi_1-\xi_2=I_1\cdot 6+I_2\cdot 2.

Первое уравнение показывает обход по нижнему контуру по часовой стрелке. Во втором обход верхнего контура против часовой стрелки. Что, если сложить эти уравнения? Поскольку в первом уравнении всё взято “по часовой стрелке”, а во втором “против часовой”, то если эти уравнения отнять, то выйдет

\xi_3-\xi_1 = I_3\cdot(2+1)-I_1\cdot 6.

И ого, если приглядеться, то это по сути правило Кирхгофа, записанное для большого контура.

А значит неважно какие именно мы берём контуры, какие именно берём обходы, и даже какие именно направления токов. Если сумма токов в каждом узле и равенство напряжений записаны с правильным учётом знаков, то после расчётов ответы сами станут положительными или отрицательными, из чего можно делать вывод о том, как именно направлены у нас токи.

4 лайка

MegaBit 02.Март.2023 02:19:46

12

Можешь кстати открыть канал Edlight Physics на ютубе, на этом канале много роликов по теме электричество

Dayana (Deya) 02.Март.2023 04:31:17

13

Ох, спасибо Вам огромное! Наконец-то более менее поняла

Dayana (Deya) 02. Март.2023 04:31:32

14

Спасибо большое! Обязательно посмотрю

1 лайк

Симметрия | Бесплатный полнотекстовый | Индекс Кирхгофа и аддитивный индекс Кирхгофа, основанный на мультипликативной степени для случайной цепочки полимино

1. Введение

Расстояние сопротивления рассматривается как функция графа расстояний, которая необходима для случайного блуждания графа и пружинной сети. Основываясь на идее электрических сетей, Клейн и Рандич [1] в 1993 г. предложили понятие индекса Кирхгофа и расстояния сопротивления графов. Предположим, что G — симметричный граф с множеством вершин {υ˘1,υ˘2,υ˘ 3,…,υ˘η}, а соответствующая электрическая сеть N получается при замене каждого ребра графа фиксированным сопротивлением (единичным сопротивлением). Для графа G расстояние сопротивления между любыми двумя вершинами обозначается через γ˘(υ˘i,υ˘j), где υ˘i,υ˘j∈G. Однако в электрических сетях расстояние сопротивления известно как эффективное сопротивление между узлами. Эффективное сопротивление можно рассчитать из законов Кирхгофа и законов Ома. Сумма всех пар вершин расстояний сопротивления известна как индекс Кирхгофа группы G, представляется как Kf(G) и записывается как

где

Чен и Чжан [2] представили современный инвариант графа в 2007 году, который сформулирован как

где δ˘i указывает степень вершины υ˘i графа G.

Gutman et al. [3] в 2012 году ввел идею аддитивного индекса степени Кирхгофа, определяемого как

Было проведено множество исследований по вычислению индексов Кирхгофа для конкретных классов графов, по нахождению оценок индексов Кирхгофа графов и по нахождению характеристических экстремальных графов [4,5,6,7,8,9].,10]. Недавно было проведено исследование индекса Кирхгофа, основанного на степени вершин неправильных многоугольных цепей.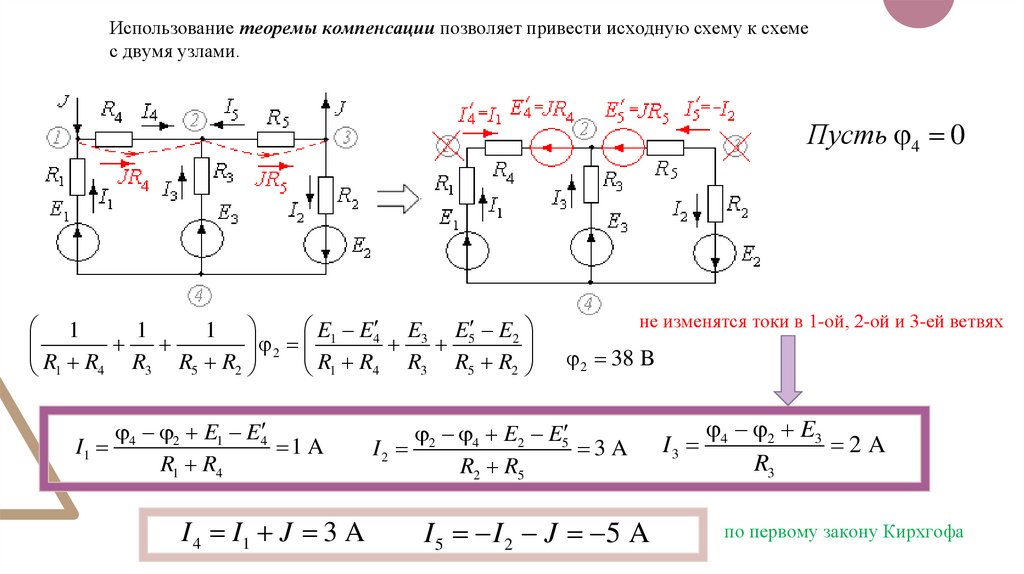 Эти усилия привели к получению ожидаемых значений показателей степени Кирхгофа (как аддитивного, так и мультипликативного), индекса Гутмана и индекса Шульца случайной полифениленовой цепи [11]. Для расширенных исследований случайных полигональных цепочек читатели в основном ссылались на недавние статьи [12,13,14,15]. Мотивация целевого исследования может быть сформулирована следующим образом:

• Некоторые ученые изучают методы расчета степени Кирхгофа для некоторых специальных классов графов, таких как линейная шестиугольная цепочка, шестиугольная цепочка, лестничная диаграмма, лестничная цепочка, линейная полиномиальная цепочка, линейная шестиугольная цепочка и так далее. Эта работа осталась без внимания для случайной цепочки полимино.

• В [2] авторы установили красивую связь между мультипликативным индексом степени Кирхгофа и собственными значениями нормированной матрицы Лапласа.

Вдохновленная вышеупомянутой литературой, эта статья посвящена установлению точных формул для ожидаемых значений индексов Кирхгофа в аддитивной и мультипликативной степени через случайную цепь полимино. При этом характеризуется и наивысшая степень ожидаемых значений этих показателей.

Граф полимино [16] (известный также как шахматная доска [17] или расположение, использующее квадратные ячейки [18]) — это симметричный геометрический граф, который получается, когда два конгруэнтных обычных квадрата (имеют либо общее ребро, либо не пересекаются) со сторонами на расстоянии 1 (известный как ячейка) расположены в плоскости. Полимино-графы имеют множество приложений в структурной химии и статистической физике. Нерегулярная полиминоцепь известна как подграф полиминографа [19].]. Полимино-цепь Qη, имеющая «η» квадратов, которую следует рассматривать как полиамино-цепь Qη-1, имеющую «η-1» квадратов, смежную с указанным на рисунке новым конечным квадратом с обрезанным краем, как показано на рисунке 1.

Если Qη=ϝ˘1,ϝ˘2,⋯,ϝ˘η — цепь полимино, состоящая из η(≥2) квадратов, ϝ˘κ — это κ-й квадрат Qη, соединенный с ϝ˘κ−1 разрезанным ребром µ˘κ−1ω˘κ, где µ˘κ−1∈ϝ˘κ−1 и ω˘κ∈ϝ˘κ, (2≤κ≤η). Вершина υ˘ называется орто-вершиной (o˘κ) и пара-вершиной (p˘κ) ϝ˘κ, если расстояние между υ˘ и ω˘κ равно единице и двум соответственно.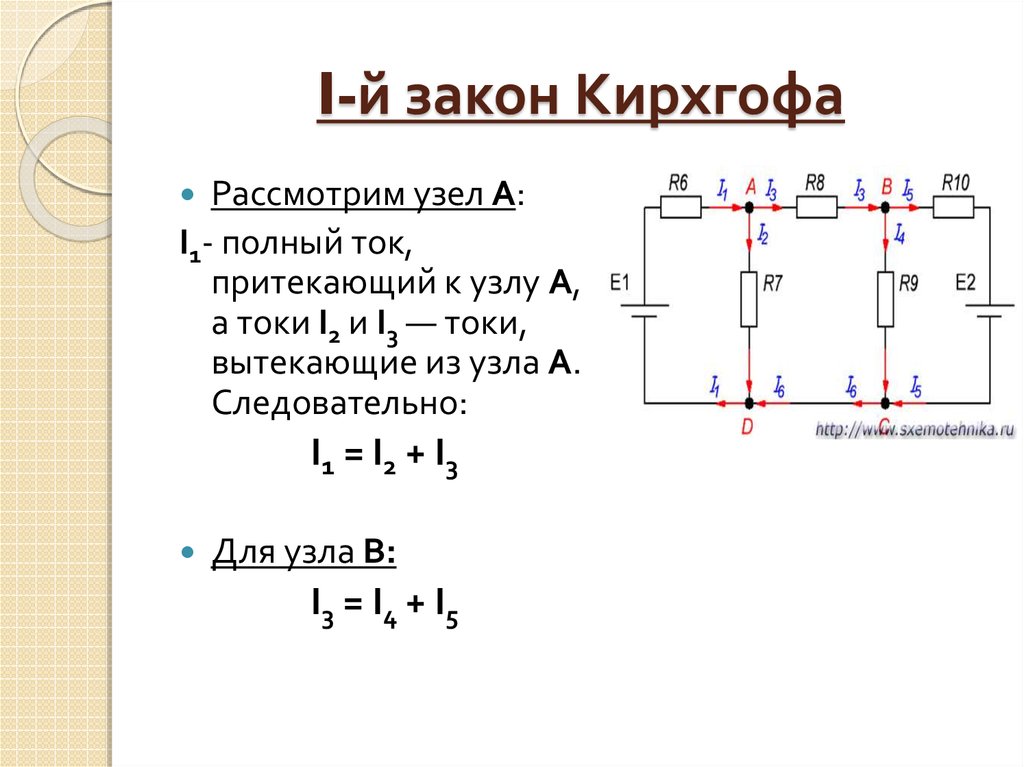 Легко установить, что ω˘η=λ˘1, o˘η=λ˘2,λ˘4 и p˘η=λ˘3 в ϝ˘η (см. рис. 1).

Цепь полимино Qη называется орто-цепью полимино Qηo и парацепью полимино Qηp, если μ˘κ=o˘κ и μ˘κ=p˘κ с 2≤κ≤η−1 соответственно.

Два различных соединения с пара- или орто-вершинами возможны для конечного квадрата η≥2, чтобы обеспечить локальные расположения, записанные как Qη+11Qη+12 (см. рис. 2).

Полиминоцепь известна как полиаминоцепь Q(η,t) с η квадратами, если концевые квадраты добавляются постепенно. На каждом этапе κ=(3,4,⋯,η) осуществляется случайный выбор из следующих построений:

1.

Qκ−1→Qκ1 с вероятностью t,

2.

Qκ−1→Qκ2 с вероятностью 1−t,

где вероятность не зависит от шага t,

вероятность параметр κ. В частности, нерегулярная цепь полимино Q(η,1) известна как орто-цепь полимино Qηo. Кроме того, Q(η,0) называется пара-цепью полимино Qηp.

2. Ожидаемое значение мультипликативного индекса степени Кирхгофа случайной цепочки полимино

Мультипликативный индекс степени Кирхгофа Kf*(Qη) для случайной цепи полимино Qη является случайной величиной.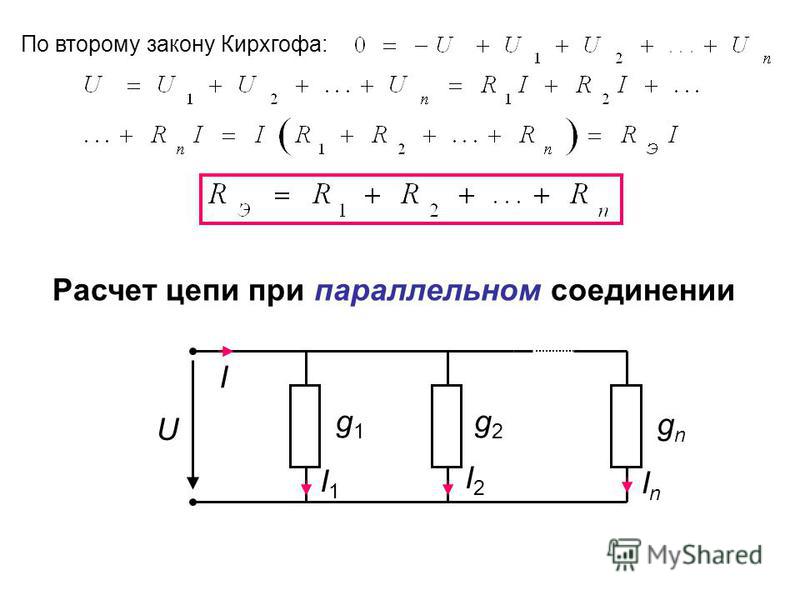 Здесь мы предлагаем точную формулу для его ожидаемого значения E(Kf*(Qη)).

Пусть конечный квадрат натянут на вершины {λ˘1,λ˘2,λ˘3,λ˘4}, а новое ребро помечено как µ˘ηλ˘1 (как показано на рисунке 1). Для каждого υ˘∈VQη имеем

Тем временем,

Доказательство.  

Из уравнения (3) видно, что

Обратите внимание, что

Из уравнений (5) и (6) получаем

Затем,

Для случайной цепочки полимино Qη случайная величина задается как ∑v∈VQηδ˘(υ˘)γ˘(µ˘η,υ˘). Мы пишем Rη=E(∑υ˘∈VQηδ˘(υ˘)γ˘(µ˘η,υ˘)) для представления его ожидаемого значения. Рассмотрим, например, две важные ситуации:

• Случай 1:  Qη→Qη+11

  Здесь µ˘η соотносится с вершиной, помеченной λ˘2 или λ˘4. В результате ∑υ˘∈VQηδ˘(υ˘)γ˘(µ˘η,υ˘) эквивалентно ∑υ˘∈VQηδ˘(υ˘)γ˘(λ˘2,υ˘).

• Случай 2:  Qη→Qη+12

  Здесь µ˘η соответствует вершине с номером λ˘3. В результате ∑υ˘∈VQηδ˘(υ˘)γ˘(µ˘η,υ˘) эквивалентно ∑υ˘∈VQηδ˘(υ˘)γ˘(λ˘3,υ˘).

Поскольку вероятности для упомянутых выше двух случаев в случайных цепочках полимино равны t и 1−t соответственно, мы можем определить ожидаемое значение Rη как:

Теперь, применяя свойства математического ожидания и проверяя, что E(Rη)=Rη, получаем

Граничное условие

Используя рекуррентное соотношение в уравнении (15), получаем

Используя оператор ожидания и уравнение (14), мы получаем

Состояние б/у

а уравнение (16) можно переписать как

Используя рекуррентное соотношение в приведенном выше уравнении, мы получаем

Особенно,

• Если t=1, E(Kf*(Qηo))=1756η3+52η2−323η−1.

• Если t=0, E(Kf*(Qηp))=1003η3−10η2−73η−1.

□

3. Ожидаемое значение индекса аддитивной степени Кирхгофа случайной цепи полимино

Доказательство.  

Как описано выше, цепь полимино Qη+1 получается путем присоединения Qη к новому терминальному полимино с помощью режущего края, как показано на рисунке 2. Используя уравнение (4), можно получить

где;

Положим γ˘(µ˘η|Qη)=∑υ˘∈VQηγ˘(µ˘η,υ˘), как обсуждалось в теореме 1, имеем

По уравнениям (5) и (6) имеем

Обратите внимание, что,

Тогда уравнение (17) можно переписать как

Для случайной цепочки полимино Qη,γ˘(µ˘η|Qη) — случайная величина с математическим ожиданием

Следующие два возможных случая помогли нам продолжить нашу работу.

• Случай 1:  Qη→Qη+11

  Здесь µ˘η совпадает с вершинами λ˘2 или λ˘4. Следовательно, γ˘(µ˘η|Qη) задается формулой γ˘(λ˘2|Qη).

• Случай 2:  Qη→Qη+12

  Здесь µ˘η совпадает с вершиной λ˘3. Следовательно, γ˘(µ˘η|Qη) задается выражением γ˘(λ˘3|Qη).

Поскольку в вышеописанных нерегулярных цепочках полимино с вероятностью случаются два сценария, t и 1−t соответственно, мы можем получить следующий результат:

Применяя свойства математического ожидания к упомянутому выше уравнению и учитывая, что E(Dη)=Dη, получаем

Граничное условие

Используя рекуррентное соотношение в уравнении (19), можно получить

Применяя свойства математического ожидания к уравнению (18), получаем

Таким образом,

Граничное условие задается как

Используя рекуррентное соотношение в уравнении (20) и граничное условие, получаем

В частности,

• Если t=1, E(Kf+(Qηo))=703η3+11η2−433η.

• Если t=0, E(Kf+(Qηp))=803η3+η2−233η.

□

4. Выводы

В этой статье мы вычислили точные формулы для очень специфической категории полиминографа, известной как подграфы или полимино-цепи, используя топологические индексы, а именно индекс мультипликативной степени-Кирхгофа и аддитивная степень-индекс Кирхгофа. Это исследование также характеризует высшую степень математического ожидания для упомянутого графа. Данная стратегия позволяет вычислить математическое ожидание для индекса Шульца и индекса Гутмана, что очень удобно для случайной цепочки полимино. Эти результаты ограничены случайными цепочками полимино. В будущем мы надеемся создать несколько новых структур/графов, а затем изучить их топологические индексы, чтобы лучше понять лежащие в их основе топологии.

Авторские взносы

Написание — подготовка первоначального проекта, М.Л.; написание — обзор и редактирование, PA; программное обеспечение, MA и HA; валидация, H. A.; формальный анализ, FM; методология, M.A. Все авторы прочитали и согласились с опубликованной версией рукописи.

Финансирование

Эта работа поддерживается Фондом естественных наук провинции Фуцзянь в рамках гранта № 2022J011149; Проект для молодежи и среднего возраста Департамента образования провинции Фуцзянь, номер гранта JAT200599.

Заявление Институционального контрольного совета

Неприменимо.

Заявление об информированном согласии

Неприменимо.

Заявление о доступности данных

В этом исследовании данные не использовались.

Конфликт интересов

Авторы заявляют об отсутствии конфликта интересов.

Ссылки

1. Клейн, Д.Дж.; Рэндич, М. Расстояние сопротивления. Дж. Матем. хим. 1993 , 12, 81–95. [Академия Google] [CrossRef]
2. Чен, Х .; Чжан, Ф. Расстояние сопротивления и нормализованный лапласовский спектр. Дискретный. заявл. Мат. 2007 , 155, 654–661. [Google Scholar] [CrossRef][Зеленая версия]
3. Гутман И.; Фэн, Л .; Ю, Г. Дистанция сопротивления степеней унициклических графов. Транс. Гребень. 2012 , 1, 27–40. [Google Scholar]
4. Yang, Y. Индекс Кирхгофа подразделений графов. Дискретный. заявл. Мат. 2014 , 171, 153–157. [Google Scholar] [CrossRef]
5. Ян, Ю.; Кляйн, Д.Дж. Графовые инварианты подразделений и триангуляции графов, основанные на сопротивлении. Дискретный. заявл. Мат. 2015 , 181, 260–274. [Google Scholar] [CrossRef]
6. Лю, Х.; Чжоу, Дж .; Bu, C. Расстояние сопротивления и индекс Кирхгофа соединения R-вершин и соединения R-ребер двух графов. Дискретный. заявл. Мат. 2015 , 187, 130–139. [Google Scholar] [CrossRef]
7. Du, J.; Су, Г.; Ту, Дж.; Гутман И. Степень сопротивления кактусов. Дискретный. заявл. Мат. 2015 , 188, 16–24. [Google Scholar] [CrossRef]
8. Qun, L. Некоторые результаты измерения расстояния сопротивления и индекса Кирхгофа короны вершины-ребра подразделения для графов. ИАЕНГ, международный Дж. Заявл. Мат. 2016 , 46, 346–352. [Google Scholar]
9. Бапат Р.Б.; Карими, М .; Лю, Дж. Б. Индекс Кирхгофа и индекс степени Кирхгофа полных многодольных графов. Дискретный. заявл. Мат. 2017 , 232, 41–49. [Google Scholar] [CrossRef]
10. Qi, X.; Чжоу, Б. Об индексе степени Кирхгофа унициклических графов. Дискретный. заявл. Мат. 2020 , 284, 86–98. [Google Scholar] [CrossRef]
11. Чжан, Л.; Ли, В.; Ли, С .; Чжан, М. Ожидаемые значения для индекса Шульца, индекса Гутмана, мультипликативного индекса степени Кирхгофа и аддитивного индекса степени Кирхгофа случайной полифениленовой цепи. Дискретный. заявл. Мат. 2020 , 282, 243–256. [Google Scholar] [CrossRef]
12. «> Wei, S.; Шиу, В.К. Перечисление индексов Винера в случайных ломаных цепях. Дж. Матем. Анальный. заявл. 2019 , 469, 537–548. [Google Scholar] [CrossRef]
13. Чжан, Дж.; Пэн, X .; Чен, Х. Предельное поведение для индекса Гутмана, индекса Шульца, мультипликативного индекса степени Кирхгофа и аддитивного индекса степени Кирхгофа случайной полифениленовой цепи. Дискретный. заявл. Мат. 2021 , 299, 62–73. [Академия Google] [CrossRef]
14. Хечао, Л.И.У.; Рангвей, В.У.; Лихуа, Ю.О.У. Три типа индексов Кирхгофа в случайных циклооктановых цепочках. JS Китай Норма. ун-т (Нац. ред.) 2021 , 53, 96–103. [Google Scholar]
15. Zhu, W.; Генг, X. Перечисление мультипликативного индекса степени Кирхгофа в случайных полигональных цепях. Molecules 2022 , 27, 5669. [Google Scholar] [CrossRef]
16. Berge, C.; Чен, CC; Хватал, В .; Сеоу, К. С. Комбинаторные свойства полимино. Комбинаторика 1981 , 1, 217–224. [Google Scholar] [CrossRef]
17. Cockayne, E.J. Проблемы доминирования на шахматной доске. Дискретный. Мат. 1990 , 86, 13–20. [Google Scholar] [CrossRef][Green Version]
18. Harary, F.; Мезей, П.Г. Преобразования выделения ячеек, отношения эквивалентности и меры подобия для конфигураций с квадратными ячейками. Междунар. J. Квантовая хим. 1997 , 62, 353–361. [Google Scholar] [CrossRef]
19. Ву, Т.; Лю, Х .; Чжан, X. Экстремальная энергия согласования случайных цепочек полимино. Энтропия 2017 , 19, 684. [Google Scholar] [CrossRef][Green Version]

Рисунок 1. Цепь полимино Qη с η квадратами.

Рисунок 1. Цепь полимино Qη с η квадратами.

Рисунок 2. Два типа локального расположения в цепях полимино.

Рисунок 2. Два типа локального расположения в цепях полимино.

Отказ от ответственности/Примечание издателя: Заявления, мнения и данные, содержащиеся во всех публикациях, принадлежат исключительно отдельным авторам и участникам, а не MDPI и/или редакторам. . MDPI и/или редактор(ы) отказываются от ответственности за любой ущерб людям или имуществу в результате любых идей, методов, инструкций или продуктов, упомянутых в содержании.

© 2023 авторами. Лицензиат MDPI, Базель, Швейцария. Эта статья находится в открытом доступе и распространяется на условиях лицензии Creative Commons Attribution (CC BY) (https://creativecommons.org/licenses/by/4.0/).

Перечисление мультипликативного индекса степени-Кирхгофа в случайных полигональных цепочках

• Список журналов
• Молекулы
• PMC9457823

молекул. 2022 сен; 27(17): 5669.

Опубликовано в сети 2 сентября 2022 г. doi: 10.3390/molecules27175669

Jia-Bao Liu, академический редактор

Информация об авторе Примечания к статье Информация об авторских правах и лицензии Отказ от ответственности

Индекс мультипликативной степени Кирха интересный топологический индекс. В этой статье мы вычисляем аналитическое выражение для ожидаемого значения индекса мультипликативной степени-Кирхгофа в случайном многоугольнике. На основании вышеприведенного результата мы также получаем Мультипликативную степень-индекс Кирхгофа всех полигональных цепочек с экстремальными значениями и средними значениями.

Ключевые слова: мультипликативный индекс степени Кирхгофа, случайные ломаные цепи, математическое ожидание, экстремальное значение, среднее значение

В этой статье мы рассматриваем только простые и конечные связные графы. Топологический индекс представляет собой математический дескриптор молекулярной структуры, который получается путем выполнения некоторой числовой операции над матрицей, представляющей молекулярный граф. Это инвариантный график, созданный непосредственно из молекулярной структуры и используемый для отражения размера, формы, ветви и других структурных особенностей молекулы, чтобы реализовать числовое значение информации о молекулярной структуре. Молекулярно-топологические индексы широко используются из-за их простоты, объективности и свободы от опыта и экспериментов. Было предложено более 200 различных типов топологических индексов.

Общеизвестно, что возникновение и развитие теории графов тесно связано с изучением химических молекулярных графов. Использование топологических индексов, физико-химических свойств и параметров активности соединений для построения моделей QSPR/QSAR, а также для оценки и прогнозирования их свойств стало одной из самых активных областей химических исследований. В последние годы все большее внимание уделяется повышению квалификации рабочих-химиков. Графическое представление соединения содержит атомы в виде узлов и связи в виде ребер. Для получения более подробной информации мы можем обратиться к [1,2,3,4].

Топологические индексы могут использоваться для описания химических структур и связаны с физическими свойствами, термодинамическими параметрами, химическими свойствами, биологической активностью и канцерогенностью соединений. Граф — это упорядоченная двойка G=(V(G),E(G)), где V(G) — непустое множество, а E(G) — множество, не пересекающееся с V(G). V(G) и E(G) — набор вершин и набор ребер G . Число ребер, инцидентных v в G , называется степенью вершины 9.0359 v в G и обозначается dG(v). Если u и v находятся в одном компоненте G , мы определяем d(u,v) как длину кратчайшего пути u−v в G [5,6,7].

В 1993 году Клейн и Рандич, академики Международной академии математических химиков, обсудили применение эффективного сопротивления в химии и назвали эффективное сопротивление графа расстоянием сопротивления графа. Впервые в мире была выдвинута концепция дистанции сопротивления, и ее авторы указывали, что дистанция сопротивления имеет больше преимуществ, чем кратчайшее расстояние, в изучении дистанции молекулярной коммуникации и других аспектов [8].

Индекс Кирхгофа определяется как

Kf(G)=∑{x,y}⊆VGr(x,y).

(1)

В 2007 г. мультипликативный индекс степени Кирхгофа был определен как [9]

Kf*(G)=∑{x,y}⊆VGd(x)d(y)r(x,y).

(2)

Случайная полигональная цепочка Gn из n полигонов составлена ​​из полигональной цепочки Gn−1 из n−1 полигонов, где новый терминальный многоугольник Hn примыкает к ребру, см. . При n≥3 конечный многоугольник Hn можно соединить через м способов, которые можно описать как перестановку Gn1,Gn2,Gn3,…,Gnm. видеть . Случайная цепочка многоугольников Gn(p1,p2,p3,…,pm−1) — это цепочка многоугольников, полученная последовательным добавлением концевых многоугольников. В каждом сложении m(=3,4,…,n) можно случайным образом выбрать один из m режимов соединения:

• Gm−1→G2m1 с вероятностью p1,

• Gm−1→G2m2 с вероятностью p2,

• Gm−1→G2m3 с вероятностью p3,

• ⋮          ⋮                         ⋮ 9где вероятности p1, p2, p3, …, pm−1 — константы, не зависящие от параметра m .

  Открыть в отдельном окне

  Полигональная цепочка Gn из n полигонов.

  Открыть в отдельном окне

  м виды локальных расположений полигональной цепочки.

  Пусть Gn — полигональная цепь с n полигонов h2, h3, …, Hn. utωt связывает Ht и Ht+1 с ut∈VHt в Gn, ωt∈VHt+1 для t=1,2,⋯,n−1. Очевидно, что и ωt, и ut+1 являются вершинами в Ht+1 и d(ωt,ut+1)∈{1,2,3,…,n}. В частности, Gn — это метацепь Mn(pm=1), ортоцепь On1,On2,…, Onm−2(pi+1=1,1≤i≤m−2) и парацепь Ln (pm=1), если d(ωt,ut+1)=1 (т.е. p1=1), d(ωt,ut+1) = 2 (т.е. p2=1), d(ωt,ut+1) = 3 (т.е. p3=1), …, d(ωt,ut+1)= m(т.е. pm=1) для всех t∈{1,2,…,n−2} соответственно.

  Huang, Kuang и Deng [10] рассчитали случайные полифенильные и спироцепи, а Zhang и Li et al. [11] рассчитали ожидаемые значения случайных полифениленовых цепей мультипликативного индекса Кирхгофа. Для получения дополнительной информации мы можем обратиться к [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]. Мы вычисляем аналитическое выражение для ожидаемого значения мультипликативного индекса степени Кирхгофа в случайном многоугольнике. Мы также получаем мультипликативный индекс степени Кирхгофа с экстремальными значениями и средними значениями всех ломаных цепочек. Эти результаты сыграют положительную роль в изучении химических и физических свойств соединений, разработке лекарств и прогнозировании загрязнения окружающей среды [31,32].

  В этой части в случайной полигональной цепочке мы вычислим ожидаемое значение коэффициента мультипликативной степени-Кирхгофа. Для случайной полигональной цепи Gn мультипликативная степень Кирхгофа является случайной величиной. На самом деле Gn+1 — это Gn, соединенный ребром с новым концевым многоугольником Hn+1, здесь Hn+1 состоит из вершин x1, x2, x3,…,x2m, а новое ребро равно unx1; видеть . Для всех v∈VGn

  r(x1,v)=r(un,v)+1,r(x2,v)=r(un,v)+1+1·(2m−1)1+(2m−1)=r (un,v)+1+2m−12m,r(x3,v)=r(un,v)+1+2·(2m−2)2+(2m−2)=r(un,v)+ 1+4m−42m,⋮⋮⋮r(xm,v)=r(un,v)+1+(m−1)·(m+1)(m−1)+(m+1)=r( un,v)+1+m2−12m,r(xm+1,v)=r(un,v)+1+m·mm+m=r(un,v)+1+m22m,r(xm+ 2,v)=r(un,v)+1+(m+1)·(m−1)(m+1)+(m−1)=r(un,v)+1+m2−12m, ⋮⋮⋮r(x2m−1,v)=r(un,v)+1+(2m−2)·2(2m−2)+2=r(un,v)+1+4m−42m,r (x2m,v)=r(un,v)+1+(2m−1)·1(2m−1)+1=r(un,v)+1+2m−12m.

  (3)

  ∑v∈VGndGn+1(v)=[(2m−2)·2+2·3]n−1=(4m+2)n−1.

  (4)

  И,

  ∑i=12md(xi)r(x1,xi)=4m2−13=8m3−2m6m,∑i=12md(xi)r(x2,xi)=4m2−13+1·(2m−1)2m =8m3+4m−36m,∑i=12md(xi)r(x3,xi)=4m2−13+2·(2m−2)2m=8m3+10m−126m,⋮⋮⋮∑i=12md(xi) r(xm,xi)=4m2−13+(m−1)·(m+1)2m=8m3+3m2−2m−36m,∑i=12md(xi)r(xm+1,xi)=4m2− 13+m·m2m=8m2+3m−26m,∑i=12md(xi)r(xm+2,xi)=4m2−13+(m+1)·(m−1)2m=8m3+3m2−2m −36m,⋮⋮⋮∑i=12md(xi)r(x2m−1,xi)=4m2−13+(2m−2)·22m=8m3+10m−126m,∑i=12md(xi)r(x2m ,xi)=4m2−13+(2m−1)·12m=8m3+4m−36m.

  (5)

  Напомним, что d(x1)=3 и d(xi)=2 для i∈{2,3,4,…,2m}. Из (3) и (4) имеем

  ∑v∈VGn∑xi∈VHn+1d(v)d(xi)r(v,xi)=∑v∈VGnd(v)[3(r(un,v)+1)+2(r( un,v)+1+1·(2m−1)2m)+2(r(un,v)+1+2·(2m−2)2m)+2(r(un,v)+1+3 ·(2m−3)2m)+⋯+2(r(un,v)+1+(m−1)·(m+1)2m)+2(r(un,v)+1+m·m2m )+2(r(un,v)+1+(m+1)·(m−1)2m)+⋯+2(r(un,v)+1+(2m−2)·22m)+2 (r(un,v)+1+(2m−1)·12m)]=∑v∈VGnd(v)[(4m+1)r(un,v)+4m2+12m+23]=(4m+ 1)∑v∈VGnd(v)r(un,v)+4m2+12m+23[(4m+2)n−1].

  Из (5) есть,

  ∑{xixj}⊆VHn+1d(xi)d(xj)r(xi,xj)=12∑i=12md(xi)(∑j=12md(xj)r(xi,xj))=12[ 3×4m2−13+2×(4m2−13+1·(2m−1)2m)+2×(4m2−13+2·(2m−2)2m)+⋯+2×(4m2−13+( m−1)·(m+1)2m)+2×(4m2−13+m·m2m)+2×(4m2−13+(m+1)·(m−1)2m)+⋯+2× (4м2-13+(2м-1)·12м)]=8м3+4м2-2м-13.

  Тогда

  Kf*(Gn+1)=Kf*(Gn)+(4m+2)∑v∈VGnd(v)r(un,v)+4m2+12m+23[(4m+2)n−1] +8м3+4м2-2м-13.

  (6)

  Для случайной многоугольной цепочки Gn математическое ожидание числа ∑v∈VGnd(v)r(un,v) является случайной величиной. Мы можем представить это

  Rn:=E(∑v∈VGnd(v)r(un,v)).

  Подставляя Rn в (6), можно получить рекуррентную формулу E(Kf*(Gn))

  E(Kf*(Gn+1))=E(Kf*(Gn))+(4m+2 )Rn+16m3+56m2+32m+43n+8m3−14m−33.

  Продолжаем рассматривать следующие м возможностей.

  • Путь 1. Gn⟶Gn+11. Таким образом, un дает тот же результат с вершиной x2 или x2m. Тогда ∑v∈VGnd(v)r(un,v) описывается как ∑v∈VGnd(v)r(x2,v) или ∑v∈VGnr(v)d(x2m,v) с вероятностью p1.

  • Путь 2. Gn⟶Gn+12. Таким образом, un дает тот же результат с вершиной x3 или x2m−1. Тогда ∑v∈VGnd(v)r(un,v) описывается как ∑v∈VGnd(v)r(x3,v) или ∑v∈VGnd(v)r(x2m−1,v) с вероятностью p2 .

  • Способ 3. Gn⟶Gn+13. Таким образом, un дает тот же результат с вершиной x4 или x2m−2. Тогда ∑v∈VGnd(v)r(un,v) описывается как ∑v∈VGnd(v)r(x4,v) или ∑v∈VGnd(v)r(x2m−2,v) с вероятностью p3 .

  • ⋮      ⋮                       ⋮

  • Путь м-3. Gn⟶Gn+1m−3. Таким образом, un дает тот же результат с вершиной xm−2 или xm+4. Тогда ∑v∈VGnd(v)r(un,v) описывается как ∑v∈VGnd(v)r(xm−2,v) или ∑v∈VGnd(v)r(xm+4,v) с вероятность pm−3.

  • Путь м-2. Gn⟶Gn+1m−2. Таким образом, un дает тот же результат с вершиной xm−1 или xm+3. Тогда ∑v∈VGnd(v)r(un,v) описывается как ∑v∈VGnd(v)r(xm−1,v) или ∑v∈VGnd(v)r(xm+3,v) с вероятность pm−2.

  • Путь м-1. Gn⟶Gn+1m−1. Таким образом, un дает тот же результат с вершиной xm или xm+2. Тогда ∑v∈VGnd(v)r(un,v) описывается как ∑v∈VGnd(v)r(xm,v) или ∑v∈VGnd(v)r(xm+2,v) с вероятностью pm −1.

  • Путь м. Gn⟶Gn+1m, то un есть вершина xm+1. Тогда ∑v∈VGnd(v)r(un,v) описывается как ∑v∈VGnd(v)r(xm+1,v) с вероятностью 1−p1−p2−p3−…−pm−3−pm −2−pm−1.

  Согласно приведенному выше обсуждению, мы получаем

  Rn=p1∑v∈VGnd(v)r(x2,v)+p2∑v∈VGnd(v)r(x3,v)+p3∑v∈VGnd(v)r(x4,v)+⋯ +pm−3∑v∈VGnd(v)r(xm−2,v)+pm−2∑v∈VGnd(v)r(xm−1,v)+pm−1∑v∈VGnd(v)r (xm,v)+(1−p1−p2−p3−…−Pm−3−Pm−2−pm−1)∑v∈VGnd(v)r(xm+1,v)=p1[∑v∈ VGn−1d(v)r(un−1,v)+(1+1·(2m−1)2m)((4m+2)n−1)+(4m2−13+1·(2m−1) 2m)]+p2[∑v∈VGn−1d(v)r(un−1,v)+(1+2·(2m−2)2m)((4m+2)n−1)+(4m2− 13+2·(2m−2)2m)]+p3[∑v∈VGn−1d(v)r(un−1,v)+(1+3·(2m−3)2m)((4m+2 )n−1)+(4m2−13+3·(2m−3)2m)]+⋯+pm−3[∑v∈VGn−1d(v)r(un−1,v)+(1+( m−3)·(m+3)2m((4m+2)n−1)+(4m2−13+(m−3)·(m+3)2m)]+pm−2[∑v∈VGn −1d(v)r(un−1,v)+(1+(m−2)·(m+2)2m((4m+2)n−1)+(4m2−13+(m−2) ·(m+2)2m)]+pm−1[∑v∈VGn−1d(v)r(un−1,v)+(1+(m−1)·(m+1)2m((4m +2)n−1)+(4m2−13+(m−1)·(m+1)2m)]+(1−p1−p2−⋯−pm−1)[∑v∈VGn−1d(v )r(un−1,v)+(1+m·m2m)((4m+2)n−1)+(4m2−13+m·m2m)].0005

  Подставим математическое ожидание в вышеприведенное уравнение, E(Rn)=Rn, получим

  Rn=Rn−1+{(2m2+5m+2)−∑i=1m−1[(2m2+5m+2)−2m+i·(2m−i)m(2m+1)]pi} n+∑i=1m−1[(2m2+5m+2)−2m+i·(2m−i)m(2m+1)]pi−2m2+15m+103.

  Лет

  V=∑i=1m−1[(2m2+5m+2)−2m+i·(2m−i)m(2m+1)]pi.

  Wi=(2m+1)[(2m2+5m+2)−2m+i·(2m−i)m(2m+1)].

  Следовательно,

  Rn=Rn-1+[(2m2+5m+2)-V]n+V-2m2+15m+103.

  По расчету

  R1=E(∑v∈VGnd(v)r(u1,v))=4m2−13.

  На основании приведенных выше результатов имеем

  Rn={(2m2+5m+2)2−12∑i=1m−1[(2m2+5m+2)−2m+i·(2m−i)m(2m+1)]pi}n2+{ 12∑i=1m−1[(2m2+5m+2)−2m+i·(2m−i)m(2m+1)]pi+2m2−15m−146}n+1.

  Таким образом,

  Rn=[(2m2+5m+2)2−12В]n2+[12В+2m2−15m−146]n+1.

  Подставляя Rn в (6), имеем

  E(Kf*(Gn+1))=E(Kf*(Gn))+(4m+2)Rn+16m3+56m2+32m+43n+8m3−14m−33=E(Kf*(Gn) )+(4m+2){[(2m2+5m+2)2−12V]n2+[12V+2m2−15m−146]n+1}+16m3+56m2+32m+43n+8m3−14m−33.

  По этим расчетам E(Kf*(G1))=8м3−2м3.

  Наконец, мы получаем формулу ожидаемого значения

  E(Kf*(Gn))={(4m3+12m2+9m+2)−(2m+1)∑i=1m−1[(2m2+5m+2)−2m+i(2m−i) m(2m+1)]pi}n33+{4m3−4m2−19m−83+(2m+1)∑i=1m−1[(2m2+5m+2)−2m+i(2m−i)m(2m +1)]pi}n2−{(8m2−8m−9)+2(2m+1)∑i=1m−1[(2m2+5m+2)−2m+i(2m−i)m(2m+ 1)]pi}n3−1.

  Таким образом,

  E(Kf*(Gn))=[(4m3+12m2+9m+2)−(2m+1)V]n33+[4m3−4m2−19m−83+(2m+1)V]n2−[( 8m2−8m−9)+2(2m+1)V]n3−1.

  по желанию.

  В частности, если положить (p1,p2,p3,…,pm−1,pm) = (1,0,0,…,0,0), (0,1,0,…,0,0 ), (0,0,1,…,0,0), …, (0,0,0,…,1,0), (0,0,0,…,0,1) или (0,0 ,0,…,0,0), по теореме 1 можно получить мультипликативный индекс степени Кирхгофа полигональной метацепи Mn(p1=1), полигональной ортоцепи On1, On2, On3, …, Onm −2(pi+1=1,1≤i≤m−2), многоугольная парацепь Ln(pm=1), как

  Kf*(Mn)=16m3+12m2-13mn3+16m4-16m3-28m2-2m+33mn2-8m4-14m2-5m+23mn-1,Kf*(On1)=24m3+8m2-10m-43mn3+16m4- 40м3-16м2+28м+123мн2-8м4-16м3-6м2+15м+83мн-1,Кф*(Он2)=32м3-4м2-28м-93мн3+16м4-64м3+20м2+82м+273мн2-8м4-32м3+18м2+ 51m+183mn−1,⋮⋮⋮Kf*(Onm−3)=4m4+12m3−7m2−14m−43mn3+4m4−4m3+29m2+40m+123mn2−8m3+24m2+23m+83mn−1,Kf*( Onm−2)=4m4+12m3+5m2−2m−13mn3+4m4−4m3−7m2+4m+33mn2−8m3−m+23mn−1,Kf*(Ln)=4m4+12m3+9m2+2m3mn3+4m4−4m3 −19м2−8м3мн2−8м3−8м2−9м3мн−1.

  Kf*(Oni)=[(4m3+12m2+9m+2)−Wi+1]n33+[4m3−4m2−19m−83+Wi+1]n2−[(8m2−8m−9)+2Wi+1]n3−1,

  Очевидно,

  Kf*(Mn)+Kf*(Ln)=Kf*(On1)+Kf*(On2)+⋯+Kf*(Onm−2).

  Когда n≥3, взяв частную производную от E(Kf*(Gn)), можно получить

  ∂E(Kf*(Gn))∂pi=−Win33+Win2−23Win<0,∂E(Kf*(Gn))∂p1=−4m4−4m3−3m2+2m+1mn33+4m4−4m3− 3m2+2m+1mn2−23·4m4−4m3−3m2+2m+1mn<0,∂E(Kf*(Gn))∂p2=−4m4−12m3+m2+12m+4mn33+4m4−12m3+m2+12m +4mn2−23·4m4−12m3+m2+12m+4mn<0,∂E(Kf*(Gn))∂p3=−4m4−20m3+13m2+30m+9mn33+4m4−20m3+13m2+30m+9mn2− 23·4м4−20м3+13м2+30м+9mn<0,⋮⋮⋮∂E(Kf*(Gn))∂pm−1=−4m2+4m+1mn33+4m2+4m+1mn2−23·4m2+4m+1mn<0.

  Когда (p1,p2,p3,…,pm−1,pm)=(0,0,0,…,0,1)(т.е. pm=1), парацепь Ln достигает максимума E (Kf*(Gn)), (т.е. Gn≅Ln). Если p1+p2+p3+…+pm−1=1, пусть pm−1=1−p1−p2−…−pm−2(0≤p1≤1,0≤p2≤1,…,0≤pm−2 ≤1), тогда

  E(Kf*(Gn))=∑i=1m−2(−Win33+Win2−2Win3)pi+(−Wm−1n33+Wm−1n2−2Wm−1n3)(1−p1−p2−⋯−pm −2)+(4m3+12m2+9m+2)n33+4m4−4m2−19m−83n2−8m2−8m−93n−1.

  Следовательно,

  ∂E(Kf*(Gn))∂pi=−(Wi−Wm−1)n33+(Wi−Wm−1)n2−23(Wi−Wm−1)n<0,∂E(Kf*( Gn))∂p1=−(4m3−4m2−7m−2)n33+(4m3−4m2−7m−2)n2−23·(4m3−4m2−7m−2)n<0,∂E(Kf*(Gn ))∂p2=−4m4−12m3−3m2+8m+3mn33+4m4−12m3−3m2+8m+3mn2−23·4m4−12m3−3m2+8m+3mn<0,⋮⋮⋮∂E(Kf*(Gn ))∂pm−2=−12m2+12m+3mn33+12m2+12m+3mn2−23·12m2+12m+3mn<0.

  Таким образом, (p1,p2,p3,…,pm−1,pm)=(0,0,0,…,1,0)(т. е. pm−1=1), E(Kf*(Gn) ) нельзя минимизировать. Как и выше, если p1+p2+p3+…+pi=1, пусть pi=1−p1−p2−…−pi−1(0≤p1≤1,0≤p2≤1,…,0≤pi−1≤ 1), (i≥3); тогда у нас есть

  E(Kf*(Gn))=∑i=1m−3(−Win33+Win2−2Win3)pi+(−Wm−2n33+Wm−2n2−2Wm−2n3)(1−p1−p2−⋯−pm −3)+(4m3+12m2+9m+2)n33+4m3−4m2−19m−83n2−8m2−8m−93n−1.

  Следовательно,

  ∂E(Kf*(Gn))∂pi=−(Wi−Wm−2)n33+(Wi−Wm−2)n2−23(Wi−Wm−2)n<0,(m−3≥3 ).

  Минимальное значение может быть достигнуто, только если p1+p2=1. Тогда пусть p1=1−p2(0≤p2≤1)

  E(Kf*(Gn))=(−W1n33+W1n2−2W1n3)(1−p2)+(−W2n33+W2n2−2W2n3)p2+(4m3+12m2+9m+2)n33+4m3−4m2−19m −83n2−8m2−8m−93n−1.

  Таким образом,

  ∂E(G(Kfn*))∂p2=(W1−W2)n33−(W1−W2)n2+23(W1−W2)n>0.

  Следовательно, E(Kf*(Gn)) достигает своего минимального значения, когда p2=0 (т. е. p1=1); то есть Gn≅Mn.

  □

  Пусть Θn — множество всех полигональных цепочек из n полигонов. Здесь мы вычисляем среднее значение мультипликативного индекса степени Кирхгофа.

  Kfavr*(Θn)=1|Θn|∑G∈ΘnKf*(G).

  Чтобы получить среднее значение Kfavr*(Θn), положим p1=p2=…=pm=1m в случайной полигональной цепочке E(Kf*(Gn)). Согласно теореме 1 имеем

  После вычислений получаем уравнения

  Kfavr*(Θn)=1mKf*(Mn)+1mKf*(On1)+1mKf*(On2)+⋯+1mKf*(Onm−2)+1mKf*(Ln).

  В этой статье мы вычисляем выражение для ожидаемого значения мультипликативного индекса степени Кирхгофа случайной полигональной цепи. Мы также вычисляем экстремальное значение и среднее значение этого показателя. Полигональные химические вещества имеют различную молекулярную структуру, и их физико-химические свойства приобретают все большее значение; см. [33,34,35]. Эти исследования имеют важное значение для нас, чтобы решить некоторые химические проблемы, связанные с жизнью и производством, а также для нас, чтобы предсказать физические и химические свойства молекул и синтезировать новые соединения и новые лекарства.

  В настоящее время химики-вычислители могут определять различные физические, химические и фармацевтические свойства молекул с помощью статистических методов, используя большое количество данных. Топологические индексы, основанные на расстоянии между вершинами графов, играют важную роль в характеристике молекулярных графов и установлении связи между молекулярными структурами и признаками и используются для прогнозирования физико-химических свойств и биологической активности соединений. С быстрым развитием науки и техники спрос на новые материалы и лекарства в производственной и фармацевтической областях растет день ото дня. Чтобы целенаправленно и быстро синтезировать новые вещества, топологический индекс снова стал горячей точкой исследований [36,37].

  Исследование частично поддержано Национальным научным фондом Китая (грант № 12171190), проектом Фонда инноваций для выпускников Аньхойского университета науки и технологий (грант № 149), Фондом естественных наук провинции Аньхой (грант № 2008085MA01) и Исследовательский фонд Института экологически чистых материалов и гигиены труда (Уху) Аньхойского университета науки и технологий (грант № ALW2021YF09).

  Все авторы внесли одинаковый вклад в эту статью. Все авторы прочитали и согласились с опубликованной версией рукописи.

  Авторы заявляют, что у них нет конкурирующих интересов.

  Примечание издателя: MDPI сохраняет нейтралитет в отношении юрисдикционных претензий в опубликованных картах и ​​институциональной принадлежности.

  1. Бонди Дж., Мерти У. Тексты для выпускников по теории графов по математике. Спрингер; Нью-Йорк, штат Нью-Йорк, США: 2008. с. 244. [Google Scholar]

  2. Chung F.R., Graham F.C. Теория спектральных графов. Том 92 Американское математическое общество Провиденс; Провиденс, Род-Айленд, США: 1997. [Google Scholar]

  3. Эстрада Э., Бончев Д. Дискретная математика и ее приложения. Тейлор и Фрэнсис; Лондон, Великобритания: 2013. Химическая теория графов; стр. 1–24. [Google Scholar]

  4. Флауэр Д.Р. О свойствах мер химического сходства на основе битовых строк. Дж. Хим. Инф. вычисл. науч. 1998; 38: 379–386. doi: 10.1021/ci970437z. [CrossRef] [Google Scholar]

  5. Бакли Ф., Харари Ф. Структурный анализ сложных сетей. Биркхойзер; Бостон, Массачусетс, США: 1990. Расстояние в графиках. [Google Scholar]

  6. Entringer R.C., Jackson D.E., Snyder D. Расстояние в графах. Чехослов. Мат. Дж. 1976; 26: 283–296. doi: 10.21136/CMJ.1976.101401. [CrossRef] [Google Scholar]

  7. Клейн Д.Дж., Рэндич М. Расстояние сопротивления. Дж. Матем. хим. 1993; 12:81–95. doi: 10.1007/BF01164627. [CrossRef] [Google Scholar]

  8. Гутман И., Фэн Л., Ю Г. Дистанция сопротивления степеней одноциклических графов. Транс. Гребень. 2012; 1:27–40. [Академия Google]

  9. Хуанг Г., Куанг М., Дэн Х. Ожидаемые значения индексов Кирхгофа в случайных полифенильных и спироцепях. Арс Математика. Контемп. 2014;9:197–207. doi: 10.26493/1855-3974.458.7b0. [CrossRef] [Google Scholar]

  10. Чжан Л., Ли К., Ли С., Чжан М. Ожидаемые значения для индекса Шульца, индекса Гутмана, мультипликативного индекса Кирхгофа и аддитивного индекса Кирхгофа. случайная полифениленовая цепь. Дискретный. заявл. Мат. 2020; 282: 243–256. doi: 10.1016/j.dam.2019.11.007. [Перекрестная ссылка] [Академия Google]

  11. Хуанг Г., Куанг М., Дэн Х. Ожидаемые значения индекса Хосоя и индекса Меррифилда-Симмонса в случайной полифениленовой цепи. Дж. Комб. Оптим. 2016; 32: 550–562. doi: 10.1007/s10878-015-9882-x. [CrossRef] [Google Scholar]

  12. Чен Х., Чжан Ф. Расстояние сопротивления и нормализованный лапласовский спектр. Дискретный. заявл. Мат. 2007; 155: 654–661. doi: 10.1016/j.dam.2006.09.008. [CrossRef] [Google Scholar]

  13. Бай Ю., Чжао Б., Чжао П. Экстремальный индекс Меррифилда-Симмонса и индекс Хосоя для полифенильных цепей. Соответствие коммун. Мат. вычисл. хим. 2009 г.;62:649–656. [Google Scholar]

  14. Чен А., Чжан Ф. Индекс Винера и совершенные паросочетания в случайных фениленовых цепях. Соответствие коммун. Мат. вычисл. хим. 2009; 61: 623–630. [Google Scholar]

  15. Wei S., Shiu W.C. Перечисление индексов Винера в случайных ломаных цепях. Дж. Матем. Анальный. заявл. 2019; 469: 537–548. doi: 10.1016/j.jmaa.2018.09.027. [CrossRef] [Google Scholar]

  16. Zhou Q., Wang L., Lu Y. Индекс Винера и индекс Харари на гамильтоново-связных графах с большой минимальной степенью. Дискретный. заявл. Мат. 2018; 247:180–185. doi: 10.1016/j.dam.2018.03.063. [Перекрестная ссылка] [Академия Google]

  17. Wiener H. Структурное определение точек кипения парафинов. Варенье. хим. соц. 1947; 69: 17–20. doi: 10.1021/ja01193a005. [PubMed] [CrossRef] [Google Scholar]

  18. He F., Zhu Z. Кактусы с максимальным эксцентриситетом суммы сопротивления-расстояния. Дискретный. заявл. Мат. 2017;219:117–125. doi: 10.1016/j.dam.2016.10.032. [CrossRef] [Google Scholar]

  19. Huang S., Zhou J., Bu C. Некоторые результаты по индексу Кирхгофа и индексу степени Кирхгофа. Соответствие коммун. Мат. вычисл. хим. 2016;75:207–222. [Академия Google]

  20. Лю Дж.-Б., Чжан Т., Ван Ю., Линь В. Индекс Кирхгофа и остовные деревья восьмиугольной цепи Мёбиуса/цилиндра. Дискретный. заявл. Мат. 2022; 307: 22–31. doi: 10.1016/j.dam.2021.10.004. [CrossRef] [Google Scholar]

  21. Qi J., Fang M., Geng X. Ожидаемое значение индекса Винера в случайных спироцепях. Полицикл. аромат. комп. 2022;2022:2038218. doi: 10.1080/10406638.2022.2038218. [CrossRef] [Google Scholar]

  22. Хейдари А. Об модифицированном индексе Шульца C ₄ C ₈ ( S ) нанотрубки и нанотор. Дайджест. Дж. Наноматер. Биоструктур. 2010;5:51–56. [Google Scholar]

  23. Yang Y., Klein D.J. Замечание об индексах Кирхгофа и аддитивных показателях степени Кирхгофа графов. З. Натурфорш. А. 2015;70:459–463. doi: 10.1515/зна-2014-0274. [CrossRef] [Google Scholar]

  24. Liu J.B., Wang C., Wang S., Wei B. Загребские индексы и мультипликативные загребские индексы эйлеровых графов. Бык. малайцы. Мат. науч. соц. 2019;42:67–78. doi: 10.1007/s40840-017-0463-2. [CrossRef] [Google Scholar]

  25. Лю Дж. Б., Чжао Дж., Мин Дж. , Цао Дж. Индекс Хосоя графов, образованных фрактальным графом. Фракталы. 2019;27:1950135. doi: 10.1142/S0218348X19501354. [CrossRef] [Google Scholar]

  26. Person W.B., Pimentel G.C., Pitzer K.S. Структура циклооктатетраена. Варенье. хим. соц. 1952; 74: 3437–3438. doi: 10.1021/ja01133a524. [CrossRef] [Google Scholar]

  27. Муквемби С., Муньира С. Градусное расстояние и минимальный градус. Бык. Ауст. Мат. соц. 2013; 87: 255–271. дои: 10.1017/S0004972712000354. [CrossRef] [Google Scholar]

  28. Танг М., Прибе К.Э. Предельные теоремы для собственных векторов нормализованного лапласиана для случайных графов. Анна. Стат. 2018;46:2360–2415. дои: 10.1214/17-AOS1623. [CrossRef] [Google Scholar]

  29. Liu J.B., Zhao J., He H., Shao Z. Топологические дескрипторы на основе валентности и структурные свойства обобщенных сетей Серпинского. Дж. Стат. физ. 2019;177:1131–1147. doi: 10.1007/s10955-019-02412-2. [CrossRef] [Google Scholar]

  30. Георгакопулос А. Единственность электрических токов в сети конечного полного сопротивления. Дж. Лонд. Мат. соц. 2010; 82: 256–272. doi: 10.1112/jlms/jdq034. [Перекрестная ссылка] [Академия Google]

  31. Гупта С., Сингх М., Мадан А. Сумма эксцентричных расстояний: инвариант нового графа для прогнозирования биологических и физических свойств. Дж. Матем. Анальный. заявл. 2002; 275:386–401. doi: 10.1016/S0022-247X(02)00373-6. [CrossRef] [Google Scholar]

  32. Evans WC, Evans D. Trease and Evans’ Pharmacognosy. Биркхойзер; Лондон, Великобритания: 2009 г. Углеводороды и производные; стр. 173–193. [Google Scholar]

  33. Цинкир З. Тождества удаления и сокращения для значений сопротивления и индекса Кирхгофа. Междунар. J. Квантовая хим. 2011;111:4030–4041. doi: 10.1002/qua.22942. [CrossRef] [Google Scholar]

  34. Сомоди М. О дзета-функции Ихара и индексах сопротивления, основанных на расстоянии. Приложение линейной алгебры. 2016;513:201–209. doi: 10.1016/j.laa.2016.09.042. [CrossRef] [Google Scholar]

  35. Li S., Wei W. Некоторые трансплантационные преобразования суммы сопротивления эксцентриситета и расстояния и их приложения.