Уравнение моментов в физике
Определение и уравнение моментов
Пусть О — какая-либо неподвижная точка в инерциальной системе отсчета. Ее называют началом или полюсом. Обозначим через радиус-вектор, проведенный из этой точки к точке приложения силы (рис. 1) .
рис. 1.
Моментом нескольких сил относительно точки называется векторная сумма моментов этих сил относительно той же точки:
Момент импульса материальной точки
Системы n материальных точек моментом импульса относительно некоторой точки О называется векторная сумма моментов импульсов этих точек относительно того же начала:
Производная по времени от момента импульса механической системы относительно неподвижной точки (полюса О) равна сумме моментов внешних сил , действующих на систему:
Для материальной точки уравнение моментов записывается:
Уравнение (6) называется уравнением моментов для системы материальных точек. Это основной закон динамики твердого тела, вращающегося вокруг неподвижной точки.
В проекциях на оси неподвижной декартовой системы координат с началом в полюсе О уравнение моментов системы записывается в виде:
где — проекции момента импульса на соответствующую ось; — проекции суммарного момента сил на соответствующую ось.
Уравнение моментов позволяет получить ответ на следующие вопросы:
- найти момент силы ( суммарного момента внешних сил) относительно интересующей нас точки в любой момент времени, если известна зависимость от времени момента импульса частицы (системы частиц) относительно той же точки;
- определить приращение момента импульса частицы (системы частиц) относительно точки О за любой промежуток времени, если известна зависимость от времени момента силы (суммарного момента внешних сил), действующей на эту частицу ( систему частиц) относительно той же точки.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
Уравнение моментов | Все Формулы
![Rendered by QuickLaTeX.com \[ \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-9b26b31cc88858c6b01bc73f6d36171f_l3.png)
Пусть О — какая-либо неподвижная точка в инерциальной системе отсчета. Ее называют началом или полюсом. Обозначим через
![Rendered by QuickLaTeX.com \[\overline{r}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-2f0114750810f37c45ff1402ffdd4a95_l3.png)
радиус-вектор, проведенный из этой точки к точке приложения силы
![Rendered by QuickLaTeX.com \[\overline{F}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-61173749746bf44710bfd975071d1557_l3.png)
.
ОПРЕДЕЛЕНИЕ
Моментом силы
![Rendered by QuickLaTeX.com \[\overline{F}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-61173749746bf44710bfd975071d1557_l3.png)
относительно точки О называется векторное произведение радиуса-вектора
![Rendered by QuickLaTeX.com \[\overline{r}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-2f0114750810f37c45ff1402ffdd4a95_l3.png)
на силу
![Rendered by QuickLaTeX.com \[\overline{F}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-61173749746bf44710bfd975071d1557_l3.png)
:
![Rendered by QuickLaTeX.com \[\overline{M}=\overline{r}\times \overline{F} \qquad \qquad (1)\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-70f218f7090b1b8251811a91e2d8539a_l3.png)
направление
![Rendered by QuickLaTeX.com \[\overline{M}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-1e055106be3a19cb2f9bb76b4fbdab87_l3.png)
выбирается так, чтобы последовательность векторов
![Rendered by QuickLaTeX.com \[\overline{r},\overline{F},\overline{M} \]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-254b48dc7043fd17e104ea4649318bde_l3.png)
образовывала правовинтовую систему, т. е. если смотреть вдоль вектора
![Rendered by QuickLaTeX.com \[\overline{M}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-1e055106be3a19cb2f9bb76b4fbdab87_l3.png)
, то поворот по кратчайшему пути от первого сомножителя в (1) ко второму осуществлялся по часовой стрелке, таким образом
![Rendered by QuickLaTeX.com \[\overline{M\ }\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-d4e4dd913f63aa2e43b31b23d86e0178_l3.png)
совпадает с направлением поступательного движения правого буравчика, рукоятка которого вращается от
![Rendered by QuickLaTeX.com \[ \overline{r}, к \[\overline{F}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-e70c0c28290497762823a561c415c4b4_l3.png)
по наикратчайшему пути.
Моментом
![Rendered by QuickLaTeX.com \[\overline{M\ }\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-d4e4dd913f63aa2e43b31b23d86e0178_l3.png)
нескольких сил относительно точки называется векторная сумма моментов этих сил относительно той же точки:
![Rendered by QuickLaTeX.com \[ \[\overline{M}=\sum^n_{i=1}{{\overline{r}}_i\times \overline{F_i}} \qquad \qquad (2)\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-b4fd33c9df4e49ee49b97bf1d3d01232_l3.png)
Момент импульса материальной точки
ОПРЕДЕЛЕНИЕ
Моментом импульса материальной точки относительно точки О называется векторное произведение радиуса-вектора
![Rendered by QuickLaTeX.com \[\overline{r}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-2f0114750810f37c45ff1402ffdd4a95_l3.png)
на импульс
![Rendered by QuickLaTeX.com \[\overline{p}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-9b31deb7d4ef1795edd68bd965496fc3_l3.png)
:
![Rendered by QuickLaTeX.com \[\overline{L}=\overline{r}\times \overline{p} \qquad \qquad (3)\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-83ea4ddbd83fa6ef436a433b8e585d56_l3.png)
![Rendered by QuickLaTeX.com \[\overline{L}=J\overline{w} \qquad \qquad (4)\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-49a8df9b2379bfadc0e2c8c9a5d547d2_l3.png)
где J— момент инерции,
![Rendered by QuickLaTeX.com \[\overline{w}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-a186d95fcf7476fbc23728e38f405a78_l3.png)
— угловая скорость вращения тела.
Системы n материальных точек моментом импульса относительно некоторой точки О называется векторная сумма моментов импульсов этих точек относительно того же начала:
![Rendered by QuickLaTeX.com \[\overline{L}=\sum^n_{i=1}{{\overline{r}}_i\times \overline{p_i}} \qquad \qquad (5)\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-5c009771014f51911b34df4dda06a049_l3.png)
Производная по времени от момента импульса \overline{L} механической системы относительно неподвижной точки (полюса О) равна сумме моментов внешних сил {\overline{M}}^{vnesh}, действующих на систему:
![Rendered by QuickLaTeX.com \[\frac{d\overline{L}}{dt}={\overline{M}}^{vnesh} \qquad \qquad (6)\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-aff0a3d864c45da23a7bd00e13444227_l3.png)
Для материальной точки уравнение моментов записывается:
![Rendered by QuickLaTeX.com \[\frac{d\overline{L}}{dt}={\overline{M}}\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-51fc957114b1fa52fcf34dd216f0559b_l3.png)
Уравнение (6) называется уравнением моментов для системы материальных точек. Это основной закон динамики твердого тела, вращающегося вокруг неподвижной точки.
В проекциях на оси неподвижной декартовой системы координат с началом в полюсе О уравнение моментов системы записывается в виде:
![Rendered by QuickLaTeX.com \[\frac{dL_x}{dt}=M^{vnesh}_x,\ \frac{dL_y}{dt}=M^{vnesh}_y,\ \frac{dL_z}{dt}=M^{vnesh}_z \qquad (7)\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-dbfb0c850c3ed1cb30eaea8df64749fa_l3.png)
где
![Rendered by QuickLaTeX.com \[L_x,L_y,L_z\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-a5cdb2a1e4124cc693ec2c5bf46fb8ba_l3.png)
— проекции момента импульса на соответствующую ось;
![Rendered by QuickLaTeX.com \[M^{vnesh}_x,M^{vnesh}_y,\ M^{vnesh}_z\]](/800/600/https/xn----ctbjzeloexg6f.xn--p1ai/wp-content/ql-cache/quicklatex.com-3a5dd83b91f6d8ca9f2c747261bcfff5_l3.png)
— проекции суммарного момента сил на соответствующую ось.
Уравнение моментов позволяет получить ответ на следующие вопросы:
найти момент силы ( суммарного момента внешних сил) относительно интересующей нас точки в любой момент времени, если известна зависимость от времени момента импульса частицы (системы частиц) относительно той же точки;
определить приращение момента импульса частицы (системы частиц) относительно точки О за любой промежуток времени, если известна зависимость от времени момента силы (суммарного момента внешних сил), действующей на эту частицу ( систему частиц) относительно той же точки.Примеры решения задач
Уравнение моментов | Все формулы
Определение и уравнение моментов
Пусть О — какая-либо неподвижная точка в инерциальной системе отсчета. Ее называют началом или полюсом. Обозначим через радиус-вектор, проведенный из этой точки к точке приложения силы (рис. 1) .
рис. 1.
Моментом нескольких сил относительно точки называется векторная сумма моментов этих сил относительно той же точки:
Момент импульса материальной точки
Системы n материальных точек моментом импульса относительно некоторой точки О называется векторная сумма моментов импульсов этих точек относительно того же начала:
Производная по времени от момента импульса механической системы относительно неподвижной точки (полюса О) равна сумме моментов внешних сил , действующих на систему:
Для материальной точки уравнение моментов записывается:
Уравнение (6) называется уравнением моментов для системы материальных точек. Это основной закон динамики твердого тела, вращающегося вокруг неподвижной точки.
В проекциях на оси неподвижной декартовой системы координат с началом в полюсе О уравнение моментов системы записывается в виде:
где — проекции момента импульса на соответствующую ось; — проекции суммарного момента сил на соответствующую ось.
Уравнение моментов позволяет получить ответ на следующие вопросы:
- найти момент силы ( суммарного момента внешних сил) относительно интересующей нас точки в любой момент времени, если известна зависимость от времени момента импульса частицы (системы частиц) относительно той же точки;
- определить приращение момента импульса частицы (системы частиц) относительно точки О за любой промежуток времени, если известна зависимость от времени момента силы (суммарного момента внешних сил), действующей на эту частицу ( систему частиц) относительно той же точки.Примеры решения задач
Уравнение трёх моментов — Википедия
Уравнение трёх моментов — уравнение для расчёта моментов в задаче об изгибе неразрезной многопролётной балки[1].
Известно, что балка при наличии дополнительных опор становится статически неопределимой. Одним из методов расчёта таких балок является метод сил. С помощью данного метода выводится уравнение трёх моментов[2]:
- Mi−1li+2Mi(li+li+1)+Mi+1li+1=−6(Ωiaili+Ωi+1bi+1li+1).{\displaystyle M_{i-1}l_{i}+2M_{i}(l_{i}+l_{i+1})+M_{i+1}l_{i+1}=-6\left({\frac {\Omega _{i}a_{i}}{l_{i}}}+{\frac {\Omega _{i+1}b_{i+1}}{l_{i+1}}}\right).}
Здесь Ωi{\displaystyle \Omega _{i}} — площадь эпюры моментов i-й статически определимой балки, ai{\displaystyle a_{i}} — расстояние от центра тяжести i-й эпюры до левого конца балки, bi{\displaystyle b_{i}} — расстояние от центра тяжести i-й эпюры до правого конца балки, li=ai+bi{\displaystyle l_{i}=a_{i}+b_{i}} — длина i-й балки.
Вывод уравнения трёх моментов предусматривает, что после введения шарниров над опорами получается статически определимая система из n{\displaystyle n} балок, каждая из которых представляет простую балку с опорами по концам. Неизвестные в методе сил — моменты, приложенные по концам независимых балок.

Впервые уравнение для расчёта неразрезных балок применил мостостроитель и путейский инженер Берто (Bertot) в 1855 г[3]. Сам же метод применялся ранее (1849) при реконструкции моста через Сену в Аньере (пригород Парижа, ныне известный как Аньер-сюр-Сен, фр. Asnières-sur-Seine), но опубликован Клапейроном в трудах Академии наук только в 1857 г. Так как идея основной системы с неизвестными моментами над опорами впервые была высказана Клапейроном, уравнение трёх моментов связывают с его именем[4]. Дальнейшее развитие теория неразрезных балок получила в работах Отто Мора, который обобщил теорию на случай, когда опоры расположены на разной высоте (1860).
Процедура решения задачи с использованием уравнения трёх моментов такова.
1. Балка режется на отдельные части (простые балки) дополнительными внутренними шарнирами в местах крепления опор.
Обозначения реакций образовавшихся связей: — моменты M0,M1,…,Mn{\displaystyle M_{0},M_{1},…,M_{n}}.
2. Нумеруются пролёты (участки балки между опорами). Число пролётов равно n{\displaystyle n}. Левая консоль считается нулевым пролётом, правая имеет номер n+1{\displaystyle n+1}. Длины пролётов: li{\displaystyle l_{i}}, i=0,…,n+1{\displaystyle i=0,…,n+1}.
3. Из условия равновесия консольных частей определяются моменты M0{\displaystyle M_{0}} и Mn{\displaystyle M_{n}}. Остальные моменты являются неизвестными системы n−1{\displaystyle n-1} уравнений трёх моментов.
4. Строятся эпюры моментов Mp{\displaystyle M_{p}} и перерезывающих сил Qp{\displaystyle Q_{p}} в пролётах и консолях (если они есть) балки от действия внешней нагрузки. Каждый пролёт представляет собой отдельную статически определимую балку.
5. Вычисляются площади эпюр моментов Ωi{\displaystyle \Omega _{i}}, i=1,…,n{\displaystyle i=1,…,n} в пролётах и расстояния от центров тяжести этих площадей до левой (ai{\displaystyle a_{i}}) и правой (bi{\displaystyle b_{i}}) опоры соответствующего пролёта.
6. Решение системы уравнений трёх моментов складывается с эпюрами моментов от внешней нагрузки. Полученная эпюра есть эпюра моментов в неразрезной балке.
Построить эпюру моментов в неразрезной балке длиной 19 метров с четырьмя опорами (рис. 1). На балку действует распределённая нагрузка q1=10{\displaystyle q_{1}=10} кН/м, q2=12{\displaystyle q_{2}=12} кН/м и сосредоточенная сила P=9{\displaystyle P=9} кН.
Рис. 1Длина консоли: l0=4{\displaystyle l_{0}=4} м. Длины пролетов: l1=l2=l3=5{\displaystyle l_{1}=l_{2}=l_{3}=5} м. Получаем основную систему метода сил, вводя шарниры над опорами (рис. 2). Моменты M0{\displaystyle M_{0}} и M3{\displaystyle M_{3}} — величины известные и определяются из условия равновесия консолей. Правой консоли здесь нет, M3=0{\displaystyle M_{3}=0}. Для левой консоли получаем M0=q1l02/2{\displaystyle M_{0}=q_{1}l_{0}^{2}/2}.
Рис. 2Строим эпюры моментов от внешней нагрузки в независимых балках основной (статически определимой) системы (рис. 3). Эпюры строим на сжатом волокне (как принято в машиностроении; в строительстве и архитектуре эпюры моментов принято строить на растянутом волокне).
Рис. 3Записываем уравнения трёх моментов:
l1M0+2M1(l1+l2)+M2l2=−6(Ω1a1/l1+Ω2b2/l2),{\displaystyle l_{1}M_{0}+2M_{1}(l_{1}+l_{2})+M_{2}l_{2}=-6(\Omega _{1}a_{1}/l_{1}+\Omega _{2}b_{2}/l_{2}),}
l2M1+2M2(l2+l3)+M3l3=−6(Ω2a2/l2+Ω3b3/l3).{\displaystyle l_{2}M_{1}+2M_{2}(l_{2}+l_{3})+M_{3}l_{3}=-6(\Omega _{2}a_{2}/l_{2}+\Omega _{3}b_{3}/l_{3}).}
Здесь Ω1=10.8⋅5/2=27,{\displaystyle \Omega _{1}=10.8\cdot 5/2=27,} a1=(2+5)/3=2.333,{\displaystyle a_{1}=(2+5)/3=2.333,} Ω2=Ω3=2fl2/3=125,{\displaystyle \Omega _{2}=\Omega _{3}=2fl_{2}/3=125,} a2=b2=a3=b3=2.5.{\displaystyle a_{2}=b_{2}=a_{3}=b_{3}=2.5.} Решаем систему уравнений M1=7.301{\displaystyle M_{1}=7.301} кНм, M2=−39.325{\displaystyle M_{2}=-39.325} кНм. Строим эпюру от этих моментов (рис. 4).
Рис. 4Складываем (по точкам) эпюры от нагрузки (рис. 3) и от моментов (рис. 4). Получаем эпюру моментов в балке (рис. 5).
Рис. 5Очевидным достоинством метода является простота матрицы системы линейных уравнения задачи. Эта матрица — трёхдиагональная, что позволяет применять различные упрощённые численные схемы решения.
- ↑ Кирсанов М. Н. . Maple и Maplet. Решения задач механики. — СПб.: Лань, 2012. — 512 с. — ISBN 978-5-8114-1271-6. — С. 179—181.
- ↑ Феодосьев В. И. . Сопротивление материалов. — М.: Государственное издательство физико-математической литературы, 1960. — 536 с. — С. 217.
- ↑ Бернштейн С.А. Очерки по истории строительной механики. — М.: Государственное издательство литературы по строительству и архитектуре, 1957. — 236 с. — С. 209.
- ↑ Тимошенко С. П. . История науки о сопротивлении материалов. 2-е изд. — М.: URSS, 2006. — 536 с. — ISBN 5-484-00449-7. — С. 176.
- Киселёв В. А. . Строительная механика. Общий курс. — М.: Стройиздат, 1986. — 520 с.
- Горшков А. Г., Трошин В. Н., Шалашилин В. И. . Сопротивление материалов. — М.: ФИЗМАТЛИТ, 2002. — 544 с. — ISBN 5-9221-0181-1.
6.2. Уравнение моментов
Предположим, что точка О неподвижна. В случае одной материальной точки, дифференцируя (3), получаем
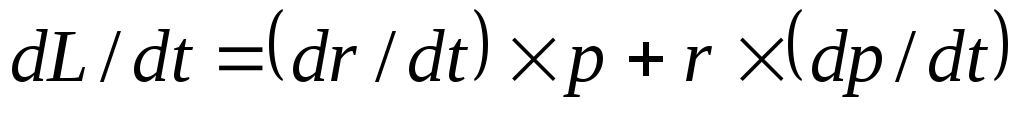 .
.
При
неподвижной точке О вектор  ,
равный
,
равный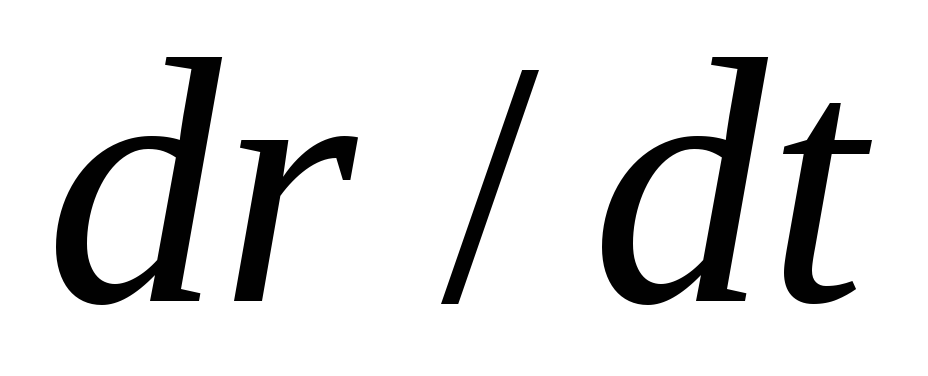 , параллелен
, параллелен 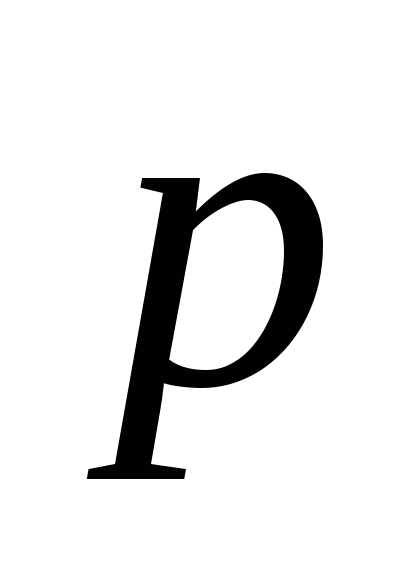 и поэтому
и поэтому 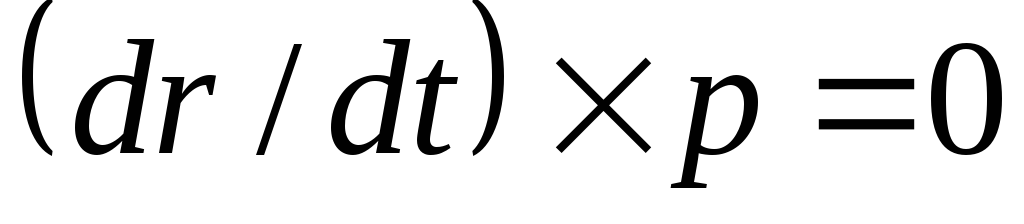 . Кроме того
. Кроме того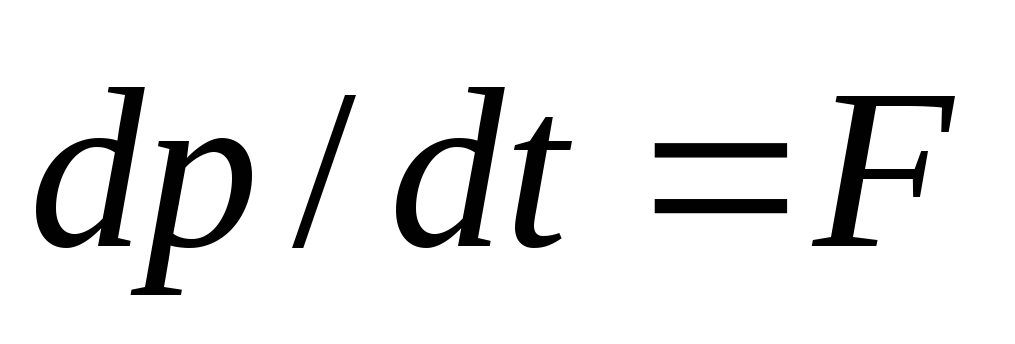 .
.
Таким
образом 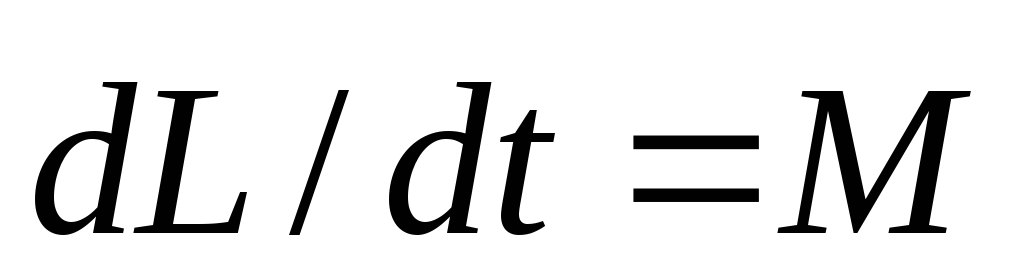 .
(5)
.
(5)
Э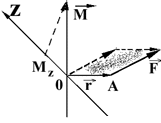
Рис. 2
то уравнение моментов для одной материальной точки. Распространим его на систему материальных точек, для чего запишем уравнение (5) для каждой материальной точки механической системы, понимая подМ момент всех действующих на нее сил, как внутренних так и внешних. Затем сложим все эти уравнения. Внутренние силы входят в систему попарно так, что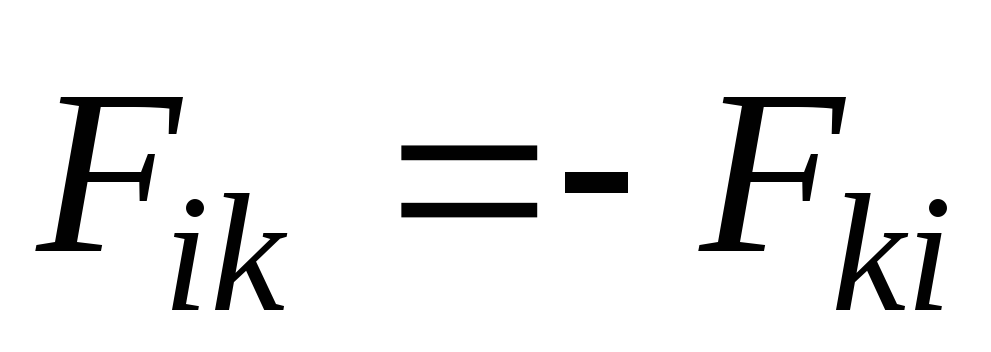 где
где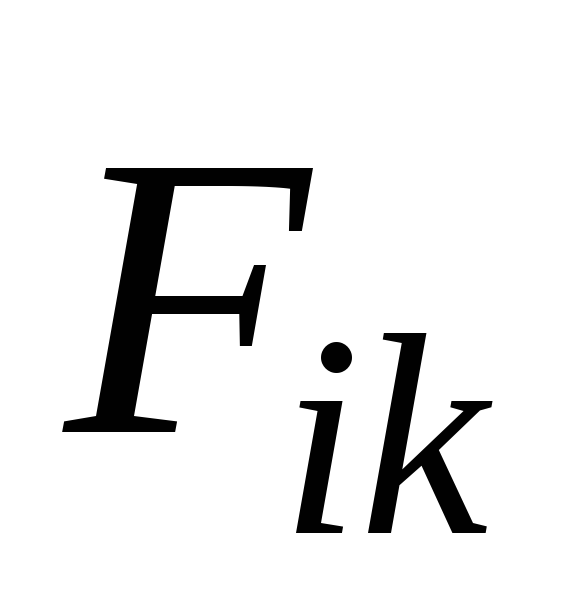 – сила воздействия k-й
материальной точки на i-ю.
Кроме того, эти силы
– сила воздействия k-й
материальной точки на i-ю.
Кроме того, эти силы 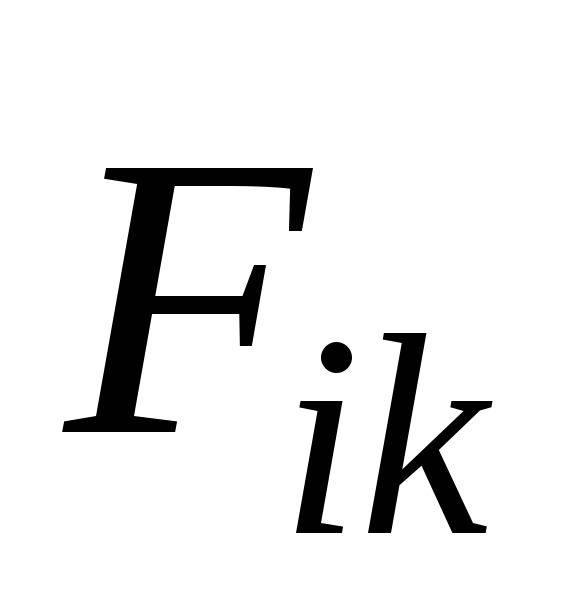 и
и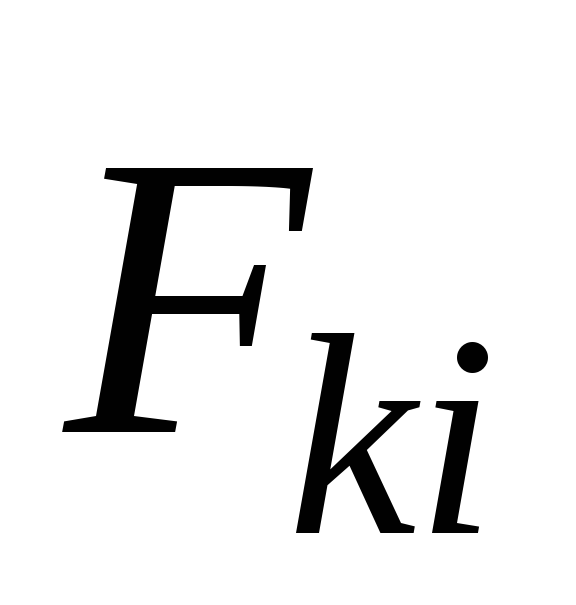 , действуют вдоль одной и
той же прямой. Момент таких двух сил, а
значит и моменты всех внутренних сил
равны нулю. В результате опять получается
уравнение моментов типа (5) только для
системы материальных точек, в котором
, действуют вдоль одной и
той же прямой. Момент таких двух сил, а
значит и моменты всех внутренних сил
равны нулю. В результате опять получается
уравнение моментов типа (5) только для
системы материальных точек, в котором 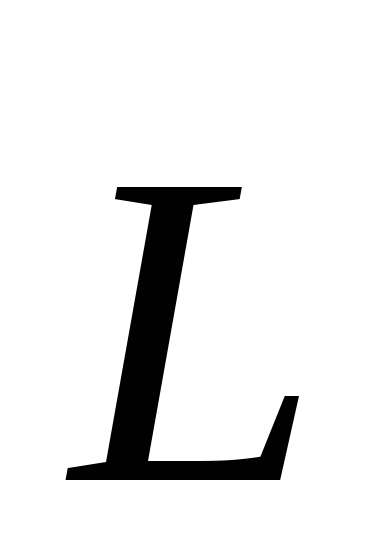 определяется
выражением (4), а
определяется
выражением (4), а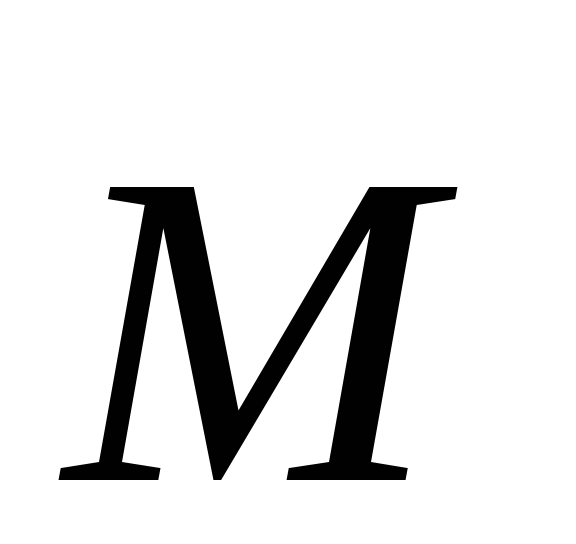 – выражением (2) для внешних
сил, т. е.
– выражением (2) для внешних
сил, т. е. 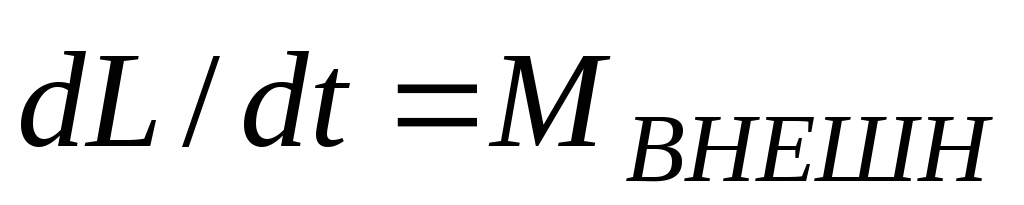 .
(6)
.
(6)
Моментом силы механической системы относительно оси называется проекция на эту ось вектора момента силы системы относительно любой точки, выбранной на рассматриваемой оси (рис. 2). Соответственно, моментом импульса относительно оси называется проекция на эту ось вектора момента импульса относительно любой точки на данной оси.
Можно
доказать, что выбор точки на оси влияет
на значения моментов импульса 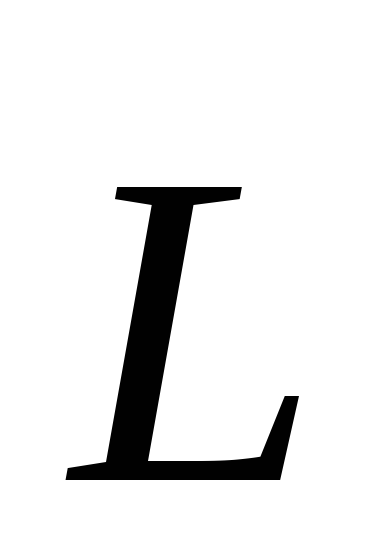 и
и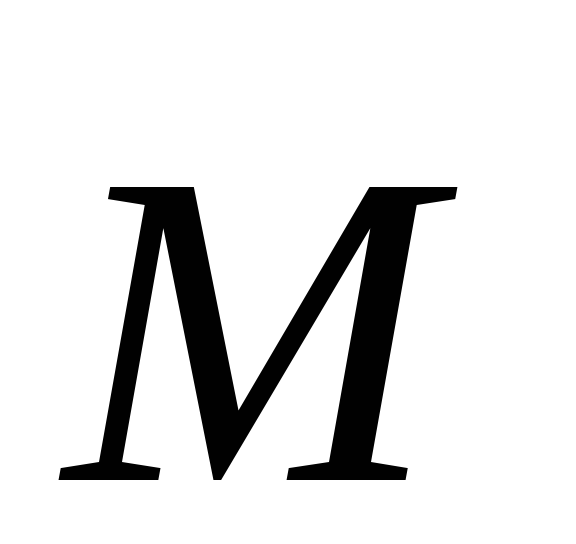 относительно
точки, но не влияет на значения
соответствующих проекций моментов на
эту ось.
относительно
точки, но не влияет на значения
соответствующих проекций моментов на
эту ось.
Если мы выбираем прямоугольную систему координат с началом, совпадающим с полюсом, то имеем:
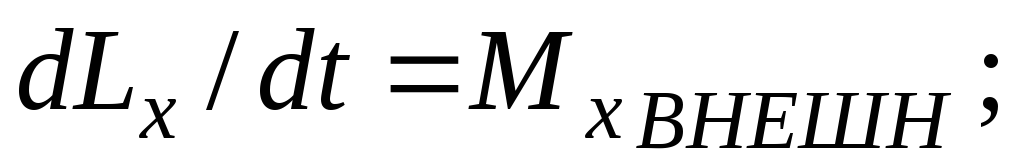
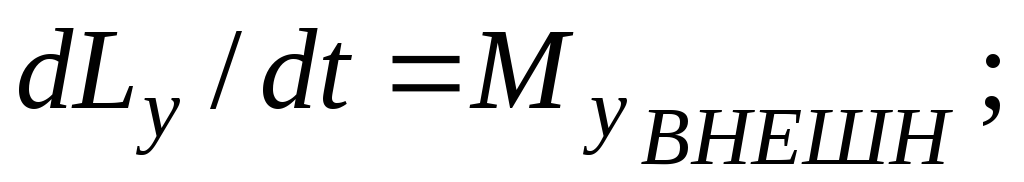
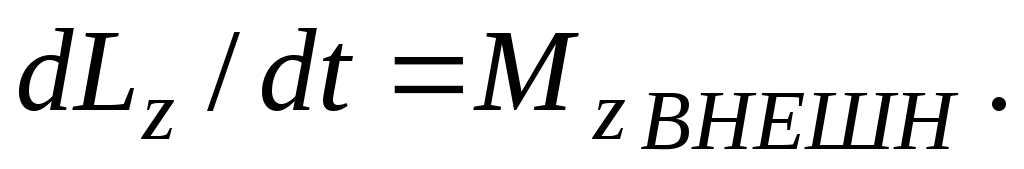 (7)
(7)
6.3. Закон сохранения момента импульса
Если
система замкнута (т. е. внешних сил нет),
то  и, следовательно, согласно уравнению
(6) вектор
и, следовательно, согласно уравнению
(6) вектор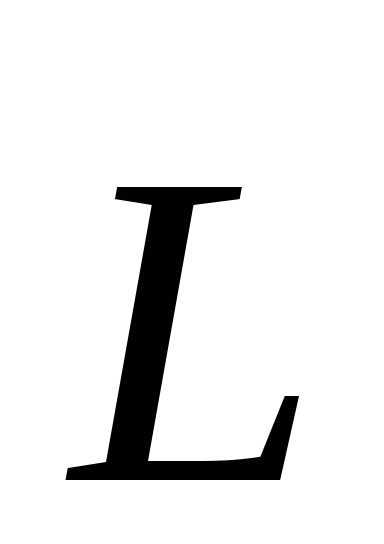 не изменяется со временем, т.е.
не изменяется со временем, т.е.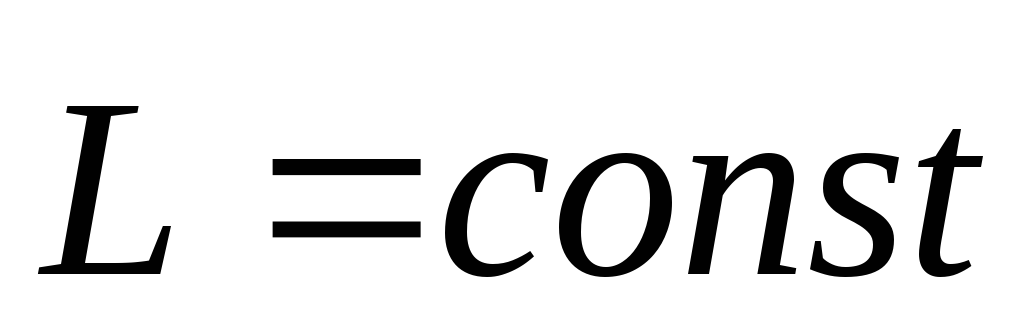 . Отсюда
вытекает закон сохранения момента
импульса, который гласит, что
. Отсюда
вытекает закон сохранения момента
импульса, который гласит, что
МОМЕНТ ИМПУЛЬСА ЗАМКНУТОЙ СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК ОСТАЕТСЯ ПОСТОЯННЫМ.
Момент импульса сохраняется и для незамкнутой системы, если сумма моментов внешних сил равна нулю.
В основе закона сохранения момента импульса лежит изотропия пространства, т. е. одинаковость свойств пространства по всем направлениям.
Поворот замкнутой системы частиц без изменения их взаимного расположения и относительных скоростей не изменяет механических свойств системы. Движение частиц после поворота будет таким же, каким оно было бы, если бы поворот не был осуществлен.
Наряду с законом сохранения импульса и энергии закон сохранения момента импульса является одним из фундаментальных законов физики. Такой расширенный закон сохранения момента импульса уже не является теоремой механики, а должен рассматриваться как самостоятельный общефизический принцип, являющийся обобщением опытных фактов.
6.4. Движение в поле центральных сил
Если на материальную точку действует сила вида
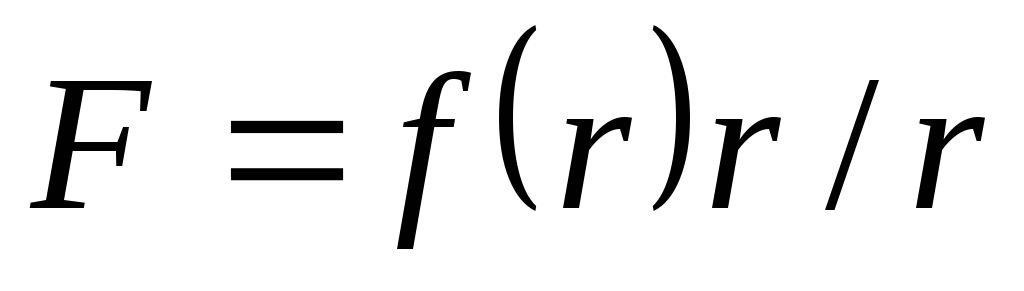 ,
(8)
,
(8)
то говорят, что материальная точка находится в поле центральных сил, если начало координат совпадает с центром сил.
Примерами материальных точек в таком поле являются искусственные спутники Земли.
Очевидно,
что момент 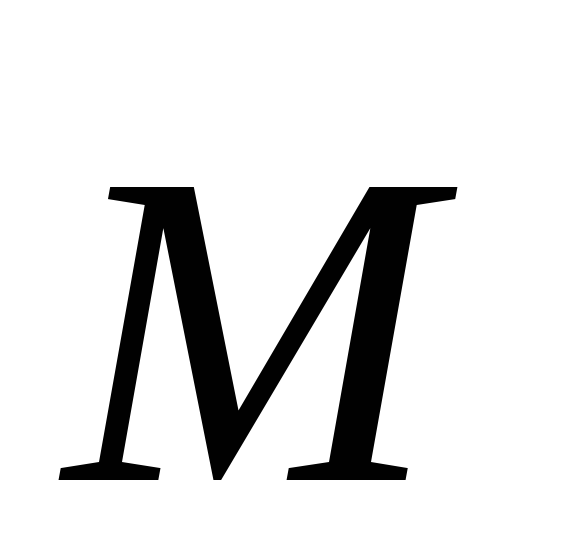 центральных
сил
центральных
сил  относительно центра сил 0 равен нулю.
Следовательно, при движении в центральном
поле момент импульса материальной точки
остается постоянным.
относительно центра сил 0 равен нулю.
Следовательно, при движении в центральном
поле момент импульса материальной точки
остается постоянным.
Вектор 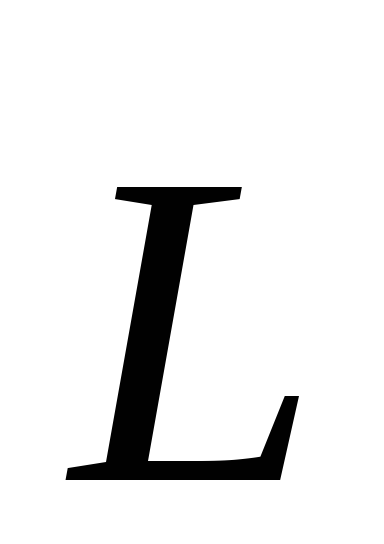 всегда ортогонален плоскости векторов
всегда ортогонален плоскости векторов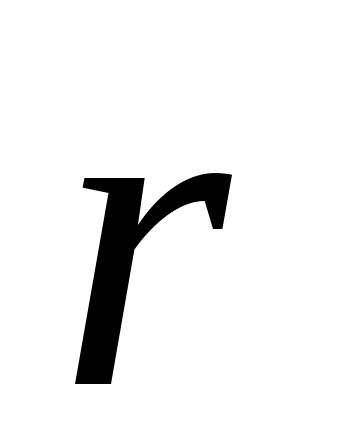 и
и
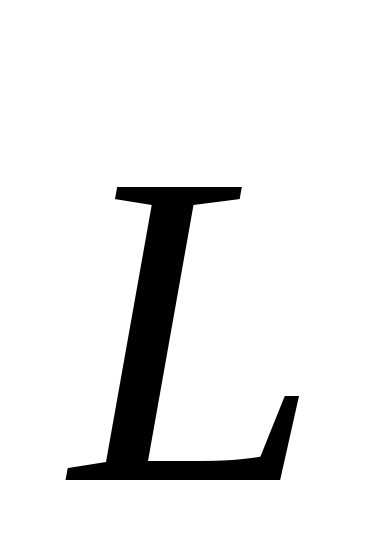 свидетельствует о том, что движение
материальной точки в поле центральных
сил происходит в одной плоскости.
свидетельствует о том, что движение
материальной точки в поле центральных
сил происходит в одной плоскости.Материальная точка, движущаяся в поле центральных сил, представляет собой консервативную систему. Поэтому при движении материальной точки сохраняется и полная механическая энергия точки, т. е.
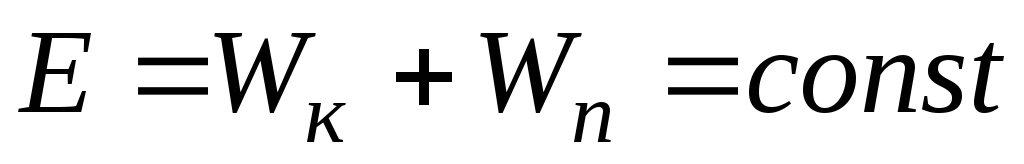 . (9)
. (9)
Для гравитационного центрального поля большой массы М имеем
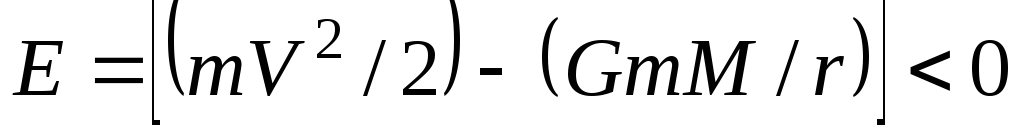
В этом случае траекторией материальной точки является эллипс, один из фокусов которого совпадает с центром силы, т. е. с положением центра массы М. При E = 0 траекторией частицы является парабола, а при Е > О – гипербола.
Определение моментов импульса, силы и инерции. Уравнение моментов. Пример решения задачи :: SYL.ru
Динамика вращения является одним из важных разделов современной механики, которая рассматривает законы вращательного перемещения тел вокруг осей и точек. В данной статье подробно изучим главное уравнение динамики вращения — уравнение моментов.
Момент импульса
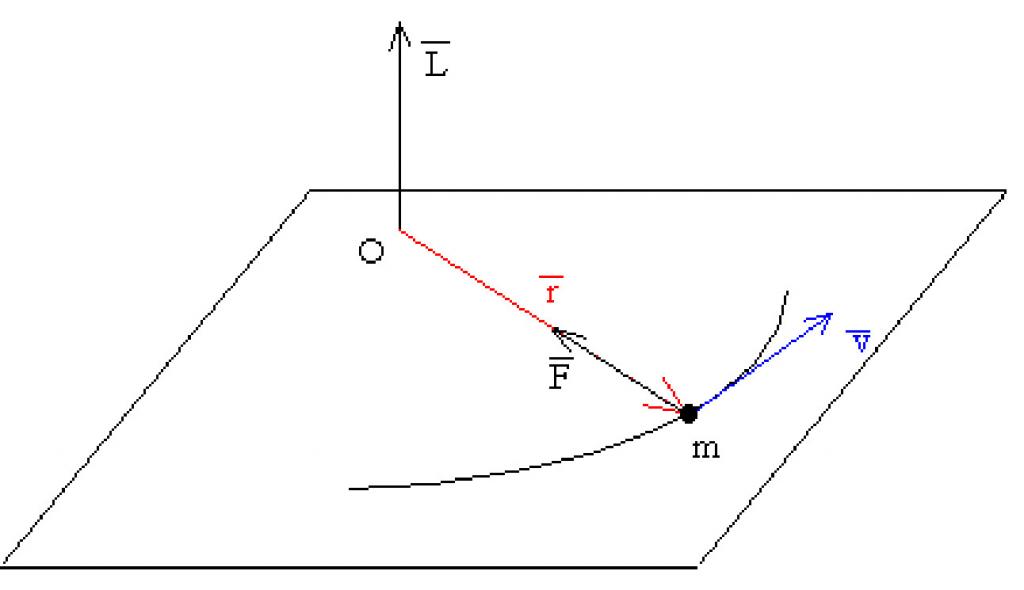
Каждому школьнику известно, что представляет собой механический импульс, который более правильно называть количеством движения. Теперь предположим, что материальная точка, имеющая массу m, вращается вокруг оси O с линейной скоростью v. Если радиус вращения обозначить как r, тогда можно записать следующее выражение:
L¯ = [m*v¯*r¯].
Первые два множителя в правой части равенства являются линейным импульсом точки. Произведение векторное этого импульса на вектор r¯, направленный от оси вращения к точке, называется моментом импульса L¯.
Величина L¯ является векторной. Направлена она перпендикулярно плоскости вращения точки. Направление момента импульса материальной точки определяется с помощью правила правой руки либо правила буравчика. Вращение точки против часовой стрелки создает положительный момент импульса.
Поскольку скорость вращения v¯ направлена по касательной к круговой траектории, то векторное выражение можно переписать в скалярной форме:
L = m*v*r.
Момент силы
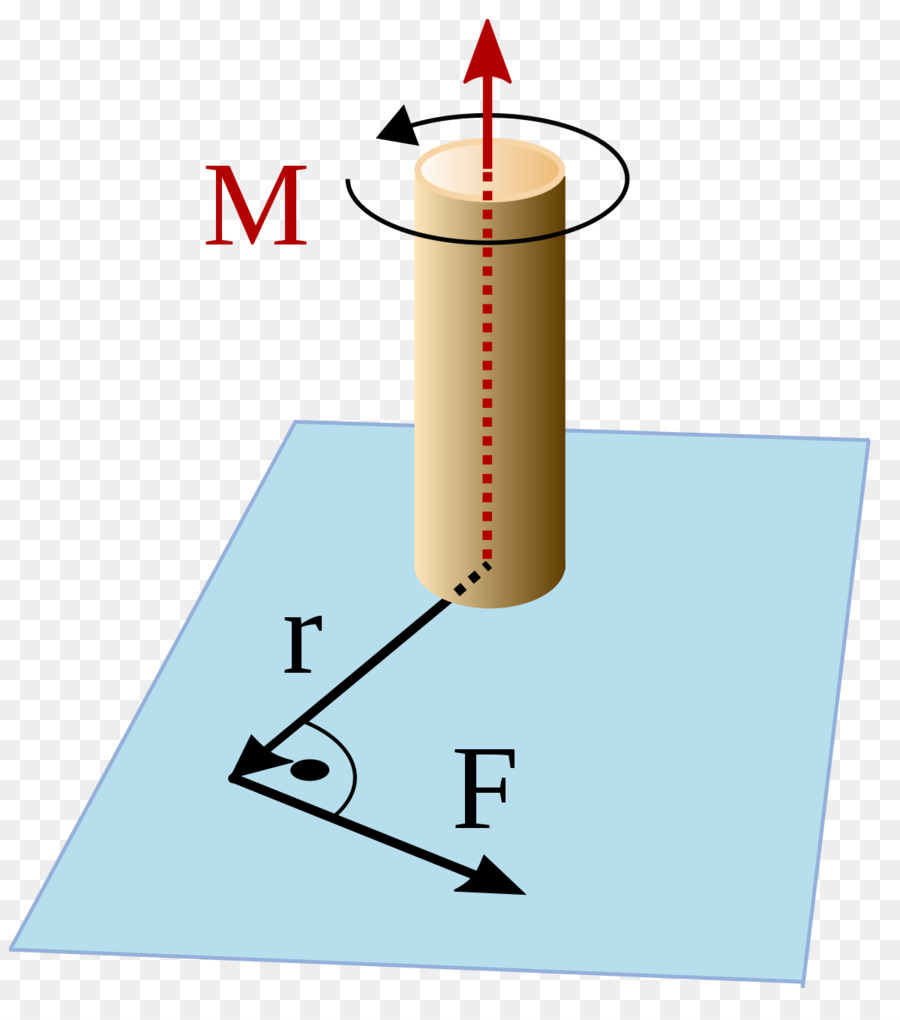
Это еще одна важная характеристика вращательного перемещения. Вводится в физике эта величина аналогичным образом, как и момент импульса материальной точки, только вместо количества движения в записанную выше формулу следует подставить касательную силу. Имеем:
M¯ = [r¯*F¯].
Момент силы, который также называется вращательным моментом, характеризует способность последней совершить поворот системы и придать ей угловое ускорение.
Направление вектора вращающего момента M¯ определяется по тем же правилам, что и для вектора L¯. Если система совершает ускоренное вращение, тогда M¯ и L¯ по направлению совпадают, если замедленное, то они будут противоположно направленными.
Если сила F¯ и радиус-вектор r¯ будут взаимно перпендикулярными, тогда векторная форма записи перейдет в аналогичную скалярную:
M = r*F.
Величину r называют рычагом силы. Чем больше его значения, тем больший момент создает сила F, и тем большим будет угловое ускорение системы.
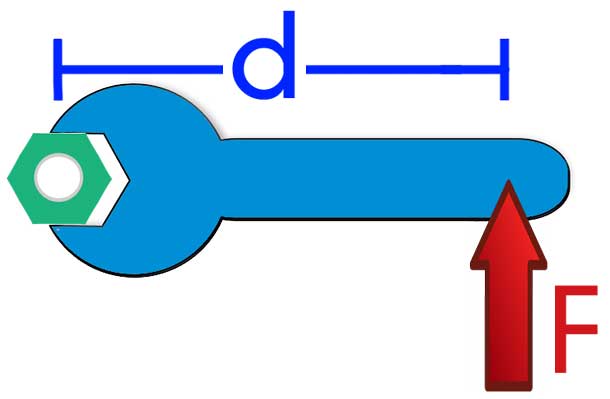
Примерами, которые позволят яснее представить, в чем заключается физический смысл величины M¯, являются откручивание гайки специальным длинным ключом, процесс открывания двери с помощью ее толчка около ручки и около дверных петель, а также процесс удержания тела некоторой массы на вытянутой и прижатой к телу руке.
Момент инерции
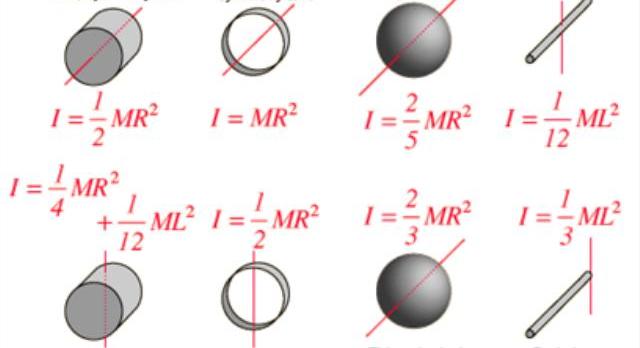
Осталось дать определение третьему моменту, который используется для количественного описания процесса вращения. Момент инерции материальной точки, параметры которой были записаны в начале статьи, рассчитывается по формуле:
I = m*r2.
В отличие от двух других моментов (M¯ и L¯), момент инерции является скаляром. С помощью него описывают инерционные свойства системы (аналогия с массой при поступательном движении).
Очевидно, что для определения значения I для твердого тела сложной формы и неравномерной плотности, следует воспользоваться интегральным счислением:
I = ∫m(r2*dm).
По сути, формула отражает суммирование величин Ii для каждой материальной точки i.
Момент инерции I является характеристикой не только формы и распределения массы в системе вращения, но также он зависит от расположения оси. Например, многие замечали, что вращать металлический стержень или деревянную швабру вдоль оси, проходящей через их длину, гораздо проще, чем вдоль перпендикулярной оси. Во втором случае момент инерции принимает большее значение.
Уравнение моментов для материальной точки
Теперь пришло время перейти непосредственно к теме статьи. Если вращающий момент M действует в течение времени dt, тогда он приводит к изменению момента импульса на величину dL, то есть:
dL = M*dt.
Это равенство является дифференциальной формой записи уравнения моментов в физике. Перенесем член dt в левую часть равенства и перепишем dL в явном виде, получим:
dL/dt = M =>
m*dv*r/dt = M.
Вспомним, что линейная скорость в кинематике связана с угловой следующим равенством:
v = ω*r.
Подставляя его в уравнение моментов, получаем:
m*dω*r2/dt = M =>
I*α = M, где α = dω/dt, I = m*r2.
Полученное равенство часто используется для определения кинематических характеристик вращающейся системы, если известны момент внешних сил M и момент инерции I.
Закон сохранения величины L
Уравнение моментов показывает, как изменяется момент импульса, если действует внешний момент M. Что будет происходить с системой, если M окажется равным нулю? В таком случае величина L будет сохраняться. Математическая формула для такой ситуации записывается следующим образом:
L = const или
L = m*r*v = m*r2*ω = I*ω = const.
Заметим, что условие M = 0 должно соблюдаться только для внешних сил. Внутренние силы, создающие момент M, не могут изменить момент импульса системы.
Закон сохранения L используется для поворота искусственных спутников в космическом пространстве и в фигурном катании. Так, группируясь различным образом, спортсмен изменяет значение своего момента инерции, что приводит к пропорциональному изменению скорости его углового вращения.

Пример задачи
На материальную точку массой 2 кг действует сила 10 Н. Зная, что радиус вращения материальной точки вокруг оси составляет 0,5 м, а также учитывая, что сила действует по касательной к траектории, необходимо найти угловую скорость вращения точки через 5 секунд после начала движения.
Запишем уравнение моментов и выразим ускорение α:
I*α = M =>
α = M/I.
Подставим теперь выражения для M и I, учитывая условия задачи, имеем:
α = F*r/(m*r2) = F/(m*r).
Поскольку рассматриваемое движение происходит с постоянным ускорением α, то для вычисления величины ω подойдет следующая формула:
ω = α*t.
Подставляя в нее полученное выражение для α, приходим к конечной рабочей формуле:
ω = F*t/(m*r).
С учетом данных задачи, можно записать ответ: ω = 50 рад/c. Это значение соответствует практически 8 полным оборотам вокруг оси в секунду.
Закон сохранения момента импульса. Уравнение моментов.
Моментом
импульса механической системы называется
векторная сумма моментов импульса
частиц, образующих эту систему 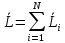
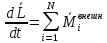 .
Если система замкнута (
.
Если система замкнута (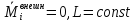 ),
то выполняется закон
сохранения момента импульса:
момент импульса замкнутой системы
материальных точек остаётся постоянным.
Закон
сохранения момента импульса выполняется
также для незамкнутых систем, если
суммарный момент внешних сил = 0.
),
то выполняется закон
сохранения момента импульса:
момент импульса замкнутой системы
материальных точек остаётся постоянным.
Закон
сохранения момента импульса выполняется
также для незамкнутых систем, если
суммарный момент внешних сил = 0.Уравнение
моментов: производная момента импульса относительно
некоторой оси по времени равна моменту
действующей на материальную точку силы
относительно той же оси. 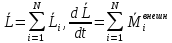
Движение в центральном поле сил.
Пусть
частица массы m
движется в центральном силовом поле.
Момент сил, действующих на частицу 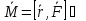 момент импульса частицы
момент импульса частицы 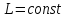 .
В силу сохранения
.
В силу сохранения 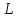 ,
направление движения частицы должно
происходить перпендикулярно направлению
,
направление движения частицы должно
происходить перпендикулярно направлению 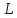
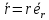 ,
, 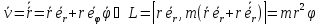 – проекция моментов на ось Z
сохраняется. Т.к. силовое поле является
центральным, то оно консервативное,
значит, для него можно найти выражение
для потенциальной энергии U.
При движении в консервативном силовом
поле сохраняется полная механическая
энергия.
– проекция моментов на ось Z
сохраняется. Т.к. силовое поле является
центральным, то оно консервативное,
значит, для него можно найти выражение
для потенциальной энергии U.
При движении в консервативном силовом
поле сохраняется полная механическая
энергия. 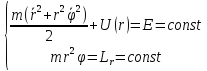 , таким образом, задача по движению
частицы в центральном силовом поле
свелась к решению системы 2-ух
дифференциальных уравнений 1-ого порядка.
При этом мы используем момент энергии
и момент сил.
, таким образом, задача по движению
частицы в центральном силовом поле
свелась к решению системы 2-ух
дифференциальных уравнений 1-ого порядка.
При этом мы используем момент энергии
и момент сил.Задача 2-ух тел.
Задача
2-ух тел по движению изолированной
системы 2-ух материальных точек,
взаимодействующих друг с другом. В силу
изолированности системы её импульс
сохраняется, а центр масс движется с
постоянной скорость, относительно
системы отсчёта К’. Это позволяет
перейти в систему центра масс (она будет
инерциальная, как и К’). 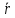 – радиус-вектор
– радиус-вектор 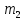 относительно
относительно 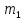 .
. 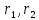 — радиус-векторы
— радиус-векторы 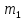 и
и 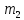 относительно С. Составляем систему:
относительно С. Составляем систему: 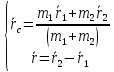 .
Решая систему, получаем:
.
Решая систему, получаем: 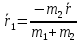 ,
, 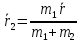 .
Движение тел определяется силами
.
Движение тел определяется силами 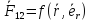 ,
, 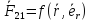 .
Учли 3-ий
закон Ньютона и изотропность
пространства (если поворот СО на произвольный угол
не приведёт к изменению результатов
измерений). Получаем уравнения:
.
Учли 3-ий
закон Ньютона и изотропность
пространства (если поворот СО на произвольный угол
не приведёт к изменению результатов
измерений). Получаем уравнения: 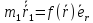 ,
, 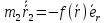 .
Решаем, в
результате получаем:
.
Решаем, в
результате получаем: 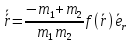 .
.
Центр масс твёрдого тела движется таким же образом, как двигалась бы материальная точка массы m под действием всех внешних сил, действующих на твёрдое тело.
Уравнение моментов относительно движущегося начала и движущейся оси.
Уравнение моментов может быть записано не только относительно неподвижной точки, но и относительно любой точки, движущейся с постоянной скоростью в силу равноправия всех ИСО.
Точку приложения любой силы можно перемещать по прямой, на которой лежит эта сила.
При действии на тело нескольких параллельных сил их можно заменить равнодействующей, приложенной к такой точке, чтобы момент равнодействующей = сумме моментов действующих сил:
 ,
С – точка, к которой приложена
равнодействующая.
,
С – точка, к которой приложена
равнодействующая.
В однородном поле силы тяжести точка приложения равнодействующей совпадает с центром масс. Если гравитационное поле неоднородно, то положение центра масс и центра тяжести не совпадает.
Пусть
точка А, относительно которой будет
вычисляться момент импульса и сил,
движется с произвольной скоростью 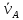 ,
точка О – неподвижна. Тогда скорость
изменения момента импульса
,
точка О – неподвижна. Тогда скорость
изменения момента импульса 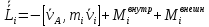 (уравнение моментов относительно
движущего начала). Уравнение
моментов относительно точки А:
(уравнение моментов относительно
движущего начала). Уравнение
моментов относительно точки А: 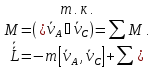 Если А
совпадает с С, то можно использовать
выражение для момента импульса как
скорость
Если А
совпадает с С, то можно использовать
выражение для момента импульса как
скорость 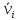 и скорость
относительно движущегося центра масс:
и скорость
относительно движущегося центра масс: 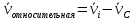 .
.


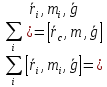 ,
С – точка, к которой приложена
равнодействующая.
,
С – точка, к которой приложена
равнодействующая.