(30-4)

Это первое уравнение Максвелла.

Интеграл в правой части берется по произвольной поверхности S, опирающейся на контур ℓ (рис. 30.3).

(Поскольку в общем случае может быть

функцией и координат, то берем частную

производную )

Смысл первого уравнения соответствует

максвелловской трактовке явления ЭМИ, то

есть, изменяющееся со временем магнитное поле порождает вихревое электрическое поле.

Второе уравнение Максвелла

(30-5)

Это уравнение выражает тот факт, что силовые линии магнитного поля не имеют источника

Третье уравнение Максвелла

(30-6)

Это обобщенный закон полного тока (см. часть 3, лекция №24), который подчеркивает тот факт, что магнитное поле может создаваться не только токами проводимости ( ), но и перемещенным электрическим полем

Четвертая теорема Максвелла (см. часть 3, лекция №18).

(30-7)

Физически эта теорема подчеркивает тот факт, что электрическое поле может создаваться зарядами, то есть источниками силовых линий электрического поля являются электрические заряды.

Уравнения (30-3,5,6,7) представляют уравнения Максвелла в интегральной форме.

Уравнения Максвелла подчеркивают тот факт, что электрическое поле может создаваться как зарядами, так и переменным магнитным полем, а магнитное поле может создаваться как токами проводимости, так и переменным электрическим полем.

В вакууме, где нет зарядов и токов, магнитное поле может создаваться

Эту совокупность непрерывно изменяющихся и порождающих друг друга электрического и магнитного полей Максвелл назвал электромагнитным полем.

Кроме четырех рассмотренных уравнений в полную систему уравнений Максвелла входят еще три уравнения, называемых материальными. В них входят характеристики вещества («материи»), такие как диэлектрическая и магнитная проницаемости ℰ и µ, проводимость σ.

Связь и (лекция №18, часть 3)

Связь и (лекция №23, часть 3)

Закон Ома в локальной форме (лекция №20, часть 3)

Уравнения Максвелла (30-4) ÷ (30-7) можно представить в дифференциальной форме, т. е. в виде системы дифференциальных уравнений. Для этого используем теоремы Стокса

(30-8)

и Остроградского – Гаусса:

(30-9)

где — некоторый вектор в нашем случае: (О функции rot см. примечание к п.2).

С другой стороны, используя теорему Стокса, получим

Поскольку равны левые части, равны и правые

откуда следует

(30-10)

Второе уравнение Максвелла

С другой стороны из теоремы Остроградского – Гаусса

получаем (30-11)

Третье уравнение запишем, предварительно выразив токи проводимости через плотность токов проводимости

,

тогда

с другой стороны

получим

(30-12)

Аналогичный подход для четвертого уравнения дает систему уравнений

,

(в последнем уравнении мы заменили — объемная плотность заряда) из которой следует:

(30-13)

Сведем четыре уравнения Максвелла в интегральной и дифференциальной формах, а также три материальных уравнения в таблицу:

Уравнения Максвелла

ℰℰ ; μμ ; σ

Отметим, что физический смысл уравнений в дифференциальной форме такой же, что и соответствующих уравнений в интегральной форме. Интегрируя их, можно получить , , , .

Примечание.Вихревое электрическое поле характеризуется особой векторной величиной, называемой ротором напряженности поля: . Вектор ротора приложен в центре поля перпендикулярно плоскости его силовых линий (в случае круговых линий – в центре окружностей) и направлен относительно них согласно правилу правого винта.

По определению

.

Наглядное представление о роторе вектора можно получить, представив себе небольшую легкую турбинку, помещенную в данную точку текущей жидкости.

3. Волновые уравнения для электромагнитного поля и их решения. Скорость распространения электромагнитных волн в средах. Основные свойства электромагнитных волн.

Пусть имеется однородная и изотропная среда вдали от зарядов и токов. Возбудим в какой-либо точке пространства переменное электрическое гармоническое поле (Предположим Для простоты рассматриваем этот частный случай).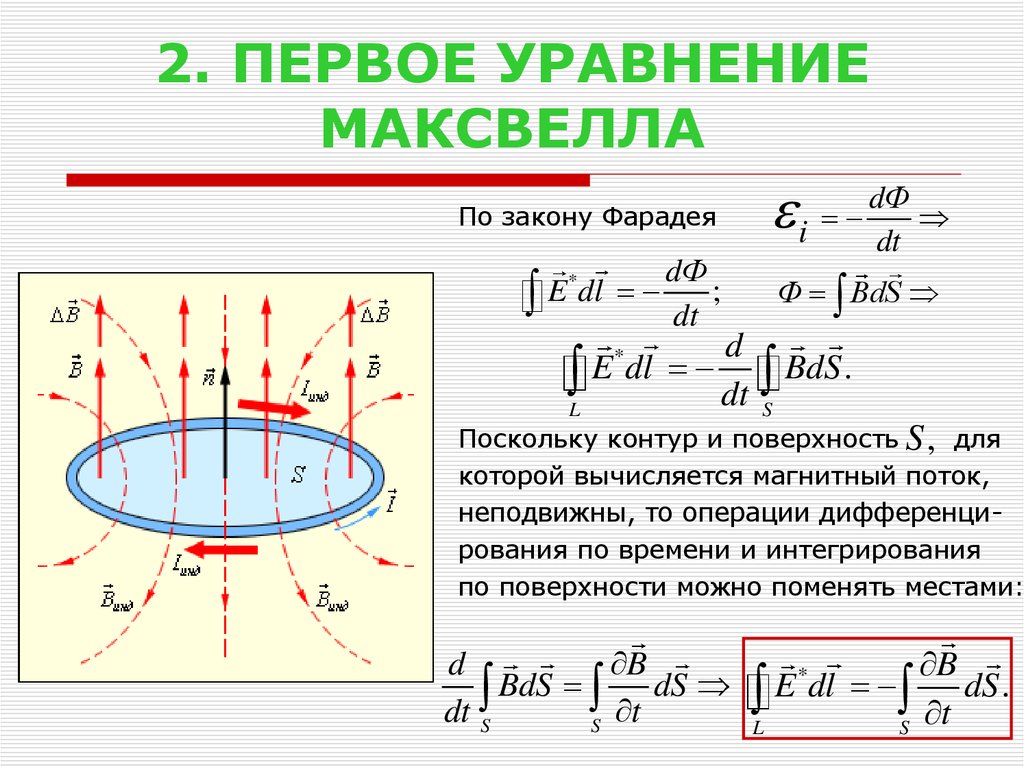

Из уравнений Максвелла при условии сделанных предположений можно получить волновые уравнения электромагнитного поля

, (30-14)

где — скорость распространения электро-

магнитной волны.

Процесс распространения электромагнитного поля в пространстве называется электромагнитной волной.

Подставим ℰ = 8,85 μ = в выражение для скорости u. Если среда – вакуум, то ℰ = 1, μ = 1, тогда получим u = ,то есть скорость электромагнитной волны в вакууме равна скорости света в вакууме. Это обстоятельство приводит к выводу, что свет — электромагнитная волна.

Решения уравнений (30-14)

(30-15)

Выражения (30-15) – уравнения электромагнитной волны. Их графическое

Как показывает опыт, электромагнитные волны проходят через диэлектрики и отражаются от металлов. Для них свойственны такие явления как интерференция, дифракция, поляризация, дисперсия (рассмотрим далее в разделе «Оптика»).

Итак, из решения уравнений Максвелла получаются следующие выводы:

– если в какой-либо ограниченной области пространства возникает электромагнитное поле, то оно не остается локализованным в этой области, а распространяется с конечной скоростью, зависящей от свойств среды;

– если электрическое и магнитные поля меняются по простому гармоническому закону, то электромагнитное поле распространяется в пространстве в виде плоской электромагнитной волны.



Уравнения Максвелла для электромагнитного поля

| на главную | доп. материалы | физика как наука и предмет | электричество и электромагнетизм |

Организационные, контрольно-распорядительные и инженерно-технические услуги
в сфере жилой, коммерческой и иной недвижимости. Московский регион. Официально.

Введение Максвеллом понятия тока смещения привело его к завершению созданной им макроскопической теории электромагнитного поля, позволившей с единой точки зрения не только объяснить электрические и магнитные явления, но и предсказать новые, существование которых было впоследствии подтверждено.

В основе теории Максвелла лежат рассмотренные выше четыре уравнения:

1. Электрическое поле может быть как потенциальным (Е_Q), так и вихревым (Е_B), поэтому напряженность суммарного поля Е = Е_Q + Е_B. Так как цир­куляция вектора Е_Q равна нулю (см. (137.3)), а циркуляция вектора Е_B определяется выражением (137.2), то циркуляция вектора напряженности суммарного поля

Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.

2. Обобщенная теорема о циркуляции вектора Н (см. (138.4)):

Это уравнение показывает, что магнитные поля могут возбуждаться либо движущими­ся зарядами (электрическими токами), либо переменными электрическими полями.

3. Теорема Гаусса для поля D (см. (89.3)):

                                                                      (139.1)

Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью r, то формула (139.1) запишется в виде

4. Теорема Гаусса для поля В (см. (120.3)):

Итак, полная система уравнений Максвелла в интегральной форме:

Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует следующая связь (изотропные несегнетоэлектрические и неферромагнитные среды):

где e₀ и m₀ — соответственно электрическая и магнитная постоянные, e и m — соответст­венно диэлектрическая и магнитная проницаемости, g — удельная проводимость веще­ства.

Из уравнений Максвелла вытекает, что источниками электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля, а магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями. Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе существуют электрические заряды, но нет зарядов магнитных.

Для стационарных полей (E=const и B=const) уравнения Максвелла примут вид

т.е. источниками электрического поля в данном случае являются только электрические заряды, источниками магнитного — только токи проводимости. В данном случае электрические и магнитные поля независимы друг от друга, что и позволяет изучать отдельно постоянные электрическое и магнитное поля.

Воспользовавшись известными из векторного анализа теоремами Стокса и Гаусса

можно представить полную систему уравнении Максвелла в дифференциальном форме (характеризующих поле в каждой точке пространства):

Если заряды и токи распределены в пространстве непрерывно, то обе формы уравнений Максвелла — интегральная и дифференциальная — эквивалентны. Однако если имеются поверхности разрыва – поверхности, на которых свойства среды или полей меняются скачкообразно, то интегральная форма уравнений является более общей.

Уравнения Максвелла в дифференциальной форме предполагают, что все величины в пространстве и времени изменяются непрерывно. Чтобы достичь математической эквивалентности обеих форм уравнений Максвелла, дифференциальную форму дополняют граничными условиями, которым должно удовлетворять электромагнитное поле на границе раздела двух сред. Интегральная форма уравнений Максвелла содержит эти условия. Они были рассмотрены раньше:

(первое и последнее уравнения отвечают случаям, когда на границе раздела нет ни свободных зарядов, ни токов проводимости).

Уравнения Максвелла — наиболее общие уравнения для электрических и магнитных полей в покоящихся средах. Они играют в учении об электромагнетизме такую же роль, как законы Ньютона в механике. Из уравнений Максвелла следует, что переменное магнитное поле всегда связано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнитным, т. е. электрическое и магнитное поля неразрывно связаны друг с другом — они образуют единое электромагнитное поле.

Теория Максвелла, являясь обобщением основных законов электрических и магнит­ных явлений, не только смогла объяснить уже известные экспериментальные факты, что также является важным ее следствием, но и предсказала новые явления. Одним из важных выводов этой теории явилось существование магнитного поля токов смещения, что позволило Максвеллу предсказать существование электромагнитных волн — переменного электромагнитного поля, распространяющегося в пространстве с конечной скоростью. В дальнейшем было доказано, что скорость распространения свободного электромагнитного поля (не связанного с зарядами и токами) в вакууме равна скорости света с = 3×10⁸ м/с. Этот вывод и теоретическое исследование свойств электромагнитных волн привели Максвелла к созданию электромагнитной теории света, согласно которой свет представляет собой также электромагнитные волны. Электромагнитные волны на опыте были получены немецким физиком Г. Герцем (1857—1894), доказавшим, что законы их возбуждения и распространения полностью описываются уравнениями Максвелла. Таким образом, теория Максвелла была экспериментально подтверждена.

К электромагнитному полю применим только принцип относительности Эйн­штейна, так как факт распространения электромагнитных волн в вакууме во всех системах отсчета с одинаковой скоростью с не совместим с принципом относи­тельности Галилея.

Согласно принципу относительности Эйнштейна, механические, оптические и элект­ромагнитные явления во всех инерциальных системах отсчета протекают одинаково, т. е. описываются одинаковыми уравнениями. Уравнения Максвелла инвариантны относительно преобразований Лоренца: их вид не меняется при переходе от одной инерциальной системы отсчета к другой, хотя величины Е, В, D, Н в них преобразуются по определенным правилам.

Из принципа относительности вытекает, что отдельное рассмотрение электрического и магнитного полей имеет относительный смысл. Taк, если электрическое поле создается системой неподвижных зарядов, то эти заряды, являясь неподвижными относительно одной инерциальной системы отсчета, движутся относительно другой и, следовательно, будут порождать не только электрическое, но и магнитное поле. Аналогично, неподвижный относительно одной инерциальной системы отсчета проводник с постоянным током, возбуждая в каждой точке пространства постоянное магнитное поле, движется относительно других инерциальных систем, и создаваемое им переменное магнитное поле возбуждает вихревое электрическое поле.

Таким образом, теория Максвелла, ее экспериментальное подтверждение, а также принцип относительности Эйнштейна приводят к единой теории электрических, магнитных и оптических явлений, базирующейся на представлении об электромагнитном поле.

электромагнетизм — Интегральная и дифференциальная формы уравнений Максвелла

Интегральная и дифференциальная версии эквивалентны, поэтому кажется, что ваш текст просто не знает, как использовать дифференциальную версию в таком общем виде, как ваш текст знает, как использовать интегральная версия.

Например, вам не нужно знать частные производные для определения дивергенции и/или ротора, но если у вас есть частные производные, то есть простые формулы для дивергенции и ротора в этой ситуации , вы можете использовать эти формулы в качестве определения, но они не являются правильным общим определением.

Эти две формы действительно эквивалентны, и они эквивалентны, потому что на самом деле они не говорят ничего другого. Понимание интегральных форм состоит в том, что они выполняются для каждой замкнутой/открытой поверхности в любой ограниченной области. Понимание дифференциальной формы состоит в том, что они выполняются в любой ограниченной области.

Похоже, ваш текст знает, как настроить интегральные формы в довольно общем виде. Дифференциальные формы можно настроить таким же общим образом, поскольку существуют очень общие способы определения дивергенции и завитка. Один из способов — взять теорему о дивергенции и теорему о роторе в качестве определений операторов (вместо того, чтобы допускать частные производные, затем составлять случайные комбинации, а затем составлять теорему). Например

$$\vec{\nabla}\cdot\vec{A}@(x,y,z)=\lim_{DiameterV\стрелка вправо 0, V\стрелка вправо\{(x,y,z)\}}\ frac{\iint_{\partial V}\шляпа{n}\cdot\vec{A}dS}{\iiint_VdV}$$

и

$$\шляпа{S}\cdot\left(\vec{\ nabla}\times\vec{A}@(x,y,z)\right)=\lim_{Диаметр S\стрелка вправо 0, S\стрелка вправо\{(x,y,z)\}}\frac{\int_ {\partial S}\vec{A}\cdot d\vec{l}}{\iint_SdS}$$

не требуют частных производных, только поля должны быть достаточно хорошими, чтобы иметь пределы, которые допускают расхождение и теоремы о завитках, ни больше, ни меньше. Но этот уровень общности основан на предположении, что ваша интегральная версия использует интеграцию Римана. Это самый простой вариант интеграции (но не самый общий), и я хочу, чтобы вы увидели, как нам не нужно произвольно делать один вариант более общим, чем другой. 93(\vec{r}-\vec{r}_0)dxdydz=f(\vec{r}_0)$. И это всего лишь одна из многих таких карт, называемых распределениями, которые передают тестовые функции числам красивым (линейным и непрерывным) способом. Поэтому, если мы ожидаем, что производные дадут нам распределения, то мы должны определить их так, чтобы они это делали.

Прежде всего заметим, что любая хорошая функция $g$ является распределением в том смысле, что она отправляет пробную функцию $f$ на число $\iiint fg dxdydz$, обозначим это через $G:f\mapsto\iiint fg dxdydz =G(f)$, а затем обратите внимание, что если функция $g$ имеет частную производную $\partial g$, которая является хорошей функцией, то $\iiint f\partial g dxdydz$ = $-\iiint g\partial f dxdydz $. Это приводит к обобщению частных производных. Для любого распределения $G$, которое отправляет тестовые функции $f$ в $G(f)$, мы можем определить его производную как распределение, которое отправляет $f$ в $-G(\partial f)$. Для любой хорошей функции это определение согласуется с исходным определением производных в том смысле, что они действуют одинаково под интегралами. Но сейчас у любого дистрибутива есть производная.

Но даже при таком обобщении дивергенция может быть определена более широко. Используя $$\int \phi \vec{\nabla}\cdot \vec{A}=\int \vec{\nabla}\cdot (\phi\vec{A})-\int\vec{A}\cdot \nabla\phi,$$ мы можем отбросить полный член расходимости (поскольку на границе все обнуляется достаточно быстро), чтобы получить

$$\int \phi \vec{\nabla}\cdot \vec{A }=\int -\vec{A}\cdot\nabla\phi.$$

Таким образом, для обычных функций $\vec{A}$ дивергенция превращает их во что-то, что действует на тестовые функции $\phi$, посылая им на номер, на который $\vec{A}$ отправляет $ -\nabla \phi$. Таким образом, для любого векторного распределения $\vec{G}$, которое переводит векторные тестовые функции $\vec{f}$ в $\vec{G}(\vec{f})$, расходимость $\vec{G}$ равна распределение, которое отправляет скалярную тестовую функцию $\phi$ в $-\vec{G}(\nabla\phi)$. Это очень общий вид дивергенции как в отношении того, на что оно может воздействовать, так и в отношении того, что оно может дать.

Просто несправедливо распространяться о том, насколько общие вещи вы позволяете делать своим интегралам, и не быть столь же общими в отношении того, что вы позволяете делать своим производным. Но никто на самом деле не хочет определять их производные и интегралы как нечто иное, кроме одинаково общего, в этом просто нет смысла.

Физика для науки и техники II

из Office of Academic Technologies на Vimeo.

9.12 Уравнения Максвелла Дифференциальная форма

Вспомним уравнения Максвелла. В интегральной форме мы видели, что уравнения Максвелла были такими, что первым из них был закон Гаусса для электрического поля, и это электрическое поле, усеянное вектором приращения площади d A , интегрированное по замкнутой поверхности S , равно чистый заряд, заключенный в объеме, окруженном этой замкнутой поверхностью S , разделенный на диэлектрическую проницаемость свободного пространства ε 0 . Следовательно, это был закон Гаусса для E поле.

Вторым уравнением Максвелла был закон Гаусса для магнитного поля, и это было B точка d A , проинтегрированное, опять же, по замкнутой поверхности, равной 0. Причина этого заключалась в том, что не может быть никаких магнитных монополий , поэтому мы не можем иметь в качестве источника магнитного поля единственный северный полюс, изолированный северный полюс, магнитный северный полюс или магнитный южный полюс. Это был случай закона Гаусса для поля B .

Третьим уравнением Максвелла был закон индукции Фарадея, и он был таким, что интеграл от E точка d l по замкнутому контуру C , по замкнутому контуру, равно отрицательному изменению магнитного потока, dΦ B  по dt. И это был закон индукции Фарадея.

Последним уравнением Максвелла был закон Ампера-Максвелла, и он имел вид ток, проходящий через область, окруженную этим замкнутым контуром, плюс μ 0 ε 0 , изменение электрического поля во времени. Где ε 0 раз это изменение электрического потока было током смещения, и это просто указывало на то, что изменение электрического поля генерирует магнитное поле. В случае закона Фарадея изменение магнитного поля порождает электрическое поле. Следовательно, это был закон Ампера-Максвелла.

Эти четыре уравнения представляют собой интегральную форму уравнений Максвелла. Как вы помните из исчисления, взять производную всегда намного проще, чем взять интеграл. Итак, мы попытаемся выразить эти четыре уравнения в виде дифференциальных уравнений. Для этого мы сначала вспомним оператор, который мы ввели ранее, когда изучали электрическое поле и электрический потенциал. Мы обозначили этот оператор с помощью дельта, и в исчислении он известен как «оператор дель» ( ∇ ).

В прямоугольной системе координат или в декартовой системе координат явный вид этого оператора был следующим: ∂ свыше ∂x умножить на х единиц плюс ∂ на ∂ y умножить на х единиц плюс ∂ на 8 z 9004 x k̂ единиц, где х , х и k̂ — единичные векторы в прямоугольной системе координат вдоль направлений x , y и z .

Как мы видим из определения этого оператора, он просто берет частную производную функции, когда бы он ни воздействовал на нее, вдоль этих конкретных направлений. Как вы помните, мы видели это как физическое применение этого оператора, когда мы вычисляли электрическое поле из потенциала, и оно было равно – ∇ -кратной функции потенциала. Мы назвали этот процесс «градиентом». Другими словами, всякий раз, когда оператор ∇ действовал на скалярную функцию, как в случае с потенциалом, это называлось градиентом потенциала. Итак, отрицательный градиент потенциала дал нам электрическое поле.

Здесь с математической точки зрения интересен тот факт, что здесь оператор воздействует на скалярную функцию, оператор ∇ , и преобразует ее в вектор. Как вы помните, когда мы берем частную производную потенциальной функции по определенным направлениям, мы получаем компоненты электрического поля по этим направлениям.

Если мы посмотрим на этот оператор и возьмем его скалярное произведение с самим собой, то оно будет равно ∂ над ∂x î плюс ∂ над ∂ y ĵ plus ∂ over ∂ z k̂ dotted with the same vector, which is ∂x î plus ∂ over ∂ y ĵ  and plus ∂ over ∂ z к̂ . Опять же, как вы помните, частная производная заключается в том, что если функция, которую мы берем в качестве производной, является функцией разных координат, то, когда мы берем частную производную по определенной координате, мы сохраняем другие значения постоянными. В этом смысле процесс получения производной ничем не отличается от получения полной производной этой функции.

Если мы посмотрим сюда и запишем это скалярное произведение в явной форме, мы получим ∂ на ∂ x , умноженное на ∂ на ∂ x , что даст нам вторую частную производную по отношению к x . Это ∂2 на ∂ x 2 и у нас будет х точка х для векторной части и мы будем иметь ∂2 на ∂ х ∂ y , 04 х , 03 х 9040 4 точка для второго члена плюс ∂2 сверх ∂ x ∂ z , î точка k̂ . Затем, двигаясь дальше, для продукта второго члена, плюс ∂2 над ∂ Y ∂ x , ĵ DOT î , плюс ∂2 над ∂ Y 2, ĵ DOT ∂ Y 2, ĵ DOT ∂ Y 2, ĵ DOT , плюс ∂2 над ∂ y ∂ z , х точка k̂ . И умножение или взятие скалярного произведения всех этих трех членов здесь, во второй скобке, на ∂ на ∂ z , даст нам ∂2 на ∂ z ∂ x , K̂ DOT î , плюс ∂2 над ∂ Z ∂ Y , K̂ DOT ĵ , и последний термин будет ∂2 более Z Z Z Z Z Z . k̂ точка k̂ .

Здесь, если мы посмотрим на х точка х , х точка х и k̂ точка k̂ , то эти векторы равны 1 и имеют угол между ними в том же направлении, будет 0. Следовательно, 1 умножить на 1, модуль единичного вектора х , умноженный на косинус 0, что равно 1, даст нам только 1. И затем аналогичным образом, х точка х даст нам 1, а k̂ точка k даст нам только 1.

When we look at these cross products, î dot ĵ , î dot k̂ , ĵ dot î , ĵ dot k̂ , there the magnitude of the first вектор равен 1, умножен на величину второго вектора, который равен 1, и умножен на косинус угла между этими двумя векторами, что равно косинусу 90, потому что х перпендикулярно х , которое также перпендикулярно k̂ , и аналогично, х перпендикулярно k̂ . Таким образом, все эти перекрестные члены, поскольку косинус 90 равен 0, дадут нам только 0. Следовательно, единственными оставшимися членами будут ∂2 на ∂ x 2, ∂2 на ∂ y 2 и ∂2 на ∂ y 2 ∂ z 2.

∇ точка ∇ представляется как ∇ 2, поэтому этот оператор будет равен ∂2 на ∂ x 2 плюс ∂2 на ∂ y 2 плюс ∂2 на ∂ x 2. Это еще один важный оператор в векторной алгебре. Он известен как «оператор Лапласа». Вы собираетесь подробно изучить эти операторы позже, когда будете проходить курс векторной алгебры. Итак, первый — оператор ∇, второй — оператор ∇ 2.

На этом этапе мы собираемся снова ввести две важные теоремы векторного исчисления, которые вы собираетесь подробно изучить позже в курсе векторной алгебры. Первая известна как теорема Стокса. Если мы скажем, пусть β — любой вектор, то теорема Стокса утверждает, что замкнутый интеграл от β dot d l , поэтому интеграл этого вектора смещения d l , интегрированный по замкнутому контуру, равен к ∇ кресту β точка d A интегрирована по поверхности S , и это поверхность, заключенная в этот замкнутый контур C . Таким образом, теорема Стокса просто утверждает, что если мы возьмем замкнутый интеграл вектора, β точка d l , что будет равно ∇ cross β точка d A .

Вторая важная теорема известна как теорема о расходимости. Опять же, для векторной величины β эта теорема может быть выражена как интеграл от β dot d A по замкнутой поверхности S равен ∇ dot β умноженному на dV 90 объем, окруженный замкнутой поверхностью С . Таким образом, в теореме Стокса петлевой интеграл преобразуется в поверхностный интеграл или наоборот, а в случае теоремы о дивергенции интеграл по замкнутой поверхности преобразуется в интеграл по объему.

Здесь давайте введем пару определений. Как я упоминал ранее, когда оператор ∇ действует на скалярную функцию, этот процесс называется градиентом U , а когда оператор ∇ действует на векторную величину через скалярное произведение, это называется дивергенцией β этого вектора. Если он действует на вектор через перекрестное произведение, он называется завитком β . Если мы посмотрим, с чем связаны эти процессы, завиток вектора представляет собой направление вращения и расхождение вектора. Если он положительный, он указывает на вектор, созданный в этой точке, а если отрицательный, то он представляет вектор, уничтоженный в этой точке. Это интересные термины, связанные с векторным исчислением.

Хорошо. Теперь давайте рассмотрим каждое из уравнений Максвелла одно за другим, начиная с первого. Это был закон Гаусса для электрического поля, которое равнялось E точка d A , интегрированное по замкнутой поверхности, равно суммарному заряду, заключенному в объеме, окруженном поверхностью, деленному на ε 0 диэлектрическую проницаемость свободного пространства. Суммарный заряд, заключенный внутри объема, окруженного этой поверхностью, также может быть выражен через плотность заряда: объемная плотность заряда ρ , умноженная на дВ по ε 0 , интегрированная по объему, окруженному этой поверхностью. поверхность С .

Хорошо. Итак, интеграл от E dot d A по замкнутой поверхности равен ρ умножить на dV по ε 0 проинтегрирован по объему, который окружен этой замкнутой поверхностью . Что ж, если мы вернемся к теореме о дивергенции, она гласит, что β точка d , проинтегрированное по замкнутой поверхности, равно дивергенции β , проинтегрированной по объему, окруженному поверхностью. Если мы применим эту теорему для нашего случая, то для нашего вектора мы будем иметь электрическое поле вместо β имеем E , поэтому E точка d A по замкнутой поверхности S будет равна интегралу по объему дивергенции E , умноженному на 8 d. То есть опять объем, окруженный S .

Итак, это прямо из теоремы о дивергенции. Но правая часть также равна ρ , умноженному на dV на ε 0 , интегрированному по тому же объему, объем окружен С . Оба эти интеграла берутся по одному и тому же объему. Мы можем избавиться от интегралов. Тогда мы получаем расхождение E равно ρ на ε 0 . Это дифференциальная форма закона Гаусса для поля E .

Когда мы смотрим на второе уравнение, которое было законом Гаусса для магнитного поля, B точка d A над замкнутой поверхностью S было равно 0, поэтому применяя теорему о расходимости и следуя аналогичному типу процедуры, мы получаем здесь расхождение B равно 0 как второе уравнение Максвелла в дифференциальной форме, которое является законом Гаусса для поля B .

Теперь давайте рассмотрим третье уравнение Максвелла, которое является законом индукции Фарадея, и которое было задано как E точка d l по замкнутому контуру равно – dΦ B по 4t 8 . Изменение потока во времени. Здесь поток, о котором мы говорим, является чистым потоком, протекающим через поверхность, окруженную этим замкнутым контуром. Таким образом, правая часть в явном виде может быть выражена как минус d над dt of, и тогда поток в его явной форме будет B точка d A , интегрированный по поверхности S , и это поверхность, окруженная петлей C . Поскольку интеграл берется по пространственным переменным, мы можем легко поместить оператор производной внутрь интеграла. Таким образом, если мы это сделаем, мы получим минус интеграл от d по dt от B точка d A интегрирована поверх этой закрытой поверхности S , которая окружена петлей C .

С другой стороны, левая часть закона Фарадея может быть выражена, опять же, в форме поверхностного интеграла, применяя теорему Стокса, которая просто утверждает, что любой вектор, усеянный точками вектором смещения, интегрированным по замкнутому петля равна curl этого вектора с точками d инкрементный вектор площади поверхности, интегрированный по поверхности, заключенной в эту петлю С . Здесь вместо β в нашем случае мы имеем вектор электрического поля. Следовательно, этот интеграл может быть выражен как интеграл от ∇ cross E или curl от E , разделенный вектором приращения площади d A , интегрированным по поверхности S , которая представляет собой поверхность, окруженную замкнутым контуром . С . Эти две поверхности являются одними и теми же поверхностями, поэтому мы можем избавиться от поверхностных интегралов.

Тогда остается ∇ cross E или завиток E равен минус d B больше dt . Теперь здесь мы можем выразить это в самой общей форме как ∂ B над ∂ t , потому что магнитное поле может быть функцией не только времени, но может быть функцией пространственных координат. Поэтому отрицательная частная производная магнитного поля становится равной ∇ cross E . Из этого выражения, которое является дифференциальной формой закона Фарадея, мы можем легко увидеть, что изменение магнитного поля создает или порождает электрическое поле. Это другой способ вспомнить или выразить закон индукции Фарадея. Это также известно как изменение 9Поле 0043 B генерирует поле E .

Хорошо. Теперь, если мы рассмотрим последнее уравнение Максвелла, которое является законом Ампера-Максвелла, и оно задается как B точка d l , интегрированное по замкнутому контуру, равно μ 0 умножить на i — заключенный плюс μ 0 умноженный на ток смещения, который равен ε 0 , изменение потока электрического поля во времени. Опять же, Б точка d l , интегрированная по этому замкнутому контуру, может быть выражена как μ 0 раз, для i -вложенных мы можем выразить это через плотность тока, и это будет Дж точка dA , проинтегрированная по поверхности S , которая окружена этим замкнутым контуром C , плюс для второго слагаемого имеем μ 0 ε 0 , снова выразим поток , в явном виде. Здесь речь идет о потоке электрического поля через область, окруженную этим контуром C , поэтому d над dt из E точка d A интегрирована по поверхности S , опять же, это поверхность, окруженная петлей C .

Здесь μ 0 — константа, мы можем поместить ее внутрь этого интеграла, как и μ 0 ε 0 и производную по времени можно поместить внутрь этого интеграла, потому что интеграл берутся за пространственные переменные. Мы можем выразить B dot d l , применяя теорему Стокса, как мы делали это в предыдущем случае в виде ∇ cross B dot d A , и это из теоремы Стокса, интегрированной по surface S surrounded by this loop C will be equal to integral of μ 0 J dot d A integrated over the same surface S plus integral of μ 0 ε 0 d над dt из E точка d A , опять же, объединены на той же поверхности S .

Таким образом, все эти интегралы берутся по одной и той же поверхности S , которая окружена замкнутым контуром C , и тогда мы можем избавиться от интегралов, оставив нам дифференциальное уравнение в виде ротора B магнитного поля. поле равно мк 0 Дж плюс μ 0 ε 0 . Опять же, используя самую общую форму, учитывая, что электрическое поле может быть функцией как положения, так и времени, поэтому использование здесь частной производной, ∂ E по ∂ t , даст нам дифференциальную форму Ампера Закон Максвелла. Опять же, легко увидеть, что это выражение можно интерпретировать как изменяющееся электрическое поле, в данном случае генерирующее магнитное поле. Так что здесь мы можем сказать, что это закон Ампера-Максвелла, и он также известен как изменение 9Поле 0043 E генерирует поле B .

Итак, как только мы получим эти дифференциальные формы уравнений Максвелла, мы можем выразить их здесь прямо напротив интегральных форм уравнений.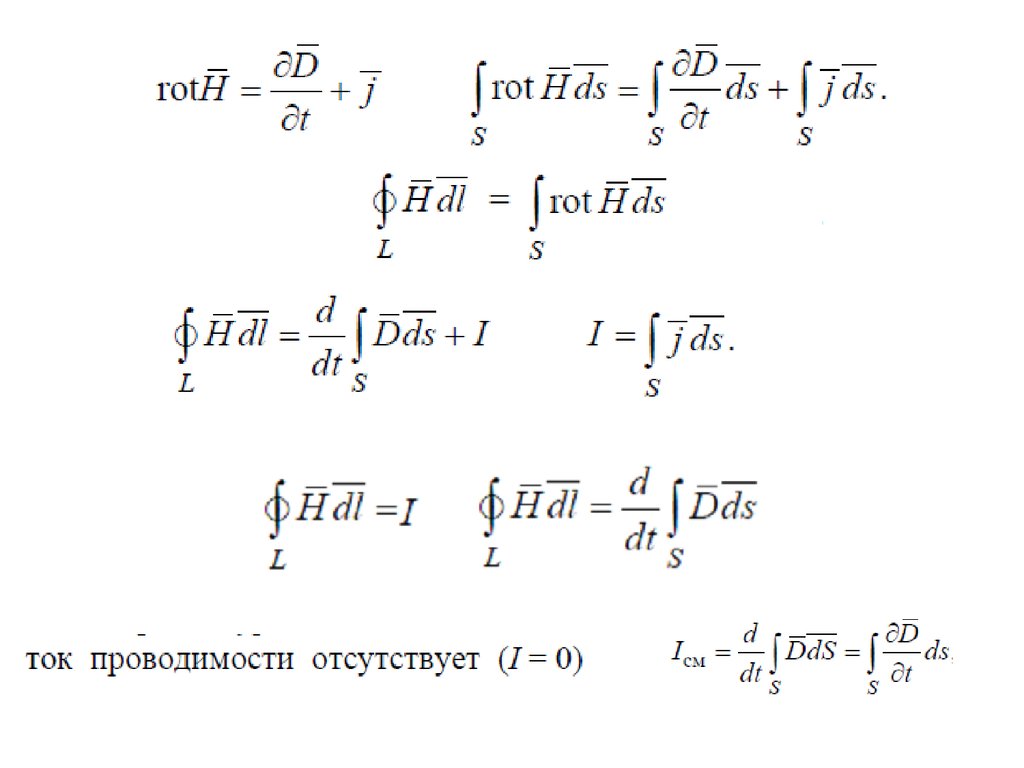 Для закона Гаусса имеем расхождение E равно ρ на ε 0 . Для закона Гаусса для магнитного поля расходимость B равна 0. Для закона индукции Фарадея имеем ∇ cross E равно -∂ B свыше ∂ t , изменение магнитного поля порождает электрическое поле.

Finally, for the Ampere-Maxwell’s law, we have ∇ cross B is equal to plus μ 0 J plus μ 0 ε 0 ∂ E over ∂ t , изменение электрического поля порождает магнитное поле. Итак, это дифференциальные формы уравнений Максвелла. Эти четыре уравнения являются фундаментальными уравнениями электромагнитной теории, и с их помощью можно анализировать и объяснять любое электромагнитное явление. Допустим, это дифференциальная форма, а это интегральные формы.

Обзор уравнений Максвелла — Электромагнитная геофизика

Цель

Предоставив набор формообразующих законов для электромагнетизма, мы представляем четыре общих представления уравнений Максвелла. Эта страница предназначена для использования в качестве краткого руководства. Для конкретных задач может оказаться полезным начать с менее распространенных форм уравнений Максвелла. Обратите внимание, однако, что все формы могут быть получены из выражений, представленных здесь.

Уравнения Максвелла состоят из первых четырех формообразующих законов; то есть закон Гаусса для электрических полей, закон Гаусса для магнитных полей, закон Фарадея и закон Ампера-Максвелла. Уравнения могут быть записаны по-разному и характеризуют физические соотношения между полями (e,h) и потоками (b,d). Конкретные формулировки могут быть получены за счет использования определяющих соотношений. Уравнения Максвелла можно записать по частоте или по времени, а также в дифференциальной или интегральной форме:

1. Дифференциальная форма во временной области

2. Дифференциальная форма в частотной области

3. Интегральная форма во временной области

4. Интегральная форма в частотной области

Эта страница предназначена для быстрого доступа к соответствующим уравнениям с правильным обозначение и единицы. Уравнения подходят для электромагнитных полей в материи. Если поля находятся в свободном пространстве, то используются те же определяющие отношения, но с \(\sigma = 0\), \(\mu_0\) и \(\varepsilon_0\). Определяющие уравнения также записываются в предположении, что физические свойства изотропны и недисперсионны. Более подробную информацию об этом можно найти в [WH88] (стр. 133) или на странице физических свойств.

Переменные и единицы измерения

Здесь приведены переменные и единицы для соответствующих величин в уравнениях Максвелла.

Поля

Флюсы

Физические свойства

Дифференциальная форма во временной области

Здесь мы представляем дифференциальные формы для закона Гаусса для электрических полей, закона Гаусса для магнитных полей, закона Фарадея и уравнения Ампера-Максвелла во временной области.

\[\begin{split}\begin{align} \textbf{Гаусс для E-поля:}\;\; &\nabla\cdot\mathbf{d}=\rho_f \\ \textbf{Гаусс для B-поля:}\;\; &\nabla\cdot\mathbf{b}=0 \\ \textbf{Фарадей:} \;\; &\nabla\times\mathbf{e}=-\dfrac{\partial \mathbf{b}}{\partial t} \\ \textbf{Ампер-Максвелл:} \;\; &\nabla\times\mathbf{h}=\mathbf{j} + \dfrac{\partial \mathbf{d}}{\ partial t} \end{выравнивание}\end{split}\]

, где \(\rho_f\) — плотность свободных изменений, а \(\mathbf{j}\) — плотность свободного тока. Для замены полей и потоков можно использовать следующие определяющие отношения:

\[\begin{split}\begin{align} \mathbf{j} &= \sigma \mathbf{e}\\ \mathbf{b} &= \mu \mathbf{h}\\ \mathbf{d} &= \varepsilon \mathbf{e} \конец{выравнивание}\конец{разделение}\]

Дифференциальная форма в частотной области

Здесь мы представляем дифференциальные формы для закона Гаусса для электрических полей, закона Гаусса для магнитных полей, закона Фарадея и уравнения Ампера-Максвелла в частотной области:

\[\begin{split}\begin{align} \textbf{Гаусс для E-поля:} \;\; &\nabla\cdot\mathbf{D}=\rho_f \\ \textbf{Гаусс для B-поля:} \;\; &\nabla\cdot\mathbf{B}=0 \\ \textbf{Фарадей:} \;\; &\nabla\times\mathbf{E}=-i\omega\mathbf{B} \\ \textbf{Ампер-Максвелл:} \;\; &\nabla\times\mathbf{H}=\mathbf{J} + i\omega \mathbf{D} \конец{выравнивание}\конец{разделение}\]

, где \(\rho_f\) — плотность свободных изменений, а \(\mathbf{J}\) — плотность свободного тока. Для замены полей и потоков можно использовать следующие определяющие соотношения:

\[\begin{split}\begin{align} \mathbf{J} &= \sigma \mathbf{E}\\ \mathbf{B} &= \mu \mathbf{H}\\ \mathbf{D} &= \varepsilon \mathbf{E} \конец{выравнивание}\конец{разделение}\]

Интегральная форма во временной области

Здесь мы представляем интегральные формы для закона Гаусса для электрических полей, закона Гаусса для магнитных полей, закона Фарадея и уравнения Ампера-Максвелла во временной области.

\[\begin{split}\begin{align} \textbf{Гаусс для E-поля:} \; & \int_V\nabla\cdot\mathbf{d}\; дВ\! =\!\oint_S\mathbf{d}\cdot d\mathbf{a} \! знак равно Q_f \\ \textbf{Гаусс для B-поля:} \; & \oint_S \mathbf{b} \cdot d \mathbf{a}=0 \\ \textbf{Фарадей:} \; & \oint_C \mathbf{e}\cdot d\mathbf{l}=-\int_S\dfrac{\partial \mathbf{b}}{\partial t}\cdot d\mathbf{a} \\ \textbf{Ампер-Максвелл:} \; & \oint_C \!\mathbf{h} \cdot d\mathbf{l} = \! \int_S \!\Big ( \mathbf{j} \!+\! \dfrac{\partial \mathbf{d}}{\partial t} \Big ) \!\cdot d\mathbf{a} \end{выравнивание}\end{split}\]

, где \(Q_f\) — общий свободный электрический заряд, а \(\mathbf{j}\) — плотность свободного тока. \(d \mathbf{a}\) — бесконечно малая единица площади поверхности с направлением вектора по нормали к поверхности \(S\). \(d \mathbf{l}\) — бесконечно малая длина с направлением вектора вдоль замкнутого пути \(C\). Для замены полей и потоков можно использовать следующие определяющие отношения:

\[\begin{split}\begin{align} \mathbf{j} &= \sigma \mathbf{e}\\ \mathbf{b} &= \mu \mathbf{h}\\ \mathbf{d} &= \varepsilon \mathbf{e} \end{выравнивание}\end{split}\]

Интегральная форма в частотной области

Здесь мы представляем интегральные формы для закона Гаусса для электрических полей, закона Гаусса для магнитных полей, закона Фарадея и уравнения Ампера-Максвелла в частотной области.

\[\begin{split}\begin{align} \textbf{Гаусс для E-поля:} \; &\int_V\nabla\cdot\mathbf{D}\; dV=\oint_S\mathbf{D}\cdot d \mathbf{a} \! знак равно Q_f \\ \textbf{Гаусс для B-поля:} \; &\oint_S \mathbf{B} \cdot d\mathbf{a}=0 \\ \textbf{Фарадей:} \; &\oint_C \mathbf{E}\cdot d\mathbf{l}=-i\omega\int_S\mathbf{B}\cdot d\mathbf{a} \\ \textbf{Ампер-Максвелл:} \; & \oint_C \!\mathbf{H} \cdot d\mathbf{l} = \! \int_S \!\big ( \mathbf{J} \!+\! i\omega \mathbf{D} \big ) \!\cdot d\mathbf{a} \end{выравнивание}\end{split}\]

, где \(Q_f\) — общий свободный электрический заряд, а \(\mathbf{J}\) — плотность свободного тока.