Уравнения Максвелла в дифференциальной и интегральной форме: физический смысл
Уравнения Максвелла — основная идея и физическая суть
Закономерности, выведенные Максвеллом, в электродинамике имеют такое значение, как, к примеру, законы Ньютона для классической механики и постулаты Эйнштейна в теории относительности. Это фундаментальные уравнения, которые подтверждены экспериментальным путем.
Определение
Уравнения Максвелла являются системой уравнений в дифференциальном или интегральном виде, которые описывают любые электромагнитные поля, взаимосвязи токов и электрических зарядов в разных средах, включая вакуум.
Уравнения Максвелла подвергались критике со стороны современников ученого, так как не вписывались в установленные стандарты и представления того времени. Однако закономерности послужили началом активного развития науки и причиной переворота в восприятии картины мира. Постулаты предшествовали открытию радиоволн и продемонстрировали электромагнитную природу света. Формулы Максвелла справедливы для макромира и области квантовой механики.
Формулы Максвелла справедливы для макромира и области квантовой механики.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Что описывают четыре уравнения
- Из первой закономерности рассматривается поток электрического поля Е сквозь какую-либо поверхность замкнутого типа. Можно наблюдать зависимость между потоком и суммарным зарядом. Уравнение является законом или теоремой Гаусса.
- Второе уравнение Максвелла выражает закон Фарадея, на основе которого функционируют электрические моторы. В двигателях возникает ток в катушке в процессе вращения магнита.
- Третье уравнение Максвелла

- Четвертый постулат Максвелла имеет наибольшее значение. Исходя из уравнения, был введен термин тока смещения. Данная формула получила название теоремы о циркуляции вектора магнитной индукции. Согласно этому утверждению, вихревое магнитное поле образовано электрическим током и изменением электрического поля.
Смысл уравнений Максвелла:
- Первое уравнение — электрическое поле сформировано электрическим зарядом.
- Второе уравнение — вихревое электрическое поле формируется в результате изменений магнитного поля.
- Третье уравнение — магнитные заряды отсутствуют в природе.
- Четвертое уравнение — вихревое магнитное поле является результатом электрического тока и изменений электрической индукции.
Как записать в интегральной форме
Первое уравнение
Первое уравнение Максвелла представляет собой дифференциальную формулировку закона полного тока.
Запись уравнения Максвелла в дифференциальной форме
\(roh\vec{H}=\sigma \vec{E}+\left(\frac{d\vec{D}}{dt} \right)\)
\(roh\vec{H}=\vec{\delta _{pr}+\vec{\delta _{sm}}}\)
\(rot\vec{E}=-\left(\frac{d\vec{B}}{dt} \right)\)
\(div\vec{D}=p\)
\(div\vec{B}=0\)
\(div\vec{\delta }=-\left(\frac{dpV}{dt} \right)\)
Возбуждение электромагнитных волн
Возбуждение электромагнитных волн
ОглавлениеПРЕДИСЛОВИЕГлава первая. УРАВНЕНИЯ МАКСВЕЛЛА 1.1. УРАВНЕНИЯ МАКСВЕЛЛА В ДИФФЕРЕНЦИАЛЬНОЙ И ИНТЕГРАЛЬНОЙ ФОРМЕ 1-3. ТЕОРЕМА УМОВА—ПОЙНТИНГА 1-4. УРАВНЕНИЯ МАКСВЕЛЛА И ТЕОРЕМА УМОВА—ПОЙНТИНГА ДЛЯ КОМПЛЕКСНЫХ АМПЛИТУД ПОЛЯ 1-5. 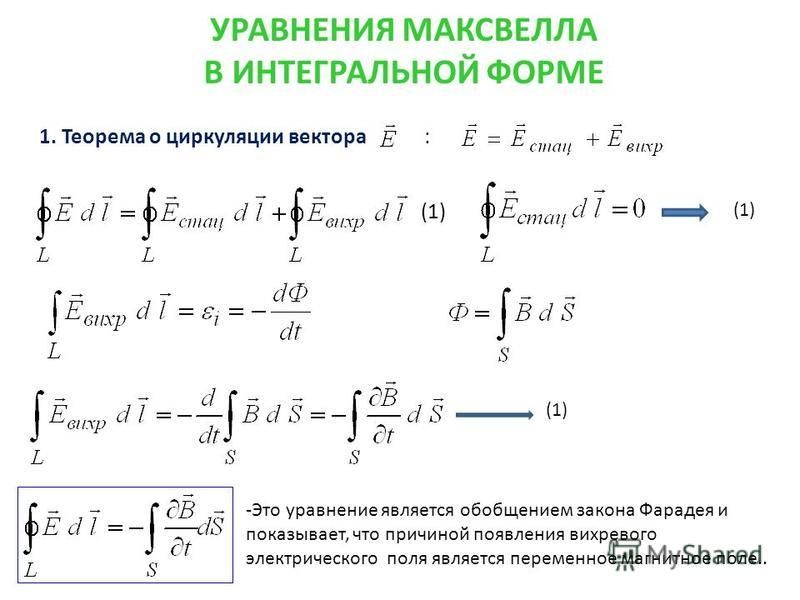 ВОЛНОВЫЕ УРАВНЕНИЯ И ЭЛЕКТРОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ ВОЛНОВЫЕ УРАВНЕНИЯ И ЭЛЕКТРОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ1-6. УРАВНЕНИЯ СТАТИЧЕСКИХ И СТАЦИОНАРНЫХ ЭЛЕКТРОМАГНИТНЫХ ПОЛЕЙ 1-7. УРАВНЕНИЯ МАКСВЕЛЛА ПРИ ВЕСЬМА ВЫСОКИХ ЧАСТОТАХ 1-8. ОРТОГОНАЛЬНЫЕ СИСТЕМЫ КООРДИНАТ Глава вторая. ИНТЕГРИРОВАНИЕ НЕОДНОРОДНЫХ УРАВНЕНИЙ МАКСВЕЛЛА ДЛЯ СВОБОДНОГО ПРОСТРАНСТВА 2-1. РЕШЕНИЕ ВЕКТОРНОГО ВОЛНОВОГО УРАВНЕНИЯ 2-2. ПРЕДСТАВЛЕНИЯ ФУНКЦИИ ГРИНА 2-3. ЭЛЕКТРИЧЕСКИЕ И МАГНИТНЫЕ ВОЛНЫ В ПРЯМОУГОЛЬНОЙ СИСТЕМЕ КООРДИНАТ 2-5. ПЛОСКАЯ ТЕМ ВОЛНА В ОДНОРОДНОМ ПРОСТРАНСТВЕ 2-6. ЭЛЕКТРИЧЕСКИЕ И МАГНИТНЫЕ ВОЛНЫ В ЦИЛИНДРИЧЕСКОЙ СИСТЕМЕ КООРДИНАТ 2-7. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ БЕСКОНЕЧНО ПРОТЯЖЕННОГО ЛИНЕЙНОГО ТОКА 2-8. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ БЕСКОНЕЧНО ПРОТЯЖЕННОЙ ТРУБКИ ТОКА 2-9. ЭЛЕКТРИЧЕСКИЕ И МАГНИТНЫЕ ВОЛНЫ В СФЕРИЧЕСКОЙ СИСТЕМЕ КООРДИНАТ 2-10. ПОЛЕ ЭЛЕКТРИЧЕСКОГО ДИПОЛЯ 2-11. ПОЛЕ СФЕРИЧЕСКОГО ИЗЛУЧАТЕЛЯ Глава третья. ОСНОВНЫЕ ПРИНЦИПЫ В ТЕОРИИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 3-1.  3-2. ТЕОРЕМА ЕДИНСТВЕННОСТИ 3-3. ЛЕММА ЛОРЕНЦА 3-4. ТЕОРЕМА ЭКВИВАЛЕНТНОСТИ 3-5. ТЕОРЕМА ВЗАИМНОСТИ 3-6. ПРИНЦИП ДВОЙСТВЕННОСТИ 3-7. ЭЛЕКТРИЧЕСКИЕ И МАГНИТНЫЕ ТОКИ ПОЛЯРИЗАЦИИ Глава четвертая. ВОЗБУЖДЕНИЕ ПЛОСКОЙ ГРАНИЦЫ РАЗДЕЛА ДВУХ СРЕД 4-1. ВОЗБУЖДЕНИЕ ПЛОСКОЙ ГРАНИЦЫ РАЗДЕЛА БЕСКОНЕЧНОЙ НИТЬЮ ЭЛЕКТРИЧЕСКОГО (МАГНИТНОГО) ТОКА. ОБЩЕЕ РЕШЕНИЕ 4-2. ПРИМЕНЕНИЕ МЕТОДА ПЕРЕВАЛА К ОПРЕДЕЛЕНИЮ ПОЛЯ НИТИ ТОКА НАД ПЛОСКОСТЬЮ В ЗОНЕ ИЗЛУЧЕНИЯ 4-3. ПРИБЛИЖЕННЫЕ ГРАНИЧНЫЕ УСЛОВИЯ ЛЕОНТОВИЧА 4-4. ВОЗБУЖДЕНИЕ ПЛОСКОЙ ГРАНИЦЫ РАЗДЕЛА ДВУХ СРЕД ЭЛЕКТРИЧЕСКИМ ДИПОЛЕМ (задача Зоммерфельда) Глава пятая. ВОЗБУЖДЕНИЕ КРУГЛОГО БЕСКОНЕЧНОГО ЦИЛИНДРА 5-2. ВОЗБУЖДЕНИЕ ЦИЛИНДРА ЭЛЕКТРИЧЕСКИМИ ДИПОЛЯМИ 5-3. ВОЗБУЖДЕНИЕ ЦИЛИНДРА МАГНИТНЫМИ ТОКАМИ 5-4. ВОЗБУЖДЕНИЕ ЦИЛИНДРА БОЛЬШОГО ЭЛЕКТРИЧЕСКОГО РАДИУСА 5-5. ДИФРАКЦИЯ ПЛОСКОЙ ВОЛНЫ НА ЦИЛИНДРЕ Глава шестая.  ВОЗБУЖДЕНИЕ ШАРА ВОЗБУЖДЕНИЕ ШАРА6-1. ОБЩЕЕ РЕШЕНИЕ ЗАДАЧИ О ВОЗБУЖДЕНИИ ИДЕАЛЬНО ПРОВОДЯЩЕГО ШАРА 6-2. ПОЛЕ РАДИАЛЬНОГО ДИПОЛЯ НАД ШАРОМ 6-3. ПОЛЕ МЕРИДИОНАЛЬНОГО ДИПОЛЯ НАД ШАРОМ 6-4. ПОЛЕ КОЛЬЦЕВОЙ ЩЕЛИ НА ШАРЕ 6-5. ДИФРАКЦИЯ ПЛОСКОЙ ВОЛНЫ НА ШАРЕ 6-6. ВОЗБУЖДЕНИЕ ШАРА БОЛЬШОГО ЭЛЕКТРИЧЕСКОГО РАДИУСА Глава седьмая. ВОЗБУЖДЕНИЕ БЕСКОНЕЧНОГО ИДЕАЛЬНО ПРОВОДЯЩЕГО КЛИНА 7-1. ОБЩЕЕ РЕШЕНИЕ ЗАДАЧИ О ВОЗБУЖДЕНИИ ИДЕАЛЬНО ПРОВОДЯЩЕГО КЛИНА 7-2. ВОЗБУЖДЕНИЕ КЛИНА РАДИАЛЬНЫМ ЭЛЕКТРИЧЕСКИМ ДИПОЛЕМ 7-3. ВОЗБУЖДЕНИЕ КЛИНА РАДИАЛЬНОЙ ЩЕЛЬЮ 7-4. МЕТОД ВИНЕРА—ХОПФА И ПРИМЕНЕНИЕ ЕГО К РЕШЕНИЮ ЗАДАЧИ О ВОЗБУЖДЕНИИ ИДЕАЛЬНО ПРОВОДЯЩЕЙ ПОЛУПЛОСКОСТИ Глава восьмая. ВОЗБУЖДЕНИЕ ПОВЕРХНОСТНЫХ ВОЛН 8-1. ПРИМЕНЕНИЕ ИМПЕДАНСНЫХ ГРАНИЧНЫХ УСЛОВИЙ В ТЕОРИИ ПОВЕРХНОСТНЫХ ВОЛН 8-2. ВОЗБУЖДЕНИЕ ПЛОСКОЙ ИМПЕДАНСНОЙ ПОВЕРХНОСТИ 8-3. ПОВЕРХНОСТНЫЕ ВОЛНЫ НАД ПЛОСКОСТЬЮ С МОДУЛИРОВАННЫМ ИМПЕДАНСОМ 8-4. РАСЧЕТ ТОКОВ НА ИМПЕДАНСНОЙ ПЛОСКОСТИ МЕТОДОМ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ  ВОЗБУЖДЕНИЕ ПЛОСКОГО ЭКРАНА СО СЛОЕМ ДИЭЛЕКТРИКА ВОЗБУЖДЕНИЕ ПЛОСКОГО ЭКРАНА СО СЛОЕМ ДИЭЛЕКТРИКАГлава девятая. РЕШЕНИЕ ГРАНИЧНЫХ ЗАДАЧ ЭЛЕКТРОДИНАМИКИ В КОРОТКОВОЛНОВОМ ПРИБЛИЖЕНИИ 9-2. МЕТОД ГЕОМЕТРИЧЕСКОЙ ОПТИКИ 9-3. МЕТОД ФИЗИЧЕСКОЙ ОПТИКИ 9-4. МЕТОД ДИФРАКЦИОННЫХ ЛУЧЕЙ Глава десятая. ВОЗБУЖДЕНИЕ ВОЛНОВОДОВ 10-1. ВОЗБУЖДЕНИЕ ВОЛН МЕЖДУ ДВУМЯ ПЛОСКОСТЯМИ 10-2. ВОЗБУЖДЕНИЕ ПРЯМОУГОЛЬНОГО ВОЛНОВОДА 10-3. ВОЗБУЖДЕНИЕ КРУГЛОГО ВОЛНОВОДА 10-4. ВОЗБУЖДЕНИЕ РАДИАЛЬНОГО ВОЛНОВОДА Глава одиннадцатая. ВОЗБУЖДЕНИЕ ОБЪЕМНЫХ РЕЗОНАТОРОВ 11-1. ВОЗБУЖДЕНИЕ ПРЯМОУГОЛЬНОГО РЕЗОНАТОРА 11-2. ВОЗБУЖДЕНИЕ КРУГЛОГО ЦИЛИНДРИЧЕСКОГО РЕЗОНАТОРА 12-1. ТЕНЗОР ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ ПИРОЭЛЕКТРИЧЕСКОЙ СРЕДЫ 12-2. ОБЩЕЕ РЕШЕНИЕ ЗАДАЧИ О ВОЗБУЖДЕНИИ ВОЛН В НЕОГРАНИЧЕННОЙ ГИРОЭЛЕКТРИЧЕСКОЙ СРЕДЕ 12-3. ВОЗБУЖДЕНИЕ ГИРОЭЛЕКТРИЧЕСКОЙ СРЕДЫ ПЛОСКИМ СЛОЕМ СИНФАЗНОГО ТОКА ПРИЛОЖЕНИЯ |
2.
 4: Связь между интегральной и дифференциальной формами уравнений Максвелла
4: Связь между интегральной и дифференциальной формами уравнений Максвелла- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 24989
- Дэвид Х. Стейлин
- Массачусетский технологический институт через MIT OpenCourseWare
Теорема Гаусса о расходимости
Две теоремы очень полезны для связи дифференциальной и интегральной форм уравнений Максвелла: теорема Гаусса о расходимости и теорема Стокса. Теорема Гаусса о расходимости (2.1.20) утверждает, что интеграл от нормальной компоненты произвольного аналитического надлинейного поля \(\overline A \) по поверхности S, ограничивающей объем V, равен объемному интегралу от \( \nabla \cdot \ overline{\mathrm{A}}\) над V. Теорему можно быстро вывести, если вспомнить (2.1.3):
Теорему можно быстро вывести, если вспомнить (2.1.3):
\[\nabla \cdot \overline{A} \equiv \frac{\partial A_{x}}{\partial x}+\frac{\partial A_{y}}{\partial y}+\frac{ \partial A_{z}}{\partial z} \]
Следовательно, \( \nabla \cdot \overline{A}\) в позиции x o , y o , z o можно найти используя (2.4.1) в пределе, когда Δx, Δy и Δz стремятся к нулю:
\[\begin{align}
\nabla \cdot \overline{A}=\lim _{\Delta i \rightarrow 0} &\left\{\left[A_{x}\left(x_{0}+\Delta x/2\right)-A_{x}\left(x_{0}-\Delta x/2\right)\ вправо] / \Дельта х\вправо.\\
&+\left[A_{y}\left(y_{0}+\Delta y / 2\right)-A_{y}\left(y_{0}-\Delta y/2\right)\right] / \Delta y \nonumber\\
&\left.+\left[A_{z}\left(z_{0}+\Delta z / 2\right)-A_{z}\left(z_{0}- \Delta z / 2\right)\right] / \Delta z\right\} \nonumber
\end{align} \]
\[\begin{align}
=\lim _{\Delta i \rightarrow 0 } &\left\{\Delta y \Delta z\left[A_{x}\left(x_{0}+\Delta x / 2\right)-A_{x}\left(x_{0}-\Delta x / 2\right)\right]\right. \\
\\
&+\Delta x \Delta z\left[A_{y}\left(y_{0}+\Delta y / 2\right)-A_{y }\left(y_{0}-\Delta y / 2\right)\right] \nonnumber\\
&\left.+\Delta x \Delta y\left[A_{z}\left(z_{0}+\Delta z / 2\right)-A_{z}\left(z_{0}-\Delta z / 2\right)\right]\right\} / \Delta x \Delta y \Delta z \nonumber
\end{align} \]
\[ =\lim _{\Delta \mathbf{v} \ стрелка вправо 0} \ влево \ {\ oiint _ {\ mathrm {S} _ {\ mathrm {c}}} \ overline {\ mathrm {A}} \ пуля \ шляпа {n} \ mathrm {da} / \ Delta \ mathrm {v}\right\}\]
где \(\hat{n}\) — единичная нормальная черта для инкрементного куба размерностей Δx, Δy, Δz; da — его дифференциальная поверхность; С c – площадь его поверхности; Δv — его объем, как показано на рис. 2.4.1 (а).
Теперь мы можем сложить произвольное количество таких бесконечно малых кубов, чтобы сформировать объем V, подобный показанному на рис. 2.4.1(b). Затем мы можем просуммировать (2.4.4) по всем этим кубам, чтобы получить:
\[ \lim _{\Delta v \rightarrow 0} \sum_{i}(\nabla \bullet \overline{A}) \Delta v_ {i}=\lim _{\Delta v \rightarrow 0} \sum_{i}\left\{\oiint_{S_{c}} \overline{A} \bullet \hat{n} d a_{i}\ right\}\]
Рисунок \(\PageIndex{1}\): Вывод теоремы Гаусса о расходимости.
Поскольку все вклады в \(\sum_{i}\left\{\oiint_{S} \overline{A} \bullet \hat{n} d a_{i}\right\} \) от обращенного внутрь смежного куба грани сокращаются, в правой части (2.4.5) остаются только вклады от внешней поверхности объема V. Переходя к пределу, получаем Теорема Гаусса о расходимости }(\nabla \bullet \overline{A}) d v=\oiint_{S}(\overline{A} \cdot \hat{n}) d a\]
Теорема Стокса
Теорема Стокса утверждает, что интеграл ротора надлинеторного поля над ограниченной поверхностью равен линейному интегралу этого надлинейторного поля по контуру C, ограничивающему эту поверхность. Его вывод аналогичен выводу теоремы Гаусса о расходимости (раздел 2.4.1), начиная с определения z-компоненты оператора ротора [из уравнения (2.1.4)]:
\[ (\nabla \times \overline{\mathrm{A}})_{\mathrm{z}} \equiv \hat{z}\left(\frac{\partial \mathrm{A}_{\ mathrm{y}}}{\partial\mathrm{x}}-\frac{\partial\mathrm{A}_{\mathrm{x}}}{\partial\mathrm{y}}\right)\]
\[ \begin{align}
=\hat{z} \lim _{\Delta x, \Delta y \rightarrow 0} &\left\{\left[A_{y}\left(x_{0}+ \Delta x / 2\right)-A_{y}\left(x_{0}-\Delta x / 2\right)\right] / \Delta x\right. \\
\\
&\left.-\left[ A_{x}\left(y_{0}+\Delta y/2\right)-A_{x}\left(y_{0}-\Delta y/2\right)\right]/\Delta y\right \}\номер
\end{align}\]
\[ \begin{align}
=\hat{z} \lim _{\Delta x, \Delta y \rightarrow 0}\{& \Delta y\left[A_{ y}\left(x_{0}+\Delta x / 2\right)-A_{y}\left(x_{0}-\Delta x/2\right)\right] / \Delta x \Delta y \ \
&\left.-\Delta x\left[A_{x}\left(y_{0}+\Delta y/2\right)-A_{x}\left(y_{0}-\Delta y/ 2\right)\right] / \Delta x \Delta y\right\} \nonumber
\end{align}\]
Рассмотрим поверхность в плоскости x-y, перпендикулярную \(\hat{z}\) и \(\hat{n}\), локальная нормаль к поверхности, как показано на рис. 2.4.2(a).
Рисунок \(\PageIndex{2}\): Вывод теоремы Стокса.Тогда (2.4.9) применительно к ΔxΔy принимает следующий вид: n}=\oint_{\mathrm{C}} \overline{\mathrm{A}} \bullet \mathrm{d} \overline{\mathrm{s}} \]
, где d\(\overline s\) представляет собой дифференциальную длину линии над линией [м] вдоль контура C, ограничивающего инкрементальную область, определяемую ΔxΔy = da. Контур C трансверсирован в правом направлении относительно \(\hat{n}\). Мы можем собрать такие бесконечно малые области, чтобы сформировать поверхности произвольной формы и площади A, как показано на рис. 2.4.2(b). Суммируя (2.4.10) по всем этим бесконечно малым площадям da, мы находим, что все вклады в правую внутренность области A сокращаются, остаются только вклады от контура C вдоль границы A. Таким образом, (2.4. 10) становится Теорема Стокса :
Контур C трансверсирован в правом направлении относительно \(\hat{n}\). Мы можем собрать такие бесконечно малые области, чтобы сформировать поверхности произвольной формы и площади A, как показано на рис. 2.4.2(b). Суммируя (2.4.10) по всем этим бесконечно малым площадям da, мы находим, что все вклады в правую внутренность области A сокращаются, остаются только вклады от контура C вдоль границы A. Таким образом, (2.4. 10) становится Теорема Стокса :
\[ \int \int _{\mathrm{A}}(\nabla \times \overline{\mathrm{A}}) \bullet \hat{n} \mathrm{da}=\ oint_{\mathrm{C}} \overline{\mathrm{A}} \cdot \mathrm{d} \overline{\mathrm{s}}\]
где соотношение между направлением интегрирования вокруг контура и ориентация \(\шляпа{n}\) подчиняется правилу правой руки (если пальцы правой руки сгибаются в направлении d\(\над чертой s\), то большой палец указывает в направлении \(\шляпа{ п}\)).
Уравнения Максвелла в интегральной форме
Дифференциальную форму уравнений Максвелла (2. 1.5–8) можно преобразовать в интегральную форму с помощью теоремы Гаусса о дивергенции и теоремы Стокса. Закон Фарадея (2.1.5):
1.5–8) можно преобразовать в интегральную форму с помощью теоремы Гаусса о дивергенции и теоремы Стокса. Закон Фарадея (2.1.5):
\[\nabla \times \overline{\mathrm{E}}=-\frac{\partial \overline{\mathrm{B}}}{\partial \mathrm{t }} \]
Применяя теорему Стокса (2.4.11) к криволинейной поверхности A, ограниченной контуром C, получаем:
\[ \iint_{\mathrm{A}}(\nabla \times \overline{ \mathrm{E}}) \bullet \hat{n} \mathrm{d} \mathrm{a}=\oint _{\mathrm{C}} \overline{\mathrm{E}} \bullet \mathrm{d} \ overline {\ mathrm {s}} = — \ iint _ {\ mathrm {A}} \ frac {\ partial \ overline {\ mathrm {B}}} {\ partial \ mathrm {t}} \ bullet \ hat {n } \mathrm{d} \mathrm{a}\]
Это становится интегральной формой закона Фарадея: } \overline{B} \bullet \hat{n} d a \quad\quad\quad\quad\quad(\text {Закон Фарадея} a w)\]
Аналогичное применение теоремы Стокса к дифференциальной форме уравнения Ампера закон дает свою интегральную форму:
\[ \oint_{\mathrm{C}} \overline{\mathrm{H}} \bullet \mathrm{d} \overline{\mathrm{s}}=\iint_{\mathrm {A}}\left[\overline{\mathrm{J}}+\frac{\partial \overline{\mathrm{D}}}{\partial \mathrm{t}}\right] \bullet\hat{n } \mathrm{d} \mathrm{a} \quad\quad\quad\quad\quad \text { (Закон Ампера) }\]
Теорему Гаусса о расходимости (2. {\prime} s \text {Закон заряда}\right)\]
{\prime} s \text {Закон заряда}\right)\]
\[\oiint_{\mathrm{A}}(\overline{\mathrm{B}} \bullet \hat{n}) \mathrm{d} \mathrm{a}=0 \quad \quad \quad \ quad \quad \text{ (Закон Гаусса для } \overline{B}) \]
Наконец, закон сохранения заряда (1.3.19) может быть преобразован к интегральной форме, как и законы Гаусса:
\[ \oiint_{\ mathrm {A}} (\ overline {\ mathrm {J}} \ bullet \ hat {n}) \ mathrm {d} \ mathrm {a} = — \ int \ int \ int _ {\ mathrm {V}} \ frac {\ парциальное \ rho} {\ парциальное \ mathrm {t}} \ mathrm {d} \ mathrm {v} \ quad \ quad \ quad \ quad \ quad (\ text {сохранение заряда}) \]
Рисунок \(\PageIndex{3}\): уравнения Максвелла в эскизной форме.Четыре схемы уравнений Максвелла, представленные на рис. 2.4.3, могут облегчить запоминание; их можно интерпретировать как в дифференциальной, так и в интегральной форме, поскольку они охватывают основную физику.
Пример \(\PageIndex{A}\)
Используя закон Гаусса, найдите \(\overline E\) на расстоянии r от точечного заряда q.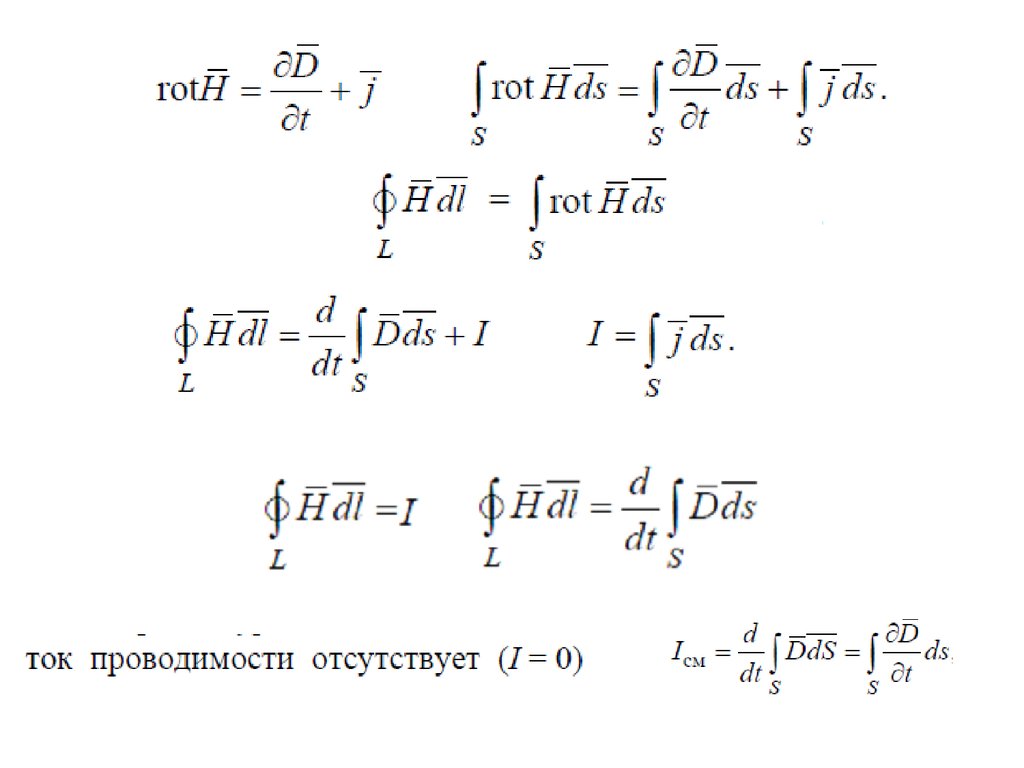 {2}\).
{2}\).
Пример \(\PageIndex{B}\)
Что такое \(\overline H\) на расстоянии r = 1 см от тока линии \(\overline I\) = \(\hat{z}\) [ ампер] расположен на r = 0?
Решение
Поскольку геометрия этой задачи цилиндрически симметрична, решение тоже. Используя интегральную форму закона Ампера (2.4.15) и интегрируя в правом смысле по окружности радиуса r с центром в токе и в плоскости, ортогональной ему, получаем 2\(\pi\)rH = I , поэтому \(\overline H\) = \(\hat{\theta}\) 100/2\(\pi\) [A m -1 ].
Эта страница под названием 2.4: Связь между интегральной и дифференциальной формами уравнений Максвелла распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Дэвидом Х. Стелином (MIT OpenCourseWare) через исходный контент это было отредактировано в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Дэвид Х.
 Стаелин
Стаелин
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Программа ООР или издатель
- MIT OpenCourseWare
- Теги
- source@https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-013-electromagnetics-and-applications-spring-2009
- Теорема Стокса
электромагнетизм — Интегральная и дифференциальная формы уравнений Максвелла
Интегральная и дифференциальная версии эквивалентны, поэтому похоже, что ваш текст просто не знает, как использовать дифференциальную версию так же широко, как ваш текст знает, как использовать интегральную версию.
Например, вам не нужно иметь частные производные для определения дивергенции и/или завихрения, но если у вас есть частные производные, то есть простые формулы для дивергенции и завихрения в этой ситуации вы можете использовать к этим формулам в качестве определения, но они не являются надлежащим общим определением.
Эти две формы действительно эквивалентны, и они эквивалентны, потому что на самом деле не говорят ничего другого. Понимание интегральных форм состоит в том, что они выполняются для каждой замкнутой/открытой поверхности в любой ограниченной области. Понимание дифференциальной формы состоит в том, что они выполняются в любой ограниченной области.
Похоже, ваш текст знает, как настроить интегральные формы в довольно общем виде. Дифференциальные формы можно настроить таким же общим образом, поскольку существуют очень общие способы определения дивергенции и завитка. Один из способов — взять теорему о дивергенции и теорему о роторе в качестве определений операторов (вместо того, чтобы допускать частные производные, затем составлять случайные комбинации, а затем составлять теорему). Например
Например
$$\vec{\nabla}\cdot\vec{A}@(x,y,z)=\lim_{DiameterV\стрелка вправо 0, V\стрелка вправо\{(x,y,z)\}}\ frac{\iint_{\partial V}\шляпа{n}\cdot\vec{A}dS}{\iiint_VdV}$$
и
$$\шляпа{S}\cdot\left(\vec{\ nabla}\times\vec{A}@(x,y,z)\right)=\lim_{Диаметр S\стрелка вправо 0, S\стрелка вправо\{(x,y,z)\}}\frac{\int_ {\partial S}\vec{A}\cdot d\vec{l}}{\iint_SdS}$$
не требуют частных производных, только поля должны быть достаточно хорошими, чтобы иметь пределы, которые допускают расхождение и теоремы о завитках, ни больше, ни меньше. Но этот уровень общности основан на предположении, что ваша интегральная версия использует интеграцию Римана. Это самый простой вариант интеграции (но не самый общий), и я хочу, чтобы вы увидели, как нам не нужно произвольно делать один вариант более общим, чем другой. 93(\vec{r}-\vec{r}_0)dxdydz=f(\vec{r}_0)$. И это всего лишь одна из многих таких карт, называемых распределениями, которые передают тестовые функции числам красивым (линейным и непрерывным) способом. Поэтому, если мы ожидаем, что производные дадут нам распределения, то мы должны определить их так, чтобы они это делали.
Поэтому, если мы ожидаем, что производные дадут нам распределения, то мы должны определить их так, чтобы они это делали.
Сначала отметим, что любая хорошая функция $g$ является распределением в том смысле, что она отправляет тестовую функцию $f$ на число $\iiint fg dxdydz$, обозначим это через $G:f\mapsto\iiint fg dxdydz =G(f)$, а затем обратите внимание, что если функция $g$ имеет частную производную $\partial g$, которая является хорошей функцией, то $\iiint f\partial g dxdydz$ = $-\iiint g\partial f dxdydz $. Это приводит к обобщению частных производных. Для любого распределения $G$, которое отправляет тестовые функции $f$ в $G(f)$, мы можем определить его производную как распределение, которое отправляет $f$ в $-G(\partial f)$. Для любой хорошей функции это определение согласуется с исходным определением производных в том смысле, что они действуют одинаково под интегралами. Но сейчас у любого дистрибутива есть производная.
Но даже при таком обобщении дивергенция может быть определена более широко.



 Формулируются общие теоремы и принципы в теории электромагнитного поля. Изучаются свойства электромагнитных волн, в частности быстрых и медленных волн в свободном пространстве, а также при возбуждении цилиндра, шара, клина и замедляющих структур. Изучается возбуждение волн в волноводах а колебаний в резонаторах. Кратко рассматриваются некоторые приближенные методы решений граничных задач электродинамики. Решение ряда задач доводится до численных результатов.
Формулируются общие теоремы и принципы в теории электромагнитного поля. Изучаются свойства электромагнитных волн, в частности быстрых и медленных волн в свободном пространстве, а также при возбуждении цилиндра, шара, клина и замедляющих структур. Изучается возбуждение волн в волноводах а колебаний в резонаторах. Кратко рассматриваются некоторые приближенные методы решений граничных задач электродинамики. Решение ряда задач доводится до численных результатов.
 Стаелин
Стаелин