Основные правила и свойства умножения вектора на число и их применение на стандартных заданиях

При обучении математике и физике в старших классах средней школы, а также в высших учебных заведениях постоянно приходится сталкиваться с понятием вектора. Учащиеся и студенты обязаны уметь проводить с векторами простейшие арифметические действия.

В статье будет показано, как умножать их на постоянные числа.

Основные понятия и определения

Чтобы в дальнейшем упростить работу со статьёй, введём некоторые формулировки и договорённости:

1. Постоянная — любое обычное число, которое может принимать определённые фиксированные значения, быть положительным, отрицательным или нулевым. Обозначать будем латинской буквой С (от греческого слова constanta, то есть постоянная).
2. Вектор — участок прямой, ограниченный двумя точками и имеющий заданное направление. Обозначать будем как (АВ). Причём точка, А является его началом, В — концом. Направление будем считать от точки, А к точке В. Допустима замена на (CD).
3. Вектора называются параллельными (коллинеарными), если они лежат на коллинеарных прямых или на одной прямой.
4. Нулевым вектором называется такой, у которого конец и начало совпадают. Называется нуль-вектор и обозначается (0).
5. Координатами (АВ) называются числа, равные его протяжённости относительно каждой из оси координат в Декартовой системе. Они находятся вычитанием из координат конца вектора координат его начала. Знак минус перед этим числом означает, что вектор направлен против направления данной оси.
6. Модулем (АВ) называется длина отрезка АВ.
7. Квадратный корень из числа или выражения условимся обозначать латинским буквосочетанием SQRT.
8. (АВ) с координатами (x, y, z) будем обозначать как (АВ) (x, y, z).

Это интересно: Как найти разность чисел в математике?

Правила умножения вектора на число

Рассмотрим, как умножить вектор на число:

1. Прежде всего отметим, что при умножении на отрицательную постоянную меняется направление на противоположное.
2. Если constanta больше -1, но меньше 1, то модуль (АВ) уменьшится. Проще говоря — отрезок станет короче.
3. Если постоянная равна нулю, С=0, то результатом вычислений окажется (0).
4. Для умножения (АВ) (x, y, z) на некую постоянную, нужно найти произведение каждой из координат с этой постоянной. Получится (А1В1) (С*x, С*y, С*z).

Интересно знать: Модуль числа в математике.

Алгебраический и геометрический смысл действия

Любое математическое действие имеет некий смысл, причём в разных науках он различается. Рассмотрим, что нам даёт этот вид умножения:

1. Геометрический смысл: (АВ)*С — это вектор, коллинеарный данному, модуль которого отличается в С раз от исходного, направление может совпадать или меняться на противоположное в зависимости от знака постоянной.
2. Алгебраический смысл: (АВ) (x, y, z)*С — это новый (А1В1) с координатами равными (С*x, С*y, С*z).
3. Физический смысл: уменьшение или увеличение в С раз силы действующей на тело или материальную точку.

Это интересно: как разложить на множители квадратный трехчлен?

Формулы умножения

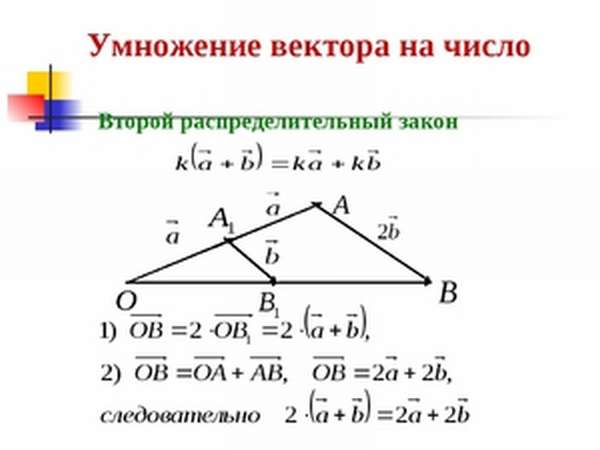При умножении проще всего использовать заранее заученные на память формулы, которые вполне можно применять по шаблону, выполняя действия буквально на полном автомате:

• С*(АВ) (x, y, z) = (А1В1) (С*x, С*y, С*z).
• 0*(АВ) = (0).

Для начала возьмём физическую задачу воздействия силы на материальную точку. Пусть на неё действует сила, описываемая (АВ) (57,63,28). Как изменится эта сила по координатам при её десятикратном увеличении?

Прежде всего следует отметить, что направление воздействия силы не изменится, а сама сила возрастёт десятикратно. При раскладке по координатам получим следующее:

10*(АВ) (57,63,28) = (А1В1) (10*57,10*63,10*28) = (А1В1) (570,630,280).

Вторую задачу возьмём аналогичную: как изменится сила, действующая на материальное тело, описываемая (АВ) (46,59,-43) при её увеличении в -0,5 раза.

Прежде всего заметим, что знак у постоянной отрицательный, следовательно, направление самой силы изменится на противоположное. Воспользуемся пунктом 2 вышеизложенных правил умножения, тогда сразу станет понятно, что численное выражение силы уменьшится вдвое. Проведём вычисления по шаблону:

-0,5*(АВ) (46,59,-43) = (А1В1) (-0,5*46,-0,5*59,-0,5*(-43)) = (А1В1) (-23,-29,5,21,5).

Следует заметить, что приведённые выше задачи решались для векторов, размещённых в пространстве и имеющих три координаты. В случае плоскостного размещения количество координат уменьшается до двух, а в случае линейного — до одной. Рассмотрим математические примеры для этих случаев:

• 33*(CD) (11,10) = (C1D1) (33*11,33*10) = (C1D1) (363,330).
• -0,2*(АВ) (-0,3,25) = (А1В1) (-0,2*(-0,3), -0,2*25) = (А1В1) (0,06, -5).
• 67*(CD) (2) = (C1D1) (67*2) = (C1D1) (134).
• 0*(АВ) (65,-87) = (0).

Возможные действия с векторами

Не следует думать, что все возможные действия ограничиваются умножениям на число. Прежде всего можно определить длину (АВ) — модуль. Он будет равняться SQRT из суммы квадратов координат. Поясним это на примере:

• модуль (АВ) (3,4) = SQRT (3 2+ 4 2) = SQRT (9 + 16) = SQRT25 = 5.

Кроме этого, из курса школьной математики и физики известно, что вектора можно слагать один с другим и вычитать друг из друга. При этом проводится сложение и вычитание соответствующих координат.

Наконец, высшая математика вводит понятия числового (скалярного) и векторного умножения двух векторов. В первом случае получится некое число, во втором — третий вектор, направленный перпендикулярно плоскости, содержащей два первых.

В данной статье приведены основы умножения вектора на число. Исходя из её материала, можно утверждать, что действие это простое и доступное любому школьнику с удовлетворительной успеваемостью. Рекомендуется изучить формулы и в своих вычислениях действовать по изложенному в тексте шаблону.

Умножение векторов на число — методическая рекомендация. Геометрия, 9 класс.

1.	Умножение вектора на число	2 вид — интерпретация	среднее	1 Б.	Умножение вектора на число.
2.	Понятие об умножении вектора на число и коллинеарности векторов	2 вид — интерпретация	среднее	4 Б.	Укрепление знаний об умножении вектора на число и коллинеарности векторов.
3.	Сонаправленные и противоположно направленные векторы	2 вид — интерпретация	среднее	6 Б.	Понимает, как умножать вектор на число, чтобы получились сонаправленные или противоположно направленные векторы.
4.	Соотношение отрезков	3 вид — анализ	среднее	3 Б.	Использует соотношение отрезков для определения коэффициента при умножении векторов.
5.	Умножение и разложение векторов	3 вид — анализ	среднее	4 Б.	Разлагает вектор на данные векторы, использует знания о умножении вектора на число.
6.	Умножение и вычитание векторов	3 вид — анализ	сложное	3 Б.	Проверка знаний о вычитании и умножении векторов, выражение вектора через данные векторы.

Сложение и вычитание векторов. Умножение вектора на число. Геометрия, 10 класс: уроки, тесты, задания.

1.	Выражение, содержащее векторы Сложность: лёгкое	2
2.	Сумма векторов Сложность: среднее	3
3.	Сумма и разность векторов Сложность: лёгкое	2
4.	Сложение и вычитание векторов Сложность: лёгкое	2
5.	Арифметические операции с векторами Сложность: лёгкое	2
6.	Выражение вектора суммы Сложность: среднее	3
7.	Выражение вектора разности Сложность: среднее	3
8.	Выражение с векторами Сложность: среднее	5
9.	Сложение и вычитание векторов Сложность: среднее	4
10.	Сумма нескольких векторов Сложность: среднее	3
11.	Умножение вектора на число Сложность: среднее	4
12.	Сложение и умножение на число Сложность: сложное	10
13.	Арифметические действия с векторами, длина вектора Сложность: сложное	8
14.	Уравнение с векторами Сложность: сложное	8

Умножение вектора на число — Мегаобучалка

Свойства

Ортогональность

Векторы являются ортогональными тогда и только тогда, когда их скалярное произведение равно нулю.

Часто вместо этого термина употребляют термин «перпендикулярность», однако следует учитывать, что нулевой вектор ортогонален любому вектору, но понятие перпендикулярности для него не определено, поскольку не определён угол между нулевым и другим вектором.

Пример:
Даны два вектора и , с координатами в ортонормированном базисе. Эти векторы будут ортогональными, если выражение x₁x₂ + y₁y₂ = 0.

Коллинеарность

Два не нулевых вектора называются коллиниарными, если , где

Векторы являются коллинеарными тогда и только тогда, когда их векторное произведение равно нулю.

Часто вместо этого термина употребляют термин «параллельность», однако следует учитывать, что нулевой вектор коллинеарен любому вектору, но понятие параллельности для него не определено, поскольку не определён угол между нулевым и другим вектором.

Сложение геометрических векторов

 

Два вектора u, v и вектор их суммы

Сложение двух свободных векторов можно осуществлять как по правилу параллелограмма, так и по правилу треугольника.

Правило треугольника. Для сложения двух векторов и по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора.

Правило параллелограмма. Для сложения двух векторов и по правилу параллелограмма оба эти вектора переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.

А модуль (длину) вектора суммы определяют по теореме косинусов где — угол между векторами, когда начало одного совпадает с концом другого. Так же используется формула теперь — угол между векторами выходящими из одной точки.

 

Умножение вектора на число

Произведением вектора и числа λ называется вектор, обозначаемый (или ), модуль которого равен , а направление совпадает с направлением вектора , если , и противоположно ему, если . Если же , или вектор нулевой, тогда и только тогда произведение — нулевой вектор.

• Обычно принято в записи произведения числа и вектора число записывать слева, но в принципе допустим и обратный порядок, хотя все же обычное соглашение состоит в том, чтобы его избегать, если нет прямой необходимости. Так или иначе, .

Из определения произведения вектора на число легко вывести следующие свойства: