Онлайн калькулятор умножения матриц

Данный калькулятор дает детальное решение с объяснением умножения двух матриц. Умножить две матрицы возможно только в том случае, если количество столбцов первой матрицы, равно количеству строк второй

Матрица размерности m × n – это таблица чисел у которой m строк и n столбцов. Элементы матрицы обозначаются как a_ij, где i – номер строки, j – номер столбца.
Чтобы записать дробь, воспользуйтесь знаком “ / ” например 3/5 или -3/5

Примеры умножения матриц

Умножить две матрицы размерности 3 × 2 и 2 × 3

C = A × B =

×

=

4.8 49.4 -36 15 7 0 -8.1 19.8 -18

---

Решение

Даны две матрицы

A =		где,	a11 = 4 a12 = 1 a21 = 0 a22 = 5 a31 = 2 a32 = -3
B =		где,	b11 = 0.45 b12 = 12 b13 = -9 b21 = 3 b22 = 1.4 b23 = 0

---

Умножить две матрица можно только, если число столбцов матрицы А равно числу строк матрицы В

При умножении матрицы А размерности l × m на матрицу В размерности m × n получаем матрицу С размерности l × n

C =

×

=

c11 c12 c13 c21 c22 c23 c31 c32 c33

---

Элемент матрицы с индексом C_ij находится по формуле

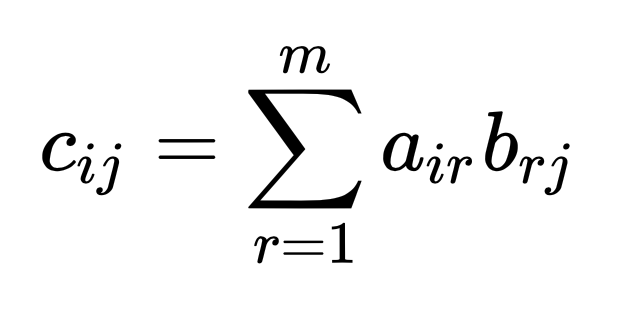
c₁₁ = a₁₁ ⋅ b₁₁ + a₁₂ ⋅ b₂₁ = 4 ⋅ 0.45 + 1 ⋅ 3 = 4.8

c₁₂ = a₁₁ ⋅ b₁₂ + a₁₂ ⋅ b₂₂ = 4 ⋅ 12 + 1 ⋅ 1.4 = 49.4

c₁₃ = a₁₁ ⋅ b₁₃ + a₁₂ ⋅ b₂₃ = 4 ⋅ (-9) + 1 ⋅ 0 = -36

c₂₁ = a₂₁ ⋅ b₁₁ + a₂₂ ⋅ b₂₁ = 0 ⋅ 0.45 + 5 ⋅ 3 = 15

c₂₂ = a₂₁ ⋅ b₁₂ + a₂₂ ⋅ b₂₂ = 0 ⋅ 12 + 5 ⋅ 1.4 = 7

c₂₃ = a₂₁ ⋅ b₁₃ + a₂₂ ⋅ b₂₃ = 0 ⋅ (-9) + 5 ⋅ 0 = 0

c₃₁ = a₃₁ ⋅ b₁₁ + a₃₂ ⋅ b₂₁ = 2 ⋅ 0.45 + (-3) ⋅ 3 = -8.1

c₃₂ = a₃₁ ⋅ b₁₂ + a₃₂ ⋅ b₂₂ = 2 ⋅ 12 + (-3) ⋅ 1.4 = 19.8

c₃₃ = a₃₁ ⋅ b₁₃ + a₃₂ ⋅ b₂₃ = 2 ⋅ (-9) + (-3) ⋅ 0 = -18

C =	4.8 49.4 -36 15 7 0 -8.1 19.8 -18

Перейти в калькулятор Умножить две матрицы размерности 2 × 2 и 2 × 4

---

Решение

Даны две матрицы

A =		где,	a11 = 7 a12 = 1 a21 = 0 a22 = 3
B =	b11 b12 b13 b14 b21 b22 b23 b24	где,	b11 = -5 b12 = 6 b13 = 2 b14 = 9 b21 = 12 b22 = 37 b23 = 1 b24 = 0

---

Умножить две матрица можно только, если число столбцов матрицы А равно числу строк матрицы В

При умножении матрицы А размерности l × m на матрицу В размерности m × n получаем матрицу С размерности l × n

C =

×

b11 b12 b13 b14 b21 b22 b23 b24

=

c11 c12 c13 c14 c21 c22 c23 c24

---

Элемент матрицы с индексом C_ij находится по формуле

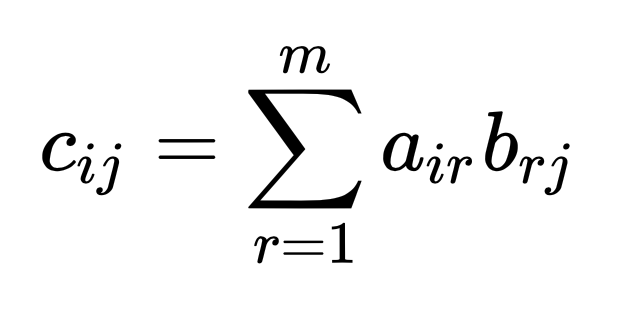
c₁₁ = a₁₁ ⋅ b₁₁ + a₁₂ ⋅ b₂₁ = 7 ⋅ (-5) + 1 ⋅ 12 = -23

c₁₂ = a₁₁ ⋅ b₁₂ + a₁₂ ⋅ b₂₂ = 7 ⋅ 6 + 1 ⋅ 37 = 79

c₁₃ = a₁₁ ⋅ b₁₃ + a₁₂ ⋅ b₂₃ = 7 ⋅ 2 + 1 ⋅ 1 = 15

c₁₄ = a₁₁ ⋅ b₁₄ + a₁₂ ⋅ b₂₄ = 7 ⋅ 9 + 1 ⋅ 0 = 63

c₂₁ = a₂₁ ⋅ b₁₁ + a₂₂ ⋅ b₂₁ = 0 ⋅ (-5) + 3 ⋅ 12 = 36

c₂₂ = a₂₁ ⋅ b₁₂ + a₂₂ ⋅ b₂₂ = 0 ⋅ 6 + 3 ⋅ 37 = 111

c₂₃ = a₂₁ ⋅ b₁₃ + a₂₂ ⋅ b₂₃ = 0 ⋅ 2 + 3 ⋅ 1 = 3

c₂₄ = a₂₁ ⋅ b₁₄ + a₂₂ ⋅ b₂₄ = 0 ⋅ 9 + 3 ⋅ 0 = 0

Перейти в калькулятор Умножить две матрицы размерности 1 × 3 и 3 × 2

---

Решение

Даны две матрицы

A =		где,	a11 = 2 a12 = -7 a13 = 0
B =		где,	b11 = 3 b12 = 6 b21 = 4 b22 = 1 b31 = 0 b32 = 8

---

Умножить две матрица можно только, если число столбцов матрицы А равно числу строк матрицы В

При умножении матрицы А размерности l × m на матрицу В размерности m × n получаем матрицу С размерности l × n

---

Элемент матрицы с индексом C_ij находится по формуле

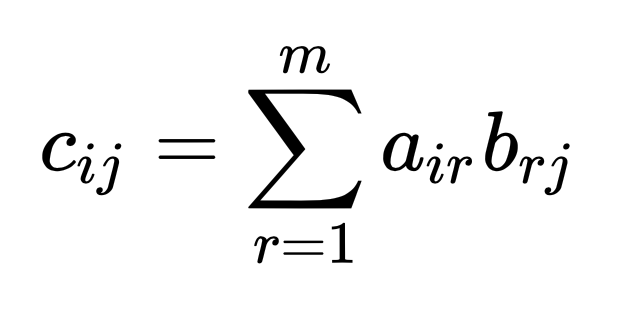
c₁₁ = a₁₁ ⋅ b₁₁ + a₁₂ ⋅ b₂₁ + a₁₃ ⋅ b₃₁ = 2 ⋅ 3 + (-7) ⋅ 4 + 0 ⋅ 0 = -22

c

12 = a₁₁ ⋅ b₁₂ + a₁₂ ⋅ b₂₂ + a₁₃ ⋅ b₃₂ = 2 ⋅ 6 + (-7) ⋅ 1 + 0 ⋅ 8 = 5

Перейти в калькулятор

Умножение вектора на число.

Геометрическая интерпретация.

Произведение ненулевого вектора на число — это вектор, коллинеарный данному (сонаправленный данному, если число положительное, имеющий противоположное направление, если число отрицательное), а его модуль равен модулю данного вектора, умноженному на модуль числа.

Алгебраическая интерпретация. Произведение ненулевого вектора на число — это вектор, координаты которого равны соответствующим координатам данного вектора, умноженным на число.

Формулы умножения вектора на число

Формула умножения вектора на число для плоских задач

В случае плоской задачи произведение вектора a = {a_x ; a_y} и числа k можно найти воспользовавшись следующей формулой:

k · a = {k · a_x; k · a_y}

Формула умножения вектора на число для пространственных задач

В случае пространственной задачи произведение вектора a = {a_x ; a_y ; a_z} и числа k можно найти воспользовавшись следующей формулой:

k · a = {k · a_x ; k · a_y ; k · a_z}

Формула умножения n -мерного вектора

В случае n-мерного пространства произведение вектора a = {a₁ ; a₂; … ; a_n} и числа k можно найти воспользовавшись следующей формулой:

k · a = {k · a

1; k · a₂; … ; k · a_n}

Свойства вектора умноженного на число

Если вектор b равен произведению ненулевого числа k и ненулевого вектора a, то есть b = k · a, тогда:

• b || a — вектора b и a параллельны

• a↑↑b, если k > 0 — вектора b и a сонаправленные, если число k > 0

• a↑↓b, если k < 0 — вектора b и a противоположно направленные, если число k < 0

• |b| = |k| · |a| — модуль вектора b равен модулю вектора a умноженному на модуль числа k

Примеры задач на умножение вектора и числа

Пример умножения вектора на число для плоских задачи

Пример 1. Найти произведение вектора a = {1; 2} на 3.

Решение: 3 · a = {3 · 1; 3 · 2} = {3; 6}.

Пример умножения вектора на число для пространственных задачи

Пример 2. Найти произведение вектора a = {1; 2; -5} на -2.

Решение: (-2) · a = {(-2) · 1; (-2) · 2; (-2) · (-5)} = {-2; -4; 10}.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Умножение комплексного вектора на матрицу

Результат умножения вектора-строки на матрицу с*A

Результат умножения матрицы на вектор-столбец A*b

Каждый вектор можно рассматривать как одностолбцовую или однострочную матрицу. Одностолбцовую матрицу будем называть вектор-столбцом, а однострочную матрицу — вектор-строкой.

Если A-матрица размера m*n, то вектор столбец b имеет размер n, а вектор строка b имеет размер m.

Таким образом, что бы умножить матрицу на вектор, надо рассматривать вектор как вектор-столбец. При умножении вектора на матрицу, его нужно рассматривать как вектор -строку.

Пример.

Умножить матрицу

 

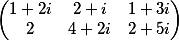
на комплексный вектор

 

Получаем результат

Результат умножения матрицы на вектор A*b

Результат умножения вектора на матрицу b*A

 

Как видите при неизменной размерности вектора, у нас могут существовать два решения.

Хотелось бы обратить Ваше внимание на то что матрица в первом и втором варианте, несмотря на одинаковые значения, совершенно разные (имеют различную размерность)

 

В первом случае вектор считается как столбец и тогда необходимо  умножать матрицу на вектор, а во втором случае у нас вектор-строка и тогда у нас произведение вектора на матрицу.

 

 

Свойства умножения матрицы на вектор

 — матрица   — вектор столбец   — вектор-строка  — произвольное число

1. Произведение матрицы на сумму векторов-столбцов равна сумме произведений матрицы на каждый из векторов

2. Произведение суммы векторов-строк на матрицу  равна сумме произведений векторов на матрицу

3. Общий множитель вектора  можно вынести за пределы произведения матрицы на вектор/вектора на матрицу

4.Произведение вектора-строки на произведение матрицы и вектора столбца, равноценно произведению произведения вектора-строки на матрицу и вектора-столбца.

 

Удачных расчетов!!

 

• Умножение матриц с комплексными значениями онлайн >>

Сложение и вычитание векторов. Онлайн калькулятор.

Как сложить или вычесть два вектора плоскости и пространства

Пример №1
Найдем сумму векторов плоскости. Координаты обоих векторов заданны точками.
Координаты точки А вектора AB: (5 ; 9)
Координаты точки B вектора AB: (-2 ; 11)
Координаты точки C вектора CD: (0 ; 12)
Координаты точки D вектора CD: (-3 ; 1)

Решение:

Для того, чтобы сложить два вектора необходимо сложить их координаты. Результатом сложения векторов AB и CD будет вектор c

Вычислим координаты первого вектора по двум точкам A и B:

AB = {x_B — x_A  ; y_B — y_A} = {-2 — 5 ; 11 — 9} = {-7 ; 2}

Вычислим координаты второго вектора по двум точкам C и D:

CD = {x_D — x_C  ; y_D — y_C} = {-3 — 0 ; 1 — 12} = {-3 ; -11}

c = AB + CD = {AB_x + CD_x ; AB_y + CD_y} = {-7 + (-3) ; 2 + (-11)} = {-10 ; -9}

Пример №2
Найдем разность векторов плоскости.
Координаты вектора a: (5 ; 9)
Координаты вектора b: (-1 ; 7)

Решение:

Для того, чтобы вычесть два вектора необходимо вычесть их координаты. Результатом вычитания векторов a и b будет вектор c
c = a — b = {a_x — b_x ; a_y — b_y} = {5 — (-1) ; 9 — 7} = {6 ; 2}

Пример №3
Найдем разность векторов пространства. Координаты обоих векторов заданны точками.
Координаты точки А вектора AB: (7; 0.2 ; 69)
Координаты точки B вектора AB: (-1 ; 0 ; 2/8)
Координаты точки C вектора CD: (-4 ; -6 ; 2)
Координаты точки D вектора CD: (3 ; 0 ; 9)

Решение:

Для того, чтобы вычесть два вектора необходимо вычесть их координаты. Результатом вычитания векторов AB и CD будет вектор c

Вычислим координаты первого вектора по двум точкам A и B:

AB = {x_B — x_A  ; y_B — y_A; z_B — z_A} = {-1 — 7 ; 0 — 0.2 ; 2/8 — 69} = {-8 ; -1/5 ; -275/4}

Вычислим координаты второго вектора по двум точкам C и D:

CD = {x_D — x_C  ; y_D — y_C; z_D — z_C} = {3 — (-4) ; 0 — (-6) ; 9 — 2} = {7 ; 6 ; 7}

c = AB — CD = {AB_x — CD_x ; AB_y — CD_y ; AB_z — CD_z} = {-8 — 7 ; -1/5 — 6 ; -275/4 — 7} = {-15 ; -31/5 ; -303/4}= {-15 ; -6.2 ; -75.75}

Пример №4
Найдем сумму векторов пространства.
Координаты вектора a: (5 ; 1 ; 7)
Координаты вектора b: (2 ; 4 ; 6)

Решение:

Для того, чтобы сложить два вектора необходимо сложить их координаты. Результатом сложения векторов a и b будет вектор c
c = a + b = {a_x + b_x ; a_y + b_y ; a_z + b_z} = {5 + 2 ; 1 + 4 ; 7 + 6} = {7 ; 5 ; 13}