Умножение векторов

Умножение вектора на вектор бывает двух типов: скалярное и векторное. В результате скалярного умножения двух векторов получаем число (скаляр). В результате векторного произведения двух векторов получаем вектор. Скалярным произведением двух ненулевых векторов и называется число, равное произведению длин этих векторов на косинус угла между ними: , где .

Свойства скалярного произведения во многом сходны со свойствами произведения действительных чисел.

Векторным произведением двух векторов и называется вектор , который:

1. имеет модуль, численно равный площади параллелограмма, построенного на векторах и : ;

2. перпендикулярен к плоскости этого параллелограмма;

3. направлен в такую сторону, с которой кратчайший поворот от к рассматривается совершающимся против часовой стрелки (такое расположение векторов , и называется правой тройкой векторов).

Отличительная особенность векторного произведения состоит в том, что для него переместительное свойство (коммутативность) не имеет места. От перестановки векторов – сомножителей векторное произведение изменяет знак на противоположный: .

Три вектора могут быть перемножены несколькими способами. Чаще всего рассматривают смешанное произведение двух векторов векторно и на третий скалярно.В результате получают число.

Смешанное произведение трех векторов , и , которое обозначается или , есть скаляр, абсолютная величина которого равна обьему параллелепипеда, построенного на векторах , и , как на ребрах.

Указанные произведения векторов и их свойства достаточно просто выражаются через их прямоугольные координаты, т.е. координаты векторов в базисе , по сравнению с аналогичными выражениями в произвольном базисе , которых мы не приводим.

Пусть заданы два вектора и .

Скалярное произведение двух ненулевых векторов равно сумме произведений соответствующих координат этих векторов:

.

Угол между векторами вычисляется по формуле

,

или в координатной форме .

Проекция вектора на ось вектора находится из соотношения:

,

или в координатной форме .

Если учесть, что — орт вектора, то .

Условием перпендикулярности ненулевых векторов и является равенство нулю их скалярного произведения:

.

Векторное произведение ненулевых векторов выражается через координаты данных векторов и следующим образом:

.

Равенство нулю векторного произведения двух ненулевых векторов является условием их коллинеарности, т.е.  .

Скаляр , представляющий смешанное произведение трех векторов, равняется определителю третьего порядка, составленному из координат этих трех векторов:

.

Равенство нулю смешанного произведения трех ненулевых векторов является условием их компланарности: .

Координаты вектора зависят от выбора базиса. Выбор базиса ничем не ограничен, и принципиальное значение имеет задача о нахождении координат вектора в одном базисе по его координатам в другом базисе. Выясним, как устанавливается связь между координатами одного и того же вектора в различных базисах.

Пусть в пространстве имеются два базиса: старый и новый . Каждый из векторов (i =1,2,3) нового базиса можно выразить в виде линейной комбинации векторов старого базиса:

.

Матрица (i,k=1,2,3) называется матрицей перехода от старого базиса к новому. Базисные векторы (i =1,2,3) линейно независимы, поэтому матрица неособенная.

Обратный переход от нового базиса к старому базису осуществляется с помощью обратной матрицы .

Найдем зависимость между координатами некоторого вектора в разных базисах. Пусть этот вектор имеет координаты относительно старого базиса и координаты относительно нового базиса, т.е. и

Подставив значения из предыдущей системы в первое равенство

для вектора и учитывая второе равенство, получим систему уравнений:

Как нетрудно заметить, матрицей перехода от новых к старым координатам будет транспонированная матрица . В матричном виде взаимосвязь между старыми координатами и новыми выражается следующими равенствами:

и .

Пример. В базисе заданы векторы и вектор . Показать, что векторы (i =1,2,3) образуют базис в трехмерном пространстве и найти координаты вектора в этом базисе.

Решение. Векторы образуют базис, если они линейно независимы. Составим векторное равенство или

Задача сводится к решению системы:

Определитель системы не равен нулю.

Следовательно, однородная система имеет только нулевое решение , значит векторы линейно независимы и образуют базис.

Связь между старым базисом и новым выражается системой уравнений:

Матрица перехода от старого базиса к новому имеет вид

Вычисляем . Она имеет вид

Находим транспонированную матрицу

Координаты в новом базисе находим из равенства

Новые координаты вектора в базисе есть (9/6, 5/6, 1/6) и вектор может быть представлен в виде:

Геометрия Умножение вектора на число

Материалы к уроку

Конспект урока

5. Умножение вектора на число

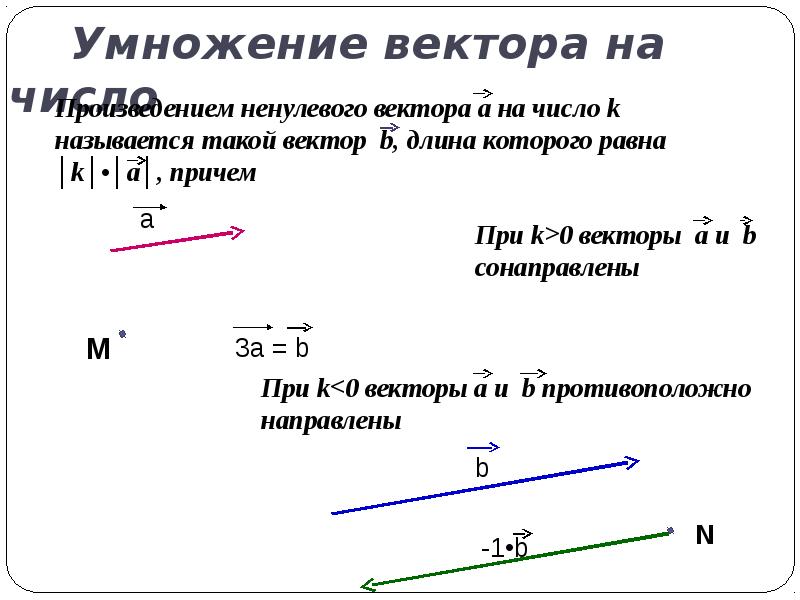
Произведением ненулевого вектора а на число k называется такой вектор  b, длина которого равна модуль |k| умноженный на модуль|а|, причем векторы а и b сонаправлены, если  k положительно и  противоположно направлены, если k отрицательно. Произведение вектора а на число k обозначается так: ka.	Текст Умножение вектора на число   Рисунок векторов
Для любого числа k и любого вектора а векторы а и ka коллинеарны. Произведением нулевого вектора на любое число считается нулевой вектор. Произведение любого вектора на число нуль есть нулевой вектор.	Текст Умножение вектора на число
Рассмотрим основные свойства умножения вектора на число. Для любых векторов а,b и любых чисел k и l справедливы равенства: Первое. Произведение k и l, умноженное на вектор а, равно произведению k на вектор lа. Это свойство известно как сочетательный закон. На рисунке, на примере показано это свойство.	Текст Свойства умножения вектора на число Сочетательный закон   Рисунок векторов   Текст
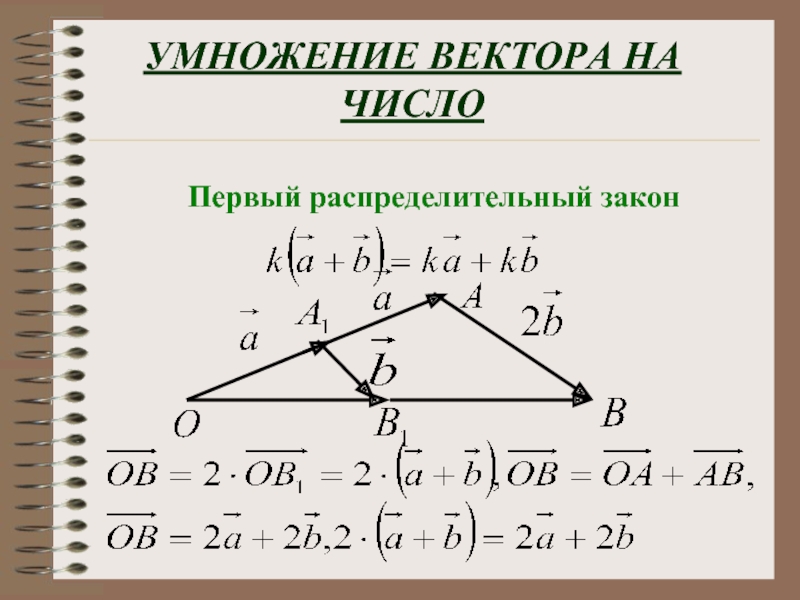
Второе свойство, первый распределительный закон. Произведение числа k на сумму векторов а и b  равно сумме произведений этого числа на векторы а и b. На рисунке, на примере показано это свойство.	Текст Свойства умножения вектора на число Первый распределительный закон
Третье свойство, второй распределительный закон. Произведение суммы чисел k и  l на вектор равно сумме произведений чисел k и l на вектор а. На рисунке, на примере показано это свойство.	Текст Свойства умножения вектора на число Второй распределительный закон
Стоит отметить, что произведение числа -1 на любой вектор дает вектор противоположный данному. Согласно определению произведения вектора на число, их длины равны, а направления противоположны. При условии, что вектор а ненулевой.	Текст
Для векторов в пространстве, как и в планиметрии, выполняется следующее условие: Если векторы a и b коллинеарны (то есть лежат на одной прямой или на параллельных прямых) и вектор а ненулевой, то существует число k такое что вектор b  равен произведению числа k на вектор а.
Решим задачу №347 (а) Необходимо упростить выражение.
Решение. Первый распределительный закон позволяет нам раскрыть скобки. А переместительное свойство сложения векторов – привести подобные.	.

Остались вопросы по теме? Наши педагоги готовы помочь!

• Подготовим к ЕГЭ, ОГЭ и другим экзаменам

• Найдём слабые места по предмету и разберём ошибки

• Повысим успеваемость по школьным предметам

• Поможем подготовиться к поступлению в любой ВУЗ

Выбрать педагогаОставить заявку на подбор

Умножение векторов — математика GCSE

Введение

Что такое векторное умножение?

Как умножить вектор

на

Рабочий лист векторного умножения

Распространенные заблуждения

Упражнения на умножение векторов

Умножение векторов GCSE вопросы

Контрольный список обучения

Следующие уроки

Вы знали?

Все еще застряли?

Индивидуальные занятия по математике, созданные для успеха KS4

Теперь доступны еженедельные онлайн-уроки повторения математики GCSE

Узнать больше

Введение

Что такое векторное умножение?

Как умножить вектор

на

Рабочий лист векторного умножения

Распространенные заблуждения

Упражнения на умножение векторов

Умножение векторов GCSE вопросы

Контрольный список обучения

Следующие уроки

Вы знали?

Все еще застряли?

Здесь мы узнаем о векторном умножении, в том числе на скалярное умножение вектора (умножение вектора на число).

Существуют также векторные рабочие листы на основе экзаменационных вопросов Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.

Что такое векторное умножение?

Умножение векторов — это умножение вектора на число. Число является скаляром и имеет только величину, тогда как вектор имеет величину и направление.

Для этого умножаем каждую из составляющих на скалярное число.

Вот пример:

Вектор a равно 

\[\textbf{a}= \left(\begin{массив}{1} 2\\ 1\\ \end{array}\right)\]

Таким образом, умножение вектора a на 3 будет

\[3\textbf{a}= 3\влево(\начать{массив}{1} 2\\ 1\\ \конец{массив}\справа) «=» \left(\begin{массив}{1} 3\раз2\\ 3\умножить на 1\\ \конец{массив}\справа) «=» \left(\begin{массив}{1} 6\\ 3\\ \end{array}\right)\]

Это работает, потому что умножение — это многократное сложение. Другим способом умножения вектора на на 3 будет 9. 0003

\[3\textbf{а}=\textbf{а}+\textbf{а}+\textbf{а}= \left(\begin{массив}{1} 2\\ 1\\ \конец{массив}\справа) +\влево(\начать{массив}{1} 2\\ 1\\ \конец{массив}\справа) +\влево(\начать{массив}{1} 2\\ 1\\ \конец{массив}\справа) =\влево(\начать{массив}{1} 6\\ 3\\ \end{array}\right)\]

Это видно на диаграмме. Вы можете видеть 3 лота компонента x и 3 лота компонента y.

Направление вектора при умножении на скалярное число такое же, как и у исходного вектора, но величина вектора (также называемая абсолютным значением вектора) изменилась.

Что такое векторное умножение?

Как умножить вектор

Чтобы умножить вектор на скаляр:

1. Умножьте компонент x на скаляр.
2. Умножьте компонент y на скаляр.
3. Запишите результирующий вектор.

Как умножить вектор

Рабочий лист векторов (включая умножение векторов)

Получите бесплатную таблицу умножения векторов, содержащую более 20 векторных вопросов и ответов. Включает рассуждения и прикладные вопросы.

СКАЧАТЬ БЕСПЛАТНО

Икс

Лист векторов (включает умножение векторов)

Получите бесплатный лист умножения векторов, содержащий более 20 вопросов и ответов по векторам. Включает рассуждения и прикладные вопросы.

СКАЧАТЬ БЕСПЛАТНО

Связанные уроки по векторам

Умножение векторов является частью нашей серии уроков для поддержки повторения на векторов . Возможно, вам будет полезно начать с урока по основным векторам, чтобы получить общее представление о том, чего ожидать, или воспользоваться пошаговыми руководствами, приведенными ниже, для получения более подробной информации по отдельным темам. Другие уроки этой серии включают:

• Векторы
• Величина вектора
• Вектор-столбец
• Векторное обозначение
• Добавление вектора
• Вычитание векторов
• Векторные проблемы

Примеры векторного умножения

Пример 1: векторное умножение

Вычисление:

\[2\left(\begin{array}{1} 4\\ 5\\ \end{массив}\right)\]

1. Умножьте компонент x на скаляр.

Умножить скалярное число на верхнее число

2\раз4=8

2 Умножьте компонент y на скаляр.

Умножить скалярное число на нижнее число

2\х5=10

3 Запишите результирующий вектор.

Запишите два ответа в виде вектор-столбца

\[2\left(\begin{array}{1} 4\\ 5\\ \конец{массив}\справа) «=» \left(\begin{массив}{1} 2\раз4\\ 2\раз5\\ \конец{массив}\справа) «=» \left(\begin{массив}{1} 8\\ 10\\ \end{array}\right)\]

Пример 2: векторное умножение

Вычисление:

\[4\left(\begin{array}{1} 8\\ 3\\ \end{массив}\right)\]

Умножьте компонент x на скаляр.

Умножить скалярное число на верхнее число

4\х8=32

Умножьте компонент y на скаляр.

Умножить скалярное число на нижнее число

4\times3=12

Запишите результирующий вектор.

Запишите два ответа в виде вектор-столбца

\[4\left(\begin{array}{1} 8\\ 3\\ \конец{массив}\справа) «=» \left(\begin{массив}{1} 4\раз8\\ 4\раз3\\ \конец{массив}\справа) «=» \left(\begin{массив}{1} 32\\ 12\\ \конец{массив}\справа)\]

Пример 3: векторное умножение, десятичный скаляр

Вычисление:

\[0,5\left(\begin{array}{1} 10\\ 8\\ \end{массив}\right)\]

Умножьте компонент x на скаляр.

Умножить скалярное число на наибольшее число

0,5\×10=5

Умножьте компонент y на скаляр.

Умножить скалярное число на нижнее число

0,5\х8=4

Запишите результирующий вектор.

Запишите два ответа в виде вектор-столбца

\[0,5\left(\begin{array}{1} 10\\ 8\\ \конец{массив}\справа) «=» \left(\begin{массив}{1} 0,5\х10\\ 0,5\х8\\ \конец{массив}\справа) «=» \left(\begin{массив}{1} 5\\ 4\\ \end{array}\right)\]

Пример 4: векторное умножение, дробный скаляр

Вычисление:

\[\frac{1}{3}\left(\begin{array}{1} -6\\ 9\\ \end{массив}\right)\]

Умножить 9Компонент 0066 x скаляром.

Умножить скалярное число на наибольшее число

\frac{1}{3}\times-6=-2

Умножьте компонент y на скаляр.

Умножить скалярное число на нижнее число

\frac{1}{3}\times9=3

Запишите результирующий вектор.

Запишите два ответа в виде вектор-столбца

\[\frac{1}{3}\left(\begin{array}{1} -6\\ 9\\ \конец{массив}\справа) «=» \left(\begin{массив}{1} \frac{1}{3}\times-6\\ \frac{1}{3}\times9\\ \конец{массив}\справа) «=» \left(\begin{массив}{1} -2\\ 3\\ \end{array}\right)\]

Пример 5: векторное умножение

Вычисление:

\[4\left(\begin{array}{1} -5\\ -2\\ \end{массив}\right)\]

Умножьте компонент x на скаляр.

Умножить скалярное число на наибольшее число

4\раз-5=-20

Умножьте компонент y на скаляр.

Умножить скалярное число на нижнее число

4\раз-2=-8

Запишите результирующий вектор.

Запишите два ответа в виде вектор-столбца

\[4\left(\begin{array}{1} -5\\ -2\\ \конец{массив}\справа) «=» \left(\begin{массив}{1} 4\раз-5\\ 4\раз-2\\ \конец{массив}\справа) «=» \left(\begin{массив}{1} -20\\ -8\\ \end{array}\right)\]

Пример 6: векторное умножение, отрицательный скаляр

Вычисление:

\[-3\left(\begin{array}{1} -2\\ 5\\ \конец{массив}\справа)\]

Умножить компонент x на скаляр.

Умножить скалярное число на наибольшее число

-3\раз-2=6

Умножьте компонент y на скаляр.

Умножить скалярное число на нижнее число

-3\times5=-15

Запишите результирующий вектор.

Запишите два ответа в виде вектор-столбца

\[-3\left(\begin{array}{1} -2\\ 5\\ \конец{массив}\справа) «=» \left(\begin{массив}{1} -3\раз-2\\ -3\раз5\\ \конец{массив}\справа) «=» \left(\begin{массив}{1} 6\\ -15\\ \конец{массив}\справа)\]

Распространенные заблуждения

• Убедитесь, что вы умножили оба компонента на скалярное число

Компоненты x и y необходимо умножить на скалярное число.

• Векторы-столбцы имеют только 2 числа в скобках

Векторы-столбцы имеют верхнее и нижнее число в скобках. Нет необходимости в каких-либо других знаках препинания, таких как запятые или точки с запятой. Нет необходимости в линии для разделения чисел.

Упражнение на умножение векторов

\begin{pmatrix} \; 5 \;\\ \; 7\; \end{pmatrix}

\begin{pmatrix} \; 6 \;\\ \; 4\; \end{pmatrix}

\begin{pmatrix} \; 12 \;\\ \; 6\; \end{pmatrix}

\begin{pmatrix} \; 6 \;\\ \; 12\; \end{pmatrix}

3\textbf{a}= 3\begin{pmatrix} \; 2 \;\\\; 4\; \end{pmatrix} = \begin{pmatrix} \; 3\умножить на 2\;\\\; 3\х4\; \end{pmatrix} = \begin{pmatrix} \; 6 \;\\\; 12\; \end{pmatrix}

\begin{pmatrix} \; 6 \;\\ \; 8\; \end{pmatrix}

\begin{pmatrix} \; 5 \;\\ \; 3 \; \end{pmatrix}

\begin{pmatrix} \; 5 \;\\ \; 15 \; \end{pmatrix}

\begin{pmatrix} \; 6 \;\\ \; 15 \; \end{pmatrix}

5\textbf{b}= 5\begin{pmatrix} \; 1 \;\\ \; 3 \; \end{pmatrix} = \begin{pmatrix} \; 5\умножить на 1\;\\\; 5\раз3\; \end{pmatrix} = \begin{pmatrix} \; 5 \;\\\; 15 \; \end{pmatrix}

\begin{pmatrix} \; 21 \;\\ \; 31\; \end{pmatrix}

\begin{pmatrix} \; 20. 1 \;\\ \; 30,1 \; \end{pmatrix}

\begin{pmatrix} \; 2 \;\\ \; 3 \; \end{pmatrix}

\begin{pmatrix} \; 20 \;\\ \; 3 \; \end{pmatrix}

0.1\textbf{c}= 0.1\begin{pmatrix} \; 20 \;\\ \; 30 \; \end{pmatrix} = \begin{pmatrix} \; 0,1\раз 20\;\\\; 0,1\х30\; \end{pmatrix} = \begin{pmatrix} \; 2 \;\\\; 3 \; \end{pmatrix}

\begin{pmatrix} \; -4 \;\\ \; 3 \; \end{pmatrix}

\begin{pmatrix} \; -4 \;\\ \; 6\; \end{pматрица}

\begin{pmatrix} \; -2 \;\\ \; 3 \; \end{pmatrix}

\begin{pmatrix} \; -10 \;\\ \; 6\; \end{pmatrix}

\frac{2}{5}\textbf{a}= \frac{2}{5}\begin{pmatrix} \; -10\;\\\; 15 \; \end{pmatrix} = \begin{pmatrix} \; \frac{2}{5}\times -10 \;\\ \; \frac{2}{5}\times15 \; \end{pmatrix} = \begin{pmatrix} \; -4\;\\\; 6\; \end{pmatrix}

\begin{pmatrix} \; 12 \;\\ \; 18 \; \end{pmatrix}

\begin{pmatrix} \; 4 \;\\ \; 3 \; \end{pmatrix}

\begin{pmatrix} \; -12 \;\\ \; -18\; \end{pматрица}

\begin{pmatrix} \; -4 \;\\ \; -3\; \end{pmatrix}

6\textbf{d}= 6\begin{pmatrix} \; -2 \;\\\; -3\; \end{pmatrix} = \begin{pmatrix} \; 6\раз -2\;\\\; 6\раз -3\; \end{pmatrix} = \begin{pmatrix} \; -12\;\\\; -18\; \end{pmatrix}

\begin{pmatrix} \; -15 \;\\ \; -12 \; \end{pmatrix}

\begin{pmatrix} \; -2 \;\\ \; -1\; \end{pmatrix}

\begin{pmatrix} \; 15 \;\\ \; 12\; \end{pmatrix}

\begin{pmatrix} \; -15 \;\\ \; -4\; \end{pматрица}

-3\textbf{f}= -3\begin{pmatrix} \; -5 \;\\\; -4\; \end{pmatrix} = \begin{pmatrix} \; -3\раз -5\;\\\; -3\раз -4\; \end{pmatrix} = \begin{pmatrix} \; 15 \;\\\; 12\; \end{pmatrix}

Умножение векторов Вопросы GCSE

1. Вектор \textbf{v} равен

 

\textbf{v}= \begin{pmatrix} \; -3 \;\\ \; 5 \; \end{pматрица}

 

Какой из приведенных ниже векторов эквивалентен 4\textbf{v} ?

 

А	\ четырехъядерный \ четырехъядерный	Б	\ четырехъядерный \ четырехъядерный	С	\ четырехъядерный \ четырехъядерный	Д
\begin{pmatrix} \; -12 \;\\ \; 5 \; \end{pmatrix}	\ четырехъядерный \ четырехъядерный	\begin{pmatrix} \; -1 \;\\ \; 20 \; \end{pmatrix}	\ четырехъядерный \ четырехъядерный	\begin{pmatrix} \; -1 \;\\ \; 5 \; \end{pmatrix}	\ четырехъядерный \ четырехъядерный	\begin{pmatrix} \; -12 \;\\ \; 20 \; \end{pматрица}

 

(1 балл)

Показать ответ

2. Вектор \textbf{a} равен

 

\textbf{а}= \begin{pmatrix} \; 3 \;\\ \; -6\; \end{pматрица}

 

Вычислить 5\textbf{a}

 

(2 балла)

Показать ответ

\begin{pmatrix} \; 15 \;\\ \; -30 \; \end{pматрица}

 

Для компонента x (верхнее число)

(1)

Для компонента y (нижний номер)

(1)

 

3. Вот векторное умножение

 

900 28 3 \begin{pmatrix} \; -4 \;\\ \; \текст{б} \; \end{pматрица} «=» \begin{pmatrix} \; \текст{а} \;\\ \; 24\; \end{pматрица}

 

(a) Найдите значение a .

 

(b) Найдите значение b .

 

(2 балла)

Показать ответ

(а)

а=-12

(1)

 

(б)

б=8

(1)

Контрольный список для обучения

Теперь вы научились:

• Умножать вектор на скаляр

Знаете ли вы?

Не входит в GCSE: мы можем транспонировать вектор-столбец, чтобы записать его как вектор-строку (и наоборот). Они выглядят как координаты, но без запятых.

Векторы также можно расширить до математики уровня A и высшей математики, научившись умножать два вектора вместе с помощью скалярного произведения. Это также известно как скалярное произведение двух векторов. Векторы можно умножать, и это известно как векторное произведение. Это также известно как векторное произведение двух векторов. Перекрестное произведение связано с правилом правой руки.

Мы также можем расширять векторы до трех измерений. Мы также можем посмотреть на вектор, перпендикулярный плоскости, чтобы получить уравнение плоскости.

Векторы-столбцы являются простым примером матриц. В математике GCSE у нас есть один столбец. Матрицы изучаются на уровне A Level Additional Maths. Количество столбцов и строк будет больше 1 . Умножение матриц можно изучать вместе с нахождением обратной матрицы. Мы также можем найти определитель матрицы и пойти дальше и изучить собственные значения и собственные векторы.

Если величина вектора равна 1 , этот вектор называется единичным вектором.

Все еще зависает?

Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning. Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.

Узнайте больше о нашей программе обучения математике GCSE.

Умножение матрицы на вектор — Мэтью Н. Бернстайн

5 минут чтения0623 19 декабря 2020 г.

Умножение матрицы на вектор — это операция между матрицей и вектором, в результате которой получается новый вектор. В этом посте я дам определение умножения матрицы на вектор, а также три угла, с которых можно рассматривать эту концепцию. Третий аспект подразумевает просмотр матриц как функций между векторными пространствами

Введение

В предыдущем посте мы обсуждали три способа просмотра матрицы: как таблицу значений, как список векторов и, наконец, как функцию . Это третий способ просмотра матриц, который действительно придает матрицам их силу. Здесь мы введем операцию между матрицами и векторами, называемую умножение матрицы на вектор , что позволит нам использовать матрицы как функции.

Умножение матрицы на вектор — это операция между матрицей и вектором, в результате которой получается новый вектор. n$ умножение матрицы на вектор $\boldsymbol{A}$ и $\boldsymbol{x}$ определяется как

$$\boldsymbol{A}\boldsymbol{x} := x_1\boldsymbol{a}_{* ,1} + x_2\boldsymbol{a}_{*,2} + \dots + x_n\boldsymbol{a}_{*,n}$$

, где $\boldsymbol{a}_{*,i}$ — $i$-й вектор-столбец $\boldsymbol{A}$.

Как и большинство математических понятий, умножение матрицы на вектор можно рассматривать с разных точек зрения на разных уровнях абстракции. Эти взгляды пригодятся, когда мы попытаемся концептуализировать различные способы использования матричного умножения на вектор для моделирования реальных проблем. Ниже приведены три способа, которые я считаю полезными для концептуализации умножения матрицы на вектор в порядке от наименее к наиболее абстрактному:0003

1. В качестве «построчного» процесса генерации вектора: Умножение матрицы на вектор определяет процесс создания нового вектора с использованием существующего вектора, где каждый элемент нового вектора «генерируется» путем взятия взвешенной суммы каждой строки матрицы с использованием элементов вектора в качестве коэффициентов
2. Как взятие линейной комбинации столбцов матрицы: Умножение матрицы на вектор — это процесс взятия линейной комбинации пространства столбцов матрицы используя элементы вектора в качестве коэффициентов
3. Как вычисление функции между векторными пространствами: Умножение матрицы на вектор позволяет матрице определить отображение между двумя векторными пространствами.

Я считаю полезными все три точки зрения. Первые две перспективы обеспечивают способ понимания механизма умножения матрицы на вектор, тогда как третья перспектива обеспечивает суть умножения матрицы на вектор. Именно эта третья перспектива умножения матрицы на вектор позволяет нам рассматривать матрицы как функции, как мы обсуждали в предыдущем посте.

Умножение матрицы на вектор как «построчный» процесс генерации вектора

Полезный способ просмотра механизма умножения матрицы на вектор между матрицей $\boldsymbol{A}$ и вектором $\boldsymbol{x }$ заключается в том, чтобы рассматривать его как своего рода «процесс» (или даже как компьютерную программу), который создает каждый элемент выходного вектора итеративным образом, когда мы перебираем каждую строку $A$. В частности, для каждой строки $i$ матрицы $\boldsymbol{A}$ мы берем $\boldsymbol{x}$ и вычисляем скалярное произведение между $\boldsymbol{x}$ и $i$-й строкой матрицы, тем самым производя $i$-й элемент выходного вектора (см.