Главная → Видеоуроки → Алгебра. 9 класс. Векторы. Описание видеоурока: Скалярным произведением двух векторов и называется число, равное произведению длин этих векторов на косинус угла между ними. Стоит вспомнить, что угол между векторами получают, откладывая данные векторы от одной точки. При этом выбирают угол меньший 180°. Результатом скалярного произведения векторов является число. Валерий Волков 2 03.02.2018 Будем рады, если Вы поделитесь ссылкой на этот видеоурок с друзьями! Новости образования | ЕГЭ по математике Профильный уровень Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 9 Задание 10 Задание 11 Задание 12 Задание 13 Задание 14 Задание 15 Задание 16 Задание 17 Задание 18 Задание 19 Задание 20 Задание 21 ГИА по математике Задача 1 Задача 2 Задача 3 Задача 4 Задача 5 Задача 6 Задача 7 Задача 8 Задача 9 Задача 10 Задача 11 Задача 12 Задача 13 Задача 14 Задача 15 Задача 16 Задача 17 Задача 18 Задача 19 Задача 20 Задача 21 Задача 22 Задача 23 Задача 24 Задача 25 Задача 26 Демонстрационные варианты ОГЭ по математике Математика. Натуральные числа Обыкновенные дроби Десятичные дроби Проценты Математика. 6 класс. Делимость чисел Сложение и вычитание дробей с разными знаменателями Умножение и деление обыкновенных дробей Отношения и пропорции Положительные и отрицательные числа Измерение величин Математика. 7 класс. Преобразование выражений Многочлены Формулы сокращенного умножения Математика. 8 класс. Модуль числа. Уравнения и неравенства. Квадратные уравнения Квадратные неравенства Уравнения с параметром Задачи с параметром Функции и их свойства Прогрессии Векторы Комбинаторика, статистика и теория вероятностей Математика. Числовые функции Тригонометрические функции Тригонометрические уравнения Преобразование тригонометрических выражений Производная Степенные функции Показательная функция Логарифмические функции Первообразная и интеграл Уравнения и неравенства Комбинаторика Создаёте видеоуроки? Если Вы создаёте авторские видеоуроки для школьников и учителей и готовы опубликовать их, то просим Вас связаться с администратором портала. Актуально Физкультминутки для школьников и дошкольников Подготовка к ЕГЭ Подготовка к ОГЭ |
5 класс.
10 — 11 класс.
4.5: Геометрический смысл скалярного умножения
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 14521
- Кен Каттлер
- Университет Бригама Янга via Lyryx 9{2}}\nonumber \] Таким образом, верно следующее.
\[\| к \vec{u} \| =\левый\верт к \правый\верт \| \vec{u} \|\nonumber \] Другими словами, умножение на скаляр увеличивает или уменьшает длину вектора в \(\left\vert k \right\vert\). Если \(\left\vert k \right\vert >А как насчет направления? Нарисуйте изображение \(\vec{u}\) и \(k\vec{u}\), где \(k\) отрицательно. Обратите внимание, что это приводит к тому, что результирующий вектор указывает в противоположном направлении, в то время как если \(k>0\), он сохраняет направление, на которое указывает вектор. Поэтому направление может либо измениться, если \(k < 0\), либо остаться прежним, если \(k >
Рассмотрим следующий пример.
Пример \(\PageIndex{1}\): графическое скалярное умножение
Рассмотрим векторы \(\vec{u}\) и \(\vec{v}\), нарисованные ниже.
Рисунок \(\PageIndex{1}\)Рисование \(-\vec{u}\), \(2\vec{v}\) и \(-\frac{1}{2}\vec{ v}\).
Решение
Чтобы найти \(-\vec{u}\), мы сохраняем длину \(\vec{u}\) и просто меняем направление. Для \(2\vec{v}\) мы удваиваем длину \(\vec{v}\), сохраняя при этом направление. Наконец, \(-\frac{1}{2}\vec{v}\) можно найти, взяв половину длины \(\vec{v}\) и изменив направление. Эти векторы показаны на следующей диаграмме.
Рисунок \(\PageIndex{2}\) 9п\) есть сумма векторов, умноженных на скаляры.В следующем примере мы исследуем геометрический смысл этого понятия.
Пример \(\PageIndex{2}\): построение графика линейной комбинации векторов
Рассмотрим следующее изображение векторов \(\vec{u}\) и \(\vec{v}\)
Рисунок \( \PageIndex{3}\)Нарисуйте изображение \(\vec{u}+2\vec{v},\vec{u}-\frac{1}{2}\vec{v}.\)
Решение
Два вектора показаны ниже.
Эта страница под названием 4.5: Геометрическое значение скалярного умножения распространяется под лицензией CC BY 4.
0 и была создана, изменена и/или курирована Кеном Каттлером (Lyryx) с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Кен Каттлер
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Показать страницу TOC
- нет
- Теги
- источник@https://lyryx. com/first-course-linear-алгебра
- источник@https://lyryx.
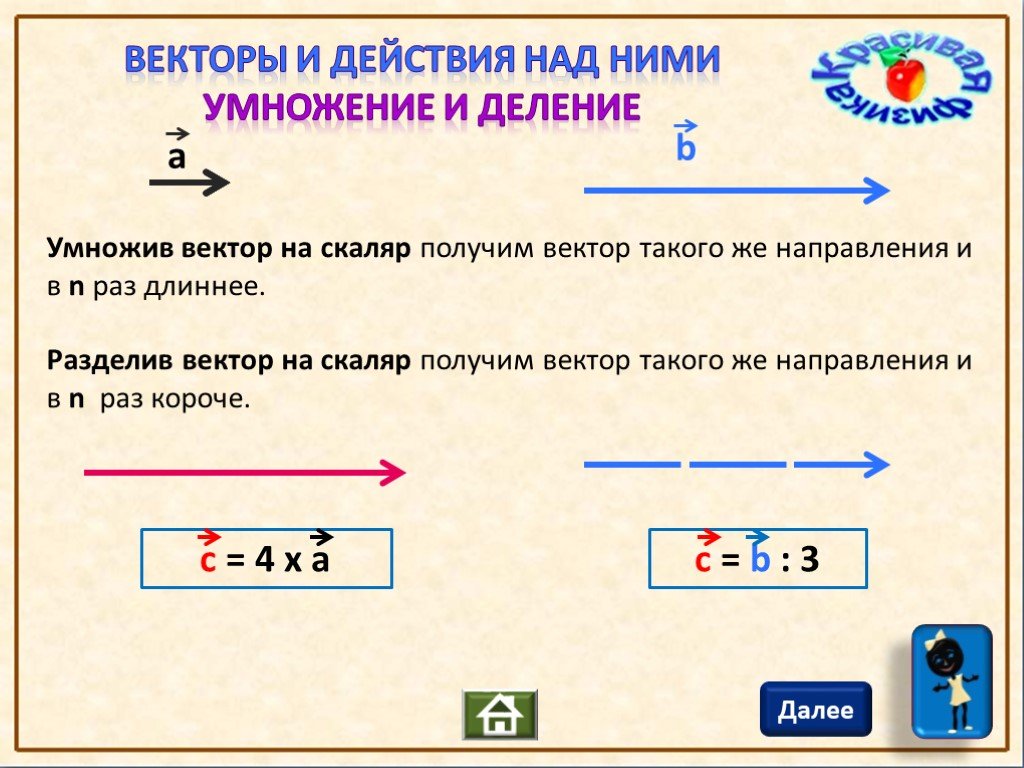
Умножение или деление вектора на скаляр
Скалярные и векторные величины — это только два вида величин. Если мы хотим измерить какое-либо количество, есть два способа измерения: либо только по величине, либо по величине и направлению. Если величина имеет только величину, она называется скалярной величиной. Если величина имеет как величину, так и направление, она называется векторной величиной. В этой статье будет рассмотрено умножение или деление вектора на скаляр.
Если есть скаляр и вектор, их произведение будет обозначаться как а.
В зависимости от значения (положительного или отрицательного) новый вектор a будет иметь то же направление, что и вектор a, или противоположное.
Величина нового вектора a равна произведению скалярной величины на величину вектора.
a = aЕсли = 1a, то a = a = 1aa = 1
Однако при условии, что вектор a равен 0. Следовательно, a не должен быть нулевым вектором, чтобы вышеуказанное условие выполнялось.
Законы распределения для сложения и умножения вектора на скаляр- b) = ka + kb
Умножить вектор на скаляр очень просто; умножьте величины вектора на скаляр.
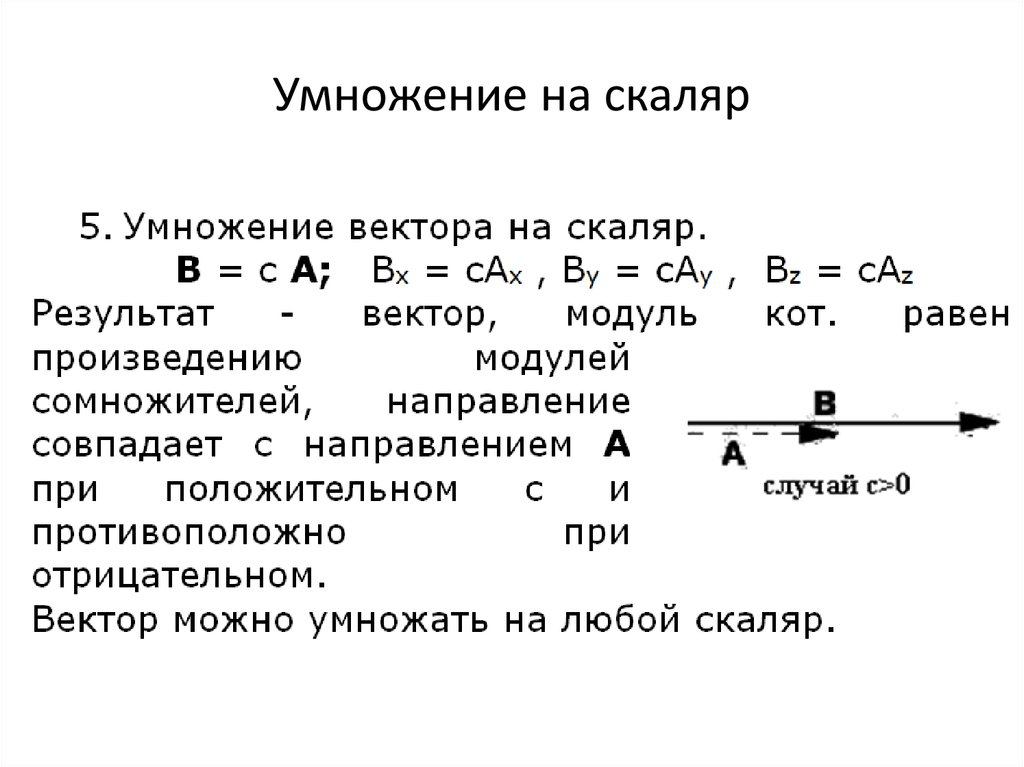
Когда мы умножаем вектор A на действительное число k, мы получаем другой вектор A’. Величина A’ в k раз больше величины A. Если она положительна, направление A’ совпадает с направлением A .
Результирующий новый вектор будет иметь то же направление.
Например, пусть c = ⟨8⟩. Найдите 7с.
Направление скалярного множителя остается таким же, как и у входного вектора.
Либо скаляр равен нулю, либо вектор равен нулю, если скаляр, кратный вектору, равен нулю.
\[\| к \vec{u} \| =\левый\верт к \правый\верт \| \vec{u} \|\nonumber \] Другими словами, умножение на скаляр увеличивает или уменьшает длину вектора в \(\left\vert k \right\vert\). Если \(\left\vert k \right\vert >
0 и была создана, изменена и/или курирована Кеном Каттлером (Lyryx) с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.
com/first-course-linear-алгебра
a = aЕдиничный вектор в направлении вектора a = 1a a = 15 (i – 2j) = 15i – 25j
Новый вектор величины 7, направленный в направлении вектора a is
7 a = 7 (15i – 25j) = 75i – 145j
Как умножить вектор на скаляр?
7C = 7⟨8⟩
= ⟨7 (8)⟩
= ⟨56⟩
Скалярные кратно изменения.
Таблица умножения вектора на вещественное число с другим коэффициентом:
Factors | Original vector | Product of vector after multiplication | The direction of the vector after multiplications |
If λ is greater чем 0 | A | λA | То же, что и A |
– λ меньше 0 | A | λA | Opposite to A |
λ equal to 0 | A | 0 = null vector | None. |
Исходное и конечное положение одинаковые.В общем случае умножение действительного числа r на вектор A дает этот результат. Это даст нам что-то в том же направлении, что и раньше, но в r раз больше исходной величины. r A имеет две составляющие: r Ax и r Ay с точки зрения составляющих.
Если r равно -1, результирующий вектор будет указывать в противоположном направлении, если A истинно.
Пример умножения или деления вектора на скаляр
Сила — это векторная величина в физическом мире. Количество выполненной работы определяется величиной и направлением силы, приложенной к предмету. Согласно второму закону линейного движения Ньютона эта сила является произведением вектора на скалярное число.
Сила следующая:
m x a = F.
В приведенном выше уравнении a — это ускорение объекта, которое является векторной величиной, а m обозначает массу объекта, которая является скалярной величиной.
