Сайт репетитора по математике Фроловой Л.А.
Решение систем уравнений — http://ru.onlinemschool.com/math/assistance/equation/matr/
http://ru.onlinemschool.com/math/assistance/
Онлайн калькуляторы. Конвертеры величин.
- Онлайн калькулятор. Конвертер единиц массы и веса
- Онлайн калькулятор. Конвертер единиц расстояния и длины.
- Онлайн калькулятор. Конвертер единиц площади
- Онлайн калькулятор. Конвертер единиц объема
- Онлайн калькулятор. Конвертер единиц времени
- Онлайн калькулятор. Преобразование скоростей (метры в секунду, километры в час)
Онлайн калькуляторы. Теория чисел
- Онлайн калькулятор. Сложение, вычитание, умножение и деление столбиком.
- Онлайн калькулятор. Сложение и вычитание в столбик.
- Онлайн калькулятор. Умножение в столбик.
- Онлайн калькулятор. Деление в столбик.
- Онлайн калькулятор. НОД и НОК двух чисел
- Онлайн калькулятор.

Онлайн калькуляторы с дробями
- Онлайн калькулятор дробей. Вычисления с двумя дробями. Сложение, вычитание, умножение и деление дробей.
- Онлайн калькулятор. Вычисления с обыкновенной и десятичной дробями.
Онлайн калькулятор. Преобразование десятичной дроби в обыкновенную дробь.
- Онлайн калькулятор. Преобразование неправильных дробей в смешанные числа.
- Онлайн калькулятор. Преобразование смешанных чисел в неправильные дроби.
- Онлайн калькулятор. Сокращение дробей.
- Онлайн калькулятор. Сравнение дробей.
- Онлайн калькуляторы. Калькуляторы с процентами
Онлайн калькулятор. Найти X
- Онлайн калькулятор. Найти число X зная его Y процентов.
- Онлайн калькулятор. Добавить или вычесть X процентов от числа.
- Онлайн калькулятор. Найти сколько процентов составляет число X от числа Y.

- Онлайн калькулятор. Калькулятор сложных процентов. Депозитный калькулятор.
- Онлайн калькуляторы. Решение уравнений
- Онлайн калькулятор. Решение квадратных уравнений.
Онлайн калькулятор. Решение биквадратных уравнений.
- Онлайн калькулятор. Решение систем линейных уравнений.
- Онлайн калькулятор. Решение систем линейных уравнений. Метод Гауса.
- Онлайн калькулятор. Решение систем линейных уравнений. Метод Крамера.
- Онлайн калькулятор. Решение систем линейных уравнений. Матричный метод.
Онлайн калькуляторы. Прогрессии
- Онлайн калькулятор. Значение n-того члена арифметической прогрессии.
- Онлайн калькулятор. Сумма арифметической прогрессии.
Онлайн калькуляторы. Пределы и производные функций
- Онлайн калькулятор. Решение пределов онлайн.
- Онлайн калькулятор. Решение производных онлайн.
Онлайн калькуляторы. Интегралы онлайн
- Онлайн калькулятор.
 Решение интегралов онлайн.
Решение интегралов онлайн. - Онлайн калькулятор. Решение определенных интегралов онлайн.
- Онлайн калькуляторы. Комбинаторика. Теория вероятности.
Онлайн калькулятор. Вычисление числа перестановок из n элементов.
- Онлайн калькулятор. Вычисление числа размещений из n по k.
- Онлайн калькулятор. Вычисление числа сочетаний из n по k.
- Онлайн калькулятор. Вычисление математического ожидания дискретного распределения.
- Онлайн калькулятор. Вычисление дисперсии дискретного распределения.
Онлайн калькуляторы с комплексными числами
- Онлайн калькулятор. Сложение, вычитание, умножение и деление комплексных чисел.
- Онлайн калькулятор. Модуль комплексного числа.
- Онлайн калькулятор. Конвертер алгебраической формы комплексного числа в тригонометрическую и показательную.
Онлайн калькуляторы с векторами
- Онлайн калькулятор. Определение вектора по двум точкам.

- Онлайн калькулятор. Длина вектора. Модуль вектора.
- Онлайн калькулятор. Направляющие косинусы вектора.
- Онлайн калькулятор. Сложение и вычитание двух векторов.
- Онлайн калькулятор. Умножение вектора на число.
- Онлайн калькулятор. Скалярное произведение векторов.
- Онлайн калькулятор. Угол между векторами.
- Онлайн калькулятор. Проекция вектора на вектор.
- Онлайн калькулятор. Векторное произведение векторов.
- Онлайн калькулятор. Смешанное произведение векторов.
- Онлайн калькулятор. Коллинеарность векторов.
- Онлайн калькулятор. Ортогональность векторов.
- Онлайн калькулятор. Компланарность векторов.
- Онлайн калькулятор. Площадь треугольника построенного на векторах.
- Онлайн калькулятор. Площадь параллелограмма построенного на векторах.
- Онлайн калькулятор. Объем пирамиды построенной на векторах.
- Онлайн калькулятор. Проверить являются ли векторы базисом.

4
5
6
i
(
)
π
e
1
2
3
sin
cos
tg
ctg
ln
.
√
sh
ch
th
cth
abs
Скрыть клавиатуру
С решением
Тригонометрическая форма
Показательная форма
Десятичных знаков:
Вычислить
Вычислено выражений:
Как пользоваться калькулятором
- Введите в поле ввода выражение с комплексными числами
- Укажите, требуется ли вывод решения переключателем «С решением»
- Нажмите на кнопку «Построить»
Ввод комплексных чисел
комплексные числа можно вводить в следующих трёх форматах:
- Только действительная часть:
2, 2.5, -6.7, 12.25 - Только мнимая часть:
i, -i, 2i, -5i, 2.16i, -12.5i - Действительная и мнимая части:
2+i, -5+15i, -7+2.5i, -6+i - Математические константы:
π, e
Поддерживаемые операции и математические функции
- Арифметические операции:
+, -, *, /, ^ - Получение абсолютного значения числа:
abs - Базовые математические функции:
exp, ln, sqrt - Получение действительной и мнимой частей:
re, im - Тригонометрические функции:
sin, cos, tg, ctg - Гиперболические функции:
sh, ch, th, cth - Обратные тригонометрические функции:
arcsin, arccos, arctg, arcctg - Обратные гиперболические функции:
arsh, arch, arth, arcth
Примеры корректных выражений
- (2+3i)*(5-7i)
- sh(i)
- (4+i) / (3 — 4i)
- sqrt(2i)
- (-3+4i)*2i / exp(2i + (15 — 8i)/4 — 3.
 75)
75)
Комплексные числа
Комплексные числа — это числа вида
x+iy, гдеx,y— вещественные числа, аi— мнимая единица (специальное число, квадрат которого равен -1, то естьi2 = -1).
Так же, как и для вещественных чисел, для комплексных чисел определены операции сложения, разности, умножения и деления, однако комплексные числа нельзя сравнивать.Примеры комплексных чисел
4+3i— действительная часть = 4, мнимая = 3-2+i— действительная часть = -2, мнимая = 1i— действительная часть = 0, мнимая = 1-i— действительная часть = 0, мнимая = -110— действительная часть = 10, мнимая = 0
Основные действия с комплексными числами
Основными операциями, определёнными для комплексных чисел, являются сложение, разность, произведение и деление комплексных чисел. Операции для двух произвольных комплексных чисел (a + bi) и (c + di) определяются следующим образом:
- сложение: (a + bi) + (c + di) = (a + c) + (b + d)i
- вычитание: (a + bi) — (c + di) = (a — c) + (b — d)i
- умножение: (a + bi) · (c + di) = ac + bci + adi + bdi2 = (ac — bd) + (bc + ad)i
- деление:
a + bi
c + di
=(a + bi)(c — di)
c2 + d2
=(ac + bd)
c2 + d2
+(bc — ad)
c2 + d2
i
Примеры
Найти сумму чисел
5+7iи5.: 5-2i
5-2i
Найдём отдельно суммы действительных частей и сумму мнимых частей: re = 5 + 5.5 = 10.5, im = 7 — 2 = 5.
Запишем их рядом, добавив к мнимой части i: 10.5 + 5i
Полученное число и будет ответом:5+7i+5.5-2i=10.5 + 5iНайти разность чисел
12-iи-2i:
Найдём отдельно разности действительных частей и разности мнимых частей: re = 12 — 0 = 12, im = -1 — (-2) = 1.
Запишем их рядом, добавив к мнимой части i: 12 + 1i
Полученное число и будет ответом:12-i—(-2i)=12 + iНайти произведение чисел
2+3iи5-7i:
Найдём по формуле действительную и мнимую части: re = 2·5 — 3·(-7) = 31, im = 3·5 + 2·(-7) = 1.
Запишем их рядом, добавив к мнимой части i: 31 + 1i
Полученное число и будет ответом:2+3i*(5-7i)=31 + iНайти отношение чисел
75-50iи3+4i:
Найдём по формуле действительную и мнимую части: re = (75·3 — 50·4) / 25 = 1, im = (-50·3 — 75·4) / 25 = -18.
Запишем их рядом, добавив к мнимой части i: 1 — 18i
Полученное число и будет ответом:75-50i/(3+4i)=1 - 18iДругие действия над комплексными числами
Помимо базовых операций сложения, вычитания, умножения и деления комплексных чисел существуют также различные математические функции. Рассмотрим некоторые из них:
- Получение действительной части числа:
Re(z) = a - Получение мнимой части числа:
Im(z) = b - Модуль числа:
|z| = √(a2 + b2) - Аргумент числа:
arg z = arctg(b / a) - Экспонента:
ez = ea·cos(b) + i·ea·sin(b) - Логарифм:
Ln(z) = ln |z| + i·arg(z) - Тригонометрические функции: sin z, cos z, tg z, ctg z
- Гиперболические функции: sh z, ch z, th z, cth z
- Обратные тригонометрические функции: arcsin z, arccos z, arctg z, arcctg z
- Обратные гиперболические функции: arsh z, arch z, arth z, arcth z
Примеры
Найти действительную и мнимую части числа z, а также его модуль, если z = 4 — 3i
Re(z) = Re(4 — 3i) = 4
Im(z) = Im(4 — 3i) = -3
|z| = √(42 + (-3)2) = √25 = 5Формы представления комплексных чисел
Комплексные числа принято представлять в одной из трёх следующих форм: алгебраической, тригонометрической и показательной.

- Алгебраическая форма — наиболее часто используемая форма комплексного числа, запись числа в виде суммы действительной и мнимой частей:
x+iy, где x — действительная часть, а y — мнимая часть - Тригонометричкая форма — запись вида
r·(cos φ + isin φ), где r — модуль комплексного числа (r = |z|), а φ — аргумент этого числа (φ = arg(z)) - Показательная форма — запись вида
r·eiφ, где r — модуль комплексного числа (r = |z|), e — число Эйлера, а φ — аргумент комплексного числа (φ = arg(z))
Пример:
Переведите число 1+i в тригонометрическую и показательную формы:
Решение:
- Найдём радиус (модуль) комплексного числа r: r = √(12 + 12) = √2
- Найдём аргумент числа: φ = arctan() = = 45°
- Запишем результат в тригонометрической форме:
√2·(cos(45°) + isin(45°)) - Запишем результат в показательной форме:
√2·eπi/4
Скалярное произведение двух векторов
Вам нужно вычислить скалярное произведение двух векторов ? Узнайте, как это сделать, здесь или воспользуйтесь нашим онлайн-калькулятором, чтобы сразу узнать результат.

Вам нужно только написать компоненты вектора и компоненты вектора , а также угол, образованный двумя векторами в градусах. Нажмите кнопку расчета, и вы автоматически узнаете их скалярное произведение.
Разделы статьи
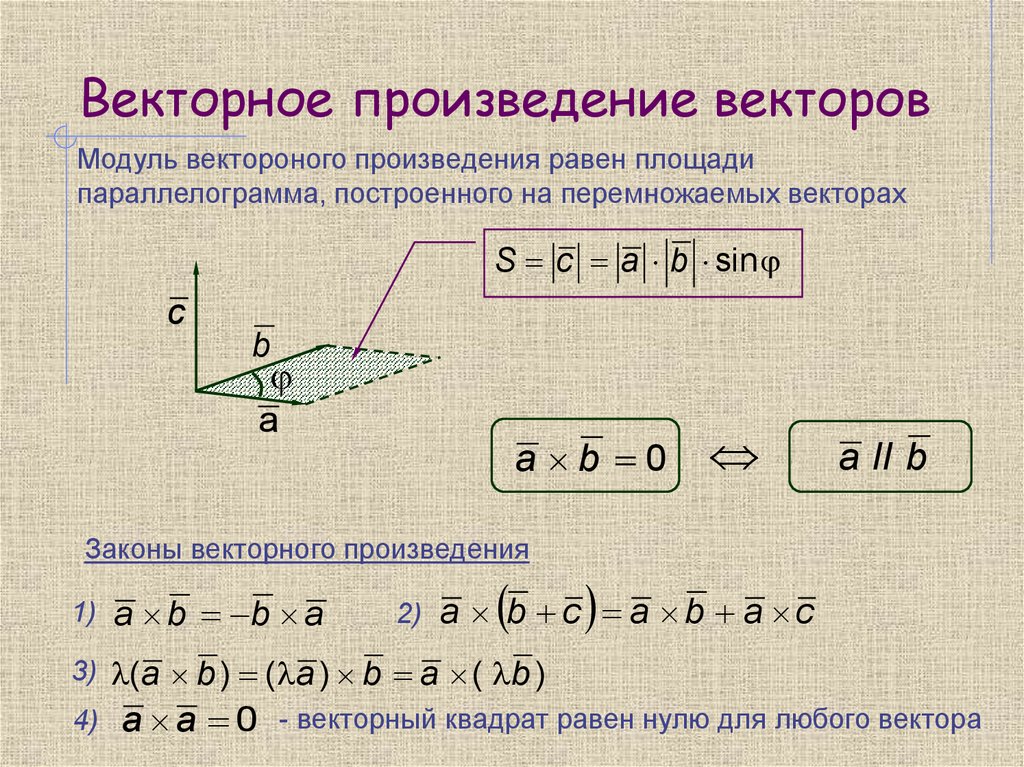
- Формула скалярного произведения двух векторов
- Аналитическая формула скалярного произведения
- Скалярное произведение вектора на себя
- Свойства скалярного произведения
- Решенные упражнения
- Вычисление скалярного произведения двух векторов в Excel
6 Расчет скалярного произведения двух векторов 902 Формула скалярного произведения двух векторов скалярное произведение двух векторов , вы должны применить следующую формулу математики:
где:
- |u| и |v| являются модулем каждого вектора (узнайте здесь, как вычислить модуль вектора).
- cosα — косинус угла, образующего два вектора.
В зависимости от того, каков этот угол α, приведенная выше формула может быть упрощена в некоторых случаях:
- Если векторов перпендикулярны (α = 90º), скалярное произведение будет равно нулю.
 Это потому, что косинус 90 равен 0, .
Это потому, что косинус 90 равен 0, . - Если вектора параллельны и имеют один и тот же смысл (α = 0º), формула сводится к произведению модулей |u|⋅|v| Это потому, что косинус 0 равен 1,
- Если вектора параллельны, но имеют противоположные направления (α = 180º), то формула sera del producto escalar será — |u|⋅|v|. Ese símbolo negativo se debe a que el coseno de 180 es igual a -1.
Следует отметить, что скалярное произведение двух векторов даст действительное число . Также очень важно не путать его с векторным произведением.
Аналитическая формула скалярного произведения
При расчете скалярное произведение двух векторов с аналитической точки зрения мы получаем в результате скалярное число, которое является результатом умножения каждой из декартовых составляющих двух векторов, как мы можем видеть в этой формуле:
скалярное произведение вектора самого по себе
Приведенная выше формула пригодится для решения задачи, в которой мы собираемся вычислить скалярное произведение вектора самого по себе .

Как видите, скалярное произведение вектора само по себе равно квадрату его модуля . Мы также могли бы решить это упражнение, применив общую формулу скалярного произведения и установив α = 0º.
Скалярное произведение вектора само по себе всегда будет положительным (пока это ненулевой вектор).
Свойства скалярного произведения
При решении упражнений будет полезно знать свойства скалярного произведения:
- Коммутативный : u ⋅ v = v ⋅ u
- Распределительный (векторная сумма): x ⋅ (u + v) = x ⋅ u + x ⋅ v
- Ассоциативный (произведение на скаляр m): m (u ⋅ v) = (mu) ⋅ v = u ⋅ (mv).
Решенные упражнения
Далее мы увидим пару упражнений, в которых мы собираемся вычислить скалярное произведение следующих векторов:
Первое, что мы собираемся сделать, это вычислить модуль каждого вектор:
Теперь применим общую формулу и у нас останется следующее:
Если вы хотите попрактиковаться с большим количеством решенных упражнений, составьте данные двух векторов и используйте наш калькулятор, чтобы проверить результат.
 Если у вас возникли проблемы с каким-либо из них, напишите нам комментарий, и мы вам поможем.
Если у вас возникли проблемы с каким-либо из них, напишите нам комментарий, и мы вам поможем.Вычислить скалярное произведение двух векторов в Excel
Как и не могло быть иначе, Excel также имеет функцию, позволяющую вычислить скалярное произведение двух векторов с помощью аналитической формулы.
Эту функцию нелегко найти в программе Microsoft, поэтому мы собираемся объяснить, как это сделать. Первое, что вам нужно сделать, это открыть новую таблицу и используйте пустую ячейку для записи каждого компонента вектора . Мы собираемся вычислить скалярное произведение векторов (-1, 3) и (2, -2), поэтому у нас есть такая форма:
Теперь мы будем использовать функцию СУММПРОИЗВ для получения скалярного произведения. В нашем примере это выглядит так:
=СУММАПРОИЗВ(B2:C2;B3:C3)
Обратите внимание, что в диапазоне ячеек B2:C2 находятся компоненты вектора 1, а в диапазоне B3:C3 являются компонентами вектора 2.
 Вам придется адаптировать эти диапазоны к ячейкам, которые вы использовали вы.
Вам придется адаптировать эти диапазоны к ячейкам, которые вы использовали вы.Теперь вам просто нужно нажать клавишу ENTER, и
Nacho
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En Esta веб-те Ayudo hacer cálculos у преобразования sencillas дие кон-эль-Пасо-де-лос-Años се-нос-ха olvidado Cómo себе Hace. Si tienes dudas, déjame un commentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, напишите мне сообщение.
- градусов с радианами
- Apothem
- Antilogarithm Calculator
- Calculator
- Exponent Calculator
- Exponential Function Calculator
- LogArithm Calculator
- NEARELENTIAL FUNCTION FUNDEITIRITIRITIRITIR
- LOGARITHM Calculator
- NEPONUEL FUNCTION FUNCAUT
- Калькулятор кубического корня
- Калькулятор n-го корня числа
- Калькулятор квадратных уравнений
- Онлайн-калькулятор факториала
- Калькулятор гипотенузы
- Калькулятор наибольшего общего делителя
- Калькулятор наименьшего общего кратного
- Калькулятор умножения
- Онлайн-калькулятор
— примеры, онлайн-калькулятор скалярного произведения
Калькулятор скалярного произведениявычисляет скалярное произведение двух заданных векторов.
 Когда два вектора умножаются с помощью скалярного произведения, полученная таким образом величина будет скаляром. Скалярный продукт может быть положительным или отрицательным действительным числом.
Когда два вектора умножаются с помощью скалярного произведения, полученная таким образом величина будет скаляром. Скалярный продукт может быть положительным или отрицательным действительным числом.Что такое калькулятор скалярного произведения?
Калькулятор скалярного произведения – это онлайн-инструмент, который помогает определить скалярную величину, являющуюся результатом скалярного произведения заданных двух векторов. Величина, полученная после скалярного произведения, будет находиться в той же плоскости, что и два заданных вектора. Чтобы использовать калькулятор скалярного произведения, введите значения в соответствующие поля ввода.
Калькулятор скалярного произведения
Как пользоваться калькулятором скалярного произведения?
Выполните следующие шаги, чтобы вычислить скалярное произведение двух заданных векторов с помощью калькулятора скалярного произведения
- Шаг 1: Перейдите к онлайн-калькулятору скалярного произведения Cuemath.

- Шаг 2: Введите коэффициенты двух векторов в указанные поля ввода.
- Шаг 3: Нажмите кнопку «Умножить» , чтобы вычислить скалярный продукт.
- Шаг 4: Нажмите кнопку «Сброс» , чтобы очистить поля и ввести новые значения.
Как найти калькулятор скалярного произведения?
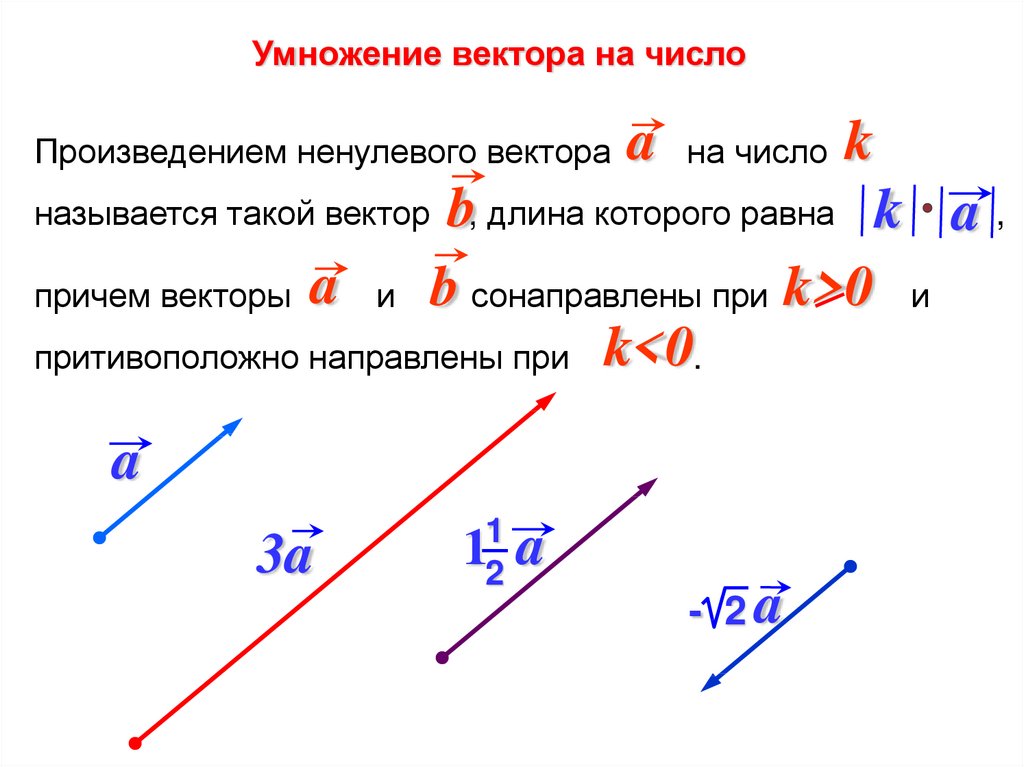
Скалярное произведение определяется как произведение величины двух векторов и косинуса угла между двумя заданными векторами. Если \(\overrightarrow{a}\) и \(\overrightarrow{b}\) являются двумя векторами, то скалярное произведение дается следующим образом:
\(\overrightarrow{a}\). \(\overrightarrow{b}\) = |\(\overrightarrow{a}\)|.|\(\overrightarrow{b}\)|cosθ.
Предположим, что нам даны два вектора, которые выражены в виде их единичных векторов i, j, k вдоль осей x, y и z. Затем шаги, которые необходимо выполнить, чтобы найти скалярное произведение между двумя векторами, приведены ниже:
\(\overrightarrow{a}\) = \(a_{1}\шляпа{i} + a_{2}\шляпа{j} + a_{3}\шляпа{k}\)
\(\ overrightarrow{b}\) = \(b_{1}\шляпа{i} + b_{2}\шляпа{j} + b_{3}\шляпа{k}\)
Чтобы найти скалярное произведение
\ (\overrightarrow{а}\).
 \(\overrightarrow{b}\) = (\(a_{1}\шляпа{i} + a_{2}\шляпа{j} + a_{3}\шляпа{k}\)).(\(b_ {1}\шляпа{i} + b_{2}\шляпа{j} + b_{3}\шляпа{k}\))
\(\overrightarrow{b}\) = (\(a_{1}\шляпа{i} + a_{2}\шляпа{j} + a_{3}\шляпа{k}\)).(\(b_ {1}\шляпа{i} + b_{2}\шляпа{j} + b_{3}\шляпа{k}\))= \((a_{1}b_{1})(\шляпа{ i}.\шляпа{i}) + (a_{1}b_{2})(\шляпа{i}.\шляпа{j}) + (a_{1}b_{3})(\шляпа{i} .\шляпа{k})\) + \((a_{2}b_{1})(\шляпа{j}.\шляпа{i}) + (a_{2}b_{2})(\шляпа{ j}.\шляпа{j}) + (a_{2}b_{3})(\шляпа{j}.\шляпа{k})\) + \((a_{3}b_{1})(\ шляпа{k}.\шляпа{i}) + (a_{3}b_{2})(\шляпа{k}.\шляпа{j}) + (a_{3}b_{3})(\шляпа{ к}.\шляпа{к})\)
\(\шляпа{i}.\шляпа{j}\) = \(\шляпа{i}.\шляпа{k}\) = \(\шляпа{k}.\шляпа{j}\) = cos 90 = 0. Это потому, что эти векторы ортогональны.
\(\шляпа{i}.\шляпа{i}\) = \(\шляпа{k}.\шляпа{k}\) = \(\шляпа{j}.\шляпа{j}\) = cos 0 = 1. Потому что эти векторы сонаправлены.
\(\overrightarrow{a}\). \(\overrightarrow{b}\) = \(a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\)
Хотите найти сложные математические решения за секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы.
 С Cuemath находите решения простыми и легкими шагами.
С Cuemath находите решения простыми и легкими шагами.Запись на бесплатный пробный урок
Решенные примеры на калькуляторе скалярного произведения
Пример 1:
Найдите скалярное произведение двух векторов \(\overrightarrow{a}\) = \(4\hat{i} + 2\шляпа{j} — 5\шляпа{k}\) и \(\overrightarrow{b}\) = \(3\шляпа{i} — 2\шляпа{j} — \шляпа{k}\). Проверьте результат с помощью калькулятора скалярного произведения.
Решение:
Учитывая \(\overrightarrow{a}\) = \(4\hat{i} + 2\hat{j} — 5\hat{k}\) и \(\overrightarrow{b }\) = \(3\шляпа{i} — 2\шляпа{j} — \шляпа{k}\)
\(\overrightarrow{a}\). \(\overrightarrow{b}\) = \(a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}\)
\(\overrightarrow{a}\ ). \(\overrightarrow{b}\) = (4 . 3) + (2 . (-2)) + ((-5) . 1)
= 12 — 4 — 5
= 3
Следовательно, скалярное произведение двух векторов равно 3.
Пример 2:
Найдите скалярное произведение двух векторов \(\overrightarrow{a}\) = \(2.





 Решение интегралов онлайн.
Решение интегралов онлайн.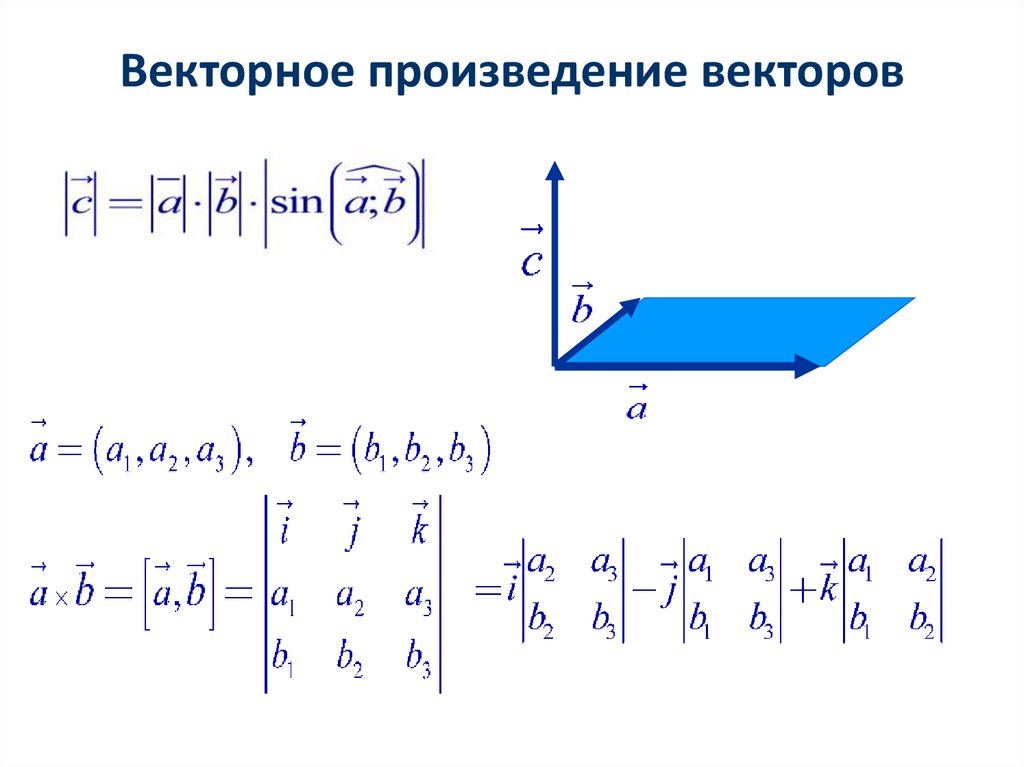

 75)
75) 5-2i
5-2i


 Это потому, что косинус 90 равен 0,
Это потому, что косинус 90 равен 0,
 Если у вас возникли проблемы с каким-либо из них, напишите нам комментарий, и мы вам поможем.
Если у вас возникли проблемы с каким-либо из них, напишите нам комментарий, и мы вам поможем.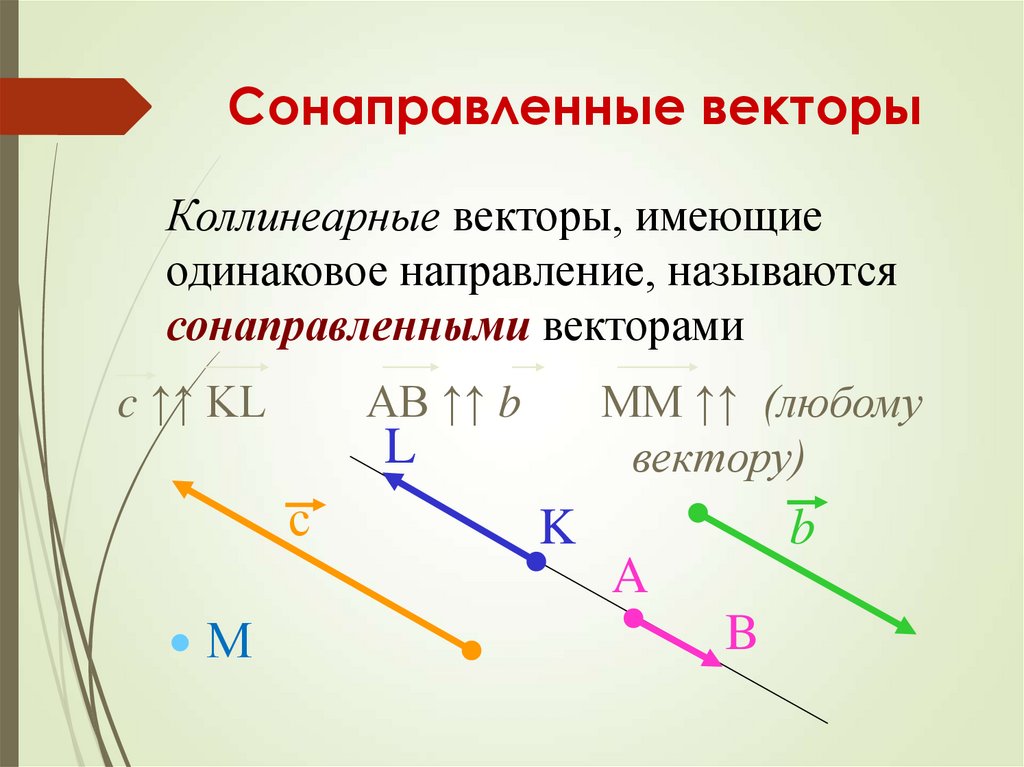 Вам придется адаптировать эти диапазоны к ячейкам, которые вы использовали вы.
Вам придется адаптировать эти диапазоны к ячейкам, которые вы использовали вы. Когда два вектора умножаются с помощью скалярного произведения, полученная таким образом величина будет скаляром. Скалярный продукт может быть положительным или отрицательным действительным числом.
Когда два вектора умножаются с помощью скалярного произведения, полученная таким образом величина будет скаляром. Скалярный продукт может быть положительным или отрицательным действительным числом.
 \(\overrightarrow{b}\) = (\(a_{1}\шляпа{i} + a_{2}\шляпа{j} + a_{3}\шляпа{k}\)).(\(b_ {1}\шляпа{i} + b_{2}\шляпа{j} + b_{3}\шляпа{k}\))
\(\overrightarrow{b}\) = (\(a_{1}\шляпа{i} + a_{2}\шляпа{j} + a_{3}\шляпа{k}\)).(\(b_ {1}\шляпа{i} + b_{2}\шляпа{j} + b_{3}\шляпа{k}\)) С Cuemath находите решения простыми и легкими шагами.
С Cuemath находите решения простыми и легкими шагами.