Умножение вектора на число — презентация онлайн
Похожие презентации:
Умножение вектора на число
Умножение вектора на число
Умножение вектора на число
Умножение вектора на число
Умножение вектора на число
Умножения вектора на число
Умножение вектора на число
Произведение вектора на число
Векторы. Понятие вектора
Векторы в пространстве. (10-11 класс)
2. ЗАДАЧА№1
Найдите:B
a ) AB BC
C
б ) CB CD
в ) AC DA
г ) DC BD AB
д) AB AD
е) AC DC
D
A
3. ЗАДАЧА№2
Докажите:B
C
а ) AB AD CB CD
б ) AD BD AC BC
D
A
4. ЗАДАЧА№3
ABCD-прямоугольникAB=5; AD=12.
Докажите:
C
B
a) AB BC 2 AO
O
б ) BA DA OD OB
Найдите:
AO DO CD
A
D
Умножение вектора на число.
Произведением ненулевого вектора
a
на число
k
b, длина которого равна k a ,
причем векторы a и b сонаправлены при k>0 и
притивоположно направлены при k<0.

называется такой вектор
a
3a
1
12
a
— 2a
Умножение вектора на число.
b
2b
a
2b b
2b = 2 b
1
a
2
1
a
2
a
2
a
=
1
2
a
Умножение вектора на число.
Для любого числа
kи
a
ka
любого вектора
векторы
a
и
коллинеарны.
1
2
— a
a
1
12
a
— 2a
Произведение нулевого вектора на любое число
считается нулевой вектор.
k o=o
Произведение любого вектора на число нуль есть
нулевой вектор.
o a=o
Назовите вектор, который получится в результате
умножения.
A
B
C
D
N
M
R
E
S
F
Q
I
H
V
O
J
T
P
K
Y
X
L
U
G
Z
JO 3
1
ML
3
4 AB
4 ЕУ
3
NZ
4
х JO
СК = -4
JO = – х1
4 CK
XD =– х3
A
B
C
D
N
0 XD
NN = х
M
R
E
S
F
ХТ = х XD
Q
V
T
Y
U
х не существует
х XT
XT = 1
I
O
P
X
G
х XT
TX = -1
H
J
K
L
Z
О – точка пересечения медиан треугольника.

ВК =3х ОК
B
х ВK
КO =– 1
3
ОВ = 2х КО
T
O
A
K
C
T
A
B
7
3
C
TВ = 7
AC = 3
х TВ
AC = 3
7
х AC
TB = 7
3
10
D
O
DO = 10
2,5
K
F
KF = 2,5
KF = – х1 DO
4
х KF
DO = –4
ABCD – трапеция.
С
8
BC =
х
– DA
0,8
х BC
DA = – 10
8
А
10
D
ABCD – параллелограмм. CS : SB = 5 : 3
В
А
С
S
D
3
BS = – х
8
DA
8
DA = – х
3
BS
Умножение вектора на число обладает следующими
основными свойствами.
Для любых
равенства:
a, b
и любых чисел
1
(kl)a = k (l a)
2
(k+l)a = ka + la
k, l
справедливы
Сочетательный закон
Первый распределительный закон
3
k (a + b) = ka + kb
Второй распределительный закон
Рисунок иллюстрирует сочетательный закон.
Представлен случай, когда
k = 2, l = 3.
1
Сочетательный закон
a
a
a
A
O
OВ = 2OA = 2(3
a a
B
a)
a a a a
B
O
OВ = 6
a = (2 3) a
Рисунок иллюстрирует первый распределительный
закон.
 Представлен случай, когда
Представлен случай, когда2
(k+l)a = ka + la
Первый
распределительный закон
B
la
a
ka
k = 3, l = 2.
A
OA =
ka;
AB =
la
O
OB =
(k+l)a = ka + la
3
k (a + b) = ka + kb
Второй
распределительный
закон
Рисунок иллюстрирует второй распределительный закон.
На рисунке ОАВ
ОА1В1, коэффициент подобия
k
A
ka
AB =
kb
OB =
k(a+b)
OB = OA + AB =
ka+kb
A1
a
O
b
a+b
B1
С другой стороны,
Таким образом,
B
k(a+b) = ka+kb
№ 781 Пусть х = m + n, y = m – n
Выразите через m и n
векторы
2х – 2у 2(m n ) 2(m n ) 2m 2n 2m 2n 4n
1
1
1
2(m n ) (m n ) 2m 2n m n
2
2
2
1
1
2 m 1 n
2
2
1
1
1
–х – 1 у (m n ) (m n ) m n m n
3
3
3
3
1
2
1 m n
3
3
2х + 1 у
2
Задача
Построить вектор
3
1
3
3
1
ВС АВ АС ( ВС АС ) АВ
7
14
7
7
14
В
С
3
1
( ВС СА) АВ
7
14
3
1
7
ВА ВА
7
14
14
А
1
ВА
2
Задача
Построить вектор
5
1
5 1
5
1
( АВ ВС АС ) ( АС АС ) АС
2
2
2 2
2
2
В
5
АС
С
4
А
Задача
2
1
2
1
СD DA BС AB =
Построить вектор.

9
3
9
3
В
С
2
1
(СD BС ) ( АВ DA)
9
3
CA
AC
2
1
(СD СB) ( АВ AD)
9
3
А
D
2
1
2
1
CA AC СА СА
9
3
9
3
АВСD – параллелограмм.
1
СА
9
Задача
Построить вектор.
2
1
2
5
10
5
В
С
2
1
( АВ DA) CА
5
10
AC
2
1
( АВ AD) CА
5
10
2
1
5
AС AC
АС
5
10
10
А
D
АВСD – параллелограмм.
1
АС
2
English Русский Правила
Умножение вектора на число презентация, доклад
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Русский язык
- Страхование
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация на тему Презентация на тему Умножение вектора на число, предмет презентации: Разное. Этот материал содержит 6 слайдов. Красочные слайды и илюстрации помогут Вам заинтересовать свою аудиторию. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций ThePresentation.ru в закладки!
Этот материал содержит 6 слайдов. Красочные слайды и илюстрации помогут Вам заинтересовать свою аудиторию. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций ThePresentation.ru в закладки!
Умножение вектора на число
9 класс
Учитель математики Тивякова Л.А.
Если b = k*a, то векторы a и b – коллинеарны.
Задание:
указать тип данных векторов при отрицательном значении числа k,
при положительном значении числа k,
при k = 0
Тивякова Л.А.
№ 1 Найти вектор х
АВ + х = АК
( PE + EF) + x = PA
PM + EF + AE + X + MA = PF
Тивякова Л.А.
№ 2 Найти число h, чтобы выполнялось равенство a = h*b, если…
Векторы сонаправлены, а длина вектора а в 4 раза больше длины вектора b.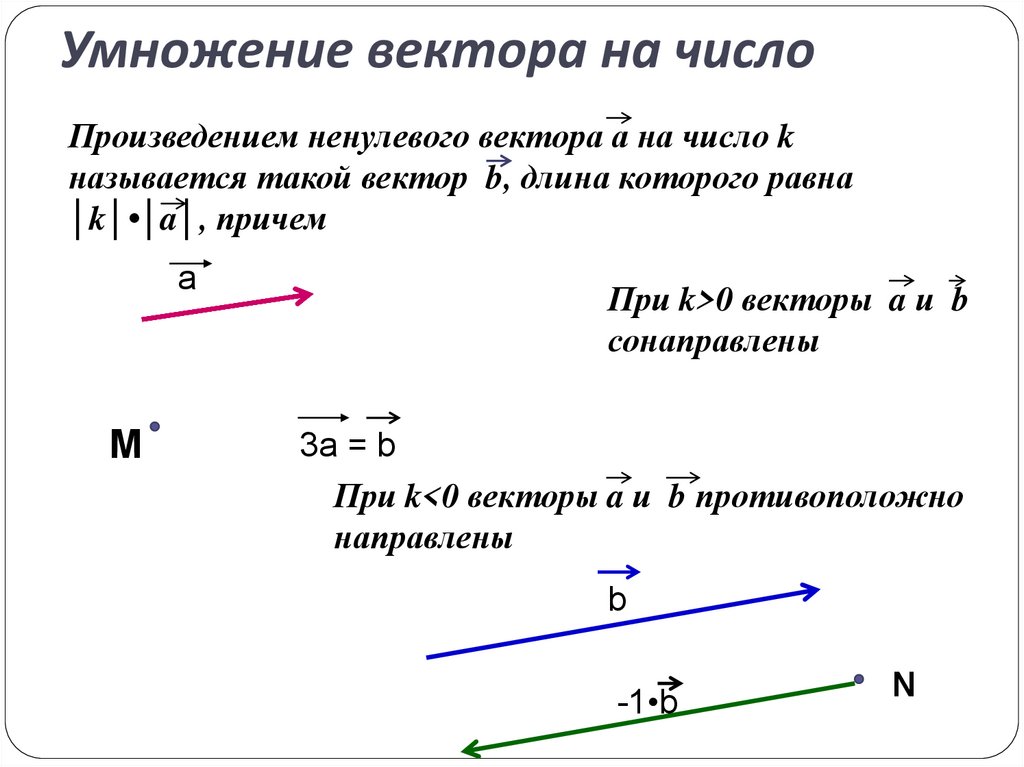
Векторы противоположно направлены, а длина вектора а в 2 раза больше длины вектора b.
Тивякова Л.А.
№ 4 Построить вектор х
Тивякова Л.А.
№ 4 Выразить векторы ВС, CD, AC, OC, OA через векторы а и b
Тивякова Л.А.
Скачать презентацию
Обратная связь
Если не удалось найти и скачать презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Email: Нажмите что бы посмотреть
Что такое ThePresentation.ru?
Это сайт презентаций, докладов, проектов, шаблонов в формате PowerPoint. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами с другими пользователями.
Для правообладателей
Понимание умножения векторов на действительные числа
Умножение векторов является важным инструментом во многих областях физики, включая расстояния, энергии, силы, проделанную работу, электрические или магнитные поля и многие другие приложения.
Умножение любого вектора на вещественное число называется скалярным умножением. Это умножение изменяет величину вектора, но не меняет его направление. Однако, если умноженная величина отрицательна, этого не будет, и направление будет обратным. Второй закон движения Ньютона и проделанная работа — два самых известных примера применения скалярного умножения векторов в физике.
Что происходит, когда мы умножаем вектор на вещественное числоКогда мы умножаем вектор на действительное число, величина вектора изменяется, однако это не влияет на направление вектора.
Например, |p·Ā| = р|А| если р>0.
Если p<0, то изменяются и величина, и направление вектора.
Умножение векторов Умножение векторов применяется в различных областях физики, таких как расстояние, энергии, силы, проделанная работа, электрическое или магнитное поле и многое другое. Векторы можно умножать двумя способами: скалярным умножением и векторным умножением. Мы обсудим скалярное умножение, то есть умножение вектора на действительное число.
Мы обсудим скалярное умножение, то есть умножение вектора на действительное число.
Умножение любого вектора на вещественное число называется скалярным умножением. Всякий раз, когда мы умножаем скалярную величину на любую векторную величину, величина вектора изменяется. Однако изменение его направления зависит от скалярной величины, на которую мы его умножаем. Если скалярная величина положительна, направление остается прежним, а если скалярная величина отрицательна, направление становится противоположным исходному направлению. Кроме того, если мы умножим вектор на ноль, он станет нулевым вектором (нулевым вектором).
Скалярное произведение двух векторов — это скалярное произведение их компонентов. Скалярное произведение двух векторов можно использовать для преобразования вектора в скаляр, представляющий его значение. Другими словами, скалярное произведение двух векторов — это скалярное значение, представляющее сумму элементов каждого вектора.
Скалярная формула произведения = A•B= |A| |Б| Cosθ
Свойства скалярного умножения- a·b — скалярная величина
- Если скалярное произведение двух векторов равно нулю, это означает, что они перпендикулярны друг другу. Это потому, что
А•В = |А| |Б| Cosθ = 0
Cosθ = 0 означает θ=90°
- Если скалярное произведение двух величин равно произведению их величин, это означает, что два вектора параллельны. Это потому, что Cosθ = 1 означает θ=0°
- Точно так же, если скалярное произведение двух векторов равно отрицательному результату произведения их величин, это означает, что они антипараллельны. Это связано с тем, что при Cos θ = -1 значение θ будет равно 180°.
- При решении скалярных произведений
i·i = j·j = k·k = 1 и i·j = i·k = j·k = 0 по тем же причинам, что и упомянутые выше.
- Cosθ = a.b/ |a||b|
- Точечные произведения (скалярные произведения) коммутативны по своей природе, т.
 е. a·b = b·a
е. a·b = b·a - Они также следуют дистрибутивному свойству a·(b+c) = a·b + a·c
Второй закон движения Ньютона — лучший пример умножения векторов на действительное число. Он утверждает, что сила прямо пропорциональна ускорению движения. Когда мы обращаемся к пропорциональности, мы умножаем уравнение на массу постоянного значения. Уравнение получается
F = ma
Здесь и сила, и ускорение являются векторными величинами, тогда как m является скалярной величиной. Сила получается умножением векторной величины на действительное число. Мы можем видеть, что это умножение ускорения только меняет его величину, чтобы дать величину силы, но не меняет направление силы. Сила приложена в направлении самого ускорения. Масса (m) всегда положительная величина. Следовательно, она не может быть меньше нуля, и, следовательно, направление силы не изменится.
Заключение Векторы можно перемножать двумя способами: скалярным умножением и векторным умножением. Умножение векторов имеет приложения в различных областях физики, таких как расстояние, энергии, силы, проделанная работа, электрическое или магнитное поле и многие другие. Всякий раз, когда мы умножаем скалярную величину на любую векторную величину, изменяется величина вектора. Если скалярная величина положительна, направление остается прежним, а если скалярная величина отрицательна, направление становится противоположным исходному направлению. Второй закон движения Ньютона утверждает, что сила прямо пропорциональна ускорению движения, и, таким образом, является хорошим примером скалярного умножения.
Умножение векторов имеет приложения в различных областях физики, таких как расстояние, энергии, силы, проделанная работа, электрическое или магнитное поле и многие другие. Всякий раз, когда мы умножаем скалярную величину на любую векторную величину, изменяется величина вектора. Если скалярная величина положительна, направление остается прежним, а если скалярная величина отрицательна, направление становится противоположным исходному направлению. Второй закон движения Ньютона утверждает, что сила прямо пропорциональна ускорению движения, и, таким образом, является хорошим примером скалярного умножения.
Умножение векторов на действительное число
Введение Умножение идет после сложения и вычитания в развитии простой арифметики. В векторном анализе умножение — это умножение вектора на скаляр, что соответствует скалярному умножению. A+A выражается как 2A, а A+ A+…n terms = n A, где n — скалярное значение. В векторном анализе есть еще один вид умножения, который включает произведение двух векторных значений. Векторные произведения введены потому, что они часто встречаются при исследовании физических задач.
Векторные произведения введены потому, что они часто встречаются при исследовании физических задач.
Существует два способа умножения двух векторов, оба из которых оказались чрезвычайно полезными при решении числовых задач. Мы знаем эти два метода как скалярное произведение и векторное произведение.
Зарегистрируйтесь, чтобы получить бесплатные пробные тесты и учебные материалы
Класс
—Класс 6Класс 7Класс 8Класс 9Класс 10Класс 11Класс 12
Вы ученик Шри Чайтаньи?
НетДа
+91
Подтвердить OTP-код (обязательно)
Я согласен с условиями и политикой конфиденциальности.
Безусловно, математика — это язык физики. Когда человек хорошо понимает математику, ему легче формулировать, интерпретировать и применять физические принципы. Мы также будем часто использовать алгебру, тригонометрию, геометрию, векторную алгебру, дифференциальное исчисление и интегральное исчисление. В этом курсе будут обсуждаться векторы, равенство векторов, единичные векторы и векторы положения. Используя простые алгебраические понятия, некоторые физические величины могут быть полностью математически описаны (с указанием единиц измерения) и добавлены. И даже если вы просто изучаете естественные науки, вам необходимо понимать векторы. Вы почти не можете думать о механике без них. Принципы необходимы для концептуальной ясности. Продолжайте изучать нашу страницу для получения дополнительной информации, связанной с физикой.
Используя простые алгебраические понятия, некоторые физические величины могут быть полностью математически описаны (с указанием единиц измерения) и добавлены. И даже если вы просто изучаете естественные науки, вам необходимо понимать векторы. Вы почти не можете думать о механике без них. Принципы необходимы для концептуальной ясности. Продолжайте изучать нашу страницу для получения дополнительной информации, связанной с физикой.
Используя два вектора в качестве входных данных, мы можем создать скалярное произведение
AB=ABcos?
Когда два вектора расположены хвост к хвосту, скалярное произведение равно произведению их модулей и косинуса меньшего угла между ними.
Геометрическая интерпретация скалярного произведенияМожно написать AB=ABcos? как AB=B(Acos?)
Таким образом, мы можем заключить, что AB=ABcos?
= Мера величины компонента в направлении A
=ABA
Свойства скалярного произведенияОтсюда следует коммутативное свойство
ab=ba
AB=ABcos?
AB=BAcos?
Отсюда следует распределительное свойство
a. (b + c) = a.b + a.c
(b + c) = a.b + a.c
Отсюда следует билинейное свойство
a.(rb + c) = r.(a.b) + (a.c)
Свойство скалярного умножения
(xa) . (yb) = xy (a.b)
Поскольку скалярное произведение скаляра и вектора запрещено, оно следует свойству неассоциативности.
Единичные векторы в направлениях осей x, y и z равны i, j и k соответственно
Если i × j = 0, то i × k = 0, а j × k = 0, тогда
Единица равна j × j, единица равна k × k, единица равна единице
Если a=a1i+a2j+a3k и b=b1i+b2j+b3k
ab=a1b1+a2b2+a3b3
Примечание: Интересный способ запомнить это — перемножить компоненты I и j, затем перемножить компоненты k и k и, наконец, просуммировать результаты. Эту форму иногда называют скалярным произведением векторов a и b. Это просто означает сумму произведений соответствующих компонентов вектора в контексте векторов.
Применение скалярного произведения Используя два вектора, найдите угол между ними Когда два вектора записаны в декартовой форме, одним из наиболее типичных применений скалярного произведения является вычисление угла между ними.
Из определения скалярного произведения
a · b = |a| |б| cos θ
Перестановкой можно получить следующее выражение для cos θ:
cos θ =a · b/|a| |б|
Сила и перемещение вместе определяют работу, совершаемую постоянной силой.
Умножение на векторГеометрически площадь параллелограмма, образованного двумя векторами, называется перекрестным произведением или векторным умножением/произведением.
Название «перекрестное произведение» происходит от символа, используемого для обозначения этой операции, который представляет собой огромный диагональный крест (). Этот продукт также известен как векторный продукт, потому что он содержит величину и направление.
AB=ABsin?n
Единичный вектор, перпендикулярный плоскости, образованной двумя векторами, равен n (n шляпа). Правило правой руки определяет направление n.
Перекрестное произведение является дистрибутивным
Это определяется как (A × B + C) = (A × B + C)
, но не коммутативно
A × B = −B × A
Стоит отметить, что величина векторного произведения любого единичного вектора на любой другой равна единице. (В конце концов, синус 90° равен единице.) Однако ориентация сразу не видна. Используя правило правой руки для перекрестного умножения, мы можем определить направление двух векторов, а также их произведение. Чрезвычайно важно правильно упорядочить операции, потому что перекрестное умножение не является коммутативным.
(В конце концов, синус 90° равен единице.) Однако ориентация сразу не видна. Используя правило правой руки для перекрестного умножения, мы можем определить направление двух векторов, а также их произведение. Чрезвычайно важно правильно упорядочить операции, потому что перекрестное умножение не является коммутативным.
- Держите правую руку горизонтально и перпендикулярно пальцам, при этом большой палец должен быть перпендикулярен пальцам. Ни в коем случае нельзя сгибать большой палец.
- Укажите пальцами в направлении первого вектора.
- Расположите ладонь так, чтобы при сгибании пальцы указывали в направлении второго вектора.
- Теперь большой палец у векторного произведения указывает правильно.
Любое циклическое произведение трех осей координат положительно, тогда как любое антициклическое произведение отрицательно в правой системе координат, которая является наиболее распространенной системой координат, используемой в физике и математике. Рассмотрим часы, которые отображают три буквы x-y-z вместо традиционных двенадцати цифр. Циклическим и положительным произведением этих трех букв является такое, которое работает круглосуточно в том же направлении, что и последовательность x-y-z. Антициклические и негативные продукты — это те, которые работают в противоположном направлении.
Рассмотрим часы, которые отображают три буквы x-y-z вместо традиционных двенадцати цифр. Циклическим и положительным произведением этих трех букв является такое, которое работает круглосуточно в том же направлении, что и последовательность x-y-z. Антициклические и негативные продукты — это те, которые работают в противоположном направлении.
Читайте также: Сложение и вычитание векторов
Часто задаваемые вопросыВопрос 1: Как вычислить векторно-скалярное умножение?
Ответ: В три простых шага можно определить скалярное умножение векторов. Для начала вычислите величину двух векторов a и b, т. е. |a| и |б|. Затем вычислите косеканс угла, образованного двумя векторами. Чтобы получить скалярное произведение двух векторов, умножьте величину двух векторов на и косеканс угла между двумя векторами. A B=ABcos?
Вопрос 2: Почему скалярное умножение векторов называется скалярным произведением?
Ответ: Поскольку все компоненты решения являются скалярными величинами, скалярное произведение называется скалярным умножением векторов.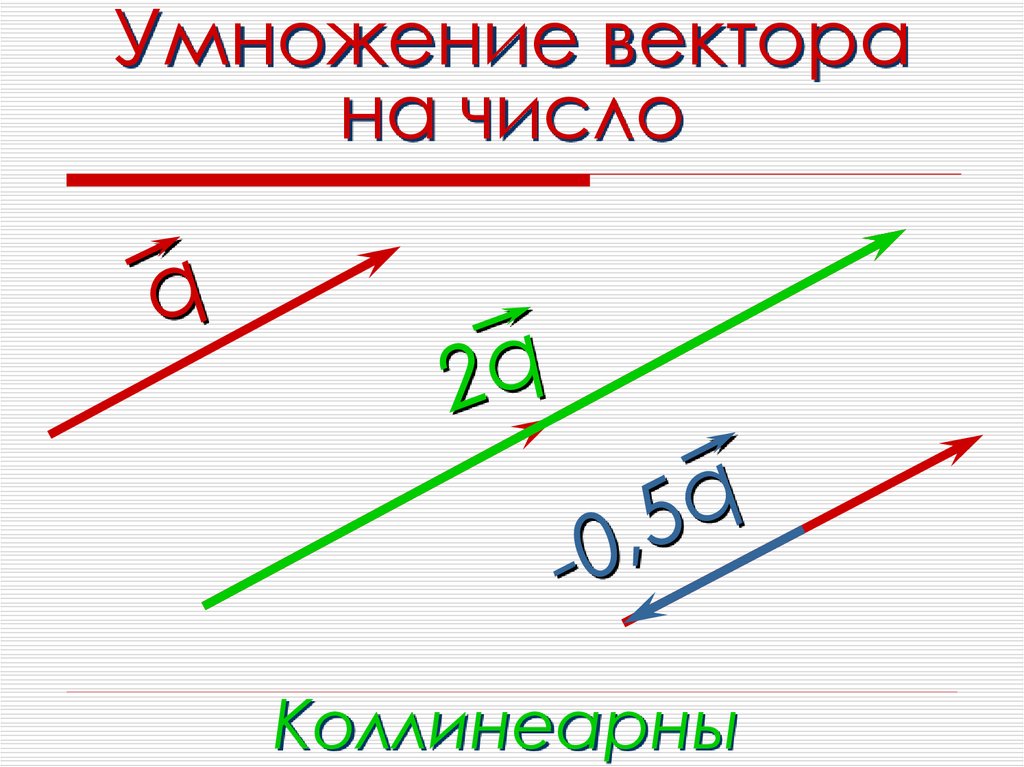


 е. a·b = b·a
е. a·b = b·a