Аналитическая геометрия
Аналитическая геометрия
ОглавлениеВВЕДЕНИЕЧАСТЬ ПЕРВАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ ГЛАВА I. МЕТОД КООРДИНАТ § 2. Координаты на прямой линии. § 3. Расстояние между двумя точками на прямой линии. § 4. Прямоугольные координаты на плоскости. § 5. Расстояние между двумя точками на плоскости. § 6. Деление отрезка в данном отношении. § 7. Угол между двумя осями. § 8. Основные положения теории проекций.  § 9. Проекции направленного отрезка на оси координат. § 10. Площадь треугольника. § 11. Полярные координаты. Упражнения ГЛАВА II. ЛИНИИ И ИХ УРАВНЕНИЯ § 1. Составление уравнений заданных линий. § 2. Геометрический смысл уравнений. § 3. Две основные задачи. § 4. Пересечение двух линий. § 5. Параметрические уравнения линий. § 6. Уравнения линий в полярных координатах. ГЛАВА III. ПРЯМАЯ ЛИНИЯ § 1. Угловой коэффициент прямой. § 2. Уравнение прямой линии с угловым коэффициентом. § 3. Геометрический смысл уравнения первой степени между двумя переменными. § 4. Исследование общего уравнения первой степени Ах + Ву + С = 0. § 5. Уравнение прямой линии в отрезках. § 7. Угол между двумя прямыми. § 8. Условия параллельности и перпендикулярности двух прямых. § 9. Уравнение прямой, проходящей через данную точку в данном направлении. § 10. Взаимное расположение двух прямых на плоскости.  § 11. Уравнение пучка прямых. § 12. Уравнение прямой, проходящей через две данные точки. § 13. Условие, при котором три данные точки лежат на одной прямой. § 14. Нормальное уравнение прямой линии. § 15. Приведение общего уравнения первой степени к нормальному виду. § 17. Уравнение прямой в полярной системе координат. Упражнения ГЛАВА IV. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ КОНИЧЕСКИХ СЕЧЕНИЙ § 2. Окружность. § 3. Эллипс. § 4. Гипербола и ее асимптоты. § 5. Парабола. § 6. Построение точек эллипса, гиперболы и параболы посредством циркуля и линейки. § 7. Эллипс, гипербола и парабола как конические сечения. § 8. Эксцентриситет и директрисы эллипса. § 9. Эксцентриситет и директрисы гиперболы. § 10. Эксцентриситет и директриса параболы. § 11. Уравнение конического сечения в полярных координатах. § 12. Диаметры зллипса. Сопряженные диаметры. § 13. Диаметры гиперболы. Сопряженные диаметры.  § 14. Диаметры параболы. § 15. Касательная. § 16. Эллипс как проекция окружности. § 17. Параметрические уравнения эллипса. Упражнения ГЛАВА V. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. КЛАССИФИКАЦИЯ ЛИНИЙ § 2. Перенос начала координат. § 3. Поворот осей координат. § 4. Общий случай. § 5. Некоторые приложения формул преобразования координат. § 6. Преобразование общего уравнения второй степени, не содержащего произведения переменных. § 7. Преобразование общего уравнения второй степени. § 8. Классификация линий. Упражнения ГЛАВА VI. ОПРЕДЕЛИТЕЛИ 2-го и 3-го ПОРЯДКА § 3. Определители 3-го порядка. § 4. Основные свойства определителей 3-го порядка. § 5. Система трех уравнений первой степени с тремя неизвестными. § 6. Однородная система. § 7. Общее исследование системы трех уравнений первой степени с тремя неизвестными. § 8. Некоторые приложения определителей к аналитической геометрии.  Упражнения ЧАСТЬ ВТОРАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ ГЛАВА I. МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ § 2. Основные задачи. § 3. Основные положения теории проекций в пространстве. § 4. Вычисление угла между двумя осями в пространстве. ГЛАВА II. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ § 2. Сложение векторов. § 3. Вычитание векторов. § 4. Умножение вектора на число. § 5. Проекции вектора. § 6. Действия над векторами, заданными своими проекциями. § 7. Скалярное произведение векторов. § 8. Основные свойства скалярного произведения. § 9. Скалярное произведение векторов, заданных проекциями. § 10. Направление вектора. § 11. Векторное произведение. § 12. Основные свойства векторного произведения. § 13. Векторное произведение векторов, заданных проекциями. § 14. Векторно-скалярное произведение. § 15. Векторно-скалярное произведение в проекциях. § 16. Двойное векторное произведение. ГЛАВА III.  ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЙ§ 1. Уравнение поверхности. § 2. Геометрический смысл уравнений. § 3. Две основные задачи. § 4. Сфера. § 5. Цилиндрические поверхности. § 6. Уравнения линии в пространстве. § 7. Пересечение трех поверхностей. Упражнения ГЛАВА IV. ПЛОСКОСТЬ § 1. Нормальное уравнение плоскости. § 2. Геометрический смысл уравнения первой степени между тремя переменными. Приведение общего уравнения первой степени к нормальному виду. § 3. Исследование общего уравнения плоскости. § 5. Уравнение плоскости, проходящей через данную точку. § 6. Уравнение плоскости, проходящей через три данные точки. § 7. Угол между двумя плоскостями. § 8. Условия параллельности и перпендикулярности двух плоскостей. § 9. Точка пересечения трех плоскостей. § 10. Расстояние от точки до плоскости. Упражнения ГЛАВА V. ПРЯМАЯ ЛИНИЯ § 1. Уравнения прямой линии. § 2. Прямая как линия пересечения двух плоскостей.  Общие уравнения прямой.§ 3. Угол между двумя прямыми линиями. § 4. Условия параллельности и перпендикулярности двух прямых. § 6. Угол между прямой и плоскостью. § 7. Условия параллельности и перпендикулярности прямой и плоскости. § 8. Уравнение пучка плоскостей. § 9. Пересечение прямой с плоскостью. § 10. Условие, при котором две прямые лежат в одной плоскости. Упражнения ГЛАВА VI. ЦИЛИНДРИЧЕСКИЕ И КОНИЧЕСКИЕ ПОВЕРХНОСТИ. ПОВЕРХНОСТИ ВРАЩЕНИЯ. ПОВЕРХНОСТИ 2-го ПОРЯДКА § 1. Классификация поверхностей. § 2. Цилиндрические поверхности (общий случай). § 3. Конические поверхности. § 4. Поверхности вращения. § 5. Эллипсоид. § 6. Однополостный гиперболоид. § 7. Двуполостный гиперболоид. § 9. Гиперболический параболоид. § 10. Конус 2-го порядка. § 11. Цилиндры 2-го порядка. § 12. Прямолинейные образующие поверхностей 2-го порядка. 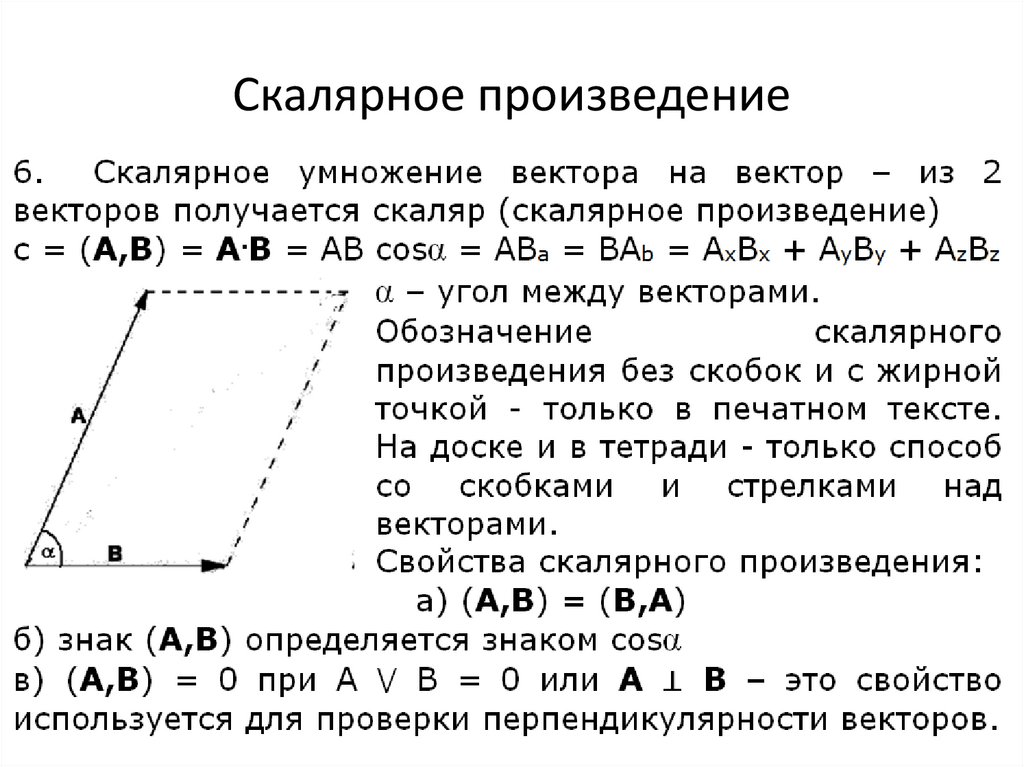 Конструкции В. Г. Шухова.Упражнения Ответы |
Координатный метод. Часть 4
Преподаватель
Князева Светлана Евгеньевна
Линейные операции над векторами
Линейные операции над элементами — операции сложения и вычитания элементов и их умножения на скаляр
Линейные операции над векторами
Сумма векторов а и b – вектор c.
В координатах: а (a x ;a y ;a z ) и b (b x ;b y ;b z ):
а + b=(a x +b x ;a y +b y ;a z +b z )
Геометрически:
Правило треугольника Правило параллелограмма
Линейные операции над векторами
Разность векторов а и b – вектор c.
В координатах: а (a x ;a y ;a z ) и b (b x ;b y ;b z ):
а — b=(a x -b x ;a y -b y ;a z -b z )
Геометрически:
3
Линейные операции над векторами
Умножение вектора а на число λ – вектор c.
В координатах: а (a x ;a y ;a z )
λ · а=( λ · a x ; λ
Геометрически:
a
λ
λ0
λ · a
λ · a
4
Скалярное произведение векторов
Скалярным произведением двух векторов называется число, равное произведению их длин на косинус угла между ними.
a
a
b
a
b
cos ( )
b
=
Скалярное произведение векторов – число (скаляр). Скаляр – лат. scale – лестница, шкала.
Ввел в 1845г. У. Гамильтон, английский математик.
5
Свойства скалярного произведения векторов
1. Скалярное произведение обладает переместительным свойством, то есть
2. Скалярное произведение обладает распределительным свойством, то есть
3. Скалярное произведение обладает сочетательным свойством относительно
числового множителя, то есть
6
Свойства скалярного произведения векторов
4. Скалярное произведение вектора самого на себя называется скалярным квадратом вектора. Скалярный квадрат вектора равен квадрату его модуля.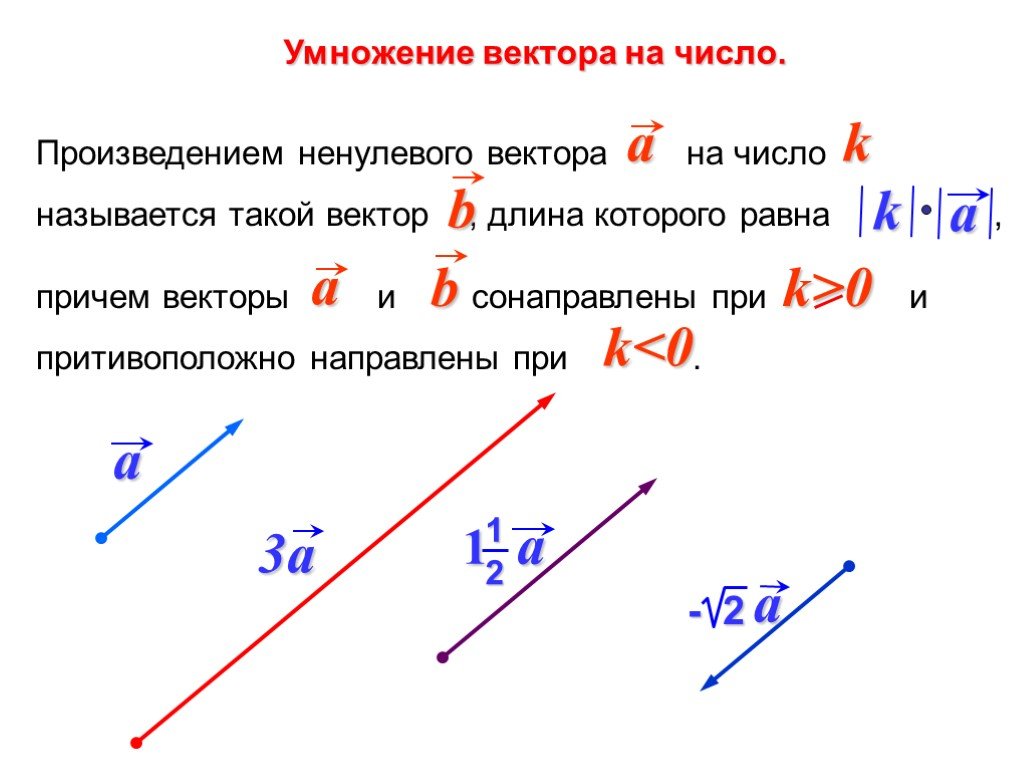
То есть
5. Скалярное произведение одноименных ортов равно единице
6
Свойства скалярного произведения векторов
6. Скалярное произведение разноименных ортов равно нулю.
7. Скалярное произведение векторов, заданных своими координатами:
6
Свойства скалярного произведения векторов
8. Угол между двумя векторами:
9. Если , то
10. Проекция вектора а на вектор b
6
Свойства скалярного произведения векторов
Следствие свойства 4 – с калярный квадрат вектора равен квадрату его модуля
8. Угол между двумя векторами:
9.
6
Свойства скалярного произведения векторов
Скалярное произведение ненулевых векторов положительно тогда и только тогда , когда угол между векторами острый.
6
Свойства скалярного произведения векторов
Скалярное произведение ненулевых векторов отрицательно тогда и только тогда , когда угол между векторами тупой.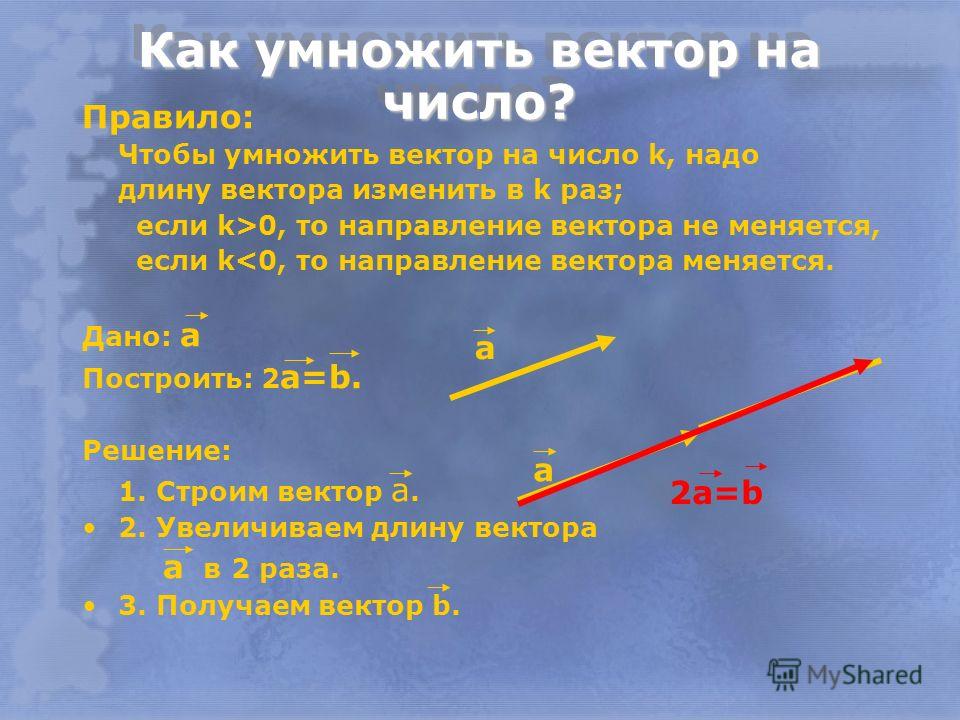
Скалярное произведение ненулевых сонаправленных векторов равно произведению длин этих векторов.
6
Свойства скалярного произведения векторов
Скалярное произведение ненулевых противоположно направленных векторов равно произведению длин этих векторов, взятых со знаком минус.
6
Пример 14
Все ребра тетраэдра АВСD равны друг другу. Точки М и
N – середины ребер АD и ВС. Докажите, что
A
M
D
B
N
C
6
Решение.
A
Проведем в основании BCD DN – медиана (по условию задачи) и в боковой грани АВС AN – медиана (по условию задачи). Все ребра тетраэдра равны между собой, следовательно, и все грани также равны друг другу, а, значит и медианы всех треугольников также равны.
Т.о.
M
D
B
N
C
равнобедренный. Т.к. М – середина AD (по условию задачи), то MN – медиана, а значит и высота, т.е.
ч.т.д
15
Пример 15
ABCDA 1 B 1 C 1 D 1 — куб, AB = a . Вычислите скалярное произведение векторов:
AD · B 1 C 1 В A 1 · В C 1
D 1
C 1
А 1
B 1
D
C
B
А
16
Решение.
D 1
C 1
а 2
а
А 1
B 1
Треугольник BA 1 C 1 правильный. Стороны его равны как диагонали равных квадратов:
D
C
а
B
А
а
17
Пример 16
Дан прямоугольный параллелепипед ABCDA 1 B 1 C 1 D 1 , DA =1, DC =2, DD 1 =3.
Найдите угол между прямыми CB 1 и D 1 B .
D 1
C 1
А 1
B 1
D
C
B
А
Решение.
Две пересекающиеся прямые образуют смежные и вертикальные углы. Вертикальные углы равны, а смежные углы дополняют друг друга до 180°. Угловая мера меньшего из них называется углом между прямыми. Как было отмечено ранее
19
z
Введём систему координат Dxyz . Рассмотрим векторы
CB 1 и D 1 B .
D 1
C 1
А 1
D 1 (0; 0; 3), B (1; 2; 0)
B 1
3
D 1 B (1; 2; – 3)
C (0; 2; 0), B 1 (1; 2; 3),
C
2
СВ 1 (1; 0; 3)
y
1
D
А
B
D 1 B · CB 1
cos(D 1 B , CB 1 )=
x
D 1 B · CB 1
D 1 B (1; 2; – 3)
СВ 1 (1; 0; 3)
D 1 B · CB 1 =?
D 1 B = ?
СВ 1 = ?
21
СВ 1 (1; 0; 3)
D 1 B (1; 2; – 3)
D 1 B · CB 1 =1·1+0 ·2+3 ·(-3)=-8
D 1 B = √ 1 2 +2 2 +(-3) 2 = √ 14
CB 1 = √ 1 2 +0 2 +3 2 = √ 10
8
8
cos(D 1 B , CB 1 )= =
√ 14 · √ 10
2 · √ 35
4
cos(D 1 B , CB 1 )=
(D 1 B , CB 1 ) 47 0
√ 35
22
Пример 17
О
Дана правильная пирамида, сторона основания которой
a = .
Высота пирамиды ОК=2.
Найдите угол между
боковым ребром пирамиды
и плоскостью ее основания.
2
C
B
К
A
D
23
Решение.
О
Будем искать угол между боковым ребром пирамиды и плоскостью ее основания, как угол между СО и СК.
Длина вектора СК – радиус описанной окружности около АВСD – квадрата, следовательно
2
B
C
К
A
D
24
О
Т.о. длина СК равна длине ОК, следовательно треугольник ОСК – равнобедренный, а значит искомый угол равен 45 0 .
2
B
C
К
A
D
25
Вопрос 1:
Как называется этот многогранник?
D 1
C 1
А 1
B 1
а
D
C
а
B
А
а
26
Вопрос 2:
Как называется BD 1 ?
D 1
C 1
А 1
B 1
D
C
B
А
27
Вопрос 3:
Как называется CB 1 ?
D 1
C 1
B 1
А 1
D
C
B
А
28
Прямые не пересекаются и не параллельны — такие прямые называются скрещивающимися .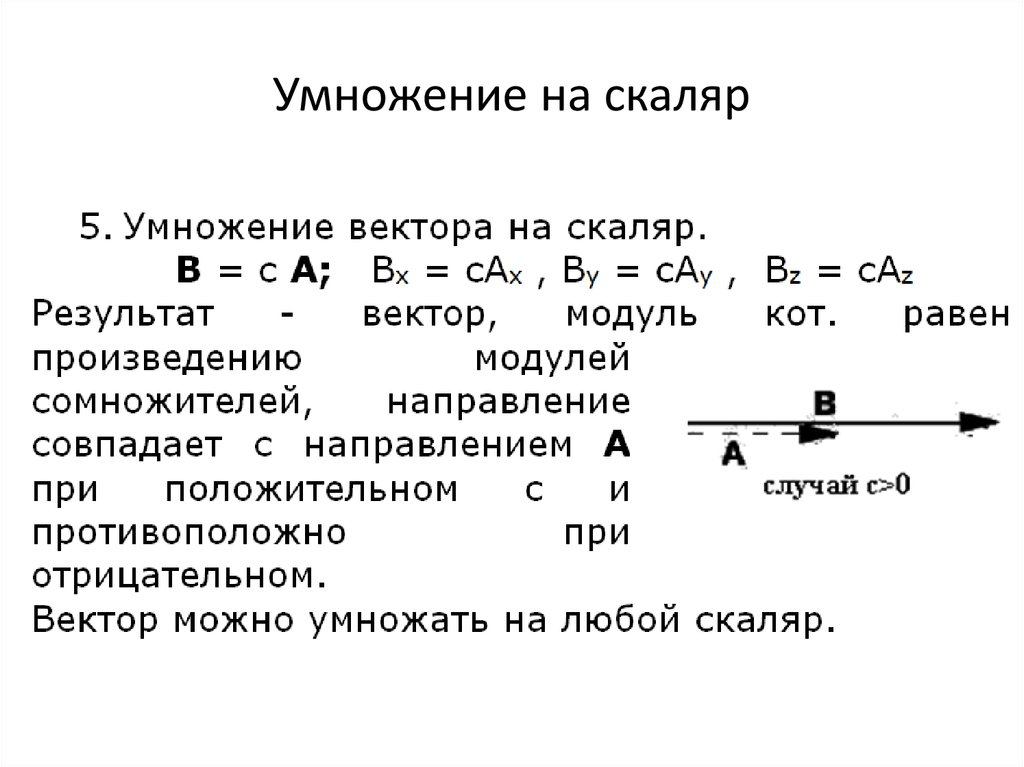
α
a
β
b
29
Теорема . Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.
a
α
b
30
Пример 18
Докажите, что угол между скрещивающимися прямыми, одна из которых содержит диагональ куба, а другая — диагональ грани куба, равен 90°.
D 1
C 1
А 1
B 1
D
C
B
А
31
Решение.
D 1
В качестве первой прямой возьмем, например, диагональ куба – BD 1 .
В качестве второй прямой возьмем диагональ грани СС 1 В 1 В, которая не имеет общих точек с BD 1 – СВ 1 .
C 1
А 1
B 1
D
C
B
А
32
Пусть ABCDA 1 B 1 C 1 D 1 — куб с ребром a.
D 1
C 1
Если прямые BD 1 и СВ 1 перпендикулярны, то вектора BD 1 и СВ 1 — ортогональны.
А 1
B 1
D
C
По свойствам скалярного произведения:
B
А
BD 1 · СВ 1 0
BD 1 СВ 1
33
D 1
C 1
Найдем BD 1 :
BD 1 =BD+DD 1 , а DD 1 =BB 1 , следовательно BD 1 =BD+ВВ 1
А 1
B 1
ВD=BA+BC, тогда
D
C
BD 1 =BA+BC+ВВ 1
B
А
34
D 1
C 1
Найдем СВ 1 :
А 1
B 1
СВ 1 =BB 1 -BC
BD 1 · СВ 1 0
D
C
BD 1 СВ 1
B
А
BD 1 =BA+BC+ВВ 1
Тогда, т.к.
(BA+BC+ВВ 1 ) ·
BD 1 · СВ 1
(ВВ 1 -ВС)
35
BD 1 · СВ 1
BA · BB 1 -BA ·BC+BC ·BB 1 -BC ·BC+BB 1 ·BB 1 -BB 1 ·BC
D 1
BA и BB 1 , ВА и ВС, ВС и ВВ 1 – ортогональны, т.
к. лежат на гранях куба, следовательно их скалярное произведение равно нулю. Тогда
C 1
А 1
B 1
D
C
B
А
BD 1 · СВ 1 — BC + BB 1
2
2
Т.к. все ребра куба – равны а, то
Ч.Т.Д.
36
Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на плоскость – угол АВК
А
В
К
37
Теорема. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.
с
b
а
α
a c и b c c
37
Пример 19
Дана пирамида с вершиной в точке D(1;10;8), основание которой – треугольник, построенный на векторах АВ и АС.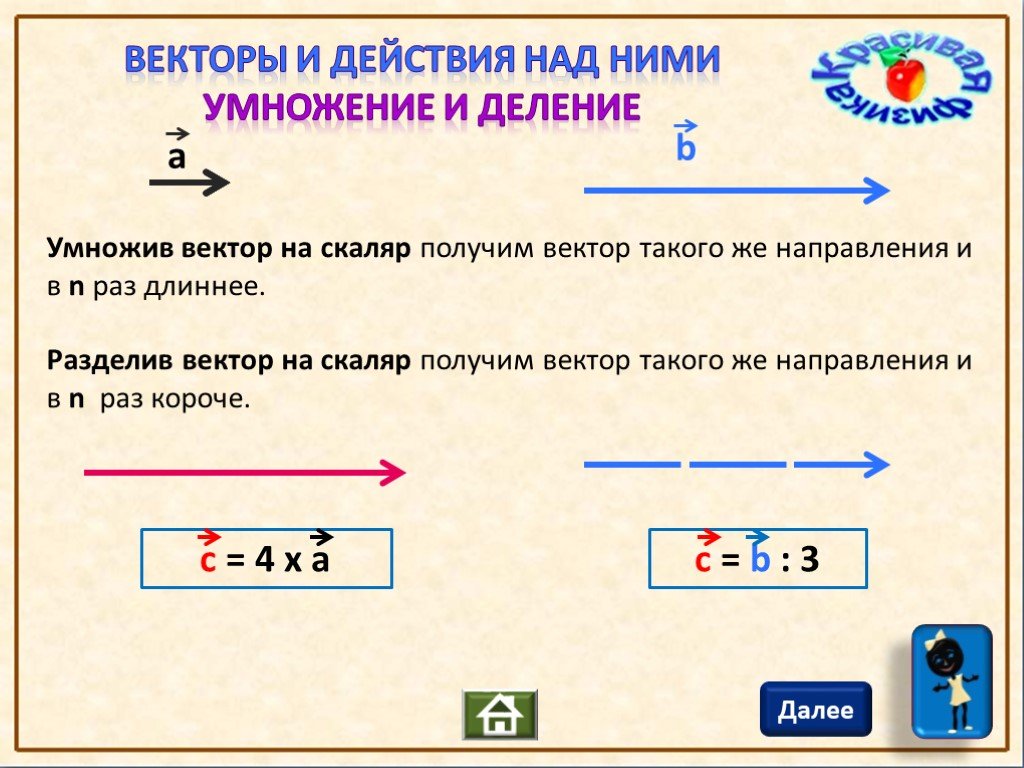
Докажите, что ребро AD перпендикулярно основанию АВС. Найдите объем пирамиды.
Решение.
Выполним чертеж: D(1;10;8), А(1;2;0), B(3;-2;4), C(3;6;-4)
z
D
B
O
y
A
x
C
Для того, чтобы доказать, что боковое ребро AD перпендикулярно основанию АВС, нам необходимо доказать, что вектор AD ортогонален векторам АВ и АС
41
D(1;10;8), А(1;2;0), B(3;-2;4), C(3;6;-4)
АD · АВ 0
АD АВ
АD · АВ =0·2+8 ·(-4)+8 ·4=0
41
D(1;10;8), А(1;2;0), B(3;-2;4), C(3;6;-4)
АD · АС 0
АD АС
АD · АС =0·2+8 ·4+8 ·(-4)=0
Итак АD ортогонален и вектору АВ и вектору АС, следовательно он ортогонален плоскости основания.
43
Объем пирамиды равен одной трети произведения площади ее основания на высоту.
Мы доказали, что AD – высота нашей пирамиды.
Найдем площадь основания по формуле Герона:
44
D(1;10;8), А(1;2;0), B(3;-2;4), C(3;6;-4)
ВС(3-3;6+2;-4-4) ВС (0;8;-8)
Найдем длины этих векторов:
44
46
46
Пусть векторы A⃗ =(2,1,−4), B⃗ =(−3,0,1) и C⃗ =(−1,−1,2). Рассчитайте следующее: — Справка по работе на дому
прасанна
#1
Пусть векторы A⃗ =(2,1,−4), B⃗ =(−3,0,1) и C⃗ =(−1,−1,2).
Вычислите следующее:
A) A⃗ ⋅B⃗ =
B) Чему равен угол θAB между A⃗ и B⃗?
C) 2B⃗ ⋅3C⃗ =
D)2(B⃗ ⋅3C⃗ ) =
E)Что из следующего можно вычислить?
F) Выразите ответ через V1: V⃗ 1⋅V⃗ 1 =
G) Если V⃗ 1 и V⃗ 2 перпендикулярны,
H) Если V⃗ 1 и V⃗ 2 параллельны,
Выразите ответ в терминах V1 и V2.
Понятия и причины
Основным понятием, используемым для решения задачи, являются векторные операции.
Сначала используйте компоненты заданных векторов, чтобы найти величину векторов. найти скалярное произведение вектора, используя компоненты вектора. Позже используйте скалярное произведение векторов и величину вектора, чтобы найти угол между векторами. Наконец, умножьте векторы на соответствующие константы и рассчитайте скалярное произведение.
Основы
Умножение вектора на константу можно выполнить, умножив компонент вектора на константу.
Скалярное произведение двух векторов является скаляром.
Ответ:
(А)
Перекрестное произведение двух векторов представляет собой сумму произведений компонентов векторов.
(Б)
Угол между двумя векторами зависит от скалярного произведения векторов и величины векторов.
(К)
Скалярное произведение вектора должно умножаться на константу, чтобы получить скалярное произведение векторов, умноженных на константы.
(D)
Скалярный продукт,
Константу можно убрать, а скалярное произведение одного только вектора можно умножить на константы.
(E)
Скалярное произведение может принимать только два вектора. Скалярное произведение дает скалярное значение.
В (a) скалярное произведение первых двух векторов дает скаляр, а третий вектор нельзя использовать для скалярного произведения. Следовательно, уравнение не вычислимо.
В (b) скалярное произведение между двумя последними векторами дает скаляр, а первый вектор не может быть взят дальше для скалярного произведения со скалярным значением. Следовательно, уравнение не вычислимо.
В (c) сложение двух последних векторов дает вектор, а первый вектор можно использовать для скалярного произведения суммы двух последних векторов.
Следовательно, уравнение вычислимо.
В (d) 3 является скаляром, следовательно, вектор не может подвергаться скалярному произведению с рубцом. Уравнение не вычислимо.
Вычислимой операцией является ( c) .
Часть E
Вычислимой операцией является (c) .
(F)
Скалярное произведение одиночного вектора с самим собой есть квадрат величины вектора.
(G)
Скалярное произведение двух векторов, перпендикулярных друг другу, равно нулю.
(H)
Скалярное произведение двух параллельных векторов равно произведению их величин.
Обзор умножения векторов на скаляр
Умножение векторов на скалярную величину
При наличии скалярной величины величина вектора изменяется пропорционально величине скаляра, но направление вектора не меняется совсем.
Векторы и скаляры перемножаются
Вопреки их представлению различных видов физических атрибутов, векторы и скаляры часто взаимодействуют друг с другом, чтобы быть полезными.
Сопоставить две скалярные и две векторные величины вместе почти невозможно из-за несоответствия размерностей между двумя типами величин. Когда речь идет о векторных величинах, их можно умножать на скалярные величины, но не наоборот. Однако невозможно произвести противоположное следствие в тот же самый момент. Поэтому, как бы вы ни старались, скаляр никогда не умножается на вектор.
Арифметическое умножение используется для объединения величин, которые подобны друг другу, когда векторы и скаляры перемножаются вместе. Другими словами, величина векторов умножается на величину скалярных величин для получения окончательного результата. Операция умножения добавления векторов к скалярам дает вектор как результат операции сложения. В отличие от исходного вектора, вектор произведения имеет такое же направление, как и вектор, умноженный на скаляр, а его величина увеличивается на число, умноженное на произведение величин вектора и скаляра, умноженных на каждый другой.
Иллюстрация
Рассмотрим следующий сценарий: у нас есть вектор a
Этот вектор умножается на скалярную величину k, и в результате получается другой вектор с величиной, равной ka, и направление вектора остается таким же, как и раньше.
А пока давайте наглядно проиллюстрируем скалярное умножение вектора.
Предположим, что значения «k» = 2,3,-3,-½ и так далее.
Из набора векторов, представленного выше, мы можем заметить, что направление каждого вектора равно
Когда значение скаляра положительное, направление стрелки остается неизменным; когда значение скаляра отрицательное, направление стрелки становится прямо противоположным; и в обоих случаях величина стрелки изменяется в зависимости от значений скалярного множителя.
В свете предыдущих рассуждений мы можем заметить, что
ka= |k|a
Предположим, что значение скалярного кратного k равно -1, и мы знаем, что результирующий вектор получается из скалярного умножения, что это
после этого
a+(-a) = 0 есть. Вектор -a
Этот символ символизирует отрицательную или аддитивную инверсию вектора.
Рассмотрим следующий сценарий: значение k =1/|a|
с учетом того, что значение a не равно нулю
В этом случае имеем свойство скалярной кратности векторов.
ка равно |k|a
=1/| a|xa
Кроме того, как обсуждалось ранее, если k = 0, вектор также сводится к нулю.
Рассмотрим следующую иллюстрацию, чтобы лучше понять, что я пытаюсь сказать:
В качестве иллюстрации вектор представлен в ортогональной системе следующим образом:
a = 3i + j + k
Что получится в результате вектор, если это произойдет?
это ответ, умноженный на 5?
Из-за того, что вектор должен быть умножен на скаляр, результирующее произведение равно
5a = 5(3i + j + k)
Или 5a = 15i + 5j + 5k
Умножение векторов
Умножение векторов — это математический термин, который относится к одной из многочисленных стратегий умножения двух (или более) векторов на самих себя.
Это может быть связано с любой из следующих статей:
«Скалярное произведение», иногда известное как «точечный продукт», — это бинарная операция, которая принимает два вектора и создает другой вектор с одной скалярной величиной. Если два вектора перемножить, произведение их величин и косинуса угла между двумя векторами можно определить как скалярное произведение. В качестве альтернативного определения он определяется как произведение проекции первого вектора на второй вектор и величины второго вектора. В результате А ⋅ В = |А| |Б| потому что θ
«Векторное произведение» — это бинарная операция над двумя векторами, которая дает другой вектор. Он также известен как «перекрестное произведение» или «векторное произведение». В частности, перекрестное произведение двух векторов в трехмерном пространстве определяется как вектор, перпендикулярный плоскости, определяемой двумя векторами, величина которых является произведением их величин, а также синусоидальной функцией, полученной из угла между двумя векторами.
