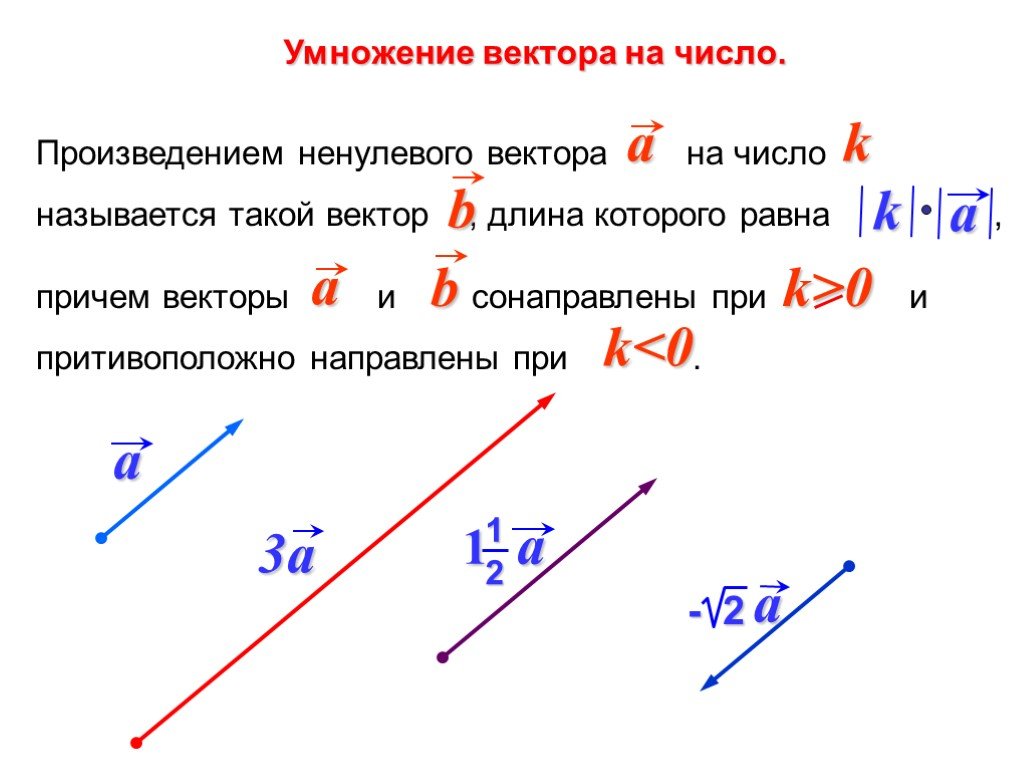
Умножение векторов
Умножение вектора на вектор бывает двух типов: скалярное и векторное. В результате скалярного умножения двух векторов получаем число (скаляр). В результате векторного произведения двух векторов получаем вектор. Скалярным произведением двух ненулевых векторов и называется число, равное произведению длин этих векторов на косинус угла между ними: , где .
Свойства скалярного произведения во многом сходны со свойствами произведения действительных чисел.
Векторным произведением двух векторов и называется вектор , который:
имеет модуль, численно равный площади параллелограмма, построенного на векторах и : ;
перпендикулярен к плоскости этого параллелограмма;
направлен в такую сторону, с которой кратчайший поворот от к рассматривается совершающимся против часовой стрелки (такое расположение векторов , и называется правой тройкой векторов).
Отличительная особенность векторного произведения состоит в том, что для него переместительное свойство (коммутативность) не имеет места. От перестановки векторов – сомножителей векторное произведение изменяет знак на противоположный: .
Три вектора могут быть перемножены несколькими способами. Чаще всего рассматривают смешанное произведение двух векторов векторно и на третий скалярно.В результате получают число.
Смешанное произведение трех векторов , и , которое обозначается или , есть скаляр, абсолютная величина которого равна обьему параллелепипеда, построенного на векторах , и , как на ребрах.
Указанные произведения векторов и их свойства достаточно просто выражаются через их прямоугольные координаты, т.е. координаты векторов в базисе , по сравнению с аналогичными выражениями в произвольном базисе , которых мы не приводим.
Пусть
заданы два вектора и .
Скалярное произведение двух ненулевых векторов равно сумме произведений соответствующих координат этих векторов:
.
Угол между векторами вычисляется по формуле
,
или в координатной форме .
Проекция вектора на ось вектора находится из соотношения:
,
или в координатной форме .
Если учесть, что — орт вектора, то .
Условием перпендикулярности ненулевых векторов и является равенство нулю их скалярного произведения:
.
Векторное произведение ненулевых векторов выражается через координаты данных векторов и следующим образом:
.
Равенство нулю векторного произведения двух ненулевых векторов является условием их коллинеарности, т.е. .
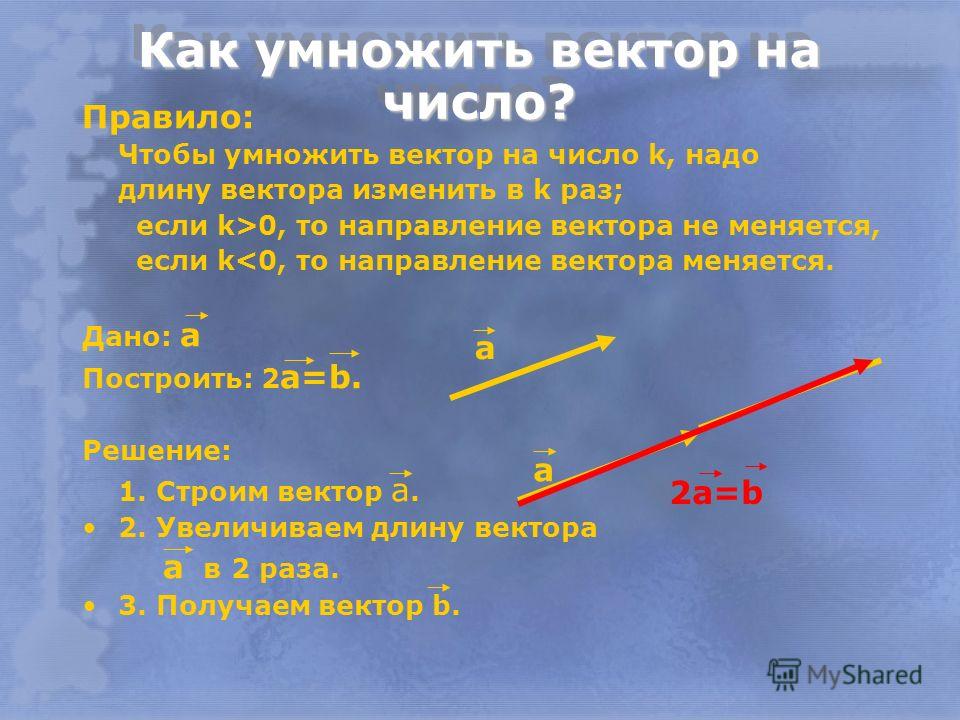
Скаляр , представляющий смешанное произведение трех векторов, равняется определителю третьего порядка, составленному из координат этих трех векторов:
.
Равенство нулю смешанного произведения трех ненулевых векторов является условием их компланарности: .
Координаты вектора зависят от выбора базиса. Выбор базиса ничем не ограничен, и принципиальное значение имеет задача о нахождении координат вектора в одном базисе по его координатам в другом базисе. Выясним, как устанавливается связь между координатами одного и того же вектора в различных базисах.
Пусть в пространстве имеются два базиса: старый и новый . Каждый из векторов (i =1,2,3) нового базиса можно выразить в виде линейной комбинации векторов старого базиса:
.
Матрица (i,k=1,2,3) называется матрицей перехода от старого базиса к новому. Базисные векторы (i =1,2,3) линейно независимы, поэтому матрица неособенная.
Обратный
переход от нового базиса к старому
базису осуществляется с помощью обратной
матрицы .
Найдем зависимость между координатами некоторого вектора в разных базисах. Пусть этот вектор имеет координаты относительно старого базиса и координаты относительно нового базиса, т.е. и
Подставив значения из предыдущей системы в первое равенство
для вектора и учитывая второе равенство, получим систему уравнений:
Как нетрудно заметить, матрицей перехода от новых к старым координатам будет транспонированная матрица . В матричном виде взаимосвязь между старыми координатами и новыми выражается следующими равенствами:
и .
Решение. Векторы образуют базис, если они линейно независимы. Составим векторное равенство или
Задача сводится к решению системы:
Определитель
системы не равен нулю.
Следовательно, однородная
система имеет только нулевое решение ,
значит векторы
линейно независимы
и образуют базис.
Связь между старым базисом и новым выражается системой уравнений:
Матрица перехода от старого базиса к новому имеет вид
Вычисляем . Она имеет вид
Находим транспонированную матрицу
Координаты в новом базисе находим из равенства
Новые координаты вектора в базисе есть (9/6, 5/6, 1/6) и вектор может быть представлен в виде:
скалярное и векторное — Студопедия
Поделись
Умножение вектора на вектор бывает двух типов: скалярное и векторное. В результате скалярного умножения двух векторов получаем число (скаляр). В результате векторного произведения двух векторов получаем вектор.
Скалярным произведением двух ненулевых векторов и называется число, равное произведению длин этих векторов на косинус угла между ними: , где .
Свойства скалярного произведения во многом сходны со свойствами произведения действительных чисел.
Векторным произведением двух векторов и называется вектор , который:
1) имеет модуль, численно равный площади параллелограмма, построенного на векторах и : ;
2) перпендикулярен к плоскости этого параллелограмма;
3) направлен в такую сторону, с которой кратчайший поворот от к рассматривается совершающимся против часовой стрелки (такое расположение векторов , и называется правой тройкой векторов).
Отличительная особенность векторного произведения состоит в том, что для него переместительное свойство (коммутативность) не имеет места. От перестановки векторов – сомножителей векторное произведение изменяет знак на противоположный: .
Три вектора могут быть перемножены несколькими способами. Чаще всего рассматривают смешанное произведение двух векторов векторно и на третий скалярно. В результате получают число.
Смешанное произведение трех векторов , и , которое обозначается или , есть скаляр, абсолютная величина которого равна обьему параллелепипеда, построенного на векторах , и , как на ребрах.
Пусть заданы два вектора и .
Скалярное произведение двух ненулевых векторов равно сумме произведений соответствующих координат этих векторов:
.
Угол между векторами вычисляется по формуле
,
или в координатной форме .
Условием перпендикулярности ненулевых векторов и является равенство нулю их скалярного произведения:
.
Векторное произведение ненулевых векторов выражается через координаты данных векторов и следующим образом:
.
Равенство нулю векторного произведения двух ненулевых векторов является условием их коллинеарности, т.е. ½½ .
Скаляр , представляющий смешанное произведение трех векторов, равняется определителю третьего порядка, составленному из координат этих трех векторов:
.
Равенство нулю смешанного произведения трех ненулевых векторов является условием их компланарности: .
Задача. Определить внутренние углы c вершинами .
Решение. Найдем .
Для этого надо найти векторы и . Зная векторы и , из формулы (2) получим
Легко видеть, что . Тогда
.
Отсюда .
Аналогично, находя предварительно, что , получим
.
Отсюда и .
Задача. Вычислить площадь треугольника с вершинами .
Решение. Найдем вначале площадь параллелограмма, построенного на векторах как на сторонах. По определению векторного произведения . Но
.
Тогда .
Следовательно, .
Задача. Вычислить объем пирамиды с вершинами .
Решение. Найдем координаты векторов . Очевидно, что .
Тогда . Но
. .
Следовательно, .
Сложение и скалярное умножение векторов — Концепция
Сложение и скалярное умножение векторов являются основными операциями, которые можно выполнять, используя их геометрическое или алгебраическое представление.
Глядя на геометрическое представление, мы можем понимать скалярное умножение векторов как масштабирование. Сложение векторов можно также выполнить двумя способами, используя геометрическое представление.
компонентов вектора горизонтальная составляющая вертикальная составляющая форма компонента сложение векторов нулевой вектор скалярное умножение
Теперь, когда у нас есть понятие компонентов векторов, мы можем переопределить способ сложения векторов, а также ввести другую операцию, называемую скалярным умножением.
Добавляя векторы алгебраически, предположим, что у нас есть два вектора, данные нам в компонентной форме, поэтому u — это u1, запятая u2, а вектор v — это v1, запятая v2.
Какова будет их сумма? Ну, сумма равна u1+v1, вы добавляете первые компоненты, а затем u2+v2 вы добавляете вторые компоненты, поэтому вы добавляете компоненты двух векторов.
Теперь я также хочу представить идею нулевого вектора. Нулевой вектор — это вектор с компонентами 0, 0 имеет длину 0. Этот вектор обладает тем свойством, что вы можете добавить его к любому другому вектору и получить этот вектор обратно, так что u плюс нулевой вектор равен u, а нулевой вектор плюс u равен u.
Векторы во многом действуют как действительные числа с точки зрения их алгебры, но они не идентичны действительным числам с точки зрения их алгебры, но они немного отличаются. Одно из отличий заключается в том, что умножение векторов немного сложнее, поэтому первый вид умножения, о котором я хочу поговорить, — скалярное умножение. Теперь вы помните, что скаляр — это величина, которая имеет только величину, а не направление, поэтому мы собираемся умножать векторы на скаляры, и давайте посмотрим так: если k — действительное число, а u — некоторый вектор u1, u2, то скаляр несколько k раз u будет определено как ku1, ku2, поэтому вы просто умножаете скаляр на каждый из компонентов, таких как распределение.
Давайте посмотрим, что делает скалярное умножение на примере, допустим, что u равно -3, 1, и я на самом деле изобразил этот вектор здесь, так что -3, 1 выглядит вот так. Каким бы ты был в 3 раза? Ну, согласно этому определению, я умножаю 3 внутри и получаю -9, 3 умножить на 1 3, так что это 3 умножить на u. -2 умножить на u, я умножаю -2 на -3 и получаю 6, -2 на 1 -2, 6, -2 и 0 скаляр 0 на s вектор u будет равен 0 на -3 0 и 0 на 1 , 0, и это, конечно, вектор 0, поэтому скалярный ноль, умноженный на любой вектор, дает вам нулевой вектор. Просто имейте в виду, что эти два нуля различны, это действительное число 0, а это вектор 0.
Теперь просто хочу, чтобы вы знали, как выглядят эти некоторые из этих векторов. Позвольте мне построить -2 раза u. Его компоненты равны 6, -2, поэтому я иду на 6 вправо и на 2 вниз, чтобы он закончился здесь, поэтому обратите внимание, что этот вектор в конечном итоге будет вдвое длиннее u, так что это -2 раза u, это вдвое больше длинный, но в противоположном направлении, потому что коэффициент k в этом случае отрицательный, и это всегда будет происходить всякий раз, когда вы умножаете вектор на отрицательное число, вы меняете его направление, поэтому скалярное умножение может удлинить или укоротить вектор, и это может изменить свое направление, но если мы умножаем на положительную константу, мы всегда получаем вектор в одном и том же направлении.
Как умножить вектор на скаляр — Помощь с IGCSE GCSE Maths
Решение примеров задач на умножение векторовТеперь вы знаете, как умножить вектор на скаляр, пора ответить на несколько примеров вопросов. Так что начните смотреть математические видеоролики ниже, остановите их и ответьте на вопросы сами, прежде чем смотреть мои решения и ответы. Это лучший способ подготовиться к следующему экзамену по математике. Удачи! Решение вопроса из прошлой статьи о векторах и одновременных уравнениях Один из вас попросил меня помочь на форуме этого веб-сайта, чтобы решить и объяснить этот вопрос прошлого экзамена по математике, связанный с векторами. Пример вопросов по математике, умножение векторов на скалярПосле того, как вы изучили предыдущие задания по математике, пришло время попытаться самостоятельно ответить на некоторые вопросы по математике. Я создал для вас этот БЕСПЛАТНЫЙ рабочий лист, который проверяет, действительно ли вы понимаете векторы и как умножать их на скаляр. На второй странице рабочего листа по математике вы найдете ответы. Вы также можете скачать и распечатать этот БЕСПЛАТНЫЙ рабочий лист по математике внизу этой страницы, чтобы вы могли закончить его для повторения по математике в удобное для вас время. Пожалуйста, поделитесь моими ресурсами с друзьями или направьте их на мой сайт.
| ||||
Изучите следующее видео во время собственного повторения математики и попросите меня помочь на форуме, если вы не понимаете векторы.
